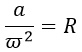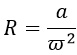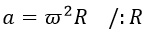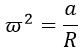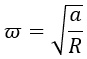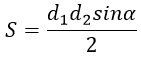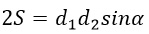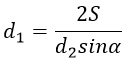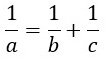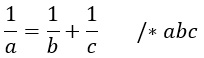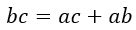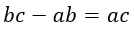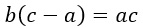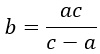Скачать материал

Скачать материал


- Сейчас обучается 137 человек из 43 регионов


- Сейчас обучается 41 человек из 29 регионов


- Сейчас обучается 98 человек из 37 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
НАХОЖДЕНИЕ ВЕЛИЧИН, ВХОДЯЩИХ В ФОРМУЛУ
Далее
Глава 11. Урок 140 -
2 слайд
Устная работа.
Далее
1. Вычислите:
2. Эстафета.
1) 1,5 · 2 + 7; 4) 1 – 2 · (–2,5);
2) –4 · 1,1 – 2; 5) –4 + 1,5 · 4;
3) 2 · (–1,2) – 3;6) 11 – 5 · 1,2.
Ответ: –6,4. -
3 слайд
Объяснение нового материала.
Далее
Пусть имеется некоторая формула N = а + b.
Что могут означать величины а, b и N?
Приведите примеры ситуаций, в которых можно будет воспользоваться этой формулой
– Если а = 130 и b = 80, то чему равно N?
– Всегда ли можно найти величину N, если известны величины а и b?
– Если бы была дана другая формула, то, зная входящие в нее величины, всегда ли можно найти ту величину, которую эта формула выражает?
– Сделайте вывод.
Зная формулу, всегда можно найти величину, которую она выражает, если известны все величины, входящие в эту формулу.
Вывод: -
4 слайд
Объяснение нового материала.
Далее
N = а + b
– Если известно, что N = 150 и а = 60, то чему равно b?
– Как можно найти b, зная N и а?
– Запишите формулу, выражающую b через N и а.
– Если бы была дана другая формула, то смогли бы мы найти входящую в нее величину?
Если известна какая-либо формула, то можно найти не только ту величину, которую она выражает, но и величины, входящие в нее.
Вывод: -
5 слайд
Объяснение нового материала.
Далее
Задача. Поезд шел 3 ч со скоростью 90 км/ч. Какой путь прошел поезд?
90 ∙ 3 = 270 (км)
s = v ∙ t
v, t и s — первые буквы латинских слов
velocitas (скорость),
tempus (время),
spatium (расстояние). -
6 слайд
Формирование умений и навыков.
Далее
№ 1123. Заполните таблицу, пользуясь в каждом случае одной из формул:
𝑠=𝑣𝑡, 𝑣= 𝑠 𝑡 , 𝑡= 𝑠 𝑣 . -
7 слайд
Формирование умений и навыков.
Далее
№ 1124. Банки с консервами пакуются в коробки. Общая масса М банок в коробке определяется по формуле М = тп. где т — масса одной банки, п — количество банок в коробке. Объясните, что определяется по формуле:
𝑛= 𝑀 𝑚 и 𝑚= 𝑀 𝑛
Заполните таблицу, пользуясь каждый раз нужной формулой. -
8 слайд
Формирование умений и навыков.
Далее
Пусть а – сторона квадрата, Р – периметр этого квадрата. Заполните таблицу:
Напишите формулу числа, кратного 7. Найдите по этой формуле два трехзначных числа, кратных 7. -
9 слайд
Формирование умений и навыков.
Далее
№ 1125. Из формулы площади прямоугольника S=ab выразите а через S и b. Найдите сторону а, если:
а) S = 30 см2, b = 5 см;б) S = 6,5 м2, b=1,3 м.
-
10 слайд
Формирование умений и навыков.
Далее
№ 1127. В кинозале п рядов no k кресел в каждом ряду. Число мест в кинозале можно вычислить по формуле N = kn.
а) Сколько мест в кинозале, если k =10, n = 12; k = 33, n = 25?
б) Сколько в кинозале рядов, если в каждом ряду 15 кресел, а всего в кинозале 300 мест? Выразите n через N и k.в) Сколько кресел в каждом ряду, если всего в кинозале 176 мест и 11 рядов? Выразите k через N и n.
-
11 слайд
Формирование умений и навыков.
Далее
№ 1129. Периметр треугольника Р можно определить по формуле Р = а + b + с, где а, b, с — длины сторон.
а) Найдите периметр треугольника, если его стороны равны: 4 см, 5 см, 3 см; 7 см. 9 см, 11 см.
б) Найдите неизвестную сторону треугольника, если Р = 18 см, b = 6 см, с = 7 см; Р=24 см, а = 8 см, b = 9 см.
в) Выразите сторону с треугольника через периметр Р и две другие стороны а и b. -
12 слайд
Формирование умений и навыков.
Далее
Чтобы отправить телеграмму, нужно уплатить за услугу 15 р. и за каждое слово в тексте по 7 рублей. Обозначьте стоимость телеграммы буквой С, а количество слов в тексте буквой n.
а) Составьте формулу для нахождения стоимости телеграммы.
б) Найдите С, если n = 11.
в) Найдите, из скольких слов состоит телеграмма, если ее стоимость составила 155 р.
г) Выразите количество слов в телеграмме через ее стоимость. -
13 слайд
Итоги урока.
Далее
– Назовите формулу, выражающую скорость движения через время движения и пройденный путь;
время движения через скорость и пройденный путь;
пройденный путь через скорость и время движения.
– Как найти одну из сторон прямоугольника, зная его площадь и другую сторону?
– Как найти сторону квадрата, зная его периметр?
– Как найти сторону треугольника, зная его периметр и две другие стороны?
Домашнее задание.
№ 1126; 1128.
Краткое описание документа:
Презентацию можно использовать как вспомогательный материал к электронному пособию «Математика. 6–7 классы: поурочные планы по учебникам под редакцией Г. В. Дорофеева» при изучении темы «О математическом языке» с целью формирования навыков выполнения вычислений по формулам и нахождения различных величин, входящих в формулу. Слайды № 6 — 12 допускают использование стилуса при работе на интерактивной доске. Презентацию удобно использовать при дистанционном обучении, при проведении индивидуальных и дополнительных занятий в режиме онлайн.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 268 697 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-
«Математика», Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. и др. / Под ред. Дорофеева Г.В., Шарыгина И.Ф.
Тема
8.3. Формулы. Вычисления по формулам
Больше материалов по этой теме
Другие материалы


Программа » Математика 10″
- Учебник: «Алгебра и начала математического анализа. Базовый и углубленный уровни», Алимов А.Ш., Колягин Ю.М. и др.
- 18.04.2021
- 135
- 3



- 18.04.2021
- 98
- 0

- 18.04.2021
- 9155
- 323
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Содержание:
- § 1 Правило нахождения пути по скорости и времени (формула пути)
- § 2 Формула нахождения периметра прямоугольника
- § 3 Формула периметра квадрата
§ 1 Правило нахождения пути по скорости и времени (формула пути)
В этом уроке Вы познакомитесь с таким понятием как формула. Научитесь составлять формулы и решать по ним различные задания.
Давайте рассмотрим задачу № 1:
Велосипедист-любитель, двигаясь по дороге на своем велосипеде со скоростью 14 километров в час, заметил, что находился в пути ровно 3 часа. Какой путь преодолел велосипедист?
Решение:
Чтобы узнать, сколько километров преодолел велосипедист, надо умножить его скорость на время пути, т.е. найти произведение:
Ответ: Велосипедист преодолел 42 км.
Запишем правило нахождения пути по скорости и времени движения в буквенном виде.
Для этого обозначим путь латинской буквой S, скорость буквой V, и время буквой t.
Получим равенство: S = Vt
Оно читается так: расстояние равно время умножить на скорость.
Это равенство называют формулой пути.
Таким образом, получили определение:
Запись какого–либо правила с помощью букв называют формулой.
Давайте рассмотрим еще несколько видов задач, которые можно решить с помощью формулы пути.
Задача № 2:
Скорость автобуса, осуществляющего междугородний рейс равна 80 км/ч.
За какое время он преодолеет путь в 640 километров?
Решение:
Заменим в формуле пути (S = Vt) буквы S и V их значениями, т.е. 640 и 80, тем самым получим уравнение: 640 = 80 t.
Значит, чтобы проехать 640 км автобус должен двигаться 8 часов.
Ответ: за 8 часов.
Задача № 3:
Группа туристов должна преодолеть участок пути протяженностью 30 километров до конца дня, т.е. за 5 часов.
С какой скоростью им следует двигаться?
Решение:
Заменим в формуле пути (S = Vt) буквы S и t их значениями 30 и 5.
Решив уравнение, получим V = 6.
Значит, туристы должны двигаться со скоростью 6 километров в час.
Ответ: 6 км в час.
§ 2 Формула нахождения периметра прямоугольника
А теперь, рассмотрим формулу для нахождения периметра прямоугольника.
Для ее записи обозначим длину прямоугольника латинской буквой а, ширину – буквой b. Сам периметр принято обозначать буквой Р.
Так как периметр прямоугольника – это сумма длин всех его сторон, то
Решим задачу:
Найдите периметр прямоугольника со сторонами 7 и 5 сантиметров.
Решение:
Периметр P = 2(а + в).
Подставим вместо а и b значения 7 и 5, получим P = 2(7 + 5), т.е. P = 2 умножить на 12, равно 24.
Ответ: Периметр прямоугольника – 24 см.
§ 3 Формула периметра квадрата
Рассмотрим еще одну формулу – формулу периметр квадрата.
Для ее записи обозначим длину стороны квадрата латинской буквой а, сам периметр снова обозначим буквой Р.
Так как периметр квадрата – это сумма длин всех его сторон, то Р = а + а + а + а = 4а.
Задача:
Найдите периметр квадрата со стороной 7 см.
Решение:
Подставляем в формулу Р =4а значение а=7, т.е. 4 умножить на 7 будет 28.
Ответ: периметр квадрата – 28 сантиметров.
Таким образом, в этом уроке Вы познакомились с таким понятием как формула. Научились составлять формулы и решать по ним различные задачи.
Список использованной литературы:
- Математика 5 класс. Виленкин Н.Я., Жохов В.И. и др. 31-е изд., стер. — М: 2013.
- Дидактические материалы по математике 5 класс. Автор — Попов М.А. – 2013.
- Вычисляем без ошибок. Работы с самопроверкой по математике 5-6 классы. Автор — Минаева С.С. – 2014.
- Дидактические материалы по математике 5 класс. Авторы: Дорофеев Г.В., Кузнецова Л.В. – 2010.
- Контрольные и самостоятельные работы по математике 5 класс. Авторы — Попов М.А. — 2012.
- Математика. 5 класс: учеб. для учащихся общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009.
Содержание материала
- Как же рассчитать скорость?
- Видео
- Молекулярная физика
- Единицы измерения времени
- Скорость
- Формулы для расчета пути и времени движения при неравномерном движении тела
- Импульс
- Самая большая единица измерения времени
- Основные формулы электричества
- График пути равномерного движения
- Решение задач
Как же рассчитать скорость?
На самом деле, рассчитать ее можно несколькими способами:
- через формулу нахождения мощности;
- через дифференциальные исчисления;
- по угловым параметрам и так далее.
В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:
v=S/t, где
- v — скорость объекта,
- S — расстояние, которое пройдено или должно быть пройдено объектом,
- t — время, за которое пройдено или должно быть пройдено расстояние.
Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.
Теперь нужно подставить имеющиеся значения вместо буквенных символов:
v=100 км/1,5 ч=66,66 км/ч
Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.
Таким нехитрым способом можно найти скорость через время и расстояние.
А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:
vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.
Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:
- vср=(S1+S2+…+Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
- S1, S2, Sn — отдельные неравномерные участки всего пути,
- t — общее время, за которое объект прошел все участки.
Можно записать использовать и такой вид вычислений:
- vср=S/(t1+t2+…+tn), где S — общее пройденное расстояние,
- t1, t2, tn — время прохождения отдельных участков расстояния S.
Но можно записать эту же формулу и в более точном варианте:
vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.
Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.
Видео
Молекулярная физика
К оглавлению…
Химическое количество вещества находится по одной из формул:
Масса одной молекулы вещества может быть найдена по следующей формуле:
Связь массы, плотности и объёма:
Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:
Определение концентрации задаётся следующей формулой:
Для средней квадратичной скорости молекул имеется две формулы:
Средняя кинетическая энергия поступательного движения одной молекулы:
Постоянная Больцмана, постоянная Авогадро и универсальная газовая постоянная связаны следующим образом:
Следствия из основного уравнения МКТ:
Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева):
Газовые законы. Закон Бойля-Мариотта:
Закон Гей-Люссака:
Закон Шарля:
Универсальный газовый закон (Клапейрона):
Давление смеси газов (закон Дальтона):
Тепловое расширение тел. Тепловое расширение газов описывается законом Гей-Люссака. Тепловое расширение жидкостей подчиняется следующему закону:
Для расширения твердых тел применяются три формулы, описывающие изменение линейных размеров, площади и объема тела:
Единицы измерения времени
Основной единицей измерения момента силы в системах СИ и СГС является: [t]=c
Единицы измерения времени основываются на периоде вращения Земли около своей оси и вокруг Солнца, Луни вокруг Земли. Внесистемные единицы измерения времени: час, минута, сутки и т.д.
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости
Чтобы найти скорость, нужно разделить путь на время:
v = s : t
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.
Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.
Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.
Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
Формулы для расчета пути и времени движения при неравномерном движении тела
При неравномерном движении мы используем определение средней скорости, которую можем найти по формуле
$$upsilon_{ср} = frac{S}{t}$$
Чтобы определить путь при неравномерном движении, нужно среднюю скорость движения умножить на время:
$$large S = upsilon_{ср} t$$
Также мы можем рассчитать время, разделив путь, пройденный телом, на среднюю скорость его движения:
$$t = frac{s}{upsilon_{ср}}$$
Импульс
К оглавлению…
Импульс тела находится по следующей формуле:
Изменение импульса тела или системы тел (обратите внимание, что разность конечного и начального импульсов векторная):
Общий импульс системы тел (важно то, что сумма векторная):
Второй закон Ньютона в импульсной форме может быть записан в виде следующей формулы:
Закон сохранения импульса. Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:
Самая большая единица измерения времени
Самая большая единица измерения времени – кальпа. Кальпа является понятием из индуизма и буддизма. Она равняется примерно 4,32 миллиардам лет, что совпадает с возрастом Земли с точностью до 5%.
Как в голову древним индуистам пришли такие цифры? Ответа на этот вопрос мы не знаем, но вся система как будто говорит нам, что тогда люди знали о Вселенной немного больше, чем мы.
Кальпу в индуизме еще называют «днем Брахмы». День сменяется ночью, равной ему по продолжительности. 30 дней и ночей составляют месяц, а год состоит из 12 месяцев. Вся жизнь Брахмы – 100 лет, по прошествии которых мир погибает вместе с ним.
Если перевести сто лет Брахмы в наши традиционные годы, получится 311 триллионов и 40 миллиардов лет! Нынешнему Брахме 51 год.
Вывод: если все это правда, то беспокоится не стоит — Вселенная будет существовать еще долгое время.
Основные формулы электричества
Для многих студентов тема про электричество сложнее, чем про термодинамика, но она не менее важна. Итак, начнём с электростатики:
Переходим к постоянному электрическому току:
Далее добавляем формулы по теме: “Магнитное поле электрического тока”
Электромагнитная индукция тоже важная тема для знания и понимания физики. Конечно, формулы по этой теме необходимы:
Ну и, конечно, куда же без электромагнитных колебаний:
График пути равномерного движения
Пример графика зависимости пути равномерного движения представлен на рисунке 3.
Здесь $S$ — ось пройденных путей, $t$ — ось времени. По этому графику мы можем найти путь, пройденный телом за определенный промежуток времени. Например, за 1 с тело проходит путь длиной 2 м, за 2 с – 4 м, за 3 с – 6 м.
Зная путь и время, мы можем рассчитать скорость. Для удобства расчета возьмем самый первый отрезок пути: $t = 1 с, s = 2 м$. Тогда,
$upsilon = frac{s}{t} = frac{2 м}{1 с} = 2 frac{м}{с}$.
Решение задач
Понять действие формул времени при равномерном движении или равноускоренном можно, решив задачу. Многие сайты предлагают онлайн-калькулятор для удобного подсчета. В соответствующие графы достаточно ввести основные данные, после чего программа рассчитает все самостоятельно.
Задача 1. Автомобиль ехал со скоростью 200 км/ч и проехал всего 80 км. Требуется определить время движения машины. Условные обозначения:
- V — скорость;
- S — расстояние;
- t — время.
Показатели нужно перевести из километров в метры, из часов в секунды: 1 км = 1 тыс. м, 1 час = 3600 секунд. Получаем S = 80000 м, V= 200000/3600 = 55,55 м/с. Находим скорость по формуле: V= S/t = 80000/55,55 = 1440,14 сек.
t = 1440
14/3600 = 0,4 часа.
Ответ: автомобиль пройдет 0,4 ч.
При неравномерном движении путь, пройденный телом, равен произведению средней скорости на время, в течение которого тело перемещалось.
Задача 2. Движение точки задано уравнением: х = 2t — 0,03t2. Нужно определить, в какой период скорость точки сближения сравняется с нулевой отметкой. Коэффициенты равны 2м/с, 0,03 м/с2.
Условия задачи содержат функцию x (t). Скорость можно вычислить по формуле V = dx/dt = 2 — 0,06t Приравниваем скорость к 0, находим t:
2 — 0,06t = 0
t = 2/0,06 = 33,33 сек.
Необходимо определить зависимость модуля ускорения от времени: A (t)= dv/dt = -0,06.
Задача 3. Самолет для взлета набирает 350 км/ч. Нужно определить время разгона, если скорость достигается в конце взлетной полосы длиной в 2 км. Движение считается равноускоренным.
При равноускоренном движении формула выглядит как S = V0t+at2/2. При этом V= V0+at. Разгон самолета начинается с состояния покоя, то есть V0 = 0.
S = at2/2
V=at.
S = (V/t)*(t2/2) = Vt/2.
S = 2000 м
V=350 км/ч = 97,2 м/с.
t= 2S/V = 2*2000/97,2 = 41,15.
Благодаря вычислению известно, что разгон самолета длится 41,15 сек.
Задача 4. Скорость конькобежца составляет 15 м/с. Нужно вычислить время, за которое он пробежит путь 3 км.
V= 15 м/с.
S = 3 км (3000 м).
t = S/V = 3000/15 = 200
Ответ: за 200 секунд конькобежец пробежит 3 км.
Современная наука распределяет известные представления о времени в разные концепции — относительную и вещественную. По мнению относительной, в природе не существует временных рамок, а понятие времени является отношением между событиями. Время — проявление свойств физических тел и изменений, оно статично, как и пространство.
Теги
Физика
В каждой задаче по физике требуется из формулы выразить неизвестную, следующим шагом подставить численные значения и получить ответ. Лучше не решать физическую задачу по шагам: найти из одной формулы значение физической величины, затем подставлять ее во вторую формулу. Почему? Во-первых, получается неточный результат в вычислениях после многократного округления. Во-вторых, многие задачи нет возможности решить таким путем, из-за того, что нет значения некоторой физической величины. Но тупик часто заключается в том, что если бы мы подставляли в буквенном виде одну формулу в другую, то та неизвестная физическая величина сократилась бы. Поэтому учимся на примерах выражать из формулы необходимую физическую величину. Главное правило: букву, которую необходимо выразить, представляем в уме за x, остальные буквы представляем известными значениями. В этом случае получим совершенно обычное математическое уравнение.
Выведение переменной из формулы
Данную статью я начну с общего алгоритма выражения переменной, а затем уже будем разбираться на конкретных примерах.
Пусть дана какая-то формула.
1) Если она содержит скобки, то раскрываем их и приводим подобные слагаемые;
2) Если есть знаменатель, то избавляемся от него, умножив обе части формулы на этот знаменатель (если знаменателей несколько, то умножаем обе части равенства на общий знаменатель);
3) Если есть корни, то обе части возводим в степень, равную показателю корня;
4) Переносим все члены с нужной нам переменной в одну сторону;
5) Если таких членов несколько, то выносим нужную нам переменную за скобку в качестве общего множителя. Если нет, то этот шаг пропускаем.
6) Делим обе части формулы на все сомножители нужной нам переменной.
7) Если нужная переменная возведена в n-ую степень, то нужно из обеих частей формулы извлечь корень n-ой степени.
На самом деле, всё не так ужасно) На ОГЭ так вообще простые задания.
Вот парочка примеров.
1) Центростремительное ускорение при движении по окружности вычисляется по формуле a=ω 2 R, где ω — угловая скорость, R — радиус окружности. Выразим из этой формулы R и ω.
Выразим радиус R, разделив обе части на его сомножитель ω 2 :
Но обычно пишут так, чтобы искомая переменная была слева:
Теперь выразим угловую скорость. Разделим обе части равенства на сомножитель угловой скорости (на R, короче говоря):
Получается вот такая запись:
Нужная нам угловая скорость возведена в квадрат. Избавиться от степени нам поможет квадратный корень:
Теперь возьмем формулу с дробью.
2) Площадь четырехугольника можно вычислить по формуле
Выразим из нее d1.
Избавляемся от знаменателя, умножив обе части равенства на 2 (т.к. знаменатель равен двум).
Чтобы выразить d1 разделим обе части на сомножители d2 и sinα.
Точно также выражаются d2 и sinα. Можешь даже самостоятельно попробовать.
Еще один пример. Последний.
3) Дана формула
Выразим из нее переменную b.
Формула содержит дроби, поэтому надо избавится от знаменателей. Умножим обе части равенства на общий знаменатель abc.
Получится такое выражение:
Перенесем все члены равенства, содержащие переменную b в левую часть.
Вынесем b за скобки как общий множитель.
Разделим обе части равенства на (с — а).
Что-то не выражается? Напиши мне свой пример. Используй функцию «Предложить новость».
Правила вывода величины из формулы (7-11 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Правила вывода величины из формулы
Формула – это правило вычисления одной величины через другие, записанное при помощи их буквенных обозначений.
Иногда для решения задач необходимо вывести неизвестную величину из формулы. Для этого существуют несколько правил.
Формулы можно преобразовывать по правилам математики. Рассмотрим примеры. В левой колонке таблицы вы видите исходные формулы. В средней колонке каждая из формул преобразована так, что «выражена» величина, обозначенная « b ». В последней колонке выражена величина « с »
Примеры вывода физической величины из формулы
Курс повышения квалификации
Педагогические основы деятельности учителя общеобразовательного учреждения в условиях ФГОС
Курс повышения квалификации
Анализ урока как инструмент развития профессиональных компетенций учителя в соответствии с требованиями ФГОС
- Сейчас обучается 26 человек из 16 регионов
Курс повышения квалификации
Теория и методика преподавания предмета «Астрономия» в условиях реализации ФГОС СОО
- Сейчас обучается 67 человек из 35 регионов
«Домашнее обучение. Лайфхаки для родителей»
- подготовка к ЕГЭ/ОГЭ и ВПР
- по всем предметам 1-11 классов
«Такие разные дети: преимущества тьюторской позиции учителя»
Свидетельство и скидка на обучение каждому участнику
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 909 890 материалов в базе
«Интеграция современного искусства в детское творчество»
Свидетельство и скидка на обучение
каждому участнику
Ищем педагогов в команду «Инфоурок»
- ЗП до 91 000 руб.
- Гибкий график
- Удаленная работа
Другие материалы
- Физика
- 7 класс
- Тесты
- Учебник: «Физика», Перышкин А.В.
- 02.05.2018
- 482
- 0
- Физика
- 7 класс
- Другие методич. материалы
- Учебник: «Физика», Перышкин А.В.
- 02.05.2018
- 8598
- 28
- Физика
- 10 класс
- Презентации
- Учебник: «Физика. Базовый и профильный уровни», Тихомирова С.А., Яворский Б.М.
- Тема: Глава 1. Кинематика
- 02.05.2018
- 3214
- 47
- Физика
- 7 класс
- Тесты
- Учебник: «Физика», Перышкин А.В.
- Тема: Глава 3. Давление твёрдых тел, жидкостей и газов
- 02.05.2018
- 13283
- 149
- Физика
- 9 класс
- Другие методич. материалы
- Учебник: «Физика», Перышкин А.В., Гутник Е.М.
- Тема: § 13 Свободное падение тел
- 02.05.2018
- 340
- 0
- Физика
- 7 класс
- Презентации
- Учебник: «Физика», Перышкин А.В.
- Тема: §55 Механическая работа. Единицы работы
- 02.05.2018
- 258
- 1
- Физика
- 10 класс
- Презентации
- Учебник: «Физика. Базовый и профильный уровни», Тихомирова С.А., Яворский Б.М.
- Тема: § 19. Сила трения
- 02.05.2018
- 2054
- 25
- Физика
- 8 класс
- Конспекты
- Учебник: «Физика», Перышкин А.В.
- Тема: Приложение к Главе 1
- 02.05.2018
- 443
- 0
«Практический подход в работе с утратой смысла жизни: логотерапия»
Свидетельство и скидка на обучение каждому участнику
Вам будут интересны эти курсы:
- Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
- Курс повышения квалификации «Основы местного самоуправления и муниципальной службы»
- Курс повышения квалификации «Организация научно-исследовательской работы студентов в соответствии с требованиями ФГОС»
- Курс повышения квалификации «Формирование компетенций межкультурной коммуникации в условиях реализации ФГОС»
- Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»
- Курс повышения квалификации «Организация маркетинга в туризме»
- Курс повышения квалификации «ЕГЭ по физике: методика решения задач»
- Курс повышения квалификации «Психодинамический подход в консультировании»
- Курс профессиональной переподготовки «Организация технической поддержки клиентов при установке и эксплуатации информационно-коммуникационных систем»
- Курс профессиональной переподготовки «Деятельность по хранению музейных предметов и музейных коллекций в музеях всех видов»
- Курс профессиональной переподготовки «Эксплуатация и обслуживание общего имущества многоквартирного дома»
- Курс профессиональной переподготовки «Организация процесса страхования (перестрахования)»
- Курс профессиональной переподготовки «Технический контроль и техническая подготовка сварочного процесса»
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
- 02.05.2018 2588
- DOCX 186.2 кбайт
- Оцените материал:
Настоящий материал опубликован пользователем Абдуллаева Гульбахор Уришовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 5 лет и 8 месяцев
- Подписчики: 9
- Всего просмотров: 1158579
- Всего материалов: 1214
40%
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!

«Политическая карта как объект изучения в школьном курсе географии. Объекты и субъекты, уникальные характеристики, динамизм и изменчивость политической карты»

«Мозаичный декор из цветного стекла»

«Развитие коммуникативных способностей школьников на уроках и во внеурочной деятельности»
Подарочные сертификаты
- Курсы «Инфоурок»
- Онлайн-занятия с репетиторами на IU.RU
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Правила вывода величины из формулы
Формула – это правило вычисления одной величины через другие, записанное при помощи их буквенных обозначений.
Иногда для решения задач необходимо вывести неизвестную величину из формулы. Для этого существуют несколько правил.
Формулы можно преобразовывать по правилам математики. Рассмотрим примеры. В левой колонке таблицы вы видите исходные формулы. В средней колонке каждая из формул преобразована так, что «выражена» величина, обозначенная «b». В последней колонке выражена величина «с»
Примеры вывода физической величины из формулы