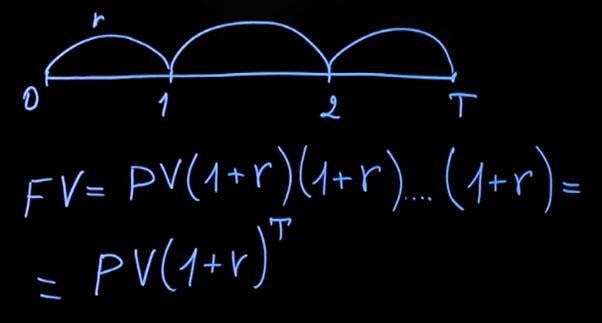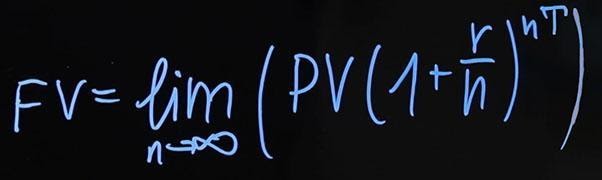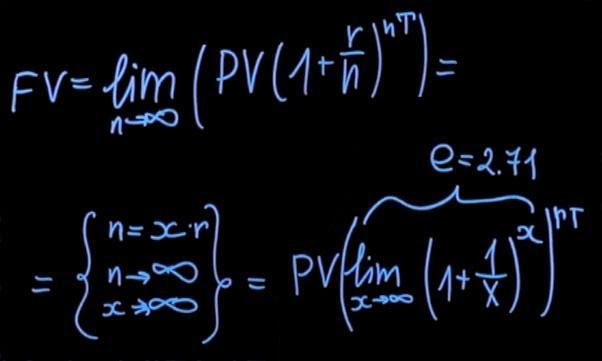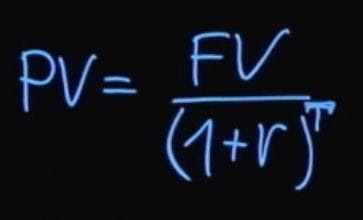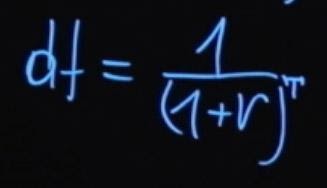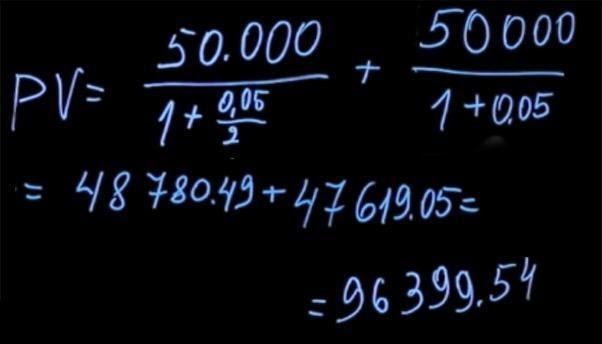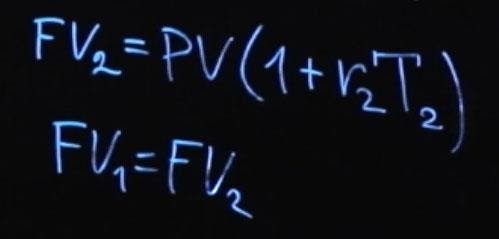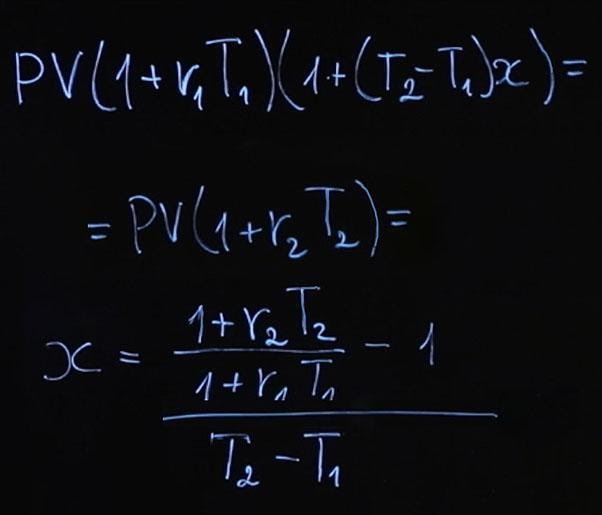Представьте себе ситуацию – вы покупаете машину, и вам предлагают два варианта: заплатить с рассрочкой в несколько месяцев или погасить всю сумму сразу и с небольшой скидкой. Какой окажется выгоднее?
Или, например, вы хотите разместить вклад на год. Можно положить на весь срок под высокий процент или на отдельные короткие сроки под более низкий. Что лучше и насколько?
Все ответы под катом. И добро пожаловать в мир, где время — всегда деньги. До этого вы знали об этом, но теперь — в деталях и с примерами.
Меня зовут Мария Абрашкина, я математик и Product Owner в команде по расчету портфельных рисков. А также один из авторов видеокурса про финансовую математику (Ч.1 – Типы начисления процентов, Ч.2 – Дисконтирование, Ч.3 – Форвардные процентные ставки). В этом посте я расскажу о стоимости денег, процентных ставках и облигациях. Эти знания помогут вам в будущем принимать финансовые решения основываясь на точном расчете, используя простую математику.
#1. Временная стоимость денег. Типы начисления процентов
Сначала поговорим о том, что такое временная стоимость денег, или Time Value of Money (TVM), почему деньги имеют стоимость и какие виды процентов существуют.
На картинке ниже показан список фильмов с максимальными кассовыми сборами.
Можем ли мы их сравнить по этим цифрам? Учитывая, что фильмы выходили в разные годы, вряд ли такое сравнение будет правильным. Как быть?
Давайте рассмотрим более простой пример. Допустим, у вас есть тысяча рублей, и я у вас прошу эту сумму в долг. Сколько вы хотите, чтобы я вам отдала через год? Возможно, вы подумаете, что на эту тысячу рублей вы сейчас можете купить бутылку вкусного вина или что-то другое. Также вы можете предположить, что через год на ту же самую тысячу рублей вы вряд ли сможете купить этот товар по причине инфляции. Кроме того, существует риск, что деньги я не верну. Поэтому, скорее всего, вы захотите компенсацию за то, что вы пока не будете покупать бутылку вина или какую-нибудь другую вещь. Также вам необходим стимул, оправдывающий риск того, что деньги я вам могу и не вернуть. Вероятно, вы потребуете от меня вернуть деньги с какой-то надбавкой, то есть с процентом.
Итак, деньги имеют стоимость, потому что их владелец хочет компенсации за то, что он не может купить какой-то товар или услугу, и за риск, который он несет, давая деньги в долг.
На языке математики это будет выглядеть так:
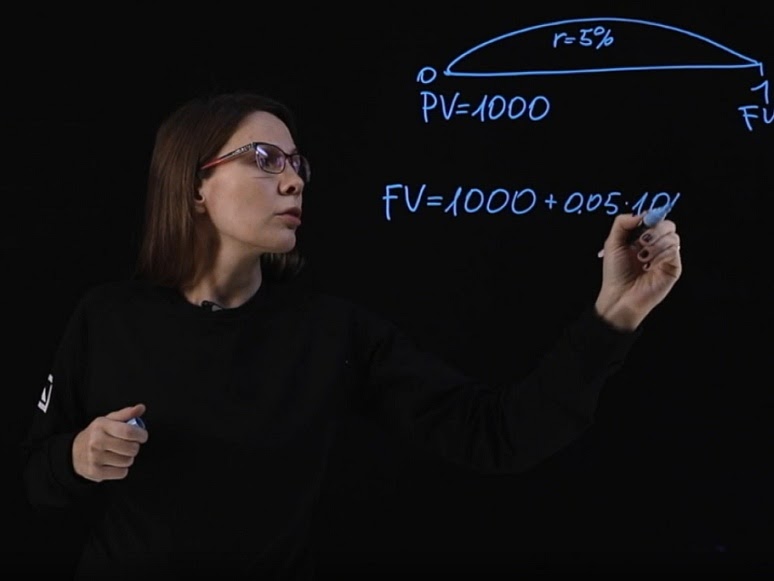
PV=1000
Сейчас вы мне даете тысячу рублей. Обозначим это как PV (Present Value). Допустим ставка (r) равна 5%, и деньги вы даете мне сроком на один год. Тогда возвращая деньги FV (Future Value), мне придется добавить к исходной сумме 50 рублей.
Если записать эту формулу в общем виде, то будущее значение равняется сумме долга, умноженной на единицу плюс процентная ставка.
А что, если начисление процентов происходит не раз в год, а чаще? Или что если проценты начисляются в течение двух, трех, десяти лет? В данном случае нам нужно всегда уточнять, каким образом происходит начисление процентов, в конце срока или с какой-то периодичностью и на сколько лет.
Простые проценты
Рассмотрим пример, когда проценты начисляются в конце срока вклада. Будущее значение будет равняться текущему значению плюс текущее значение, умноженное на годовую процентную ставку. Годовая процентная ставка будет прибавляться к сумме нашего вклада столько раз, на сколько лет мы сделали вклад.
Результат – текущее значение, умноженное на сумму единица плюс процентная ставка (r), умноженная на число лет вклада (T). Такой способ начисления процентов называется простыми процентами.
Если же процентная ставка начисляется каждый год, то формула будет выглядеть иначе.
Рассмотрим ситуацию с начислением за период в несколько лет. Считаем, что действующая процентная ставка на протяжении всего периода будет одинаковая. Тогда формула принимает следующий вид: текущее значение, умноженное на сумму единица плюс процентная ставка, затем еще раз на сумму единицы и процентной ставки и т. д. Умножать следует столько раз, на какое количество лет был сделан вклад. В общем виде формула будет выглядеть следующим образом:
Обратите внимание – если в первом случае к нашему вкладу каждый год прибавлялась сумма процентов (как в первом примере, где добавлялось к сумме вклада 50 рублей), то в случае с ежегодным начислением на 50 рублей, добавленные в первом периоде, у нас каждый раз начисляется процент.
Всегда важно обращать внимание на то, каким образом происходит начисление процентов. Проценты могут начисляться не только раз в год, но и раз в полгода, каждый день. И в принципе нам ничего не мешает начислять эти проценты непрерывно.
Непрерывное начисление процентов
Давайте рассмотрим, как будет выглядеть формула для начислений процентов чаще одного раза в год. В этом случае будущее значение будет равняться текущему значению, умноженному на сумму единица плюс годовая процентная ставка, деленная на количество периодов начислений в году (n) в степени nT. Если начисления производятся каждые полгода, то n=2, если каждый день, то n=365.
Как же будет выглядеть формула, если мы хотим начислять проценты непрерывно? Тут придется вспомнить школьную математику. Формула будет следующей:
Для того, чтобы привести наш предел к какому-то удобному виду, нам нужно сделать подстановку. В итоге мы получаем следующее:
С учетом того, что наш предел равен числу Эйлера (е=2,71), наша формула преобразуется в очень простое выражение. Текущее значение нашего вклада умножается на экспоненту, которая возводится в степень, представленную произведением процентной ставки и количества лет, на которые начисляются наши проценты.
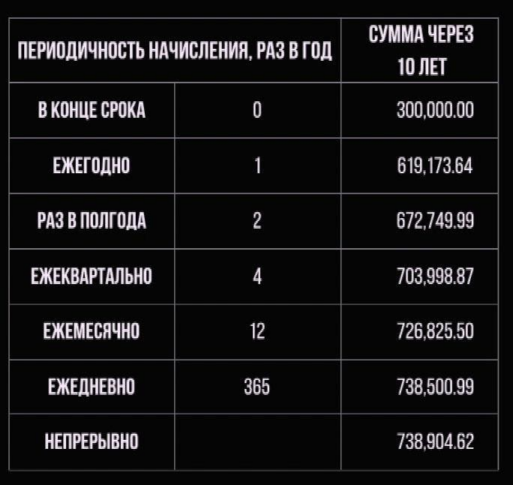
Давайте сравним, как выглядят платежи в зависимости от периодичности начислений. В таблице представлено будущее значение вклада в сто тысяч рублей, который положен на десять лет по ставке двадцать процентов.
Как вы можете видеть – 300 тысяч рублей вкладчик получит в случае, если начисления производятся в конце срока действия вклада.
Таким образом сумма вклада при начислении процентов ежегодно в два раза превышает сумму вклада при выплате процентов единожды в конце срока.
Если же начисления производятся непрерывно, то сумма вклада оказывается более 700 тысяч рублей против 300 тысяч рублей при простом начислении процентов.
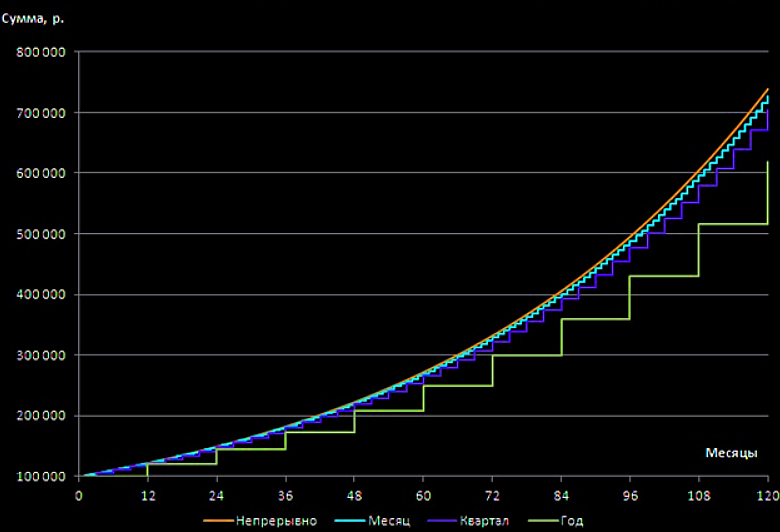
На графике ниже наглядно показано, как растет итоговая сумма вкладов при разных способах начисления процентов.
Отсюда необходимо сделать вывод:
выбирая вклад, важно смотреть не только на размер процентной ставки, но и на периодичность начисления процентов. Высокая процентная ставка не всегда является по-настоящему выгодной.
Поэтому, перед тем как сделать свой выбор, имеет смысл сделать небольшие вычисления, чтобы узнать итоговую сумму вклада при заданных условиях.
#2. Дисконтирование (помогает понять, что лучше: взять рассрочку или заплатить сейчас со скидкой)
Мы рассмотрели, какие бывают ставки и какие бывают способы начисления процентов. Если проценты выплачиваются в конце срока действия вклада, проценты называются простыми, если проценты выплачиваются с какой-то периодичностью, то такие проценты называются сложными.
Давайте решим обратную задачу. Допустим, мы знаем, сколько нам заплатят в будущем (например, нам кто-то пообещал платеж за какой-то продукт). Мы также знаем, какая сейчас процентная ставка. Как нам посчитать текущую цену этого продукта?
Как было сказано ранее, будущее значение суммы платежа будет равняться текущему значению, умноженному на единицу плюс процентная ставка. Если из этой формулы мы выразим текущее значение, то оно будет равняться будущему значению, деленному на единицу плюс процентная ставка.
Если проценты начисляются с какой-то периодичностью, то в общем виде формула выглядит так:
T – это количество периодов выплат начислений процентной ставки. Такой процесс деления будущего значения на единицу плюс процентная ставка в степени T называется дисконтированием. А множитель, единица деленная на сумму единицы плюс r в степени T, называется коэффициентом дисконтирования.
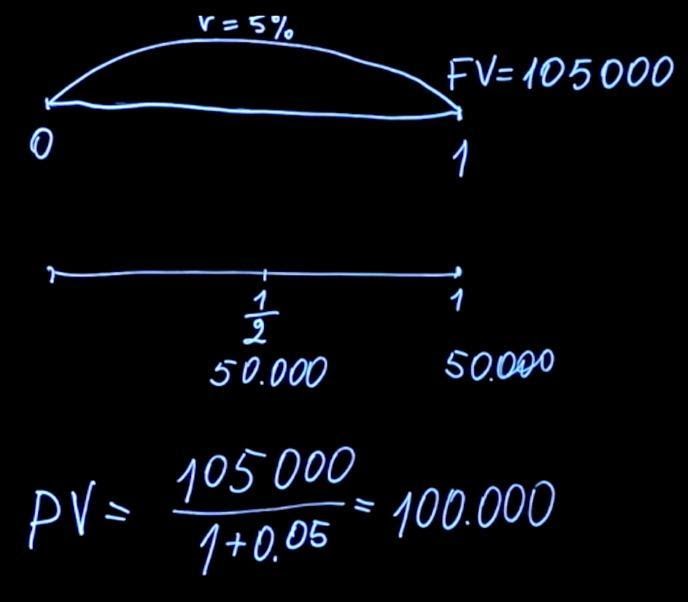
Давайте вернемся к задаче о том, какую премию лучше выбрать. В зависимости от способа премирования сумма выплат может отличаться. При этом не всегда очевидно, какой из способов предпочтительнее. Чтобы дать правильный ответ, необходимо решить математическую задачу. Предположим, у нас есть возможность взять в конце года 105 тысяч рублей при процентной ставке 5 процентов. Либо мы можем выбрать другой способ премирования, когда нам выплачивают по 50 тысяч рублей раз в полгода при той же процентной ставке.
Сравним эти два платежа. Для этого посчитаем, какое будет текущее значение для каждой из данных выплат. Воспользовавшись формулой для нахождения текущего значения, нам нужно продисконтировать 105 тысяч по ставке пять процентов (в данном случае T=1). Получаем 100 тысяч.
Чтобы найти текущее значение выплат через каждые полгода, мы должны 50 тысяч рублей (которые получим через полгода) продисконтировать по ставке два с половиной процента (потому что начисление происходит только в первые полгода. Строго говоря, ставка на 6 мес не равна половине годовой ставки. N(1+x)(1+x)=N(1+0.05) => x=2.4695% мы инвестируем на 6 мес, а потом опять на 6 и это идентично инвестиции на год), пять процентов годовых, деленные на два, плюс 50 тысяч полученные в конце года, которые мы дисконтируем по ставке 5 процентов. В результате подсчетов мы получаем цену первого платежа за полгода в размере 48780 рублей 49 копеек и второго платежа — 47619 рублей 5 копеек. Сумма ценностей составляет 96399 рублей 54 копеек.
Очевидно, что предложение получить 105 тысяч рублей через год выгоднее, чем получать по 50 тысяч раз в полгода. Хотя интуитивно вам могло показаться, что разница несущественна, при том, что деньги вы получите быстрее. Математика говорит нам о том, что это не так.
Выгоднее получить премию в 105 тыс рублей, подождав дольше.
Данный принцип работает при оценке различных жизненных ситуаций.
Например, когда вам предлагают купить автомобиль в рассрочку или заплатить полную сумму сейчас с какой-нибудь скидкой. Нужно взять будущую сумму, которую вы заплатите, привести к текущему значению, а затем сравнивать платежи, происходящие в один и тот же момент времени.
В таком случае сравнение будет корректным.
#3. Форвардные процентные ставки
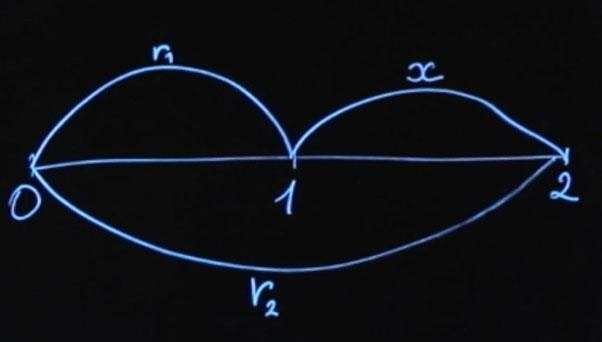
Допустим, мы с вами договоримся о процентной ставке. Под эту процентную ставку я через год возьму у вас деньги в долг, которые верну через два года плюс процент. Какова должна быть в данном случае процентная ставка, чтобы она была справедливой? Распишем этот пример подробнее.
Мы находимся сейчас в моменте времени «ноль». Через год я у вас по ставке x возьму деньги и верну их вам через два года. Как рассчитать ставку x? У нас есть несколько опций. Вы можете сейчас положить деньги по ставке r1 на год, а затем реинвестировать их по ставке x.
Либо положить деньги сразу по ставке r2 на два года.
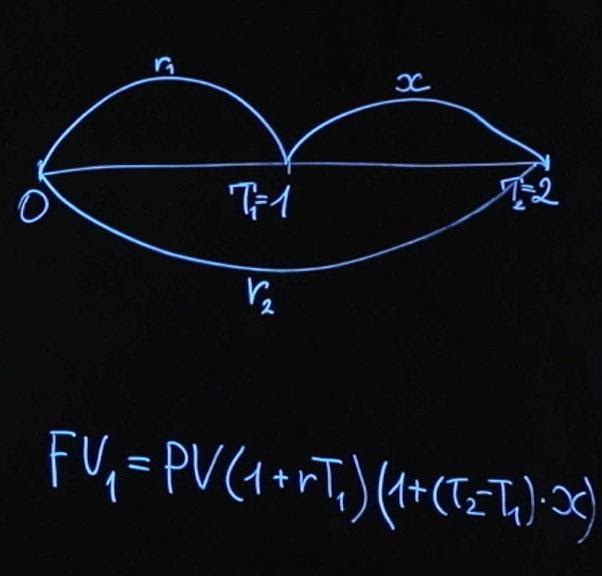
На финансовом рынке существует правило отсутствия арбитража (No-Arbitrage Condition). Оно говорит о том, что если в конце срока мы получаем одинаковые выплаты, то для инструментов с одинаковым риском начальная сумма должна быть тоже одинаковая. Давайте распишем и это. Будущее значение первого варианта инвестиции FV1 будет равняться текущему значению, умноженному на сумму единицы и rT1 (будем считать, что у нас простое начисление процентов).
Момент времени T1 у нас равняется одному году. Дальше у нас произойдет реинвестирование суммы, и мы положим на промежуток времени от T2—T1, умноженную на нашу процентную ставку x. T2 – это момент времени, в нашем случае два года.
Либо будущее значение FV2 будет равняться текущему значению PV, умноженному на единица плюс r2, умноженное на T2. Согласно условию отсутствия арбитража FV1 должно равняться FV2.
Из этого мы получаем следующее:
Формула получилась достаточно громоздкая. Давайте рассчитаем по этой формуле пример, а затем подумаем, что мы можем сделать, чтобы она выглядела проще.
Пусть процентные ставки у нас r1=4%; r2=6%. В таком случае имеем следующее:
x=(1+0,06*2)/(1+0,04*1)-1 = 1,077-1 = 0,077 = 7,7% Казалось бы странно, что ставка на два года равняется шести процентам, на год она равняется четырем процентам, а от года до двух мы получаем ставку более семи процентов. Объясняется это так. Поскольку в первый год у нас годовая ставка ниже чем на два года, в следующий год она должна быть выше, чем обе этих ставки. Это необходимо для того, чтобы компенсировать недостаток начисления процентов в первом году, и после реинвестирования можно было бы получить такую же сумму, как при инвестировании на два года по более высокой ставке. Такая ставка называется форвардной процентной ставкой.
Чтобы облегчить себе жизнь, давайте упростим эту формулу. Если мы будем использовать формулу непрерывного начисления процентов (FV=PVerT), то тогда мы можем переписать условие отсутствия арбитража следующим образом:
PVer2T2=PVer1T1e(T2-T1)x
Если мы возьмем логарифм от обеих сторон нашего равенства и сократим константы, мы получим:
r2T2=r1T1+(T2-T1)x
Далее легко найти x:
x=(r2T2—r1T1)/(T2-T1)
Согласитесь, такую формулу для будущих процентных ставок использовать гораздо проще и удобнее.
Вы можете задать вопрос – а зачем такой странный продукт и кто им пользуется?
Представьте себе ситуацию, когда у вас или у вашей компании точно будет поступление средств через год. Сейчас вы бы хотели обезопасить себя от риска изменения процентных ставок. Вы понимаете, что через год процентная ставка может увеличиться и стать более выгодной, но также вы понимаете, что она может понизиться. И вам вполне комфортно с действующей на рынке форвардной процентной ставкой. Тогда вы можете заключить контракт, указав в нем, что на те деньги которые поступят в будущем через год, вы заключаете договор по заданной ставке. Ставка фиксируется, и вы больше не переживаете о том, как будут происходить изменения процентных ставок на рынке.
Обратите внимание, что форвардная процентная ставка ни в коем случае не является предсказанием будущей цены. Это абсолютно не значит, что процентные ставки будут равны 7,7% через год, когда мы окажемся в точке T1. Они могут принимать какое угодно значение, и вот почему. В момент, когда мы рассчитываем форвардную процентную ставку из ставок, действующих на рынке, мы можем сказать, что эта ставка является ожиданием рынка относительно будущих цен. Но к моменту, когда мы перемещаемся в будущее, происходят новые события, добавляется новая информация, и рынок каким-то образом меняется. Поэтому процентные ставки через год не будут совпадать с форвардными ставками, рассчитанными на год сейчас.
Все статьи этой серии
- Стоимость денег, типы процентов, дисконтирование и форвардные ставки. Ликбез для гика, ч. 1
- Облигации: купонные и бескупонные, расчет доходности. Ликбез для гика, ч. 2
- Облигации: оценка рисков и примеры использования. Ликбез для гика, ч. 3
- Как банки берут друг у друга в долг. Плавающие ставки, процентные свопы. Ликбез для гика, ч. 4
- Построение кривой дисконтирования. Ликбез для гика, ч. 5
- Что такое опционы и кому это нужно. Ликбез для гика, ч. 6
- Опционы: пут-колл парити, броуновское движение. Ликбез для гика, ч. 7
Что такое Форвардная ставка?
Форвардная ставка — это процентная ставка, применяемая к финансовой операции, которая состоится в будущем. Форвардные ставки рассчитываются на основе спотовой ставки и корректируются с учетом затрат на перенос, чтобы определить будущую процентную ставку, которая приравнивает общий доход от долгосрочных инвестиций к стратегии пролонгации более краткосрочных инвестиций.
Термин может также относиться к ставке, установленной для будущего финансового обязательства, например, процентной ставке по выплате кредита.
Понимание форвардных ставок
На форекс форвардный курс, указанный в соглашении, является договорным обязательством, которое должны соблюдаться участвующими сторонами. Например, рассмотрим американского экспортера с крупным экспортным заказом в Европу, и экспортер обязуется продать 10 миллионов евро в обмен на доллары по форвардному курсу 1,35 евро за доллар США в течение шести месяцев. Экспортер обязан поставить 10 миллионов евро по указанному форвардному курсу в указанную дату, независимо от статуса экспортного заказа или обменного курса, преобладающего на спотовом рынке в то время.
По этой причине форвардные курсы широко используются для целей хеджирования на валютных рынках, поскольку валютные форварды могут быть адаптированы к конкретным требованиям, в отличие от фьючерсов , которые имеют фиксированные размеры контрактов и даты истечения срока действия и поэтому не могут быть настроены.
В контексте облигаций форвардные ставки рассчитываются для определения будущей стоимости . Например, инвестор может приобрести однолетний казначейский вексель или купить шестимесячный вексель и превратить его в другой шестимесячный вексель после его погашения. Инвестору будет безразлично, если обе инвестиции принесут одинаковую общую прибыль.
Например, инвестору будет известна спотовая ставка по шестимесячному векселю, а также будет известна ставка по годовой облигации на момент начала инвестирования, но он или она не будет знать стоимость шестимесячного векселя. который будет приобретен через шесть месяцев.
Форвардные ставки на практике
Чтобы снизить риски реинвестирования, инвестор мог заключить договорное соглашение, которое позволило бы ему или ей инвестировать средства через шесть месяцев по текущему форвардному курсу.
Теперь перенесемся на шесть месяцев вперед. Если рыночная спотовая ставка для новой шестимесячной инвестиции ниже, инвестор может использовать соглашение о форвардной ставке для инвестирования средств из погашенных казначейских векселей по более выгодной форвардной ставке. Если спотовая ставка достаточно высока, инвестор может отменить соглашение о форвардной ставке и инвестировать средства по преобладающей рыночной процентной ставке в новую шестимесячную инвестицию.
Форвардная ставка это процентная ставка, устанавливаемая сегодня, которая будет
выплачена за пользование деньгами, занятыми в определенный момент в будущем
на определенное время . Этот онлайн — инструмент используется для расчета форвардной ставки для (n1-n2) числа лет после n2 числа лет.
.
Калькулятор расчета форвардной ставки
S1 — Спотовая ставка до следующей будущей даты (%)
S2 — Спотовая ставка до более близкой даты в будущем (%)
n1 — Количество лет до следующей будущей даты
n2 — Количество лет до более близкой будущей даты
Как рассчитать форвардную ставку(FR%)
Формула форвардной ставки помогает расшифровать кривую доходности, которая представляет собой графическое представление доходности различных облигаций с различными сроками погашения. Он может быть рассчитан на основе спотовой ставки на более позднюю будущую дату и более близкую будущую дату, а также на количество лет до более поздней будущей даты и более близкой будущей даты.
Пример. На рынок только что были выпущены две облигации – однолетняя (т.е. на один год) и двухлетняя (т.е. на два года). Известно, что доходность однолетней облигации составляет 9% годовых, а доходность двухлетней – 14% годовых. Найти будущую доходность однолетней облигации, которая будет выпущена ровно через год.
Решение. В этой задаче нам нужно найти форвардную ставку между периодом 1 и 2. При этомнам известна спот-ставка периода 2 (она равна 14%) и спот-ставка периода 1 (она равна 9%).
Подставляем всё в формулу: (1 + 𝑓1,2)1=(1+0,14)2/(1+0,09)1
Отсюда находим 𝑓1,2 ≈ 19,23
Формула для расчета форвардной ставки
Формула форвардной ставки помогает расшифровать кривую доходности, которая представляет собой графическое представление доходности по разным облигациям с разными сроками погашения. Его можно рассчитать на основе спотовой ставки на дату в более отдаленном будущем и дату в ближайшем будущем, а также на количество лет до даты в более отдаленном будущем и на дату в ближайшем будущем.
Форвардный курс = [(1 + S1)n1 / (1 + S2)n2]1/(n1-n2) – 1
где S1 = спотовая ставка до следующей даты в будущем,
- S2 = спотовая ставка до ближайшей даты в будущем, n1 = количество лет до более поздней даты в будущем,
- n2 = Количество лет до ближайшей даты в будущем
Обозначение формулы обычно представляется как Ф(2,1), что означает годовую ставку через два года.
Оглавление
- Формула для расчета форвардной ставки
- Расчет форвардной ставки (шаг за шагом)
- Примеры
- Пример №1
- Пример #2
- Актуальность и использование
- Рекомендуемые статьи
Расчет форвардной ставки (шаг за шагом)
Его можно получить, выполнив следующие действия:
- Во-первых, определите курс спот до ближайшей будущей даты покупки или продажи ценной бумаги, и он обозначается S1. Кроме того, вычислить нет. года до более дальней даты в будущем и обозначается n1.
- Затем определите курс спот до ближайшей даты продажи или покупки той же ценной бумаги, и он обозначается S2. Затем вычислить нет. года до ближайшей даты в будущем и обозначается n2.
- Наконец, расчет форвардной ставки для (n1 – n2) нет. лет после n2 нет. лет показано ниже. Форвардный курс = [(1 + S1)n1 / (1 + S2)n2]1/(n1-n2) – 1
Примеры
.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:»»;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон Excel с формулой форвардной ставки здесь – Шаблон Excel с формулой форвардной ставки
Пример №1
Давайте возьмем пример компании PQR Ltd, которая недавно выпустила облигации, чтобы собрать деньги для своего предстоящего проекта, который должен быть завершен в ближайшие два года. Облигации, выпущенные со сроком погашения один год, обеспечивают доходность инвестиций в размере 6,5%, в то время как облигации со сроком погашения два года обеспечивают доходность инвестиций в размере 7,5%. На основе полученных данных рассчитайте годовую ставку через год.
Данный,
- Спотовая ставка на два года, S1 = 7,5%
- Спотовая ставка на один год, S2 = 6,5%
- Количество лет для 2-х облигаций, n1 = 2 года
- Количество лет для 1-й облигации, n2 = 1 год
Согласно приведенным выше данным, мы рассчитаем годовую ставку компании POR ltd.
Следовательно, расчет годовой форвардной ставки через год будет следующим:
Ф(1,1) = [(1 + S1)n1 / (1 + S2)n2]1/(n1-n2) – 1
«=» [(1 + 7.5%)2 / (1 + 6.5%)1]1/(2-1) – 1
Через год ЗА один год = 8,51%
Пример #2
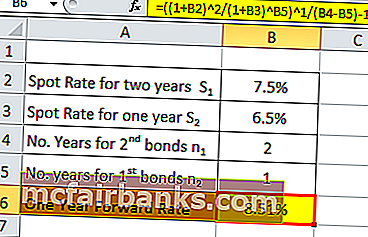
Возьмем в качестве примера брокерскую фирму, которая занимается бизнесом более десяти лет. Компания предоставила следующую информацию. В таблице дан снимок подробного расчета форвардного курса.
- Спотовая ставка на один год, S1 = 5,00%
- F(1,1) = 6,50%
- F(1,2) = 6,00%
На основе предоставленных данных рассчитайте спотовую ставкуРассчитать спотовую ставкуСпотовая ставка — это наличный курс, по которому происходит немедленная сделка и/или расчет между покупателем и продавцом. Эту ставку можно рассматривать для любых и всех видов продуктов, распространенных на рынке, от потребительских товаров до недвижимости и рынков капитала. Это дает немедленную стоимость продукта, с которым совершается сделка. Подробнее в течение двух и трех лет. Затем рассчитайте годовую форвардную ставку через два года.
- Дано, S1 = 5,00%
- F(1,1) = 6,50%
- F(1,2) = 6,00%
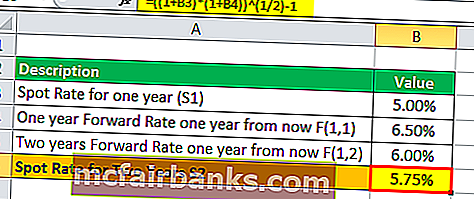
Следовательно, спотовая ставка за два года может быть рассчитана как
S2 = [(1 + S1) * (1 + F(1,1))]1/2 – 1
«=» [(1 + 5.00%) * (1 + 6.50%)]1/2 – 1
Спотовая ставка за два года = 5,75%
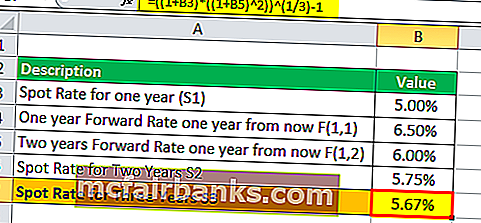
Следовательно, расчет спотовой ставки за три года будет,
S3 = [(1 + S1) * (1 + F(1,2))2]1/3 – 1
«=» [(1 + 5.00%) * (1 + 6.00%)2]1/3 – 1
Спотовая ставка за три года = 5,67%
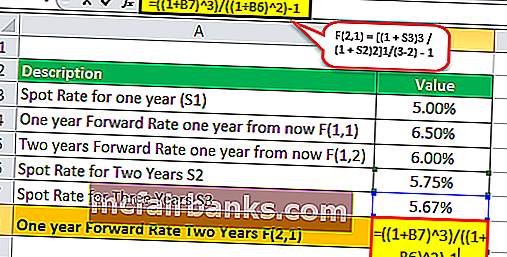
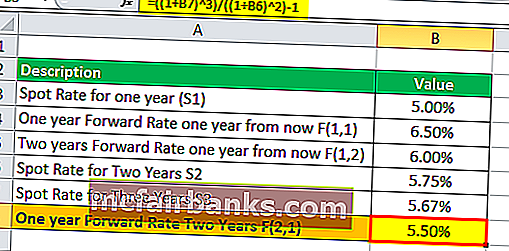
Таким образом, расчет годовой форвардной ставки через два года будет следующим:
Ф(2,1) = [(1 + S3)3 / (1 + S2)2]1/(3-2) – 1
«=» [(1 + 5.67%)3 / (1 + 5.75%)2] – 1
Актуальность и использование
Форвардная ставка относится к ставке, которая используется для дисконтирования платежа с даты в отдаленном будущем на дату в более близком будущем. Его также можно рассматривать как связующее звено между двумя будущими спотовыми ставками, т. е. более дальней спотовой ставкой и более близкой спотовой ставкой. Это оценка того, какими, по мнению рынка, будут процентные ставки в будущем для различных сроков погашения.
Например, предположим, что Джек получил деньги сегодня и хочет накопить деньги, чтобы купить недвижимость через год. Теперь он может инвестировать деньги в государственные ценные бумаги, чтобы обеспечить их безопасность и ликвидность в течение следующего года. Однако в этом случае у Джека есть два варианта: он может либо купить государственную облигацию со сроком погашения в течение одного года, либо купить еще одну государственную облигацию. в обмен на стабильный процентный доход, срок погашения которого наступит через шесть месяцев, а затем, когда наступит срок погашения первой, выделит деньги на другую шестимесячную государственную облигацию.
В случае, если оба варианта приносят одинаковую отдачу от инвестиций, Джеку будет безразлично, и он выберет любой из двух вариантов. Но что, если предлагаемая процентная ставка по шестимесячной облигации выше, чем по годовой. В этом случае он заработает больше денег, купив сейчас шестимесячную облигацию и пролонгировав ее еще на шесть месяцев. Теперь необходимо рассчитать доходность шестимесячной облигации через шесть месяцев. Таким образом, это может помочь Джеку извлечь выгоду из такой временной вариации доходности.
Рекомендуемые статьи
Это руководство по формуле форвардной ставки. Здесь мы обсудим, как рассчитать форвардную ставку по спотовой ставке, а также приведем практические примеры и загружаемый лист Excel. Вы можете узнать больше о бухгалтерском учете из следующих статей –
- Формула возврата инвестицийФормула возврата инвестицийФормула возврата инвестиций измеряет прибыль или убыток от инвестиций по отношению к вложенной сумме. Чистый доход, разделенный на первоначальную капитальную стоимость инвестиций. Формула рентабельности инвестиций = (Чистая прибыль / Стоимость инвестиций) * 100 читать далее
- Формула эффективной годовой ставкиФормула эффективной годовой ставкиЭффективная процентная ставка — это фактическая процентная ставка, полученная или выплаченная после начисления сложных процентов. Он определяется как: Формула эффективной годовой ставки = (1 + r/n)n – 1Подробнее
- Формула процентной ставки
- Формула ставки капитализацииФормула ставки капитализацииФормула ставки капитализации рассчитывается путем деления чистой операционной прибыли на текущую рыночную стоимость актива. Инвесторы используют его для оценки инвестиций в недвижимость на основе годовой доходности. Это помогает решить, является ли собственность хорошей сделкой. Формула = чистая операционная прибыль/текущая рыночная стоимость активаПодробнее
- Bear SpreadBear SpreadBear Spread — это ценовой спред, при котором вы покупаете опционы колл или пут с разными ценами исполнения, имеющими одинаковую дату истечения срока действия. Он используется, когда инвестор считает, что цена акции упадет, но не резко.
Формула для расчета форвардной ставки
Формула форвардной ставки помогает расшифровать кривую доходности, которая представляет собой графическое представление доходности по различным облигациям с разными сроками погашения. Он может быть рассчитан на основе спотового курса на более позднюю дату в будущем и более близкую дату в будущем, а также количество лет до следующей даты в будущем и более близкой даты в будущем.
Форвардная ставка = [(1 + S 1 ) n 1 / (1 + S 2 ) n 2 ] 1 / (n 1 -n 2 ) — 1
где S 1 = спот-курс до следующей даты в будущем,
- S 2 = спотовая ставка до ближайшей даты в будущем, n 1 = количество лет до следующей даты в будущем,
- n 2 = количество лет до более близкой даты в будущем
Обозначение для формулы обычно представлено как F (2,1), что означает годовую ставку через два года.
Расчет форвардной ставки (шаг за шагом)
Его можно получить, выполнив следующие действия:
- Шаг 1: Во-первых, определите спотовый курс до следующей даты в будущем для покупки или продажи ценной бумаги, и он обозначается S 1 . Кроме того, вычислите номер. года до следующей даты в будущем и обозначается n 1 .
- Шаг 2: Затем определите спотовый курс до ближайшей даты в будущем для продажи или покупки той же ценной бумаги, и он обозначается S 2 . Затем вычислите нет. года до ближайшей даты в будущем и обозначается n 2 .
- Шаг 3: Наконец, расчет форвардной ставки для (n 1 — n 2 ) no. лет после n 2 нет. лет показано ниже. Форвардная ставка = [(1 + S 1 ) n 1 / (1 + S 2 ) n 2 ] 1 / (n 1 -n 2 ) — 1
Примеры
Вы можете скачать этот шаблон формулы форвардной ставки в формате Excel здесь — шаблон формулы форвардной ставки в формате Excel
Пример # 1
Давайте возьмем пример компании PQR Ltd, которая недавно выпустила облигации, чтобы собрать деньги для своего предстоящего проекта, который должен быть завершен в следующие два года. Облигации, выпущенные со сроком погашения один год, предлагали 6,5% прибыли на инвестиции, а облигации с двухлетним сроком погашения предлагали 7,5% прибыли на инвестиции. На основании приведенных данных рассчитайте годовую ставку через год.
Данный,
- Спотовая ставка на два года S 1 = 7,5%
- Спотовая ставка на один год, S 2 = 6,5%
- Кол-во лет для 2-х облигаций, n 1 = 2 года
- Кол-во лет для 1-й облигации, n 2 = 1 год
Исходя из приведенных выше данных, мы рассчитаем годовую ставку с настоящего момента для компании POR ltd.
Следовательно, расчет годовой форвардной ставки через год будет следующим:
F (1,1) = [(1 + S 1 ) n 1 / (1 + S 2 ) n 2 ] 1 / (n 1 -n 2 ) —
= [(1 + 7,5%) 2 / (1 + 6,5%) 1] 1 / (2–1) — 1
Один год FR через год = 8,51%
Пример # 2
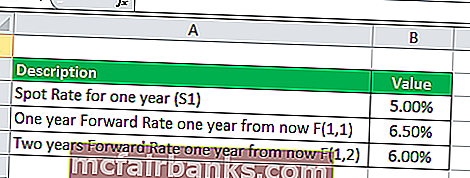
Возьмем, к примеру, брокерскую фирму, которая занимается этим бизнесом более десяти лет. Фирма предоставила следующую информацию. В таблице приведен снимок подробного расчета форвардного курса.
- Спотовая ставка на один год, S 1 = 5,00%
- F (1,1) = 6,50%
- F (1,2) = 6,00%
На основании приведенных данных рассчитайте спотовую ставку на два года и три года. Затем рассчитайте годовую форвардную ставку через два года.
- Учитывая, что S 1 = 5,00%
- F (1,1) = 6,50%
- F (1,2) = 6,00%
Таким образом, спотовая ставка на два года может быть рассчитана как
S 2 = [(1 + S 1 ) * (1 + F (1,1))] 1/2 — 1
= [(1 + 5,00%) * (1 + 6,50%)] 1/2 —
Спот-ставка на два года = 5,75%
Таким образом, расчет спотовой ставки на три года будет:
S 3 = [(1 + S 1 ) * (1 + F (1,2)) 2] 1/3 —
= [(1 + 5,00%) * (1 + 6,00%) 2] 1/3 —
Спот-ставка на три года = 5,67%
Следовательно, расчет годовой форвардной ставки через два года будет следующим:
F (2,1) = [(1 + S 3 ) 3 / (1 + S 2 ) 2] 1 / (3-2) —
= [(1 + 5,67%) 3 / (1 + 5,75%) 2] —
Актуальность и использование
Форвардная ставка относится к ставке, которая используется для дисконтирования платежа с более отдаленной даты в будущем на более близкую дату в будущем. Это также можно рассматривать как связующее звено между двумя будущими спотовыми ставками, то есть дальнейшей спотовой ставкой и более близкой спотовой ставкой. Это оценка того, какими, по мнению рынка, будут процентные ставки в будущем для различных сроков погашения.
Например, предположим, что Джек получил деньги сегодня, и он хочет сэкономить деньги, чтобы купить недвижимость через год. Теперь он может вложить деньги в государственные ценные бумаги, чтобы сохранить их в безопасности и ликвидировать в течение следующего года. Однако в этом случае у Джека есть два варианта: он может либо купить государственную облигацию, срок погашения которой составляет один год, либо он может выбрать покупку другой государственной облигации, срок погашения которой составляет шесть месяцев, а затем пролонгировать деньги еще на шесть месяцев. -месячная государственная облигация при погашении первой.
Если оба варианта приносят одинаковую отдачу от инвестиций, Джек будет безразличен и выберет любой из двух вариантов. Но что, если предлагаемая процентная ставка для шестимесячной облигации выше, чем для однолетней? В этом случае он заработает больше денег, купив шестимесячную облигацию сейчас и пролистав ее еще на шесть месяцев. Теперь самое время рассчитать доходность шестимесячной облигации через шесть месяцев. Таким образом, это может помочь Джеку воспользоваться таким изменением доходности во времени.