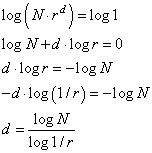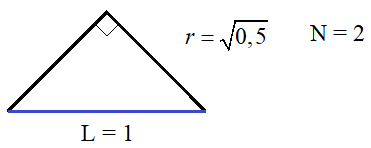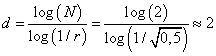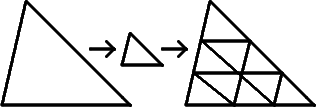Фракталы в простых числах
Время на прочтение
3 мин
Количество просмотров 150K
Я обнаружил этот фрактал, когда разглядывал интерференцию волн на поверхности речки. Волна движется к берегу, отражается и накладывается сама на себя. Есть ли порядок в тех узорах, которые создаются волнами? Попробуем найти его. Рассмотрим не всю волну, а только вектор ее движения. «Берега» сделаем гладкими, для простоты эксперимента.
Эксперимент можно провести на обычном листке в клеточку из школьной тетради.
Или используя JavaScript реализацию алгоритма.
Английская версия: New kind of fractals — Fractals in relatively prime integers (coprime integers)
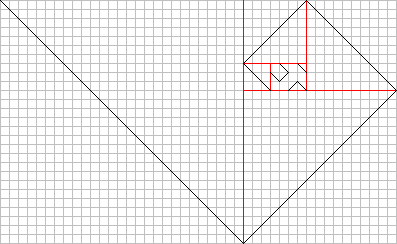
Возьмем прямоугольник со сторонами q и p. Отправим луч (вектор) из угла в угол. Луч двигается к одной из сторон прямоугольника, отражается и продолжает движение к следующей стороне. Это продолжается до тех пор, пока луч не попадет в один из оставшихся углов. Если размер стороны q и p — взаимно просты числа, то получается узор (как мы увидим позже — фрактал).
На картинке мы ясно видим, как работает этот алгоритм.
Gif-анимация:
Самое удивительное то, что с разными сторонами прямоугольника — получаем разные узоры.








Почему я называю эти узоры фракталами? Как известно, «фрактал» — это геометрическая фигура, обладающая свойствами самоподобия. Часть картинки повторяет всю картинку в целом. Если значительно увеличить размеры сторон Q и P — ясно, что эти узоры обладают свойствами самоподобия.
Попробуем увеличить. Увеличивать будем хитрым способом. Возьмем, например, узор 17×29. Следующие узоры будут: 29x(17+29=46), 46x(29+46=75)…
Одна сторона: F(n);
Вторая сторона: F(n+1)=F(n)+F(n-1);
17, 29, 46, 75, 121, 196, 317, 513, 830, 1343
Как числа Фибоначчи, только с другими первым и вторым членом последовательности: F(0)=17, F(1)=29.
Дальше фракталы циклически повторяются.
Если большая сторона четная, получается такой узор:
Если меньшая сторона четная:
Если обе стороны нечетные — получаем симметрический узор:
В зависимости от того, как начинается луч:
или
Попробую объяснить, что происходит в этих прямоугольниках.
Отделим от прямоугольника квадрат, и посмотрим, что происходит на границе.
Луч выходит в той-же точке, откуда зашел.
При этом, количество квадратиков, которые проходит луч — всегда четное число.
Поэтому, если отрезать от прямоугольника квадрат — останется не измененная часть фрактала.
Если отделять от фрактала квадраты столько раз, сколько это возможно — можно добраться до «начала» фрактала.
Похоже на спираль Фибоначчи?
Из чисел Фибоначчи тоже можно получить фракталы.
В математике числами Фибоначчи (ряд Фибоначчи, последовательность Фибоначчи) называют числа:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597…
По определению, первые две цифры в последовательности Фибоначчи 0 и 1, а каждое последующее число равно сумме двух предыдущих.
F(n)=F(n-1)+F(n-2)
F(0)=0, F(1)=1
Поехали:










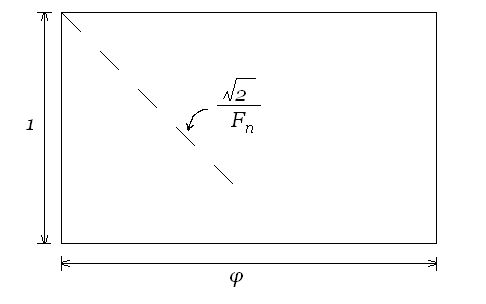
Как мы видим, чем ближе отношение сторон приближается к золотому сечению — тем больше детализация фрактала.
При этом фрактал повторяет часть фрактала, увеличенного на 
Вместо чисел Фибоначчи можно использовать иррациональные размеры сторон:
Получим тот-же фрактал.
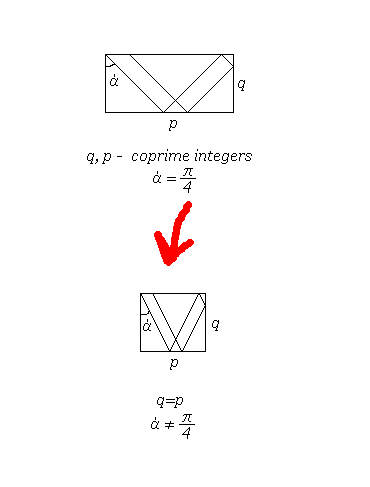
Те-же фракталы можно получить и в квадрате, если пускать луч под другим углом:
Что можно сказать в заключении?
Хаос — это тоже порядок. Со своими закономерностями. Порядок этот не изученный, но вполне поддающийся изучению. А все стремление науки — обнаружить эти закономерности. И в конечном итоге соединить детали головоломки, чтобы увидеть общую картину.
Давайте посмотрим на поверхность речки. Если бросить в нее камень — пойдут волны. Круги, вполне поддающиеся изучению. Скорость, период, длину волны — все это можно подсчитать. Но до тех пор, пока волна не дойдет до берега, не отразиться и не начнет накладываться на саму себя. Получим хаос (интерференцию), который уже трудно поддается изучению.
Что если двигаться от обратного? Упростить поведение волны на столько, на сколько это возможно. Упростить, найти закономерность и после этого попробовать описать уже полную картину происходящего.
Что можно упростить? Очевидно, что сделать отражающую поверхность прямой, без изгибов. Далее, вместо самой волны, использовать только вектор движения волны. В принципе, этого достаточно, чтобы построить простой алгоритм и смоделировать процесс на компьютере. И даже вполне достаточно, чтобы сделать «модель» поведения волны на обычном листке в клеточку.
Что имеем в результате? В результате видим, что в волновых процессах (та-же рябь на поверхности речки) имеем не хаос, а наложение фракталов (самоподобных структур) друг на друга.
Рассмотрим другой вид волн. Как известно, электромагнитная волна состоит из трех векторов — волновой вектор и вектора напряженности электрического и магнитного поля. Как видим, если «словить» такую волну в замкнутой области – там, где пересекаются эти вектора, получаем вполне четкие замкнутые структуры. Быть может, элементарные частицы – это такие-же фракталы?
Все фрактальчики в прямоугольниках от 1 до 80 (6723х6723 px):
Замкнутые области во фракталах (6723х6723 px):
Просто красивый фрактал (4078×2518 px):
Если у вас хватило терпения дочитать до конца, еще раз JavaScript реализация алгоритма 
Продолжение:
Фракталы в иррациональных числах
Фракталы в иррациональных числах. Часть 2
Фракталы, как правило, управляются довольно простыми правилами, порождая удивительную красоту. Однако я не встречал способов построения фракталов, основанных на простоте чисел. Фрактал, который получился у меня, быть может не так красив, как фрактал Мандельброта, и не содержит явного само-подобия (self-similarity), но также имеет бесконечно сложную структуру.
За 4 шага я покажу, как я его получил. Будет много картинок и мало формул.
Постоянные Фейгенбаума и теория хаоса
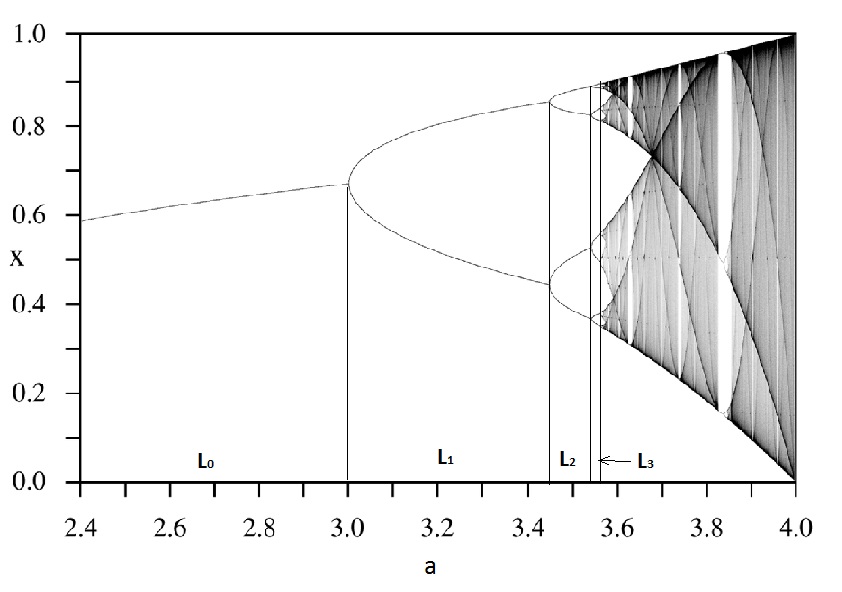
Многие уже узнали эту картинку, связанную с размножением кроликов. Пусть каждый год популяция кроликов увеличивается в a раз:
Если a, коэффициент размножения больше 1, то каждый год кроликов все больше и больше. В природе так не бывает. Пусть, если x приближается к 1, то кролики начинают умирать от болезней:
Дополнительная часть уравнения как раз отвечает за смертность кроликов, а картинка вверху показывает зависимость х (в пределе многих лет) от a. Как видно, при увеличении a до 3 равновесная плотность популяции растет, а потом мы видим неожиданное: происходит бифуркация: в один год кроликов меньше, в другой больше. Впрочем, мы такое поведение природы знаем по урожаю яблок, когда урожайные годы идут через один.
При дальнейшем увеличении a возникает вторая бифуркация, потом еще и еще, все чаще и чаще, а потом настает полный хаос. По мере приближения к хаосу время как бы ускоряется, плотность событий увеличивается. Предел отношений длин отрезков L является первой константой Фейгенбаума, 4.669… и она проявляет себя для очень широкого класса систем. Даже отношения размеров ‘бубликов’ (кардиоидов) у множества Мандельброта тоже 4.669.
Если за L0 (см. картинку вверху) взять промежуток времени 24 февраля — 21 сентября, то следующая бифуркация будет в первых числах ноября.
Фрактал Ляпунова
Фрактал назван в память о Ляпунове, который пустил себе пулю в голову за пол века до открытия фрактала, в котором используется экспонента Ляпунова. Идея генерации фрактала заключается в том, чтобы вместо одного значения a использовать два разных, a и b, и чередовать их по какому-нибудь правилу, например, abababab…:
начинаем мы с x=0.5, выбираем a и b (оси x и y), и вычисляем экспоненту Ляпунова. Для других последовательностей ab картинка будет выглядеть иначе, например для aabab:
А теперь простые числа
Что если вместо периодической последовательности ab использовать апериодическую последовательность abbababaaa…, где a одначает что число составное, а b простое:
1-a, 2-простое, b, 3-простое b, 4- составное, a, 5 — b, 6-a, 7-b итд.
Картинка стала резко ассиметричной (что не удивительно, простых чисел меньше), но стала смазанной и менее интересной, на мой взгляд.
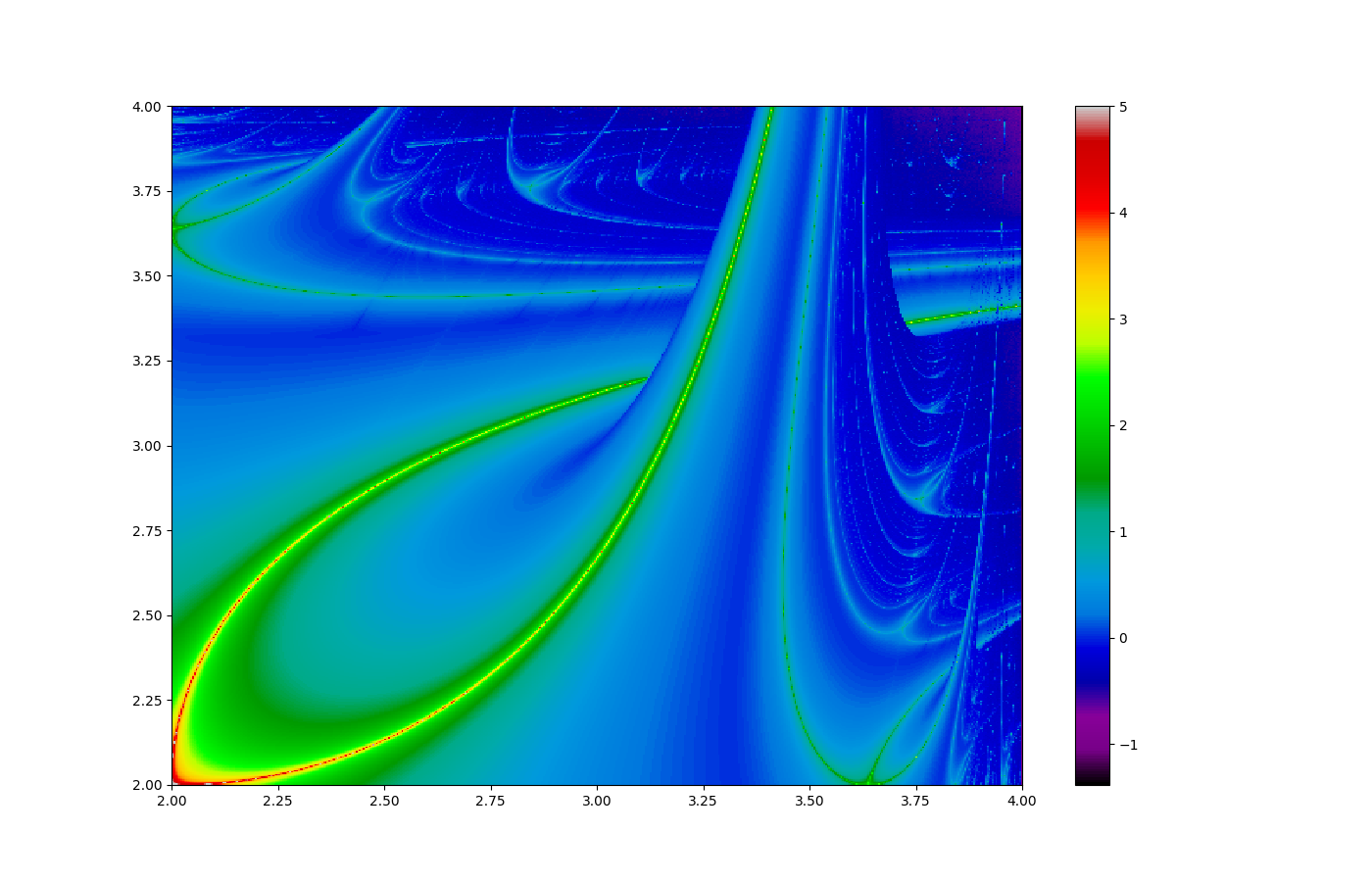
Кстати, а вы заметили, что оси у нас рисуются до значения 4? Это не случайно. При величине a>4 фрактал теряет устойчивость, значения улетают в бесконечность… Как и при отрисовке фрактала Мандельброта! Что если выкинуть экспоненту Ляпунова и отрисовывать (логарифм) количества итераций до того, как модуль x превысит некоторое значение, например, 1000?
Простые числа, вторая попытка
Теперь наши оси не ограничены значением 4:
Черный цвет означает стабильность — бесконечности не получается. Это наша знакомая область до 4. А вот дальше все интереснее/ Давайте увеличим район относительной стабильности около 4:
Картинка меняется довольно сильно, если ‘объявить’ число 3 или 5 составным, а вот большие числа (91, например) на картинку почти не влияют.
Еще один zoom:
И еще, кусочек справа:
‘Прожектора’, светящие в разные стороны, связаны с локальными сгущениями и разрежениями простых чисел. Просчитываются эти картинки довольно долго, 500×500 точек, для каждой надо скользить по простым числам до заданного предела (я брал 10-100 миллионов)
- СИФ, множества Жюлиа и Мандельброта
- Как вычисляется фрактальная размерность по Хаусдорфу
- Системы итерированных функций СИФ
- Рандомизированная система итерированных функций
- Примеры фракталов, сгенерированных СИФ
- Как построить множества Жюлиа
- Рисуем множество Мандельброта
- Главная
- Фракталы
- СИФ, множества Жюлиа и Мандельброта
Как вычисляется фрактальная размерность по Хаусдорфу
На предыдущих
занятиях мы с вами последовательно рассматривали разные вариации L-системы по
принципу «от простого к сложному». Я решил не прерывать это повествование и
довести его до логического конца. Теперь же можно вернуться к одному важному
вопросу, который остался в стороне – о вычислении размерности фрактальных
кривых.
Как я говорил во
введении, фракталы принадлежат дробной размерности. Например, кривая Коха имеет
размерность, равную, примерно, 1,2618. Но как она была вычислена? Именно это мы
и разберем на этом занятии.
Первый
математический аппарат для расчета дробных размерностей предложил немецкий
ученый Феликс Хаусдорф в 1919 году.
Феликс Хаусдорф
(1868-1942 гг.)
Чтобы получить
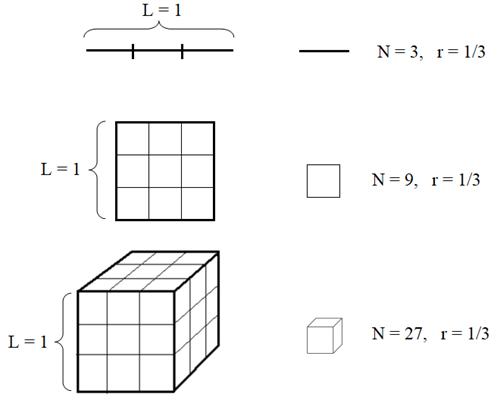
формулу расчета размерности фигуры, можно рассуждать следующим образом. Если
взять линейный отрезок и разделить его на N = 3 равные
части, то длина каждого фрагмента будет в три раза меньше исходной длины. Пусть
начальная длина, условно равна 1, тогда длины фрагментов будут равны r = 1/3.
Очевидно, что общая длина отрезка, равна:
Проделаем ту же
операцию с квадратом. Каждую из его сторон длиной в одну единицу также разделим
на три равные части. То есть, линейные размеры маленьких квадратов будут равны r = 1/3. И таких
квадратов всего N = 9. В этом случае площадь большого квадрата будет
равна:
Как вы уже
догадались, если взять куб и каждую из его сторон также разбить на три равных
отрезка, то получим N = 27 кубиков со сторонами r = 1/3. Тогда
объем куба можно выразить формулой:
То есть,
смотрите, размерность фигуры проявляется как степень коэффициента подобия r. И в общем
случае можно записать:
Чтобы из этой
формулы выразить степень d, прологарифмируем левую и правую части
этого уравнения, получим:
Логарифм можно
взять по любому основанию, обычно это 2, 10 или e – натуральный
логарифм. Величину d называют фрактальной размерностью или размерностью
подобия.
Вот это
выражение и есть формула Хаусдорфа для вычисления размерностей произвольных
кривых, которые могут быть разбиты на одинаковые фрагменты. Фрактальные кривые,
как раз обладают таким свойством – они составлены их однотипных кривых меньшей
размерности поэтому принцип расчета размерности, предложенный Хаусдорфом,
хорошо для них подходит.
Давайте
воспользуемся этой формулой, вычислим размерность кривой Коха и проверим,
действительно ли она равна 1,2816.
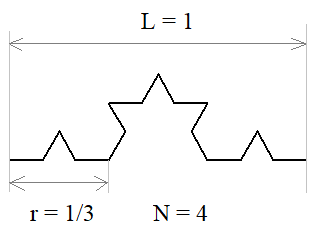
Смотрите, длина
уменьшенных сегментов равна r = 1/3 от общей длины L = 1. Всего
таких сегментов N = 4. Подставляем величины в формулу фрактальной
размерности, имеем:
Давайте
проделаем тот же ход для вычисления размерности фрактала «ковер Серпинского».
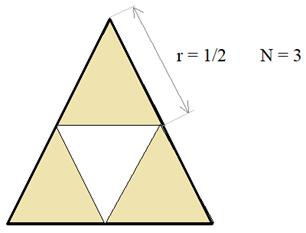
Здесь
коэффициент подобия r = 1/2. Всего уменьшенных треугольников N = 3. Получаем
размерность этого фрактала, равной:
Ну и последний
пример – размерность фрактала «дракон Хартера-Хейтуэя».
На каждой
итерации прямые заменяются на прямоугольные уголки. Если длину прямой принять
за единицу (L = 1), то длины
сторон прямоугольного уголка будут равны .
Всего таких сторон N = 2. Получаем размерность этого фрактала:
То есть, при
числе итераций стремящихся к бесконечности, дракон покроет собой все двумерное
пространство. На самом деле – это один из примеров кривой Пеано, которая будучи
одномерной, способна обходить все точки на плоскости. И метрика Хаусдорфа это
подтверждает.
Видео по теме
- Следующая
☰ Оглавление
- Первая страница
- Онлайн инструменты ▽
- Редактор иконок favicon.ico онлайн
- Игра «Жизнь» онлайн
- Онлайн навигатор по множеству (фракталу) Мандельброта
- Онлайн конвертер PNG в favicon.ico
- Интерактивная схема солнечной системы
- Пересчёт дат в Юлианские дни
- Объяснение и онлайн-демо, как работает HTML5 canvas transform
- Онлайн генератор периодических фонов
- Онлайн конвертер цветов из HSV в RGB
- Онлайн URL-перекодировщик
- Онлайн генератор QR-кодов
- Покрутить 4D-гиперкуб
- Получение географических координат точки на карте
- «Сапёр» на бесконечном поле онлайн
- Черепаший язык онлайн
- Калькулятор индекса массы тела
- Для самых маленьких ▽
- Рисовалка для детей до трёх лет
- «Робот» для детей с трёх-четырёх лет
- «Морской бой» для самых маленьких
- Простой чат
- Инструменты ▽
- Docker ▽
- Docker устанавливаем и разбираемся
- Пример использования Docker для изучения Ruby on Rails
- Пример использования Docker для запуска MySQL
- Почему docker требует root-прав
- JavaScript ▽
- Букмарклеты для JavaSctipt/HTML-разработчика
- Использование «use strict» в JavaScript
- Небольшая памятка по JavaScript
- Простой минификатор/оптимизатор JavaScript
- Мои плагины для хрома
- Python ▽
- Сводная таблица методов основных типов данных Python 2 и 3
- Инструменты для Python-разработчика
- Удобная командная строка Python
- Утечки памяти в Python: метод
__del__и сборка мусора - Работа с нитями в Python
- Файловая система ▽
- FS: перемещение, переименование, архивирование
- Монтирование sshfs с помощью systemd
- Shell ▽
- Работа с историей команд bash
- Консоль/bash. настройка
- Отправка e-mail с картинками чистым shell скриптом
- Конвертирование аудио
- Конвертирование видео
- Управляем тактовой частотой процессора
- Совместный доступ к mercurial по SSH
- Передача файлов по сети
- Безопасное хранение и передача данных
- Нотификатор
- Xorg. Настройка
- Xorg. Настройка нестандартной клавиатуры
- Synergy: Много мониторов с одной клавиатурой и мышкой
- Ssh. Настройка
- Ssh. Настройка туннелирования через NAT и firewall
- Pidgin для хакеров
- Печать
- USB-Flash. монтирование
- Доступ к данным по MTP
- Настройка aspell
- Iptables. Port knocking
- Sudo, sudoers, visudo
- Swap в файле в Linux
- Добрый kill (gdb)
- Изменить размер tmp (tmpfs)
- Установка Arch Linux на USB-Flash
- Эмуляция в QEMU
- GRUB2 вручную
- Системные утилиты
- Настройка редактора vi
- Краткое руководство по vi
- HTML-валидатор
- VDS/VPS
- Начальная настройка
- Сборка nginx
- Настройка nginx
- Сборка uWSGI (Django+CGI)
- Настройка uWSGI
- Управление сетью в Ubuntu с помощью netctl (Arch Linux)
- Настройка WiFi точки доступа под Linux
- Docker ▽
- CS: Искусственный интеллект ▽
- Метрики в машинном обучении: precision, recall и не только
- Оценка точности классификатора
- Нейронные сети на простейших примерах
- Что такое нейрон (очень коротко)
- Пример задачи и демонстрация, как нейрон её решает
- Пример обучения нейрона
- Что осталось за сценой в задаче для одного нейрона
- Деревья принятия решений
- Байесовское машинное обучение
- Примеры кода numpy, scipy, matplotlib
- Метод наименьших квадратов
- Построение системы рекомендаций, на основе текстов
- Диффузионные реакции (реакции с диффузией)
- CS: Разное ▽
- RSA-шифрование на пальцах
- SQRT-декомпозиция
- О пользе рекурсии
- Дискретная бисекция
- Top-K из N (куча)
- Быстрое возведение в степень и подсчёт чисел Фибоначчи
- Алгебра логики
- Небольшая памятка по C++
- Проблема останова
- Примеры простейших серверов на Python
- Простейший форкающийся сервер
- Простейший prefork-сервер
- Простейший многонитевой сервер
- Многонитевой сервер с простым взаимодействием между нитями
- Асинхронный сервер
- Кумулятивное вычисление статистических характеристик
- Пять задач, которые хорошо бы уметь решать за час
- Теория относительности ▽
- Об этих заметках
- Пространство-время как геометрия
- Физическая интерпретация
- Универсальность скорости света
- Эквивалентность инерциальных систем отсчёта
- Относительность пространственных и временных интервалов
- Движение быстрее света
- Парадокс близнецов
- Заключение
- Теория вероятностей ▽
- Как нас обманывает интуиция
- Парадокс Монти Холла
- Парадокс двух конвертов
- Квантовая механика ▽
- Принцип неопределённости на классических примерах
- Фракталы ▽
- Фрактальная размерность
- Фрактальные деревья
- Применение фракталов
- Комплексная размерность
- Гиперкуб
- Обучение и преподавание ▽
- О репетиторстве
- Типичные ошибки на экзаменах
- Лёгкая подготовка к экзаменам
- Как отвечать на экзамене
- Как я худел
- Личное ▽
- Обо мне (как бы резюме)
- Благодарности
- Мои ошибки
- Немного фотографий
- Копирование этих материалов
Фрактальная размерность
О фракталах говорят много. В Паутине созданы сотни сайтов,
посвящённых фракталам. Но большая часть информации сводится к тому,
что фракталы это красиво. Загадочность фракталов объясняют их
дробной размерностью, но мало кто понимает, что же такое дробная
размерность.
Где-то в 1996 меня заинтересовало, что же такое дробная размерность
и каков её смысл. Каково же было моё удивление, когда я узнал, что
это не такая уж сложная вещь, и понять её может любой школьник.
Я постараюсь изложить здесь популярно, что же такое дробная размерность.
Чтобы компенсировать острый дефицит информации по этой теме.
Измерение тел
Сперва небольшое введение, чтобы привести наши бытовые
представления об измерении тел в некоторый порядок.
Не стремясь к математической точности формулировок, давайте разберёмся,
что же такое размер, мера и размерность.
Размер
Размер объекта можно померить линейкой.
В большинстве случаев размер получается малоинформативен.
Какая «гора» больше?
Если сравнивать высоты, то больше красная, если ширины —
зелёная.
Сравнение размеров может быть информативным если
предметы подобны друг другу:
Теперь какие бы размеры мы ни сравнили: ширину, высоту, сторону,
периметр, радиус вписанной окружности или любые другие, всегда получится,
что зелёная гора больше.
Далее мы будем говорить о подобных объектах, поэтому размер
нам пригодится.
Мера
Мера тоже служит для измерения объектов, но она измеряется не
линейкой. О том, как именно она измеряется мы ещё поговорим,
а пока отметим её главное свойство — мера аддитивна.
Выражаясь на бытовом языке, при слиянии двух объектов, мера
суммы объектов равна сумме мер исходных объектов.
Для одномерных объектов мера пропорциональна размеру.
Если вы возьмёте отрезки длиной 1см и 3см, «сложите» их вместе,
то «суммарный» отрезок будет иметь длину 4см (1+3=4см).
Для не одномерных тел, мера вычисляется по некоторым правилам,
которые подбираются так, чтобы мера сохраняла аддитивность.
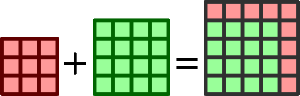
Например, если вы возьмёте квадраты со сторонами 3см и 4см и
«сложите» их (сольёте их вместе), то сложатся площади (9+16=25см²),
то есть сторона (размер) результата будет 5см.
И слагаемые, и сумма являются квадратами.
Они подобны друг другу и мы можем сравнивать их размеры.
Оказывается, что размер суммы не равен сумме размеров слагаемых
(5≄4+3).
Как же связаны мера и размер?
Размерность
Как раз размерность и позволяет связать меру и размер.
Давайте обозначим размерность — D, меру — M, размер — L.
Тогда формула, связывающая эти три величины будет имеют вид:
M = LD
Для привычных нам мер эта формула приобретает всем знакомые обличия.
Для двухмерных тел (D=2) мерой (M) является площадь (S),
для трёхмерных тел (D=3) — объём (V):
S = L2, V = L3
Внимательный читатель спросит, по какому праву мы написали знак равенства?
Ну хорошо, площадь квадрата равна квадрату его стороны, а площадь круга?
Работает ли эта формула для любых объектов?
И да и нет. Вы можете заменить равенства на пропорциональности и ввести
коэффициенты, а можете считать, что мы вводим размеры тел именно так,
чтобы формула работала. Например для круга мы будем называть размером длину дуги
равной корень из «пи» радиан. А почему нет?
В любом случае, наличие или отсутствие коэффициентов не
изменит суть дальнейших рассуждений. Для простоты, я не буду вводить
коэффициенты; если хотите, вы можете их добавить самостоятельно,
повторить все рассуждения и убедиться, что они (рассуждения) не утратили
своей справедливости.
Итого
Из всего сказанного нам следует сделать один вывод, что
если фигуру уменьшить в N раз (отмасштабировать), то
она будет укладываться в исходной ND раз.
Действительно, если уменьшить отрезок (D=1) в 5 раз, то он
поместится в исходном ровно пять раз (51=5);
Если треугольник (D=2) уменьшить в 3 раза, то он уложится в исходном
9 раз (32=9).
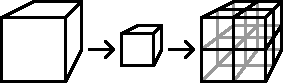
Если куб (D=3) уменьшить в 2 раза, то он
уложится в исходном 8 раз (23=8).
Верно и обратное: если при уменьшении размера фигуры в N
раз, оказалось, что она укладывается в исходной n раз
(то есть мера её уменьшилась в n раз), то размерность
можно вычислить по формуле:
D = ln(n)/ln(N)
Не очень строго и опуская многие важные детали, мы всё же получили
формулу для размерности.
Дробная размерность
Простейший пример
Про дробную размерность обычно рассказывают на примерах
различных ломаных. Я не буду изобретать велосипед и обращусь
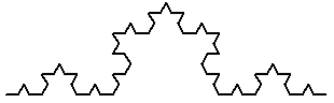
к звезде Коха.
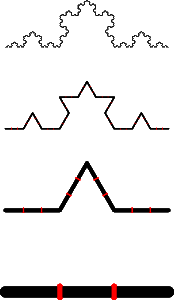
Процедура её построения показана на рисунке (снизу вверх):
В начале берётся отрезок, делится на три равные части и
средняя часть заменяется на два отрезка, равных изъятому.
Получается ломаная из четырёх равных отрезков.
На втором шаге действия повторятся с каждым из четырёх отрезков
и получается ломаная из 16 отрезков.
Эти построения повторяются бесконечное число раз и в конце концов
у нас получается ломаная, состоящая из бесконечного числа отрезков.
Сколько бы мы её не масштабировали, мы всё равно будем получать
одно и тоже.
Это и есть звезда Коха.
Строго говоря, полученное множество точек уже нельзя
называть ломаной. По определению, ломаная должна состоять из
конечного числа отрезков. Но я буду использовать слово
«ломаная» в «нестрогом» смысле для краткости.
Давайте теперь воспользуемся нашим приёмом, чтобы определить её размерность.
Из построения и рисунка видно, что звезду можно разбить на
четыре равные части, при этом размер (скажем, длина исходного
отрезка) каждой части будет равен трети размера исходной фигуры.
То есть будучи уменьшена в три раза, она уложится в себе четыре раза:
По аналогии с нашими предыдущими рассуждениями получаем, что
размерность равна
D = ln(4)/ln(3) ≈ 1.26185950714291487419
То есть это уже не просто отрезок или ломаная (длина звезды Коха бесконечна),
но и не плоская фигура, полностью покрывающая некоторую площадь.
Если мы слегка модифицируем алгоритм построения и будем извлекать
не 1/3 отрезка, а 1/9, то ломаная получится более плотной:
Какова же её размерность? Теперь фигура уложится сама в себе
четыре раза после уменьшения в 9/4 раза, то есть размерность можно
вычислить по той же формуле:
D = ln(4)/ln(9/4) ≈ 1.70951129135145477696
Как видите, «плотность» покрытия сразу отразилась на размерности.
Чуть сложнее
Давайте теперь получим более общую формулу для вычисления размерности.
Для этого снова рассмотрим пример:
Итерации снова начинаются с одного отрезка.
На каждом шаге итерации количество отрезков удваивается.
Каждый порождает два новых: один в 0.88 раз меньше (или, вернее больше)
родителя, второй — в 0.41 раз. В пределе получается следующее
множество:
Давайте вернёмся к первому шагу итераций, на котором мы
получили два отрезка, и посмотрим, какая часть фрактала
образована из каждого из них:
Если принять, что размер полного фрактала 1, то размер
зелёной части (полученной из большего отрезка) будет 0.88,
а размер красной (полученной из меньшего) — 0.41.
Та формула, которой мы располагаем, уже не годится, так как мы
имеем не один, а два коэффициента масштабирования. Но мы можем воспользоваться
нашими знаниями о свойства меры, размера и размерности. Мера, как мы
помним, аддитивна, то есть мера полного фрактала, равна сумме мер
его частей:
M0 = M1 + M2
И сам фрактал, и его части имеют одинаковую размерность (D) и мы можем
выразить меры, через размеры:
L0D = L1D + L2D
А размеры мы знаем. То есть для размерности нашего фрактала мы можем написать уравнение:
1D = 0.88D + 0.41D
или просто
1 = 0.88D + 0.41D
Решить это уравнение аналитически невозможно, но «приблизительный» ответ
можно «подобрать». В нашем случае
D ≈ 1.7835828288192
Можете проверить на калькуляторе.
1 ≈ 0.881.78358 + 0.411.78358
Таким образом, если фрактал образован из N подобных элементов, с коэффициентами
подобия k1, k2 … kN, то его
размерность можно найти из уравнения:
1 = k1D + k2D + … + kND
По этой формуле уже можно рассчитать размерность многих итерационных систем.
Обратите внимание, что, если все коэффициенты равны,
то наша формула превращается в
уже известную простую формулу:
1 = kD + kD + … + kD = N * kD
1/N = kD
D = ln(1/N)/ln(k)
или
D = ln(N)/ln(1/k)
Последнее выражение есть наша первая простая формула
для вычисления размерности простейших самоподобных фракталов.
В заключение
В этом рассказе (именно рассказе) о размерности даже не
упомянуты многие важные аспекты. Он ни сколько не претендует
на полноту, точность или строгость. Но, надеюсь, что
он будет понятен любому старшекласснику и развеет многие
непонимания и мистификации. Про одну из таких распространённых
мистификаций вы можете прочитать в
моей следующей заметке.
Немного о фракталах и множестве Мандельброта
Антон Ступин
Что породило само понятие фрактал? Изучив некоторое количество материалов об истории фрактала, я пришел к выводу, что это понятие создано все тем же неизменным двигателем человеческого прогресса и эволюции — любопытством.
В этот раз любопытство сфокусировало внимание человека на математическом описании окружающего мира. Именно стремление к познанию создало понятие фрактал. Человек стремится описать ту реальность, которая есть вокруг него. Новые открытия — это новые элементы пазла, которые добавляют целостность картине реальности.
Термин фрактал появился относительно недавно — в 1975 году математиком Бенуа Мандельбротом, в честь которого назван самый популярный фрактал. Но, прежде чем перейти к рассмотрению множества Мандельброта, окунемся в историческую сводку и постараемся выделить основную проблему, которая сподвигла Бенуа к исследованию и созданию фрактальный геометрии.

До создания фрактальный геометрии, истинной являлась Евклидова геометрия (да, та самая, которую мы изучали в школе) и именно она на протяжении более 2000 лет служила базой для описания физического мира (прямые линии, углы, треугольники, квадрат и т.д — это все из геометрии Евклида).

Если мы посмотрим на то, что нас окружает, то условно сможем разделить все на две части: то, что создано человеком и то, что создала природа. То, что построено человеком — построено по постулатам евклидовой геометрии (круги, треугольники, квадраты и т.д.). Но чем как описать деревья, горы, реки? Как описать все то, что создала природа? Да, конечно, можно описать все, используя простые фигуры, меняя их масштаб и положение относительно друг друга (что-то мне подсказывает, что мир бы выглядел как в игре Майнкрафт). Но, если серьезно, то попытка описать мир таким принципом — это лишь попытка смоделировать (построить модель), но не описать все так, как оно есть.
Именно желание описать мир, с его, казалось бы, несовершенством линий и попытка придать всему этому хаосу некие закономерности и привело к созданию понятия фрактал и фрактальный геометрии.
Определение фрактала. Примеры.
Определение из интернета «Фрактал — множество, обладающее свойством самоподобия». Звучит сложно. Попробую объяснить, используя некоторые высказывания, относительно фракталов:
- Фрактал — самоподобная сложная фигура;
- Фрактал — элемент, повторяя который бесконечное количество раз, мы получим тот же/подобный элемент другого масштаба;
- Фрактал строится за счет многократного повторения (математики называют этот процесс «итерацией«);
- Целый объект практически полностью совпадает с частью себя самого. Целые имеют ту же форму, что одна или более частей;
- Есть фигура и правило, по которому эта фигура дублируется относительно друг друга.
Как правило, итерация это многократное повторение простого действия. Фракталы были и до множества Мандельброта, но он описал эту теорию наиболее комплексно.
Чтобы упростить понимание фрактала: да, как сказано выше, природа очень самобытна и нелинейна, но она состоит из подобных элементов. Возьмем самый распространенный пример фрактала в природе — дерево. Оно состоит из подобных элементов: меленькая веточка подобна ветки крупнее и т.д.


Ниже приведем примеры фракталов с множественным повторением какого-то простого действия (итерацией):
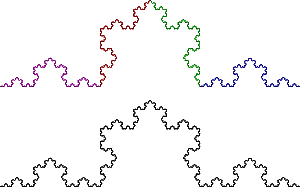
- Кривая Гильберта
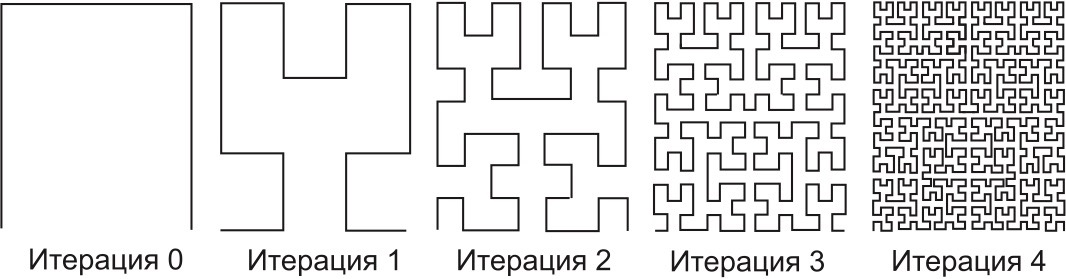
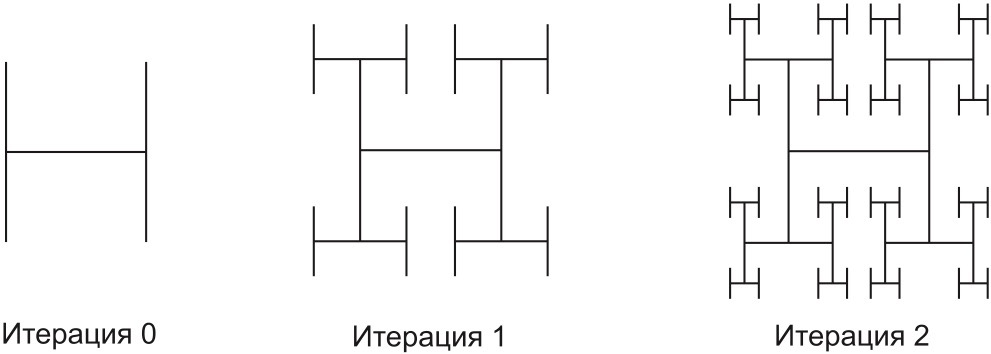
2. Н-фрактал (конечные точки буквы «Н» заменяем на «Н» и так до бесконечности)
3. Треугольник Серпинского (внутри треугольника строим перевернутый треугольник и так до бесконечности)
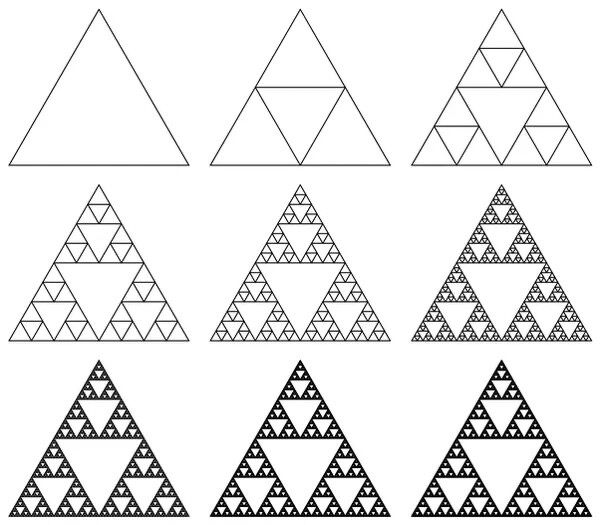
4. Кривая Коха (делим сторону равностороннего треугольника на 3, среднюю часть заменяем на равносторонний треугольник и так до бесконечности с каждой стороной каждого треугольника)
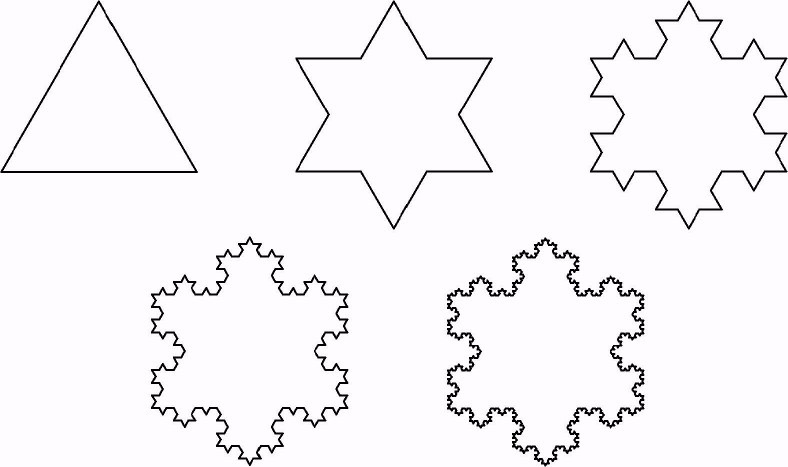
Как мы видим, что все сложные фигуры складываются из самоподобных элементов, с помощью простого правила.
Множество Мандельброта.
Повторюсь, что итерация простых элементов для построение целостной сложной фигуры были и до работы Бенуа Мандельброта. Увеличение вычислительной мощности компьютеров позволило достичь огромного числа повторений, что позволило ученому достичь такой глубины в понимании фрактальности мира:



Попутешествовать по завораживающему множеству Мандельброта можно по следующим ссылкам:
sunandstuff.com/mandelbrot/
www.michurin.net/online-tools/mandelbrot.html
Как бы вы не меняли масштаб, вы всегда будете видеть похожие на себя фигуры. Это и есть ключевой признак фракталов — самоподобие при изменении масштаба.
Принцип построения модели:
В основе модели, как и писал раньше, лежит итерация (многократное повторение). В случае множества Мандельброта — это решение уравнения.
Оно выглядит так:
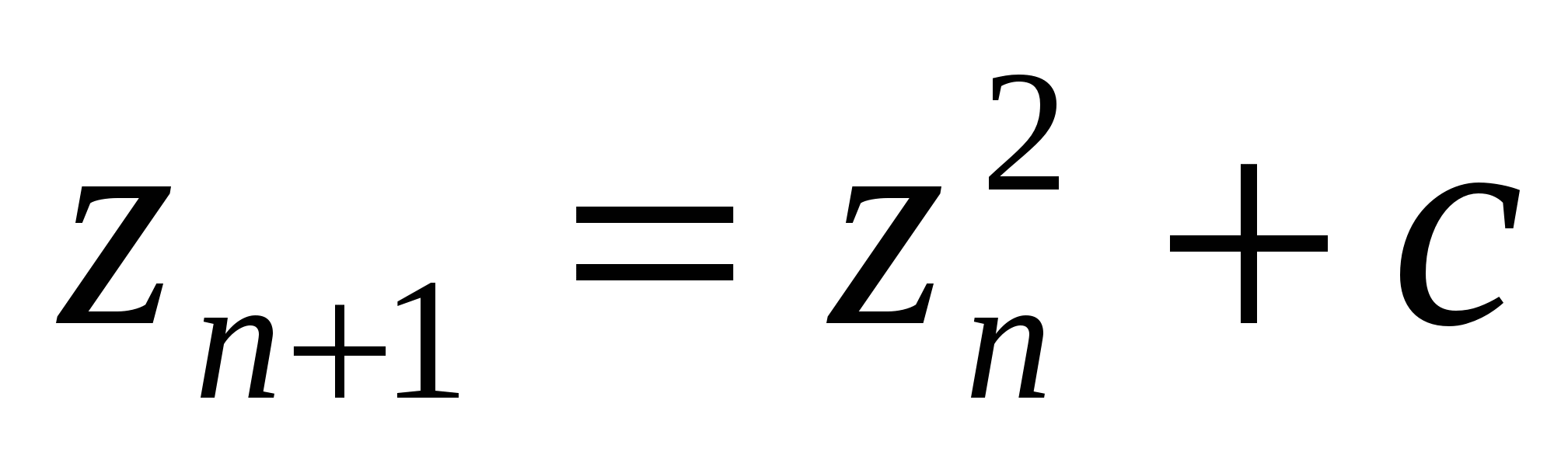
Для математика выглядит достаточно просто, но есть нюансы. Не будем вдаваться в подробности, попробуем пошагово раскрыть суть построения множества:
Чтобы определить, входит ли число в множество Мандельброта, нужно принять Z за ноль (О) возвести в квадрат и сложить с нашим числом. Полученное число Z — заново подставляем в уравнение и складываем с числом, которое тестируем. Уравнение решается и полученное решение снова подставляется в уравнение. Уравнение заново решается. Итерация! Множественное повторение решений одного и того же уравнения. Если при решении мы видим, что значение Z сильно увеличивается (стремится к бесконечности), значит изначальное число не подходит. Если же Z колеблется в пределах одного значения, значит выбранное число входит в множество. Далее полученные значения отмечают на плоскости. Уравнение решается огромное количество раз и в итоге получается графическое изображение множества Мандельброта (его мы видели выше).
P.s можно еще посмотреть что такое комплексные числа — они имеют большое значение для построение модели.
До 1975 года, фракталы встречались в истории время от времени, но после работы Бенуа Мандельброта, изучение фракталов начало приобретать массовый характер, все больше интегрируясь в мир. Изучение фракталов вызвало новый виток в изучении разных сфер жизни: в компьютерной графике, в передаче данных, в радиотехнике, в производстве, в работе мозга, в движениях человека, в росте живых существ и многом другом.
Представьте, насколько упрощается построение графических моделей, зная, что они самоподобны и вычисляются по одной простой формуле. Насколько становиться проще кодирование и передача информации, когда есть понимание, что их можно «сжать» по определённой фрактальный закономерности. И насколько понятней становится эволюция живых существ, когда мы можем найти фракталную модель их развития.
Фракталы в тейдинге.
Тема фракталов сложна и интересна, но как же она соотносится с торговлей на бирже? Думаю, что идея также проста: попытка описать и упорядочить казалось бы хаотичное и нелинейное движение цены, и найти в нем определенные закономерности.
Тема фракталов достаточно молода, но одно знаем точно, что ее глубина и охват — это «черная дыра» с огромным количеством идей и возможный векторов применения.
Первое, что мы можем выделить — это подобие графиков движения цены, вне зависимости от инструмента, таймфрема (временного масштаба). Разумеется, что найти абсолютно похожие участки крайне сложно, но ключевое свойство фрактала — это самоподобие, а не идентичность. А найти регулярные и подобные структуры в колебаниях цены — это уже более реальная задача.
Получается, что рынок, как минимум, имеет фрактальные свойства. Само наличие закономерностей в движении говорит об этом.
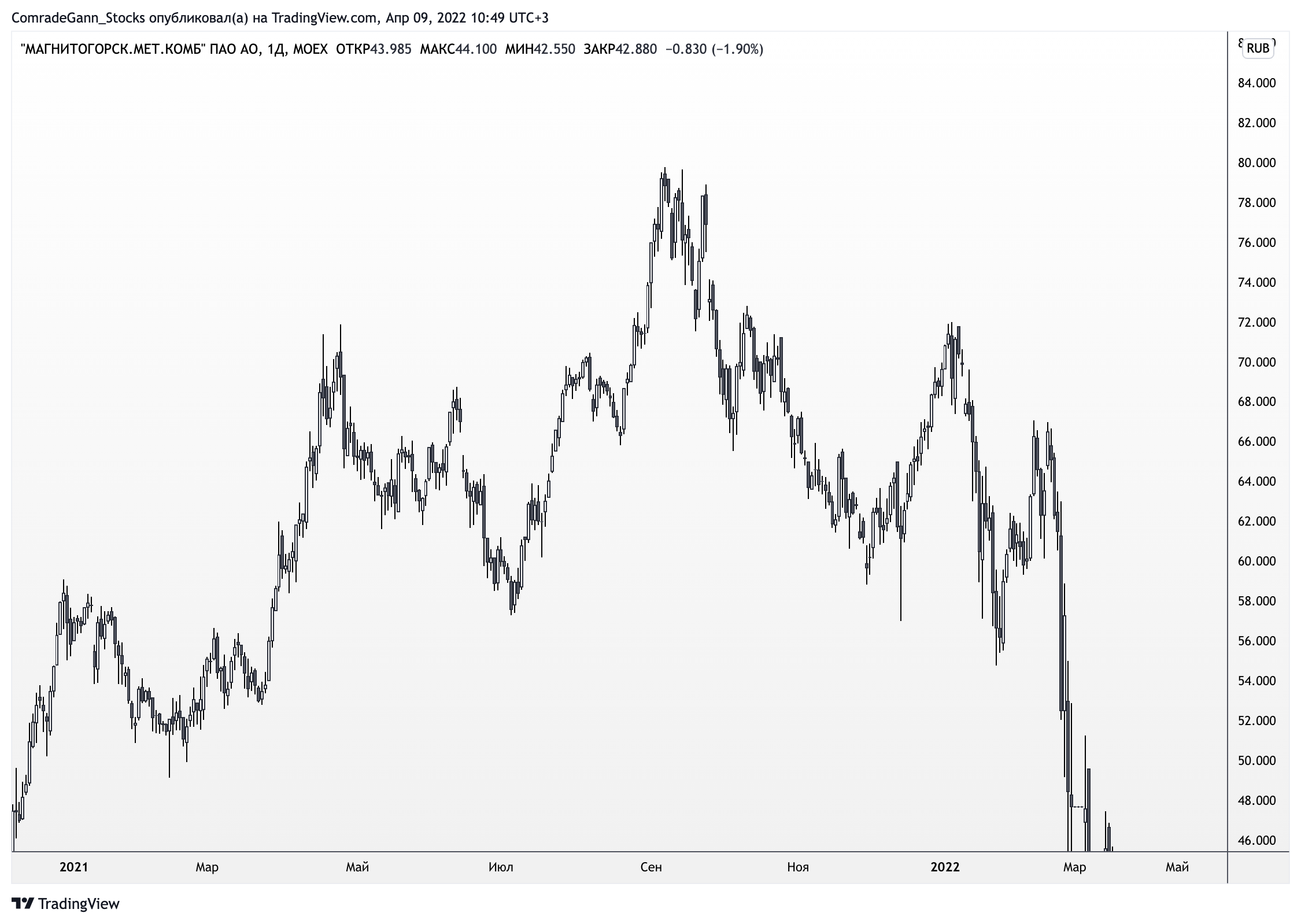
Поиск закономерностей в движении цены, похожих ценовых моделей/паттернов (фракталов) — как одно из направлений, в которое можно углубиться.
Волны Элиота — также определенная фрактальная закономерность в движении цены
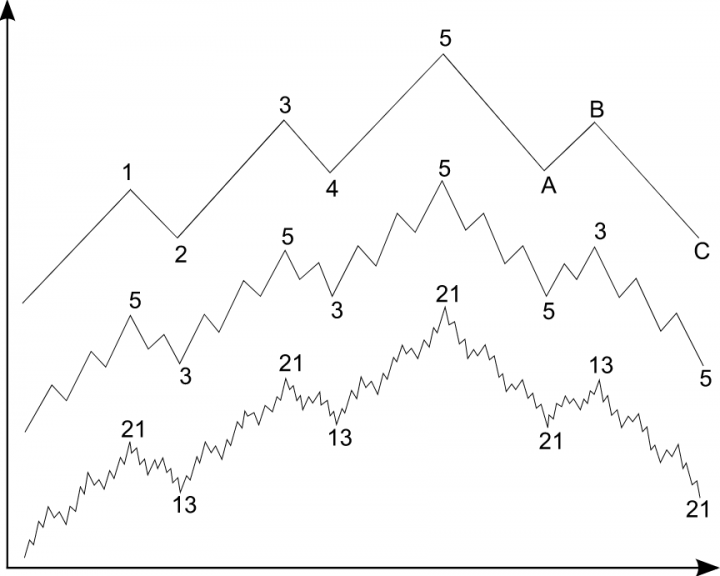
Что еще интересного можно найти на основе модели Мандельброта?
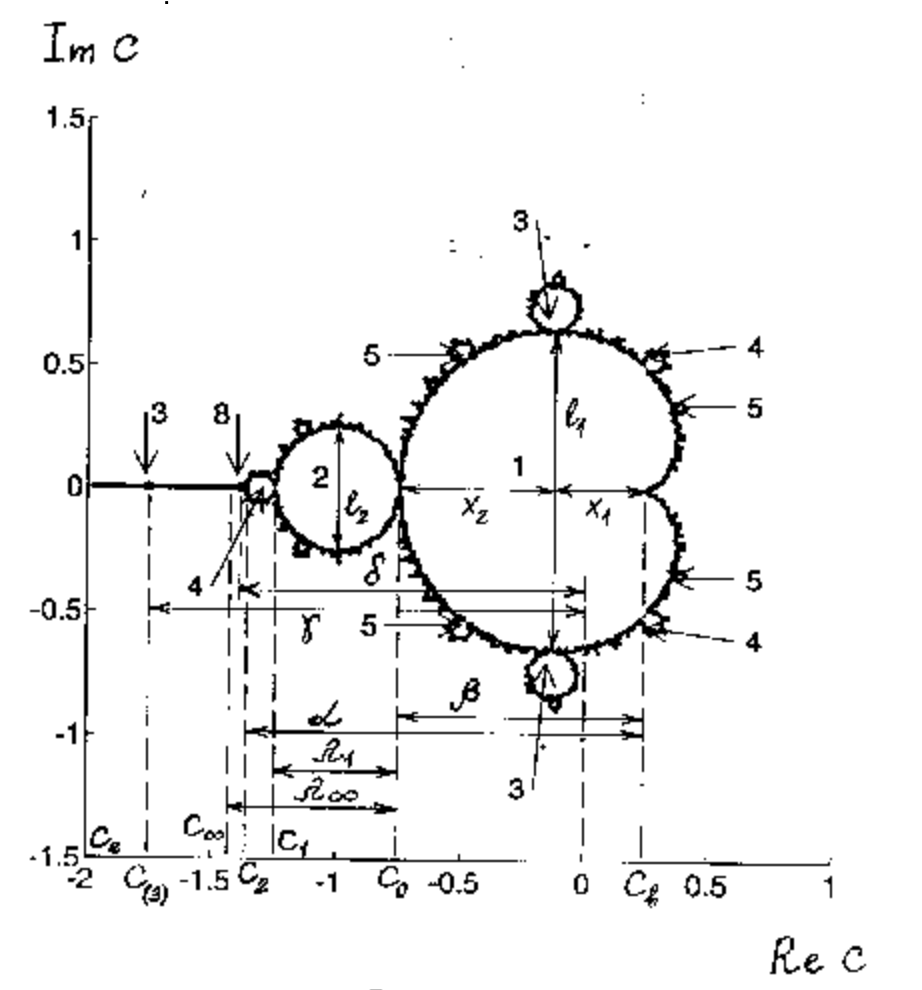
К примеру, можно взглянуть на соотношение частей этого фрактала:
Фрактальную теорию тесно связывают с принципом золотого сечения и числами Фибоначчи. Опять же, не будем вдаваться в сложные математические вычисления и доказательства.
Нас тут интересует, что определенное соотношение частей и сторон множества
Мандельброта соответствуют принципам золотого сечения и чисел Фибоначчи.
А это уже совсем другая история…
Множество Мандельброта — это удивительный мир фракталов, возможности которого, по большей части, не изучены. Но, безусловно, изучение этого направления — это «окно» в мир новых теорий и концепций.
t.me/ComradeGann