Как найти фундаментальную функцию

УДК 519.6

П.А. Акимов, М.А. Фрайнт

ФГБОУ ВПО «МГСУ»

ФУНДАМЕНТАЛЬНЫЕ ФУНКЦИИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ И ИХ ВЕЙВЛЕТ-АППРОКСИМАЦИЯ С УЧЕТОМ СПЕЦИФИКИ СТРОИТЕЛЬНЫХ ЗАДАЧ

Приведено определение фундаментальной функции линейного дифференциального оператора с постоянными коэффициентами, рассмотрен корректный универсальный метод аналитического построения фундаментальных функций, учитывающий особенности краевых задач строительной механики, изложены элементы кратномасштабного вейвлет-анализа с использованием вейвлета Хаара, представлен алгоритм осреднения коэффициентов разложения функции по базису Хаара, описан ряд примеров реализации разложения фундаментальных функций по базису Хаара.

Ключевые слова: дифференциальные уравнения, фундаментальные функции, кратно-масштабный вейвлет-анализ, задачи строительной механики.

1. Понятие о фундаментальной функции. Рассмотрим линейное неоднородное дифференциальное уравнение с постоянными коэффициентами

any(n) (х) + a„-i y(n—1) (x) + a-_2 y(n—2) (x) +… + ai y(1) (x) + ao y(x) = f (x), (1.1) где ak = const, k = 0, 1, 2, …, n — коэффициенты, f (x) — известная функция.

Решение (1.1) при f (x) = S(x) (5(x) — дельта-функция Дирака) обозначим e(x):

Le( x) = S( x). (1.2)

Функция s(x), определяемая уравнением (1.2), как известно, называется фундаментальной функцией дифференциального оператора [1]

_ » ^ d d d d d ,л,

L = ^ ak—^ = an —- + an —— + an _ 2—+… + a—+ ao. (1.3)

k=0 dx dx dx dx dx

Для произвольной f (x) общее решение уравнения может быть записано в виде

да

y(x) = s(x) *f (x) = J s(x _ f ©d5, т.е. L»1 = e*; LL_ f = e* f. (1.4)

—да

2. Аналитическое построение фундаментальной функции. Фундаментальная функция определена с точностью до однородного решения. Иными словами, если имеется некоторая функция у( x), такая, что Ly (x) = 0, то e (x) = e( x) + у (x) также удовлетворяет уравнению Le( x) = S(x).

Предлагается следующий алгоритм построения фундаментальной функции [2, 3]:

1. Записывается характеристическое уравнение, соответствующее (1.3):

anV +a-—1r—1 +… + a1X+a0 =0. (2.1)

2. Данное уравнение имеет n корней вида: X = a + /р , р = 1, …, n, часть из которых в общем случае кратные. Обозначим m кратность p-го корня.

3. Фундаментальную функцию будем искать в виде

e(x) = e+ (x) = (С , у), x > 0; e(x) = e_ (x) = (C , y), x < 0, (2.2)

где C+ = [ C0+ C+ C2+ … C-+_1 ]T; C-= [ C0 С— C_ … C^ ]T — (2.3)

векторы постоянных, подлежащих определению;

— T k i icos (Ppx)l

y = [У0 У1 у2 … у-_1] ; Ур = x exp(apxН , A k = 0 1 nip _1 (2.4)

есть векторы базисных функций (фундаментальных решений).

4. Поиск компонент векторов (2.3) ведется из следующих условий стыковки:

Де = 0; Де(1) = 0; …; Де(п-2) = 0; Де(п-1) = 0, (2.5)

где Де = е(+0)-е(-0); Де()) = е())(+0)-е())(-0), 5 = 1, 2, …, п. (2.6)

Условия (2.5) обеспечивают выполнение условия (1.2).

5. Необходимо приравнивать к нулю соответствующие коэффициенты С++, если уp (x) содержит функцию вида exp (apx) при аp > 0. Аналогично коэффициенты Ср задаются нулевыми, если уp (x) содержит функцию exp (apx) при аp < 0.

Данное условие необходимо выполнять для обеспечения отсутствия показательных функций с положительными аргументами в составе окончательной формулы для фундаментальной функции. При невыполнении этого условия, при численной реализации будет происходить накопление погрешностей, приводящих к неверным результатам или к переполнению разрядной сетки ЭВМ и остановке машины.

Следует полагать нулевыми коэффициенты С- если соответствующие yp (x) имеют вид уp (x) = xk, yp (x) = cos (Ppxj, уp (x) = sin (ppx), уp (x) = xk cos (ppx) или

yp(x) = xk sin(Ppx).

Возможны и иные подходы, в зависимости от желаемого общего вида решения.

3. Некоторые базовые сведения о вейвлетах. Одним из наиболее распространенных на сегодняшний день аппаратов раздельного исследования локального и глобального поведения функций является аппарат Фурье, однако его применение связано с некоторыми трудностями. Коэффициенты рядов Фурье в некоторых случаях убывают достаточно медленно, что вызывает необходимость учета большего количества членов ряда и, как следствие, увеличивает время решения задачи. Бурно развивающейся альтернативой анализу Фурье, по сути, приходящей на замену последнему, является вейвлет-анализ [4]. При исследовании высокочастотных и низкочастотных составляющих решения задачи применяется соответственно более сильная или более слабая локализация.

Вейвлеты представляют собой класс базисных функций {ук (x)} ю . Эти функции должны обладать следующими основными свойствами:

1) все функции получаются из базовой сдвигом уk (x — к) или сжатием уk (2k x);

2) базовая функция у( x) — решение некоторого функционального уравнения.

Можно выбрать базис {Фк (x)}¡=-m таким образом, что:

1) каждая функция Фк (x) является сдвигом Ф(x), т.е. Фк (x) = Ф(x — к);

2) для некоторой последовательности коэффициентов } _ имеем

Ф( х/2) = £ ^Ф( X — ] ). (3.1)

]=1

Усилим условие (3.1) требованием представить две линейно независимые функции Ф(х /2) и Т(х /2) в виде

Ф(х /2) = £ ^Ф(х — у); Т(х /2) = £ Ф(х — у). (3.2)

>-да у=-да

Вводя нормирующий множитель, можно переписать (3.2) в виде

да да

Ф( х/2) = ^2 £ Ф( х — к); Т (х/2) = ^2 £ gk Ф(х — к). (3.3)

к=-да к=-да

Кроме того, можно подобрать такую функцию Т(х), что gl-k = (-1)1-к^, где hk — комплексно сопряженное hk.

Выражения (3.4) и (3.5) называют масштабирующими уравнениями, функции Ф( х) и Т( х) соответственно отцовской и материнской функциями вейвлетов.

Рассмотрим такое решение масштабирующего уравнения, при котором будут иметь место только два ненулевых коэффициента /г0 = ^ = Тогда отцовская

функция (масштабирующая функция, рис. 1) определяется по формуле

Ф(x) = 1, 0 < x < 1; Ф(x) = 0, x < 0 u x > 1. 1,5

(3.4)

0,5

-0,5 0 0,5 1 1,5 -0,5 0

Рис. 1. Масштабирующая функция и вейвлет Хаара

0,5

1,5

Соответственно материнский вейвлет (вейвлет Хаара) будет иметь вид (см. рис. 1)

‘ 1, 0 < х < 1/2;

Ч(х) = | -1, 1/2 < х < 1; (3.5)

0, х < 0 и х > 1.

4. Дискретный базис Хаара на отрезке. Рассмотрим произвольный отрезок Ь]. Разделим его на (п -1) равных частей, где п = 2м ; М — максимальный уровень функций Хаара. Рассмотрим систему материнских функций (уДО}, Р = 0,1,…,М; ] = 1, 2,…,Ыр; г = 1, 2,…, п; N р — количество функций Хаара на р-м уровне.

Дискретные функции Хаара на отрезке определяются формулой 1, 2р (2] — 2) < г < 2р (2] -1);

-1, 2р (2] -1) < г < 2р2]; (4.1)

0, г < 2р (2] — 2) и г > 2р 2]. Количество функций Хаара и норма функции Хаара на р -м уровне:

И Р (0 =

1

f 2M-(Р+1) = n (2Р+1), 0 < Р < м; Г , 0 < p < M;

Np = аР = И(о Ч ^

[1, Р = M; Р 11 7 11 I 72м, p = м.

(4.2)

Пусть / — произвольная функция, определенная в точках разбиения отрезка с номерами / = 1, 2,…, п. Разложение функции /(г) по базису Хаара имеет вид

м Np

f (i) =Ц vP ИР (0

(4.3)

Р=07=1

где ур = ^ / (г)Чр (г) — коэффициенты разложения.

5. Алгоритм быстрого вычисления коэффициентов разложения дискретной функции по базису Хаара. Описываемый ниже алгоритм прямого вейвлет-преобра-зования по базису Хаара, предложенный А.Б. Золотовым, позволяет вычислить коэффициенты разложения за т • п операций, где т — некоторое целое число, не зависящее от п .

Пусть

-f (j), j = 1, 2, …, n, a 0 =V2, p = 0. Для всех Р = 0, 1, …, M — 1 производим вычисления по формулам

= (<7-1 — <7 )/aР , <+1 = иР-1 + U2J , j = 1, 2, …, N

(5.1)

>+1

Р = 0,1, …, M -1. (5.2)

a

При р = М имеем

ам = < = пМ /«М, p =М, (5.3)

где ир, ] = 1, 2, …, ^^, р = 1, 2, …, М — вспомогательные величины.

6. Алгоритм осреднения коэффициентов. Если значения (5.1) являются точными, то возникновение вычислительных ошибок при определении коэффициентов разложения по алгоритму, описанному в п. 5, исключено. С учетом специфики конкретных задач может потребоваться некоторое уменьшение точности расчета при уменьшении количества вычислительных операций. В частности, возможно использование алгоритма осреднения коэффициентов.

Введем следующие обозначения:

(Duр)2-1 =(пру -иру-1)/(2рИ);

р 1 = (<]-1 + иру )/2; р = 0,1,…,М, ] = 1, 2,…,Ыр. (6.1)

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

(БпрЦ = (йрг] -пр2]-)/(2рИ);

При вычислении коэффициентов без осреднения, используя обозначения (6.1):

ур = -ар'(2рИ)(Duр] = ар1 (2р+1 И)(Dup-l] ; р = 1, 2,…,М. (6.2)

Предположим, что требуется произвести осреднение на уровне q. Тогда для всех р = 1, 2,…, д будем полагать

(Бпр)2]- — (Бпр)2] — (Бпр)2]-,; У2Р- = У2Р; ] = 1, 2, …, Ыр+1. (6.3)

Имеем

гр ~ Р

П2 ] —

V

+2 и Щ ■ — Щ -1

р+1 = ^^^ ; = ^ ^, где р)2]-1 = 2]р+12]-1

а р+1 2 И

таким образом,

а ,

(БП р )2 ]-‘ =- ^ +I, ] = ^ 2, …, ^ (6^) Следовательно,

У2*-1 = У2р] = -ар12р И(Бпр )2]-1 — -ар12р И [-а(2р+2 И)] = = 1а р+1 уР+1 = 1 ур+1

4 ад ] 2>/2

д

откуда окончательно получим

р

Ъ] —

1 = Ур] = 1, ] = 1, 2, …, Ыр+1, где в = 1 (24г). (6.6)

7. Примеры. Во всех примерах будет использована вейвлет-аппроксимация при М = 6.

Пример 1. Рассмотрим дифференциальный оператор задачи о поперечном изгибе балки

¿V = 7(4).

соответствующая фундаментальная функция имеет вид

е(х) = х3 / 6, х > 0; е(х) = 0, х < 0.

Вейвлет-аппроксимация полностью совпадает с представленным аналитическим видом фундаментальной функции. Проиллюстрируем результаты без осреднения для данной функции на отрезке (0, 10] и с осреднением при р = 2 (рис. 2).

Пример 2. рассмотрим дифференциальный оператор задачи о поперечном изгибе балки на упругом основании (модель Винклера)

Ьу = /Ч + 4а4у, а4 > 0.

£ 80 60 40 20 0 -20

,М = 6, без осреднения э С осреднением

6 8 X Data

Рис. 2. Вейвлет-аппроксимации фундаментальной функции для примера 1

Соответствующая фундаментальная функция имеет вид б(х) = У(8а3) ехр(-а | х |)(^(ах) + sin(а | х |)).

Примем для определенности а = 1. Вейвлет-аппроксимация полностью совпадает с представленным аналитическим видом фундаментальной функции. Проиллюстрируем результаты без осреднения для данной функции на отрезке (0, 10] и с осреднением при р = 0 на отрезке (0, 5) и при р = 2 на отрезке (5, 10) (рис. 3).

0,14 и

0,12 0,10 a0,08 2 0,06 0,04 0,02 0,00 -0,02

•М = 6, без осреднения с осреднением

0 2 4

6 8 X Data

10

12

• Р = 6 о Р = 5 т Р = 4 V Р = 3 — Р = 2 □ p = 1

♦ р = 0

о Функция

0,14 0,12 0,10 0,08 0,06 0,04 0,02 0,00 -0,02 -0,04 -0,06

Рис. 3. Вейвлет-аппроксимации фундаментальной функции для примера 2 (а); вклады уровней вейвлет-аппроксимации (б)

а

Замечания. Исследования проводились в рамках следующих работ:

1) грант 2.3.8 Российской академии архитектуры и строительных наук «Разработка и исследование дискретно-континуальных методов для расчета строительных конструкций с кусочно-постоянными физико-геометрическими параметрами по одному из направлений» на 2011—2012 гг.;

2) грант 2.3.18 Российской академии архитектуры и строительных наук для молодых ученых специалистов «Разработка и верификация коррективных численных и численно-аналитических методов исследования локального напряженно-деформируемого состояния строительных конструкций на основе многоуровневого вейвлет-анализа» на 2012 г.

Библиографический список

1. Кеч В., Теодореску П. Введение в теорию обобщенных функций с приложениями в технике. М. : Мир, 1978. 518 с.

2. Дискретные и дискретно-континуальные реализации метода граничных интегральных уравнений / А.Б. Золотов, П.А. Акимов, В.Н. Сидоров, М.Л. Мозгалева. М. : МГСУ, 2011. 368 с.

3. Численные и аналитические методы расчета строительных конструкций / А.Б. Золотов, П.А. Акимов, В.Н. Сидоров, М.Л. Мозгалева. М. : Изд-во АСВ, 2009. 336 с.

4. Захарова Т.В., Шестаков О.В. Вейвлет-анализ и его приложения. М. : Инфра-М, 2012. 158 с.

Поступила в редакцию в апреле 2012 г.

Об авторах: Акимов Павел Алексеевич — доктор технических наук, член-корреспондент РААСН, профессор кафедры информатики и прикладной математики, ФГБОУ ВПО «Московский государственный строительный университет» (ФГБОУ ВПО «МГСУ»), Россия, 129337, г. Москва, Ярославское шоссе, д. 26, 8 (499) 183-59-94, pavel.akimov2@gmail.com;

Фрайнт Михаил Александрович — студент, ФГБОУ ВПО «Московский государственный строительный университет» (ФГБОУ ВПО «МГСУ»), Россия, 129337, г Москва, Ярославское шоссе, д. 26, mfraynt@gmail.com.

Для цитирования:АкимовП.А., ФрайнтМ.А. Фундаментальные функции для обыкновенных дифференциальных уравнений с постоянными коэффициентами и их вейвлет-аппроксима-ция с учетом специфики строительных задач // Вестник МГСУ 2012. № 7. С. 37—43.

P.A. Akimov, M.A. Fraynt

FUNDAMENTAL FUNCTIONS OF ORDINARY DIFFERENTIAL EQUATIONS WITH CONSTANT COEFFICIENTS AND THEIR WAVELET APPROXIMATION SPECIFIC TO CONSTRUCTION

PROBLEMS

The paper covers the analytical construction of fundamental functions of ordinary differential equations with constant coefficients and their wavelet approximations specific to problems of the structural mechanics. The definition of the fundamental function of an ordinary linear differential equation (operator) with constant coefficients is presented. A correct universal method of analytical construction of the fundamental function in the context of problems of structural analysis is described as well. Several basic elements of the multi-resolution wavelet analysis (basic definitions, wavelet transformations, the Haar wavelet etc.) are considered. Fast algorithms of analysis and synthesis (direct and inverse wavelet transformations) for the Haar basis and a corresponding algorithm of averaging are proposed. It is noteworthy that the algorithms of analysis and synthesis are the relevant constituents of all wavelet-based methods of structural analysis. Moreover, the effectiveness of these algorithms determines the global efficiency of respective methods. A few examples of fundamental functions of ordinary linear differential equations (the problem of analysis of beam, the problem of analysis of the beam resting on the elastic foundation) are presented.

Key words: fundamental function, ordinary differential equation, structural analysis, wavelet approximation, Haar basis, wavelet transformations, algorithm of averaging.

References

1. Kech V., Teodoresku P. Vvedenie v teoriyu obobshchennykh funktsiy s prilozheniyami v tekhnike [Introduction into the Theory of Generalized Functions and Their Applications in Engineering]. Moscow, Mir Publ., 1978, 518 p.

2. Zolotov A.B., Akimov P.A., Sidorov V.N., Mozgaleva M.L. Diskretnye i diskretno-kontinual’nye realizatsii metoda granichnykh integral’nykh uravneniy [Discrete and Discrete-continual Versions of the Boundary Integral Equation Method]. Moscow, MSUCE, 2011, 368 p.

3. Zolotov A.B., Akimov P.A., Sidorov V.N., Mozgaleva M.L. Chislennye i analiticheskie metody rascheta stroitel’nykh konstruktsiy [Numerical and Analytical Methods of Structural Analysis]. Moscow, ASV Publ., 2009, 336 p.

4. Zakharova T.V., Shestakov O.V. Veyvlet-analiz i ego prilozheniya [Wavelet Analysis and Its Applications]. Moscow, Infra-M Publ., 2012, 158 p.

About the authors: Akimov Pavel Alekseevich — Doctor of Technical Sciences, Associate Member of the Russian Academy of Architecture and Construction Sciences, Professor, Department of Computer Sciences and Applied Mathematics, Moscow State University of Civil Engineering (MSUCE), 26 Yaroslavskoe shosse, Moscow, 129337, Russian Federation; pavel.akimov2@gmail.com, +7 (499) 183-59-94;

Fraynt Mikhail Aleksandrovich — student, Moscow State University of Civil Engineering (MSUCE), 26 Yaroslavskoe shosse, Moscow, 129337, Russian Federation; mfraynt@gmail.com.

For citation: Akimov P.A., Fraynt M.A. Fundamental’nye funktsii dlya obyknovennykh differentsial’nykh uravneniy s postoyannymi koeffitsientami i ikh veyvlet-approksimatsiya s uchetom spetsifiki stroitel’nykh zadach [Fundamental Functions of Ordinary Differential Equations with Constant Coefficients and Their Wavelet Approximation Specific to Construction Problems]. Vestnik MGSU [Proceedings of Moscow State University of Civil Engineering]. 2012, no. 7, pp. 37—43.

Рассмотрим
произвольное уравнение порядка

(2.80)

где
.

Определение 2.8.Обобщенная функцияназываетсяобобщенным решениемуравнения (2.80), если выполнено тождество

для
.
Здесь-сопряженный дифференциальный оператор
для оператора.
■

В качестве правой
части уравнения (2.80) рассмотрим
-функцию Дирака:

. (2.81)

Любое обобщенное
решение
уравнения (2.81) называетсяфундаментальной
функцией оператора .

Очевидно, что
фундаментальная функция определяется
неоднозначно. Учитывая специфику
решаемой прикладной задачи, на
фундаментальную функцию накладывают
дополнительные условия нормировки,
которые выделяют единственную
фундаментальную функцию
,
которая называетсяфундаментальным
решением уравнения (2.81), [7, с. 348].

Фундаментальное
решение уравнения Колмогорова. В
теории вероятностей и стохастических
процессов важную роль играет уравнение
Колмогорова. Рассмотрим неоднородное
уравнение Колмогорова с-функцией
в правой части, то есть рассмотрим
уравнение вида (2.81):

,
(2.82)

которое определено
на пространстве
с координатами,Рассмотрим частный случай уравнения
[9, с. 226] когда-постоянные:

(2.83)

Не нарушая общности,
положим
.
Получим уравнение

,
(2.84)

для которого найдем
фундаментальное решение, накладывая
условие на бесконечности

при(2.85)

В уравнении (2.84)
перейдем к новым переменным
,с помощью преобразования

(2.86)

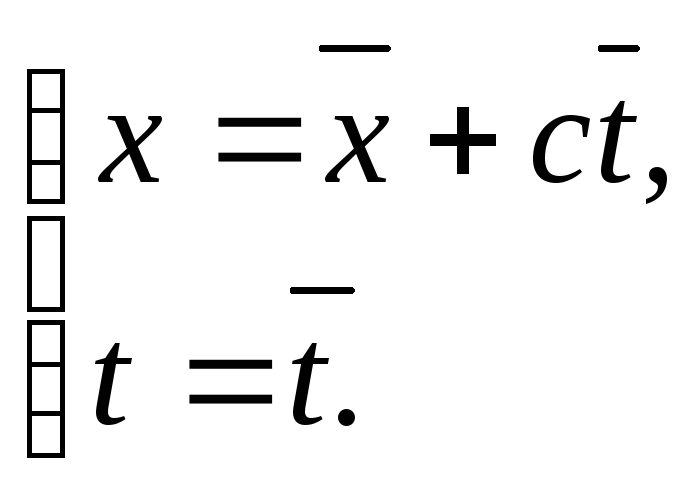
Тогда
.

На основании формулы
(2.76):
,
получим уравнение

.
(2.87)

Произведем еще
одну замену переменных
,,
где-постоянная, тогда

.

Используем формулу
(2.76) и представим правую часть уравнения
в виде

.

В результате,
заменив
,,
получим уравнение

.
(2.88)

Уравнения (2.87) и
(2.88) представляют собой одно и тоже
уравнение, решением которого при
соответствующем условии на бесконечности
(2.85) является фундаментальное решение.
В силу единственности фундаментального
решения отождествим решения уравнений
(2.87) и (2.88). В результате получим, что
функциональное соотношение
справедливо при любом

Выберем
,
тогда

.

Введем новую
переменную
,
получим представление

,
(2.89)

где
.

Подставив функцию
(2.89) в уравнение (2.87), получим обыкновенное
дифференциальное уравнение для
определения
:

.

Так как
-функция
притождественно равна нулю, то

при
.

Для наших целей
пригодным является решение этого
уравнения
,
где постоянная нормировки,
откуда

.

Возвратившись к
старым переменным
(2.86), получим фундаментальное решение
уравнения (2.84):

,,
(2.90)

которое при
доопределим нулем.

Производим сдвиг
координат
на величиныи получим фундаментальное решение
уравнения (2.83), которое совпадает с
функцией (1.90) при.
Сравнение с формулой (5.14) (см. главу 5)
показывает, что фундаментальное решение
уравнения Колмогорова совпадает с
переходной функцией плотности вероятностей
марковского процесса, то естьпри.

Фундаментальное
решение уравнения Лапласа. Рассмотрим
неоднородное уравнение Лапласа в
трехмерном пространствес-функцией в правой части:

.
(2.91)

Можно показать,
что обобщенным решением уравнения
(2.91) является фундаментальное решение
(1.86). В двухмерном случае
обобщенным решением уравнения

является фундаментальное
решение (1.84).

Соседние файлы в папке Учебник по УМФ

• #
• #
• #
• #
• #
• #
• #
• #

Фундаментальная система решений (конкретный пример)

Вы можете заказать подробное решение вашей задачи здесь!!!

Чтобы понять, что такое фундаментальная система решений вы можете посмотреть видео-урок для этого же примера кликнув здесь. Теперь перейдем собственно к описанию всей необходимой работы. Это поможет вам более детально разобраться в сути данного вопроса.

Как найти фундаментальную систему решений линейного уравнения?

Возьмём для примера такую систему линейных уравнений:

Найдём решение этой линейной системы уравнений методом Гаусса. Для начала нам надо выписать матрицу коэффициентов системы.

Преобразуем эту матрицу к треугольной. Первую строку переписываем без изменений. И все элементы, что стоят под $a_{11}$, надо сделать нулями. Что бы сделать ноль в место элемента $a_{21}$, надо от второй строки вычесть первую, и разность записать во второй строке. Что бы сделать ноль в место элемента $a_{31}$, надо от третьей строки вычесть первую и разность записать в третьей строке. Что бы сделать ноль в место элемента $a_{41}$, надо от четвёртой строки вычесть первую умноженную на 2 и разность записать в четвёртой строке. Что бы сделать ноль в место элемента $a_{31}$, надо от пятой строки вычесть первую умноженную на 2 и разность записать в пятой строке.

Первую и вторую строку переписываем без изменений. И все элементы, что стоят под $a_{22}$, надо сделать нулями. Что бы сделать ноль в место элемента $a_{32}$, надо от третьей строки вычесть вторую умноженную на 2 и разность записать в третьей строке. Что бы сделать ноль в место элемента $a_{42}$, надо от четвёртой строки вычесть вторую умноженную на 2 и разность записать в четвёртой строке. Что бы сделать ноль в место элемента $a_{52}$, надо от пятой строки вычесть вторую умноженную на 3 и разность записать в пятой строке.

Видим, что последние три строки – одинаковые, поэтому если от четвёртой и пятой вычесть третью, то они станут нулевыми.

По этой матрице записываем новую систему уравнений.

Видим, что линейно независимых уравнений у нас, только три, а неизвестных пять, поэтому фундаментальная система решений будет состоять из двух векторов. Значит, нам надо перенести две последние неизвестные вправо.

Теперь, начинаем выражать те неизвестные, что стоят в левой части через те, что стоят в правой части. Начинаем с последнего уравнения, сначала выразим $x_3$, потом полученный результат подставим во второе уравнение и выразим $x_2$, а потом в первое уравнение и тут выразим $x_1$. Таким образом мы все неизвестные, что стоят в левой части, выразили через неизвестные, что стоят в правой части.

После чего вы вместо $x_4$ и $x_5$, можем подставлять любые числа и находить $x_1$, $x_2$ и $x_3$. Каждая такая пятёрка чисел будет корнями нашей изначальной системы уравнений. Что бы найти векторы, что входят в ФСР нам надо вместо $x_4$ подставить 1, а вместо $x_5$ подставить 0, найти $x_1$, $x_2$ и $x_3$, а потом наоборот $x_4=0$ и $x_5=1$.

Какие именно векторы создают фундаментальную систему решений данной системы уравнений?

Для лучшего понимания хода роботы можете посмотреть видео-урок по данном задании.

Материалы по теме:

• Метод Гаусса (конкретный пример)
• Матрицы и определители
• Три метода решения определителя (детерминанта) матрицы!
• Сложение и вычитание матриц

Загрузка…