The likelihood function (often simply called the likelihood) is the joint probability of the observed data viewed as a function of the parameters of a statistical model.[1]
In maximum likelihood estimation, the arg max (over 

Definition[edit]
The likelihood function, parameterized by a (possibly multivariate) parameter 
where 

often written
In other words, when 






Discrete probability distribution[edit]
Let 


considered as a function of 













Given no event (no data), the likelihood is 1;[citation needed] any non-trivial event will have a lower likelihood.
Example[edit]
Figure 1. The likelihood function (
Figure 2. The likelihood function (
Consider a simple statistical model of a coin flip: a single parameter 


Imagine flipping a fair coin twice, and observing two heads in two tosses («HH»). Assuming that each successive coin flip is i.i.d., then the probability of observing HH is
Equivalently, the likelihood at 
This is not the same as saying that 


Now suppose that the coin is not a fair coin, but instead that 
Hence
More generally, for each value of 

Continuous probability distribution[edit]
Let 



considered as a function of 






Relationship between the likelihood and probability density functions[edit]
The use of the probability density in specifying the likelihood function above is justified as follows. Given an observation 
![{displaystyle [x_{j},x_{j}+h]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/beda1f8ebddb6aaaedaa2941d09321dd0a9094cf)

![{displaystyle {mathcal {L}}(theta mid xin [x_{j},x_{j}+h])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33e5808aa602eabab47f7bcd07be74842ca07ed8)
,
since 
where 
.
The first fundamental theorem of calculus provides that
Then
Therefore,
and so maximizing the probability density at 

In general[edit]
In measure-theoretic probability theory, the density function is defined as the Radon–Nikodym derivative of the probability distribution relative to a common dominating measure.[3] The likelihood function is this density interpreted as a function of the parameter, rather than the random variable.[4] Thus, we can construct a likelihood function for any distribution, whether discrete, continuous, a mixture, or otherwise. (Likelihoods are comparable, e.g. for parameter estimation, only if they are Radon–Nikodym derivatives with respect to the same dominating measure.)
The above discussion of the likelihood for discrete random variables uses the counting measure, under which the probability density at any outcome equals the probability of that outcome.
Likelihoods for mixed continuous–discrete distributions[edit]
The above can be extended in a simple way to allow consideration of distributions which contain both discrete and continuous components. Suppose that the distribution consists of a number of discrete probability masses 



where 


The fact that the likelihood function can be defined in a way that includes contributions that are not commensurate (the density and the probability mass) arises from the way in which the likelihood function is defined up to a constant of proportionality, where this «constant» can change with the observation 

Regularity conditions[edit]
In the context of parameter estimation, the likelihood function is usually assumed to obey certain conditions, known as regularity conditions. These conditions are assumed in various proofs involving likelihood functions, and need to be verified in each particular application. For maximum likelihood estimation, the existence of a global maximum of the likelihood function is of the utmost importance. By the extreme value theorem, it suffices that the likelihood function is continuous on a compact parameter space for the maximum likelihood estimator to exist.[5] While the continuity assumption is usually met, the compactness assumption about the parameter space is often not, as the bounds of the true parameter values are unknown. In that case, concavity of the likelihood function plays a key role.
More specifically, if the likelihood function is twice continuously differentiable on the k-dimensional parameter space 


is negative definite for every
at which the gradient
vanishes,
and if
i.e. the likelihood function approaches a constant on the boundary of the parameter space, 

In the proofs of consistency and asymptotic normality of the maximum likelihood estimator, additional assumptions are made about the probability densities that form the basis of a particular likelihood function. These conditions were first established by Chanda.[8] In particular, for almost all 

exist for all 


where 

is positive definite and 
The above conditions are sufficient, but not necessary. That is, a model that does not meet these regularity conditions may or may not have a maximum likelihood estimator of the properties mentioned above. Further, in case of non-independently or non-identically distributed observations additional properties may need to be assumed.
In Bayesian statistics, almost identical regularity conditions are imposed on the likelihood function in order to proof asymptotic normality of the posterior probability,[10][11] and therefore to justify a Laplace approximation of the posterior in large samples.[12]
Likelihood ratio and relative likelihood[edit]
Likelihood ratio[edit]
A likelihood ratio is the ratio of any two specified likelihoods, frequently written as:
The likelihood ratio is central to likelihoodist statistics: the law of likelihood states that degree to which data (considered as evidence) supports one parameter value versus another is measured by the likelihood ratio.
In frequentist inference, the likelihood ratio is the basis for a test statistic, the so-called likelihood-ratio test. By the Neyman–Pearson lemma, this is the most powerful test for comparing two simple hypotheses at a given significance level. Numerous other tests can be viewed as likelihood-ratio tests or approximations thereof.[13] The asymptotic distribution of the log-likelihood ratio, considered as a test statistic, is given by Wilks’ theorem.
The likelihood ratio is also of central importance in Bayesian inference, where it is known as the Bayes factor, and is used in Bayes’ rule. Stated in terms of odds, Bayes’ rule states that the posterior odds of two alternatives, 


The likelihood ratio is not directly used in AIC-based statistics. Instead, what is used is the relative likelihood of models (see below).
Relative likelihood function[edit]
Since the actual value of the likelihood function depends on the sample, it is often convenient to work with a standardized measure. Suppose that the maximum likelihood estimate for the parameter θ is 

Thus, the relative likelihood is the likelihood ratio (discussed above) with the fixed denominator 
Likelihood region[edit]
A likelihood region is the set of all values of θ whose relative likelihood is greater than or equal to a given threshold. In terms of percentages, a p% likelihood region for θ is defined to be[14][16][19]
If θ is a single real parameter, a p% likelihood region will usually comprise an interval of real values. If the region does comprise an interval, then it is called a likelihood interval.[14][16][20]
Likelihood intervals, and more generally likelihood regions, are used for interval estimation within likelihoodist statistics: they are similar to confidence intervals in frequentist statistics and credible intervals in Bayesian statistics. Likelihood intervals are interpreted directly in terms of relative likelihood, not in terms of coverage probability (frequentism) or posterior probability (Bayesianism).
Given a model, likelihood intervals can be compared to confidence intervals. If θ is a single real parameter, then under certain conditions, a 14.65% likelihood interval (about 1:7 likelihood) for θ will be the same as a 95% confidence interval (19/20 coverage probability).[14][19] In a slightly different formulation suited to the use of log-likelihoods (see Wilks’ theorem), the test statistic is twice the difference in log-likelihoods and the probability distribution of the test statistic is approximately a chi-squared distribution with degrees-of-freedom (df) equal to the difference in df’s between the two models (therefore, the e−2 likelihood interval is the same as the 0.954 confidence interval; assuming difference in df’s to be 1).[19][20]
Likelihoods that eliminate nuisance parameters[edit]
In many cases, the likelihood is a function of more than one parameter but interest focuses on the estimation of only one, or at most a few of them, with the others being considered as nuisance parameters. Several alternative approaches have been developed to eliminate such nuisance parameters, so that a likelihood can be written as a function of only the parameter (or parameters) of interest: the main approaches are profile, conditional, and marginal likelihoods.[21][22] These approaches are also useful when a high-dimensional likelihood surface needs to be reduced to one or two parameters of interest in order to allow a graph.
Profile likelihood[edit]
It is possible to reduce the dimensions by concentrating the likelihood function for a subset of parameters by expressing the nuisance parameters as functions of the parameters of interest and replacing them in the likelihood function.[23][24] In general, for a likelihood function depending on the parameter vector 


For instance, in a linear regression with normally distributed errors, 
![{displaystyle beta =left[beta _{1}:beta _{2}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acab37fb4a56ab74c722e4a6b7dd77e96623e107)
![{displaystyle mathbf {X} =left[mathbf {X} _{1}:mathbf {X} _{2}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed32253947696f7eaa8c5d7eae0c70fd1730beec)



where 

Since graphically the procedure of concentration is equivalent to slicing the likelihood surface along the ridge of values of the nuisance parameter 

Conditional likelihood[edit]
Sometimes it is possible to find a sufficient statistic for the nuisance parameters, and conditioning on this statistic results in a likelihood which does not depend on the nuisance parameters.[30]
One example occurs in 2×2 tables, where conditioning on all four marginal totals leads to a conditional likelihood based on the non-central hypergeometric distribution. This form of conditioning is also the basis for Fisher’s exact test.
Marginal likelihood[edit]
Sometimes we can remove the nuisance parameters by considering a likelihood based on only part of the information in the data, for example by using the set of ranks rather than the numerical values. Another example occurs in linear mixed models, where considering a likelihood for the residuals only after fitting the fixed effects leads to residual maximum likelihood estimation of the variance components.
Partial likelihood[edit]
A partial likelihood is an adaption of the full likelihood such that only a part of the parameters (the parameters of interest) occur in it.[31] It is a key component of the proportional hazards model: using a restriction on the hazard function, the likelihood does not contain the shape of the hazard over time.
Products of likelihoods[edit]
The likelihood, given two or more independent events, is the product of the likelihoods of each of the individual events:
This follows from the definition of independence in probability: the probabilities of two independent events happening, given a model, is the product of the probabilities.
This is particularly important when the events are from independent and identically distributed random variables, such as independent observations or sampling with replacement. In such a situation, the likelihood function factors into a product of individual likelihood functions.
The empty product has value 1, which corresponds to the likelihood, given no event, being 1: before any data, the likelihood is always 1. This is similar to a uniform prior in Bayesian statistics, but in likelihoodist statistics this is not an improper prior because likelihoods are not integrated.
Log-likelihood[edit]
Log-likelihood function is a logarithmic transformation of the likelihood function, often denoted by a lowercase l or 

Given the independence of each event, the overall log-likelihood of intersection equals the sum of the log-likelihoods of the individual events. This is analogous to the fact that the overall log-probability is the sum of the log-probability of the individual events. In addition to the mathematical convenience from this, the adding process of log-likelihood has an intuitive interpretation, as often expressed as «support» from the data. When the parameters are estimated using the log-likelihood for the maximum likelihood estimation, each data point is used by being added to the total log-likelihood. As the data can be viewed as an evidence that support the estimated parameters, this process can be interpreted as «support from independent evidence adds», and the log-likelihood is the «weight of evidence». Interpreting negative log-probability as information content or surprisal, the support (log-likelihood) of a model, given an event, is the negative of the surprisal of the event, given the model: a model is supported by an event to the extent that the event is unsurprising, given the model.
A logarithm of a likelihood ratio is equal to the difference of the log-likelihoods:
Just as the likelihood, given no event, being 1, the log-likelihood, given no event, is 0, which corresponds to the value of the empty sum: without any data, there is no support for any models.
Graph[edit]
The graph of the log-likelihood is called the support curve (in the univariate case).[34].
In the multivariate case, the concept generalizes into a support surface over the parameter space.
It has a relation to, but is distinct from, the support of a distribution.
The term was coined by A. W. F. Edwards[34] in the context of statistical hypothesis testing, i.e. whether or not the data «support» one hypothesis (or parameter value) being tested more than any other.
The log-likelihood function being plotted is used in the computation of the score (the gradient of the log-likelihood) and Fisher information (the curvature of the log-likelihood). This, the graph has a direct interpretation in the context of maximum likelihood estimation and likelihood-ratio tests.
Likelihood equations[edit]
If the log-likelihood function is smooth, its gradient with respect to the parameter, known as the score and written 
The equations defined by the stationary point of the score function serve as estimating equations for the maximum likelihood estimator.
In that sense, the maximum likelihood estimator is implicitly defined by the value at 










The second derivative evaluated at 
Exponential families[edit]
The log-likelihood is also particularly useful for exponential families of distributions, which include many of the common parametric probability distributions. The probability distribution function (and thus likelihood function) for exponential families contain products of factors involving exponentiation. The logarithm of such a function is a sum of products, again easier to differentiate than the original function.
An exponential family is one whose probability density function is of the form (for some functions, writing 
Each of these terms has an interpretation,[a] but simply switching from probability to likelihood and taking logarithms yields the sum:
The 

In words, the log-likelihood of an exponential family is inner product of the natural parameter 


Example: the gamma distribution[edit]
The gamma distribution is an exponential family with two parameters, 

Finding the maximum likelihood estimate of 

To maximize the log-likelihood, we first take the partial derivative with respect to 
If there are a number of independent observations 
To complete the maximization procedure for the joint log-likelihood, the equation is set to zero and solved for 
Here 

Background and interpretation[edit]
[edit]
The term «likelihood» has been in use in English since at least late Middle English.[40] Its formal use to refer to a specific function in mathematical statistics was proposed by Ronald Fisher,[41] in two research papers published in 1921[42] and 1922.[43] The 1921 paper introduced what is today called a «likelihood interval»; the 1922 paper introduced the term «method of maximum likelihood». Quoting Fisher:
[I]n 1922, I proposed the term ‘likelihood,’ in view of the fact that, with respect to [the parameter], it is not a probability, and does not obey the laws of probability, while at the same time it bears to the problem of rational choice among the possible values of [the parameter] a relation similar to that which probability bears to the problem of predicting events in games of chance. . . . Whereas, however, in relation to psychological judgment, likelihood has some resemblance to probability, the two concepts are wholly distinct. . . .»[44]
The concept of likelihood should not be confused with probability as mentioned by Sir Ronald Fisher
I stress this because in spite of the emphasis that I have always laid upon the difference between probability and likelihood there is still a tendency to treat likelihood as though it were a sort of probability. The first result is thus that there are two different measures of rational belief appropriate to different cases. Knowing the population we can express our incomplete knowledge of, or expectation of, the sample in terms of probability; knowing the sample we can express our incomplete knowledge of the population in terms of likelihood.[45]
Fisher’s invention of statistical likelihood was in reaction against an earlier form of reasoning called inverse probability.[46] His use of the term «likelihood» fixed the meaning of the term within mathematical statistics.
A. W. F. Edwards (1972) established the axiomatic basis for use of the log-likelihood ratio as a measure of relative support for one hypothesis against another. The support function is then the natural logarithm of the likelihood function. Both terms are used in phylogenetics, but were not adopted in a general treatment of the topic of statistical evidence.[47]
Interpretations under different foundations[edit]
Among statisticians, there is no consensus about what the foundation of statistics should be. There are four main paradigms that have been proposed for the foundation: frequentism, Bayesianism, likelihoodism, and AIC-based.[48] For each of the proposed foundations, the interpretation of likelihood is different. The four interpretations are described in the subsections below.
Frequentist interpretation[edit]
|
This section is empty. You can help by adding to it. (March 2019) |
Bayesian interpretation[edit]
In Bayesian inference, although one can speak about the likelihood of any proposition or random variable given another random variable: for example the likelihood of a parameter value or of a statistical model (see marginal likelihood), given specified data or other evidence,[49][50][51][52] the likelihood function remains the same entity, with the additional interpretations of (i) a conditional density of the data given the parameter (since the parameter is then a random variable) and (ii) a measure or amount of information brought by the data about the parameter value or even the model.[49][50][51][52][53] Due to the introduction of a probability structure on the parameter space or on the collection of models, it is possible that a parameter value or a statistical model have a large likelihood value for given data, and yet have a low probability, or vice versa.[51][53] This is often the case in medical contexts.[54] Following Bayes’ Rule, the likelihood when seen as a conditional density can be multiplied by the prior probability density of the parameter and then normalized, to give a posterior probability density.[49][50][51][52][53] More generally, the likelihood of an unknown quantity 



Likelihoodist interpretation[edit]
In frequentist statistics, the likelihood function is itself a statistic that summarizes a single sample from a population, whose calculated value depends on a choice of several parameters θ1 … θp, where p is the count of parameters in some already-selected statistical model. The value of the likelihood serves as a figure of merit for the choice used for the parameters, and the parameter set with maximum likelihood is the best choice, given the data available.
The specific calculation of the likelihood is the probability that the observed sample would be assigned, assuming that the model chosen and the values of the several parameters θ give an accurate approximation of the frequency distribution of the population that the observed sample was drawn from. Heuristically, it makes sense that a good choice of parameters is those which render the sample actually observed the maximum possible post-hoc probability of having happened. Wilks’ theorem quantifies the heuristic rule by showing that the difference in the logarithm of the likelihood generated by the estimate’s parameter values and the logarithm of the likelihood generated by population’s «true» (but unknown) parameter values is asymptotically χ2 distributed.
Each independent sample’s maximum likelihood estimate is a separate estimate of the «true» parameter set describing the population sampled. Successive estimates from many independent samples will cluster together with the population’s «true» set of parameter values hidden somewhere in their midst. The difference in the logarithms of the maximum likelihood and adjacent parameter sets’ likelihoods may be used to draw a confidence region on a plot whose co-ordinates are the parameters θ1 … θp. The region surrounds the maximum-likelihood estimate, and all points (parameter sets) within that region differ at most in log-likelihood by some fixed value. The χ2 distribution given by Wilks’ theorem converts the region’s log-likelihood differences into the «confidence» that the population’s «true» parameter set lies inside. The art of choosing the fixed log-likelihood difference is to make the confidence acceptably high while keeping the region acceptably small (narrow range of estimates).
As more data are observed, instead of being used to make independent estimates, they can be combined with the previous samples to make a single combined sample, and that large sample may be used for a new maximum likelihood estimate. As the size of the combined sample increases, the size of the likelihood region with the same confidence shrinks. Eventually, either the size of the confidence region is very nearly a single point, or the entire population has been sampled; in both cases, the estimated parameter set is essentially the same as the population parameter set.
AIC-based interpretation[edit]
|
This section needs expansion. You can help by adding to it. (March 2019) |
Under the AIC paradigm, likelihood is interpreted within the context of information theory.[55][56][57]
See also[edit]
- Bayes factor
- Conditional entropy
- Conditional probability
- Empirical likelihood
- Likelihood principle
- Likelihood-ratio test
- Likelihoodist statistics
- Maximum likelihood
- Principle of maximum entropy
- Pseudolikelihood
- Score (statistics)
Notes[edit]
- ^ See Exponential family § Interpretation
References[edit]
- ^ Casella, George; Berger, Roger L. (2002). Statistical Inference (2nd ed.). Duxbury. p. 290. ISBN 0-534-24312-6.
- ^ Zellner, Arnold (1971). An Introduction to Bayesian Inference in Econometrics. New York: Wiley. pp. 13–14. ISBN 0-471-98165-6.
- ^ Billingsley, Patrick (1995). Probability and Measure (Third ed.). John Wiley & Sons. pp. 422–423.
- ^ Shao, Jun (2003). Mathematical Statistics (2nd ed.). Springer. §4.4.1.
- ^ Gouriéroux, Christian; Monfort, Alain (1995). Statistics and Econometric Models. New York: Cambridge University Press. p. 161. ISBN 0-521-40551-3.
- ^ Mäkeläinen, Timo; Schmidt, Klaus; Styan, George P.H. (1981). «On the existence and uniqueness of the maximum likelihood estimate of a vector-valued parameter in fixed-size samples». Annals of Statistics. 9 (4): 758–767. doi:10.1214/aos/1176345516. JSTOR 2240844.
- ^ Mascarenhas, W.F. (2011). «A mountain pass lemma and its implications regarding the uniqueness of constrained minimizers». Optimization. 60 (8–9): 1121–1159. doi:10.1080/02331934.2010.527973. S2CID 15896597.
- ^ Chanda, K.C. (1954). «A note on the consistency and maxima of the roots of likelihood equations». Biometrika. 41 (1–2): 56–61. doi:10.2307/2333005. JSTOR 2333005.
- ^ Greenberg, Edward; Webster, Charles E. Jr. (1983). Advanced Econometrics: A Bridge to the Literature. New York, NY: John Wiley & Sons. pp. 24–25. ISBN 0-471-09077-8.
- ^ Heyde, C. C.; Johnstone, I. M. (1979). «On Asymptotic Posterior Normality for Stochastic Processes». Journal of the Royal Statistical Society. Series B (Methodological). 41 (2): 184–189. doi:10.1111/j.2517-6161.1979.tb01071.x.
- ^ Chen, Chan-Fu (1985). «On Asymptotic Normality of Limiting Density Functions with Bayesian Implications». Journal of the Royal Statistical Society. Series B (Methodological). 47 (3): 540–546. doi:10.1111/j.2517-6161.1985.tb01384.x.
- ^ Kass, Robert E.; Tierney, Luke; Kadane, Joseph B. (1990). «The Validity of Posterior Expansions Based on Laplace’s Method». In Geisser, S.; Hodges, J. S.; Press, S. J.; Zellner, A. (eds.). Bayesian and Likelihood Methods in Statistics and Econometrics. Elsevier. pp. 473–488. ISBN 0-444-88376-2.
- ^ Buse, A. (1982). «The Likelihood Ratio, Wald, and Lagrange Multiplier Tests: An Expository Note». The American Statistician. 36 (3a): 153–157. doi:10.1080/00031305.1982.10482817.
- ^ a b c d Kalbfleisch, J. G. (1985), Probability and Statistical Inference, Springer (§9.3).
- ^ Azzalini, A. (1996), Statistical Inference—Based on the likelihood, Chapman & Hall, ISBN 9780412606502 (§1.4.2).
- ^ a b c Sprott, D. A. (2000), Statistical Inference in Science, Springer (chap. 2).
- ^ Davison, A. C. (2008), Statistical Models, Cambridge University Press (§4.1.2).
- ^ Held, L.; Sabanés Bové, D. S. (2014), Applied Statistical Inference—Likelihood and Bayes, Springer (§2.1).
- ^ a b c Rossi, R. J. (2018), Mathematical Statistics, Wiley, p. 267.
- ^ a b Hudson, D. J. (1971), «Interval estimation from the likelihood function», Journal of the Royal Statistical Society, Series B, 33 (2): 256–262.
- ^ Pawitan, Yudi (2001). In All Likelihood: Statistical Modelling and Inference Using Likelihood. Oxford University Press.
- ^ Wen Hsiang Wei. «Generalized Linear Model — course notes». Taichung, Taiwan: Tunghai University. pp. Chapter 5. Retrieved 2017-10-01.
- ^ Amemiya, Takeshi (1985). «Concentrated Likelihood Function». Advanced Econometrics. Cambridge: Harvard University Press. pp. 125–127. ISBN 978-0-674-00560-0.
- ^ Davidson, Russell; MacKinnon, James G. (1993). «Concentrating the Loglikelihood Function». Estimation and Inference in Econometrics. New York: Oxford University Press. pp. 267–269. ISBN 978-0-19-506011-9.
- ^ Gourieroux, Christian; Monfort, Alain (1995). «Concentrated Likelihood Function». Statistics and Econometric Models. New York: Cambridge University Press. pp. 170–175. ISBN 978-0-521-40551-5.
- ^ Pickles, Andrew (1985). An Introduction to Likelihood Analysis. Norwich: W. H. Hutchins & Sons. pp. 21–24. ISBN 0-86094-190-6.
- ^ Bolker, Benjamin M. (2008). Ecological Models and Data in R. Princeton University Press. pp. 187–189. ISBN 978-0-691-12522-0.
- ^ Aitkin, Murray (1982). «Direct Likelihood Inference». GLIM 82: Proceedings of the International Conference on Generalised Linear Models. Springer. pp. 76–86. ISBN 0-387-90777-7.
- ^ Venzon, D. J.; Moolgavkar, S. H. (1988). «A Method for Computing Profile-Likelihood-Based Confidence Intervals». Journal of the Royal Statistical Society. Series C (Applied Statistics). 37 (1): 87–94. doi:10.2307/2347496. JSTOR 2347496.
- ^ Kalbfleisch, J. D.; Sprott, D. A. (1973). «Marginal and Conditional Likelihoods». Sankhyā: The Indian Journal of Statistics. Series A. 35 (3): 311–328. JSTOR 25049882.
- ^
Cox, D. R. (1975). «Partial likelihood». Biometrika. 62 (2): 269–276. doi:10.1093/biomet/62.2.269. MR 0400509. - ^ Kass, Robert E.; Vos, Paul W. (1997). Geometrical Foundations of Asymptotic Inference. New York: John Wiley & Sons. p. 14. ISBN 0-471-82668-5.
- ^ Papadopoulos, Alecos (September 25, 2013). «Why we always put log() before the joint pdf when we use MLE (Maximum likelihood Estimation)?». Stack Exchange.
- ^ a b Edwards, A. W. F. (1992) [1972]. Likelihood. Johns Hopkins University Press. ISBN 0-8018-4443-6.
- ^ Foutz, Robert V. (1977). «On the Unique Consistent Solution to the Likelihood Equations». Journal of the American Statistical Association. 72 (357): 147–148. doi:10.1080/01621459.1977.10479926.
- ^ Tarone, Robert E.; Gruenhage, Gary (1975). «A Note on the Uniqueness of Roots of the Likelihood Equations for Vector-Valued Parameters». Journal of the American Statistical Association. 70 (352): 903–904. doi:10.1080/01621459.1975.10480321.
- ^ Rai, Kamta; Van Ryzin, John (1982). «A Note on a Multivariate Version of Rolle’s Theorem and Uniqueness of Maximum Likelihood Roots». Communications in Statistics. Theory and Methods. 11 (13): 1505–1510. doi:10.1080/03610928208828325.
- ^ Rao, B. Raja (1960). «A formula for the curvature of the likelihood surface of a sample drawn from a distribution admitting sufficient statistics». Biometrika. 47 (1–2): 203–207. doi:10.1093/biomet/47.1-2.203.
- ^ Ward, Michael D.; Ahlquist, John S. (2018). Maximum Likelihood for Social Science : Strategies for Analysis. Cambridge University Press. pp. 25–27.
- ^ «likelihood», Shorter Oxford English Dictionary (2007).
- ^ Hald, A. (1999). «On the history of maximum likelihood in relation to inverse probability and least squares». Statistical Science. 14 (2): 214–222. doi:10.1214/ss/1009212248. JSTOR 2676741.
- ^ Fisher, R.A. (1921). «On the «probable error» of a coefficient of correlation deduced from a small sample». Metron. 1: 3–32.
- ^ Fisher, R.A. (1922). «On the mathematical foundations of theoretical statistics». Philosophical Transactions of the Royal Society A. 222 (594–604): 309–368. Bibcode:1922RSPTA.222..309F. doi:10.1098/rsta.1922.0009. JFM 48.1280.02. JSTOR 91208.
- ^ Klemens, Ben (2008). Modeling with Data: Tools and Techniques for Scientific Computing. Princeton University Press. p. 329.
- ^ Fisher, Ronald (1930). «Inverse Probability». Mathematical Proceedings of the Cambridge Philosophical Society. 26 (4): 528–535. Bibcode:1930PCPS…26..528F. doi:10.1017/S0305004100016297.
- ^ Fienberg, Stephen E (1997). «Introduction to R.A. Fisher on inverse probability and likelihood». Statistical Science. 12 (3): 161. doi:10.1214/ss/1030037905.
- ^ Royall, R. (1997). Statistical Evidence. Chapman & Hall.
- ^ Bandyopadhyay, P. S.; Forster, M. R., eds. (2011). Philosophy of Statistics. North-Holland Publishing.
- ^ a b c d I. J. Good: Probability and the Weighing of Evidence (Griffin 1950), §6.1
- ^ a b c d H. Jeffreys: Theory of Probability (3rd ed., Oxford University Press 1983), §1.22
- ^ a b c d e E. T. Jaynes: Probability Theory: The Logic of Science (Cambridge University Press 2003), §4.1
- ^ a b c d D. V. Lindley: Introduction to Probability and Statistics from a Bayesian Viewpoint. Part 1: Probability (Cambridge University Press 1980), §1.6
- ^ a b c d A. Gelman, J. B. Carlin, H. S. Stern, D. B. Dunson, A. Vehtari, D. B. Rubin: Bayesian Data Analysis (3rd ed., Chapman & Hall/CRC 2014), §1.3
- ^ Sox, H. C.; Higgins, M. C.; Owens, D. K. (2013), Medical Decision Making (2nd ed.), Wiley, chapters 3–4, doi:10.1002/9781118341544, ISBN 9781118341544
- ^ Akaike, H. (1985). «Prediction and entropy». In Atkinson, A. C.; Fienberg, S. E. (eds.). A Celebration of Statistics. Springer. pp. 1–24.
- ^ Sakamoto, Y.; Ishiguro, M.; Kitagawa, G. (1986). Akaike Information Criterion Statistics. D. Reidel. Part I.
- ^ Burnham, K. P.; Anderson, D. R. (2002). Model Selection and Multimodel Inference: A practical information-theoretic approach (2nd ed.). Springer-Verlag. chap. 7.
Further reading[edit]
- Azzalini, Adelchi (1996). «Likelihood». Statistical Inference Based on the Likelihood. Chapman and Hall. pp. 17–50. ISBN 0-412-60650-X.
- Boos, Dennis D.; Stefanski, L. A. (2013). «Likelihood Construction and Estimation». Essential Statistical Inference : Theory and Methods. New York: Springer. pp. 27–124. doi:10.1007/978-1-4614-4818-1_2. ISBN 978-1-4614-4817-4.
- Edwards, A. W. F. (1992) [1972]. Likelihood (Expanded ed.). Johns Hopkins University Press. ISBN 0-8018-4443-6.
- King, Gary (1989). «The Likelihood Model of Inference». Unifying Political Methodology : the Likehood Theory of Statistical Inference. Cambridge University Press. pp. 59–94. ISBN 0-521-36697-6.
- Lindsey, J. K. (1996). «Likelihood». Parametric Statistical Inference. Oxford University Press. pp. 69–139. ISBN 0-19-852359-9.
- Rohde, Charles A. (2014). Introductory Statistical Inference with the Likelihood Function. Berlin: Springer. ISBN 978-3-319-10460-7.
- Royall, Richard (1997). Statistical Evidence : A Likelihood Paradigm. London: Chapman & Hall. ISBN 0-412-04411-0.
- Ward, Michael D.; Ahlquist, John S. (2018). «The Likelihood Function: A Deeper Dive». Maximum Likelihood for Social Science : Strategies for Analysis. Cambridge University Press. pp. 21–28. ISBN 978-1-316-63682-4.
External links[edit]
Look up likelihood in Wiktionary, the free dictionary.
- Likelihood function at Planetmath
- «Log-likelihood». Statlect.
Конспект по «Машинному обучению». Математическая статистика. Метод максимального правдоподобия
Время на прочтение
3 мин
Количество просмотров 11K
Вспомним некоторые определения математической статистики
Пусть задано вероятностное пространство
.
Определение 1:
Случайной величиной
, принимающей значения в множестве
c
-алгеброй
подмножеств
называется любая
-измеримая функция
, то есть
выполняется условие
.
Определение 2:
Выборочное пространство — это пространство всех возможных значений наблюдения или выборки вместе с
-алгеброй измеримых подмножеств этого пространства.
Обозначение:
.
Определённые на вероятностном пространстве
случайные величины
порождают на пространстве
вероятностные меры
На выборочном пространстве определяются не одна вероятностная мера, а конечное или бесконечное семейство вероятностных мер.
В задачах математической статистики известно семейство вероятностных мер
, определённых на выборочном пространстве, и требуется по выборке определить, какой из вероятностных мер этого семейства соответствует выборка.
Определение 3:
Статистическая модель — совокупность, состоящая из выборочного пространства и семейства определённых на нём вероятностных мер.
Обозначение:
, где
.
Пусть
и
— выборочное пространство.
Выборку
можно рассматривать, как совокупность
действительных чисел. Припишем каждому элементу выборки вероятность, равную
.
Пусть
Определение 4:
Эмпирическим распределением, построенным по выборке X, называется вероятностная мера
:
То есть
— отношение числа элементов выборки, которые принадлежат
, к общему числу элементов выборки:
.
Определение 5:
Выборочным моментом порядка
называется
— выборочное среднее.
Определение 6:
Выборочный центральный момент порядка
определяется равенством
— выборочная дисперсия.
В машинном обучении многие задачи заключаются в том, чтобы по имеющимся данным научиться подбирать параметр
, который наилучшим образом описывает эти данные. В математической статистике для решения подобной задачи часто используют метод максимального правдоподобия.
В реальной жизни часто распределение ошибок имеет нормальное распределение. Для некоторого обоснования приведём формулировку центральной предельной теоремы.
Теорема 1 (ЦПТ):
Если случайные величины
— независимы, одинаково распределены, математическое ожидание
, дисперсия
, то
Ниже сформулируем метод максимального правдоподобия и рассмотрим его работу на примере семейства нормальных распределений.
Метод максимального правдоподобия
Пусть для статистической модели
выполнены два условия:
Определение 7:
Оценкой максимального правдоподобия (о.м.п)
параметра
называется построенное по эмпирической мере
, соответствующей выборке
, значение
, при котором достигается
Определение 8:
Функция
, как функция от
, называется функцией правдоподобия, а функция
— логарифмическая функция правдоподобия.
Эти функции достигают максимума при одних и тех же значениях
, так как
— монотонная возрастающая функция.
Пример:
— семейство нормальных распределений с плотностями
. По выборке
Получили оценки для математического ожидания и дисперсии.
Если внимательно посмотреть на формулу
можно сделать вывод, что функция
принимает своё максимальное значение, когда
минимальна. В задачах машинного обучения часто используют метод наименьших квадратов, в котором минимизируют сумму квадратов отклонений предсказанных значений от истинных.
Список используемой литературы:
- Конспект лекций по математической статистике, автор неизвестен;
- «Глубокое обучение. Погружение в мир нейронных сетей», С. Никуленко, А. Кадурин, Е. Архангельская, ПИТЕР, 2018.
Аннотация: Цель работы: практически освоить метод максимального правдоподобия для точечной оценки неизвестных параметров заданного вероятностного распределения случайной величины. Среда программирования — MATLAB.
Теоретическая часть
Метод максимального или наибольшего правдоподобия предложен Р. Фишером [6, 13]. С помощью этого метода производится точечная оценка неизвестных параметров априорно известного закона распределения случайной величины.
Рассмотрим сначала суть метода при оценке параметров дискретного распределения случайной величины [6].
Обозначим вероятность того, что в результате испытания величина 
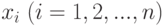

Определение. Функцией правдоподобия случайной дискретной величины 

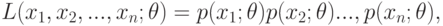 |
( 7.1) |
где 

В качестве точечной оценки параметра 
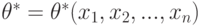

Для упрощения расчетов в рассмотрение вводится логарифм функции правдоподобия 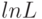

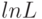

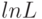
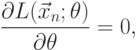 |
( 7.2) |
или
 |
( 7.3) |
где 
Уравнение правдоподобия (7.3) с логарифмической функцией, как правило, более простое относительно функции правдоподобия (7.2).
Если распределение случайной величины 

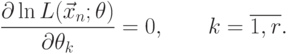 |
( 7.4) |
Именно уравнения (7.3) и (7.4) принято называть уравнениями правдоподобия [13]. Во многих случаях решение системы (7.4), являющейся, как правило, нелинейной, приходится искать численными методами.
Рассмотрим применение метода максимального правдоподобия для оценки параметров непрерывного распределения случайных величин генеральной совокупности 
Пусть 




Определение. Функцией правдоподобия непрерывной случайной величины 
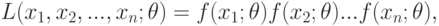 |
( 7.5) |
где 
Оценку максимального правдоподобия неизвестного параметра 
Замечание. Если плотность распределения непрерывной случайной величины 

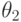

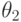
 |
( 7.6) |
Как для дискретных распределений, так и для непрерывных точку максимума логарифмической функции распределения 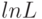

- найти производную
;
- приравнять производную нулю и найти критическую точку — корень полученного уравнения (его называют уравнением правдоподобия);
- найти вторую производную
; если вторая производная при
отрицательна, то
– точка максимума [6].
Найденную точку максимума 

Метод максимального правдоподобия имеет ряд достоинств: его оценки, вообще говоря, состоятельны (но они могут быть смещенными), распределены асимптотически нормально (при больших значениях 



Практическая часть
1. Оценка параметра экспоненциального распределения
Рассматривается пример поиска методом максимального правдоподобия оценки параметра 
 |
( 7.7) |
К характеристикам экспоненциального распределения относятся математическое ожидание ![M[X]](https://intuit.ru/sites/default/files/tex_cache/3c68892dcbe5fa2f2bec99c61aebef95.png)
![D[X]](https://intuit.ru/sites/default/files/tex_cache/170537c0284a060429415faa254a8407.png)
![M[X]=frac{1}{lambda},](https://intuit.ru/sites/default/files/tex_cache/fcafad1f5dd710e1f436d7162c051f12.png) |
( 7.8) |
![D[X]=frac{1}{lambda^2}.](https://intuit.ru/sites/default/files/tex_cache/75ae0b68f47752031afcf0251fa5bf00.png) |
( 7.9) |
Замечание. Во встроенных функциях MATLAB параметром экспоненциального распределения является математическое ожидание случайной величины.
Возможная программная реализация точечной оценки параметра экспоненциального распределения:
clear,clc,close all
%%% Проверка на закрытие диалоговых окон
try
global h11
close(h11);
end
try
global n11
close(n11);
end
try
global v11
close(v11)
end
%% ВВОД ТЕОРЕТИЧЕСКОГО ПАРАМЕТРА РАСПРЕДЕЛЕНИЯ
options.Resize = 'on';
options.WindowStyle = 'modal'; %%'normal';
options.Interpreter = 'tex';
P1 = inputdlg({'bfВвод параметра:......................................................'},...
sprintf('Теоретическая величина параметра'),1,{'1.23'},options);
%% ПРЕОБРАЗОВАНИЕ К СТРОКОВОЙ ПЕРЕМЕННОЙ
P2 = char(P1);
%% ПРЕОБРАЗОВАНИЕ К ЧИСЛУ С ДВОЙНОЙ ТОЧНОСТЬЮ
P0 = str2num(P2);
%% КОНТРОЛЬ ВВОДА ПАРАМЕТРА
if isempty(P0)
h11 = errordlg('Параметр должен быть действительным положительным числом!','Ошибка ввода');
return
end
%% КОНТРОЛЬ ВВОДА ПАРАМЕТРА
global h11
if P0 <= 0 | ~isreal(P0) | ~isfinite(P0)
h11 = errordlg('Параметр должен быть конечным действительным положительным числом!','Ошибка ввода');
return
end
% ВВОД ЧИСЛА ПРОГОНОВ ПРОГРАММЫ
n1 = inputdlg({'bfВвод числа прогонов программы..........................'},...
'Число прогонов программы',1,{'10'}, options);
% ПРЕОБРАЗОВАНИЕ К ЧИСЛОВОЙ ПЕРЕМЕННОЙ
n = str2num(char(n1));
%% Контроль ввода цифр
if isempty(n)
global n11
n11 = errordlg('Число прогонов программы должно быть целым положительным числом!', 'Ошибка ввода');
return
end
if ~isreal(n) | ~isfinite(n)
global n11
n11 = errordlg('Число прогонов программы должно быть целым положительным числом!', 'Ошибка ввода');
return
end
%% Контроль целого положительного числа циклов
if n <= 0 | n ~= round(n)
global n11
n11 = errordlg('Число прогонов программы должно быть целым положительным числом!', 'Ошибка ввода');
return
end
% ВВОД ЧИСЛА ИЗМЕРЕНИЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
v1 = inputdlg({'bfВвод числа измерений случайной величины...................................'},...
'Число измерений случайной величины',1,{'1234'}, options);
% ПРЕОБРАЗОВАНИЕ К ЧИСЛОВОЙ ПЕРЕМЕННОЙ
v = str2num(char(v1));
if isempty(v)
global v11
v11 = errordlg('Число измерений должно быть положительным целым числом!','Ошибка ввода');
return
end
if ~isreal(v) | ~isfinite(v)
global v11
v11 = errordlg('Число измерений должно быть положительным целым числом!','Ошибка ввода');
return
end
% КОНТРОЛЬ ЦЕЛОГО ЧИСЛА ИЗМЕРЕНИЙ
% СЛУЧАЙНОЙ ВЕЛИЧИНЫ
if v <= 0 | v ~= round(v)
global v11
v11 = errordlg('Число измерений должно быть положительным целым числом!','Ошибка ввода');
return
end
syms m
k = 0;
%% ЦИКЛ ЗАДАННОГО ЧИСЛА ПРОГОНОВ ПРОГРАММЫ
for I = 1:n
k=k+1;
%% ФОРМИРОВАНИЕ ЧИСЛА ИЗМЕРЕНИЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
t = exprnd(1/P0,v,1);
%% ФОРМИРОВАНИЕ ФУНКЦИИ МАКСИМАЛЬНОГО
%% ПРАВДОПОДОБИЯ
L = m^(length(t))*exp(-m*sum(t));
%% ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ МАКСИМАЛЬНОГО
%% ПРАВДОПОДОБИЯ
Lg = log(L);
%% ДИФФЕРЕНЦИРОВАНИЕ
dLg = diff(Lg,m);
%% ПРЕОБРАЗОВАНИЕ СИМВОЛЬНОЙ ПЕРЕМЕННОЙ К СТРОКОВОЙ
dLg = char(dLg);
%% РЕШЕНИЕ УРАВНЕНИЯ ОТНОСИТЕЛЬНО ОЦЕНИВАЕМОГО
%% ПАРАМЕТРА
as1(k) = double(solve(dLg));
%% УСРЕДНЕНИЕ ОЦЕНИВАЕМОГО ПАРАМЕТРА
as(k) = mean(as1);
end
%% ОКОНЧАНИЕ ЦИКЛА ЗАДАННОГО ЧИСЛА ПРОГОНОВ ПРОГРАММЫ
mcp = mean(as);
%% ВЫВОД РЕЗУЛЬТАТОВ В КОМАНДНОЕ ОКНО
fprintf('nt%s%gn t%s%gn','Теоретический параметр: ',P0,...
'Оценка параметра: ', mcp)
fprintf('tОтносительная погрешность: %g%sn',abs(P0-mcp)/P0*100,'%')
%% ГРАФИЧЕСКИЕ ПОСТРОЕНИЯ
figure(1)
%% set(gcf,'position',[a(3)/90,a(3)/20,a(3)/2.1,a(4)/2])
plot(1:n,as1,'r:','linew',2),grid off,hold on,
plot(1:n,as,'linew',2),
title(sprintf('%s%g','bfТеоретический параметрfontsize{12} lambdafontsize{10} = ',P0))
xlabel('bf Количество циклов'),
ylabel('bf Эмпирический параметрfontsize{14} lambda'),
legend('bf Измеряемая величинаfontsize{12} lambda',...
'bf Средняя величинаfontsize{12} lambda'),
set(gcf,'color','w')
%% ПОСТРОЕНИЕ ТЕОРЕТИЧЕСКОЙ И ЭМПИРИЧЕСКОЙ
%% ФУНКЦИИ ПЛОТНОСТИ
t = 0 : 0.1 : 4;
y1 = P0*exp(-P0*t); %exppdf(t,1/P0); % встроенная функция
y2 = mcp*exp(-mcp*t); %exppdf(t,1/mcp);
figure(2)
plot(t, y1, 'r', 'linew',2),
hold on
plot(t, y2, 'bo', 'linew',2)
grid off
legend('bf Теоретическая функция плотности (PDF)',...
'bf Эмпирическая функция плотности'),
text(t(end)/3,2/3*max(max([y1,y2])),['bf',...
sprintf('Теоретический параметр: %gn Эмпирический параметр: %g',P0,mcp)])
xlabel('bf Случайная величина'),
ylabel('bf Функция плотности'),
set(gcf,'color','w')
Задание 1
- Видоизмените программу так, чтобы параметры задачи вводились в одном диалоговом окне
.
- В соответствии с номером компьютера задайте следующие значения параметра:
№ 1:
; № 2:
; № 3:
; № 4:
; № 5:
;
№ 6:
; № 7:
; № 8:
; № 9:
; № 10:
.
- Рассчитайте оценку параметра при следующих объемах выборок (в соответствии с номером компьютера):
№ 1: n = 200; № 2: n = 300; № 3: n = 400; № 4: n = 500; № 5: n = 600; № 6: n = 700; № 7: n = 800; № 8: n = 900; № 9: n = 1000; № 10: n = 2000;
Число прогонов программы выберите по равномерному закону из следующих интервалов (в соответствии с номером компьютера):
№ 1: (10-19); № 2: (20-29); № 3: (30-39); № 4: (40-49); № 5 (50-59); № 6: (60-69); № 7: (70-79); № 8: (80-89); № 9: (90-99); № 10: (100-110).
- Проверьте, доставляет ли максимум функции правдоподобия найденная оценка параметра экспоненциального распределения?
- Напишите программу по оценке параметров нормального закона по методу максимального правдоподобия.
Принцип максимального правдоподобия является спорным принципом статистического вывода, который предполагает, что вся информация о статистической выборке содержится в функции правдоподобия.
Функция правдоподобия основывается на условной вероятности взятием ее как функции от второго аргумента при фиксировании первого. Например рассмотрим модель в которой плотность вероятности случайной величины X зависит от параметра θ. Тогда для некоторого конкретного значения x случайной величины X функция L(θ | x) = P(X=x | θ) и есть функция правдоподобия θ, определяющая насколько правдоподобно каждое конкретное значение параметра θ при условии, что нам известно значение x величины X. Две функции правдоподобия являются равными, если одна есть произведение второй на некоторую скалярную величину.
Пример[]
Рассмотрим случайные величины
- X количество успехов в двенадцати независимых испытаний с распределением Бернулли с вероятностью успеха θ в каждом из них.
- Y количество независимых испытаний с распределением Бернулли, необходимых для получения трех успехов. Вероятность успеха в каждом из испытаний θ.
Тогда рассмотрение X = 3 даст функцию правдоподобия
а рассмотрение Y = 12 даст функцию правдоподобия
Они равносильны, так как одна равняется произведению второй на скалярное значение. Принцип максимального правдоподобия в данном случае говорит, что выводы, сделанные о значении переменной θ должны быть одинаковы в обоих случаях.
Разница в наблюдении X = 3 и наблюдении Y = 12 исключительно в дизайне эксперимента: в одном случае изначально было решено делать двенадцать попыток, а в другом делать попытки, пока не будет трех успешных. Результат будет одинаковым в обоих случаях. Поэтому принцип максимального правдоподобия иногда выражают следующим образом:
- Вывод должен зависеть только от исхода эксперимента, а не от дизайна эксперимента.
Закон максимального правдоподобия[]
Связанная с принципом максимального правдоподобия концепция — это закон максимального правдоподобия, говорящий, что отношение того, какое значение параметра более применимо, равняется отношению их функций правдоподобия.
Тогда отношение
является мерой того, насколько величина x принимает параметр a в отношении к b.
Таким образом, если отношение равняется 1, то разницы нет, а если больше 1, то a предпочтительней b, и наоборот.
Из принципа максимального правдоподобия и закона максимального правдоподобия следует, что параметр, который максимизирует функцию правдоподобия, является лучшим. Это и является основой широко известного метода максимального правдоподобия.
Историческая справка[]
Принцип максимального правдоподобия был впервые упомянут в печати в 1962 г. Однако основы принципа и применение его на практике были опубликованы ранее в работах Р. А. Фишера в 1920 г.
Аргументы за и против принципа максимального правдоподобия[]
Принцип максимального правдоподобия принимается не всеми.
Некоторые широко используемые методы традиционной статистики, как например проверка статистических гипотез противоречат принципу максимального правдоподобия. Рассмотрим кратко некоторые за и против этого принципа.
Зависимость результата от организации эксперимента[]
Неосуществленные события действительно играют роль в некоторых общих статистических методах. Например результат проверки статистической гипотезы может зависеть от доверительной вероятности так же или даже более, чем распределение неизвестного параметра. А сама доверительная вероятность может зависеть организации эксперимента.
Некоторые классичекие методы проверки гипотез базируются не на правдоподобии. Часто приводимый пример это проблема оптимальной остановки. Предположим я сказал, что бросил монету 12 раз и получил 3 решки. Из этого вы сможете сделать некоторые выводы о вероятности выпадения решки у этой монеты. А теперь предположим, что я бросал монету пока решка не выпала 3 раза, и получилось 12 бросков. Сделаете ли вы теперь другие выводы?
Функция правдоподобия одинакова в обоих случаях и пропорциональна
.
В соответствии с принципом правдоподобия выводы должны быть одинаковы в обоих случаях.
Предположим некоторая группа ученых определяет вероятность некоторого исхода (который мы будем называть ‘успехом’) серией экспериментов. Здравый смысл подсказывает нам, что если нет оснований считать что успех более вероятен, чем неудача, и наоборот, то следует положить вероятность успеха равной 0.5. Ученый Адам сделал 12 испытаний, в которых получил 3 успеха и 9 неудач, после чего умер.
Его коллега по лаборатории Билл продолжил работу Адама и опубликовал результат проверки гипотезы. Он проверил гипотезу что вероятность успеха p=0.5 против p < 0.5. Вероятность того, что в 12 испытаниях наступит не более 3 успехов, равна
что есть 299/4096 = 7.3 %. Таким образом гипотеза не отвергается при 5 % уровне доверия.
Шарлотта, прочитав статью Билла, пишет письмо. Она считает, что Адам, возможно, продолжал испытания пока не умер, успев получить к этому моменту 3 успеха. Вероятность того, что для трех успехов потребуется 12 или более испытаний равна
что есть 134/4096 = 3.27 %. И теперь результат отвергается при уровне в 5 %.
Для этих ученых зависимость результата испытаний зависит от организации эксперимента, а не только от правдоподобия результата.
Очевидно, парадоксы такого рода некоторые считают аргументом против принципа правдоподобия, для других они же иллюстрирует значимость принципа.
Литература[]
- Barnard, G.A.; G.M. Jenkins, and C.B. Winsten (1962). «Likelihood Inference and Time Series». J. Royal Statistical Society, A 125 (3): 321-372. ISSN 0035-9238.
- J.O. Berger The Likelihood Principle. — 2nd edition. — Haywood, CA: The Institute of Mathematical Statistics, 1988. — ISBN 0-940600-13-7
- Birnbaum, Allan (1962). «On the foundations of statistical inference». J. Amer. Statist. Assoc. 57 (298): 269-326. ISSN 0162-1459.
(With discussion.)
- Anthony W.F. Edwards Likelihood. — 1st edition. — Cambridge: Cambridge University Press, 1972.
- Anthony W.F. Edwards Likelihood. — 2nd edition. — Baltimore: Johns Hopkins University Press, 1992. — ISBN 0-8018-4445-2
- Edwards, Anthony W.F. (1974). «The history of likelihood». Int. Statist. Rev. 42 (1): 9-15. ISSN 0306-7734.
- Fisher, Ronald A. (1922). «On the Mathematical Foundations of Theoretical Statistics» (PDF fulltext). Phil. Trans. Royal Soc. A 222: 326. DOI:10.1098/rsta.1922.0009. ISSN 0264-3952.
- Ian Hacking Logic of Statistical Inference. — Cambridge: Cambridge University Press, 1965. — ISBN 0-521-05165-7
- Harold Jeffreys The Theory of Probability. — The Oxford University Press, 1961.
- Richard M. Royall Statistical Evidence: A Likelihood Paradigm. — London: Chapman & Hall, 1997. — ISBN 0-412-04411-0
- Leonard J. Savage The Foundations of Statistical Inference. — London: Methuen, 1962.
См. также[]
- Функция правдоподобия.
- Метод максимального правдоподобия.
Ссылки[]
- Anthony W.F. Edwards. «Likelihood». http://www.cimat.mx/reportes/enlinea/D-99-10.html
- Jeff Miller. Earliest Known Uses of Some of the Words of Mathematics (L)
- John Aldrich. Likelihood and Probability in R. A. Fisher’s Statistical Methods for Research Workers












![{displaystyle operatorname {argmax} _{theta }{mathcal {L}}(theta mid xin [x_{j},x_{j}+h])=operatorname {argmax} _{theta }{frac {1}{h}}{mathcal {L}}(theta mid xin [x_{j},x_{j}+h])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b6797a0c2b5bae9a317a32b352296ab5280cfb3)
![{displaystyle operatorname {argmax} _{theta }{frac {1}{h}}{mathcal {L}}(theta mid xin [x_{j},x_{j}+h])=operatorname {argmax} _{theta }{frac {1}{h}}Pr(x_{j}leq xleq x_{j}+hmid theta )=operatorname {argmax} _{theta }{frac {1}{h}}int _{x_{j}}^{x_{j}+h}f(xmid theta ),dx,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/522da72c12286e9b3307c091c946e9933c95fda5)
![{displaystyle operatorname {argmax} _{theta }{mathcal {L}}(theta mid xin [x_{j},x_{j}+h])=operatorname {argmax} _{theta }{frac {1}{h}}int _{x_{j}}^{x_{j}+h}f(xmid theta ),dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/287d682ce342c6403977e98cb2c9f632f24b1b2b)

![{displaystyle {begin{aligned}&operatorname {argmax} _{theta }{mathcal {L}}(theta mid x_{j})=operatorname {argmax} _{theta }left[lim _{hto 0^{+}}{mathcal {L}}(theta mid xin [x_{j},x_{j}+h])right]\[4pt]={}&operatorname {argmax} _{theta }left[lim _{hto 0^{+}}{frac {1}{h}}int _{x_{j}}^{x_{j}+h}f(xmid theta ),dxright]=operatorname {argmax} _{theta }f(x_{j}mid theta ).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c379434595f33938e8eeebebbde00c1451edc4b)


![{displaystyle mathbf {H} (theta )equiv left[,{frac {partial ^{2}L}{,partial theta _{i},partial theta _{j},}},right]_{i,j=1,1}^{n_{mathrm {i} },n_{mathrm {j} }};}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db07bfbff65917f8ca27dee1406b9e1ff2302e11)
![{displaystyle ;nabla Lequiv left[,{frac {partial L}{,partial theta _{i},}},right]_{i=1}^{n_{mathrm {i} }};}](https://wikimedia.org/api/rest_v1/media/math/render/svg/538a4e516eda07a4834956dbec52e16a95ccb1ac)





















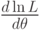 ;
; ; если
; если  отрицательна, то
отрицательна, то  .
.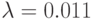 ; № 2:
; № 2:  ; № 3:
; № 3: 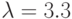 ; № 4:
; № 4: 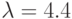 ; № 5:
; № 5: 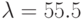 ;
;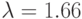 ; № 7:
; № 7:  ; № 8:
; № 8:  ; № 9:
; № 9: 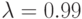 ; № 10:
; № 10: 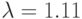 .
.




