Функция Эйлера — функция, равная количеству чисел ряда
, взаимно
простых с . Заметим, что из определения
.
Пояснение: взаимно простыми называются числа, которые не имеют общих делителей, отличных от 1. Так как
делителями нуля являются все натуральные числа, то 0 взаимно прост только с 1.
Вычисление функции Эйлера
Представим число в виде
где числа простые и попарно различные. Тогда
Мультипликативность функции Эйлера
Для взаимно простых чисел и
справедливо
Это свойство называется свойством мультипликативности функции Эйлера и может быть использовано для её вычисления.
Функция Эйлера онлайн
Программа вычисляет функцию Эйлера онлайн для любого числа, меньшего .
См. также: разложение числа на простые множители.
Интересное и простое из комбинаторики. Функция Эйлера
Время на прочтение
2 мин
Количество просмотров 7.7K
Предисловие
Прежде всего хочу сказать, мне всего 14 лет. Я надеюсь, что информация, которой поделюсь, будет для кого-то интересна.
Речь пойдет о некоторых задачах комбинаторики.
Сколько вариантов расставить n предметов?
Способ №1
Первое, что приходит на ум обычному человеку: «Возьму-ка я 3 предмета и начну их расставлять в ряд. Сколько разных комбинаций получится — столько вариантов расстановок и есть». Да, это так. Но есть способ, который по своей простоте опережает приведенный ранее способ.
Способ №2
Факториал — количество способов расставить n предметов.
Факториал высчитывается перемножением чисел от 1 до n.
Обозначается n! (читать как факториал n).
Допустим, нам нужно узнать, сколько вариантов в расстановке 10 предметов. Умножаем: 1x2x3..x10
Получим: 10! = 3628800
Как из n предметов выбрать k предметов?
Способ №1
Допустим, вы — организатор лотереи. Из 10 участников вам нужно выбрать 2 победителя. Вы можете узнать количество способов сделать это.
Так же как и в случае с факториалом, можно посчитать вручную. Выбирать n предметов, пока не иссякнут все варианты.
Цитирую: но есть способ, который по своей простоте опережает приведенный ранее способ.
Способ №2
Число сочетаний — это количество способов из n предметов выбрать k предметов.
Обозначается так:
Высчитывается по формуле:
Итак, сколько же способов из 10 участников выбрать 2 победителя?
Ответ вполне себе простой —
Числа Фибоначчи
Стоит отдать должное человеку, который «придумал» эти числа. Леонардо Пизанский. Думаю достаточно, чтобы Вы запомнили имя этого великого человека.
Приступим. Числа Фибоначчи применяются в Теории Чисел. Если сказать честно, я знаю не слишком много об этих числах.
Числа Фибоначчи — это последовательность чисел, в котором каждое последующее числовое значение равно сумме двух предыдущих. Первые два числа Фибоначии — единицы. Соответственно, 3-е число = 2.
Первые 22 числа Фибоначчи:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946.
Еще раз повторюсь — я знаю не слишком много об этих числах. Если я еще не слишком вас утомил/отпугнул/надоел — идем дальше.
Функция Эйлера
В этом пункте я попытаюсь выложить все, что знаю об этом. Я потратил достаточно времени и сил, чтобы изучить эту, между прочим абсолютно простою вещь.
По правде говоря, я очень горжусь тем, что такой человек как Леонард Эйлер жил в России.
К делу. Есть три разных способа посчитать функцию Эйлера. На выбор одного из способов влияют некоторые факторы.
Функция Эйлера обозначается (читать как фи от n).
Способ №1
Увы, но этот способ применять следует для высчитывания функции простых чисел.
Например, функция Эйлера для 3 =
Способ №2
Данный способ следует применять если число можно представить как степень какого-то числа. Например, 9 — это
Посчитаем функцию для 9.
Получаем:
Способ №3
Если число нельзя представить как степень, но можно представить как два множителя — этот способ нам и нужен.
Тут немного сложнее. Нужно разложить число на два множителя, посчитать функцию для каждого из множителей и полученные результаты перемножить.
Также хочу отметить, что если число можно представить и как степень и как два множителя, то в преимуществе всегда степень какого-то числа (о как, в рифму).
Таким образом получаем:
Спасибо за внимание.
Расчет значения функции Эйлера
| Целое положительное число |
Функция Эйлера — такая функция от целого положительного числа, значение которой равно количеству натуральных чисел, меньших заданного числа и взаимно простых с ним.
При этом полагают, что число 1 взаимно просто со всеми натуральными числами.
Если заданное число N является простым то логично предложить что функция Эйлера будет равна N-1, так как все числа меньше N, являются взаимно простыми к заданному.
Например, значение функции Эйлера числа 33 равно 20. Как такое получилось?
Разложим 33 на множители получим 3*11. Запомним их и будем сравнивать с рядом чисел от 1 до 32.
Напомним, что взаимно простыми числами являются таки числа, которые не имеют общих делителей.
Считаем взаимно простые числа: 1,2 ,3(не учитываем),4,5,6(делится на 3),7,8,9,10,11(делится на 11),12,13,14,15,16,17,18,19,20,21(делится на три),22(делится на 11),23,24,25,26,27,28,29,30,31,32
Посчитаем сколько получилось зачеркнутых чисел?
Их 12, ряд чисел содержит 32 элемента ( от 1 до 33) тогда количество не зачёркнутых (взаимно простых) чисел будет 32-12 =20
Есть еще простой способ рассчитывать значения функции
Разложим произвольное число например 4832 на простые множители.
Получим
Функция Эйлера равна
То есть, если у вас число N представлено в виде простых сомножителей вида
то функция Эйлера будет равна
Вот еще пример
Рассчитаем значение фунции числа 100
тогда значение функции Эйлера равно
Применимость числа Эйлера в теории чисел и криптографии достаточно велико, но мы будем её использовать для расчета линейных диофантовых уравнений с двумя неизвестными.
Напоследок, представляем таблицу значений функции Эйлера для первых 500 чисел
| 1 | 1 | 101 | 100 | 201 | 132 | 301 | 252 | 401 | 400 |
| 2 | 1 | 102 | 32 | 202 | 100 | 302 | 150 | 402 | 132 |
| 3 | 2 | 103 | 102 | 203 | 168 | 303 | 200 | 403 | 360 |
| 4 | 2 | 104 | 48 | 204 | 64 | 304 | 144 | 404 | 200 |
| 5 | 4 | 105 | 48 | 205 | 160 | 305 | 240 | 405 | 216 |
| 6 | 2 | 106 | 52 | 206 | 102 | 306 | 96 | 406 | 168 |
| 7 | 6 | 107 | 106 | 207 | 132 | 307 | 306 | 407 | 360 |
| 8 | 4 | 108 | 36 | 208 | 96 | 308 | 120 | 408 | 128 |
| 9 | 6 | 109 | 108 | 209 | 180 | 309 | 204 | 409 | 408 |
| 10 | 4 | 110 | 40 | 210 | 48 | 310 | 120 | 410 | 160 |
| 11 | 10 | 111 | 72 | 211 | 210 | 311 | 310 | 411 | 272 |
| 12 | 4 | 112 | 48 | 212 | 104 | 312 | 96 | 412 | 204 |
| 13 | 12 | 113 | 112 | 213 | 140 | 313 | 312 | 413 | 348 |
| 14 | 6 | 114 | 36 | 214 | 106 | 314 | 156 | 414 | 132 |
| 15 | 8 | 115 | 88 | 215 | 168 | 315 | 144 | 415 | 328 |
| 16 | 8 | 116 | 56 | 216 | 72 | 316 | 156 | 416 | 192 |
| 17 | 16 | 117 | 72 | 217 | 180 | 317 | 316 | 417 | 276 |
| 18 | 6 | 118 | 58 | 218 | 108 | 318 | 104 | 418 | 180 |
| 19 | 18 | 119 | 96 | 219 | 144 | 319 | 280 | 419 | 418 |
| 20 | 8 | 120 | 32 | 220 | 80 | 320 | 128 | 420 | 96 |
| 21 | 12 | 121 | 110 | 221 | 192 | 321 | 212 | 421 | 420 |
| 22 | 10 | 122 | 60 | 222 | 72 | 322 | 132 | 422 | 210 |
| 23 | 22 | 123 | 80 | 223 | 222 | 323 | 288 | 423 | 276 |
| 24 | 8 | 124 | 60 | 224 | 96 | 324 | 108 | 424 | 208 |
| 25 | 20 | 125 | 100 | 225 | 120 | 325 | 240 | 425 | 320 |
| 26 | 12 | 126 | 36 | 226 | 112 | 326 | 162 | 426 | 140 |
| 27 | 18 | 127 | 126 | 227 | 226 | 327 | 216 | 427 | 360 |
| 28 | 12 | 128 | 64 | 228 | 72 | 328 | 160 | 428 | 212 |
| 29 | 28 | 129 | 84 | 229 | 228 | 329 | 276 | 429 | 240 |
| 30 | 8 | 130 | 48 | 230 | 88 | 330 | 80 | 430 | 168 |
| 31 | 30 | 131 | 130 | 231 | 120 | 331 | 330 | 431 | 430 |
| 32 | 16 | 132 | 40 | 232 | 112 | 332 | 164 | 432 | 144 |
| 33 | 20 | 133 | 108 | 233 | 232 | 333 | 216 | 433 | 432 |
| 34 | 16 | 134 | 66 | 234 | 72 | 334 | 166 | 434 | 180 |
| 35 | 24 | 135 | 72 | 235 | 184 | 335 | 264 | 435 | 224 |
| 36 | 12 | 136 | 64 | 236 | 116 | 336 | 96 | 436 | 216 |
| 37 | 36 | 137 | 136 | 237 | 156 | 337 | 336 | 437 | 396 |
| 38 | 18 | 138 | 44 | 238 | 96 | 338 | 156 | 438 | 144 |
| 39 | 24 | 139 | 138 | 239 | 238 | 339 | 224 | 439 | 438 |
| 40 | 16 | 140 | 48 | 240 | 64 | 340 | 128 | 440 | 160 |
| 41 | 40 | 141 | 92 | 241 | 240 | 341 | 300 | 441 | 252 |
| 42 | 12 | 142 | 70 | 242 | 110 | 342 | 108 | 442 | 192 |
| 43 | 42 | 143 | 120 | 243 | 162 | 343 | 294 | 443 | 442 |
| 44 | 20 | 144 | 48 | 244 | 120 | 344 | 168 | 444 | 144 |
| 45 | 24 | 145 | 112 | 245 | 168 | 345 | 176 | 445 | 352 |
| 46 | 22 | 146 | 72 | 246 | 80 | 346 | 172 | 446 | 222 |
| 47 | 46 | 147 | 84 | 247 | 216 | 347 | 346 | 447 | 296 |
| 48 | 16 | 148 | 72 | 248 | 120 | 348 | 112 | 448 | 192 |
| 49 | 42 | 149 | 148 | 249 | 164 | 349 | 348 | 449 | 448 |
| 50 | 20 | 150 | 40 | 250 | 100 | 350 | 120 | 450 | 120 |
| 51 | 32 | 151 | 150 | 251 | 250 | 351 | 216 | 451 | 400 |
| 52 | 24 | 152 | 72 | 252 | 72 | 352 | 160 | 452 | 224 |
| 53 | 52 | 153 | 96 | 253 | 220 | 353 | 352 | 453 | 300 |
| 54 | 18 | 154 | 60 | 254 | 126 | 354 | 116 | 454 | 226 |
| 55 | 40 | 155 | 120 | 255 | 128 | 355 | 280 | 455 | 288 |
| 56 | 24 | 156 | 48 | 256 | 128 | 356 | 176 | 456 | 144 |
| 57 | 36 | 157 | 156 | 257 | 256 | 357 | 192 | 457 | 456 |
| 58 | 28 | 158 | 78 | 258 | 84 | 358 | 178 | 458 | 228 |
| 59 | 58 | 159 | 104 | 259 | 216 | 359 | 358 | 459 | 288 |
| 60 | 16 | 160 | 64 | 260 | 96 | 360 | 96 | 460 | 176 |
| 61 | 60 | 161 | 132 | 261 | 168 | 361 | 342 | 461 | 460 |
| 62 | 30 | 162 | 54 | 262 | 130 | 362 | 180 | 462 | 120 |
| 63 | 36 | 163 | 162 | 263 | 262 | 363 | 220 | 463 | 462 |
| 64 | 32 | 164 | 80 | 264 | 80 | 364 | 144 | 464 | 224 |
| 65 | 48 | 165 | 80 | 265 | 208 | 365 | 288 | 465 | 240 |
| 66 | 20 | 166 | 82 | 266 | 108 | 366 | 120 | 466 | 232 |
| 67 | 66 | 167 | 166 | 267 | 176 | 367 | 366 | 467 | 466 |
| 68 | 32 | 168 | 48 | 268 | 132 | 368 | 176 | 468 | 144 |
| 69 | 44 | 169 | 156 | 269 | 268 | 369 | 240 | 469 | 396 |
| 70 | 24 | 170 | 64 | 270 | 72 | 370 | 144 | 470 | 184 |
| 71 | 70 | 171 | 108 | 271 | 270 | 371 | 312 | 471 | 312 |
| 72 | 24 | 172 | 84 | 272 | 128 | 372 | 120 | 472 | 232 |
| 73 | 72 | 173 | 172 | 273 | 144 | 373 | 372 | 473 | 420 |
| 74 | 36 | 174 | 56 | 274 | 136 | 374 | 160 | 474 | 156 |
| 75 | 40 | 175 | 120 | 275 | 200 | 375 | 200 | 475 | 360 |
| 76 | 36 | 176 | 80 | 276 | 88 | 376 | 184 | 476 | 192 |
| 77 | 60 | 177 | 116 | 277 | 276 | 377 | 336 | 477 | 312 |
| 78 | 24 | 178 | 88 | 278 | 138 | 378 | 108 | 478 | 238 |
| 79 | 78 | 179 | 178 | 279 | 180 | 379 | 378 | 479 | 478 |
| 80 | 32 | 180 | 48 | 280 | 96 | 380 | 144 | 480 | 128 |
| 81 | 54 | 181 | 180 | 281 | 280 | 381 | 252 | 481 | 432 |
| 82 | 40 | 182 | 72 | 282 | 92 | 382 | 190 | 482 | 240 |
| 83 | 82 | 183 | 120 | 283 | 282 | 383 | 382 | 483 | 264 |
| 84 | 24 | 184 | 88 | 284 | 140 | 384 | 128 | 484 | 220 |
| 85 | 64 | 185 | 144 | 285 | 144 | 385 | 240 | 485 | 384 |
| 86 | 42 | 186 | 60 | 286 | 120 | 386 | 192 | 486 | 162 |
| 87 | 56 | 187 | 160 | 287 | 240 | 387 | 252 | 487 | 486 |
| 88 | 40 | 188 | 92 | 288 | 96 | 388 | 192 | 488 | 240 |
| 89 | 88 | 189 | 108 | 289 | 272 | 389 | 388 | 489 | 324 |
| 90 | 24 | 190 | 72 | 290 | 112 | 390 | 96 | 490 | 168 |
| 91 | 72 | 191 | 190 | 291 | 192 | 391 | 352 | 491 | 490 |
| 92 | 44 | 192 | 64 | 292 | 144 | 392 | 168 | 492 | 160 |
| 93 | 60 | 193 | 192 | 293 | 292 | 393 | 260 | 493 | 448 |
| 94 | 46 | 194 | 96 | 294 | 84 | 394 | 196 | 494 | 216 |
| 95 | 72 | 195 | 96 | 295 | 232 | 395 | 312 | 495 | 240 |
| 96 | 32 | 196 | 84 | 296 | 144 | 396 | 120 | 496 | 240 |
| 97 | 96 | 197 | 196 | 297 | 180 | 397 | 396 | 497 | 420 |
| 98 | 42 | 198 | 60 | 298 | 148 | 398 | 198 | 498 | 164 |
| 99 | 60 | 199 | 198 | 299 | 264 | 399 | 216 | 499 | 498 |
| 100 | 40 | 200 | 80 | 300 | 80 | 400 | 160 | 500 | 200 |
Удачных расчетов!
«φ(n)» redirects here. For other uses, see Phi.
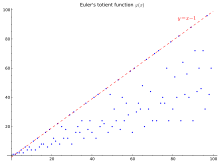
The first thousand values of φ(n). The points on the top line represent φ(p) when p is a prime number, which is p − 1.[1]
In number theory, Euler’s totient function counts the positive integers up to a given integer n that are relatively prime to n. It is written using the Greek letter phi as 

For example, the totatives of n = 9 are the six numbers 1, 2, 4, 5, 7 and 8. They are all relatively prime to 9, but the other three numbers in this range, 3, 6, and 9 are not, since gcd(9, 3) = gcd(9, 6) = 3 and gcd(9, 9) = 9. Therefore, φ(9) = 6. As another example, φ(1) = 1 since for n = 1 the only integer in the range from 1 to n is 1 itself, and gcd(1, 1) = 1.
Euler’s totient function is a multiplicative function, meaning that if two numbers m and n are relatively prime, then φ(mn) = φ(m)φ(n).[4][5]
This function gives the order of the multiplicative group of integers modulo n (the group of units of the ring 
History, terminology, and notation[edit]
Leonhard Euler introduced the function in 1763.[7][8][9] However, he did not at that time choose any specific symbol to denote it. In a 1784 publication, Euler studied the function further, choosing the Greek letter π to denote it: he wrote πD for «the multitude of numbers less than D, and which have no common divisor with it».[10] This definition varies from the current definition for the totient function at D = 1 but is otherwise the same. The now-standard notation[8][11] φ(A) comes from Gauss’s 1801 treatise Disquisitiones Arithmeticae,[12][13] although Gauss didn’t use parentheses around the argument and wrote φA. Thus, it is often called Euler’s phi function or simply the phi function.
In 1879, J. J. Sylvester coined the term totient for this function,[14][15] so it is also referred to as Euler’s totient function, the Euler totient, or Euler’s totient. Jordan’s totient is a generalization of Euler’s.
The cototient of n is defined as n − φ(n). It counts the number of positive integers less than or equal to n that have at least one prime factor in common with n.
Computing Euler’s totient function[edit]
There are several formulae for computing φ(n).
Euler’s product formula[edit]
It states
where the product is over the distinct prime numbers dividing n. (For notation, see Arithmetical function.)
An equivalent formulation is
where 


The proof of these formulae depends on two important facts.
Phi is a multiplicative function[edit]
This means that if gcd(m, n) = 1, then φ(m) φ(n) = φ(mn). Proof outline: Let A, B, C be the sets of positive integers which are coprime to and less than m, n, mn, respectively, so that |A| = φ(m), etc. Then there is a bijection between A × B and C by the Chinese remainder theorem.
Value of phi for a prime power argument[edit]
If p is prime and k ≥ 1, then
Proof: Since p is a prime number, the only possible values of gcd(pk, m) are 1, p, p2, …, pk, and the only way to have gcd(pk, m) > 1 is if m is a multiple of p, that is, m ∈ {p, 2p, 3p, …, pk − 1p = pk}, and there are pk − 1 such multiples not greater than pk. Therefore, the other pk − pk − 1 numbers are all relatively prime to pk.
Proof of Euler’s product formula[edit]
The fundamental theorem of arithmetic states that if n > 1 there is a unique expression 
This gives both versions of Euler’s product formula.
An alternative proof that does not require the multiplicative property instead uses the inclusion-exclusion principle applied to the set 
Example[edit]
In words: the distinct prime factors of 20 are 2 and 5; half of the twenty integers from 1 to 20 are divisible by 2, leaving ten; a fifth of those are divisible by 5, leaving eight numbers coprime to 20; these are: 1, 3, 7, 9, 11, 13, 17, 19.
The alternative formula uses only integers:
Fourier transform[edit]
The totient is the discrete Fourier transform of the gcd, evaluated at 1.[16] Let
where xk = gcd(k,n) for k ∈ {1, …, n}. Then
The real part of this formula is
For example, using 

Unlike the Euler product and the divisor sum formula, this one does not require knowing the factors of n. However, it does involve the calculation of the greatest common divisor of n and every positive integer less than n, which suffices to provide the factorization anyway.
Divisor sum[edit]
The property established by Gauss,[17] that
where the sum is over all positive divisors d of n, can be proven in several ways. (See Arithmetical function for notational conventions.)
One proof is to note that φ(d) is also equal to the number of possible generators of the cyclic group Cd ; specifically, if Cd = ⟨g⟩ with gd = 1, then gk is a generator for every k coprime to d. Since every element of Cn generates a cyclic subgroup, and all subgroups Cd ⊆ Cn are generated by precisely φ(d) elements of Cn, the formula follows.[18] Equivalently, the formula can be derived by the same argument applied to the multiplicative group of the nth roots of unity and the primitive dth roots of unity.
The formula can also be derived from elementary arithmetic.[19] For example, let n = 20 and consider the positive fractions up to 1 with denominator 20:
Put them into lowest terms:
These twenty fractions are all the positive k/d ≤ 1 whose denominators are the divisors d = 1, 2, 4, 5, 10, 20. The fractions with 20 as denominator are those with numerators relatively prime to 20, namely 1/20, 3/20, 7/20, 9/20, 11/20, 13/20, 17/20, 19/20; by definition this is φ(20) fractions. Similarly, there are φ(10) fractions with denominator 10, and φ(5) fractions with denominator 5, etc. Thus the set of twenty fractions is split into subsets of size φ(d) for each d dividing 20. A similar argument applies for any n.
Möbius inversion applied to the divisor sum formula gives
where μ is the Möbius function, the multiplicative function defined by 



An example:
Some values[edit]
The first 100 values (sequence A000010 in the OEIS) are shown in the table and graph below:
Graph of the first 100 values
-
φ(n) for 1 ≤ n ≤ 100
+ 1 2 3 4 5 6 7 8 9 10 0 1 1 2 2 4 2 6 4 6 4 10 10 4 12 6 8 8 16 6 18 8 20 12 10 22 8 20 12 18 12 28 8 30 30 16 20 16 24 12 36 18 24 16 40 40 12 42 20 24 22 46 16 42 20 50 32 24 52 18 40 24 36 28 58 16 60 60 30 36 32 48 20 66 32 44 24 70 70 24 72 36 40 36 60 24 78 32 80 54 40 82 24 64 42 56 40 88 24 90 72 44 60 46 72 32 96 42 60 40
In the graph at right the top line y = n − 1 is an upper bound valid for all n other than one, and attained if and only if n is a prime number. A simple lower bound is 
Euler’s theorem[edit]
This states that if a and n are relatively prime then
The special case where n is prime is known as Fermat’s little theorem.
This follows from Lagrange’s theorem and the fact that φ(n) is the order of the multiplicative group of integers modulo n.
The RSA cryptosystem is based on this theorem: it implies that the inverse of the function a ↦ ae mod n, where e is the (public) encryption exponent, is the function b ↦ bd mod n, where d, the (private) decryption exponent, is the multiplicative inverse of e modulo φ(n). The difficulty of computing φ(n) without knowing the factorization of n is thus the difficulty of computing d: this is known as the RSA problem which can be solved by factoring n. The owner of the private key knows the factorization, since an RSA private key is constructed by choosing n as the product of two (randomly chosen) large primes p and q. Only n is publicly disclosed, and given the difficulty to factor large numbers we have the guarantee that no one else knows the factorization.
Other formulae[edit]
Menon’s identity[edit]
In 1965 P. Kesava Menon proved
where d(n) = σ0(n) is the number of divisors of n.
Generating functions[edit]
The Dirichlet series for φ(n) may be written in terms of the Riemann zeta function as:[26]
where the left-hand side converges for 
The Lambert series generating function is[27]
which converges for |q| < 1.
Both of these are proved by elementary series manipulations and the formulae for φ(n).
Growth rate[edit]
In the words of Hardy & Wright, the order of φ(n) is «always ‘nearly n‘.»[28]
First[29]
but as n goes to infinity,[30] for all δ > 0
These two formulae can be proved by using little more than the formulae for φ(n) and the divisor sum function σ(n).
In fact, during the proof of the second formula, the inequality
true for n > 1, is proved.
We also have[20]
Here γ is Euler’s constant, γ = 0.577215665…, so eγ = 1.7810724… and e−γ = 0.56145948….
Proving this does not quite require the prime number theorem.[31][32] Since log log n goes to infinity, this formula shows that
In fact, more is true.[33][34][35]
and
The second inequality was shown by Jean-Louis Nicolas. Ribenboim says «The method of proof is interesting, in that the inequality is shown first under the assumption that the Riemann hypothesis is true, secondly under the contrary assumption.»[35]: 173
For the average order, we have[22][36]
due to Arnold Walfisz, its proof exploiting estimates on exponential sums due to I. M. Vinogradov and N. M. Korobov.
By a combination of van der Corput’s and Vinogradov’s methods, H.-Q. Liu (On Euler’s function.Proc. Roy. Soc. Edinburgh Sect. A 146 (2016), no. 4, 769–775)
improved the error term to
(this is currently the best known estimate of this type). The «Big O» stands for a quantity that is bounded by a constant times the function of n inside the parentheses (which is small compared to n2).
This result can be used to prove[37] that the probability of two randomly chosen numbers being relatively prime is 6/π2.
Ratio of consecutive values[edit]
In 1950 Somayajulu proved[38][39]
In 1954 Schinzel and Sierpiński strengthened this, proving[38][39] that the set
is dense in the positive real numbers. They also proved[38] that the set
is dense in the interval (0,1).
Totient numbers[edit]
A totient number is a value of Euler’s totient function: that is, an m for which there is at least one n for which φ(n) = m. The valency or multiplicity of a totient number m is the number of solutions to this equation.[40] A nontotient is a natural number which is not a totient number. Every odd integer exceeding 1 is trivially a nontotient. There are also infinitely many even nontotients,[41] and indeed every positive integer has a multiple which is an even nontotient.[42]
The number of totient numbers up to a given limit x is
for a constant C = 0.8178146….[43]
If counted accordingly to multiplicity, the number of totient numbers up to a given limit x is
where the error term R is of order at most x/(log x)k for any positive k.[44]
It is known that the multiplicity of m exceeds mδ infinitely often for any δ < 0.55655.[45][46]
Ford’s theorem[edit]
Ford (1999) proved that for every integer k ≥ 2 there is a totient number m of multiplicity k: that is, for which the equation φ(n) = m has exactly k solutions; this result had previously been conjectured by Wacław Sierpiński,[47] and it had been obtained as a consequence of Schinzel’s hypothesis H.[43] Indeed, each multiplicity that occurs, does so infinitely often.[43][46]
However, no number m is known with multiplicity k = 1. Carmichael’s totient function conjecture is the statement that there is no such m.[48]
Perfect totient numbers[edit]
A perfect totient number is an integer that is equal to the sum of its iterated totients. That is, we apply the totient function to a number n, apply it again to the resulting totient, and so on, until the number 1 is reached, and add together the resulting sequence of numbers; if the sum equals n, then n is a perfect totient number.
Applications[edit]
Cyclotomy[edit]
In the last section of the Disquisitiones[49][50] Gauss proves[51] that a regular n-gon can be constructed with straightedge and compass if φ(n) is a power of 2. If n is a power of an odd prime number the formula for the totient says its totient can be a power of two only if n is a first power and n − 1 is a power of 2. The primes that are one more than a power of 2 are called Fermat primes, and only five are known: 3, 5, 17, 257, and 65537. Fermat and Gauss knew of these. Nobody has been able to prove whether there are any more.
Thus, a regular n-gon has a straightedge-and-compass construction if n is a product of distinct Fermat primes and any power of 2. The first few such n are[52]
- 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40,… (sequence A003401 in the OEIS).
Prime number theorem for arithmetic progressions[edit]
The RSA cryptosystem[edit]
Setting up an RSA system involves choosing large prime numbers p and q, computing n = pq and k = φ(n), and finding two numbers e and d such that ed ≡ 1 (mod k). The numbers n and e (the «encryption key») are released to the public, and d (the «decryption key») is kept private.
A message, represented by an integer m, where 0 < m < n, is encrypted by computing S = me (mod n).
It is decrypted by computing t = Sd (mod n). Euler’s Theorem can be used to show that if 0 < t < n, then t = m.
The security of an RSA system would be compromised if the number n could be efficiently factored or if φ(n) could be efficiently computed without factoring n.
Unsolved problems[edit]
Lehmer’s conjecture[edit]
If p is prime, then φ(p) = p − 1. In 1932 D. H. Lehmer asked if there are any composite numbers n such that φ(n) divides n − 1. None are known.[53]
In 1933 he proved that if any such n exists, it must be odd, square-free, and divisible by at least seven primes (i.e. ω(n) ≥ 7). In 1980 Cohen and Hagis proved that n > 1020 and that ω(n) ≥ 14.[54] Further, Hagis showed that if 3 divides n then n > 101937042 and ω(n) ≥ 298848.[55][56]
Carmichael’s conjecture[edit]
This states that there is no number n with the property that for all other numbers m, m ≠ n, φ(m) ≠ φ(n). See Ford’s theorem above.
As stated in the main article, if there is a single counterexample to this conjecture, there must be infinitely many counterexamples, and the smallest one has at least ten billion digits in base 10.[40]
Riemann hypothesis[edit]
The Riemann hypothesis is true if and only if the inequality
is true for all n ≥ p120569# where γ is Euler’s constant and p120569# is the product of the first 120569 primes.[57]
See also[edit]
- Carmichael function
- Duffin–Schaeffer conjecture
- Generalizations of Fermat’s little theorem
- Highly composite number
- Multiplicative group of integers modulo n
- Ramanujan sum
- Totient summatory function
- Dedekind psi function
Notes[edit]
- ^ «Euler’s totient function». Khan Academy. Retrieved 2016-02-26.
- ^ Long (1972, p. 85)
- ^ Pettofrezzo & Byrkit (1970, p. 72)
- ^ Long (1972, p. 162)
- ^ Pettofrezzo & Byrkit (1970, p. 80)
- ^ See Euler’s theorem.
- ^ L. Euler «Theoremata arithmetica nova methodo demonstrata» (An arithmetic theorem proved by a new method), Novi commentarii academiae scientiarum imperialis Petropolitanae (New Memoirs of the Saint-Petersburg Imperial Academy of Sciences), 8 (1763), 74–104. (The work was presented at the Saint-Petersburg Academy on October 15, 1759. A work with the same title was presented at the Berlin Academy on June 8, 1758). Available on-line in: Ferdinand Rudio, ed., Leonhardi Euleri Commentationes Arithmeticae, volume 1, in: Leonhardi Euleri Opera Omnia, series 1, volume 2 (Leipzig, Germany, B. G. Teubner, 1915), pages 531–555. On page 531, Euler defines n as the number of integers that are smaller than N and relatively prime to N (… aequalis sit multitudini numerorum ipso N minorum, qui simul ad eum sint primi, …), which is the phi function, φ(N).
- ^ a b Sandifer, p. 203
- ^ Graham et al. p. 133 note 111
- ^ L. Euler, Speculationes circa quasdam insignes proprietates numerorum, Acta Academiae Scientarum Imperialis Petropolitinae, vol. 4, (1784), pp. 18–30, or Opera Omnia, Series 1, volume 4, pp. 105–115. (The work was presented at the Saint-Petersburg Academy on October 9, 1775).
- ^ Both φ(n) and ϕ(n) are seen in the literature. These are two forms of the lower-case Greek letter phi.
- ^ Gauss, Disquisitiones Arithmeticae article 38
- ^ Cajori, Florian (1929). A History Of Mathematical Notations Volume II. Open Court Publishing Company. §409.
- ^ J. J. Sylvester (1879) «On certain ternary cubic-form equations», American Journal of Mathematics, 2 : 357-393; Sylvester coins the term «totient» on page 361.
- ^ «totient». Oxford English Dictionary (2nd ed.). Oxford University Press. 1989.
- ^ Schramm (2008)
- ^ Gauss, DA, art 39
- ^ Gauss, DA art. 39, arts. 52-54
- ^ Graham et al. pp. 134-135
- ^ a b Hardy & Wright 1979, thm. 328
- ^ Dineva (in external refs), prop. 1
- ^ a b c Walfisz, Arnold (1963). Weylsche Exponentialsummen in der neueren Zahlentheorie. Mathematische Forschungsberichte (in German). Vol. 16. Berlin: VEB Deutscher Verlag der Wissenschaften. Zbl 0146.06003.
- ^ Lomadse, G. (1964), «The scientific work of Arnold Walfisz» (PDF), Acta Arithmetica, 10 (3): 227–237, doi:10.4064/aa-10-3-227-237
- ^ a b Sitaramachandrarao, R. (1985). «On an error term of Landau II». Rocky Mountain J. Math. 15 (2): 579–588. doi:10.1216/RMJ-1985-15-2-579.
- ^ Bordellès in the external links
- ^ Hardy & Wright 1979, thm. 288
- ^ Hardy & Wright 1979, thm. 309
- ^ Hardy & Wright 1979, intro to § 18.4
- ^ Hardy & Wright 1979, thm. 326
- ^ Hardy & Wright 1979, thm. 327
- ^ In fact Chebyshev’s theorem (Hardy & Wright 1979, thm.7) and
Mertens’ third theorem is all that is needed. - ^ Hardy & Wright 1979, thm. 436
- ^ Theorem 15 of Rosser, J. Barkley; Schoenfeld, Lowell (1962). «Approximate formulas for some functions of prime numbers». Illinois J. Math. 6 (1): 64–94. doi:10.1215/ijm/1255631807.
- ^ Bach & Shallit, thm. 8.8.7
- ^ a b Ribenboim (1989). «How are the Prime Numbers Distributed? §I.C The Distribution of Values of Euler’s Function». The Book of Prime Number Records (2nd ed.). New York: Springer-Verlag. pp. 172–175. doi:10.1007/978-1-4684-0507-1_5. ISBN 978-1-4684-0509-5.
- ^ Sándor, Mitrinović & Crstici (2006) pp.24–25
- ^ Hardy & Wright 1979, thm. 332
- ^ a b c Ribenboim, p.38
- ^ a b Sándor, Mitrinović & Crstici (2006) p.16
- ^ a b Guy (2004) p.144
- ^ Sándor & Crstici (2004) p.230
- ^ Zhang, Mingzhi (1993). «On nontotients». Journal of Number Theory. 43 (2): 168–172. doi:10.1006/jnth.1993.1014. ISSN 0022-314X. Zbl 0772.11001.
- ^ a b c Ford, Kevin (1998). «The distribution of totients». Ramanujan J. Developments in Mathematics. 2 (1–2): 67–151. arXiv:1104.3264. doi:10.1007/978-1-4757-4507-8_8. ISBN 978-1-4419-5058-1. ISSN 1382-4090. Zbl 0914.11053.
- ^ Sándor et al (2006) p.22
- ^ Sándor et al (2006) p.21
- ^ a b Guy (2004) p.145
- ^ Sándor & Crstici (2004) p.229
- ^ Sándor & Crstici (2004) p.228
- ^ Gauss, DA. The 7th § is arts. 336–366
- ^ Gauss proved if n satisfies certain conditions then the n-gon can be constructed. In 1837 Pierre Wantzel proved the converse, if the n-gon is constructible, then n must satisfy Gauss’s conditions
- ^ Gauss, DA, art 366
- ^ Gauss, DA, art. 366. This list is the last sentence in the Disquisitiones
- ^ Ribenboim, pp. 36–37.
- ^ Cohen, Graeme L.; Hagis, Peter Jr. (1980). «On the number of prime factors of n if φ(n) divides n − 1«. Nieuw Arch. Wiskd. III Series. 28: 177–185. ISSN 0028-9825. Zbl 0436.10002.
- ^ Hagis, Peter Jr. (1988). «On the equation M·φ(n) = n − 1«. Nieuw Arch. Wiskd. IV Series. 6 (3): 255–261. ISSN 0028-9825. Zbl 0668.10006.
- ^ Guy (2004) p.142
- ^ Broughan, Kevin (2017). Equivalents of the Riemann Hypothesis, Volume One: Arithmetic Equivalents (First ed.). Cambridge University Press. ISBN 978-1-107-19704-6. Corollary 5.35
References[edit]
The Disquisitiones Arithmeticae has been translated from Latin into English and German. The German edition includes all of Gauss’ papers on number theory: all the proofs of quadratic reciprocity, the determination of the sign of the Gauss sum, the investigations into biquadratic reciprocity, and unpublished notes.
References to the Disquisitiones are of the form Gauss, DA, art. nnn.
- Abramowitz, M.; Stegun, I. A. (1964), Handbook of Mathematical Functions, New York: Dover Publications, ISBN 0-486-61272-4. See paragraph 24.3.2.
- Bach, Eric; Shallit, Jeffrey (1996), Algorithmic Number Theory (Vol I: Efficient Algorithms), MIT Press Series in the Foundations of Computing, Cambridge, MA: The MIT Press, ISBN 0-262-02405-5, Zbl 0873.11070
- Dickson, Leonard Eugene, «History Of The Theory Of Numbers», vol 1, chapter 5 «Euler’s Function, Generalizations; Farey Series», Chelsea Publishing 1952
- Ford, Kevin (1999), «The number of solutions of φ(x) = m«, Annals of Mathematics, 150 (1): 283–311, doi:10.2307/121103, ISSN 0003-486X, JSTOR 121103, MR 1715326, Zbl 0978.11053.
- Gauss, Carl Friedrich (1986), Disquisitiones Arithmeticae (Second, corrected edition), translated by Clarke, Arthur A., New York: Springer, ISBN 0-387-96254-9
- Gauss, Carl Friedrich (1965), Untersuchungen uber hohere Arithmetik (Disquisitiones Arithmeticae & other papers on number theory) (Second edition), translated by Maser, H., New York: Chelsea, ISBN 0-8284-0191-8
- Graham, Ronald; Knuth, Donald; Patashnik, Oren (1994), Concrete Mathematics: a foundation for computer science (2nd ed.), Reading, MA: Addison-Wesley, ISBN 0-201-55802-5, Zbl 0836.00001
- Guy, Richard K. (2004), Unsolved Problems in Number Theory, Problem Books in Mathematics (3rd ed.), New York, NY: Springer-Verlag, ISBN 0-387-20860-7, Zbl 1058.11001
- Hardy, G. H.; Wright, E. M. (1979), An Introduction to the Theory of Numbers (Fifth ed.), Oxford: Oxford University Press, ISBN 978-0-19-853171-5
- Long, Calvin T. (1972), Elementary Introduction to Number Theory (2nd ed.), Lexington: D. C. Heath and Company, LCCN 77-171950
- Pettofrezzo, Anthony J.; Byrkit, Donald R. (1970), Elements of Number Theory, Englewood Cliffs: Prentice Hall, LCCN 77-81766
- Ribenboim, Paulo (1996), The New Book of Prime Number Records (3rd ed.), New York: Springer, ISBN 0-387-94457-5, Zbl 0856.11001
- Sandifer, Charles (2007), The early mathematics of Leonhard Euler, MAA, ISBN 978-0-88385-559-1
- Sándor, József; Mitrinović, Dragoslav S.; Crstici, Borislav, eds. (2006), Handbook of number theory I, Dordrecht: Springer-Verlag, pp. 9–36, ISBN 1-4020-4215-9, Zbl 1151.11300
- Sándor, Jozsef; Crstici, Borislav (2004). Handbook of number theory II. Dordrecht: Kluwer Academic. pp. 179–327. ISBN 1-4020-2546-7. Zbl 1079.11001.
- Schramm, Wolfgang (2008), «The Fourier transform of functions of the greatest common divisor», Electronic Journal of Combinatorial Number Theory, A50 (8(1)).
External links[edit]
- «Totient function», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Euler’s Phi Function and the Chinese Remainder Theorem — proof that φ(n) is multiplicative
- Euler’s totient function calculator in JavaScript — up to 20 digits
- Dineva, Rosica, The Euler Totient, the Möbius, and the Divisor Functions
- Plytage, Loomis, Polhill Summing Up The Euler Phi Function
Содержание
- 1 Функция Эйлера
- 2 Функции [math]sigma(n)[/math], [math]tau(n)[/math] и [math]varphi(n)[/math], их мультипликативность и значения
- 2.1 Функция [math]sigma(n)[/math]
- 2.2 Функция [math]tau(n)[/math]
- 2.3 Функция [math]varphi(n)[/math]
- 3 Малая теорема Ферма и теорема Эйлера
- 4 Различные свойства функции Эйлера
- 5 Применение теоремы Эйлера в других задачах
- 5.1 Задача об ожерельях
- 6 Алгоритм
- 7 См. также
- 8 Ссылки
Функция Эйлера
| Определение: |
| Функция Эйлера определяется как количество натуральных чисел, не превосходящих и взаимно простых с . |
| Определение: |
| Функция называется мультипликативной, если для любых взаимно простых . |
| Теорема (Мультипликативность функции Эйлера): |
|
Для любых взаимно простых чисел |
| Доказательство: |
|
Запишем натуральных чисел, не превосходящих , в виде прямоугольной таблицы с столбцами и строками, располагая первые чисел в первой строке, вторые чисел во второй и т.д. Поскольку и взаимно просты, то целое взаимно просто с тогда и только тогда, когда оно взаимно просто как с , так и с . Итак, нужно доказать, что количество чисел в таблице, взаимно простых с и с равно . В данном доказательстве мы используем тот факт, что число взаимно просто с натуральным тогда и только тогда, когда остаток деления на тоже взаимно прост с . Данный факт довольно очевиден и используется в Алгоритме Евклида. Теперь приступим непосредственно к доказательству. Число находящееся в -ой строке и -ом столбце нашей таблицы можно представить в виде . Если это число взаимно просто с , то и остаток этого числа по модулю тоже взаимно прост с . Но тогда и все числа в данном столбце тоже взаимно просты с , так как весь столбец можно представить в виде арифметической прогрессии с разностью , а при добавлении остаток деления по модулю не меняется. Поэтому, числа взаимно простые с в таблице занимают ровно столбцов. Перед тем как продолжить доказательство, давайте рассмотрим небольшое утверждение. Пусть нам даны последовательных членов арифметической прогрессии . Тогда, если , то остатки всех этих чисел по модулю разные, а значит, образуют все множество остатков , причем каждый остаток получается ровно из одного из членов прогрессии. Воспользуемся данным утверждением, подставив разность арифметической прогресии . Тогда в каждом из столбцов есть ровно чисел, взаимно простых с . Следовательно всего чисел, взаимно простых и с и с равно , что и требовалось доказать. |
Функции , и , их мультипликативность и значения
Каноническое разложение числа , где — количество простых делителей числа , — -ый простой делитель, — максимальная степень вхождения этого простого делителя.
Функция
Функция определяется как сумма делителей натурального числа :
Если и взаимно просты, то каждый делитель произведения может быть единственным образом представлен в виде произведения делителей и делителей , и обратно, каждое такое произведение является делителем . Отсюда следует, что функция мультипликативна:
Для простого числа легко посчитать . При этом легко обобщается для некоторой степени :
В силу мультипликативности функции:
Функция
Функция определяется как число положительных делителей натурального числа :
Если и взаимно просты, то каждый делитель произведения может быть единственным образом представлен в виде произведения делителей и делителей , и обратно, каждое такое произведение является делителем . Отсюда следует, что функция мультипликативна:
Для простого числа легко посчитать . При этом легко обобщается для некоторой степени :
В силу мультипликативности функции:
Функция
Для простого числа легко посчитать . На некоторую степень формулу можно обобщить:
Обосновывается следующим образом: Все не взаимно простые с числа в диапазоне от 1 до , очевидно, кратны . Всего таких чисел .
В силу мультипликативности функции:
Малая теорема Ферма и теорема Эйлера
| Теорема (Теорема Эйлера): |
|
Если и — взаимно простые целые числа, то |
| Доказательство: |
|
Число называется вычетом по модулю , если . Вычет называется обратимым вычетом, если существует вычет , такой что . Заметим, что вычет обратим тогда и только тогда, когда и взаимно просты. Это обосновывается тем, что данное выражение можно представить в виде линейного диофантово уравнения второго порядка . Как видно из статьи, решение существует только при . В таком случае, у числа существует всего обратимых вычетов. Пусть — множество всех обратимых вычетов по модулю . Достаточно доказать данную теорему только для вычетов, так как мы знаем, что если остаток числа по модулю взаимно прост с , то и само число взаимно просто с . Напомним, что данный факт был ранее доказан в доказательстве мультипликативности функции Эйлера. Рассмотрим вычеты по модулю . Так как и взаимно просты, то вычет обратим. Пусть — все обратимые вычеты по модулю . Тогда вычет , равный произведению всех обратимых вычетов, тоже обратим. Заметим, что отображение , заданное формулой является биекцией. Действительно, мы просто умножаем каждый остаток на какую-то константу, от этого множество вычетов не изменится. В таком случае в выражении , в правой части стоит произведение всех обратимых вычетов, но взятое в другом порядке. Тогда . Умножая обе части на вычет, обратный к , получим, что , что и требовалось доказать. |
Следствием теоремы Эйлера является малая теорема Ферма. У нее также есть доказательство без использования более общей теоремы Эйлера, однако его мы приводить не будем.
| Теорема (Малая теорема Ферма): |
|
Если целое число и простое число — взаимно просты, то |
| Доказательство: |
| Так как — простое, то . Воспользуемся теоремой Эйлера, тогда , что и требовалось доказать. |
Различные свойства функции Эйлера
| Теорема: |
|
Если для каких-то натуральных чисел и верно, что , тогда верно и |
| Доказательство: |
|
Воспользуемся формулой для . При этом, так как , то , а также Значит, , а значит, , что и требовалось доказать. |
| Теорема: |
|
Для любого натурального числа выполнено равенство |
| Доказательство: |
|
Данную теорему можно доказать разложив по формуле , а можно более элегантно: Рассмотрим дробей . Каждую дробь представим в виде несократимой дроби . Заметим, что множество значений — это множество делителей числа . Так как дробь несократима, то и взаимно просты. Зная, что , легко понять, что всего дробей со знаменателем ровно . Так как, все дробей мы представили в несократимом виде, где знаменатель является делителем , то , так как всего дробей , что и требовалось доказать. |
| Теорема (Обобщённая мультипликативность): |
|
Пусть и — любые два натуральных числа, а , тогда: |
| Доказательство: |
|
Пусть тогда причем в общем случае и Поэтому можно записать: Здесь первые делителей являются также делителями а последние делителей являются делителями Распишем: В силу мультипликативности функции Эйлера, а также с учётом формулы где — простое, получаем: В первой строке записано во второй — а третью можно представить, как Поэтому: |
Применение теоремы Эйлера в других задачах
Задача об ожерельях
| Задача: |
| Требуется посчитать количество ожерелий из бусинок, каждая из которых может быть покрашена в один из цветов. При сравнении двух ожерелий их можно поворачивать, но не переворачивать (т.е. разрешается сделать циклический сдвиг). |
В ходе решения задачи мы приходим к формуле
Мы можем улучшить эту формулу, если рассмотрим выражение . Пусть , тогда числа и оба делятся на и больше не имеют общих делителей. Тогда . Таких натуральных и имеющих ровно .
Пользуясь функцией Эйлера, мы можем привести формулу к более лаконичному виду .
Алгоритм
Основной идеей алгоритма является формула . Для решения задачи нам нужны только простые делители числа . Их можно найти с помощью алгоритма факторизации. Написанный ниже алгоритм использует факторизацию числа, работающую за , однако есть более эффективные алгоритмы.
Асимптотика вычисления .
function phi (n):
result = n
i = 2
while (i*i <= n):
if n % i == 0:
while n % i == 0:
n /= i
result -= result / i
i++
if (n > 1):
result -= result/n
return result
См. также
- Задача об ожерельях
Ссылки
- Wikipedia — Функция Эйлера
- Алгоритм нахождения функции Эйлера
- Функция

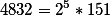
*(151^{1}-151^{0})=(32-16)(151-1)=2400)
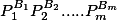
(P_2^{B_2}-P_2^{B_2-1}).....(P_m^{B_m}-P_m^{B_m-1}))
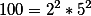
(5^{2}-5^{1})=(4-2)(25-5)=40)




![{displaystyle {begin{array}{rcl}varphi (n)&=&varphi (p_{1}^{k_{1}}),varphi (p_{2}^{k_{2}})cdots varphi (p_{r}^{k_{r}})\[.1em]&=&p_{1}^{k_{1}-1}(p_{1}-1),p_{2}^{k_{2}-1}(p_{2}-1)cdots p_{r}^{k_{r}-1}(p_{r}-1)\[.1em]&=&p_{1}^{k_{1}}left(1-{frac {1}{p_{1}}}right)p_{2}^{k_{2}}left(1-{frac {1}{p_{2}}}right)cdots p_{r}^{k_{r}}left(1-{frac {1}{p_{r}}}right)\[.1em]&=&p_{1}^{k_{1}}p_{2}^{k_{2}}cdots p_{r}^{k_{r}}left(1-{frac {1}{p_{1}}}right)left(1-{frac {1}{p_{2}}}right)cdots left(1-{frac {1}{p_{r}}}right)\[.1em]&=&nleft(1-{frac {1}{p_{1}}}right)left(1-{frac {1}{p_{2}}}right)cdots left(1-{frac {1}{p_{r}}}right).end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/595bed4719c49a400b24755d6bca6e759e7a8503)


![{displaystyle {mathcal {F}}{mathbf {x} }[m]=sum limits _{k=1}^{n}x_{k}cdot e^{{-2pi i}{frac {mk}{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44406da8bf27ff396599d35e91d4328c3f961a81)
![{displaystyle varphi (n)={mathcal {F}}{mathbf {x} }[1]=sum limits _{k=1}^{n}gcd(k,n)e^{-2pi i{frac {k}{n}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a88a09856ce4f73559b80fb01e44bdd70af8309)






![{displaystyle {begin{aligned}varphi (20)&=mu (1)cdot 20+mu (2)cdot 10+mu (4)cdot 5+mu (5)cdot 4+mu (10)cdot 2+mu (20)cdot 1\[.5em]&=1cdot 20-1cdot 10+0cdot 5-1cdot 4+1cdot 2+0cdot 1=8.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a4ce2d54734e410d4eea1d1a6b0d62ad7fbfed9)













![{displaystyle {begin{aligned}lim inf {frac {varphi (n+1)}{varphi (n)}}&=0quad {text{and}}\[5px]lim sup {frac {varphi (n+1)}{varphi (n)}}&=infty .end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc005e44784aa197220263d20f9a495ee655b528)




