Как найти функцию отображающую данную - Исправление недочетов и поиск решений вместе с Examum.ru

Содержание

Глава 3. Конформные отображения

Геометрический смысл аргумента и модуля производной функции комплексного переменного

Пусть дана аналитическая в области $D$ функция $f(z)$. Возьмем точку $z_0in D$, пусть производная функции в этой точке не равна нулю
$$f'(z_0)ne0.$$

Функция $w=f(z)$ отображает область $D$ на плоскости z на множество $E$ в плоскости $w$.

Точке $z_0in D$ соответствует точка $w_0=f(z_0)in E$.

Аргумент $arg f'(z_0)$ есть угол поворота касательной к любой
кривой, проведенной через точку $z_0$ при ее отображении с помощью функции $w=f(z)$ на плоскость $w$.

Модуль $|f'(z_0)|$ можно рассматривать как
величину масштаба в точке $z_0$ при отображении $w$. Если $|f'(z_0 )|>1$, то происходит растяжение бесконечно малого элемента, выходящего из
точки $z_0$. Если $|f'(z_0 )|<1$, то происходит сжатие, при $|f'(z_0 )|=1$ масштаб в окрестности точки $z_0$ не меняется.

Надо заметить, что все сказанное относится к точке и ее малой окрестности. В других точках кривой параметры отображения (коэффициент растяжения и угол поворота) изменяются.

Конформные отображения

Отображение одной плоскости на другую называется
конформным в точке $z$, если все бесконечно малые дуги, выходящие из этой точки, при отображении поворачиваются на один и тот же угол и получают одно и то же растяжение (сжатие).

Иными словами, при конформном отображении сохраняется подобие в бесконечно малых частях. Отображение с помощью аналитической функции является
конформным везде, кроме, быть может, точек, в которых производная данной аналитической функции равна нулю.

Отображение окрестности точки $z_0 $ на окрестность точки
$w_0$, осуществляемое аналитической функцией $w=f(z)$ и обладающее в точке $z_0$ свойством сохранения углов и постоянством растяжений,
называется конформным отображением первого рода, если поворот касательных происходит против часовой стрелки, тогда как в
конформном отображении второго рода касательные поворачиваются по часовой стрелке).

В дальнейшем будем рассматривать только конформные отображения первого рода.

В теории Конформных Отображений различают две основные задачи:

1. При известной функции $f(z)$ найти образ заданной области $D$;

2. Найти функцию $f(z)$, отображающую одну данную область $D$ на
другую данную область $G$.

Конформное отображение $f(z)$ при этом чаще всего рассматривается как взаимно однозначное (однолистное), когда для размещения
образа хватает плоскости $w$. Когда одного листа плоскости $w$ недостаточно, вводим римановы поверхности, которые позволяют строить конформные отображения с помощью многозначных функций.

При осуществлении Конформных Отображений следует использовать следующие общие принципы.

Принцип соответствия границ:
При конформном отображении друг на друга двух областей,
ограниченных замкнутыми жордановыми (без самопересечений) кривыми, между их границами всегда устанавливается взаимно однозначное и взаимно
непрерывное соответствие с сохранением направления обхода границы.

Принцип симметрии:
Пусть область $D$, содержащая в составе своей границы некоторый прямолинейный отрезок $gamma$ (конечной или бесконечной длины), отображается функций $w=f(z)$ на область $E$ так, что $gamma$ переходит в прямолинейный отрезок $Gamma$, входящий в границу области. Тогда область $D^{*}$, симметричная области $D$, относительно $gamma$, с помощью аналитической функции $w=f(z)$ отображается в область $E^{*}$, симметричную $E$, относительно $Gamma$.

Линейная функция

Отображение, осуществляемое линейной функцией $$ w = az + b,$$ где $a$ и $b$ — постоянные комплексные числа ($aneq0$), является конформным в расширенной комплексной плоскости.

Геометрический смысл.
Отображение, осуществляемое линейной функцией, складывается из

преобразования подобия (растяжение или сжатие с коэффициентом $r=|a|$) относительно начала координат,
поворота на угол $alpha=mbox{arg } a$ вокруг начала координат,
сдвига на вектор $b$.

Линейное отображение преобразует прямые в прямые (углы между прямыми сохраняются) и окружности в окружности. Покажем это свойство для окружностей.
$$
|z-z_0|=R, quad w=az+b ,,Rightarrow
$$
$$
z=displaystylefrac{w-b}{a}, quad |z-z_0|=displaystylefrac{|w-b-az_0|}{|a|}=R ,,Rightarrow
$$
$$
|w-b-az_0|=R|a| mbox{ — окружность с центром в точке } w_0=b+az_0.
$$

Замечание.

1. Линейное отображение будет однозначно определено, если известны $z_1neq z_2$, переходящие в $w_1neq w_2$:
$$
displaystylefrac{z-z_1}{z_2-z_1}=displaystylefrac{w-w_1}{w_2-w_1}.
$$

2. Линейное отображение будет однозначно определено, если известны $z_1rightarrow w_1$, $k=w’$:
$$
w-w_1=k(z-z_1).
$$

Инверсия

Инверсия $$ w=frac{1}{z}$$ является конформным отображением в расширенной комплексной плоскости.

Точка $z=0$ конформно отображается в $w=infty$, точка $z=infty$ конформно отображается в $w=0$. Доказательство конформности дано далее для более общего случая с дробно-линейной функцией.

Геометрический смысл.
Отображение, осуществляемое инверсией, складывается из двух симметричных отображений

относительно единичной окружности,
относительно действительной оси.

Круговое свойство.
Инверсия преобразует в окружность всякую окружность (прямые линии условно считаются окружностями с бесконечно большим радиусом).

Докажем это свойство.

Для окружности с центром в точке $z=0$ доказательство очевидно (например, через показательную форму комплексного числа):
$$
|z|=R ,, rightarrow ,, |w|=displaystylefrac{1}{R}.
$$
Рассмотрим произвольную окружность (включая, прямую):
$$
A(x^2+y^2)+Bx+Cy+D=0.
$$
$$
w=displaystylefrac{1}{z} ,, z=displaystylefrac{1}{w},
$$
$$
z=displaystylefrac{1}{u+mathbf iv}=displaystylefrac{u-mathbf i v}{u^2+v^2}.
$$
Подставим
$$
x=displaystylefrac{u}{u^2+v^2}, ,, y=-displaystylefrac{v}{u^2+v^2}
$$
в уравнение окружности и получим уравнение окружности (включая прямую) на плоскости $w$.
$$
D(u^2+v^2)+Bu-Cv+A=0
$$
Нетрудно заметить, что если линия (окружность или прямая) на плоскости $z$ проходит через точку $z=0$, то на плоскости $w$ ее образом является прямая. В противном случае — окружность.

Дробно-линейное отображение

Дробно-линейная функция
$$
w=frac{az+b}{cz+d},
$$
где $a$, $b$, $c$, $d$ – постоянные комплексные числа ($cneq0$, $ad-bcneq0$), является конформным в расширенной комплексной плоскости.

Считаем, что $cneq0$ (иначе получим линейную функцию) и $ad-bcneq0$ (иначе получим функцию тождественно равную константе).

Покажем, что отображение конформно во всех точках расширенной комплексной плоскости, включая $z=-frac{d}{c}$ и $z=infty$.

Круговое свойство:

Дробно-линейная функция отображает всякую окружность (включая прямую) в окружность.

Докажем это, записав $w$ как суперпозицию трех отображений (линейного, инверсии, линейного) для каждого из которых круговое свойство доказано:
$$
w=frac{az+b}{cz+d}= frac{caz+cb+ad-ad}{c(cz+d)}=
$$
$$
=frac{a(cz+d)}{c(cz+d)}+ frac{bc-ad}{c(cz+d)}=
$$
$$
=frac{a}{c}+frac{bc-ad}{c}frac{1}{cz+d}.
$$

Замечание 1.
При решении прямой задачи (нахождение образа области при известном отображении) удобно пользоваться принципом сохранения границ, определяя сначала образ границы области на плоскости $w$.

Замечание 2.
Если граница $Gamma$ области $D$ проходит через точку $z=-displaystylefrac{d}{c}$, то ее образом при дробно-линейном отображении $w=displaystylefrac{az+b}{cz+d}$ является прямая. Если не проходит — образом будет окружность.

Замечание 3.
Если образ границы $Gamma$ области $D$ — прямая, то ее уравнение можно найти по двум точкам.

Замечание.

Дробно-линейное отображение будет однозначно определено, если известны $z_1neq z_2neq z_3$, переходящие в $w_1neq w_2neq w_3$:
$$
displaystylefrac{z-z_1}{z-z_2}cdotdisplaystylefrac{z_3-z_2}{z_3-z_1}=displaystylefrac{w-w_1}{w-w_2}cdotdisplaystylefrac{w_3-w_2}{w_3-w_1}.
$$

Принцип симметрии

При решении обратной задачи (нахождение отображения по известной области $D$ на плоскости $z$ и ее образу $E$ на плоскости $w$) удобно пользоваться принципом симметрии:

Произвольное дробно-линейное отображение преобразует любые точки $z$ и $z^{*}$, симметричные относительно окружности $Gamma$ (в том числе и прямой) на плоскости $z$, в точки $w$ и $w^{*}$, симметричные относительно образа $w(Gamma)$ этой окружности на плоскости $w$.

Точки $z$ и $z^{*}$ называются симметричными относительно прямой, если они лежат по разные стороны от этой прямой на одинаковом от нее расстоянии, а соединяющий их отрезок перпендикулярен этой прямой.

Точки $z$ и $z^{*}$ называются симметричными относительно окружности $Gamma$ в $mathbb C_{}$, если они лежат на одном луче, выходящим из центра $z_0$ окружности $Gamma$, и произведение их расстояний до центра окружности равно квадрату радиуса $R$ этой окружности, то есть $$mbox{arg}, (z^{*}-z_0)=mbox{arg}, (z-z_0),$$
$$|z^{*}-z_0|cdot|z-z_0|=R^2.$$

При приближении точки $z$ к центру окружности $Gamma$ симметричная ей точка $z^{*}$ стремится к бесконечно удаленной точке. Тогда центр $z_0$ окружности $Gamma$ и бесконечно удаленную точку $z=infty$ будем считать симметричным относительно окружности $Gamma$.

Введенное определение симметрии относительно окружности можно рассматривать как развитие понятия симметрии относительно прямой.

Основные задачи нахождения ДЛО

Найти общий вид функции $w$: $$ z_1rightarrow0, ,, z_2rightarrowinfty.$$
Найти общий вид функции $w$: $$ mathfrak{I}mathbf{m}(z)>0rightarrow |w|<1, ,, z_0 (mathfrak{I}mathbf{m}(z_0)>0) rightarrow w_0=0. $$
Найти общий вид функции $w$: $$ |z|<1 rightarrow |w|<1, ,, z_1 (|z_1|<1) rightarrow w_1=0. $$

Целая степенная функция

$$ w=z^n, quad nin mathbb Z_{}, quad n>1. $$

Функция $w=z^n$ отображает расширенную комплексную плоскость $z$ на расширенную комплексную плоскость $w$.

Не является конформным при $z=0$, так как $$w’=n,z^{n-1} =0 ,, mbox{при } z=0.$$

Не является однолистной, так как всякая точка $w$, отличная от $w=0$ и $w=infty$, имеет $n$ различных прообразов. Для однолистности отображения следует брать на плоскости $z$ лишь сектор вида
$$kcdotdisplaystylefrac{2pi}{n}leqslant mbox{arg},zleqslant(k+1)cdotdisplaystylefrac{2pi}{n},,, kin mathbb Z_{}.$$

Исследуем поведение функции около точки $z=0$.
При помощи степенной функции $$ w=z^n $$ угол с вершиной в начале координат плоскости $z$ отображается в угол с вершиной в начале координат плоскости $w$ c раствором в $n$ раз большим:
$$
z=rho e^{mathbf i varphi},, rightarrow ,, w = z^n=rho^n e^{mathbf i nvarphi}.
$$
Отображение будет взаимно однозначным, если раствор угла на плоскости $w$ будет не более $2pi$.

Найти в какую область преобразуется квадрат
$$ 0le xle 1,quad 0le yle 1 $$ функцией $w=z^2+z-1$.

Решение. Выделим вещественную и мнимую части: $$
begin{array}{l}
u=x^2-y^2+x-1, v=2xy+y.
end{array}
$$

Определим образы участков границ данного квадрата:
begin{equation}
OA:quadleft{begin{array}{l} y=0, 0le xle1
end{array}right.quadhbox{дает}quad
left{begin{array}{l}
u=x^2+x-1, v=0.
end{array}right.
end{equation}
это отрезок вещественной оси $-1le ule 1$.
begin{equation}
AB:quadleft{begin{array}{l} x=1, 0le yle1
end{array}right.quadhbox{дает}quad
left{begin{array}{l}
u=1-dfrac{v^2}9, 0le vle3
end{array}right.hskip17.5pt
end{equation}
это часть параболы в первом квадранте.

Образы отрезков $BC$ и $CO$ также являются дугами парабол:
begin{equation}label{eq g3 p5 3}
BC:quad u=frac14big(v^2-9big),quad 1le vle 3,
end{equation}
begin{equation}label{eq g3 p5 4}
CO:quad u=-1-v^2,quad 0le vle1.
end{equation}
Так как точка $z=displaystylefrac12(1+i)$ переходит в точку $w=i-displaystylefrac12$, то внутренность квадрата переходит во внутренность криволинейного
четырехугольника.

Ответ: Внутренность квадрата переходит во внутренность криволинейного четырехугольника.

Радикал

Рассмотрим функцию
begin{equation}
w=sqrt[n]{z},
end{equation}
обратную степенной функции $z=w^n$.

Примем, что $$w=infty mbox{ при } z=infty.$$

Во всех точках расширенной плоскости $z$, кроме точек
$z=0$ и $z=infty$ (где эта функция соответственно равна $w=0$ и $w=infty)$, эта функция $n$-значна и все ее $n$ различных значений для каждого
фиксированного $z=re^{ivarphi}$ (не равные 0 и $infty$) дает формула:
$$ w=sqrt[n]{r}cdot e^{itfrac{scriptstylearg z+2pi k}
{scriptstyle n}} =sqrt[n]{r}cdot e^{itfrac{scriptstylearg z} {scriptstyle n}}cdot e^{itfrac{scriptstyle2pi k}{scriptstyle
n}}quadhbox{при}
quad k=0,1,dots,n-1.
$$

Через $w_k$ обозначим множество всех точек $w$, соответствующих данному фиксированному значению $k$. В результате получим $n$ функций
$w_k$, $k=0,2,dots,n-1$, называемых ветвями многозначной функции $w=sqrt[n]{z}$.
$$ w_k= sqrt[n]{r}cdot e^{itfrac{scriptstylearg z} {scriptstyle n}}cdot e^{itfrac{scriptstyle2pi k}{scriptstyle
n}}quadhbox{при}
quad k=0,1,dots,n-1.
$$

Очевидно, $$ w_{k+1}=w_k cdot
e^{itfrac{scriptstyle 2pi k}{scriptstyle n}}.
$$

Рассмотрим какую-нибудь ветвь $w_k$ функции
и заставим точку $z$ описать в плоскости какую-нибудь замкнутую
кривую.

Если эта кривая не содержит внутри себя точку $z=0$ (сплошная кривая на рисунке), то непрерывно
изменяющийся аргумент точки $z$ вернется к прежнему значению с возвращением точки $z$ в исходное положение. В силу этого и ветвь $w_k$ радикала
останется прежней (т.е. мы вернемся к прежнему значению корня в исходной точке).

Картина изменится, если кривая $l$ будет содержать внутри себя
точку $z=0$ (пунктирная кривая на рисунке). В этом случае после полного обхода кривой $l$ аргумент точки $z$ в исходном положении
увеличится на $pm 2pi k$ (в зависимости от того, совершается ли обход кривой против или по часовой стрелки), в силу чего мы от значения $w_k$
корня в исходной точке перейдем либо к значению
$$ w_kcdot e^{itfrac{scriptstyle2pi}{scriptstyle n}}=w_{k+1},$$
либо к значению
$$ w_kcdot e^{-itfrac{scriptstyle2pi}{scriptstyle n}}=w_{k-1}. $$

Повторяя обход вокруг начала координат в
том или ином направлении достаточное количество раз, мы можем перейти от исходной ветви $w_k$ радикала к любой другой ветви. Очевидно, что после
$n$ обходов начала координат в одном направлении мы возвращаемся к исходной ветви радикала.

Точка, обладающая тем свойством, что обход вокруг нее переводит от одной ветви многозначной функции к другой ветви, называется точкой
разветвления этой функции. Таким образом, точка $z=0$ будет точкой разветвления функции $w=sqrt[n]{z}$.

Из сказанного следует, что мы можем выделить $n$ однозначных ветвей $w_k$ функции $w=sqrt[n]{z}$ только в такой области $D$, которая не
содержит ни одной замкнутой кривой, заключающей внутри себя точку $z=0$.

Расширенная плоскость $z$ с любым разрезом от точки $z=0$ до точки $z=infty$ и, в частности, с разрезом вдоль положительной части вещественной
оси (левая часть рисунка) не содержит ни одной замкнутой кривой, обходящей точку $z=0$. На ней можно выделить $n$ однозначных ветвей
$w_k$, $k=0,1,dots,n-1$, радикала, принимающих каждая одно из значений $sqrt[n]{z}$.

Эти ветви будут однолистно отображать расширенную плоскость $z$ с разрезом вдоль положительной части вещественной оси на секторы $$
kfrac{2pi}n<arg wle(k+1)frac{2pi}n,quad k=0,1,dots,n-1, $$ расширенной плоскости $w$ (правая часть рисунка, где $n=6$). Отображения обратны рассмотренному ранее отображению $w=z^n$ и непрерывны. Для того чтобы фиксировать какую-либо из ветвей $w_k$ радикала,
достаточно лишь указать, в каком из секторов должно изменяться $w$.

Показательная функция

Рассмотрим показательную функцию $$ w=e^z,quad z=x+iy. $$

Перепишем $$ w=e^x(cos y+isin y)=r(cosvarphi+isinvarphi), $$
поэтому
$$
r=|w|=e^x,quadvarphi=mbox{arg},w=y. $$

Линии $x=hbox{const}$ переходят в окружности $r=hbox{const}$ ($y$ и $varphi$ — любые),

Линии $y=mbox{const}$ переходят в лучи $varphi=mbox{const}$ ($x$ и $r$ — любые).

Для взаимной однозначности при отображении с помощью функции $w=e^z$ необходимо и
достаточно, чтобы отображаемая область не содержала никакой пары различных точек $z_1$ и $z_2$, для которых $z_1-z_2=2pi ki$, $kin N$. Этому
условию удовлетворяет любая горизонтальная полоса шириной меньше $2pi$, например, полосы $2pi k<mathfrak{Im}, z<2pi(k+1)$.

Полоса $0<mathfrak{Im}, z<pi$ плоскости $z$ отображается функцией $w=e^z$ на верхнюю полуплоскость плоскости $w$
Полоса $0<mathfrak{Im}, z<2pi$ — на плоскость $w$ с разрезом по положительной части вещественной оси, при этом прямые $y=0$ и $y=2pi$ отображаются в лучи $varphi=0$ и $varphi=2pi$, т.е. обе в положительную вещественную ось (поэтому нужен разрез).
Полуполоса $-infty<mathfrak{Re}, z<0$, $0<mathfrak{Im} z<pi$ отображается в единичный полукруг $|w|<1$, $mathfrak{Im} w>0$.
Полуполоса $0<mathfrak{Re}, z<infty$, $0<mathfrak{Im},z<pi$ — на полуплоскость $mathfrak{Im}, w>0$, из которой удален единичный полукруг.

Логарифмическая функция

Логарифмическая функция обратна показательной, бесконечнозначна, все ее значения вычисляются по формуле
$$ w=mbox{Ln }z=mbox{ln }|z|+imbox{Arg }z=mbox{ln }|z|+i(mbox{arg }z+2pi k),quad k=0,pm1,pm2,dots . $$
Дополнительно примем, что $w=infty$ при $z=0$ и $z=infty$.

Обозначив через $w_k$ множество всех
точек $w$, соответствующих данному фиксированному значению $k$, получим бесконечное множество функций, которые называются ветвями многозначной функции $w=mbox{Ln }z$
$$ w_k= mbox{ln }|z|+imbox{Arg }z=mbox{ln }|z|+i(mbox{arg }z+2pi k),quad k=0,pm1,pm2,dots . $$

Бесконечнозначность логарифма связана с бесконечнозначностью его мнимой части $mbox{Arg }z$. Поэтому область не должна допускать обхода начала координат по непрерывной кривой, так как при таком обходе значение $mbox{Arg }z$ изменяется на $2pi$. Область
указанного типа будет сектором концентрического кольца: $$ 0<r_1le rle r_2,quad -pileftarrowvarphi_1levarphilevarphi_2<pi. $$

Каждая ветвь $w_k$ является однозначной функцией. Например, его главное значение $$
mbox{ln }z=mbox{ln }|z|+imbox{arg }z.
$$

Функция $mbox{Ln }z$ отображает всю плоскость с разрезом на горизонтальную полосу однозначно. Если аргумент $z$ увеличить на $2pi$, будет другая ветвь, которая отображает всю плоскость с разрезом (другой лист римановой поверхности) на другую полосу.

$z=0$ — точка разветвления.

Вещественная и мнимая части этой функции
$$
u=displaystylefrac12mbox{ln }(x^2+y^2), ,, v=mbox{arctg }frac{y}{x}+2pi k.
$$
имеют непрерывные частные производные, удовлетворяющие условиям Коши-Римана.

А это значит, что выделенная ветвь логарифма представляет собой дифференцируемую функцию комплексного переменного $z$ в области $D$. Производная ее не обращается в нуль и, следовательно, функция $w=mbox{ln }z$ осуществляет конформное отображение области $D$ на некоторую область плоскости $w$.

Найти образ плоскости с разрезом вдоль
положительной части вещественной оси при отображении однозначной ветвью логарифма, когда $z_0=i$ переходит в $w_0=displaystylefrac52pi i$.

Решение. В области $D$, представляющей собой плоскость $z$ с разрезом вдоль положительной части вещественной оси, $$
z=|z|(cosvarphi+isinvarphi),quad |z|>0, 0<varphi<2pi, $$ выделим ветвь логарифма $$ w=ln|z|+ivarphi. $$ Эта ветвь отображает $D$ на
полосу $0<v<2pi$ (здесь принимаем $w=u+iv$). Далее имеем $$ w(i)=displaystylefrac12pi i. $$ Чтобы получить $w_0 =displaystylefrac52pi i$, надо взять $w(i)+2pi
i=displaystylefrac52pi i$. А ветвь $$ w=ln|z|+i(varphi+2pi) $$ отображает $D$ на полосу $2pi!<!v!<!4pi$, содержащую точку $w_0=displaystylefrac52pi i$.

Ответ: $2pi<v<4pi$.

Функция Жуковского

Так называют функцию
begin{equation}label{eq g3 p9 1}
w=frac12left(z+frac1{z}right).
end{equation}
Ее производная $$ w’=frac12left(1-frac1{z^2}right) $$ конечна и отлична от нуля во всех точках плоскости $z$, кроме точек $z=0,+1,-1$, в
силу чего отображение конформно в плоскости $z$, исключая три упомянутые точки.

Установим условие однолистности отображения. Пусть $z_1!ne!z_2$, но $w_1=w_2$, т.е. $$
frac12left(z_1+frac1{z_1}right)=
frac12left(z_2+frac1{z_2}right).
$$ Переписав последнее равенство в виде $$
big(z_1-z_2big)left(1-frac1{z_1z_2}right)=0
$$ найдем из него, что
$$z_1z_2 =1.$$
Следовательно, отображение будет однолистным в любой области, не содержащей никаких двух точек, связанных
равенством $z_1z_2 =1$.

Этому условию удовлетворяют, в частности, круг $|z|<1$ и внешность круга $|z|>1$.

Для того чтобы лучше представить себе рассматриваемое отображение, положим $$ z=re^{ivarphi},quad w=u+iv $$ и произведя соответствующие замены
в функции Жуковског и отделив вещественные и мнимые части, получим два вещественных равенства, зависящие от двух параметров
$$ u=frac12left(r+frac1rright)cosvarphi,quad v=frac12left(r-frac1rright)sinvarphi. $$

Рассмотрим две упомянутые выше области $|z|<1$ и $|z|>1$.

В области $|z|<1$ возьмем окружность
$$|z|=r<1.$$
Из параметрической записи исключим
угол $varphi$. Получим, что эта окружность при отображении перейдет в эллипс $$
frac{u^2}{a^2}+frac{v^2}{b^2}=1
$$ с полуосями $$ a=frac12left(r+frac1rright),quad b=frac12left|r-frac1rright| $$ и полуфокусным расстоянием $$ c=sqrt{a^2-b^2}=1, $$
не зависящим от радиуса $r$ окружности $|z|=r$. Таким образом, окружности $|z|=r$, $0<r<1$, при данном отображении перейдут в софокусные эллипсы
с полуосями $a$ и $b$, фокусы которых находятся в точках $(pm1,0)$.

Так как $r-dfrac1r<0$ при $r<1$, то из представления вещественной и мнимой частей следует, что при положительном направлении обхода окружностей
$|z|=r$ соответствующие эллипсы обходятся в отрицательном направлении. При $rto0$ будет $atoinfty$ и $btoinfty$. Следовательно, при $rto0$
эллипсы, постепенно округляясь, увеличиваются и заполняют всю плоскость $w$. При $rto1-0$ будет $ato1$ и $bto0$, и эллипсы постепенно
вырождаются в разрез вдоль интервала $[-1,1]$ вещественной оси плоскости $w$.

Рассмотрим, во что преобразуются лучи, выходящие из начала координат.

Для этого исключим $r$ из уравнений для вещественной и мнимой частей. Получим $$
frac{u^2}{cos^2varphi}-frac{v^2}{sin^2varphi}=1
$$ уравнение гиперболы с полуфокусным расстоянием $$ c=sqrt{a^2+b^2}=1. $$ Следовательно, отображение переводит лучи $arg z=varphi$ в
семейство гипербол с теми же фокусами $(pm1,0)$, что и у семейства эллипсов (вершины гипербол выколоты).

Итак, функция Жуковского однолистно и конформно отображает круг $|z|<1$ на всю плоскость $w$ с разрезом вдоль вещественной оси от точки
$w=-1$ до точки $w=1$. При этом верхняя полуокружность переходит в нижний берег разреза, а нижняя полуокружность — в верхний берег разреза.

Верхний единичный полукруг $|z|<1$, $mathfrak{Im} z>0$ функция Жуковского отобразит на нижнюю полуплоскость $mathfrak{Im} w<0$, а нижний
полукруг $|z|<1$, $mathfrak{Im} z<0$ — на верхнюю полуплоскость $mathfrak{Im} w>0$.

Рассмотрим теперь в области $|z|>1$ окружности $|z|=r$, где $1<r<+infty$.

Проведя точно такой же анализ, как и в предыдущем случае, легко
доказать, что функция Жуковского отображает эти окружности на те же самые эллипсы, что и в предыдущем случае, но проходимые в
положительном направлении.

При $rto1+0$ эти эллипсы вырождаются в разрез $[-1,1]$ вещественной оси $u$, а при $rto+infty$ эллипсы,
округляясь, увеличиваются и заполняют всю плоскость $w$.

Таким образом, функция $w=frac12left(z+frac1{z}right)$ однолистно и конформно отображает
область $|z|>1$ на всю плоскость $w$ с разрезом вдоль вещественной оси от точки $w=-1$ до точки $w=1$. При этом верхний полукруг отображается на
верхнюю полуплоскость, а нижний полукруг — на нижнюю полуплоскость.

Обратная к функции Жуковского функция $$ w=z+sqrt{z^2+1} $$ двузначна, что обусловлено двузначностью квадратного корня. Каждую точку $z$ она
отображает в две точки $w_1$ и $w_2$, связанные условием $w_1w_2=1$. Легко показать, что точки $z=-1$ и $z=1$ будут точками разветвления этой
функции. Таким образом, в любой области, не содержащей замкнутых кривых, обходящих лишь одну из этих точек, можно выделить две однозначные ветви
обратной функции. Этому условию, в частности, удовлетворяет вся плоскость $z$ с разрезом вдоль отрезка $[-1,1]$ вещественной оси. Ветви обратной
функции однолистно отображают плоскость $z$ с указанным разрезом либо на круг $|w|<1$, либо на круг $|w|>1$ и аналитичны.

Тригонометрические функции

Теорема Римана. Основные принципы конформных отображений

Теорема 1 (Римана).

Всякую односвязную область $D$
комплексной плоскости $z$, граница которой состоит более чем из одной точки, можно конформно отобразить на внутренность единичного круга $|w|<1$
плоскости $w$ и притом бесконечно многими способами.

Теорема 2 (Римана).

Функция $w=f(z)$, осуществляющая
конформное отображение заданной односвязной области $D$ $($граница которой состоит более чем из одной точки$)$ на единичный круг $|w|<1$
определена единственным образом, если выполняются условия: $$ w_0=f(z_0)quadhbox{и}quadarg f'(z_0)=alpha, $$ где $z_0in D$, $w_0$ —
центр круга, $alpha$ — заданное вещественное число.

Применения конформных отображений

Конформные отображения имеют многочисленные применения.

Например, они применяются в картографии при построении географических карт [Маркушевич А.И. «Комплексные числа и конформные отображения»]. Каждая географическая карта изображает часть земной поверхности на плоскости (на листе бумаги). При таком изображении очертания материков и морей подвергаются искажению. Оказывается, однако, что можно строить карту, не изменяя величины углов между различными линиями на земной поверхности, с помощью стереографической проекции и конформных отображений.

Наиболее важные применения конформных отображений относятся к вопросам физики и механики [Маркушевич А.И. «Комплексные числа и конформные отображения»]. Например, задачи, где требуется вычислить электрический потенциал в точках пространства, окружающего заряженный конденсатор, или вычислить температуру внутри нагретого тела, вычислить скорости частиц жидкости или газа в потоке, движущемся в некотором канале и обтекающем при этом какие-либо препятствия и т.п, решаются без больших трудностей случае, когда тела имеют простую форму. Конформные отображения простой фигуры посредством некоторой функции комплексного переменного позволяют перейти к фигуре с более сложной формой, когда задача в простейшем случае уже решена.

Известный пример — расчет профиля крыла самолета [Маркушевич А.И. «Комплексные числа и конформные отображения»]. Задача о скоростях частиц потока воздуха, обтекающего крыло самолета, сводится к более простой задаче обтекания круглого цилиндра с помощью функции Жуковского (Николай Егорович Жуковский (1847-1921) широко использовал комплексные числа и конформные отображения для расчета самолетов). На рисунке показан профиль крыла самолета в поперечном сечении (рис. снизу) и более простая форма — круг, то есть само тело — круглый цилиндр (рис. сверху)

Источник

Ответ:
Отображением множества E в
множество F,
или функцией,
определенной на E со
значениями в F,
называется правило, или закон f,
который каждому элементу ставит
в соответствие определенный элемент.

Элемент называютнезависимым
элементом,
или аргументом функции f,
элемент называютзначением
функции f,
илиобразом;
при этом элемент называетсяпрообразом элемента .

Отображение
(функцию) обычно обозначают буквой f или
символом ,
указывая тем самым, чтоf отображает
множество E в F.
Употребляется также обозначение ,
указывающее, что элементуx соответствует
элемент f(x).
Иногда функцию удобно задавать посредством
равенства, в котором содержится закон
соответствия. Например, можно говорить,
что «функция f определена
равенством «.
Если «y»
— общее наименование элементов множества F,
т. е. F =
{y},
то отображение записывают
в виде равенстваy = f(x)
и говорят, что это отображение задано
явно.

2.
Образ и прообраз множества при заданном
отображении

Пусть
задано отображение и
множество.

Множество
элементов из F,
каждый из которых является образом хотя
бы одного элемента из D при
отображении f,
называется образоммножества D и
обозначается f(D).

Очевидно, .

Пусть
теперь задано множество .

Множество
элементов таких,
что,
называетсяпрообразом множества Y при
отображении f и
обозначается f^-1(Y).

Если ,
то.
Если при каждоммножествоf^-1(y)
состоит не более чем из одного элемента ,
тоf называетсявзаимно
однозначным отображением E в F.
Впрочем, можно определить взаимно
однозначное отображение f множества E на F.

Отображение называется:

— инъективным (или инъекцией,
или взаимно
однозначным отображением множества E в F),
если ,
или еслиуравнениеf(x)
= y имеет
не более одного решения;

— сюръективным (или сюръекцией,
или отображением
множества E на F),
если f(E)
= F и
если уравнениеf(x)
= y имеет
по крайней мере одно решение;

— биективным (или биекцией,
или взаимно
однозначным отображением множества E на F),
если оно инъективно и сюръективно, или
если уравнениеf(x)
= y имеет
одно и только одно решение.

3.
Суперпозиция отображений. Обратное,
параметрическое и неявное отображения

1) Пусть и.
Поскольку,
то отображениеg каждому
элементу относит
определенный элемент.

Таким
образом, каждому посредством
правилапоставлен
в соответствие элемент

Тем
самым определено новое отображение
(или новая функция), которое
назовем композицией
отображений,
или суперпозицией
отображений,
или сложным
отображением.

2) Пусть —
биективное отображение иF =
{y}.
В силу биективности f каждому соответствует
единичный образx,
который обозначим через f^-1(y),
и такой, что f(x)
= y.
Таким образом, определено отображение ,
которое называетсяобратным
отображению f,
или обратной
функцией функции f.

Очевидно,
отображение f обратно
отображению f^-1.
Поэтому отображения f и f^-1 называют взаимно
обратными.
Для них справедливы соотношения

3) Пусть

причем
хотя бы одно из этих отображений,
например ,
биективно. Тогда существует обратное
отображение,
а значит,.

Определенное
таким образом отображение называется
заданным параметрически с помощью
отображений ;
причем переменная изназываетсяпараметром.

4) Пусть
на множестве определено
отображение,
где множествосодержит
нулевой элемент. Предположим, что
существуют множестватакие,
что при каждом фиксированномуравнениеимеет
единственное решение.
Тогда на множествеE можно
определить отображение ,
ставящее каждомув
соответствие то значение,
которое при указанномx является
решением уравнения .

Относительно
так определенного отображения

говорят,
что оно задано неявно посредством
уравнения .

5) Отображение называетсяпродолжением отображения ,
аg — сужением отображения f,
если и.

Сужение
отображения на
множествоиногда
обозначают символом.

6) Графиком отображения называется
множество

Ясно,
что .

12.
монотонные функции. Обратная функция,
теорема существования. Функции y=arcsinx
y=arcos
x
х свойства и графики.

Ответ:
Моното́нная
фу́нкция —
это функция, приращение которой
не меняет знака, то есть либо всегда
неотрицательно, либо всегда неположительно.
Если в дополнение приращение не равно
нулю то функция называется стро́го
моното́нной.

.Пусть
имеется функция f(x) определенная на
отрезке <a,b>, значения которой
принадлежат некоторому отрезку <c,d>.
Если

то
говорят, что на отрезке <c,d> определена
функция, обратная к функции f(x) и
обозначают это так:x=f^(-1)(y).

Обратите
внимание на отличие этого определения
от определения заполненности отрезка
<c,d> сплошь. В определении f^(-1)(…)
стоит квантор , т.е. значение х,
обеспечивающее равенство y=f(x), должно
быть единственным, в то время как в
определении заполненности отрезка<c,d>
сплошь стоит квантор , что говорит о
том, что может быть несколько значений
х, удовлетворяющих равенству y=f(x).

Обычно,
говоря об обратной функции, заменяют х
на у а y на x(x «y) и пишут y=f^(-1)(x).
Очевидно, что исходная функция f(x) и
обратная функция f^(-1)(x)
удовлетворяют соотношению

f^(-1)(f(x))=f(f^(-1)(x))=x.

Графики
исходной и обратной функции получаются
друг из друга зеркальным отображением
относительно биссектрисы первого
квадранта.

Теорема. Пусть
функция f(x) определена, непрерывна и
строго монотонно возрастает (убывает)
на отрезке [a,b]. Тогда на отрезке [f(a),f(b)]
определена обратная функция f^(-1)(x),
которая также непрерывна и строго
монотонно возрастает (убывает).

Доказательство.

Докажем
теорему для случая, когда f(x) строго
монотонно возрастает.

Существование
обратной функции.

Так
как по условию теоремы f(x) непрерывна,
то, согласно предыдущей теореме, отрезок
[f(a),f(b)] заполнен сплошь. Это означает,
что .

Докажем,
что х единственно. Действительно, если
взять х’>x, то будет f(x’)>f(x)=y и поэтому
f(x’)>y. Если взять х’’<x, то будет
f(x’’)<f(x)=y и поэтому f(x’’)<y. В обоих
случаях f(x)¹ y и поэтому x единственно.
Следовательно, х=f^(-1)(y)
и f^(-1)(…)
существует.

Монотонность
обратной функции.

Сделаем
обычную замены x «y и будем писать y=
f^(-1)(x).
Это значит, что x=f(y).

Пусть
x₁>x₂.
Тогда:

y₁=
f^(-1)(x₁);
x₁=f(y₁)

y₂=
f^(-1)(x₂);
x₂=f(y₂)

Какое
же соотношение между y₁ и
y₂?
Проверим возможные варианты.

а)
y₁<y₂?
Но тогда f(y₁)<f(y₂)
и x₁<x₂,
а у нас было x₁>x₂.

б)
y₁=y₂?
Но тогда f(y₁)=f(y₂)
и x₁=x₂,
а у нас было x₁>x₂.

в)
Остается единственный вариант y₁>y₂,
т.е. Но тогда f^(-1)(x₁)>f^(-1)(x₂),
а это и означает, что f^(-1)(…)
строго монотонно возрастает.

Непрерывность
обратной функции.

Т.к.
значения обратной функции заполняют
сплошь отрезок [a,b], то по
предыдущей теоремеf^(-1)(…)
непрерывна. <

<=»» a=»»
style=»color: rgb(255, 68, 0);»>

y = arcsin x	y = arccos x
функция обратная функции y = sin x, —/ 2x/ 2	функция обратная функции y = cos x, 0 x

<=»»
a=»» style=»color: rgb(0, 0, 0); font-family: Arial;
font-size: 11px; font-style: normal; font-variant: normal;
font-weight: normal; letter-spacing: normal; line-height: normal;
orphans: auto; text-align: start; text-indent: 0px; text-transform:
none; white-space: normal; widows: auto; word-spacing: 0px;
-webkit-text-stroke-width: 0px; background-color: rgb(0, 171, 160);»>

Свойства
функций

	y = arcsin x	y = arccos x
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ:	[-1; 1]	[-1; 1]
ОБЛАСТЬ ЗНАЧЕНИЙ:		[0; )
ЧЕТНОСТЬ, НЕЧЕТНОСТЬ:	нечетная	ни четная, ни нечетная
НУЛИ:	y = 0 при x = 0	y = 0 при x = 1
ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА:	y > 0, при x (0;]y < 0, при x [-1; 0)	y = 0 при x = 1 y > 0 при x [-1; 1)
ЭКСТРЕМУМЫ:	нет		нет
ПРОМЕЖУТКИ МОНОТОННОСТИ:	возрастает на всей области определения	убывает на всей области определения

arcsin
x + arccos x = /2

<=»»
a=»» style=»color: rgb(255, 68, 0); font-family:
Arial; font-size: 11px; font-style: normal; font-variant: normal;
font-weight: normal; letter-spacing: normal; line-height: normal;
orphans: auto; text-align: start; text-indent: 0px; text-transform:
none; white-space: normal; widows: auto; word-spacing: 0px;
-webkit-text-stroke-width: 0px; background-color: rgb(0, 171, 160);»>

y = arctg x	y = arcctg x
функция обратная функции y = tg x, —/ 2 < x </ 2	функция обратная функции y = ctg x, 0 < x <

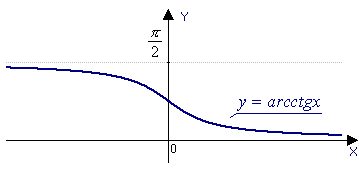
13.композиция
функций. Элементарные функции. Функции
y=arctg
x
, y
= arcctg
x,
их свойства и графики.

Ответ:
В математике компози́ция
фу́нкций (суперпози́ция
фу́нкций) —
это применение одной функции к
результату другой.

Композиция
функций G и F обычно
обозначается G∘F,
что обозначает применение функции G к
результату функции F.

Пусть F:X→Y и G:F(X)⊂Y→Z две
функции. Тогда их композицией называется
функция G∘F:X→Z,
определённая равенством:

(G∘F)(x)=G(F(x)),x∈X.

Элементарные
функции — функции,
которые можно получить с помощью
конечного числа арифметических действий
и композиций из
следующих основных элементарных
функций^[1]:

алгебраические:
- степенная;
- рациональная.
трансцендентные:
- показательная и логарифмическая;
- тригонометрические и обратные
  тригонометрические.

Каждую
элементарную функцию можно задать
формулой, то есть набором конечного
числа символов, соответствующих
используемым операциям. Все элементарные
функции непрерывны на
своей области определения.

Иногда
к основным элементарным функциям относят
также гиперболические
и обратные гиперболические функции,
хотя они могут быть выражены через
перечисленные выше основные элементарные
функции.

y = arctg x	y = arcctg x
функция обратная функции y = tg x, —/ 2 < x </ 2	функция обратная функции y = ctg x, 0 < x <

	y = arctg x	y = arcctg x
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ:	R	R
ОБЛАСТЬ ЗНАЧЕНИЙ:		(0; )
ЧЕТНОСТЬ, НЕЧЕТНОСТЬ:	нечетная	ни четная, ни нечетная
НУЛИ:	y = 0 при x = 0	нулей нет
ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА:	y > 0, при x (0;]y < 0, при x (-; 0)	y > 0 при x R
ЭКСТРЕМУМЫ:	нет	нет
ПРОМЕЖУТКИ МОНОТОННОСТИ:	возрастает при x R	убывает при x R

arctg
x + arcctg x = /2

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Виды отображений

Пусть %%f%% — отображение множества %%X%% в множество %%Y%%.

Инъективное отображение

Отображение %%f%% называется инъективным,

если для любых элементов %%x_1, x_2 in X%%, %%x_1 neq x_2%%, следует, что %%f(x_1) neq f(x_2)%%.
$$
forall x_1, x_2 in X~~x_1 neq x_2 rightarrow f(x_1) neq f(x_2).
$$

Другими словами, отображение %%f%% инъективно, если образы различных элементов из %%X%% также различны.

Пример

Функция %%f(x) = x^2%%, определенная на множестве %%mathbb{R}%%, не является инъективной, так как при %%x_1 = -1, x_2 = 1%% получаем одно и тоже значение функции %%f(x_1) = f(x_2) = 1%%.

Сюръективное отображение

Отображение %%f%% называется сюръективным,
если для всякого элемента %%y in Y%% существует элемент %%x in X%% с условием, что %%f(x) = y%%.
$$
forall y in Y~exists x in X : f(x) = y.
$$

Другими словами, отображение %%f%% сюръективно, если каждый элемент %%y in Y%% является образом хотя бы одного элемента %%x in X%%.

Пример

Отображение %%f(x) = sin(x)%%, определенное на множестве %%mathbb R%%, с множеством %%Y = [-2,2]%% не является сюръективным, т.к. для элемента %%y = 2 in Y%% нельзя найти прообраз %%x in X%%.

Биективное отображение

Отображение %%f%% называется биективным,
если оно инъективно и сюръективно. Биективное отображение также называется взаимно однозначным или преобразованием.

Обычно, словосочетания «инъективное отображение», «сюрьективное отображение» и «биективно отображение» заменяют на «инъекция», «сюръекция» и «биекция» соответственно.

Обратное отображение

Пусть %%f: X to Y%% — некоторая биекция и пусть %%y in Y%%. Обозначим через %%f^{-1}(y)%% единственный элемент %%x in X%% такой, что %%f(x) = y%%. Тем самым мы определим некоторое новое отображение %%g: Y to X%%, которое снова является биекцией. Ее называют обратным отображением.

Пример

Пусть %%X, Y = mathbb R%% — множество действительных чисел. Функция %%f%% задана формулой %%y = 3x + 3%%. Имеет ли данная функция обратную? Если да, то какую?

Для того чтобы узнать имеет ли данная функция обратную ей, необходимо проверить является ли она биекцией. Для этого проверим является ли данное отображение инъективным и сюръективным.

Проверим инъекцию. Пусть %%x_1 neq x_2%%. Проверим, что %%f(x_1) neq f(x_2)%%, то есть %%3 x_1 + 3 neq 3 x_2 + 3%%. Предположим противное, %%3 x_1 + 3 = 3 x_2 + 3%%. Тогда получается, что %%x_1 = x_2%%. Получили противоречие, т.к. %%x_1 neq x_2%%. Следовательно, %%f%% — инъекция.
Проверим сюръекцию. Пусть %%y in Y = mathbb{R}%%. Найдем элемент %%x in X = mathbb{R}%% c условием, что %%f(x) = y%%, то есть %%3x + 3 = y%%. В данном равенстве задан элемент %%y in mathbb{R}%% и нужно найти элемент %%x%%. Очевидно, что
$$
x = frac{y-3}{3} text{ и } x in mathbb R
$$
Следовательно, отображение %%f%% сюръективно.

Так как %%f%% — инъекция и сюръекция, то %%f%% — биекция. И, соответственно, обратным отображением является %%x = frac{y-3}{3}%%.

Источник

Помогаю со студенческими работами здесь

Отобразить конформно область
Отобразить конформно на верхнюю полуплоскость область {{zin C: alpha < arg z <pi — alpha }} {…

Найти целую линейную функцию, отображающую треугольник с вершинами в точках
Здравствуйте! Может ли кто нибудь помочь решить вот такую вот задачу, а то совершенно не понимаю…

Найти одну из линейных функций, отображающих область Dz на область Dw , если:
Посмотрите, пожалуйста, правильно ли я начертила? не уверена в знаке: если по часовой стрелке то…

Найти область определения, область значения, инверсию, и композиции данного бинарного отношения:
Вот собственно бинарное отношение rho ={(x,y) | x,y epsilon R и x^2+y^2>8} Вот композиции rho…

Установить область определения и область значения операторов, найти образ x0 при данном отображении
Здравствуйте,помогите пожалуйста…нужно установить область определения и область значения…

Указать область определения и область значения, найти композицию
Пусть множество A={a,b,c} B={1,2,3,4}
p1subset A x B
p2subset {B}^{2}
Изобразить р1 и р2…

Искать еще темы с ответами

Или воспользуйтесь поиском по форуму:

Источник

Линейная аппроксимация

При обработке экспериментальных данных часто возникает необходимость аппроксимировать их линейной функцией.

Аппроксимацией (приближением) функции f(x) называется нахождение такой функции ( аппроксимирующей функции ) g(x) , которая была бы близка заданной. Критерии близости функций могут быть различные.

В случае если приближение строится на дискретном наборе точек, аппроксимацию называют точечной или дискретной .

В случае если аппроксимация проводится на непрерывном множестве точек (отрезке), аппроксимация называется непрерывной или интегральной . Примером такой аппроксимации может служить разложение функции в ряд Тейлора, то есть замена некоторой функции степенным многочленом.

Наиболее часто встречающим видом точечной аппроксимации является интерполяция – нахождение промежуточных значений величины по имеющемуся дискретному набору известных значений.

Пусть задан дискретный набор точек, называемых узлами интерполяции , а также значения функции в этих точках. Требуется построить функцию g(x) , проходящую наиболее близко ко всем заданным узлам. Таким образом, критерием близости функции является g(xi)=yi .

В качестве функции g(x) обычно выбирается полином, который называют интерполяционным полиномом .

В случае если полином един для всей области интерполяции, говорят, что интерполяция глобальная .

В случае если между различными узлами полиномы различны, говорят о кусочной или локальной интерполяции.

Найдя интерполяционный полином, мы можем вычислить значения функции между узлами, а также определить значение функции даже за пределами заданного интервала (провести экстраполяцию ).

Аппроксимация линейной функцией

Любая линейная функция может быть записана уравнением

Аппроксимация заключается в отыскании коэффициентов a и b уравнения таких, чтобы все экспериментальные точки лежали наиболее близко к аппроксимирующей прямой.

С этой целью чаще всего используется метод наименьших квадратов (МНК), суть которого заключается в следующем: сумма квадратов отклонений значения точки от аппроксимирующей точки принимает минимальное значение:

Решение поставленной задачи сводится к нахождению экстремума указанной функции двух переменных. С этой целью находим частные производные функции функции по коэффициентам a и b и приравниваем их к нулю.

Решаем полученную систему уравнений

Определяем значения коэффициентов

Для вычисления коэффициентов необходимо найти следующие составляющие:
МНК
Тогда значения коэффициентов будут определены как

Пример реализации

Для примера реализации воспользуемся набором значений, полученных в соответствии с уравнением прямой

y = 8 · x — 3

Рассчитаем указанные коэффициенты по методу наименьших квадратов.
Результат сохраняем в форме двумерного массива, состоящего из 2 столбцов.
При следующем запуске программы добавим случайную составляющую к указанному набору значений и снова рассчитаем коэффициенты.

Реализация на Си

Результат выполнения
Запуск без случайной составляющей

Запуск со случайной составляющей

Построение графика функции

Для наглядности построим график функции, полученный аппроксимацией по методу наименьших квадратов. Подробнее о построении графика функции описано здесь.

Реализация на Си

Результат выполнения

Аппроксимация с фиксированной точкой пересечения с осью y

В случае если в задаче заранее известна точка пересечения искомой прямой с осью y, в решении задачи останется только одна частная производная для вычисления коэффициента a.

В этом случае текст программы для поиска коэффициента угла наклона аппроксимирующей прямой будет следующий (имя функции getApprox() заменено на getApproxA() во избежание путаницы).

Результат выполнения программы поиска коэффициента угла наклона аппроксимирующей прямой при фиксированном значении b=0:

Как по точкам определить функцию: Как по точкам найти функцию найти функцию по точкам Математика

Построение графиков функций — урок. Алгебра, 10 класс.

построить график функции y=x2+4×2−4.

Решение 1. Обозначим: f(x)=x2+4×2−4. Область определения этой функции: D(f)=(−∞;−2)∪(−2;2)∪(2;+∞), так как x≠2,x≠−2.

2. Проведём исследование функции на чётность/нечётность:

Функция чётная. Следовательно, можно построить ветви графика функции для x≥0 и отобразить их симметрично относительно оси ординат.

3. Определим асимптоты. Вертикальная асимптота: прямая (x=1), т. к. при (x=1) знаменатель дроби равен нулю, а числитель при этом не равен нулю. Для определения горизонтальной асимптоты вычисляем limx→∞f(x):

Следовательно, (y=1) — горизонтальная асимптота.

4. Определим стационарные и критические точки, точки экстремума и промежутки монотонности функции:

Производная существует на всей области определения функции, следовательно, критических точек у функции нет.

Стационарные точки определим из уравнения y′=0. Получаем: (-16x=0) — откуда получаем, что (x=0). При (x<0) имеем: y′>0; при (x>0) имеем: y′<0. Таким образом, в точке (x=0) функция имеет максимум, причём ymax=f(0)=02+402−4=−1.

При (x>0) имеем: y′<0. Учитывая точку разрыва (x=2), делаем вывод: функция убывает на промежутках 0;2) и (2;+∞).

5. Найдём несколько точек, принадлежащих графику функции f(x)=x2+4×2−4 при x≥0:

(0. 5)

6. Сначала нарисуем часть графика при x≥0, потом — часть, симметричную ей относительно оси (y). Полученный график имеет точку максимума ((0;-2)), горизонтальную асимптоту (y=1) и вертикальную асимптоту (x=2).

Как построить график функции

В этой статье разобран самый простой метод получения графика функции.

Суть метода: найти несколько точек принадлежащих графику, расставить их на координатной плоскости и соединить. Этот способ не лучший (лучший – построение графиков с помощью элементарных преобразований), но если вы все забыли или ничего не учили, то знайте, что у вас всегда есть план Б – возможность построить график по точкам.

Итак, алгоритм по шагам:

1. Представьте, как выглядит ваш график.

Строить гораздо легче, если вы понимаете, что примерно должны получить в итоге. Поэтому сначала посмотрите на функцию и представьте, как примерно должен выглядеть ее график. Все виды графиков элементарных функций вы можете найти здесь. Этот пункт желательный, но не обязательный.

Пример: Построить график функции (y=-)(frac)

Данная функция — гипербола с ветвями расположенными во второй и четвертой четверти. Её график выглядит как-то так:

2. Составьте таблицу точек, принадлежащих графику:

Теперь подставим разные значения «иксов» в функцию, и для каждого икса посчитаем значение «игрека».

(y) — не существует (делить на ноль нельзя)

Результат вычислений удобно представлять в виде таблицы, примерно такой:

Как вы могли догадаться, полученные пары «икс» и «игрек» — это точки, лежащие на нашем графике.

4. Постройте координатную плоскость и отметьте на ней точки из таблицы.

5. Если нужно, найдите еще несколько точек и нанесите их на координатную плоскость.

Пример: Чтобы построить график мне не хватает нескольких точек из отрицательной части, а также рядом с осью игрек, поэтому я добавлю столбцы с (x=-2), (x=-4), (x=)(frac) и (x=-)(frac)

6. Постройте график

Теперь аккуратно и плавно соединяем точки.

Онлайн уравнение прямой по двум точкам с подробным решением

Калькулятор уравнения прямой онлайн составлет общее уравнение прямой и уравнение прямой с угловым коэффициентом k по двум точкам.

Исходные данные:

A x + B y + C = 0 — общее уравнение прямой, где A и B одновременно не равны нулю:

составление общее уравнение прямой, где

расчет коэффициента А для общего уравнения прямой

расчет коэффициента B для общего уравнения прямой

расчет коэффициента C для общего уравнения прямой

y = k x + b — уравнение прямой с угловым коэффициентом k, равным тангенсу угла, образованного данной прямой и положительным направлением оси ОХ (ось абсцисс):

составление уравнения прямой с угловым коэффициентом, где

расчет углового коэффициента k

расчет коэффициента b

I. Порядок действий при составлении уравнения прямой, проходящей через 2 точки онлайн калькулятором:

Для составления уравнения прямой требуется ввести значеня координат 2 точек ([X₁, Y₁]; [X₂, Y₂]).

прямая (прямая линия) — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя ее точками. интерполяция — способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. линейная интерполяция — нахождение промежуточного значения функции по двум точкам (условно проведя прямую между ними). квадратичная интерполяция — нахождение промежуточного значения функции по трем точкам (интерполирующая функция многочлен второго порядка — парабола).

Аппроксимация в Matlab — CodeTown.ru

Приветствую! Сегодня продолжаем говорить об обработке экспериментальных данных. Сегодняшняя статья — продолжение предыдущей темы: Интерполяция в Matlab. Настоятельно советую с ней ознакомиться перед чтением данной статьи. По сути аппроксимация в Matlab очень похожа на интерполяцию, однако, для её реализации используются другие правила и функции.

Аппроксимация

Относительно интерполяции, аппроксимация получила более широкое распространение. Сущность этого метода состоит в том, что табличные данные аппроксимируют кривой, которая не обязательно должна пройти через все узловые точки, а должна как бы сгладить все случайные помехи табличной функции.

МНК (Метод Наименьших Квадратов)

Одним из самых популярных методов аппроксимации в Matlab и в других средах, это Метод Наименьших Квадратов ( МНК ). В этом методе при сглаживании опытных данных аппроксимирующую кривую стремятся провести так, чтобы её отклонения от табличных данных по всем узловым точкам были минимальными.

Суть МНК заключается в следующем: для табличных данных, полученных в результате эксперимента, отыскать аналитическую зависимость, сумма квадратов уклонений которой от табличных данных во всех узловых точках была бы минимальной.

Аппроксимация в Matlab по МНК осуществляется с помощью функции polyfit. Функция p = polyfit(x, y, n) находит коэффициенты полинома p(x) степени n, который аппроксимирует функцию y(x) в смысле метода наименьших квадратов. Выходом является строка p длины n+1, содержащая коэффициенты аппроксимирующего полинома.

Примеры задач

Разберём задачу, в которой разрешается использование встроенных матлабовских функций.

Осуществить аппроксимацию в Matlab табличных данных x = [0, 0.1 , 0.2, 0.3, 0.5] и y = [3, 4.5, 1.7, 0.7, -1] . Применяя метод наименьших квадратов, приблизить ее многочленами 1-ой и 2-ой степени. 2+coeff2(2)*x+coeff2(3)))

Вывод:
ans = 0.9253
ans = 0.8973

Однако, встречаются задачи, где требуется реализовать аппроксимацию в Matlab без использования специальных функций.

Найти у(0.25) путём построения аппроксимирующего полинома методом наименьших квадратов согласно данным:
x: 0, 0.1, 0.2, 0.3, 0.5
y: 3, 4.5, 1.7, 0.7, -1
p: 0.5, 0.8, 1.6, 0.8, 0.1
Построить этот полином без учёта весовых коэффициентов с использованием определителя Вандермонда и стандартных операторов.

Вывод:
a =
228.1447
-176.0984
22.7745
3.1590
qq = 228.1447 -176.0984 22.7745 3.1590
y2 = 1.4113

Как видите встроенные функции для аппроксимации в Matlab укорачивают алгоритм почти вдвое.

Существует также возможность реализации всего алгоритма через одну функцию, но для преподавателей студентов она скорее всего будет не приемлема. С помощью функции lsqcurvefit(fun,x0,xdata,ydata), где:
xdata,ydata– табличные значения аппроксимируемой функции;
x0 –стартовое значение параметров функции;
fun – функция аппроксимации, задаваемая пользователем

С аналитически-теоретической стороны, существуют такие виды аппроксимации:

Аппроксимация ортогональными классическими полиномами.
Аппроксимация каноническим полиномом

Но на практике их реализацию требуют редко.

Вот и вся основная информация по аппроксимации в Matlab, если остались вопросы, задавайте их в комментариях.

Скачать исходник первой задачи
Скачать исходник второй задачи

Поделиться ссылкой:

Получить функцию по точкам. Как по точкам найти функцию

Как построить график по n точкам? Самое простое — отметить их маркерами на координатной сетке. Однако для наглядности их хочется соединить, чтобы получить легко читаемую линию. Соединять точки проще всего отрезками прямых. Но график-ломаная читается довольно тяжело: взгляд цепляется за углы, а не скользит вдоль линии. Да и выглядят изломы не очень красиво. Получается, что кроме ломаных нужно уметь строить и кривые. Однако тут нужно быть осторожным, чтобы не получилось вот такого:

Метрика программного обеспечения — это функция системы, документации или процесса, которые могут быть объективно измерены. Вот некоторые примеры: размер программного обеспечения, количество зарегистрированных дефектов, количество тестовых примеров на случай использования, количество людей, необходимых для разработки системного модуля, среди прочих. Метрики можно разделить на контроль или прогнозирование. Элементы управления обычно связаны с программными процессами, такими как: среднее усилие и время, необходимое для исправления дефекта.

Немного матчасти

Функции f i могут быть самыми разными, но чаще всего используют полиномы некоторой степени. В этом случае итоговая интерполирующая функция (кусочно заданная на промежутках, ограниченных точками P i ) называется сплайном .

Прогнозирующие показатели напрямую связаны с самой системой. Примерами являются: цикломатрическая сложность, строки кода, размер класса и другие. Прогнозирующие показатели могут влиять на принятие решений руководителями проектов. Менеджеры используют показатели процесса, чтобы решить, нужно ли вносить изменения в процесс. Предиктивные меры также используются для оценки усилий, необходимых для создания или внесения изменений в программное обеспечение. В этой статье, когда мы ссылаемся на показатели программного обеспечения, мы будем иметь дело с теми, которые классифицируются как прогноз.

В разных инструментах для построения графиков — редакторах и библиотеках — задача «красивой интерполяции» решена по-разному. В конце статьи будет небольшой обзор существующих вариантов. Почему в конце? Чтобы после ряда приведённых выкладок и размышлений можно было поугадывать, кто из «серьёзных ребят» какие методы использует.

Показатели программного обеспечения являются индикаторами, возникающими в результате измерительной деятельности процесса разработки программного обеспечения, которые помогают в управлении проектами. Существует несколько способов измерения системы. Еще некоторые, другие менее эффективны и эффективны. Некоторые вызывают больше, другие меньше влияют на команду. Некоторые из них могут применяться во всем программном процессе. В качестве примера можно привести строки кода, которые измеряют размер продукта.

Другим примером метрики является человекоподобное усилие или человеко-час. Ротация работоспособности также может считаться метрикой. Другими примерами являются точка использования и функциональная точка, которая является одной из наиболее часто используемых и широко распространенных показателей.

Ставим опыты

Однако, как отмечалось выше, иногда хочется получить в итоге гладкую кривую.

Анализ по функциональной точке имеет в качестве основной цели измерение функциональности системы на основе представления пользователя в соответствии со следующими характеристиками.

База основана на представлении пользователя.
Тем имеет смысл для конечных пользователей.
Используются оценки Утилиза.

Что есть гладкость? Бытовой ответ: отсутствие острых углов. Математический: непрерывность производных. При этом в математике гладкость имеет порядок, равный номеру последней непрерывной производной, и область, на которой эта непрерывность сохраняется. То есть, если функция имеет гладкость порядка 1 на отрезке [a ;&nbspb ], это означает, что на [a ;&nbspb ] она имеет непрерывную первую производную, а вот вторая производная уже терпит разрыв в каких-то точках.
У сплайна в контексте гладкости есть понятие дефекта. Дефект сплайна — это разность между его степенью и его гладкостью. Степень сплайна — это максимальная степень использованных в нём полиномов.
Важно отметить, что «опасными» точками у сплайна (в которых может нарушиться гладкость) являются как раз P i , то есть точки сочленения сегментов, в которых происходит переход от одного полинома к другому. Все остальные точки «безопасны», ведь у полинома на области его определения нет проблем с непрерывностью производных.
Чтобы добиться гладкой интерполяции, нужно повысить степень полиномов и подобрать их коэффициенты так, чтобы в граничных точках сохранялась непрерывность производных.

Он в основном количественно определяет функции, содержащиеся в программном обеспечении, в значимых терминах для пользователей. Эта мера напрямую связана с функциональными требованиями. Хотя он очень популярен, его также критикуют многие авторы, которые считают, что это не объективная мера.

Чтобы рассказать о функциональной точке, необходимо выполнить несколько шагов, как показано на рисунке 1. Первый — это определить тип счета. На этом этапе вы определяете, что будет измеряться, тип подсчета, который будет использоваться для измерения дизайна программного обеспечения, как в процессе, так и в продукте. Возможны три типа подсчетов.

Традиционно для решения такой задачи используют полиномы третьей степени и добиваются непрерывности первой и второй производной. То, что получается, называют кубическим сплайном дефекта 1 . Вот как он выглядит для наших данных:

Счетчик проекта развития, счетчик проектов улучшения, количество приложений. . В упрощенном виде первая измеряет функциональность, предоставляемую конечным пользователям, когда проект готов к моменту его установки. Этот счет также охватывает преобразование данных, необходимых для развертывания программного обеспечения.

Второе измеряет модификации существующего приложения, которое включает в себя функции, включенные, измененные и исключенные из системы проектом, в дополнение к функциям преобразования данных. Важно помнить, что всегда после подсчета обслуживания и его реализации количество функциональных точек приложения должно обновляться в соответствии с изменениями, внесенными в функциональные возможности. Это призвано постоянно обновлять подсчет точек функции приложения.

Кривая, действительно, гладкая. Но если предположить, что это график некоторого процесса или явления, который нужно показать заинтересованному лицу, то такой метод, скорее всего, не подходит. Проблема в ложных экстремумах. Появились они из-за слишком сильного искривления, которое было призвано обеспечить гладкость интерполяционной функции. Но зрителю такое поведение совсем не кстати, ведь он оказывается обманут относительно пиковых значений функции. А ради наглядной визуализации этих значений, собственно, всё и затевалось.
Так что надо искать другие решения.

Третий и последний тип счета измеряет функциональность, предоставляемую пользователю установленным приложением и в процессе производства, так что текущая функциональность имеет меру. Шаги операций функции рисунка. Второй шаг для подсчета — это идентификация объема счета и границы приложения. На этом этапе область оцениваемой системы и ее граница ограничены.

Граница приложения определяет, что является внешним для приложения. — концептуальный интерфейс между приложением и внешними пользователями. Область определяет набор или подмножество программного обеспечения известного размера. Третий и четвертый шаги — это подсчет функций данных и функций транзакции. На этих шагах подсчитываются нескорректированные функциональные точки. На этих этапах рассматриваются.

Другое традиционное решение, кроме кубических сплайнов дефекта 1 — полиномы Лагранжа. Это полиномы степени n &nbsp–&nbsp1, принимающие заданные значения в заданных точках. То есть членения на сегменты здесь не происходит, вся последовательность описывается одним полиномом.
Но вот что получается:

Функции данных: внутренние логические файлы, файлы внешнего интерфейса, функции транзакции: внешние записи, внешние выходы и внешние запросы. Логическая обработка не должна иметь математической формулы или вычисления и не должна генерировать производные данные.

Пятым шагом для подсчета является расчет коэффициента корректировки. Эти факторы связаны с характеристиками приложения. Он отвечает за исправление искажений предыдущего шага и основывается на общих характеристиках системы, в которой определены 14 элементов, которые определяют значение уровня влияния каждого из этих элементов размера системы.

Гладкость, конечно, присутствует, но наглядность пострадала так сильно, что… пожалуй, стоит поискать другие методы. На некоторых наборах данных результат выходит нормальный, но в общем случае ошибка относительно линейной интерполяции (и, соответственно, ложные экстремумы) может получаться слишком большой — из-за того, что тут всего один полином на все сегменты.

Легкость изменения. Шестой и последний шаг счетчика — это вычисление скорректированных точек функции. На этом шаге исправлены возможные искажения, возникающие при расчете нескорректированных функциональных точек, приближая измерения к реальной ситуации. Обычно и по контракту корректирующие коэффициенты равны 1, так что они не влияют на нескорректированные функциональные точки.

Он делится на циклы, называемые спринтами. Именно в этих спринтах выполняются мероприятия по проекту. Его практика осуществляется по этапам, известным как «Совещание по планированию», «Ежедневный анализ», «Обзор и ретроспектива». Существует также «Заготовка продукта» и «Спринт-отставание», где перечислены действия по проекту и будут разделены спринтами. Для этого расчет производится по следующей формуле.

В компьютерной графике очень широко применяются кривые Безье , представленные полиномами k -й степени.
Они не являются интерполирующими, так как из k &nbsp+&nbsp1 точек, участвующих в построении, итоговая кривая проходит лишь через первую и последнюю. Остальные k &nbsp–&nbsp1 точек играют роль своего рода «гравитационных центров», притягивающих к себе кривую.
Вот пример кубической кривой Безье:

Как применить это в реальном случае? Пример 2 практической части этой статьи. Пример 1 — Регистрация клиентов. В этом примере рассмотрим экран «Мастер клиента», показанный на рисунке 2. Рисунок каркаса клиента. Давайте рассмотрим все этапы только для примера.

Регистрация клиентов. . Подсчет транзакций. Извлекая сложность и общие функциональные точки как функций данных, так и функций транзакций, необходимо вычислить нескорректированные функциональные точки, умножив количество функций, определенных для заданной сложности, на их вклад. Наконец, добавьте все найденные точки функции. Давайте рассмотрим пример нашего клиента, как показано на рисунке 3.

Как это можно использовать для интерполяции? На основе этих кривых тоже можно построить сплайн. То есть на каждом сегменте сплайна будет своя кривая Безье k -й степени (кстати, k &nbsp=&nbsp1 даёт линейную интерполяцию). И вопрос только в том, какое k взять и как найти k &nbsp–&nbsp1 промежуточную точку.
Здесь бесконечно много вариантов (поскольку k ничем не ограничено), однако мы рассмотрим классический: k &nbsp=&nbsp3.
Чтобы итоговая кривая была гладкой, нужно добиться дефекта 1 для составляемого сплайна, то есть сохранения непрерывности первой и второй производных в точках сочленения сегментов (P i ), как это делается в классическом варианте кубического сплайна.
Решение этой задачи подробно (с исходным кодом) рассмотрено .
Вот что получится на нашем тестовом наборе:

Расчет коэффициента корректировки выполняется для каждого приложения для каждого счета. Важно помнить, что показанные факторы связаны с характеристиками приложения и могут влиять на его размер. После вычислений нескорректированных функциональных точек и коэффициента корректировки вычисляется функция, скорректированная по формуле.

Коэффициент корректировки тока: значение корректировки, обнаруженное после проекта технического обслуживания. Таким образом, размер функциональности, который будет реализован, будет составлять 13 пунктов. Пример 2 — Отчет о регистрации клиентов. В этом примере только один спринт будет использоваться для реализации функциональных возможностей и доведения его до завершения тестирования. Запрос был подан в уже существующую систему и в производстве на клиенте.

Стало лучше: ложные экстремумы всё ещё есть, но хотя бы не так сильно отличаются от реальных.

Думаем и экспериментируем

В качестве прямых, на которых лежат точки C i &nbsp–&nbsp1 (2) , P i и C i (1) , целесообразно взять касательные к графику интерполируемой функции в точках P i . Это гарантирует отсутствие ложных экстремумов, так как кривая Безье оказывается ограниченной ломаной, построенной на её контрольных точках (если эта ломаная не имеет самопересечений).

Будет использоваться владелец продукта клиента, специалист, который будет поднимать, описывать и определять приоритеты требований и правил, которые должны быть разработаны. Прогноз «Идеальный день» был сделан для каждого вида деятельности с использованием шкалы, поэтому определение создания функциональности было всего лишь одним спринтом. При кодировании у нас будет 14, 5 дней. Остальные дни будут для документации, тестов и любых исправлений ошибок, обнаруженных командой тестирования.

Для расчета Идеального Дня было определено, что это будет считаться производительностью 90% в день 8 часов в день. Планирование показателей по Покеру было применено, и после нескольких обсуждений в итоге было достигнуто 125 баллов. Для каждой точки оценивалось почасовое значение в общей сложности 220 часов.

Методом проб и ошибок эвристика для расчёта расстояния от точки интерполируемой последовательности до промежуточной контрольной получилась такой:

Эвристика 1

Первая и последняя промежуточные контрольные точки равны первой и последней точке графика соответственно (точки C 1 (1) и C n &nbsp–&nbsp1 (2) совпадают с точками P 1 и P n соответственно).
В этом случае получается вот такая кривая:

Как видно, ложных экстремумов уже нет. Однако если сравнивать с линейной интерполяцией, местами ошибка очень большая. Можно сделать её ещё меньше, но тут в ход пойдут ещё более хитрые эвристики.

Отчет о регистрации клиентов. Для дидактических целей счет будет проходить через все этапы, как в примере 1. Проект улучшения. . Идентификация границы приложения. Извлекая сложность и общие функциональные точки как функций данных, так и функций транзакции, необходимо вычислить нескорректированные функциональные точки. Давайте посмотрим на наш пример отчета о записи клиентов на рисунке.

Рисунок Всего необычных точек функции. Коэффициент корректировки = 0, 65. Расчет скорректированных функциональных точек. После вычислений нескорректированных функциональных точек и коэффициента корректировки будет рассчитана функция, скорректированная в соответствии с формулой, представленной в примере 1.

К текущему варианту мы пришли, уменьшив гладкость на один порядок. Можно сделать это ещё раз: пусть сплайн будет иметь дефект 3. По факту, тем самым формально функция не будет гладкой вообще: даже первая производная может терпеть разрывы. Но если рвать её аккуратно, визуально ничего страшного не произойдёт.
Отказываемся от требования равенства расстояний от точки P i до точек C i &nbsp–&nbsp1 (2) и C i (1) , но при этом сохраняем их все лежащими на одной прямой:

Таким образом, размер функциональности, который будет реализован, будет составлять 3. 03 функциональных пункта. Мы можем заключить, что точка функции является метрикой, ориентированной на пользователя. Они описывают, что программное обеспечение должно делать с точки зрения задач и услуг.

Тем не менее, это очень распространенный, стандартизированный и один из наиболее широко используемых сегодня. И главное, не учитывает ни язык программирования, ни «чувство» профессионала на момент разработки, как и многие другие стратегии. Тем не менее, можно сделать совместное из двух методов, где сложность может быть оценена с учетом оценок, сделанных разработчиками, и размера, с учетом взгляда пользователя.

Эвристика для вычисления расстояний будет такой:

Эвристика 2

Расчёт l 1 и l 2 такой же, как в «эвристике 1».
При этом, однако, стоит ещё проверять, не совпали ли точки P i и P i &nbsp+&nbsp1 по ординате, и, если совпали, полагать l 1 &nbsp=&nbspl 2 &nbsp=&nbsp0. Это защитит от «вспухания» графика на плоских отрезках (что тоже немаловажно с точки зрения правдивого отображения данных).

Результат получается такой:

В результате на шестом сегменте ошибка уменьшилась, а на седьмом — увеличилась: кривизна у Безье на нём оказалась больше, чем хотелось бы. Исправить ситуацию можно, принудительно уменьшив кривизну и тем самым «прижав» Безье ближе к отрезку прямой, которая соединяет граничные точки сегмента. Для этого используется следующая эвристика:

Эвристика 3

Если абсцисса точки пересечения касательных в точках P i (x i ,&nbspy i ) и P i &nbsp+&nbsp1 (x i &nbsp+&nbsp1 ,&nbspy i &nbsp+&nbsp1) лежит в отрезке [x i ;&nbspx i &nbsp+&nbsp1 ], то l 1 либо l 2 полагаем равным нулю. В том случае, если касательная в точке P i направлена вверх, нулю полагаем максимальное из l 1 и l 2 , если вниз — минимальное.

На этом было принято решение признать цель достигнутой.
Может быть, кому-то пригодится код .

А как люди-то делают?

MS Excel

Это очень похоже на рассмотренный выше сплайн дефекта 1, основанный на кривых Безье. Правда, в отличие от него в чистом виде, тут всего два ложных экстремума — первый и второй сегменты (у нас было четыре). Видимо, к классическому поиску промежуточных контрольных точек тут добавляются ещё какие-то эвристики. Но ото всех ложных экстремумов они не спасли.

LibreOffice Calc

В настройках это названо кубическим сплайном. Очевидно, он тоже основан на Безье, и вот тут уже точная копия нашего результата: все четыре ложных экстремума на месте.

Есть там ещё один тип интерполяции, который мы тут не рассматривали: B-сплайн. Но для нашей задачи он явно не подходит, так как даёт вот такой результат:)

Highcharts , одна из самых популярных JS-библиотек для построения диаграмм

Тут налицо «метод касательных» в варианте равенства расстояний от точки интерполируемой последовательности до промежуточных контрольных. Ложных экстремумов нет, зато есть сравнительно большая ошибка относительно линейной интерполяции (седьмой сегмент).

amCharts , ещё одна популярная JS-библиотека

Картина очень похожа на экселевскую, те же два ложных экстремума в тех же местах.

Coreplot , самая популярная библиотека построения графиков для iOS и OS X

Есть ложные экстремумы и видно, что используется сплайн дефекта 1 на основе Безье.
Библиотека открытая, так что можно посмотреть в код и убедиться в этом.

aChartEngine , вроде как самая популярная библиотека построения графиков для Android

Больше всего похоже на кривую Безье степени n &nbsp–&nbsp1, хотя в самой библиотеке график называется «cubic line». Странно! Как бы то ни было, тут не только присутствуют ложные экстремумы, но и в принципе не выполняются условия интерполяции.

Вместо заключения

Метки: Добавить метки

Определите степень полинома, который будет использован для интерполирования. Он имеет вид: Кn*Х^n + К(n-1)*Х^(n-1) +.0.

Если вы не можете найти линейную функцию , а точнее распознать ее среди многих, то не переживайте. Трудного в этом ничего нет. Всего лишь пару простых правил, и вы будете всегда отличать функции друг от друга.

Линейная функция является самой просто из основных школьных функций. Если вы только начали изучать их, то, несомненно, у вас могут возникнуть некоторые трудности по распознаванию. Учителя зачастую считают, что дети легко и быстро усваивают материал. Но бывает , что пропустишь всего лишь одно занятие, а уже материал стал более сложны и непонятным, и самому его не разобрать . Поэтому первым делом вам нужно начать с определения, в котором говорится, что линейной функцией называется функция вида f(x)=ax+b. То есть вам необходимо запомнить общий вид, с помощью которого вы сможете находить подобные и определять, что данные функции линейные.

Если общий вид не помогает, и вы все равно никак не разыщите линейную функцию , то вам поможет график. По точкам постройте чертеж (можно даже схематический). Запомните одну важную вещь: у линейной функции график всегда прямая. Поэтому, сделав рисунок , вы сразу же увидите, линейная она у вас либо нет.

В случае, если график не удается построить, есть еще один способ распознавания , который является одним из наиболее простых. Запомните раз и навсегда, что линейная функция имеет степень не выше второй, то есть квадратичная функция никак не может быть линейной, также как и кубическая, и функция четвертой, пятой степеней и так далее. Даже если функция равна числу и в левой части не содержит х, то все равно она будет линейной.

Функция поиска уравнения по таблице точек

Поиск по уравнениям функций

Инструмент для нахождения уравнения функции по ее точкам, ее координатам x, y = f (x) в соответствии с некоторыми методами интерполяции и алгоритмами поиска уравнений

Функция поиска уравнений — dCode

dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Ответы на вопросы (FAQ)

Как найти уравнение кривой?

Чтобы найти уравнение на графике:

Метод 1 (подгонка): проанализируйте кривую (посмотрев на нее), чтобы определить, какой тип функции это (линейная, экспоненциальная, логарифмическая, периодическая и т. Д.).) и укажите некоторые значения в таблице, и dCode найдет функцию, которая ближе всего подходит к этим точкам.

Метод 2 (интерполяция): из конечного числа точек существуют формулы, позволяющие создать многочлен, который проходит точно через эти точки (см. Интерполяция Лагранжа), указать значения определенных точек, и dCode вычислит проходящий полином по этим точкам. точки.

Как найти уравнение из набора точек?

Чтобы вывести уравнение функции из таблицы значений (или кривой), существует несколько математических методов.

Метод 1: обнаруживает замечательные решения , как и замечательные идентичности, иногда легко найти уравнение, анализируя значения (сравнивая два последовательных значения или идентифицируя определенные точные значения).

Пример: функция имеет для точек (пары $ (x, y) $) координаты: $ (1,2) (2,4), (3,6), (4,8) $, ординаты увеличиваются на 2, а абсциссы увеличиваются на 1, решение тривиально: $ f (x) = 2x $

Метод 2: использовать функцию интерполяции , более сложный, этот метод требует использования математических алгоритмов, которые могут найти многочлены, проходящие через любые точки.Наиболее известными интерполяциями являются лагранжева интерполяция, ньютоновская интерполяция и интерполяция Невилля.

NB: для данного набора точек существует бесконечное количество решений, потому что через определенные точки проходят бесконечные функции. dCode пытается предложить максимально упрощенные решения, основанные на аффинной функции или полиноме низкой степени (степени 2 или 3).

Как найти уравнение линии?

Исходный код

dCode сохраняет за собой право собственности на исходный код онлайн-инструмента Function Equation Finder.За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любой алгоритм, апплет или фрагмент «Function Equation Finder» (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любая «Функция» Функция Equation Finder (вычисление, преобразование, решение, расшифровка / шифрование, дешифрование / шифрование, декодирование / кодирование, перевод), написанная на любом информационном языке (Python, Java, PHP, C #, Javascript, Matlab и т. Д.), Без загрузки данных , скрипт, копипаст или доступ к API для «Function Equation Finder» будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.

Нужна помощь?

Пожалуйста, посетите наше сообщество dCode Discord для запросов о помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!

Вопросы / комментарии

уравнение, координата, кривая, точка, интерполяция, таблица

Источник: https: //www.dcode.2 + bx + c> ) задается тремя числами, разумно предположить, что мы могли бы подогнать параболу к трем точкам на плоскости. Это действительно так, и это полезная идея. На этом шаге мы увидим, как алгебраически подогнать параболу к трем точкам на декартовой плоскости. Это включает в себя вспоминание или обучение тому, как решить три уравнения с тремя неизвестными. Это полезный навык сам по себе.

Уникальный круг, проходящий через три неколлинеарных точки

Решение трех линейных уравнений с тремя неизвестными

Линейные уравнения в координатной плоскости (Алгебра 1, Визуализация линейных функций) — Mathplanet

Линейное уравнение — это уравнение с двумя переменными, график которого представляет собой линию. График линейного уравнения — это набор точек на координатной плоскости, которые все являются решениями уравнения. Если все переменные представляют собой действительные числа, можно изобразить уравнение, нанеся на график достаточно точек для распознавания шаблона, а затем соединить точки, чтобы включить все точки.

Если вы хотите построить график линейного уравнения, у вас должно быть как минимум две точки, но обычно рекомендуется использовать более двух точек. При выборе очков старайтесь включать как положительные, так и отрицательные значения, а также ноль.

Пример

Постройте функцию y = x + 2

Начните с выбора пары значений для x, например -2, -1, 0, 1 и 2 и вычислите соответствующие значения y.

X	Y = х + 2	Заказанная пара
-2	-2 + 2 = 0	(-2, 0)
-1	-1 + 2 = 1	(-1, 1)
0	0 + 2 = 2	(0, 2)
1	1 + 2 = 3	(1, 3)
2	2 + 2 = 4	(2, 4)

Теперь вы можете просто нанести пять упорядоченных пар на координатную плоскость

На данный момент это пример дискретной функции.Дискретная функция состоит из изолированных точек.

Проведя линию через все точки и продолжая линию в обоих направлениях, мы получаем противоположность дискретной функции, непрерывную функцию, которая имеет непрерывный график.

Если вы хотите использовать только две точки для определения вашей линии, вы можете использовать две точки, где график пересекает оси. Точка, в которой график пересекает ось x, называется отрезком x, а точка, в которой график пересекает ось y, называется отрезком y.Пересечение по оси x находится путем нахождения значения x, когда y = 0, (x, 0), а точка пересечения по оси y находится путем нахождения значения y, когда x = 0, (0, y).

Стандартная форма линейного уравнения —

$$ Ax + By = C, : : A, B neq 0 $$

Прежде чем вы сможете построить линейное уравнение в его стандартной форме, вы сначала должны решить уравнение относительно y.

Отсюда вы можете построить уравнение, как в примере выше.

График y = a представляет собой горизонтальную линию, где прямая проходит через точку (0, a)

В то время как график x = a представляет собой вертикальную линию, проходящую через точку (a, 0)

Постройте график линейного уравнения y = 3x — 2

Функции: графики и пересечения

Предполагать ж ( Икс ) а также грамм ( Икс ) это две функции, которые принимают на входе действительное число и выводят действительное число.

Тогда точки пересечения ж ( Икс ) а также грамм ( Икс ) эти числа Икс для которого ж ( Икс ) знак равно грамм ( Икс ) .

Иногда точные значения легко найти, решив уравнение ж ( Икс ) знак равно грамм ( Икс ) алгебраически.

Пример 1:

Какие точки пересечения функций ж ( Икс ) а также грамм ( Икс ) если ж ( Икс ) знак равно Икс + 6 а также грамм ( Икс ) знак равно — Икс ?

Точки пересечения ж ( Икс ) а также грамм ( Икс ) эти числа Икс для которого ж ( Икс ) знак равно грамм ( Икс ) .

Это, Икс + 6 знак равно — Икс .

Икс + 6 знак равно — Икс 2 Икс + 6 знак равно 0 2 Икс знак равно — 6 Икс знак равно — 3

Теперь вы можете использовать значение Икс найти соответствующий у -координата точки пересечения.

Подставьте значение Икс в любой из двух функций.

грамм ( — 3 ) знак равно — ( — 3 ) знак равно 3

Уравнения также можно решить графически, построив две функции на координатной плоскости и указав точку их пересечения.

В других случаях бывает сложно найти точные значения. Возможно, вам потребуется использовать технологию для их оценки.

Пример 2:

Найдите точку (точки) пересечения двух функций.

ж ( Икс ) знак равно | Икс — 5 | грамм ( Икс ) знак равно бревно Икс

Здесь не так-то просто решить алгебраически.Решения уравнения | Икс — 5 | знак равно бревно Икс не являются красивыми рациональными числами.

Изобразите функции на координатная плоскость .

Вы можете использовать графическую утилиту, чтобы определить, что координаты точек пересечения приблизительно равны ( 4,36 , 0,64 ) а также ( 5.76 , 0,76 ) .

1.1: Четыре способа представления функции

Определите, представляет ли отношение функцию.
Найдите значение функции.
Определите, является ли функция взаимно однозначной.
Используйте тест вертикальной линии для определения функций.
Изобразите функции, перечисленные в библиотеке функций.

Авиалайнер меняет высоту по мере увеличения расстояния от точки старта полета.Вес подрастающего ребенка со временем увеличивается. В каждом случае одно количество зависит от другого. Между двумя величинами существует взаимосвязь, которую мы можем описывать, анализировать и использовать для прогнозирования. В этом разделе мы разберем такие отношения.

Определение того, представляет ли отношение функцию

Отношение — это набор упорядоченных пар. Набор первых компонентов каждой упорядоченной пары называется областью, а набор вторых компонентов каждой упорядоченной пары называется диапазоном.Рассмотрим следующий набор упорядоченных пар. Первые числа в каждой паре — это первые пять натуральных чисел. Второе число в каждой паре вдвое больше первого.

Обратите внимание, что каждое значение в домене также известно как входное значение или независимая переменная и часто обозначается строчной буквой (x ).Каждое значение в диапазоне также известно как выходное значение или зависимая переменная и часто обозначается строчной буквой (y ).

Функция (f ) — это отношение, которое присваивает одно значение в диапазоне каждому значению в домене. Другими словами, никакие (x ) — значения не повторяются. Для нашего примера, который связывает первые пять натуральных чисел с числами, удваивающими их значения, это отношение является функцией, потому что каждый элемент в домене, , связан ровно с одним элементом в диапазон, ( ).

Теперь давайте рассмотрим набор упорядоченных пар, который связывает термины «четный» и «нечетный» с первыми пятью натуральными числами. Он будет выглядеть как

Обратите внимание, что каждый элемент в домене не связан ровно с одним элементом в диапазоне ( ). Например, термин «нечетный» соответствует трем значениям из области ( ), а термин «четный» соответствует двум значениям из диапазона ( ).Это нарушает определение функции, поэтому это отношение не является функцией.

На рисунке ( PageIndex ) сравниваются отношения, которые являются функциями, а не функциями.

Рисунок ( PageIndex ): (a) Это отношение является функцией, потому что каждый вход связан с одним выходом. Обратите внимание, что входные (q ) и (r ) оба дают выход (n ). (б) Эта связь также является функцией. В этом случае каждый вход связан с одним выходом. (c) Это отношение не является функцией, потому что вход (q ) связан с двумя разными выходами.

Функция — это отношение, в котором каждое возможное входное значение приводит ровно к одному выходному значению. Мы говорим: «Выход — это функция входа».

Входные значения составляют область , а выходные значения составляют диапазон .

Как сделать: учитывая связь между двумя величинами, определите, является ли связь функцией

Определите входные значения.
Определите выходные значения.
Если каждое входное значение приводит только к одному выходному значению, классифицируйте отношение как функцию. Если какое-либо входное значение приводит к двум или более выходам, не классифицируйте отношение как функцию.

Пример ( PageIndex ): определение того, являются ли прайс-листы меню функциями

Меню кофейни, показанное на рисунке ( PageIndex ), состоит из предметов и их цен.

Цена зависит от товара?
Является ли товар функцией цены?

Решение

Начнем с рассмотрения ввода как пунктов меню. Выходные значения — это цены. См. Рисунок ( PageIndex ).

У каждого элемента в меню есть только одна цена, поэтому цена зависит от элемента.

Два пункта меню имеют одинаковую цену.Если мы рассматриваем цены как входные значения, а товары как выходные, то с одним и тем же входным значением может быть связано несколько выходных данных. См. Рисунок ( PageIndex ).

Следовательно, товар не зависит от цены.

Пример ( PageIndex ): определение того, являются ли правила оценки класса функциями

В конкретном математическом классе общая процентная оценка соответствует среднему баллу.Является ли средний балл функцией процентной оценки? Является ли процентная оценка функцией среднего балла? В таблице ( PageIndex ) показано возможное правило назначения оценок.

Процентное содержание	0–56	57–61	62–66	67–71	72–77	78–86	87–91	92–100
Средний балл	0.0	1,0	1,5	2,0	2,5	3,0	3,5	4,0

Таблица ( PageIndex ): баллы успеваемости за класс.

Решение

Для любой процентной оценки существует связанный средний балл, поэтому средний балл является функцией процентной оценки. Другими словами, если мы введем процентную оценку, на выходе получится конкретный средний балл.

В данной системе оценок существует диапазон процентных оценок, соответствующих одному и тому же среднему баллу. Например, учащиеся, получившие средний балл 3,0, могут иметь различные процентные оценки от 78 до 86. Таким образом, процентная оценка не является функцией среднего балла.

Таблица ( PageIndex ) перечисляет пять величайших бейсболистов всех времен в порядке рангов.

Является ли ранг функцией имени игрока?
Имя игрока зависит от ранга?

Ответ б

да.(Примечание: если бы два игрока были разделены, скажем, за 4-е место, то имя не зависело бы от ранга.)

Использование обозначения функций

Как только мы определим, что отношение является функцией, нам нужно отобразить и определить функциональные отношения, чтобы мы могли понять и использовать их, а иногда также, чтобы мы могли программировать их в компьютерах. Есть разные способы представления функций. Стандартные обозначения функций — это одно из представлений, облегчающих работу с функциями.

Чтобы представить «рост является функцией возраста», мы начинаем с определения описательных переменных (h ) для роста и (a ) для возраста. Буквы (f ), (g ) и (h ) часто используются для обозначения функций точно так же, как мы используем (x ), (y ) и (z ) для обозначения числа и (A ), (B ) и (C ) для представления множеств.

Помните, мы можем использовать любую букву для названия функции; обозначение (h (a) ) показывает нам, что (h ) зависит от (a ). Значение (a ) необходимо поместить в функцию (h ), чтобы получить результат. Скобки указывают, что возраст вводится в функцию; они не указывают на умножение.

Мы также можем дать алгебраическое выражение в качестве входных данных для функции.Например, (f (a + b) ) означает «сначала сложите (a ) и (b ), и результат будет входом для функции (f )». Для получения правильного результата операции необходимо выполнять именно в таком порядке.

Запись (y = f (x) ) определяет функцию с именем (f ). Это читается как « (y ) является функцией (x )». Буква (x ) представляет входное значение или независимую переменную. Буква (y ) или (f (x) ) представляет выходное значение или зависимую переменную.

Пример ( PageIndex ): использование обозначения функций для дней в месяце

Используйте обозначение функции для представления функции, вход которой является названием месяца, а выход — количеством дней в этом месяце.

Решение

Использование обозначения функций для дней в месяце

Количество дней в месяце является функцией названия месяца, поэтому, если мы назовем функцию (f ), мы напишем ( text = f ( text ) ) или (d = f (m) ). Название месяца — это вход в «правило», которое связывает определенное число (выход) с каждым входом.

Рисунок ( PageIndex ): функция (31 = f (январь) ), где 31 — результат, f — правило, а январь — вход.

Например, (f ( text ) = 31 ), потому что в марте 31 день. Обозначение (d = f (m) ) напоминает нам, что количество дней, (d ) (выход), зависит от названия месяца (m ) (вход).

Анализ

Обратите внимание, что входные данные функции не обязательно должны быть числами; входные данные функции могут быть именами людей, метками геометрических объектов или любым другим элементом, определяющим какой-либо вид вывода.Однако большинство функций, с которыми мы будем работать в этой книге, будут иметь числа как входы и выходы.

Пример ( PageIndex ): интерпретация обозначения функции

Функция (N = f (y) ) дает количество полицейских (N ) в городе в году (y ). Что означает (f (2005) = 300 )?

Решение

Когда мы читаем (f (2005) = 300 ), мы видим, что входной год — 2005. Выходное значение, количество полицейских ((N) ), равно 300.Помните, (N = f (y) ). Утверждение (f (2005) = 300 ) говорит нам, что в 2005 году в городе было 300 полицейских.

Используйте обозначение функций, чтобы выразить вес свиньи в фунтах как функцию ее возраста в днях (d ).

Ответ

Вопросы и ответы

Вместо обозначения, такого как (y = f (x) ), можем ли мы использовать тот же символ для вывода, что и для функции, например, (y = y (x) ), означающий « (y ) является функцией (x )? »

Да, это часто делается, особенно по прикладным предметам, использующим высшую математику, например физике и инженерии.Однако, исследуя математику, нам нравится проводить различие между такой функцией, как (f ) , которая является правилом или процедурой, и выходом y, который мы получаем, применяя (f ) к конкретному ввод (x ) . Вот почему мы обычно используем такие обозначения, как (y = f (x), P = W (d) ) и т. Д.

Представление функций с помощью таблиц

Общий метод представления функций — в виде таблицы. Строки или столбцы таблицы отображают соответствующие входные и выходные значения.В некоторых случаях эти значения представляют все, что мы знаем об отношениях; в других случаях таблица предоставляет несколько избранных примеров из более полных отношений.

Таблица ( PageIndex ) перечисляет входное число каждого месяца ( ( text = 1 ), ( text = 2 ) и т. Д.) И вывод значение количества дней в этом месяце. Эта информация представляет все, что мы знаем о месяцах и днях для данного года (который не является високосным). Обратите внимание, что в этой таблице мы определяем функцию дней в месяце (f ), где (D = f (m) ) идентифицирует месяцы целым числом, а не именем.

Номер месяца, (м ) (ввод)

Таблица ( PageIndex ) определяет функцию (Q = g (n) ) Помните, это обозначение говорит нам, что (g ) — это имя функции, которая принимает входные данные (n ) и дает результат (Q ).

(п )

Таблица ( PageIndex ) отображает возраст детей в годах и соответствующий им рост.В этой таблице показаны лишь некоторые из имеющихся данных о росте и возрасте детей. Мы сразу видим, что эта таблица не представляет функцию, потому что одно и то же входное значение, 5 лет, имеет два разных выходных значения, 40 дюймов и 42 дюйма.

Возраст в годах, (a ) (ввод)

Как: по таблице входных и выходных значений определить, представляет ли таблица функцию

Определите входные и выходные значения.
Проверьте, сопряжено ли каждое входное значение только с одним выходным значением. Если это так, таблица представляет функцию.

Пример ( PageIndex ): определение таблиц, представляющих функции

Какая таблица, Таблица ( PageIndex ), Таблица ( PageIndex ) или Таблица ( PageIndex ), представляет функцию (если есть)?

Решение

Таблица ( PageIndex ) и Таблица ( PageIndex ) определяют функции.В обоих случаях каждое входное значение соответствует ровно одному выходному значению. Таблица ( PageIndex ) не определяет функцию, потому что входное значение 5 соответствует двум различным выходным значениям.

Когда таблица представляет функцию, соответствующие входные и выходные значения также могут быть указаны с использованием обозначения функции.

Функция, представленная таблицей ( PageIndex ), может быть представлена записью

[f (2) = 1 text f (5) = 3 text f (8) = 6 nonumber ]

[g (−3) = 5 text g (0) = 1 text g (4) = 5 nonumber ]

представляют функцию в таблице ( PageIndex ).

Таблица ( PageIndex ) не может быть выражена аналогичным образом, потому что она не представляет функцию.

Представляет ли таблица ( PageIndex ) функцию?

Поиск входных и выходных значений функции

Когда мы знаем входное значение и хотим определить соответствующее выходное значение для функции, мы оцениваем функцию.Оценка всегда дает один результат, потому что каждое входное значение функции соответствует ровно одному выходному значению.

Когда мы знаем выходное значение и хотим определить входные значения, которые будут производить это выходное значение, мы устанавливаем выход равным формуле функции и решаем вход. Решение может дать более одного решения, потому что разные входные значения могут давать одно и то же выходное значение.

Вычисление функций в алгебраических формах

Когда у нас есть функция в форме формулы, вычислить ее обычно несложно.2 + 2p − 3 = 0 & text \ (p + 3) (p − 1) = 0 & text End nonumber ]

Если ((p + 3) (p − 1) = 0 ), либо ((p + 3) = 0 ), либо ((p − 1) = 0 ) (или оба они равны (0 )). Мы установим каждый множитель равным (0 ) и решим относительно (p ) в каждом случае.

[(p + 3) = 0, ; p = −3 nonumber ]

[(p − 1) = 0, , p = 1 nonumber ]

Это дает нам два решения. Выход (h (p) = 3 ), когда вход либо (p = 1 ), либо (p = −3 ). Мы также можем проверить, построив график, как на рисунке ( PageIndex ).2 + 2п )

Учитывая функцию (g (m) = sqrt ), решите (g (m) = 2 ).

Ответ

Вычисление функций, выраженных в формулах

Некоторые функции определяются математическими правилами или процедурами, выраженными в форме уравнения . Если можно выразить выход функции с помощью формулы, включающей входную величину, то мы можем определить функцию в алгебраической форме.Например, уравнение (2n + 6p = 12 ) выражает функциональную связь между (n ) и (p ). Мы можем переписать его, чтобы решить, является ли (p ) функцией (n ).

Как: Для данной функции в форме уравнения напишите ее алгебраическую формулу.

Решите уравнение, чтобы изолировать выходную переменную с одной стороны от знака равенства, а другую сторону как выражение, которое включает только входную переменную.
Используйте все обычные алгебраические методы для решения уравнений, такие как сложение или вычитание одной и той же величины с обеих сторон или от них, или умножение или деление обеих сторон уравнения на одинаковую величину.

Пример ( PageIndex ): поиск уравнения функции

Выразите отношение (2n + 6p = 12 ) как функцию (p = f (n) ), если это возможно.

Решение

Чтобы выразить отношение в этой форме, нам нужно иметь возможность записать отношение, где (p ) является функцией (n ), что означает запись его как (p = [ text п] ).

Следовательно, (p ) как функция от (n ) записывается как

[p = f (n) = 2− frac n nonumber ]

Анализ

Важно отметить, что не все отношения, выраженные уравнением, можно также выразить как функцию с формулой. 2 = 1 ) функцию с (x ) на входе и (y ) на выходе? Если это так, выразите отношение как функцию (y = f (x) ).y ), если мы хотим выразить y как функцию от x, не существует простой алгебраической формулы, включающей только (x ), которая равна (y ). Однако каждый (x ) определяет уникальное значение для (y ), и существуют математические процедуры, с помощью которых (y ) можно найти с любой желаемой точностью. В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для (y ) как функции (x ), даже если формулу нельзя записать явно.

Оценка функции, заданной в табличной форме

Как мы видели выше, мы можем представлять функции в виде таблиц.И наоборот, мы можем использовать информацию в таблицах для написания функций, и мы можем оценивать функции с помощью таблиц. Например, насколько хорошо наши питомцы вспоминают теплые воспоминания, которыми мы с ними делимся? Существует городская легенда, что у золотой рыбки память 3 секунды, но это всего лишь миф. Золотая рыбка может помнить до 3 месяцев, в то время как бета-рыба имеет память до 5 месяцев. И хотя продолжительность памяти щенка не превышает 30 секунд, взрослая собака может запоминать 5 минут. Это скудно по сравнению с кошкой, у которой объем памяти составляет 16 часов.

Функция, которая связывает тип питомца с продолжительностью его памяти, легче визуализировать с помощью таблицы (Table ( PageIndex )).

Память питомца

интервал в часах

Иногда оценка функции в табличной форме может быть более полезной, чем использование уравнений. Здесь вызовем функцию (P ). Область функции — это тип домашнего животного, а диапазон — это действительное число, представляющее количество часов, в течение которых хранится память питомца.Мы можем оценить функцию (P ) при входном значении «золотая рыбка». Мы бы написали (P (золотая рыбка) = 2160 ). Обратите внимание, что для оценки функции в табличной форме мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функции P кажется идеально подходящей для этой функции, больше, чем запись ее в форме абзаца или функции.

Как сделать: для функции, представленной в виде таблицы, определить конкретные выходные и входные значения

1.Найдите данный вход в строке (или столбце) входных значений.
2. Определите соответствующее выходное значение в паре с этим входным значением.
3. Найдите заданные выходные значения в строке (или столбце) выходных значений, отмечая каждый раз, когда это выходное значение появляется.
4. Определите входные значения, соответствующие заданному выходному значению.

Пример ( PageIndex ): Вычисление и решение табличной функции

Использование таблицы ( PageIndex ),

а. Оцените (g (3) ).
г. Решите (g (n) = 6 ).

(п )

Решение

а.Вычисление (g (3) ) означает определение выходного значения функции (g ) для входного значения (n = 3 ). Выходное значение таблицы, соответствующее (n = 3 ), равно 7, поэтому (g (3) = 7 ).
г. Решение (g (n) = 6 ) означает определение входных значений n, которые производят выходное значение 6. Таблица ( PageIndex ) показывает два решения: 2 и 4.

(п )

Когда мы вводим 2 в функцию (g ), на выходе получается 6.Когда мы вводим 4 в функцию (g ), наш результат также равен 6.

Используя Table ( PageIndex ), вычислите (g (1) ).

Ответ

Поиск значений функций из графика

Оценка функции с помощью графика также требует нахождения соответствующего выходного значения для данного входного значения, только в этом случае мы находим выходное значение, глядя на график.Решение функционального уравнения с использованием графика требует нахождения всех экземпляров данного выходного значения на графике и наблюдения за соответствующими входными значениями.

Пример ( PageIndex ): чтение значений функций из графика

Учитывая график на рисунке ( PageIndex ),

Вычислить (f (2) ).
Решите (f (x) = 4 ).

Решение

Чтобы оценить (f (2) ), найдите точку на кривой, где (x = 2 ), затем прочтите координату y этой точки.Точка имеет координаты ((2,1) ), поэтому (f (2) = 1 ). См. Рисунок ( PageIndex ).

( PageIndex ): график положительной параболы с центром в ((1, 0) ) с отмеченной точкой ((2, 1) ), где (f (2) = 1 ) .

Чтобы решить (f (x) = 4 ), мы находим выходное значение 4 на вертикальной оси. Двигаясь горизонтально по прямой (y = 4 ), мы обнаруживаем две точки кривой с выходным значением 4: ((- 1,4) ) и ((3,4) ). Эти точки представляют два решения (f (x) = 4 ): −1 или 3. Это означает (f (−1) = 4 ) и (f (3) = 4 ), или когда вход — -1 или 3, выход — 4.См. Рисунок ( PageIndex ).

Рисунок ( PageIndex ): График обращенной вверх параболы с вершиной в ((0,1) ) и помеченными точками в ((- 1, 4) ) и ((3 , 4) ). Прямая в точке (y = 4 ) пересекает параболу в отмеченных точках.

Учитывая график на рисунке ( PageIndex ), решите (f (x) = 1 ).

Ответ

(x = 0 ) или (x = 2 )

Определение того, является ли функция однозначной

Некоторые функции имеют заданное выходное значение, соответствующее двум или более входным значениям.Например, на биржевой диаграмме, показанной на рисунке в начале этой главы, цена акции составляла 1000 долларов в пять разных дат, что означает, что было пять различных входных значений, которые все привели к одному и тому же выходному значению в 1000 долларов.

Однако некоторые функции имеют только одно входное значение для каждого выходного значения, а также имеют только один выход для каждого входа. Мы называем эти функции взаимно однозначными функциями. В качестве примера рассмотрим школу, в которой используются только буквенные оценки и десятичные эквиваленты, как указано в Таблице ( PageIndex ).

Letter Grade	Средний балл
A	4,0
В	3,0
С	2,0
D	1,0

Таблица ( PageIndex ): буквенные оценки и десятичные эквиваленты.

Эта система оценок представляет собой функцию «один-к-одному», потому что каждая вводимая буква дает один конкретный выходной средний балл, а каждый средний балл соответствует одной вводимой букве.

Чтобы визуализировать эту концепцию, давайте еще раз посмотрим на две простые функции, изображенные на рисунках ( PageIndex ) и ( PageIndex ). Функция в части (a) показывает взаимосвязь, которая не является взаимно однозначной, потому что входы (q ) и (r ) оба дают выход (n ). Функция в части (b) показывает взаимосвязь, которая является функцией «один-к-одному», потому что каждый вход связан с одним выходом.

Однозначная функция — это функция, в которой каждое выходное значение соответствует ровно одному входному значению.2 ). Поскольку площади и радиусы являются положительными числами, существует ровно одно решение: ( sqrt > ). Таким образом, площадь круга однозначно зависит от радиуса круга.

Является ли остаток функцией номера банковского счета?
Является ли номер банковского счета функцией баланса?
Является ли баланс однозначной функцией номера банковского счета?

а.да, потому что на каждом банковском счете в любой момент времени имеется единый баланс;

г. нет, потому что несколько номеров банковских счетов могут иметь одинаковый баланс;

г. нет, потому что один и тот же выход может соответствовать более чем одному входу.

Если каждая процентная оценка, полученная на курсе, соответствует одной буквенной оценке, является ли буквенная оценка функцией процентной оценки?
Если да, то функция взаимно однозначная?

а.Да, буквенная оценка является функцией процентной оценки;
г. Нет, не один на один. Мы могли бы получить 100 различных процентных чисел, но только около пяти возможных буквенных оценок, поэтому не может быть только одного процентного числа, соответствующего каждой буквенной оценке.

Использование теста вертикальной линии

Как мы видели в некоторых примерах выше, мы можем представить функцию с помощью графика. Графики отображают огромное количество пар ввода-вывода на небольшом пространстве. Предоставляемая ими визуальная информация часто упрощает понимание взаимоотношений.Обычно графики строятся с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.

Наиболее распространенные графики называют входное значение (x ) и выходное значение (y ), и мы говорим, что (y ) является функцией (x ), или (y = f (x) ), когда функция названа (f ). График функции — это совокупность всех точек ((x, y) ) на плоскости, которая удовлетворяет уравнению (y = f (x) ). Если функция определена только для нескольких входных значений, то график функции представляет собой только несколько точек, где координата x каждой точки является входным значением, а координата y каждой точки является соответствующим выходным значением.Например, черные точки на графике на рисунке ( PageIndex ) говорят нам, что (f (0) = 2 ) и (f (6) = 1 ). Однако множество всех точек ((x, y) ), удовлетворяющих (y = f (x) ), является кривой. Показанная кривая включает ((0,2) ) и ((6,1) ), потому что кривая проходит через эти точки

. Рисунок ( PageIndex ): График многочлена.

Тест вертикальной линии можно использовать для определения того, представляет ли график функцию. Если мы можем нарисовать любую вертикальную линию, которая пересекает график более одного раза, то график не определяет функцию, потому что функция имеет только одно выходное значение для каждого входного значения.См. Рисунок ( PageIndex ) .

Рисунок ( PageIndex ): три графика, наглядно демонстрирующие, что является функцией, а что нет.

Практическое руководство. Имея график, используйте тест вертикальной линии, чтобы определить, представляет ли график функцию

Проверьте график, чтобы увидеть, пересекает ли нарисованная вертикальная линия кривую более одного раза.
Если такая линия есть, определите, что график не представляет функцию.

Пример ( PageIndex ): Применение теста вертикальной линии

Какой из графиков на рисунке ( PageIndex ) представляет (ы) функцию (y = f (x) )?

Рисунок ( PageIndex ): график полинома (a), наклонной вниз прямой (b) и круга (c).

Решение

Если какая-либо вертикальная линия пересекает график более одного раза, отношение, представленное на графике, не является функцией. Обратите внимание, что любая вертикальная линия будет проходить только через одну точку двух графиков, показанных в частях (a) и (b) рисунка ( PageIndex ). Из этого можно сделать вывод, что эти два графика представляют функции. Третий график не представляет функцию, потому что не более чем значений x вертикальная линия пересекает график более чем в одной точке, как показано на рисунке ( PageIndex ).

Рисунок ( PageIndex ): График круга.

Представляет ли график на рисунке ( PageIndex ) функцию?

Рисунок ( PageIndex ): График функции абсолютного значения. Ответ

Использование теста горизонтальной линии

После того, как мы определили, что график определяет функцию, простой способ определить, является ли она взаимно однозначной функцией, — это использовать тест горизонтальной линии .Проведите через график горизонтальные линии. Если какая-либо горизонтальная линия пересекает график более одного раза, то график не представляет собой взаимно однозначную функцию.

Практическое руководство. Имея график функции, используйте тест горизонтальной линии, чтобы определить, представляет ли график однозначную функцию

Проверьте график, чтобы увидеть, пересекает ли нарисованная горизонтальная линия кривую более одного раза.
Если такая линия есть, определите, что функция не взаимно однозначна.

Пример ( PageIndex ): Применение теста горизонтальной линии

Рассмотрим функции, показанные на рисунке ( PageIndex ) и рисунке ( PageIndex ). Являются ли какие-либо функции взаимно однозначными?

Решение

Функция на рисунке ( PageIndex ) не является взаимно однозначной. Горизонтальная линия, показанная на рисунке ( PageIndex ), пересекает график функции в двух точках (и мы даже можем найти горизонтальные линии, которые пересекают его в трех точках.)

Рисунок ( PageIndex ): График многочлена с горизонтальной линией, пересекающей 2 точки

Функция на рисунке ( PageIndex ) взаимно однозначна. Любая горизонтальная линия будет пересекать диагональную линию не более одного раза.

Является ли график, показанный на рисунке ( PageIndex ), взаимно однозначным?

Ответ

Нет, потому что он не проходит тест горизонтальной линии.

Ключевые понятия

Отношение — это набор упорядоченных пар.Функция — это особый тип отношения, в котором каждое значение домена или вход приводит ровно к одному значению диапазона или выходу.
Функциональная нотация — это сокращенный метод соотнесения ввода и вывода в форме (y = f (x) ).
В табличной форме функция может быть представлена строками или столбцами, которые относятся к входным и выходным значениям.
Чтобы оценить функцию, мы определяем выходное значение для соответствующего входного значения. Алгебраические формы функции можно оценить, заменив входную переменную заданным значением.
Чтобы найти конкретное значение функции, мы определяем входные значения, которые дают конкретное выходное значение.
Алгебраическая форма функции может быть записана из уравнения.
Входные и выходные значения функции можно определить по таблице.
Связь входных значений с выходными значениями на графике — еще один способ оценить функцию.
Функция взаимно однозначна, если каждое выходное значение соответствует только одному входному значению.
График представляет функцию, если любая вертикальная линия, проведенная на графике, пересекает график не более чем в одной точке.
График функции «один к одному» проходит проверку горизонтальной линии.

Глоссарий

зависимая переменная
выходная переменная

домен
набор всех возможных входных значений для отношения

функция
отношение, в котором каждое входное значение дает уникальное выходное значение

Проверка горизонтальной линии
Метод проверки взаимно однозначности функции путем определения того, пересекает ли какая-либо горизонтальная линия график более одного раза

независимая переменная
входная переменная

введите
каждый объект или значение в домене, который относится к другому объекту или значению посредством отношения, известного как функция

однозначная функция
функция, для которой каждое значение вывода связано с уникальным значением ввода

вывод
каждый объект или значение в диапазоне, который создается, когда входное значение вводится в функцию

диапазон
набор выходных значений, которые являются результатом входных значений в отношении

отношение
набор заказанных пар

Проверка вертикальной линии
Метод проверки того, представляет ли график функцию, путем определения того, пересекает ли вертикальная линия график не более одного раза

Авторы и авторство

Как рассчитать уклон в точке — Видео и стенограмма урока

Нахождение уклона в точке Шаги

Хорошо, теперь мы знаем взаимосвязь между производными и уклонами.Это соотношение уступает место этапам нахождения наклона функции в заданной точке ( x 1, y 1):

Найдите производную функции (есть много разных способов сделать это, в зависимости от на функции) и
Вставьте значение x , x 1 точки в производную (это наклон функции в точке)

Довольно просто, правда? Давайте применим это на практике! Снова рассмотрим наш пример с бассейном.Предположим, вода стекает 15 минут. Мы можем подключить 15 для x , чтобы увидеть, сколько воды осталось в бассейне:

A (15) = 4 (15) 2 — 320 (15) + 6400 = 2500

Через 15 минут слива , в бассейне осталось 2500 галлонов воды. Если мы хотим узнать скорость, с которой пул истощается в этот момент, мы просто выполняем функцию через предыдущие шаги.

Сначала находим производную функции. Для этой функции мы используем следующие факты, чтобы найти производную:

Производная суммы или разницы — это сумма или разность производных, соответственно
Производная константы равна 0, а
Производная от axn is тревогаn -1

Таким образом, производная A ( x ) = 4 x 2 — 320 x + 6400 равна A ‘( x ) = 8 x — 320

Следующий шаг состоит в том, чтобы вставить x = 15 в A ‘:

A ‘ (15) = 8 * 15 — 320 = -200

. вода, выходящая из бассейна, составляет 200 галлонов в минуту.Не позволяйте отрицательному ответу сбивать вас с толку. Это отрицательно, потому что вода уходит из бассейна, поэтому количество воды уменьшается. Если бы мы наполняли бассейн, то было бы положительно. В общем, когда значение функции уменьшается, ее наклон отрицательный, а когда значение функции увеличивается, ее наклон положительный.

Обратите внимание: если мы проведем касательную линию к графику функции, где x = 15, мы увидим, что это выглядит так, как будто наклон линии составляет примерно -200.

Мы видим, что мы вычислили наклон кривой в точке (15, 2500).

Дополнительная практика

Предположим, мы хотели узнать, как быстро истощается пул через 20 минут. Это тот же процесс. Мы уже нашли производную, поэтому просто подставляем x = 20 в производную A :

A ‘(20) = 8 * 20 — 320 = -160

Мы видим, что через 20 минут слива, вода выходит из бассейна со скоростью 160 галлонов в минуту.Опять же, мы можем заметить, что наклон касательной к кривой при x = 20 выглядит примерно как -160, поэтому мы знаем, что сделали это правильно.

Резюме урока

Хорошо, давайте на минутку рассмотрим то, что мы узнали. Производная функции дает формулу, которая позволяет нам вычислить наклон функции в любой заданной точке. Чтобы найти наклон функции в точке ( x 1, y 1), мы используем следующие шаги:

Найдите производную функции и
Вставьте x 1 в производную для x

Это дает вам наклон функции в точке ( x 1, y 1).

По сути, когда мы находим наклон функции в данной точке, мы находим скорость изменения этой функции в этой точке. Поскольку скорость изменений в мире вокруг нас постоянно меняется, это чрезвычайно полезное знание!

Линейные функции и их графики

Обзор линий графика

Напомним, что множество всех решений линейного уравнения может быть представлено на прямоугольной координатной плоскости с использованием прямой линии, проходящей по крайней мере через две точки; эта линия называется ее графиком.Например, чтобы построить график линейного уравнения 8x + 4y = 12, мы сначала решим для y .

8x + 4y = 12 Вычтем 8x с обеих сторон. 4y = −8x + 12 Разделим обе части на 4.y = −8x + 124 Упростим. Y = −8×4 + 124y = −2x + 3

В таком виде мы видим, что y зависит от x ; другими словами, x — это независимая переменная, которая определяет значения других переменных. Обычно мы думаем о x -значении упорядоченной пары ( x , y ) как о независимой переменной.и y — зависимая переменная — переменная, значение которой определяется значением независимой переменной. Обычно мы думаем о значении y упорядоченной пары ( x , y ) как о зависимой переменной. Выберите по крайней мере два значения x и найдите соответствующие значения y . Рекомендуется выбирать ноль, некоторые отрицательные числа, а также некоторые положительные числа. Здесь мы выберем пять значений x , определим соответствующие значения y , а затем сформируем репрезентативный набор упорядоченных парных решений.

Как найти функцию зная только точки?

Судя по всему, то, о чем Вы говорите — аппроксимация функции. В Википедии более подробна статья про интерполяцию.

По сути, Ваша задача сводится к 2м шагам:
1. По точкам и общим зависимостям выбирается форма функции (например, полиномиальная, экспоненциальная и.т.п).
2. Строится модель, в которой задаётся функция с неизвестными параметрами. Задача — найти такие параметры, чтобы минимизировать функцию невязки(часто это квадрат разности между реальными значениями в заданых точках и значениями модельной функции, см. МНК).

Источник

Содержание

Глава 3. Конформные отображения

Геометрический смысл аргумента и модуля производной функции комплексного переменного

Конформные отображения

Линейная функция

Инверсия

Дробно-линейное отображение

Целая степенная функция

Радикал

Показательная функция

Логарифмическая функция

Функция Жуковского

Тригонометрические функции

Теорема Римана. Основные принципы конформных отображений

Применения конформных отображений

Виды отображений

Инъективное отображение

Пример

Сюръективное отображение

Пример

Биективное отображение

Обратное отображение

Пример

Линейная аппроксимация

Аппроксимация линейной функцией

Пример реализации

Построение графика функции

Аппроксимация с фиксированной точкой пересечения с осью y

Как по точкам определить функцию: Как по точкам найти функцию найти функцию по точкам Математика

Построение графиков функций — урок. Алгебра, 10 класс.

Как построить график функции

Онлайн уравнение прямой по двум точкам с подробным решением

Аппроксимация в Matlab — CodeTown.ru

Аппроксимация

МНК (Метод Наименьших Квадратов)

Примеры задач

Поделиться ссылкой:

Получить функцию по точкам. Как по точкам найти функцию

Немного матчасти

Ставим опыты

Думаем и экспериментируем

А как люди-то делают?

MS Excel

LibreOffice Calc

Highcharts , одна из самых популярных JS-библиотек для построения диаграмм

amCharts , ещё одна популярная JS-библиотека

Coreplot , самая популярная библиотека построения графиков для iOS и OS X

aChartEngine , вроде как самая популярная библиотека построения графиков для Android

Вместо заключения

Рекомендуем также

Функция поиска уравнения по таблице точек

Ответы на вопросы (FAQ)

Как найти уравнение кривой?

Как найти уравнение из набора точек?

Как найти уравнение линии?

Исходный код

Нужна помощь?

Вопросы / комментарии

Уникальный круг, проходящий через три неколлинеарных точки

Решение трех линейных уравнений с тремя неизвестными

Линейные уравнения в координатной плоскости (Алгебра 1, Визуализация линейных функций) — Mathplanet

Функции: графики и пересечения

1.1: Четыре способа представления функции

Определение того, представляет ли отношение функцию

Использование обозначения функций

Представление функций с помощью таблиц

Поиск входных и выходных значений функции

Вычисление функций в алгебраических формах

Вычисление функций, выраженных в формулах

Оценка функции, заданной в табличной форме

Поиск значений функций из графика

Определение того, является ли функция однозначной

Использование теста вертикальной линии

Использование теста горизонтальной линии

Ключевые понятия

Глоссарий

Авторы и авторство

Как рассчитать уклон в точке — Видео и стенограмма урока

Нахождение уклона в точке Шаги

Дополнительная практика