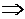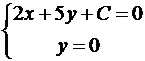Как найти функцию параллельную данной прямой - Исправление недочетов и поиск решений вместе с Examum.ru

В этой статье мы рассмотрим линейную функцию, график линейной функции и его свойства. И, как обычно, решим несколько задач на эту тему.

Линейной функцией называется функция вида y=kx+b

В уравнении функции число , которое мы умножаем на называется коэффициентом наклона.

Например, в уравнении функции y=-2x+3 ;

в уравнении функции y=-2+3x ;

в уравнении функции y=-x ;

в уравнении функции y=5 .

Графиком линейной функции является прямая линия.

1. Чтобы построить график функции, нам нужны координаты двух точек, принадлежащих графику функции. Чтобы их найти, нужно взять два значения х, подставить их в уравнение функции, и по ним вычислить соответствующие значения y.

Например, чтобы построить график функции , удобно взять x=0 и x=3 , тогда ординаты эти точек будут равны y=2 и y=3 .

Получим точки А(0;2) и В(3;3). Соединим их и получим график функции :

2. В уравнении функции y=kx+b коэффициент отвечает за наклон графика функции:

Коэффициент отвечает за сдвиг графика вдоль оси :

На рисунке ниже изображены графики функций y=2x+3 ; ; y=x+3

Заметим, что во всех этих функциях коэффициент больше нуля, и все графики функций наклонены вправо. Причем, чем больше значение , тем круче идет прямая.

Во всех функциях b=3 — и мы видим, что все графики пересекают ось OY в точке (0;3)

Теперь рассмотрим графики функций y=-2x+3 ; ; y=-x+3

На этот раз во всех функциях коэффициент меньше нуля, и все графики функций наклонены влево.

Заметим, что чем больше |k|, тем круче идет прямая. Коэффициент b тот же, b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3)

Рассмотрим графики функций y=2x+3 ; y=2x ; y=2x-2

Теперь во всех уравнениях функций коэффициенты равны. И мы получили три параллельные прямые.

Но коэффициенты b различны, и эти графики пересекают ось OY в различных точках:

График функции y=2x+3 (b=3) пересекает ось OY в точке (0;3)

График функции y=2x (b=0) пересекает ось OY в точке (0;0) — начале координат.

График функции y=2x-2 (b=-2) пересекает ось OY в точке (0;-2)

Итак, если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции y=kx+b .

Если k<0 и b>0, то график функции y=kx+b имеет вид:

Если k>0 и b>0, то график функции y=kx+b имеет вид:

Если k>0 и b<0, то график функции y=kx+b имеет вид:

Если k<0 и b<0, то график функции y=kx+b имеет вид:

Если k=0 , то функция y=kx+b превращается в функцию y=b и ее график имеет вид:

Ординаты всех точек графика функции y=b равны

Если b=0, то график функции y=kx проходит через начало координат:

Это график прямой пропорциональности.

3. Отдельно отмечу график уравнения x=a . График этого уравнения представляет собой прямую линию, параллельую оси все точки которой имеют абсциссу x=a .

Например, график уравнения x=3 выглядит так:

Внимание! Уравнение x=a не является функцией, так как различным значениям функции соответствует одно и то же значение аргумента, что не соответствует определению функции.

4. Условие параллельности двух прямых:

График функции $y=k_1{x}+b_1$ параллелен графику функции $y=k_2{x}+b_2$ , если k_1=k_2

5. Условие перпендикулярности двух прямых:

График функции $y=k_1{x}+b_1$ перпендикулярен графику функции $y=k_2{x}+b_2$ , если или $k_1=-1/{k_2}$

6. Точки пересечения графика функции с осями координат.

С осью ОY. Абсцисса любой точки, принадлежащей оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY нужно в уравнение функции вместо х подставить ноль. Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).

С осью ОХ: Ордината любой точки, принадлежащей оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ нужно в уравнение функции вместо y подставить ноль. Получим 0=kx+b. Отсюда x=-b/k . То есть точка пересечения с осью OX имеет координаты ( -b/k ;0):

Рассмотрим решение задач.

1. Постройте график функции , если известно, что он проходит через точку А(-3;2) и параллелен прямой y=-4x.

В уравнении функции y=kx+b два неизвестных параметра: k и b. Поэтому в тексте задачи должны быть два условия, характеризующих график функции.

а) Из того, что график функции y=kx+b параллелен прямой y=-4x, следует, что k=-4. То есть уравнение функции имеет вид y=-4x+b

б) Нам осталось найти b. Известно, что график функции y=-4x+b проходит через точку А(-3;2). Если точка принадлежит графику функции, то при подстановке ее координат в уравнение функции, мы получим верное равенство:

отсюда b=-10

Таким образом, нам надо построить график функции

Точка А(-3;2) нам известна, возьмем точку B(0;-10)

Поставим эти точки в координатной плоскости и соединим их прямой:

2. Написать уравнение прямой, проходящей через точки A(1;1); B(2;4).

Если прямая проходит через точки с заданными координатами, следовательно, координаты точек удовлетворяют уравнению прямой y=kx+b . То есть если мы координаты точек подставим в уравнение прямой, то получим верное равенство.

Подставим координаты каждой точки в уравнение y=kx+b и получим систему линейных уравнений.

Вычтем из второго уравнения системы первое, и получим k=3 . Подставим значение k в первое уравнение системы, и получим b=-2.

Итак, уравнение прямой y=3x-2 .

3. Постройте график уравнения

Чтобы найти, при каких значениях неизвестного произведение нескольких множителей равно нулю, нужно каждый множитель приравнять к нулю и учесть ОДЗ каждого множителя.

Это уравнение не имеет ограничений на ОДЗ. Разложим на множители вторую скобку и приравняем каждый множитель к нулю. Получим совокупность уравнений:

Построим графики всех уравнений совокупности в одной коорднатной плоскости. Это и есть график уравнения :

4. Постройте график функции , если он перпендикулярен прямой и проходит через точку М(-1;2)

Мы не будем строить график, только найдем уравнение прямой.

а) Так как график функции y=kx+b , если он перпендикулярен прямой , следовательно , отсюда k=2 . То есть уравнение функции имеет вид y=2x+b

б) Мы знаем, что график функции y=2x+b проходит через точку М(-1;2). Подставим ее координаты в уравнение функции. Получим:

, отсюда b=4 .

Следовательно, наша функция имеет вид: y=2x+4 .

5. Постройте график функции $y=(x^2-1)(1/{x-1}-1/{x+1})+x$

Упростим выражение, стоящее в правой части уравнения функции.

Важно! Прежде чем упрощать выражение, найдем его ОДЗ.

Знаменатель дроби не может быть равен нулю, поэтому x<>1 , x<>-1 .

$(x^2-1)(1/{x-1}-1/{x+1})+x =$

Тогда наша функция принимает вид:

То есть нам надо построить график функции y=x+2 и выколоть на нем две точки: с абсциссами x=1 и x=-1:

И.В. Фельдман, репетитор по математике.

Источник

График линейной функции, его свойства и формулы

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие функции

Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Графический способ — наглядно.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.

График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.

Понятие линейной функции

Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.

Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.

Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.

Если известно конкретное значение х, можно вычислить соответствующее значение у.

Нам дана функция: у = 0,5х — 2. Значит:

если х = 0, то у = -2;
если х = 2, то у = -1;
если х = 4, то у = 0;
и т. д.

Для удобства результаты можно оформлять в виде таблицы:

Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.

Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.

Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.

Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».

Функция	Коэффициент «k»	Коэффициент «b»
y = 2x + 8	k = 2	b = 8
y = −x + 3	k = −1	b = 3
y = 1/8x − 1	k = 1/8	b = −1
y = 0,2x	k = 0,2	b = 0

Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».

Еще не устали? Изучать математику веселее с опытным преподавателем на курсах по математике в Skysmart!

Свойства линейной функции

Область определения функции — множество всех действительных чисел.
Множеством значений функции является множество всех действительных чисел.
График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.
Функция не имеет ни наибольшего, ни наименьшего значений.
Четность и нечетность линейной функции зависят от значений коэффициентов k и b:
b ≠ 0, k = 0, значит y = b — четная;
b = 0, k ≠ 0, значит y = kx — нечетная;
b ≠ 0, k ≠ 0, значит y = kx + b — функция общего вида;
b = 0, k = 0, значит y = 0 — как четная, так и нечетная функция.
Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.
График функции пересекает оси координат:
ось абсцисс ОХ — в точке (-b/k, 0);
ось ординат OY — в точке (0; b).
x=-b/k — является нулем функции.
Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.
Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.
Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0: функция принимает отрицательные значения на промежутке (-∞, — b /_k) и положительные значения на промежутке (- b /_k, +∞)
При k b /_k, +∞) и положительные значения на промежутке (-∞, — b /_k).
Коэффициент k характеризует угол, который образует прямая с положительным направлением Ох. Поэтому k называют угловым коэффициентом.
Если k > 0, то этот угол острый, если k

Построение линейной функции

В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.

Например, чтобы построить график функции y = 1 /₃x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:

В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:

если k > 0, то график наклонен вправо;
если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
если b 1 /₂x + 3, y = x + 3.

Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.

В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).

Теперь рассмотрим графики функций y = -2x + 3, y = — 1 /₂x + 3, y = -x + 3.

В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.

Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).

Рассмотрим графики функций y = 2x + 3, y = 2x, y = 2x — 2.

Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.

При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:

график функции y = 2x + 3 (b = 3) пересекает ось OY в точке (0; 3);
график функции y = 2x (b = 0) пересекает ось OY в точке начала координат (0; 0);
график функции y = 2x — 2 (b = -2) пересекает ось OY в точке (0; -2).

Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.

Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.

Если k 0, то график функции y = kx + b выглядит так:

0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>

Если k > 0 и b > 0, то график функции y = kx + b выглядит так:

0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>

Точки пересечения графика функции y = kx + b с осями координат:

С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
Координаты точки пересечения с осью OY: (0; b).
С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = — b /_k.
Координаты точки пересечения с осью OX: (- b /_k; 0)

Решение задач на линейную функцию

Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!

Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.

В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
2 = -4(-3) + b
b = -10
Таким образом, нам надо построить график функции y = -4x — 10
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
Поставим эти точки в координатной плоскости и соединим прямой:

Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).

Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.
Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
Вычтем из второго уравнения системы первое, и получим k = 3.
Подставим значение k в первое уравнение системы, и получим b = -2.

Прямые на координатной плоскости

Линейная функция

Линейной функцией называют функцию, заданную формулой

где k и b – произвольные (вещественные) числа.

При любых значениях k и b графиком линейной функции является прямая линия .

Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом .

График линейной функции

При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 1, 2 и 3.

Рис.1

Рис.2

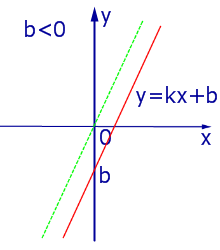Рис.3

При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.

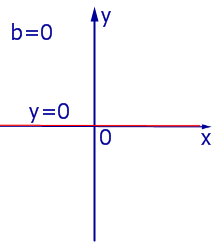Рис.4

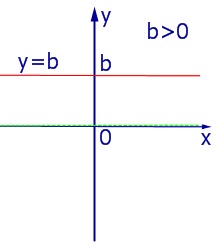Рис.5

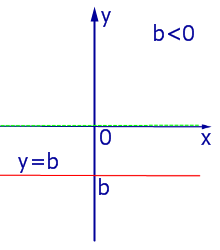Рис.6

При k линейная функция (1) убывает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 7, 8 и 9.

k y = kx + b₁ и y = kx + b₂ ,

имеющие одинаковые угловые коэффициенты и разные свободные члены , параллельны .

имеющие разные угловые коэффициенты , пересекаются при любых значениях свободных членов.

y = kx + b₁ и

перпендикулярны при любых значениях свободных членов.

Угловой коэффициент прямой линии

равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2).

Рис.10

Рис.11

Рис.12

Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b .

При прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле

Прямые, параллельные оси ординат

Прямые, параллельные оси Oy , задаются формулой

где c – произвольное число, и изображены на рис. 13, 14, 15.

Рис.13

Рис.14

Рис.15

Замечание 1 . Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .;

Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые

где p, q, r – произвольные числа.

В случае, когда уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .

что и требовалось.

В случае, когда получаем:

откуда вытекает, что уравнение (4) задает прямую линию вида (3).

В случае, когда q = 0, p = 0, уравнение (4) имеет вид

и при r = 0 его решением являются точки всей плоскости:

В случае, когда уравнение (5) решений вообще не имеет.

Замечание 2 . При любом значении r₁ , не совпадающем с r прямая линия, заданная уравнением

параллельна прямой, заданной уравнением (4) .

Замечание 3 . При любом значении r₂ прямая линия, заданная уравнением

перпендикулярна прямой, заданной уравнением (4) .

Пример . Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и

параллельной к прямой
перпендикулярной к прямой (8).

В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде

где r₁ – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство

Итак, уравнение прямой, параллельной к прямой

В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде

где r₂ – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство

Уравнение параллельной прямой

Альтернативная формула:
Прямая, проходящая через точку M₁(x₁; y₁) и параллельная прямой Ax+By+C=0 , представляется уравнением

назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения параллельной прямой (см. также как составить уравнение перпендикулярной прямой).

Пример №2 . Написать уравнение прямой, параллельной прямой 2x + 5y = 0 и образующей вместе с осями координат треугольник, площадь которого равна 5.
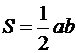
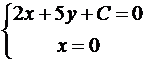
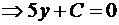
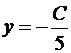
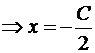
Решение. Так как прямые параллельны, то уравнение искомой прямой 2x + 5y + C = 0. Площадь прямоугольного треугольника , где a и b его катеты. Найдем точки пересечения искомой прямой с осями координат:
;
.
Итак, A(-C/2,0), B(0,-C/5). Подставим в формулу для площади: 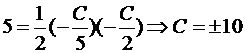. Получаем два решения: 2x + 5y + 10 = 0 и 2x + 5y – 10 = 0 .

Пример №3 . Составить уравнение прямой, проходящей через точку (-2; 5) и параллельной прямой 5x-7y-4=0 .
Решение. Данную прямую можно представить уравнением y = 5 /₇x – 4 /₇ (здесь a = 5 /₇). Уравнение искомой прямой есть y – 5 = 5 / 7(x – (-2)), т.е. 7(y-5)=5(x+2) или 5x-7y+45=0 .

Пример №4 . Решив пример 3 (A=5, B=-7) по формуле (2), найдем 5(x+2)-7(y-5)=0.

Пример №5 . Составить уравнение прямой, проходящей через точку (-2;5) и параллельной прямой 7x+10=0.
Решение. Здесь A=7, B=0. Формула (2) дает 7(x+2)=0, т.е. x+2=0. Формула (1) неприменима, так как данное уравнение нельзя разрешить относительно y (данная прямая параллельна оси ординат).

источники:

http://www.resolventa.ru/spr/algebra/degree1.htm

http://math.semestr.ru/line/parallel.php

Источник

Рассматривая линейную функцию вида (y=kx + b), особо выделяют случай, когда (b=0).

Тогда линейная функция принимает вид (y=kx) и называется прямой пропорциональностью.

Графиком функции (y=kx) является прямая, проходящая через начало координат.

Важно уметь переходить от аналитической модели (y=kx) к геометрической и, наоборот, от геометрической к аналитической модели.

Например, рассмотрим прямую, изображённую на рисунке.

Эта прямая является графиком линейной функции (y=kx), так как проходит через начало координат. Нужно лишь определить значение коэффициента (k).

Из формулы (y=kx) получим, что

k=yx

Чтобы определить коэффициент (k), необходимо выбрать некоторую точку на прямой и вычислить частное ординаты и абсциссы заданной точки.

Прямая проходит через точку (M(4; 2)), следовательно получим

24=0,5

. Значит, (k=0,5), и данная прямая является графиком линейной функции (y=0,5x).

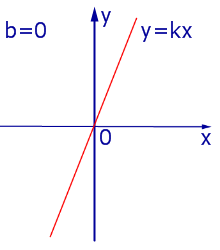
Если в формуле (y=kx) вместо (x) подставим (1), то получим (y=k). Это означает, что прямая (y=kx) проходит через точку ((1; k)). Поэтому график линейной функции можно строить по двум точкам: ((0;0)) и ((1; k)).

Иногда вместо точки ((1; k)) удобнее взять другую точку.

Коэффициент (k) определяет угол между прямой и положительным направлением оси (x).

Если (k>0), то этот угол острый (как на первом рисунке), а

если (k<0), то этот угол тупой (как на втором рисунке).

Поэтому коэффициент (k) в записи (y=kx) называют угловым коэффициентом.

Обобщая сведения о линейных функциях, можно сделать вывод:

прямая, служащая графиком линейной функции (y=kx + b), параллельна прямой, служащей графиком линейной функции (y=kx).

На рисунке показаны параллельные прямые с одним и тем же коэффициентом (k = 4).

Поэтому коэффициент (k) в записи (y=kx + b) также называют угловым коэффициентом, и

если (k>0), то прямая (y=kx + b) образует с положительным направлением оси (x) острый угол;

если (k<0), то этот угол тупой.

Источник

Линейная функция — функция вида График линейной функции — прямая.

Для построения графика линейной функции достаточно двух точек — потому что через две несовпадающие точки всегда можно провести прямую, причем единственную.

Угловой коэффициент прямой

Величина k в формуле линейной функции называется угловым коэффициентом прямой

Если , линейная функция возрастает. Чем больше х, тем больше у, то есть график идет вправо и вверх.

Если , линейная функция убывает. Чем больше х, тем меньше у, то есть график идет вправо и вниз.

Угловой коэффициент k равен тангенсу угла наклона графика линейной функции к положительному направлению оси Х.

Пусть Чем больше k, тем круче вверх идет график функции.

А что же будет, если k=0 ? Мы получим горизонтальную прямую y = b. На рисунке показан график функции y = 3.

Заметим, что прямая x = 3 (также изображенная на рисунке) не является графиком функции в нашем обычном, школьном смысле слова. В самом деле — мы помним, что функция — это соответствие между двумя множествами, причем каждому элементу множества Х соответствует один и только один элемент множества Y.

Для прямой x = 3 это не выполняется: значению x = 3 соответствует бесконечно много значений у.

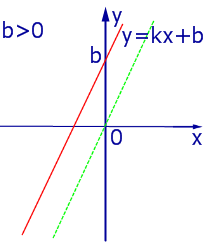
Если $k_1{=k}_2,$ прямые параллельны.

При этом, чем больше b, тем выше расположен на координатной плоскости график функции.

Например, прямые и параллельны. Их угловые коэффициенты равны.

Если прямые перпендикулярны. Например, прямые и пересекаются под прямым углом. Произведение их угловых коэффициентов равно — 1.

Построение графика линейной функции

График линейной функции построить легко — достаточно двух точек.

Оказывается, что привычный нам вид уравнения прямой — не единственно возможный.

Уравнение прямой можно записать также в виде

Построим, например, прямую, заданную уравнением

При x = 0 получаем, что y = 3.

При y = 0 получаем, что x = 4.

Значит, наша прямая проходит через точки и

Выразив у из уравнения , получим уравнение прямой вида

Если вы поступаете в вуз на специальность, связанную с математикой, — уже на первом курсе вы познакомитесь и с другими видами уравнения прямой.

Зачем изучать линейную функцию?

Дело в том, что многие зависимости в природе и технике описываются формулой виде

Например, закон Ома для участка цепи: Напряжение U прямо пропорционально силе тока I.

Формула для равномерного прямолинейного движения: S= vt . Пройденное расстояние S прямо пропорционально времени.

Закон теплового расширения , который вам встретится в одной из задач под номером 10 варианта Профильного ЕГЭ по математике — тоже линейная функция. И таких примеров можно привести очень много.

Обратите внимание, что в формулу линейной функции аргумент х входит в первой степени. Мы просто умножаем х на угловой коэффициент k и прибавляем b.

Если в формулу функции входит аргумент в любой другой степени — например, в квадрате или в кубе, если мы делим на х, если в формуле присутствует $sin x, frac{1}{x}$ или sqrt{x} , или показательные или логарифмические выражения, зависящие от х, — график функции уже не будет прямой линией.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Линейная функция» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
07.05.2023

Источник