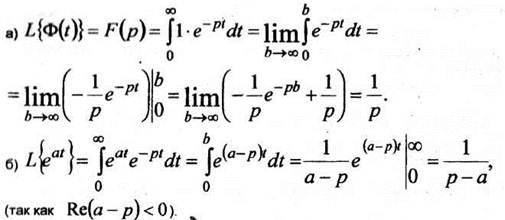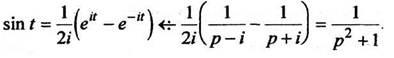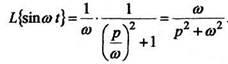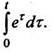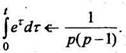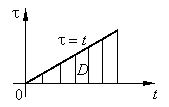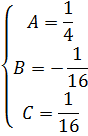Как найти функцию по ее преобразованию лапласа

Была ли эта статья полезной?

ОРИГИНАЛ И ЕГО ИЗОБРАЖЕНИЕ
ПО ЛАПЛАСУ.

Функцией-
оригиналом — называют функцию действительного
аргумента

удовлетворяющую
условиям:

1)
для всех отрицательных значений аргумента
функция тождественно равна нулю, т.е.

2)
функция при возрастает
не быстрее показательной
функции,
т.е. существ.уют такие постоянные что

3)
на любом конечном отрезке положительной
полуоси функция 
и
ее производные достаточно высокого
порядка непрерывны или имеют конечное
число разрывов 1-го рода.

Простейшей
функцией — оригиналом является единичная
функция Хевисайда

(1)

Если
функция не
удовлетворяет условию то
произведение уже
ему удовлетворяет, т.е. будет оригиналом.

Для
простоты записи множитель опускается,
например, пишут вместо вместо и
т.д.

Изображением
функции по
Лапласу (преобразованием по Лапласу) называют
функцию комплексной переменной определяемую
соотношением

(2)

Интеграл
(1.2) называют интегралом Лапласа.

Функция определяется
в полуплоскости и
является в этой области аналитической
функцией.

То,
что функция комплексной переменной является
изображением по Лапласу функции
действительного аргумента обозначается или

Изображение
элементарных функций получается
непосредственно с помощью интеграла
(2).

Пример
1 Найти изображение по Лапласу функции 

РЕШЕНИЕ

Таким
образом, получаем

Преобразование,
основанное на интеграле Лапласа (2),
обладает линейными свойсгыами.

1.
Преобразование суммы функций равно
сумме преобразований этих функций

2
Постоянный множитель можно выносить
за знак преобразования:

Из
этих двух свойств следует, что линейной
комбинации оригиналов соответствует
линейная комбинация их преобразований:

(3)

Пример
2. Найти изображение функции 

РЕШЕНИЕ

Используем
формулу (2) для функции Тогда

СВОЙСТВА ПРЕОБРАЗОВАНИЯ
ЛАПЛАСА

1.
Теорема подобияЕсли то
для любого постоянногоа > 0

(4)

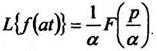
Пример
3. НайдемИз
примера2 _.По
Формуле (4)

2.Дифференцирование
оригиналаЕсли то

(5)

Методом
индукции на основании формулы (5) получены
формулы изображения высших производных:

(6)

(7)

(8)

Пример
4. ОпределимТак
как 

то
по формуле (5) получим:

3.
Дифференцирование изображения.Если то
т.е.
дифференцирование изображения сводится
к умножению на оригинала.
В общем случае,

(9)

Пример
5. Определить изображения функций 

РЕШЕНИЕ

Так
как 

В
общем случае 

4.
Интегрирование оригинала.Интегрирование
оригинала сводится к делению изображения
на р:

(10)

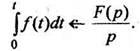
Пример
6. Найти изображение функци 

РЕШЕНИЕ
Так как то
по формуле (10) 

5.
Интегрирование изображения.Интефирование
изображения равносильно делению
на tоригинала
(если существует конечный предел 

(11)

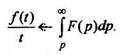
Пример
7. Найдем изображение функции 

Так
как 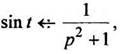то
по формуле (11) получаем

6.
Теорема смещенияПри
умножении оригинала на изображение
получается смещение аргумента на 

(12)

Пример
8. В примерах 3, 4, 5 найдены изображения
функций По
формуле (12) находим:

7.
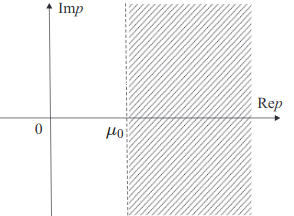
Теорема запаздывания.«Включение»
оригинала с запаздыванием на равносильно
умножению изображения на 

(13)

В
данной формуле важно подчеркнуть, что
функция поэтому
она умножена на единичную функцию
Хевисайда с запаздыванием .График
единичной функции Хевисайда с запаздывающим
аргументом показан на рисунке 1.

Изображение 

 ТАБЛИЦА
ОРИГИНАЛОВ И ИЗОБРАЖЕНИЙ.

СВЁРТКА ОРИГИНАЛОВ И ЕЁ
ПРИМЕНЕНИЕ. ТЕОРЕМА БОРЕЛЯ.

Свертка
односторонних функций, ее свойства.
Теорема Бореля

Сверткой
функций  и ,
заданных на ,
называется функция, равная интегралу , ;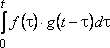
она обозначается ,
т.е.

, . 
(21)

Свойства
свертки 

1.
Симметрия, т.е. .

В
самом деле, изменяя порядок интегрирования
и полагая ,
получаем равенство

.

2.
Если  и  –
оригиналы, то и их свертка также является
оригиналом с показателем роста, равным
наибольшему из показателей роста
функций  
и .
Рекомендуем доказать самостоятельно
это утверждение или же посмотреть в
[3].

ПРИМЕР
32. Найти свертку функций  и .

Решение. ,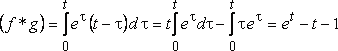
здесь ко второму интегралу применено
интегрирование по частям.

Теорема
Бореля

Если
функции  и  –
оригиналы и ,  и , ,
то произведение изображений  является
изображением свертки соответствующих
оригиналов для :

. 
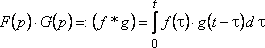
(22)

В
самом деле, по определению изображения
имеем

.

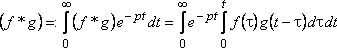
Замечаем,
что справа стоит двойной интеграл с
областью интегрирования ,
изображенной на рисунке. Изменяя в этом
интеграле порядок интегрирования,
получаем

.

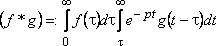
Замена
переменной интегрирования  позволяет
записать

.

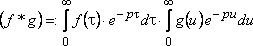
Поскольку
внутренний интеграл не зависит от ,
а внешний от ,
то двойной интеграл равен произведению
двух интегралов, т.е.

.

Теорема
Бореля применяется для нахождения
оригинала в случае, когда изображение
представлено в виде двух множителей,
для каждого из которых оригинал
устанавливается.

 ПРИМЕНЕНИЕ ОПЕРАЦИОННОГО
ИСЧИСЛЕНИЯ ДЛЯ РЕШЕНИЯ ЛИНЕЙНЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ
 КОЭФФИЦИЕНТАМИ

Пусть
имеем линейное неоднородное уравнение
с постоянными коэффициентами:

где
функция удовлетворяет условиям,
налагаемым на оригиналы.

Уравнение
(38) надо решить при нулевых начальных
условиях

Применяя
к обеим частям уравнения (38) преобразование
Лапласа и учитывая начальные условия,
найдем согласно (12):

,

откуда

.

Из
равенства (40), пользуясь известными
приемами операционного исчисления,
рассмотренными выше, найдем по
изображению  оригинал ,
который и будет являться искомым решением
уравнения (38) при .

Если
уравнение (40) требуется решить при
ненулевых начальных условиях

,

то
после применения к (40) преобразования
Лапласа найдем согласно (11): 

или

где  известная
целая рациональная функция от .

откуда
определим оригинал , являющийся искомым
решением уравнения (38).

Нетрудно
видеть, что в случае однородного уравнения

ПРИМЕНЕНИЕ ОПЕРАЦИОННОГО
ИСЧИСЛЕНИЯ ДЛЯ РЕШЕНИЯ  СИСТЕМ
ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
С  ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ.

оставим 
систему  уравнений:

Решив 
ее,  получаем

Итак  X(p)=  , 
откуда 

x(t)=— 
решение  данного  дифференциального 
уравнения.

Системы 
линейных  дифференциальных 
уравнений  с  постоянными 
коэффициентами  можно  решать 
операционными  методами  совершенно 
так  же,  как  и  отдельные 
уравнения;  все  отличие 
заключается  лишь  в  том, 
что  вместо  одного  изображающего 
уравнения  приходим  к  системе 
таких  уравнений,  причем 
система  эта  в  отношении 
изображений  искомых  функций 
будет  линейно  алгебраической. 
При  этом  никаких  предварительных 
преобразований  исходной  системы 
дифференциальных  уравнений 
производить  не  требуется  [3, 
с.  134].

Преобразование Лапласа и его свойства

Основные определения

1. Оригинал — это комплекснозначная функция действительного аргумента , которая удовлетворяет следующим условиям:

а) при ;

б) на любом конечном отрезке функция имеет не более чем конечное число точек разрыва первого рода;

в) имеет ограниченный рост, т.е. возрастает не быстрее показательной функции: существуют такие постоянные и , что при .

Замечания 5.1

1. Величина называется показателем роста функции . Для любой ограниченной функции, являющейся оригиналом, можно принять .

2. Обозначим , если пределы существуют и конечны.

3. Совокупность всех оригиналов называется пространством оригиналов.

4. В точке разрыва первого рода функция имеет конечные односторонние пределы: .

Пример 5.1

2. Изображение функции — функция комплексного переменного , определяемая равенством

Область существования этой функции определяется областью сходимости интеграла Лапласа, стоящего в правой части равенства (5.1). Исследование интeгpaлa позволяет определить эту область и установить свойства функции . Имеет место следующее утверждение.

Утверждение 5.1. Если функция , является оригиналом, то интеграл Лапласа сходится абсолютно в области (рис. 5.1) , где — показатель роста оригинала. Внутри этой области, т.е. на любом замкнутом подмножестве , интеграл сходится равномерно и определяет аналитическую функцию .

Замечания 5.2

1. Утверждение 5.1 аналогично свойствам степенных рядов, сходящихся в круге и равномерно сходящихся внутри этого круга, где сумма ряда является аналитической функцией.

2. Свойство аналитичности изображения имеет важное значение в теории и практике применения преобразования Лапласа, так как позволяет использовать в пространстве изображений методы теории аналитических функций, в частности разложения функций в ряды и теорию вычетов.

3. Совокупность всех изображений называется пространством изображений.

4. Переход, определяющий изображение по оригиналу , называется преобразованием Лапласа:

Запись означает, что оригиналу соответствует изображение .

5. Оригинал по изображению находится с помощью обратного преобразования Лапласа по формуле обращения

где путь интегрирования — любая прямая , параллельная мнимой оси и лежащая правее прямой (рис. 5.1).

Непосредственное применение формулы обращения часто затруднительно. Поэтому на практике пользуются методами, изложенными ранее.

Замечания 5.3

1. Для преобразования Лапласа используются различные обозначения, на пример и , что означает: оригиналу соответствует изображение и изображению соответствует оригинал . В некоторых учебниках вместо аргумента применяется , то есть и .

2. Для компактной записи оригиналов используется единичная ступенчатая функция

где — точка приложения (рис. 5.2). Так как во многих практических задачах аргумент имеет смысл текущего времени, то также называется моментом приложения единичной ступенчатой функции. В системах автоматического регулирования и управления функция рассматривается как типовой входной сигнал.

При функция является функцией Хевисайда:

Тогда, если функция удовлетворяет условиям «б», «в» в определении оригинала (п. 1), но не удовлетворяет условию «а», то функция будет оригиналом, так как

Далее под заданной с помощью аналитической формулы функцией , там, где это не вызывает недоразумений, будем понимать произведение этой функции на функцию Хевисайда, а множитель опускать.

3. Функции , являющиеся изображениями, удовлетворяют необходимому условию: если есть изображение, то при . Поэтому функции не являются изображениями. Однако в практических задачах функции типа и другие встречаются. Это требует расширения понятий оригинала и изображения.

Класс оригиналов можно расширить, включив в него функции, которые могут быть не ограничены в окрестности некоторых конечных точек, но такие, что интеграл Лапласа от них, тем не менее, сходится абсолютно в некоторой полуплоскости . К числу таких обобщенных оригиналов относятся степенная функция при и некоторые другие.

4. Во всякой точке , являющейся точкой разрыва функции , правая часть формулы (5.3) равна .

Примеры 5.2-5.3

---

Свойства преобразования Лапласа

Будем предполагать, что рассматриваемые далее функции являются оригиналами. Соответствующие им изображения (при ) обозначим .

1. Линейность. Если — оригиналы, то для любых комплексных чисел , функция также является оригиналом и справедливо равенство

Заметим, что для функции существенно, что все слагаемыс являются оригиналами, так как, например, функция является оригиналом, а слагаемые и не являются.

Справедливо и обратное утверждение: если — изображения, то

Здесь также важно, что слагаемые функции являются изображениями, поскольку из того, что — изображение, не следует, что — изображения. Например, функция является изображением, а слагаемые и не являются.

Примеры 5.4-5.5

2. Подобие (теорема подобия). Для любого из следует

и обратно: .

Пример 5.6

3. Смещение (теорема смещения). При любом комплексном из следует

то есть умножению оригинала на соответствует смещение изображения на .

Пример 5.7

---

Запаздывание оригинала

4. Запаздывание (теорема запаздывания). Для любого из следует

где (рис. 5.3), т.е. запаздыванию оригинала на соответствует умножение изображения на .

Примеры 5.8-5.10

Замечание 5.4. Дельта-функция часто встречается в инженерных приложениях как идеализация импульса конечной длительности. В теории автоматического регулирования и управления δ-функция вместе с единичной ступенчатой являются типовыми входными воздействиями.

Очевидно, изображение дельта-функции не удовлетворяет необходимому условию (п.2 замечаний 5.3). Этот факт свидетельствует о практическом требовании расширения понятия оригинала. Дельта-функция относится к обобщенным функциям и задается соотношением

---

Дифференцирование оригинала

5. Если функции являются оригиналами и , то

где .

Примеры 5.11-5.12

Интегрирование оригинала

Если функция является оригиналом и , то

т.е. интегрированию оригинала соответствует деление изображения на .

Пример 5.13

---

Дифференцирование изображения

Если функция является оригиналом и . то

Примеры 5.14-5.15

---

Интегрирование изображения

Если функция является оригиналом, то из следует

Пример 5.16

---

Умножение изображений (теорема Бореля)

Из и следует

т.е. свертке оригиналов соответствует произведение изображений. Функция определяется формулой

и называется сверткой оригиналов и .

Пример 5.17

---

Дифференцирование свертки (интеграл Дюамеля)

10. Согласно свойствам 9 и 5 найдем преобразование Лапласа от производной свертки двух функций:

С другой стороны,

или, применяя правило дифференцирования интеграла, зависящего от параметра, имеем

Здесь при дифференцировании интеграла, зависящего от параметра, применялась формула Лейбница, которая для общего случая имеет вид

Объединяя полученные результаты, можно записать:

Формула (5.17) называется интегралом Дюамеля. Интеграл Дюамеля применяется для решения дифференциальных уравнений.

Пример 5.18

---

Теорема о связи «начальных» и «конечных» значений оригинала и изображения

Начальное значение оригинала находится по формуле

Если существует конечный предел , то

Из соотношений (5.18),(5.19) следует, что для нахождения начальных и конечных значений оригинала не требуется знания оригинала, а достаточно иметь соответствующее изображение. На практике соотношение (5.19) применяется, например, для нахождения установившегося значения выходного сигнала в системах автоматического регулирования.

Пример 5.19

---

Нахождение изображения по оригиналу

Для нахождения изображения требуется применить свойства преобразования Лапласа Так, чтобы к функции или ее составляющим можно было применить результаты, содержащиеся в табл. 5.1.

Таблица 5.1. Таблица основных преобразований Лапласа

Посмотреть

Пример 5.21

---

Нахождение изображений функций, заданных графиком

При решении прикладных задач оригинал часто задан графиком. Это может быть, например, входной сигнал, действующий на систему автоматической регулирования. В этом случае рекомендуется сначала записать аналитическое выражение оригинала с помощью единичной ступенчатой функции (5.4), привести полученное выражение к виду, удобному для применения табл. 5.1 и свойстве преобразования Лапласа.

Пример 5.22

---

Нахождение изображений периодических функций

Во многих приложениях используются оригиналы, являющиеся периодическими функциями.

Пусть — оригинал с периодом (рис. 5.6,в), образованный повторением функции (рис. 5.6,б):

Для нахождения изображения периодической функции следует:
1. Найти изображение функции .
2. Найти изображение по формуле

Пример 5.23.

---

Нахождение оригинала по изображению

Непосредственное применение формулы обращения (5.3) затруднительно, поэтому для нахождения оригинала применяются теоремы разложения и правила преобразования изображения к виду, представленному в табл. 5.1.

Применение теорем разложения

Теорема 5.1 (первая теорема разложения). Если функция аналитична в некоторой окрестности бесконечно удаленной точки и ее разложение в ряд по степеням имеет вид , то функция (5.21) является оригиналом, соответствующим изображению .

Теорема 5.2 (вторая теорема разложения). Если изображение является однозначной функцией и имеет лишь конечное число особых точек лежащих в конечной части плоскости, то

Замечания 5.5

1. Формула (5.21) может быть записана в виде . Задача нахождения оригинала при выполнении условий теоремы сводится к нахождению коэффициентов разложения функции в ряд Лорана в окрестности бесконечно удаленной точки.

2. Формула (5.22) принимает наиболее простой вид в случае — рационального изображения, т.е. , где — многочлены степеней /пил соответственно, не имеющие общих корней. Если все полюсы функции простые, то по формуле (4.24) получаем , а формула (5.22) принимает вид

3. Если при выполнении условий п.2 коэффициенты многочлена — лействительные числа, то его комплексные корни, как известно, являются по парно сопряженными. Нахождение суммы вычетов в таких точках можно заме нить нахождением действительной части вычета в одной из них. Действительио, вычет в точке , используя свойства сопряженных чисел, можно записать следующим образом:

Это означает, что вычет в точке есть число, сопряженное вычету в точке , а сумма таких чисел равна их удвоенной действительной части:

Пример 5.24

---

Применение таблицы и свойств преобразования Лапласа

Приведем ряд известных приемов нахождения оригинала.

1. Если изображение отличается от табличного на постоянный множитель, то его следует умножить и одновременно поделить на этот множитель, а затем воспользоваться свойством линейности.

Пример 5.25

2. Изображение, заданное в виде дроби , разлагается на сумму дробей.

Пример 5.26

3. Если знаменатель дроби содержит квадратный трехчлен, то в нем выде ляется полный квадрат: . При этом числитель дроби представляется в виде многочлена от .

Пример 5.27

4. Если оригинал представляет собой правильную рациональную дробь, то следует разложить ее на простейшие дроби и для каждой из полученных дробей найти оригинал.

Примеры 5.28-5.29

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Преобразование Лапласа — интегральное преобразование, связывающее функцию $$F(p)$$ комплексного переменного (изображение) с функцией $$f(t)$$ вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения. Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так, свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими.

Определение

Прямое преобразование

Преобразованием Лапласа действительнозначной функции $$f(t)$$ называется функция $$F(p)$$ комплексной переменной такая, что

begin{equation}label{intLapl}
boxed{F(p) = intlimits^{+infty}_0 f(t) e^{-pt} dt, quad p in mathbb(C).}
end{equation}

Правая часть этого выражения называется интегралом Лапласа.

Для преобразования Лапласа используется обозначение $$f(t) supset F(t)$$.

Выясним, при каких условиях существует интеграл Лапласа для заданной функции $$f(t)$$. Будем рассматривать функцию $$f_mu(t) = e^{-mu t} f(t)$$, $$mu in mathbb{R}$$. Пусть существуют константы $$A$$, $$mu_0$$ такие, что $$|f(t)| le Ae^{-mu_0 t}$$ $$forall tge T$$. Тогда для любого $$mu ge mu_0$$ $$exists intlimits_0^{+infty} |e^{-mu t} f(t)|dt < infty$$. Поставим в соответствие функции $$f_mu(t)$$ функцию $$F_mu(t)$$, определяемую как прямое преобразование Фурье функции $$f_mu(t)$$:
[
F_mu(t) = intlimits_0^{+infty} f_mu(t) e^{-iomega t} dt = intlimits_0^{+infty} f(t) e^{-mu t} e^{-iomega t} dt = left{text{обозначим } p = mu + iomegain mathbb{C}right} = intlimits_0^{+infty} f(t) e^{-pt} dt equiv F(p).
]
Получаем следующие достаточные условия существования прямого преобразования Лапласа:

1. Функция $$f$$ растёт не быстрее показательной функции, т.е.
   begin{equation}label{growth_cond}
   exists A, mu_0 text{ такие, что } |f(t)|le Ae^{-mu_0 t} quad forall tge T.end{equation}
2. Интеграл $$intlimits_0^{+infty}|f(t) dt|$$ существует и конечен.

Обратное преобразование

Будем рассматривать физически реализуемую функцию $$chi(t)f_mu(t)$$, где функция $$chi(t)$$ — функция Хевисайда:
[
chi(t) = left{begin{align*}
1, &tge0,\
0, &t<0.
end{align*}right.
]

В этом случае $$t$$ может иметь смысл времени, поэтому получаем, что функция $$f(t)chi(t)$$ задана только на положительной полуоси $$tge0$$.

Рассмотрим обратное преобразование Фурье от функции $$F_mu(omega)$$:
[
f(t) e^{-mu t} chi(t) = f_mu(t) chi(t) = frac{1}{2pi} intlimits_{-infty}^{+infty} F_mu(omega) e^{iomega t} dt = frac{1}{2pi} intlimits_{-infty}^{+infty} F(p) e^{iomega t} dt.
]

Сделаем замену $$p = mu + iomega$$. Тогда $$domega = frac{dp}{i}$$, а верхний и нижний пределы интегрирования равны: $$omega = +infty Rightarrow p = mu + iinfty$$, $$omega = -infty Rightarrow p = mu — iinfty$$. Получаем:

[
f(t) e^{-mu t} chi(t) = frac{1}{2pi i} e^{-mu t} intlimits_{mu-iinfty}^{mu+iinfty} F(p) e^{pt} dp quad forall mu > tilde{mu}.
]

Домножив обе части равенства на $$e^{mu t}$$, окончательно получим формулу обратного преобразования Лапласа:

begin{equation}label{Mellins_formula}
boxed{f(t)chi(t) = frac{1}{2pi i} intlimits_{mu-iinfty}^{mu+iinfty} F(p)e^{pt} dp.}
end{equation}

Правая часть этого выражения называется формулой Меллина.

Теорема об области существовании изображения

Для всякого оригинала $$f(t)$$ изображение по Лапласу $$F(p)$$ определено в полуплоскости (mathrm{Re} p > mu_0) и является в этой области аналитической функцией.

Доказательство. Докажем, сначала, что интеграл Лапласа eqref{intLapl} сходится абсолютно в области $$mathrm{Re} p = mu > mu_0$$. В силу общего признака сравнения и условия роста eqref{growth_cond} получаем, что

[
left|intlimits_0^{+infty} f(t) e^{pt} dtright| le intlimits_0^{+infty} |f(t)| e^{-mu t} dt < A intlimits_0^{+infty} e^{-(mu-mu_0)t} dt.
]

Итак, для $$mu>mu_0$$:
begin{equation}label{int_bounds}
left| intlimits_0^{+infty} f(t) e^{-pt} dt right| < frac{A}{mu-mu_0},
end{equation}
то есть интеграл Лапласа сходится абсолютно.

Докажем теперь существование производной несобственного интеграла eqref{intLapl} по параметру $$p$$. Для этого убедимся в равномерной сходимости в области $$mathrm{Re},p > mu_0$$ интеграла
[
F'(p) = J(p) = intlimits_0^{+infty} (-t) f(t) e^{(mu + iomega)t} dt.
]

Выберем произвольное положительное действительное число $$mu_1$$ такое, что $$mathrm{Re},p ge mu_1 > mu_0$$. Тогда, в соответствии с признаком Вейерштрасса равномерной сходимости получаем, что

[
|J(p)| le intlimits_0^{+infty} t |f(t)| e^{-mu_1 t} dt < Aintlimits_0^{+infty} t e^{-(mu_1-mu_0)t} dt = frac{A}{(mu_1-mu_0)^2} < infty,
]

что и доказывает возможность дифференцирования интеграла eqref{intLapl} по параметру $$p$$ в области $$mathrm{Re},p ge mu_1 > mu_0$$. В силу произвольности выбора $$mu_1$$ мы доказали аналитичность изображения в области $$mathrm{Re},p > mu_0$$. $$blacksquare$$

Замечание. Из неравенства eqref{int_bounds} вытекает, что $$limlimits_{mu to +infty} F(p) = 0$$. Отсюда следует, что изображение $$F(p)to 0$$ при $$p to infty$$, оставаясь внутри угла $$-frac{pi}{2} + delta < arg p < frac{pi}{2} — delta$$, где $$delta$$ — сколь угодно малое положительное число.
Если же функция $$F(p)$$ аналитична в бесконечно удалённой точке $$p=infty$$, то $$F(p)toinfty$$ при $$ptoinfty$$ по любому пути.

Элементарные преобразования

Будем обозначать за $$F(p), G(p)$$ изображение по Лапласу функций $$f(t), g(t)$$. Выпишем таблицу основных преобразований:

$$f(t)$$	$$F(t)$$
[chi(t)]	[frac{1}{p}]
[ chi(t) e^{beta t} ]	[ frac{1}{p-beta} ]
[ chi(t) g(t)e^{beta t} ]	[ G(p-beta) ]
[ chi(t) g(t)e^{-beta t} ]	[ G(beta-p) ]
[ chi(t) t^alpha e^{beta t} ]	[ frac{Gamma(alpha + 1)}{(p-beta)^{alpha + 1}} ]
[ chi(t) t^n, ninmathbb{N} ]	[ frac{n!}{p^{n+1}} ]
[ chi(t) t^alpha, alphainmathbb{R} ]	[ frac{Gamma(alpha+1)}{p^{alpha+1}} ]
[ chi(t) sin beta t ]	[ frac{beta}{p^2+beta^2} ]
[ chi(t) cos beta t ]	[ frac{p}{p^2+beta^2} ]
[ chi(t) t^alpha sin beta t ]	[ frac{Gamma(alpha + 1)}{2i}left( frac{1}{(p-ibeta)^{alpha + 1}} — frac{1}{(p + ibeta)^{alpha+1}} right) ]
[ chi(t) t^alpha cos beta t ]	[ frac{Gamma(alpha + 1)}{2}left( frac{1}{(p-ibeta)^{alpha + 1}} + frac{1}{(p + ibeta)^{alpha+1}} right) ]
[ chi(t) sinh t ]	[ frac{beta}{p^2-beta^2} ]
[ chi(t) cosh t ]	[ frac{p}{p^2-beta^2} ]
[ chi(t) t^alpha sinh t ]	[ frac{Gamma(alpha + 1)}{2} left( frac{1}{(p-beta)^{alpha + 1}} — frac{1}{(p+beta)^{alpha + 1}} right) ]
[ chi(t) t^alpha cosh t ]	[ frac{Gamma(alpha + 1)}{2} left( frac{1}{(p-beta)^{alpha + 1}} + frac{1}{(p+beta)^{alpha + 1}} right) ]
[ delta(t) ]	[ 1 ]

Приведём доказательства для некоторых из этих формул.

1. Пусть $$f(t)=1$$.
   [
   intlimits_0^{+infty} t e^{-pt} dt = left. -frac{1}{p} e^{-pt} right|^{+infty}_0 = frac{1}{p}.
   ]
   Легко видеть, что данный интеграл сходится при любом $$mu>0$$.
2. Пусть теперь $$f(t) supset F(p)$$.
   [
   intlimits_0^{+infty} f(t) e^{(beta-p)t} dt = F(p-beta).
   ]
3. Найдём преобразование Лапласа для функции $$f(t) = chi(t) t^alpha$$, $$alpha > 0$$.
   [
   forall pinmathbb{R} : intlimits_0^{+infty} t^alpha e^{-pt} dt = left{ begin{matrix} pt = s \ ds = pdt end{matrix} right} = intlimits_0^{+infty} left( frac{s}{p} right)^alpha e^{-s} frac{1}{p} ds = frac{1}{p^{alpha + 1}} intlimits_0^{+infty} s^alpha e^{-s} ds = frac{1}{p^{alpha + 1}} Gamma(alpha + 1).
   ]
   Эту функцию можно аналитически продолжить на всю комплексную плоскость, т.е. [
   forall pinmathbb{C} : chi(t) t^alpha supset frac{Gamma(alpha + 1)}{p^{alpha + 1}} quad forall alpha > 0.
   ]
4. Рассмотрим функции $$chi(t) t^alpha cos beta t$$ и $$chi(t) t^alpha sin beta t$$. По формуле Эйлера: [
   cos beta t = frac{e^{ibeta t} + e^{-ibeta t}}{2}, quad sin beta t = frac{e^{ibeta t} — e^{-ibeta t}}{2}.
   ]
   Отсюда, используя результаты пункта 3, легко получить формулы изображений для указанных функций.
   Аналогично выводятся формулы для гиперболических тригонометрических функций: [
   sinh x = frac{e^x — e^{-x}}{2}, quad cosh x = frac{e^x + e^{-x}}{2}.
   ]

Свойства преобразования Лапласа

Будем обозначать через $$F(p)$$, $$G(p)$$, $$H(p)$$ и т.д. изображения по Лапласу оригиналов $$f(t)$$, $$g(t)$$, $$h(t)$$ и тд.

Линейность

Для любых $$alpha, beta in mathbb{C}$$ справедливо:

[
alpha f(t) + beta g(t) supset alpha F(p) + beta G(p).
]

Это соотношение является прямым следствием линейности преобразования Фурье.

Масштабируемость

[
begin{matrix} dfrac{1}{a} fleft( dfrac{t}{a} right) supset F(pa) \
f(ta) supset dfrac{1}{a} Fleft( dfrac{p}{a} right) end{matrix}
quad forall a>0.
]

Доказательство. Рассмотрим преобразование Лапласа функции $$fleft( frac{t}{a} right)$$:
[
intlimits_0^{+infty} fleft( dfrac{t}{a} right) e^{-pt} dt = left{ begin{matrix} z = at \ dz = adt end{matrix} right} = intlimits_0^{+infty} f(z) e^{-paz} a,dz = aF(pa).
]

Аналогично доказывается вторая формула. $$blacksquare$$

Сдвиг №1

Пусть $$chi(t) f(t) supset F(t)$$. Тогда $$forall tau>0$$ справедливо:
[
chi(t-tau)f(t-tau) supset e^{-ptau}F(p).
]

Доказательство. Применим преобразование Лапласа к функции $$chi(t-tau) f(t-tau)$$. Сделав замену переменной $$xi = t-a$$, получим
[
intlimits_tau^{+infty} f(t-tau) e^{-pt} dt = int_0^{+infty} f(xi) e^{-p(tau+xi)} dxi = e^{-ptau} F(xi). quad blacksquare
]

Сдвиг №2

Пусть $$chi(t) f(t) supset F(t)$$. Тогда $$forall tau>0$$ справедливо:

[
chi(t) f(t+a) supset e^{pa} left( F(p) — intlimits_0^a f(xi) e^{-pxi} dxi right).
]

Доказательство. Найдём преобразование Лапласа для функции $$chi(t) f(t+a)$$:
[
intlimits_0^{+infty} f(t+a)e^{-pt} dt = intlimits_0^{+infty} e^{-p(xi-a)} dxi — intlimits_0^a f(xi) e^{-p(xi-a)} dxi. quad blacksquare
]

Заметим, что вычитаемое в этой формуле соответствует утерянной части сигнала.

Дифференцирование оригинала

Если функция $$f(t) in C'(0, +infty)$$ и она удовлетворяет достаточным условиям существования прямого преобразования Лапласа, тогда выполнено следующее соотношение:
begin{equation}label{LT_Deriv}
f'(t) supset pF(p) -f(0+0).
end{equation}

В общем случае: если $$f(t) in C^{(k)}(0,+infty)$$ и выполнены достаточные условия существования прямого преобразования, то
begin{equation}label{LT_Derivk}
f^{(k)}(t) supset p^k F(p) — p^{k-1} f(0+0) — p^{k-2} f'(0+0) — dots — pf^{(k-2)}(0+0) — f^{(k-1)}(0+0).
end{equation}

Доказательство. Посчитаем преобразование Лапласа от функции $$f'(t)$$. Используя интегрирование по частям, получаем:
[
intlimits_0^{+infty} f'(t) e^{-pt} dt = f(t) e^{-pt} bigg|_0^{+infty} — intlimits_0^{+infty} f(t) (-p) e^{-pt} dt = 0 — f(0+0) + pF(p).
]

Далее найдём изображение второй производной, дважды применив формулу eqref{LT_Deriv}:
[
f»(t) = left( f(t) right)’ supset pBigl( pF(p) — f(0+0) Bigr) — f'(0+0) = p^2 F(p) — pf(0+0) — f'(0+0).
]

Далее, по методу математической индукции, находим:
[
f^{(k)} = left( f^{(k-1)}(t) right) supset p left( p^{k-1} F(p) -sumlimits_{l=1}^{k-2} p^{k-2-l} f^{(l)}(0+0) right) — f^{(k-1)}(0+0).
]

Раскрывая скобки, перейдём к выражению eqref{LT_Derivk}. $$blacksquare$$

Дифференцирование изображения

[
(-t)^k f(t) supset F^{(k)} (p).
]

Доказательство. Как уже было установлено, изображение $$F(p)$$ является аналитической функцией в полуплоскости $$mathrm{Re},p = mu > mu_0$$, а значит её можно дифференцировать по $$p$$ как интеграл, зависящий от параметра. Применим к формуле eqref{intLapl} $$k$$-кратное дифференцирование:
[
F^{(k)}(p) = intlimits_0^{+infty} (-t)^k f(t) e^{-pt} dt. quad blacksquare
]

Интегрирование оригинала

[
intlimits_0^t f(tau) dtau supset dfrac{F(p)}{p}.
]

Доказательство. По формуле eqref{intLapl} получаем, что
[
F(p) = intlimits_0^{+infty} e^{-pt} f(t) dt = intlimits_0^{+infty} e^{-pt} dleft( intlimits_0^t f(tau) dtau right).
]
Далее применим формулу интегрирования по частям:
[
intlimits_0^{+infty} e^{-pt} dleft( intlimits_0^t f(tau) dtau right) = e^{-pt} intlimits_0^t f(t) dt Bigg|_{t=0}^{+infty} + pint_0^{+infty} e^{-pt} dt intlimits_0^t f(tau) dtau = pintlimits_0^{+infty} e^{-pt} dtintlimits_0^t f(tau) dtau.
]
Так как функция $$f(t)$$ возрастает не быстрее показательной, то мы можем избавиться от первого слагаемого. $$blacksquare$$

Интегрирование образа

Если интеграл $$int_p^infty F(xi) dxi$$ сходится по любому пути, целиком лежащему в области $$mathrm{Re},p > mu_0$$, то он является изображением функции $$f(t)/t$$, т.е.
[
dfrac{f(t)}{t} supset intlimits_p^infty F(xi) dxi.
]

Доказательство. Согласно eqref{intLapl}:
begin{equation}label{double_int}
int_p^infty F(xi) dxi = int_p^infty dxi intlimits_0^{+infty} f(t) e^{-xi t} dt.
end{equation}

Предположим, что путь интегрирования $$(p,infty)$$ целиком лежит в полуплоскости $$mathrm{Re},xi ge mu > mu_0$$. Дадим оценку внутреннего интеграла:
[
left| intlimits_0^{+infty} f(t) e^{-qt} dt right| < A intlimits_0^{+infty} e^{-(mu-mu_0)t} dt = dfrac{M}{mu-mu_0} < infty.
]

Отсюда по достаточному признаку Вейерштрасса следует равномерная сходимость данного интеграла по параметру $$xi$$ в области $$mathrm{Re},p > mu_0$$. Тогда в интеграле eqref{double_int} можно сменить порядок интегрирования:
[
intlimits_p^infty F(xi) dxi = intlimits_0^{+infty} f(t) dt intlimits_p^infty e^{-xi t} dxi = int_0^{+infty} f(t) dfrac{e^{-pt}}{t} dt. quad blacksquare
]

Свёртка

Напомним, что свёрткой функций $$f(t)$$ и $$g(t)$$ называют функцию вида:
[
f(t)*g(t) equiv intlimits_{-infty}^{+infty} f(tau)g(t-tau) dtau = intlimits_{-infty}^{+infty} g(tau) f(t-tau) dtau.
]
Для функций-оригиналов с учётом того, что $$f(t)equiv 0$$ и $$g(t)equiv 0$$ при $$t<0$$ получаем, что
begin{equation}label{convolution}
f(t)*g(t) equiv intlimits_0^t f(tau)g(t-tau) dtau.
end{equation}

Свёртка оригиналов соответствует произведению изображений:
[
(f*g)(t) supset F(p) cdot G(p).
]

Доказательство. Сначала покажем, что свёртка оригиналов eqref{convolution} является оригиналом, то есть выполняются достаточные условия существования прямого образования Лапласа. Очевидно, что $$f(t)*g(t) equiv 0$$ при $$t<0$$. Покажем, что свёртка имеет скорость сходимости не выше экспоненциальной. Так как оригиналы удовлетворяют следующим условиям:
[
|f(t)| < A e^{mu_0 t}, quad |g(t)| < B e^{mu_1 t},
]
то мы имеем следующую оценку абсолютной величины свёртки:
[
|f(t) * g(t)| = left| intlimits_0^t f(tau) g(t-tau) dtau right| < AB intlimits_0^t e^{mu_0 tau} e^{mu_1 (t-tau)} dtau le AB te^{mu t},
]
где $$mu = max{ mu_0, mu_1 }$$. Отсюда получаем, что $$|f(t) * g(t)| < C e^{(mu + varepsilon) t}$$.

Докажем теперь справедливость формулы для образа свёртки. Согласно eqref{intLapl}:
[
f(t) * g(t) supset intlimits_0^{+infty} e^{-pt} dt int_0^t f(tau) g(t-tau) dtau.
]

Поменяем порядок интегрирования в двойном интеграле:
[
intlimits_0^{+infty} e^{-pt} dt int_0^t f(tau) g(t-tau) dtau = int_0^{+infty} f(tau) dtau intlimits_tau^{+infty}g(t-tau) e^{-pt} dt = Bigl{ t-tau = theta Bigr} = intlimits_0^{infty} f(tau) dtau intlimits_0^{+infty} g(theta) e^{-p(theta + tau)} dtheta. quad blacksquare
]

Периодическая функция

Пусть $$f(t)$$ — периодическая функция с периодом $$T>0$$.

[
intlimits_0^{+infty} f(t) e^{-pt} dt = sumlimits_{k=1}^{+infty} int_{(k-1)T}^{kT} f(t) e^{-pt} dt = left{ t = (k-1)T + s right} = sumlimits_{k=1}^{+infty} int_0^T f(s) e^{-ps} e^{-p(k-1)T} ds = left( sumlimits_{k=1}^{+infty} e^{-p(k-1)T} right) intlimits_0^T f(s) e^{-ps} ds = dfrac{1}{1-e^{-pT}} intlimits_0^T f(s) e^{-ps} ds,
]
то есть в случае периодической функции достаточно посчитать интеграл Лапласа на одном периоде.

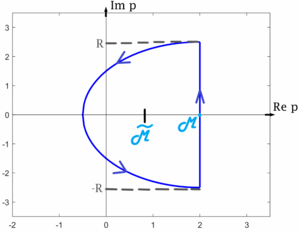
Вычисление обратного преобразования Лапласа

Общий случай

Рассмотрим формулу Меллина eqref{Mellins_formula}:
[
f(t)chi(t) = frac{1}{2pi i} intlimits_{mu — iinfty}^{mu + iinfty} F(p)e^{pt} dp.
]

В области $$mu > mu_0$$ функция $$F(p)$$ является аналитичной (по теореме об области существования). Пусть функция $$F(p)$$ имеет конечное число особых точек $$p_1, p_2, dots, p_n$$, лежащих в конечной части плоскости (т.е. существует такая полуокружность, которая содержит все эти особые точки). Тогда для этой функции применима лемма Жордана, то есть $$F(p) e^{pt} overset{Omega_R}{underset{R to +infty}{rightrightarrows}} 0$$. Отсюда получаем:
[
f(t)chi(t) = frac{1}{2pi i } cdot 2pi i sumlimits_{i=1}^n mathbb{res},(F(p)e^{pt}, p_i) = sumlimits_{i=1}^n mathbb{res},(F(p)e^{pt}, p_i).
]

Рациональный образ

Напомним, что $$delta(t) supset 1$$. Используя элементарные преобразования и свойства преобразования Лапласа можем выписать следующие выражения:
begin{equation}label{delta}
delta^{(k)}(t) supset p^k, quad delta(t-alpha) supset e^{-palpha}, quad delta^{(k)}(t-alpha) supset e^{-palpha} p^k.
end{equation}

Пусть функция $$F(p)$$ — рациональная, то есть она имеет вид $$F(p) = dfrac{Q(p)}{P(p)}$$, где $$Q(p)$$ и $$P(p)$$ — многочлены от переменной $$p$$.

• Пусть $$deg Q ge deg P$$. Тогда можем выполнить деление многочленов и воспользоваться выражениями eqref{delta}.
• Пусть $$deg Q le deg P$$. Тогда эту дробь можно разложить в следующую сумму:

[
dfrac{Q(p)}{P(p)} = dfrac{A_{1m_1}}{(p-alpha_1)^{m_1}} + dfrac{A_{1(m_1-1)}}{(p-alpha_1)^{m_1-1}} + dots + dfrac{A_{11}}{p-alpha_1} + dfrac{A_{2m_2}}{(p-alpha_2)^{m_2}} + dots + dfrac{A_{21}}{p-alpha_2} + dots + dfrac{B_{11}(p-eta) + C_{11}}{p^2 + beta_1 p + gamma_1} + dots + dfrac{B_{1n_1}p + C_{1n_1}}{(p^2 + beta_1 p + gamma_1)^{n_1}} + dots .
]

Теперь, пользуясь линейностью преобразования Лапласа, можем искать прообразы каждого слагаемого по-отдельности. В случае, если в знаменателе стоит выражение степени $$k>1$$, нужно воспользоваться свойством дифференцирования для понижения степени. Иначе, используя элементарные преобразования, получаем, что
[
A_{11} e^{alpha_1 t} supset dfrac{A_{11}}{p-alpha_1}.
]

Для дробей с квадратным трёхчленом в знаменателе воспользуемся методом выделения полного квадрата:
[
dfrac{B_{11}p + C_{11}}{p^2 + beta_1 p + gamma_1} = dfrac{B_{11}(p-eta) + left( C_{11} + B_{11}eta right)}{(p-eta)^2 + w^2)} = dfrac{B_{11}(p-eta)}{(p-eta)^2 + w^2)} + dfrac{C_{11} + B_{11}eta}{(p-eta)^2 + w^2} supset B_{11}e^{eta t} cos wt + tilde{C} e^{eta t} sin wt .
]