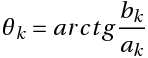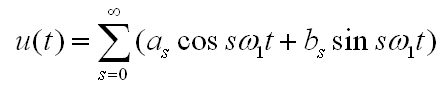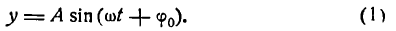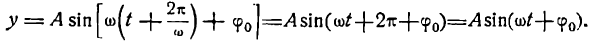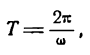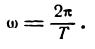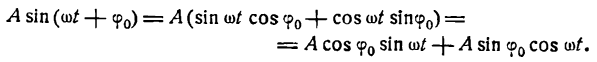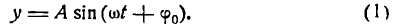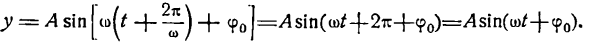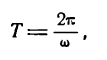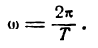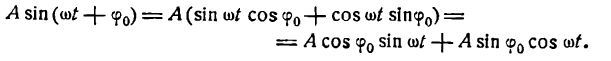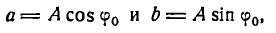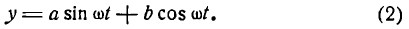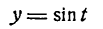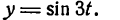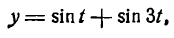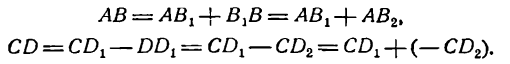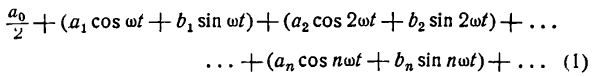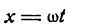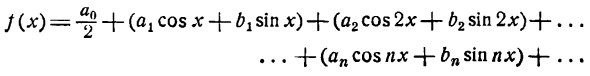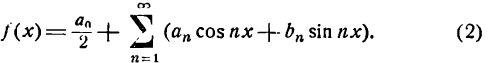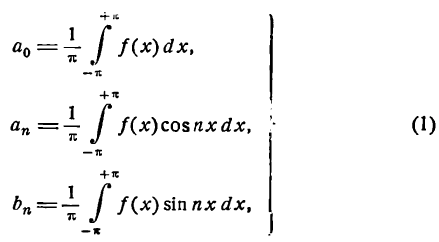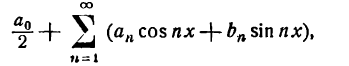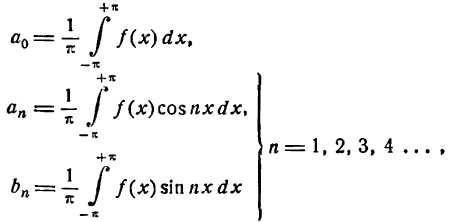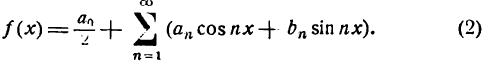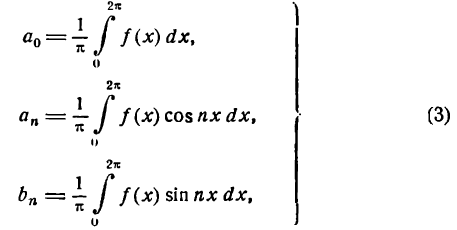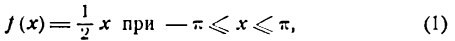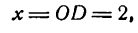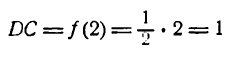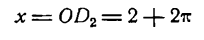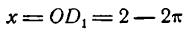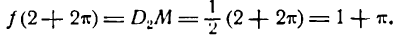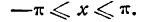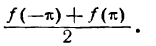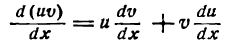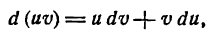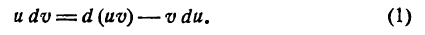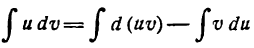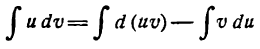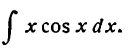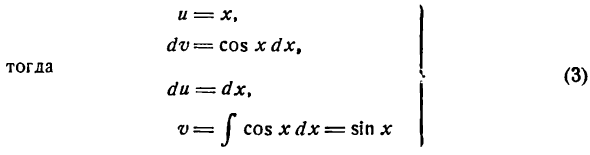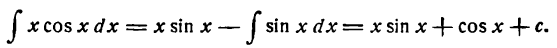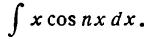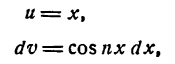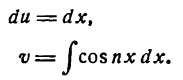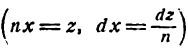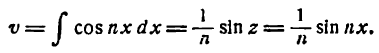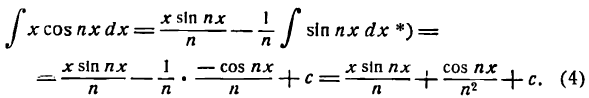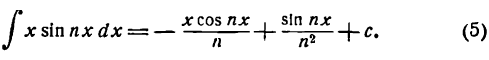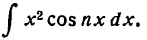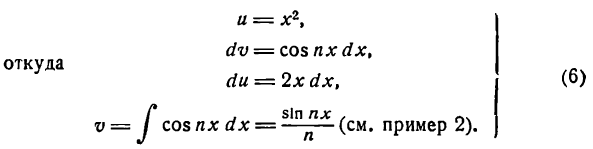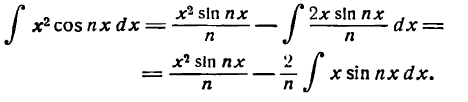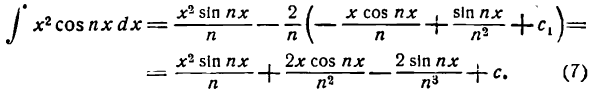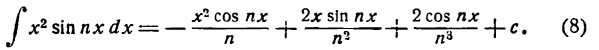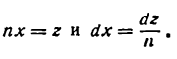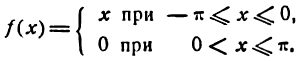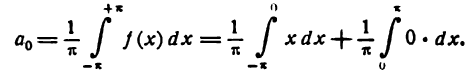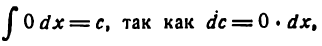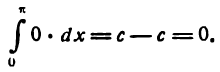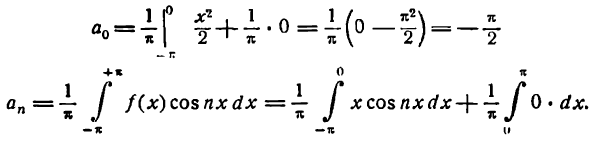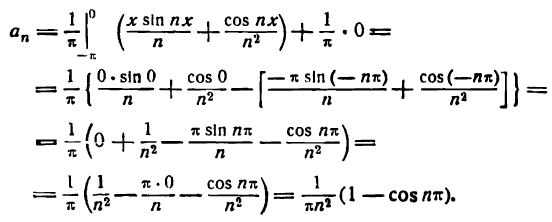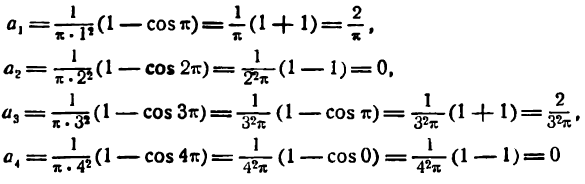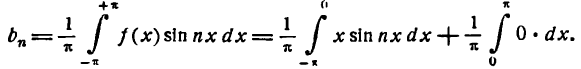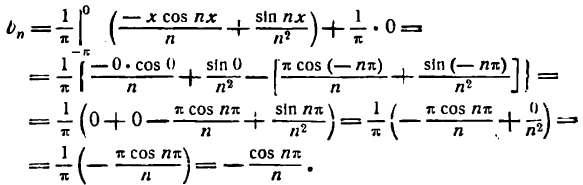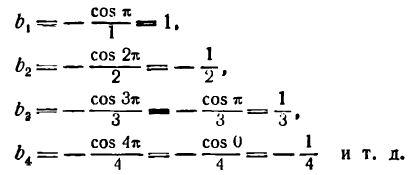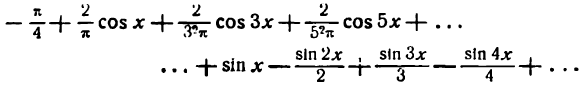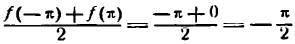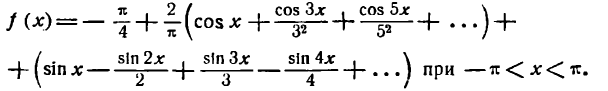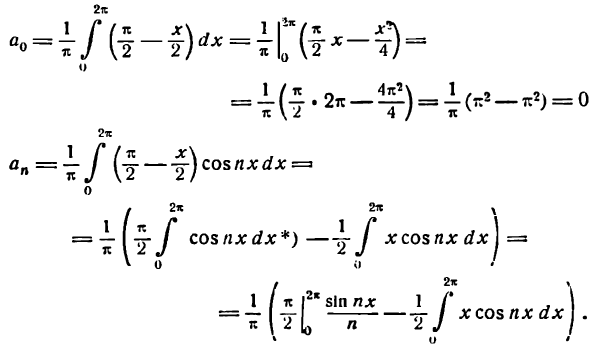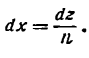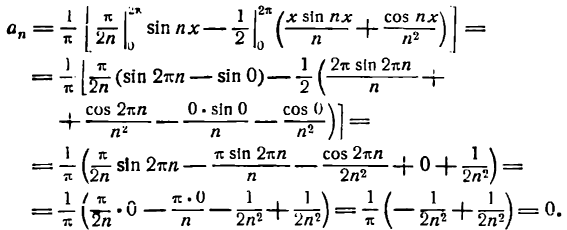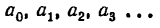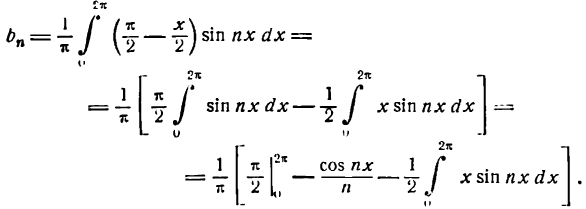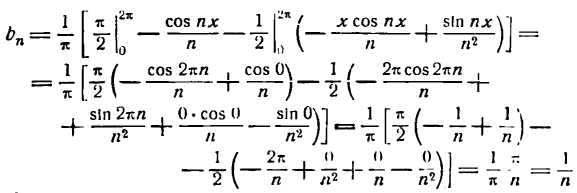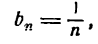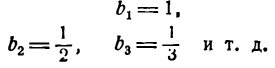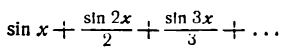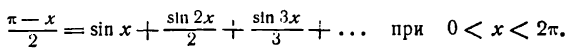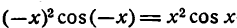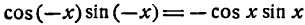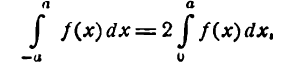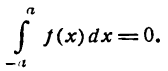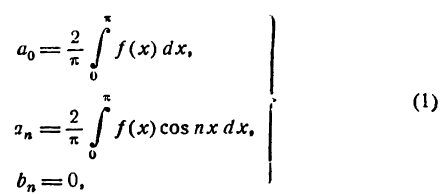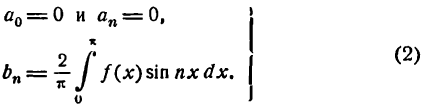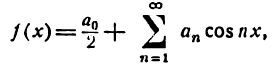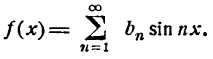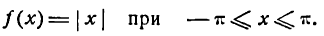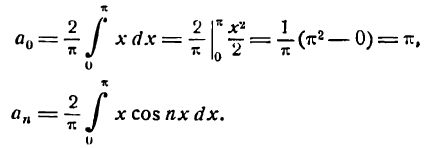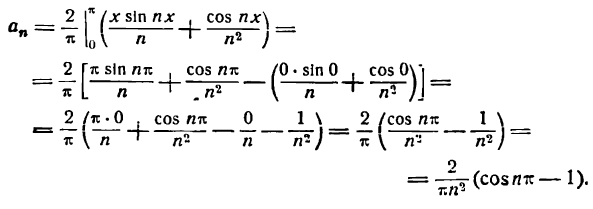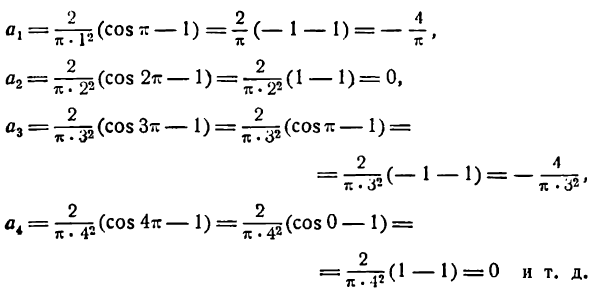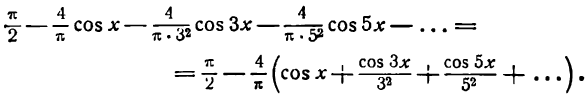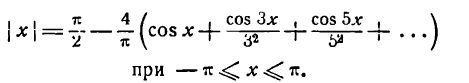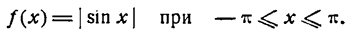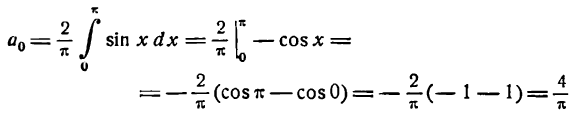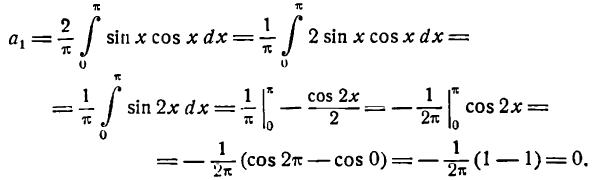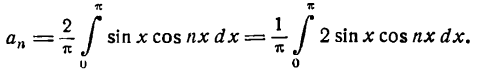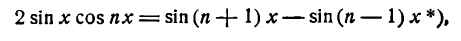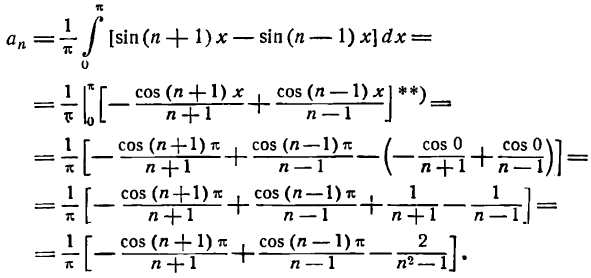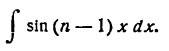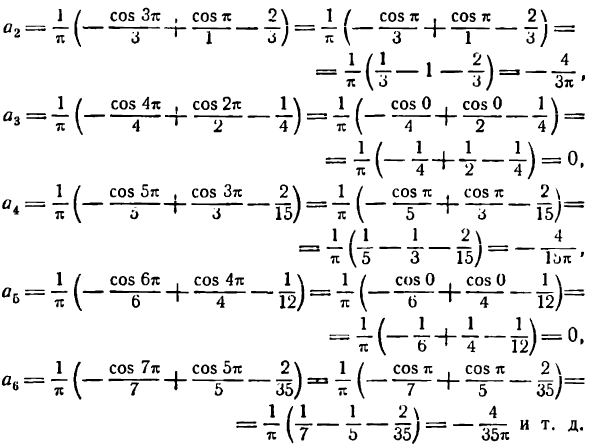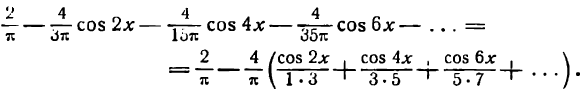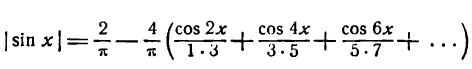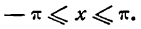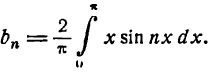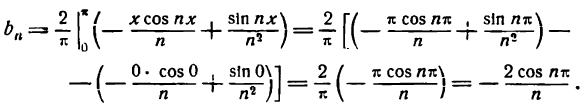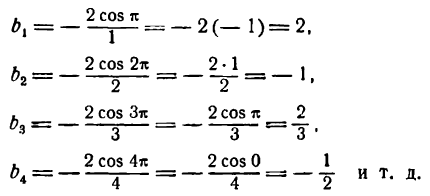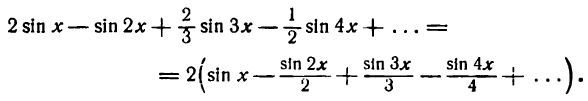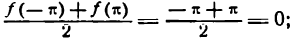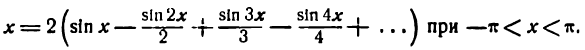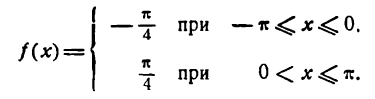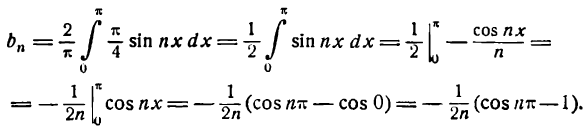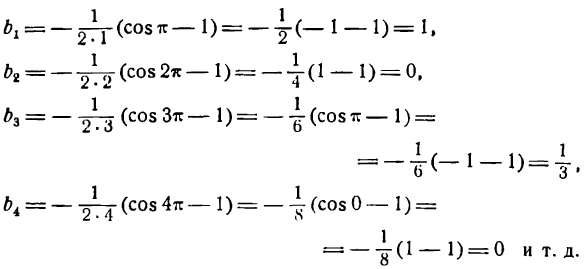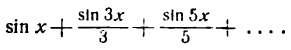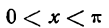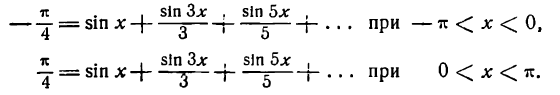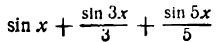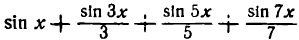Практическое применение преобразования Фурье для анализа сигналов. Введение для начинающих
Время на прочтение
9 мин
Количество просмотров 256K
1. Преобразование Фурье и спектр сигнала
Во многих случаях задача получения (вычисления) спектра сигнала выглядит следующим образом. Имеется АЦП, который с частотой дискретизации Fd преобразует непрерывный сигнал, поступающий на его вход в течение времени Т, в цифровые отсчеты — N штук. Далее массив отсчетов подается в некую программку, которая выдает N/2 каких-то числовых значений (программист, который утянул из инета написал программку, уверяет, что она делает преобразование Фурье).
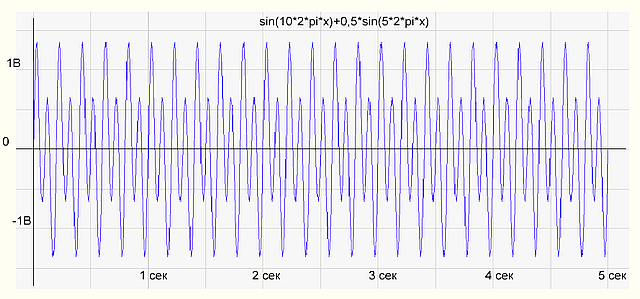
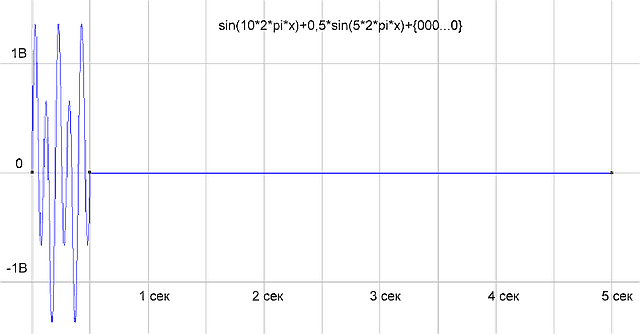
Чтобы проверить, правильно ли работает программа, сформируем массив отсчетов как сумму двух синусоид sin(10*2*pi*x)+0,5*sin(5*2*pi*x) и подсунем программке. Программа нарисовала следующее:
рис.1 График временной функции сигнала
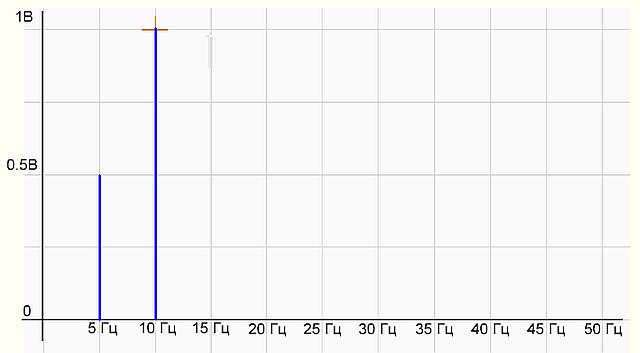
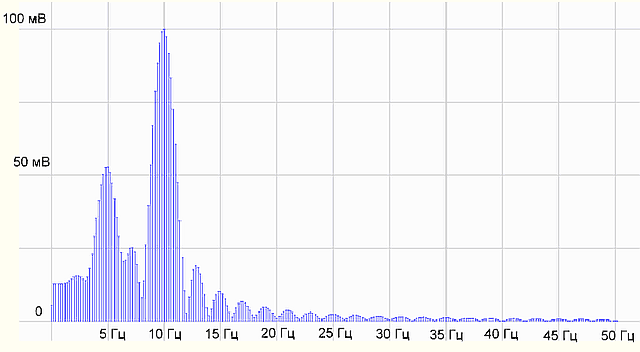
рис.2 График спектра сигнала
На графике спектра имеется две палки (гармоники) 5 Гц с амплитудой 0.5 В и 10 Гц — с амплитудой 1 В, все как в формуле исходного сигнала. Все отлично, программист молодец! Программа работает правильно.
Это значит, что если мы подадим на вход АЦП реальный сигнал из смеси двух синусоид, то мы получим аналогичный спектр, состоящий из двух гармоник.
Итого, наш реальный измеренный сигнал, длительностью 5 сек, оцифрованный АЦП, то есть представленный дискретными отсчетами, имеет дискретный непериодический спектр.
С математической точки зрения — сколько ошибок в этой фразе?
Теперь
начальство решило
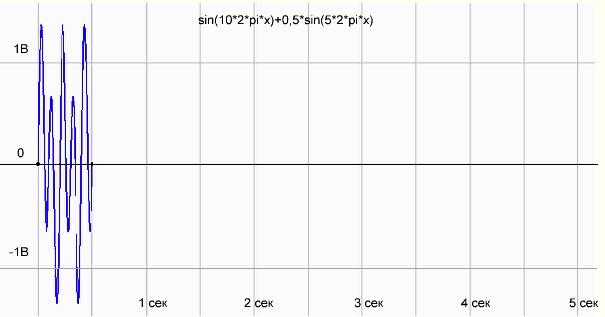
мы решили, что 5 секунд — это слишком долго, давай измерять сигнал за 0.5 сек.
рис.3 График функции sin(10*2*pi*x)+0,5*sin(5*2*pi*x) на периоде измерения 0.5 сек
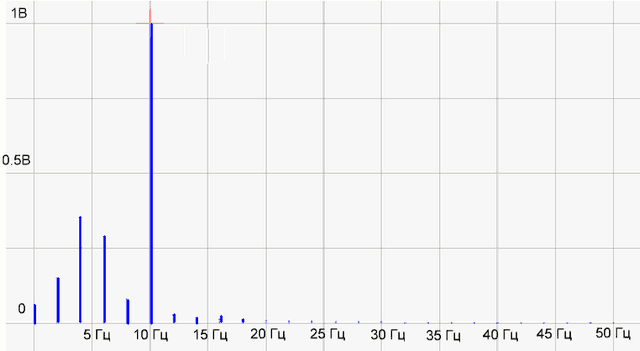
рис.4 Спектр функции
Что-то как бы не то! Гармоника 10 Гц рисуется нормально, а вместо палки на 5 Гц появилось несколько каких-то непонятных гармоник. Смотрим в интернетах, что да как…
Во, говорят, что в конец выборки надо добавить нули и спектр будет рисоваться нормальный.
рис.5 Добили нулей до 5 сек
рис.6 Получили спектр
Все равно не то, что было на 5 секундах. Придется разбираться с теорией. Идем в Википедию — источник знаний.
2. Непрерывная функция и представление её рядом Фурье
Математически наш сигнал длительностью T секунд является некоторой функцией f(x), заданной на отрезке {0, T} (X в данном случае — время). Такую функцию всегда можно представить в виде суммы гармонических функций (синусоид или косинусоид) вида:
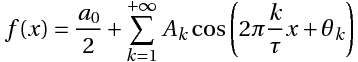
k — номер тригонометрической функции ( номер гармонической составляющей, номер гармоники)
T — отрезок, где функция определена (длительность сигнала)
Ak — амплитуда k-ой гармонической составляющей,
θk- начальная фаза k-ой гармонической составляющей
Что значит «представить функцию в виде суммы ряда»? Это значит, что, сложив в каждой точке значения гармонических составляющих ряда Фурье, мы получим значение нашей функции в этой точке.
(Более строго, среднеквадратичное отклонение ряда от функции f(x) будет стремиться к нулю, но несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно. См. https://ru.wikipedia.org/wiki/Ряд_Фурье.)
Этот ряд может быть также записан в виде:
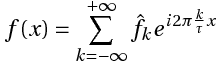
где 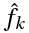
или
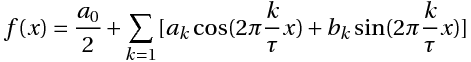
Связь между коэффициентами (1) и (3) выражается следующими формулами:
и
Отметим, что все эти три представления ряда Фурье совершенно равнозначны. Иногда при работе с рядами Фурье бывает удобнее использовать вместо синусов и косинусов экспоненты мнимого аргумента, то есть использовать преобразование Фурье в комплексной форме. Но нам удобно использовать формулу (1), где ряд Фурье представлен в виде суммы косинусоид с соответствующими амплитудами и фазами. В любом случае неправильно говорить, что результатом преобразования Фурье действительного сигнала будут комплексные амплитуды гармоник. Как правильно говорится в Вики «Преобразование Фурье (ℱ) — операция, сопоставляющая одной функции вещественной переменной другую функцию, также вещественной переменной.»
Итого:
Математической основой спектрального анализа сигналов является преобразование Фурье.
Преобразование Фурье позволяет представить непрерывную функцию f(x) (сигнал), определенную на отрезке {0, T} в виде суммы бесконечного числа (бесконечного ряда) тригонометрических функций (синусоид иили косинусоид) с определёнными амплитудами и фазами, также рассматриваемых на отрезке {0, T}. Такой ряд называется рядом Фурье.
Отметим еще некоторые моменты, понимание которых требуется для правильного применения преобразования Фурье к анализу сигналов. Если рассмотреть ряд Фурье (сумму синусоид) на всей оси Х, то можно увидеть, что вне отрезка {0, T} функция представленная рядом Фурье будет будет периодически повторять нашу функцию.
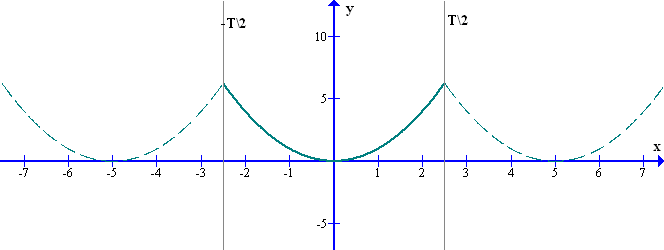
Например, на графике рис.7 исходная функция определена на отрезке {-T2, +T2}, а ряд Фурье представляет периодическую функцию, определенную на всей оси х.
Это происходит потому, что синусоиды сами являются периодическими функциями, соответственно и их сумма будет периодической функцией.
рис.7 Представление непериодической исходной функции рядом Фурье
Таким образом:
Наша исходная функция — непрерывная, непериодическая, определена на некотором отрезке длиной T.
Спектр этой функции — дискретный, то есть представлен в виде бесконечного ряда гармонических составляющих — ряда Фурье.
По факту, рядом Фурье определяется некоторая периодическая функция, совпадающая с нашей на отрезке {0, T}, но для нас эта периодичность не существенна.
Далее.
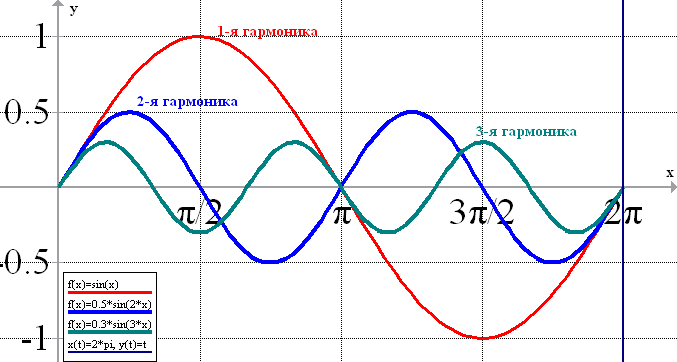
Периоды гармонических составляющих кратны величине отрезка {0, T}, на котором определена исходная функция f(x). Другими словами, периоды гармоник кратны длительности измерения сигнала. Например, период первой гармоники ряда Фурье равен интервалу Т, на котором определена функция f(x). Период второй гармоники ряда Фурье равен интервалу Т/2. И так далее (см. рис. 8).
рис.8 Периоды (частоты) гармонических составляющих ряда Фурье (здесь Т=2π)
Соответственно, частоты гармонических составляющих кратны величине 1/Т. То есть частоты гармонических составляющих Fk равны Fk= кТ, где к пробегает значения от 0 до ∞, например к=0 F0=0; к=1 F1=1T; к=2 F2=2T; к=3 F3=3T;… Fk= кТ (при нулевой частоте — постоянная составляющая).
Пусть наша исходная функция, представляет собой сигнал, записанный в течение Т=1 сек. Тогда период первой гармоники будет равен длительности нашего сигнала Т1=Т=1 сек и частота гармоники равна 1 Гц. Период второй гармоники будет равен длительности сигнала, деленной на 2 (Т2=Т/2=0,5 сек) и частота равна 2 Гц. Для третьей гармоники Т3=Т/3 сек и частота равна 3 Гц. И так далее.
Шаг между гармониками в этом случае равен 1 Гц.
Таким образом сигнал длительностью 1 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 1 Гц.
Чтобы увеличить разрешение в 2 раза до 0,5 Гц — надо увеличить длительность измерения в 2 раза — до 2 сек. Сигнал длительностью 10 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 0,1 Гц. Других способов увеличить разрешение по частоте нет.
Существует способ искусственного увеличения длительности сигнала путем добавления нулей к массиву отсчетов. Но реальную разрешающую способность по частоте он не увеличивает.
3. Дискретные сигналы и дискретное преобразование Фурье
С развитием цифровой техники изменились и способы хранения данных измерений (сигналов). Если раньше сигнал мог записываться на магнитофон и храниться на ленте в аналоговом виде, то сейчас сигналы оцифровываются и хранятся в файлах в памяти компьютера в виде набора чисел (отсчетов).
Обычная схема измерения и оцифровки сигнала выглядит следующим образом.
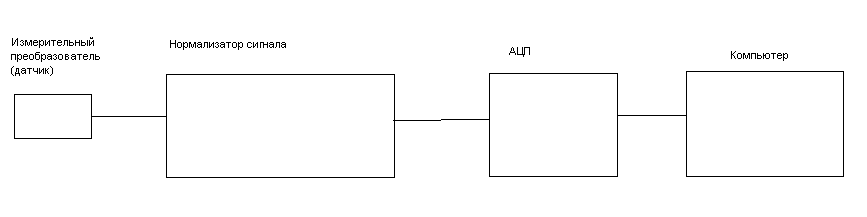
рис.9 Схема измерительного канала
Сигнал с измерительного преобразователя поступает на АЦП в течение периода времени Т. Полученные за время Т отсчеты сигнала (выборка) передаются в компьютер и сохраняются в памяти.
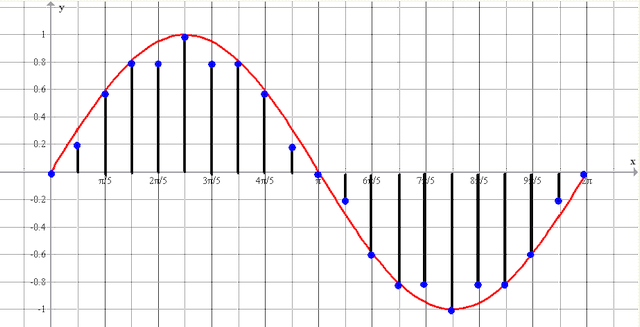
рис.10 Оцифрованный сигнал — N отсчетов полученных за время Т
Какие требования выдвигаются к параметрам оцифровки сигнала? Устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал) называется аналого-цифровой преобразователь (АЦП, англ. Analog-to-digital converter, ADC) ( Wiki).
Одним из основных параметров АЦП является максимальная частота дискретизации (или частота семплирования, англ. sample rate) — частота взятия отсчетов непрерывного во времени сигнала при его дискретизации. Измеряется в герцах. (( Wiki))
Согласно теореме Котельникова, если непрерывный сигнал имеет спектр, ограниченный частотой Fмакс, то он может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятым через интервалы времени 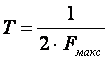
А что будет, если мы будем брать отсчеты с меньшей частотой, чем требуется по теореме Котельникова?
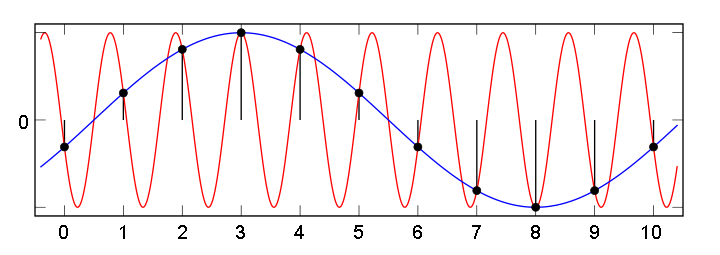
В этом случае возникает эффект «алиасинга» (он же стробоскопический эффект, муаровый эффект), при котором сигнал высокой частоты после оцифровки превращается в сигнал низкой частоты, которого на самом деле не существует. На рис. 11 красная синусоида высокой частоты — это реальный сигнал. Синяя синусоида более низкой частоты — фиктивный сигнал, возникающий вследствие того, за время взятия отсчета успевает пройти больше, чем пол-периода высокочастотного сигнала.
Рис. 11. Появление ложного сигнала низкой частоты при недостаточно высокой частоте дискретизации
Чтобы избежать эффекта алиасинга перед АЦП ставят специальный антиалиасинговый фильтр — ФНЧ (фильтр нижних частот), который пропускает частоты ниже половины частоты дискретизации АЦП, а более высокие частоты зарезает.
Для того, чтобы вычислить спектр сигнала по его дискретным отсчетам используется дискретное преобразование Фурье (ДПФ). Отметим еще раз, что спектр дискретного сигнала «по определению» ограничен частотой Fмакс, меньшей половине частоты дискретизации Fd. Поэтому спектр дискретного сигнала может быть представлен суммой конечного числа гармоник, в отличие от бесконечной суммы для ряда Фурье непрерывного сигнала, спектр которого может быть неограничен. Согласно теореме Котельникова максимальная частота гармоники должна быть такой, чтобы на нее приходилось как минимум два отсчета, поэтому число гармоник равно половине числа отсчетов дискретного сигнала. То есть если в выборке имеется N отсчетов, то число гармоник в спектре будет равно N/2.
Рассмотрим теперь дискретное преобразование Фурье (ДПФ).
Сравнивая с рядом Фурье
видим, что они совпадают, за исключением того, что время в ДПФ имеет дискретный характер и число гармоник ограничено величиной N/2 — половиной числа отсчетов.
Формулы ДПФ записываются в безразмерных целых переменных k, s, где k – номера отсчетов сигнала, s – номера спектральных составляющих.
Величина s показывает количество полных колебаний гармоники на периоде Т (длительности измерения сигнала). Дискретное преобразование Фурье используется для нахождения амплитуд и фаз гармоник численным методом, т.е. «на компьютере»
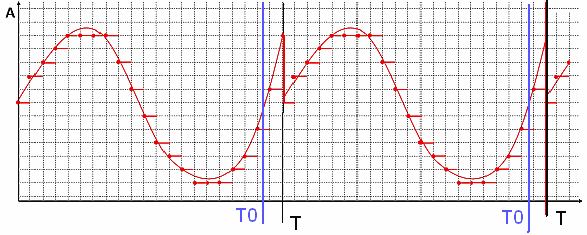
Возвращаясь к результатам, полученным в начале. Как уже было сказано выше, при разложении в ряд Фурье непериодической функции (нашего сигнала), полученный ряд Фурье фактически соответствует периодической функции с периодом Т. (рис.12).
рис.12 Периодическая функция f(x) с периодом Т0, с периодом измерения Т>T0
Как видно на рис.12 функция f(x) периодическая с периодом Т0. Однако из-за того, что длительность измерительной выборки Т не совпадает с периодом функции Т0, функция, получаемая как ряд Фурье, имеет разрыв в точке Т. В результате спектр данной функции будет содержать большое количество высокочастотных гармоник. Если бы длительность измерительной выборки Т совпадала с периодом функции Т0, то в полученном после преобразования Фурье спектре присутствовала бы только первая гармоника (синусоида с периодом равным длительности выборки), поскольку функция f(x) представляет собой синусоиду.
Другими словами, программа ДПФ «не знает», что наш сигнал представляет собой «кусок синусоиды», а пытается представить в виде ряда периодическую функцию, которая имеет разрыв из-за нестыковки отдельных кусков синусоиды.
В результате в спектре появляются гармоники, которые должны в сумме изобразить форму функции, включая этот разрыв.
Таким образом, чтобы получить «правильный» спектр сигнала, являющегося суммой нескольких синусоид с разными периодами, необходимо чтобы на периоде измерения сигнала укладывалось целое число периодов каждой синусоиды. На практике это условие можно выполнить при достаточно большой длительности измерения сигнала.
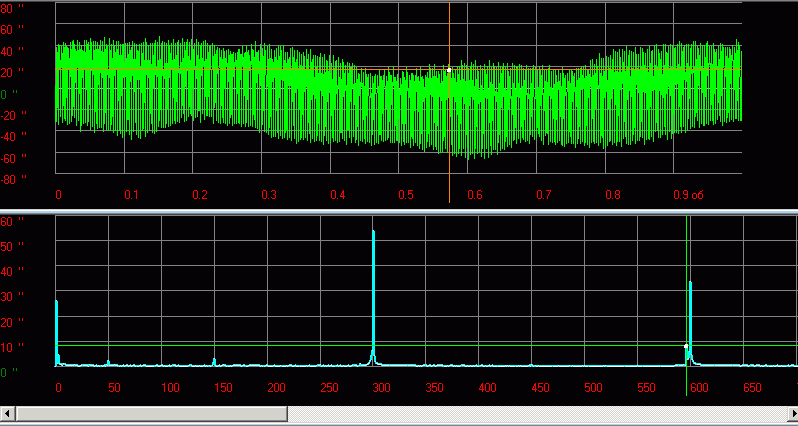
Рис.13 Пример функции и спектра сигнала кинематической погрешности редуктора
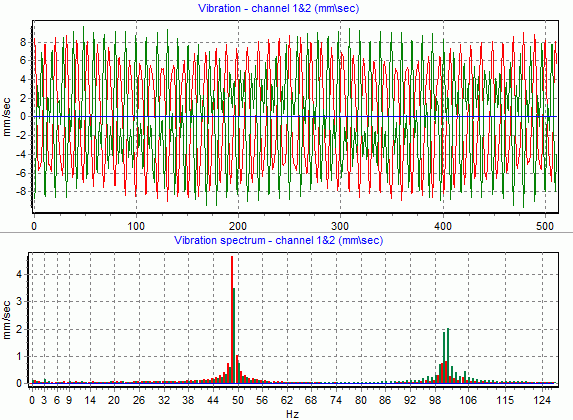
При меньшей длительности картина будет выглядеть «хуже»:
Рис.14 Пример функции и спектра сигнала вибрации ротора
На практике бывает сложно понять, где «реальные составляющие», а где «артефакты», вызванные некратностью периодов составляющих и длительности выборки сигнала или «скачками и разрывами» формы сигнала. Конечно слова «реальные составляющие» и «артефакты» не зря взяты в кавычки. Наличие на графике спектра множества гармоник не означает, что наш сигнал в реальности из них «состоит». Это все равно что считать, будто число 7 «состоит» из чисел 3 и 4. Число 7 можно представить в виде суммы чисел 3 и 4 — это правильно.
Так и наш сигнал… а вернее даже не «наш сигнал», а периодическую функцию, составленную путем повторения нашего сигнала (выборки) можно представить в виде суммы гармоник (синусоид) с определенными амплитудами и фазами. Но во многих важных для практики случаях (см. рисунки выше) действительно можно связать полученные в спектре гармоники и с реальными процессами, имеющими циклический характер и вносящими значительный вклад в форму сигнала.
Некоторые итоги
1. Реальный измеренный сигнал, длительностью T сек, оцифрованный АЦП, то есть представленный набором дискретных отсчетов (N штук), имеет дискретный непериодический спектр, представленный набором гармоник (N/2 штук).
2. Сигнал представлен набором действительных значений и его спектр представлен набором действительных значений. Частоты гармоник положительны. То, что математикам бывает удобнее представить спектр в комплексной форме с использованием отрицательных частот не значит, что «так правильно» и «так всегда надо делать».
3. Сигнал, измеренный на отрезке времени Т определен только на отрезке времени Т. Что было до того, как мы начали измерять сигнал, и что будет после того — науке это неизвестно. И в нашем случае — неинтересно. ДПФ ограниченного во времени сигнала дает его «настоящий» спектр, в том смысле, что при определенных условиях позволяет вычислить амплитуду и частоту его составляющих.
Использованные материалы и другие полезные материалы.
FourierScope — программа для построения радио сигналов и их спектрального анализа.
Graph — программа с открытым кодом, предназначенная для построения математических графиков.
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ – КАК ЭТО ДЕЛАЕТСЯ
Дискретное преобразование Фурье (ДПФ)
Ряд Фурье в виде простых гармоник. Спектры.
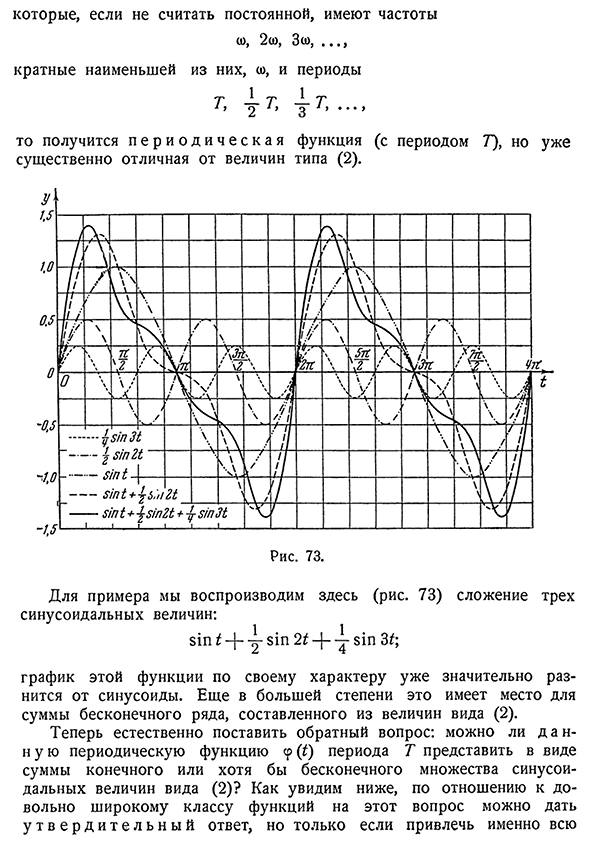
Практически любую периодическую функцию
можно разложить на простые гармоники
с помощью тригонометрического ряда
(ряда Фурье):
f(x)
=
+
(
ancos
nx
+ bnsin
nx
), (*)
Запишем данный ряд в виде суммы
простых гармоник, полагая коэффициенты
равными an=
Ansinn
, bn=
Ancosn
. Получим: ancos
n + bnsinn
= Ansin(
nx + n
), где
An
=
,
tg n
=
.
(**)
Тогда ряд (*)примет
вид f(x)
=
.
Ряд Фурье представляет периодическую
функцию суммой хотя и бесконечного
числа синусоид, но с частотами, имеющими
определенное дискретное значение.
Иногда n-ую гармонику записывают
в виде ancos
nx + bnsin
nx = Ancos(nx
– n)
, где an
= Ancosn
, bn
= An
sinn
.
При этом An и n
определяются по формулам (**). Тогда
ряд (*) примет вид
f(x)
=
.
Опр. 9. Операция представления
периодической функции f(x) рядом
Фурье называется гармоническим
анализом.
Выражение (*) встречается и в другой,
более употребительной форме:
Коэффициенты an, bn
определяются по формулам:
величина C0 выражает среднее
значение функции за период и называется
постоянной составляющей, которая
вычисляется по формуле:
В теории колебаний и спектрального
анализа представление функции f(t)
в ряд Фурье записывается в виде:
(***)
т.е. периодическая функция представлена
суммой слагаемых, каждое из которых
есть синусоидальное колебание с
амплитудой Сn и начальной
фазой n,
то есть ряд Фурье периодической функции
состоит из отдельных гармоник с частотами,
отличающимися друг от друга на постоянное
число. Причем каждая гармоника имеет
определенную амплитуду. Значения Сn
и n
должны быть надлежащим образом подобраны
для того, чтобы равенство (***) выполнялось,
то есть определяются по формулам
(**) [Сn = Аn].
Перепишем ряд Фурье (***) в виде
где
1 –
основная частота. Отсюда можно сделать
вывод: сложная периодическая функция
f(t) определяется совокупностью
величин Сn и n
.
Опр. 10. Совокупность величин Сn
, то есть зависимость амплитуды от
частоты, называется амплитудным
спектром функции или спектром
амплитуд.
Опр. 11. Совокупность величин
n носит
название спектра фаз.
Когда говорят просто “спектр”, то
подразумевают именно амплитудный
спектр, в остальных случаях делают
соответствующие оговорки. Периодическая
функция имеет дискретный спектр
(то есть она может быть представлена в
виде отдельных гармоник).
Спектр периодической функции можно
изобразить графически. Выберем для
этого координаты Сn
и = n1.
Спектр будет изображен в этой системе
координат совокупностью дискретных
точек, т.к. каждому значению n1
соответствует одно определенное
значение Сn . График,
состоящий из отдельных точек, неудобен.
Поэтому принято изображать амплитуды
отдельных гармоник вертикальными
отрезками соответствующей длины (рис.
2).
Сn
Рис. 2.
Этот дискретный спектр часто называют
линейчатым. Он — гармонический спектр,
т.е. состоит из равноотстоящих спектральных
линий; частоты гармоник находятся в
простых кратных соотношениях. Отдельные
гармоники, в том числе первая, могут
отсутствовать, т.е. амплитуды их могут
равняться нулю, но это не нарушает
гармоничности спектра.
Дискретные, или линейчатые, спектры
могут принадлежать как периодическим,
так и непериодическим функциям. В первом
случае спектр обязательно гармонический.
Разложение в ряд Фурье может быть
обобщено на случай непериодической
функции. Для этого надо применить
предельный переход при Т∞,
рассматривая непериодическую функцию
как предельный случай периодической
при неограниченно возрастающем периоде.
Вместо 1/Т введем круговую основную
частоту 1=
2/Т. Эта величина
– есть частотный интервал между соседними
гармониками, частоты которых равны
2n/Т. Если Т
∞, то 1
d
и 2n/Т
, где
– текущая частота, изменяющаяся
непрерывно, d
– ее приращение. При этом ряд Фурье
перейдет в интеграл Фурье, который
представляет собой разложение
непериодической функции в бесконечном
интервале (–∞;∞) на гармонические
колебания, частоты которых
непрерывно меняются от 0 до ∞:
Непериодическая функция имеет непрерывный
или сплошной спектры, т.е. вместо отдельных
точек спектр изображается непрерывной
кривой. Это получается в результате
предельного перехода от ряда к интегралу
Фурье: интервалы между отдельными
спектральными линиями неограниченно
сокращаются, линии сливаются, и вместо
дискретных точек спектр изображается
непрерывной последовательностью точек,
т.е. непрерывной кривой. Функции a()
и b()
дают закон распределения амплитуд и
начальных фаз в зависимости от частоты
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Графики функций вида 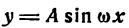
В дальнейшем изложении нам придется использовать функции вида 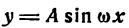
Пример:
Построить график функции у = sin Зx
Решение:
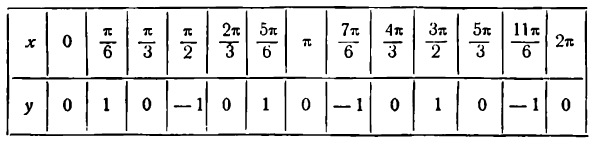
Данная функция — периодическая; областью ее существования служат все действительные числа. Построим график этой функции для значений аргумента от х = 0 до х = 2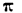
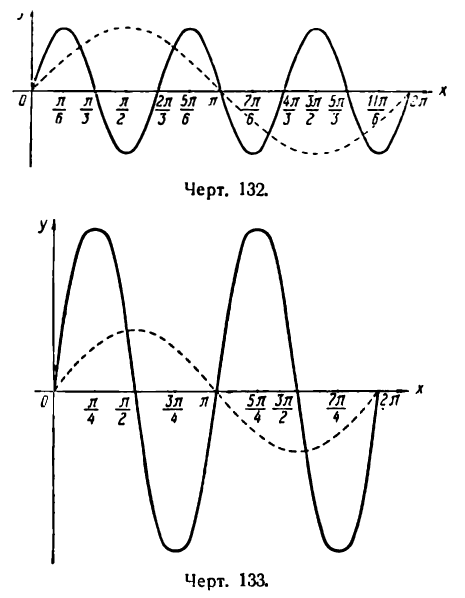
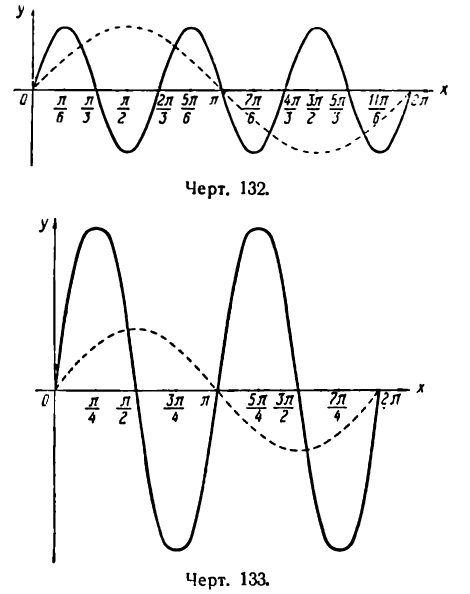
Рассматривая каждую пару значений х и у как координаты точек графика данной функции, построим эти точки и, проведя через них плавную линию, получим график функции у = sin Зx , представленный на рисеже 132 в виде сплошной линии — синусоиды с наименьшим периодом 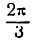
Как видно из рисежа, этот график можно получить из графика функции у = sin x , изображенного на том же рисеже пунктирной линией, уменьшив масштаб по оси Ох в три раза.
Пример:
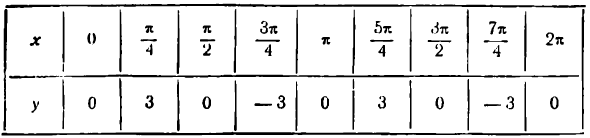
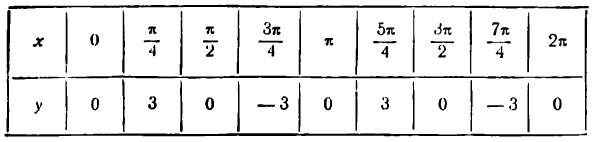
Построить график функции у = 3 sin 2x .
Решение:
Составим таблицу значений х и у.
График, построенный по точкам с вычисленными координатами, представляет синусоиду с наименьшим периодом
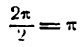
График функции у = 3 sin 2x можно получить и из графика функции у = sin х, представленного на том же рисеже пунктирной линией, уменьшив масштаб по оси Ох вдвое и увеличив его по оси Оу втрое.
Гармонические колебания
1. Простые гармонические колебания. В естествознании и технике часто наблюдаются периодические процессы, т. е. такие явления, которые повторяются через определенный промежуток времени. Например, колебания маятника, явления переменного тока и др.
Простейшее периодическое явление — гармоническое колебание, совершаемое по закону
В равенстве (1) постоянный множитель А, представляющий наибольшую величину, которую может иметь у, называется амплитудой колебания, 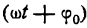
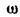
Функция (1) — периодическая с наименьшим-периодом 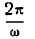
Величина 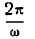
откуда
Так как Т—время одного колебания, то 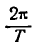
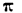
Решение:
Составим таблицу значений х и у.
График, построенный по точкам с вычисленными координатами, представляет синусоиду с наименьшим периодом
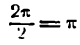
График функции у = 3 sin 2x можно получить и из графика функции у = sin х, представленного на том же рисеже пунктирной линией, уменьшив масштаб по оси Ох вдвое и увеличив его по оси Оу втрое.
Гармонические колебания. I. Простые гармонические колебания. В естествознании и технике часто наблюдаются периодические процессы, т. е. такие явления, которые повторяются через определенный промежуток времени. Например, колебания маятника, явления переменного тока и др.
Простейшее периодическое явление — гармоническое колебание, совершаемое по закону
В равенстве (1) постоянный множитель А, представляющий наибольшую величину, которую может иметь у, называется амплитудой колебания, 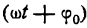
Функция (1) — периодическая с наименьшим-периодом 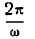
Величина 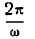
откуда
Так как Т—время одного колебания, 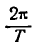
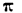
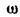
Обозначив
получим:
Колебательное движение, происходящее по закону функции (1) или, что то же, по закону функции (2), называется простым гармоническим колебанием, а график его — простой гармоникой.
ІІ. Сложные гармонические колебания. Не всякий периодический процесс можно рассматривать как простое гармоническое колебание. Очень часты случаи,
когда периодическое явление есть результат сложения нескольких простых гармонических колебаний. Полученное результирующее движение называется сложным гармоническим колебанием, а график его — сложной гармоникой.
Итак, сложная гармоника есть результат сложения нескольких простых гармоник или иначе — результат наложения простых гармоник друг на друга.
Рассмотрим пример. Пусть даны две простые гармоники, определяемые уравнениями:
и
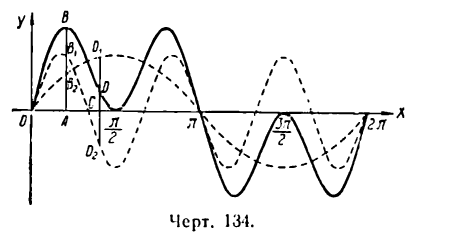
На рисеже 134 эти гармоники изображены пунктирными линиями, сложная же гармоника, являющаяся графиком функции
представлена сплошной линией. Любая точка сложной гармоники имеет ординату, равную сумме ординат точек, лежащих на простых гармониках и имеющих одну и ту же абсциссу. Так, например,
Как видно из рисежа, результирующая гармоника будет повторяться через каждый промежуток 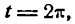
Можно доказать, что вообще при сложении простых гармоник с разными частотами получается сложная гармоника не синусоидального вида, а при сложении гармоник с одинаковыми частотами — гармоника того же вида, что и простые.
Тригонометрические ряды
Как было указано, наблюдаются периодические процессы, которые нельзя рассматривать как простые колебательные явления. Положим, что какое-либо периодическое движение задано при помощи некоторой периодической функции, отличной от (1). Чтобы иметь представление о характере этого движения, данную функцию разлагают в ряд простых гармоник, имеющий следующий вид:
Ряд (1) называется тригонометрическим рядом, а числа
— коэффициентами ряда.
Положим для простоты
и будем считать, что ряд (1) сходится при всех действительных значениях х к данной функции [т. е. сумма ряда равна функции f(х)], тогда можно написать:
или короче
Как видно, функция f(x) — периодическая с периодом 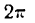
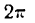
Отсюда следует, что тригонометрический ряд достаточно рассматривать только для значений x от 0 до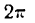
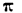
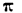
Чем больше простых гармоник ряда (2) мы сложим, тем точнее результирующая гармоника будет представлять периодическое движение, заданное функцией f(x). Поэтому вопрос о разложении функции в тригонометрический ряд приобретает очень важное значение в прикладных науках.
Процесс разложения функции, представляющей сложное периодическое движение, в тригонометрический ряд называется гармоническим анализом.
Коэффициенты Фурье
Ряд Фурье. Чтобы разложить периодическую функцию f(x) с периодом 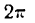
где n = 1, 2, 3, 4, ……….
Числа, полученные по формулам (1), называются коэффициентами Фурье *), а тригонометрический ряд с этими коэффициентами — рядом Фурье.
*) Формулы (1) были даны еще Эйлером (1707—1783), но широко использовал их французский математик Ж. Фурье (1768—1830).
Определение:
Ряд
где
называется рядом Фурье функции f(x).
Если ряд Фурье сходится к функции f(x), то можно записать:
Следует заметить, что величина интегралов в формулах (1) не изменится, если пределами их взять 0 и 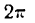
где п = 1, 2, 3, 4 …
Формулы (3) представляют иногда большие удобства, чем формулы (1).
Возможность разложения непериодической функции в ряд Фурье
Периодическая функция, как мы уже знаем, определяет колебательное движение. Однако бывают колебательные явления, которые совершаются по закону непериодической функции. Поэтому для изучения колебательного движения, подчиняющегося непериодической функции, выгодно разложить эту функцию в ряд Фурье, что оказывается возможным при некоторых условиях.
Пусть, например, задана функция
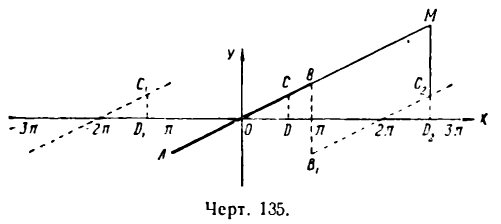
график которой изображен на рисеже 135 отрезком прямой АВ. Покажем, что для разложения данной функции в ряд Фурье
можно и к ней применить правила. Для этого введем вспомогательную периодическую функцию 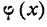
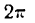
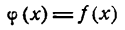
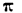
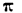
за пределами же указанного промежутка
К функции 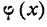
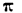
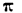
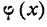
Величина суммы ряда Фурье, полученного для функции (1), вследствие периодичности его членов будет повторяться через каждый промежуток, равный 2




тогда ордината
даст величину суммы ряда Фурье функции (1) при х = 2. Ясно, что при
или
величина ординат D2С2 и D1С1, а следовательно, и сумма ряда при тех же значениях х не изменится и будет равна по-прежнему единице.
Обратим внимание, что для значений х вне промежутка от —


Все сказанное выше подтверждает мысль, что ряд Фурье функции имеет смысл рассматривать только в промежутке
Условия Дирихле
Теорема Дирихле:
Как было уже сказано, функция f(х) с областью существования 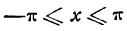
1) функция должна быть непрерывной в промежутке значений х от —

2) функция должна иметь конечное число максимумов и минимумов ила не иметь их совсем.
Одной из основных теорем, применяемых при исследовании рядов Фурье, является теорема Дирихле.
Теорема Дирихле:
Если функция f(х) с областью существования —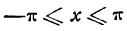
1) ряд Фурье функции f(x) сходится в указанном промежутке значений х;
2) сумма этого ряда сходится к функции f(x) во всех точках ее непрерывности;
3) в каждой точке разрыва функции сумма ряда равна половине скачка функции;
4) при х = 

Примем указанную теорему без доказательства.
Заметим, что в дальнейшем изложении мы будем пользоваться только функциями, удовлетворяющими условиям Дирихле, а потому в каждом разбираемом примере не будем останавливаться на этих условиях.
Прежде чем перейти к разложению функций в ряды Фурье мы должны познакомиться с методом интегрирования по частям, без которого нельзя определять коэффициенты Фурье.
Интегрирование по частям
Пусть и и 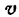
и
откуда
Взяв интеграл от обеих частей равенства (1), получим:
или
Равенство (2) служит формулой интегрирования по частям.
Пример:
Найти
Решение:
Положим
(произвольное постоянное интегрирования напишем в окончательном результате).
Подставив (3) во (2), получим:
Пример:
Найти
Решение:
Положим
тогда
Применяя метод подстановки
получим:
Согласно формуле (2) имеем:
Аналогично можно найти:
Пример:
Найти
Решение:
Положим
Подставив (6) во (2), получим:
Приняв во внимание равенство (5), будем иметь:
Таким же образом найдем:
*) Применяется подстановка
Примеры разложения функций в ряд Фурье
Пример:
Разложить в ряд Фурье функцию:
Решение:
По формулам (1) найдем коэффициенты Фурье
Но
кроме того,
Поэтому
Приняв во внимание равенство (4) получим:
Отсюда
и т.д.
Как видно, при четном значении n коэффициенты 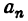
Согласно равенству (5) получим:
Отсюда
Искомый ряд напишется так:
Согласно теореме Дирихле этот ряд сходится к данной функции во всех точках промежутка значений x от — 





между тем как значения функции при х = — 


Таким образом, можно написать:
Пример:
Разложить в ряд Фурье функцию
Решение:
Здесь для определения коэффициентов Фурье используем формулы (3) .
*) 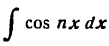
Приняв во внимание равенство (4) , будем иметь:
Таким образом, все коэффициенты
равны нулю.
Применяя к 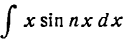
Итак,
откуда
Искомое разложение будет:
Полученный ряд сходится к функции 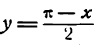
значениях х в промежутке от 0 до 2

Ряды Фурье для четных и нечетных функций
Функция f(x) называется четной, если при подстановке вместо х величины —х знак функции не меняется, т. е. f(—x) = f(x). Например, 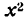
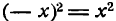
Функция f(x) называется нечетной, если при подстановке вместо х величины —х знак функции меняется на противоположный, т. е. f(—х) = — f(х). Например, 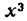
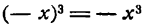
Заметим, что произведение двух четных или двух нечетных функций есть четная функция, а произведение четной функции на нечетную есть функция нечетная.
В самом деле,
—произведение двух четных функций,
— произведение четной функции на нечетную.
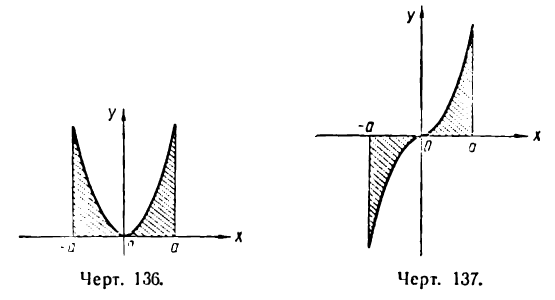
График четной функции симметричен относительно оси Оу, график нечетной функции симметричен относительно начала координат. Примеры таких графиков даны на рисеже 136 для четной функции, на рисеже 137 — для нечетной. Если f(x)—четная функция, то
если f(x)—нечетная функция, то
Эти равенства можно подтвердить геометрическими соображениями. Пусть 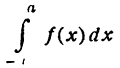
образованной тем же графиком, осью Ох и прямыми x = 0 и х = а (рис. 136); в случае нечетной функции площадь равна нулю, так как она состоит из двух равных площадей с противоположными знаками (рис. 137).
Приняв во внимание сказанное, можно упростить формулы (1) , написав их в следующем виде: для случая четной функции
для случая нечетной функции
Как видно, ряд Фурье (2) для четной функции будет состоять только из косинусов, т. е.
а для нечетной функции — только из синусов, т. е.
Пример:
Разложить в ряд Фурье функцию
Решение:
Функция у = | х | — четная (см. рис. 73), а потому согласно формулам (1) имеем:
Приняв во внимание равенство (4), найдем:
Отсюда
Искомое разложение будет:
Применяя теорему Дирихле, можно показать, что полученный ряд сходится к данной функции при всех значениях х от —
Следовательно, можно написать:
Пример:
Разложить в ряд Фурье функцию
Решение:
Данная функция четная; применяя формулы (1), получим:
Положив п = 1 в формуле для 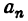
Для n = 2, 3, 4 … получим:
Представим произведение 2 sin x cos nx в следующем виде:
*) Это равенство легко проверить, применив к правой части его формулу для разности синусов двух углов.
тогда
**) 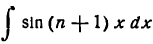
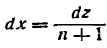
Отсюда
Искомое разложение напишется так:
Согласно теореме Дирихле полученный ряд сходится к данной функции при 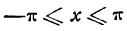
при всех значениях х указанного промежутка.
Пример:
Разложить в ряд Фурье функцию
f(x) = x при
Решение:
Применим формулы (2), так как функция f(x) = x нечетная.
Согласно равенству (5) найдем:
Отсюда
Искомое разложение таково:
Этот-ряд представляет функцию f(х) = х при всех значениях х промежутка от —

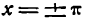
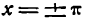
значения же функции при х = — 



Пример:
Разложить в ряд Фурье функцию
Решение:
Данная функция — нечетная, а потому, применяя формулу (2), получим:
Отсюда
Разложение напишется следующим образам:
При х = — 

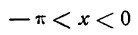
Следовательно,
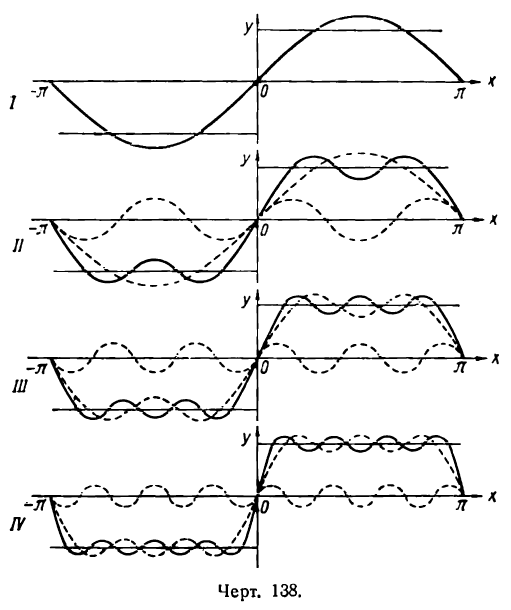
Покажем на примере разложения в ряд этой функции, что по мере увеличения числа слагаемых (простых гармоник) частичная сумма ряда (результирующая гармоника) все лучше и лучше представляет данную функцию.
На рисеже 138 I показана первая гармоника (sin х) ряда. На рисеже 138 II изображены первые две гармоники ряда (sin х и 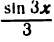
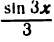
На рисеже 138 III показаны найденная сумма двух первых гармоник (sin х + 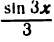
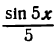
— сплошная линия).
На рисеже 138 IV — найденная сумма трех первых гармоник
— пунктирная линия), четвертая гармоника ( 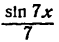
— сплошная линия).
Продолжая операцию сложения простых гармоник и дальше, мы будем получать результирующую гармонику (частичную сумму ряда), все больше и больше приближающуюся к двум параллельным отрезкам, изображающим данную функцию.
Вследствие периодичности ряда Фурье данной функции результирующая гармоника будет точно повторяться через каждый промежуток значений x, равный 2
Периодические величины и гармонический анализ
Смотрите также:
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат