Как найти гелиоцентрическое расстояние

ГЕЛИОЦЕНТРИЧЕСКОЕ РАССТОЯНИЕ

Как определить расстояние до планет

Несмотря на то, что самые ближние от нас планеты безумно далеки от Земли, расстояние это имеет конечное значение. А раз так – оно может быть определено. Причем впервые это было сделано очень давно – еще во времена Древней Греции астроном, математик и философ Аристарх с острова Самоса предложил способ определения расстояния до Луны и ее размеров. Как можно определить расстояние до планет? В основе метода лежит явление параллакса.

Вам понадобится

• — калькулятор;
• — радиолокатор;
• — секундомер;
• — справочник по астрономии.

Инструкция

Радиолокация — один из современных методов определения расстояния от Земли до планет (геоцентрического расстояния). Он основан на сравнительном анализе посланного и отраженного радиосигнала.Отправьте радиосигнал в направлении интересующей планеты и включите секундомер. Когда придет отраженный сигнал – остановите отсчет. По известной скорости распространения радиоволн и времени, за которое сигнал достиг планеты и отразился, вычислите расстояние до планеты. Оно равно произведению скорости на половину показаний секундомера.

До появления радиолокации для определения расстояния до объектов Солнечной системы использовали метод горизонтального параллакса. Погрешность этого метода составляет километр, а погрешность измерений расстояний с помощью радиолокации – сантиметр.

Суть определения расстояний до планет по методу горизонтального параллакса заключается в изменении направления на объект при перемещении точки наблюдения (параллактическое смещение) – в качестве базы берутся максимально разнесенные между собой точки: радиус Земли. То есть определение расстояния до планеты по методу горизонтального параллакса – простая тригонометрическая задача. Если известны все данные.

Умножьте 1 радиан (угол, образованный дугой, длина которой равна радиусу) выраженный в секундах (206265) на радиус Земли (6370 км) и разделите на величину параллакса планеты в данный момент времени. Полученное значение – расстояние до планеты в астрономических единицах.

По годичному или тригонометрическому параллаксу (за базу принимается большая полуось земной орбиты) вычисляют расстояния до очень далеких планет и звезд. Кстати, параллакс равный одной секунде определяет расстояние в один парсек, а 1 пс = 206265 астрономических единиц. Разделите 206265 секунд (1 радиан) на величину тригонометрического параллакса. Полученное частное – расстояние до интересующей планеты.

Ну и наконец, расстояние до планет можно вычислить по третьему закону Кеплера. Вычисления достаточно сложные, поэтому перейдем сразу к финальной части.Возведите в квадрат значение периода обращения планеты вокруг Солнца. Вычислите кубический корень из этой величины. Полученное число – расстояние от интересующей планеты до Солнца в астрономических единицах, или гелиоцентрическое расстояние. Зная гелиоцентрическое расстояние и расположение планет (угловое расстояние планеты от Солнца), можно легко вычислить геоцентрическое расстояние.

Связанная статья

Как обнаружить цель

Источники:

• Определение размеров космических объектов

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Планеты и законы их обращения

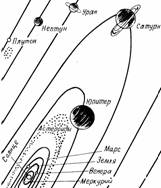
Рис.
1. Солнечная система

Солнечная
система включает девять крупных планет, которые со своими 57 спутниками
обращаются вокруг массивной звезды по эллиптическим орбитам. По своим размерам
и массе планеты можно разделить на две группы: планеты земной группы,
расположенные ближе к Солнцу, — Меркурий, Венера, Земля и Марс и
планеты-гиганты — Юпитер, Сатурн, Уран и Нептун, находящиеся на значительно
более удаленных от центральной звезды орбитах. Последняя из известных планет —
Плутон — своей орбитой с радиусом около 6 млрд. км
очерчивает
границы Солнечной системы. Плутон не относится к планетам-гигантам, его масса
почти в 10 раз меньше массы Земли. Аномальные характеристики этой крошечной
планеты позволяют рассматривать ее как бывший спутник Нептуна.

Кроме
больших планет между орбитами Марса и Юпитера вращается более 2300 малых планет
— астероидов, множество более мелких тел — метеоритов и метеорной пыли, а также
несколько десятков тысяч комет, двигающихся по сильно вытянутым орбитам,
некоторые из которых далеко выходят за границы Солнечной системы.

Все
планеты и астероиды обращаются вокруг Солнца в направлении движения Земли — с
запада на восток. Это так называемое прямое движение. Основные закономерности
движения планет полностью определяются законами Кеплера. Рассмотрим эти законы
и охарактеризуем основные элементы эллиптических орбит.

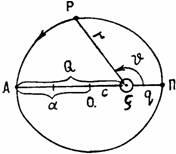
Рис.
2. Элементы планетной орбиты: АП — большая полуось орбиты, ось апсид; П —
перегилий; А — афелий;

r
— радиус-вектор

Согласно
первому закону, все планеты обращаются вокруг Солнца по эллиптическим орбитам,
в одном из фокусов которых находится Солнце. На рис. II.2 показаны элементы
планетных орбит с Солнцем (С) в фокусе. Линия АП называется линией апсид,
крайние точки которой афелий (А) и перигелий (П) характеризуют наибольшее и
наименьшее удаление от Солнца. Расстояние планет (Р)
на
орбите от Солнца (гелиоцентрическое расстояние) определяется радиусом-вектором r=СР.

Отношение полуфокального
расстояния (с) к большой
полуоси (а) называется эксцентриситетом орбиты:

e
= . (II.1)

Если
обозначить через q перигельное
расстояние, а через Q — афелийное
расстояние, то их значения легко определить из
выражений:

q = а — с = а(1 — е), (II.2)

Q = а + с = а(1 + е). (II.3)

Тогда,
определив большую полуось (а), мы найдем среднее годичное расстояние планеты до
Солнца:

а = . (II.4)

Cреднее
гелиоцентрическое расстояние Земли от Солнца равно 149,6 млн. км. Эта величина
называется астрономической единицей и принимается за единицу измерений
расстояний в пределах Солнечной системы.

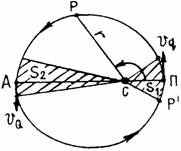
Согласно
второму закону Кеплера, радиус-вектор планеты описывает площади, прямо
пропорциональные промежуткам времени. Если обозначить через S1 площадь перигелийного
сектора (рис. II.3), а через S2 — площадь афелийного
сектора, то их отношение будет пропорционально
временам t1 и t2, за которые планета прошла соответствующие отрезки дуг орбиты:

Рис.
3. Площади, описываемые радиус-вектором планеты

 = . (II.5)

Отсюда
следует, что секториальная скорость —

V
=  =  = const — (II.6)

величина
постоянная.

Время,
в течение которого планета сделает полный оборот по орбите, называется
звездным, или сидерическим, периодом Т (рис. II.3). За полный оборот
радиус-вектор планеты опишет площадь эллипса:

S=
pab=p a2 . (II.7)

Поэтому
секториальная
скорость

V
=  =  (II.8)

оказывается
наибольшей в перигелии, а наименьшей — в афелии. Используя второй закон, можно
вычислить эксцентриситет земной орбиты по наибольшему и наименьшему суточному
смещению Солнца по эклиптике, отражающему движение Земли (см. §

2). Земля в перигелии пребывает в начале января (hmax=61′),

а в афелии в начале июля (hmax=57′).
По второму закону
Кеплера скорость Земли в афелии и перигелии определяется из выражений:

VQ=hminQ, Vq=hmaxq
. (II.9)

Учитывая
закон сохранения момента количества движения

Vq· q = VQ· Q (II.10)

и
подставив сюда значения (II.9) с учетом выражений (II.2) и (II.3), найдем:

= 1,03397, откуда е=0,0167.

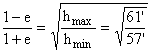
Таким
образом, орбита Земли лишь ненамного отличается от окружности.

Согласно
третьему Закону Кеплера, квадраты сидерических периодов обращения планет (Т12 и
Т22) прямо пропорциональны кубам их средних расстояний от Солнца (а13 и а23):

. (II.11)

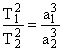
Если
одна из планет — Земля, период ее сидерического обращения равен Т1=1 году, а
расстояние от Солнца а1 положить равным а1=1 а. е., то выражение (II.11)
принимает простой вид:

Т22
= а23. (II.12)

Полученное
выражение позволяет по известным из наблюдений периодам обращения планет,
других небесных тел вокруг Солнца вычислять их средние гелиоцентрические
расстояния.

Найденные
эмпирически из наблюдательной астрономии законы Кеплера показали, что Солнечная
система представляет собой механическую систему с центром, находящимся в
солнечной массе.

Законы
Кеплера послужили Ньютону основой для вывода своего знаменитого закона
всемирного тяготения, который он сформулировал так: каждые две материальные
частицы взаимно притягиваются с силой, пропорциональной их массам и обратно
пропорциональной квадрату расстояния между ними.

Математическая
формулировка этого закона имеет вид:

F
= G, (II.13)

где
M и m — взаимодействующие массы, r
— расстояние между
ними, G — гравитационная постояная. В системе СИ G = 6,672· 10-11 м2· кг-1· с-2. Физический смысл гравитационной постоянной
заключается в следующем: она характеризует силу притяжения двух масс весом в 1
кг каждая на расстоянии в 1 м. Величина G впервые была определена в 1798 г.
английским физиком Кавендишем с помощью крутильных весов.

Закон
Ньютона решил задачу о характере действия силы, управляющей движением планет.
Это сила тяготения, создаваемая центральной массой Солнца. Именно эта сила не
дает планетам разлететься, а сохраняет их в связной системе последовательных
орбит, по которым, как на привязи, сотни миллионов лет кружатся большие и малые
планеты.

Решая
задачу движения двух тел под действием взаимного притяжения, Ньютон
аналитически определил законы движения планет в поле тяготения Солнца. Тем
самым эмпирические законы Кеплера получили строгое математическое
доказательство. Третий же закон был уточнен путем введения масс планет и
Солнца:

. (II.14)

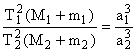
Теперь
с его помощью оказалось возможным вычислять массы небесных тел. Полагая в
выражении (II.14) массы спутников планет m1 и m2 равными нулю (ввиду их малости
в сравнении с массой планет, за исключением Луны) и приняв массу Земли M2 = 1,
получим соотношение (II.14) следующего вида:

= М1. (II.15)

Воспользуемся
законом тяготения и определим массу Земли, полагая, что взаимодействуют две
массы — Земли (М) и некоторого тела, лежащего на ее поверхности. Сила
притяжения этого тела определяется законом Ньютона:

F
= G. ( II.16)

Но
одновременно из второго закона механики эта же сила равна произведению массы на
ускорение:

F
= mg, (II.17)

где
g — ускорение силы тяжести; R — радиус Земли.

Приравнивая
правые части выражений (II.16) и (II.17): G = mg, найдем выражение для определения массы Земли:

М
= . (II.18)

Подставив
в (II.18) известные значения G = 6,672 ·
10-11 м2 · кг-1 · с-2, g = 9,81 м/с2, R = 6,371 ·
106 м, в итоге получим M3 = 5,97 · 1024
кг, или в граммах: M3 = 5,97 · 1027
г. Такова масса Земли. Обращаем внимание на формулы (II.16), (II.17), (II.18) —
их надо твердо помнить. В дальнейшем мы часто будем пользоваться ими как
исходными для определения входящих в них параметров.

Теперь
воспользуемся уточненным третьим законом Кеплера и найдем из выражения (II.15)
массу Солнца. Для этого рассмотрим две системы тел — Солнце с Землей и Землю с
Луной. В первой системе a1 = 149,6 · 106
км, Т1 = 365,26 сут; во второй системе а2 = 384,4
·103 км,
Т2 = 27,32
сут. Подставляя эти значения в формулу (II.15),
находим массу Солнца в относительных единицах массы Земли М0 =
328700 М3.
Полученный результат отличается от более точных расчетов, так
как в сравнении с массой Земли массу Луны нельзя приравнивать к нулю (масса
Луны составляет 1/81 массы Земли). Зная массу Земли в абсолютных единицах
(килограммах или граммах) и взяв более точное определение массы Солнца (М0 =
333000 М3), определим его абсолютную массу: М0 = 333000·5,97·1027 г = 1,98·1033
г.

В
настоящее время для более точного определения массы и фигуры планет и их
спутников используются параметры орбиты искусственных спутников, запускаемых с
Земли.

Список литературы

Для
подготовки данной работы были использованы материалы с сайта http://www.i-u.ru/

Дата добавления: 04.11.2005

База рефератов на портале KM.RU существует с 1999 года. Она пополнялась не только готовыми рефератами, докладами, курсовыми, но и авторскими публикациями, чтобы учащиеся могли использовать их и цитировать при самостоятельном написании работ.

Это популяризирует авторские исследования и научные изыскания, что и является целью работы истинного ученого или публициста. Таким образом, наша база — электронная библиотека, созданная в помощь студентам и школьникам.

Уважаемые авторы! Если Вы все же возражаете против размещения Вашей публикации или хотите внести коррективы, напишите нам на почту info@corp.km.ru, мы незамедлительно выполним Вашу просьбу или требование.

Определение расстояний по параллаксам космических объектов

В этой статье мы рассмотрим задачи, связанные с расчетом расстояний до небесных тел. При этом будем пользоваться понятием параллакс. О том, что такое параллактический угол, рассказывает иллюстрация. По тому, на сколько меняется видимое положение звезды на небесной сфере в связи с движением Земли по орбите, можно судить о расстоянии до нее. Если объект достаточно близко (по космическим меркам), то параллактический угол велик, если далеко – то совсем мал. Параллактический угол измеряют, как правило, в минутах или секундах.

Расстояния от Земли до тел Солнечной системы вычисляются по их горизонтальным экваториальным параллаксам и экваториальному радиусу Земли :

или

если параллакс выражен в минутах дуги () и

при параллаксе, выраженном в секундах дуги ()·

Если положить , то получается в экваториальных радиусах Земли. При вычислении в километрах следует принять км.

Если угловые размеры небесного тела , то его линейные размеры

а при , вследствие пропорциональности и ,

— в минутах дуги,

— в секундах дуги.

и

где и — в одноименных единицах измерения.

Радиусы Солнца и планет обычно выражаются в радиусах Земли (реже — в километрах), причем полярный радиус , экваториальный радиус и сжатие планеты  связаны зависимостью

а средний радиус

При совпадении направлений вращения и обращения небесного тела вокруг Солнца продолжительность его солнечных суток , период вращения и период обращения связаны зависимостью

а при противоположных направлениях одному из периодов приписывается знак минус.

Задача 1.

Вычислить средний радиус и сжатие Земли, если ее экваториальный радиус равен 6378 км, а полярный радиус— 6357 км.

Средний радиус найдем как:

Сжатие Земли:

Ответ: км, .

Задача 2.

Радиоимпульс, направленный к Венере в ее нижнем соединении на среднем расстоянии от Солнца 0,7233 а. е., возвратился к Земле через 4м36с. Вычислить геоцентрическое расстояние планеты во время радиолокации, длину астрономической единицы в километрах и средний горизонтальный экваториальный параллакс Солнца.

Вспоминаем, что нижнее соединение – это такое расположение Венеры, когда она между Землей и Солнцем. Так как сигнал возвратился через 4 минуты 36 с, следовательно, в одну сторону он шел 2 минуты 18 секунд, или 138 секунд. Сигнал идет со скоростью света. Давайте найдем расстояние до планеты:

В километрах это км.

Так как расстояние от Земли до Солнца равно 1 астрономической единице, то

Где — расстояние от Венеры до Солнца.

Тогда:

Мы получили длину астрономической единицы сразу в миллионах км.

Вычислим горизонтальный экваториальный параллакс Солнца в секундах дуги:

Откуда

Ответ: км, млн. км, .

Задача 3.

При среднем противостоянии Марса посланный к нему радиосигнал возвратился к Земле через 522,6 с. Найти среднее гелиоцентрическое расстояние Земли и соответствующий ему горизонтальный экваториальный параллакс Солнца. Сидерический период обращения Марса равен 1,881 года.

Аналогично предыдущей задаче, противостояние – это положение Марса такое, что  Земля расположена  между Солнцем и Марсом. Средним его назвали потому, что при противостоянии Марс может находиться ближе или дальше от Земли, здесь взято среднее расстояние.

Так как сигнал возвратился через 522,6 с, следовательно, в одну сторону он шел 261,3 секунды. Сигнал идет со скоростью света. Давайте найдем расстояние до планеты:

В километрах это км.

Дальше для решения нам потребуется третий закон Кеплера

Где — расстояние от Солнца до Марса, — расстояние от Солнца до Земли.

Тогда

Расстояние найдено в км.

Определяем параллакс Солнца:

Ответ: км, .

Задача 4.

Чему равен горизонтальный экваториальный параллакс Луны при ее среднем (384 400 км), ближайшем (356 410 км) и наибольшем (406 740 км) геоцентрическом расстоянии? Экваториальный радиус Земли — 6378 км.

Ответ: , , .

Задача 5.

По данным или результатам задачи 4 вычислить предельные значения диаметра лунного диска, который при среднем геоцентрическом расстоянии равен 31’05».

Если угловые размеры небесного тела , вследствие пропорциональности и ,  его линейные размеры

— в минутах дуги.

Переведем размер лунного диска в минуты: .

Тогда линейный размер

Теперь используем это при расчете минимального и максимального размеров лунного диска:

Ответ: , .

Задача 6.

Пределы геоцентрического расстояния Луны, измеренного радиолокационным методом в 1975 г., были: 16 января —406 090 км; 28 января —357 640 км и 12 февраля— 406 640 км. Найти значения большой полуоси и эксцентриситета лунной орбиты в интервалах времени, заключенных между смежными датами.

Средним расстоянием планеты от Солнца является большая полуось ее орбиты

Где и — перигельное и афелийное расстояния. То же и для Луны, только вместо перигельного будет перигейное расстояние, вместо афелийного – апогейное.

Тогда

Тогда

И эксцентриситет

Для второго периода времени

И эксцентриситет

Ответ: для периода времени от 16 января до 28 — км, эксцентриситет – 0,0634, для периода 28 января – 12 февраля км, эксцентриситет – 0,0641.

Задача 7.

Радиосигнал, направленный к Меркурию при его наибольшем сближении с Землей, вернулся на Землю через 8м52с. Определить геоцентрическое расстояние планеты и эксцентриситет ее орбиты, если большая полуось орбиты равна 0,387 а. е.

Так как сигнал возвратился через 532 с, следовательно, в одну сторону он шел 266 секунд. Сигнал идет со скоростью света. Давайте найдем расстояние до планеты:

В километрах это км, а в  астрономических единицах – 0,533 а.е.

Так как расстояние от Солнца до Земли равно 1 а.е., то расстояние от Солнца до Меркурия равно 

Это больше, чем большая полуось орбиты, поэтому это – афелийное расстояние. Тогда

И эксцентриситет

Ответ: км, .

Законы кеплера и конфигурации планет

Цель
работы:
изучение закономерностей в движении
планет и вычисление их конфигураций.

Пособия:
Астрономический календарь – постоянная
часть или Справочник любителя астрономии;
Астрономический календарь-ежегодник;
Малый звездный атлас А.А. Михайлова;
калькулятор.

Под
действием гравитационного притяжения
к Солнцу планеты обращаются вокруг него
по слабовытянутым эллиптическим орбитам.
Солнце находится в одном из фокусов
эллиптической орбиты планеты. Это
движение подчиняется законам Кеплера.

Величина
большой полуоси
эллиптической орбиты планеты является
также средним расстоянием от планеты
до Солнца. Благодаря незначительным
эксцентриситетами небольшим наклоненияморбит больших планет, можно при решении
многих задач приближенно полагать эти
орбиты круговыми с радиусоми лежащими практически в одной плоскости
– в плоскости эклиптики (плоскости
земной орбиты).

Согласно
третьему закону Кеплера, если
и– соответственно звездные (сидерические)
периоды обращения некоторой планеты и
Земли вокруг Солнца, аи– большие полуоси их орбит, то

.

(7.1)

Здесь
периоды обращения планеты и Земли могут
быть выражены в любых единицах, но
размерности
идолжны быть одинаковы. Подобное
утверждение справедливо и для больших
полуосейи.

Если
за единицу измерения времени принять
1 тропический год (– период обращения Земли вокруг Солнца),
а за единицу измерения расстояния 1
астрономическую единицу (),
то третий закон Кеплера (7.1) можно
переписать в виде

.

(7.2)

Угловая
и линейная скорости планеты при ее
движении на орбите периодически
изменяются в соответствии со вторым
законом Кеплера. Их средние значения
могут быть посчитаны по средней
удаленности
планеты от Солнца.

Средняя
суточная угловая скорость
планеты, определяется выражением

,

(7.3)

где
– сидерический период обращения планеты
вокруг Солнца, выраженный в средних
солнечных сутках.

Очевидно,
для Земли средняя угловая скорость
определяется формулой

(7.4)

и
составляет
.

Поделив
(7.3) на (7.4), получим

.

(7.5)

Если
принять за единицу измерения угловых
скоростей планеты и Земли
,
а периоды обращения измерять в тропических
годах, то формула (7.5) может быть записана
в виде

.

(7.6)

Учтя
третий закон Кеплера (7.2), запишем
зависимость средней угловой скорости
планеты от большой полуоси ее орбиты

.

(7.7)

Средняя
линейная скорость движения планеты на
орбите может быть рассчитана по формуле

,

(7.8)

Аналогичная
величина для Земли

.

(7.9)

Среднее
значение орбитальной скорости Земли
известно и составляет
.
Поделив (7.8) на (7.9) и используя третий
закон Кеплера (7.2), найдем зависимостьот

,

(7.10)

Звездный
(сидерический)
и синодическийпериоды обращения планеты связаны между
собойуравнением
синодического движения

.

(7.11)

Знак
«-» соответствует внутренним
или нижним планетам (Меркурий, Венера),
а «+» – внешним
или верхним (Марс, Юпитер, Сатурн, Уран,
Нептун). В этой формуле
ивыражены в годах. В случае необходимости
найденные значенияивсегда могут быть выражены в сутках.

Взаимное
расположение планет легко устанавливается
по их гелиоцентрическим эклиптическим
сферическим координатам, значения
которых на различные дни года публикуются
в астрономических календарях-ежегодниках,
в таблице под названием «гелиоцентрические
долготы планет».

Центром
этой системы координат (рис. 7.1) является
центр Солнца, а основным кругом –
эклиптика, полюса которой
иотстоят от нее на 90º.

Большие
круги, проведенные через полюса эклиптики,
называются кругами
эклиптической широты,
по ним отсчитывается от эклиптики
гелиоцентрическая
эклиптическая широта
,
которая считается положительной в
северном эклиптическом полушарии и
отрицательной в южном эклиптическом
полушарии небесной сферы. Гелиоцентрическая
эклиптическая долгота
отсчитывается
по эклиптике от точки весеннего
равноденствия 
против часовой стрелки до основания
круга широты светила и имеет значения
в пределах от 0º до 360º.

Из-за
малого наклонения орбит больших планет
к плоскости эклиптики, эти орбиты всегда
находятся вблизи эклиптики, и в первом
приближении можно считать их
гелиоцентрическую долготу
,
определяя положение планеты относительно
Солнца лишь одной ее гелиоцентрической
эклиптической долготой.

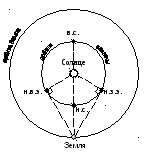
Рис.
7.1. Эклиптическая система небесных
координат

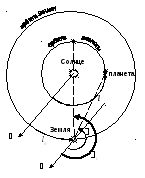
Рассмотрим
орбиты Земли и некоторой внутренней
планеты (рис. 7.2), используя гелиоцентрическую
эклиптическую систему координат.
В ней основным кругом является эклиптика,
а нуль-пунктом – точка весеннего
равноденствия .
Отсчет
эклиптической гелиоцентрической долготы
планеты ведется от направления «Солнце
– точка весеннего равноденствия »
до направления «Солнце – планета»
против часовой стрелки. Для простоты
будем считать плоскости орбит Земли и
планеты совпадающими, а сами орбиты –
круговыми. Тогда положение планеты на
орбите задается ее эклиптической
гелиоцентрической долготой
.

Если
центр эклиптической системы координат
совместить с центром Земли, то это будет
геоцентрическая
эклиптическая система координат.
Тогда угол между направлениями «центр
Земли – точка весеннего равноденствия
»
и «центр Земли – планета» называется
эклиптической
геоцентрической долготой
планеты
.
Гелиоцентрическая эклиптическая долгота
Землии геоцентрическая эклиптическая долгота
Солнца,
как видно из рис. 7.2, связаны соотношением:

.

(7.12)

Будем
называть конфигурацией
планеты
некоторое фиксированное взаимное
расположение планеты, Земли и Солнца.

Рассмотрим
раздельно конфигурации внутренних и
внешних планет.

Рис.
7.2. Гелио- и геоцентрическая системы

эклиптических координат

Различают
четыре конфигурации внутренних планет:
нижнее
соединение
(н.с.), верхнее
соединение
(в.с.), наибольшая
западная элонгация
(н.з.э.) и наибольшая
восточная элонгация
(н.в.э.).

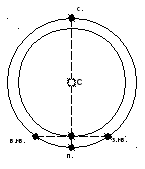
В
нижнем соединении (н.с.) внутренняя
планета находится на прямой, соединяющей
Солнце и Землю, между Солнцем и Землей
(рис. 7.3). Для земного наблюдателя в этот
момент внутренняя планета «соединяется»
с Солнцем, то есть видна на фоне Солнца.
При этом эклиптические геоцентрические
долготы Солнца и внутренней планеты
равны, то есть:
.

Вблизи
нижнего соединения планета перемещается
на небе в попятном движении около Солнца,
над горизонтом находится днем, причем
около Солнца, и наблюдать ее, разглядывая
что-либо на ее поверхности, невозможно.
Очень редко удается увидеть уникальное
астрономическое явление – прохождение
внутренней планеты (Меркурия или Венеры)
по диску Солнца.

Рис.
7.3. Конфигурации внутренних планет

Так
как угловая скорость внутренней планеты
больше угловой скорости Земли, через
некоторое время планета сместится в
положение, где направления «планета-Солнце»
и «планета-Земля» отличаются на
(рис. 7.3). Для земного наблюдателя планета
при этом удалена от солнечного диска
на максимальный угол, или говорят, что
планета в этот момент находится в
наибольшей элонгации (удалении от
Солнца). Различают две наибольших
элонгации внутренней планеты –западную
(н.з.э.) и восточную
(н.в.э.). В наибольшей западной элонгации
()
и планета заходит за горизонт и восходит
раньше, чем Солнце. Это значит, что
наблюдать ее можно утром, перед восходом
Солнца, в восточной стороне неба. Это
называетсяутренней
видимостью
планеты.

После
прохождения наибольшей западной
элонгации диск планеты начинает
приближаться на небесной сфере к диску
Солнца до тех пор, пока планета не
исчезнет за диском Солнца. Эта конфигурация,
когда Земля, Солнце и планета лежат на
одной прямой, причем планета находится
за Солнцем, называется верхним
соединением
(в.с.) планеты. Проводить в этот момент
наблюдения внутренней планеты нельзя.

После
верхнего соединения угловое расстояние
между планетой и Солнцем начинает расти,
достигая максимального значения в
наибольшей восточной элонгации (н.в.э.).
При этом гелиоцентрическая эклиптическая
долгота планеты больше, чем у Солнца
(а геоцентрическая – наоборот, меньше,
то есть).
Планета в этой конфигурации восходит
и заходит позднее Солнца, что дает
возможность наблюдать ее вечером после
захода Солнца (вечерняя
видимость).

Из-за
эллиптичности орбит планет и Земли угол
между направлениями на Солнце и на
планету в наибольшей элонгации не
постоянен, а изменяется в некоторых
пределах, для Меркурия – от
до,
для Венеры – отдо.

Наибольшие
элонгации – самые удобные моменты для
наблюдений внутренних планет. Но так
как даже в этих конфигурациях Меркурий
и Венера не отходят на небесной сфере
далеко от Солнца, наблюдать их в течение
всей ночи нельзя. Продолжительность
вечерней (и утренней) видимости у Венеры
не превышает 4 часов, а у Меркурия – не
более 1.5 часа. Можно сказать, что Меркурий
всегда «купается» в солнечных лучах –
его приходится наблюдать или непосредственно
перед восходом Солнца, или сразу после
захода, на светлом небе. Видимый блеск
(звездная величина) Меркурия меняется
со временем в пределах от
до.
Видимая звездная величина Венеры
варьируется отдо.
Венера – самый яркий объект на небе
после Солнца и Луны.

У
внешних планет также различают четыре
конфигурации (рис. 7.4): соединение
(с.), противостояние
(п.), восточная
и западная
квадратуры
(з.кв. и в.кв.).

Рис.
7.4. Конфигурации внешних планет

В
конфигурации «соединение» внешняя
планета расположена на прямой, соединяющей
Солнце и Землю, за Солнцем. В этот момент
наблюдать ее нельзя.

Так
как угловая скорость внешней планеты
меньше, чем у Земли, дальнейшее
относительное движение планеты на
небесной сфере будет попятным. При этом
она постепенно будет смещаться к западу
от Солнца. Когда угловое удаление внешней
планеты от Солнца достигнет
,
она попадет в конфигурацию «западная
квадратура». При этом планета будет
видна в восточной стороне неба всю
вторую половину ночи до восхода.

В
конфигурации «противостояние», называемой
иногда также «оппозиция», планета
отстоит на небе от Солнца на
,
тогда

,	(7.13)
.	(7.14)

После
противостояния внешняя планета постепенно
приближается к Солнцу, находясь на небе
восточнее, то есть, левее нашего дневного
светила. В этот период планету можно
наблюдать вечером после захода Солнца.
Когда угловое удаление Солнца достигнет
,
наступит конфигурация «восточная
квадратура», при этом геоцентрическая
эклиптическая долгота планеты

.

(7.15)

Планету,
находящуюся в восточной квадратуре,
можно наблюдать с вечера до полуночи.

Наиболее
благоприятны условия для наблюдений
внешних планет в эпоху их противостояния.
В это время планета доступна наблюдениям
в течение всей ночи. При этом она
максимально сближена с Землей и имеет
наибольший угловой диаметр и максимальный
блеск. Для наблюдателей немаловажно,
что все верхние планеты достигают
наибольшей высоты над горизонтом в
зимние противостояния, когда они движутся
по небу в тех же созвездиях, где Солнце
бывает летом. Летние же противостояния
на северных широтах происходят низко
над горизонтом, что может весьма
затруднить наблюдения.

При
расчете даты той или иной конфигурации
планеты ее расположение относительно
Солнца изображается на чертеже, плоскость
которого принимается за плоскость
эклиптики. Направление на точку весеннего
равноденствия 
выбирается
произвольно. Если задан день года, в
который гелиоцентрическая эклиптическая
долгота Земли
имеет определенное значение, то сначала
следует отметить на чертеже расположение
Земли.

Приближенное
значение гелиоцентрической эклиптической
долготы Земли очень легко найти по дате
наблюдения. Легко видеть (рис. 7.5), что,
например, 21 марта, смотря с Земли в
сторону Солнца, мы смотрим в точку
весеннего равноденствия ,
то
есть, направление «Солнце – точка
весеннего равноденствия» отличается
от направления «Солнце – Земля» на
,
а это значит, что гелиоцентрическая
эклиптическая долгота Земли.
Смотря на Солнце в день осеннего
равноденствия (23 сентября), мы видим его
в направлении на точку осеннего
равноденствия (на чертеже она диаметрально
противоположна точке).
При этом эклиптическая долгота Земли
.
Из рис. 7.5 видно, что в день зимнего
солнцестояния (22 декабря) эклиптическая
долгота Земли,
а в день летнего солнцестояния (22 июня)
–.

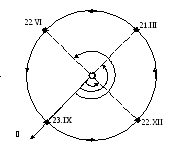
Рис.
7.5. Эклиптические гелиоцентрические
долготы Земли
в разные дни года

Для
расчета долготы Земли
в произвольный день года достаточно
вспомнить, что полный оборот ввокруг Солнца Земля совершает за 365
дней. Это значит, что за сутки Земля
смещается по своей орбите примерно на.
Например, 1 апреля эклиптическая
гелиоцентрическая долгота Земли будет,
так как эта дата наступает через 10 дней
после дня весеннего равноденствия,
когда.

Гелиоцентрическая
эклиптическая долгота Земли
в определенные дни года может быть также
найдена по геоцентрической эклиптической
долготе Солнцав эти же дни, так как если построить
подобную систему эклиптических координат
с началом в центре Земли, то всегда,
поскольку Солнце и Земля всегда находятся
на противоположных концах одного
радиуса-вектора. Но геоцентрическая
долготапланеты не связана подобной зависимостью
со своей гелиоцентрической долготой.

Затем
надо изобразить на чертеже орбиту
планеты. Как уже отмечалось, ее можно
считать круговой и изображать с помощью
циркуля. Крайне важно соблюсти пропорции
между радиусами орбит Земли и планеты,
в противном случае измерения углов
транспортиром окажутся неверными.
Напомним, что радиус орбиты Меркурия
примерно
,
Венеры –,
Марса –,
Юпитера –

Теперь
можно наносить на этот чертеж расположение
планеты либо по ее известной
гелиоцентрической эклиптической долготе
,
либо по заданной конфигурации.

Построив
на чертеже положения планет относительно
Солнца, можно измерить транспортиром
их геоцентрические долготы
и по разности

,

(7.16)

определить
условия их видимости с Земли, полагая,
что в среднем планета становится видимой
при удалении от Солнца на угол около
15º.

В
действительности же условия видимости
планет зависят не только от их удаления
от Солнца, но также и от их склонения
и от географической широтыместа наблюдения, которая влияет на
продолжительность сумерек и на высоту
планет над горизонтом.

Так
как положение Солнца на эклиптике хорошо
известно для каждого дня года, то по
звездной карте и по значениям
легко указать созвездие, в котором
находится планета в тот же день года.
Решение этой задачи облегчается тем,
что на нижнем обрезе карт Малого звездного
атласа А.А. Михайлова красными числами
проставлены даты, в которые отмеченные
ими круги склонения кульминируют в
среднюю полночь. Эти же даты показывают
приблизительное положение Земли на
своей орбите по наблюдениям с Солнца.
Поэтому, определив по карте экваториальные
координатыиточки эклиптики, кульминирующей в
среднюю полночь заданной даты, легко
найти для этой же даты экваториальные
координаты Солнца

(7.17)

и
по ним показать его положение на
эклиптике.

По
гелиоцентрической долготе планет легко
вычислить дни (даты) наступления их
различных конфигураций. Для этого
достаточно перейти к системе отсчета,
связанной с планетой. Это предполагает,
что в конечном итоге мы планету будем
считать неподвижной, а Землю – движущейся
по своей орбите, но с относительной
угловой скоростью.

Получим
необходимые формулы для изучения
движения верхней планеты. Пусть в
некоторый день года
гелиоцентрическая долгота верхней
планеты есть,
а гелиоцентрическая долгота Земли –.
Верхняя планета движется медленнее
Земли (),
которая догоняет планету, и в какой-то
день годапри гелиоцентрической долготе планетыи Землинаступит искомая конфигурация планеты.
Тогда

,	(7.18)
,	(7.19)

откуда,
обозначив
,и,
получим

(7.20)

и
найдем

.

(7.21)

Легко
видно, что
представляет собой угловой путь Земли
по орбите, проходимый Землей с относительной
угловой скоростьюза промежуток времени.
Поэтому для вычисленияможно полагать планету неподвижной и,
взяв разностьмежду разностями гелиоцентрической
долготы Земли и планеты в моменты времении(или найдяпо чертежу), сразу определить.
Для вычисления же гелиоцентрической
долготы планетыи Землина датуиспользуются формулы (7.18) и (7.19).

Очевидно,
те же формулы (7.18) – (7.21) служат для
вычисления дней наступления конфигураций
нижних планет с той лишь разницей, что
из-за большой скорости движения нижней
планеты по сравнению со скоростью
движения Земли в формулы следует
подставлять
и дугу,
которую проходит нижняя планета от
одной конфигурации до другой при условии
неподвижной Земли.

Все
рассмотренные выше задачи следует
решать приближенно, округляя значения
до 0,01 астрономической единицы,и– до 0,01 года и– до целых суток.