Как найти генеральное среднее квадратичное отклонение - Исправление недочетов и поиск решений вместе с Examum.ru

Введение

В этой статье мы научимся считать среднеквадратическое отклонение «вручную».

Любопытно, но в реальном мире статистики никогда не станет вычислять среднеквадратическое отклонение вручную. Эти расчёты достаточно сложные и трудоёмкие, велика вероятность наделать ошибок. Кроме того, считать вручную — это медленно. Очень медленно. Именно поэтому статистики полагаются в этом вопросе на электронные таблицы и компьютерные программы.

В таком случае, зачем вообще написана эта статья? Почему мы тратим время на изучение метода, который статистики на самом деле не используют? Дело в том, что научившись делать вычисления вручную, мы поймём, как на самом деле “работает”среднеквадратическое отклонение. Очень важно понять смысл этого показателя. Вместо того, чтобы рассматривать среднеквадратическое отклонение как какое-то магическое число, которое выдаёт нам наша электронная таблица или компьютерная программа, мы сможем объяснить, откуда взялась эта величина.

Общий принцип вычисления среднеквадратического отклонения

Формула среднеквадратического отклонения (СО)

start text, С, О, end text, equals, square root of, start fraction, sum, start subscript, end subscript, start superscript, end superscript, open vertical bar, x, minus, mu, close vertical bar, squared, divided by, N, end fraction, end square root

где sum означает «сумма», x — это одно значение из выборки, mu — среднее арифметическое, а N — количество элементов в выборке.

Формула среднеквадратического отклонения может показаться запутанной, но всё станет понятно, как только мы разберём её на составные части. Ниже мы пошагово рассмотрим её на примере. Вот краткое перечисление этапов:

Этап 1: Находим среднее арифметическое.

Этап 2: Для каждого элемента находим квадрат его расстояния до среднего арифметического.

Этап 3: Суммируем все результаты, полученные на втором шаге.

Этап 4: Делим полученное число на количество элементов.

Этап 5: Извлекаем квадратный корень.

Важное замечание

Приведенная выше формула предназначена для нахождения среднеквадратического отклонения генеральной совокупности. Если вы имеете дело с выборкой, вам понадобится немного другая формула (она приведена ниже), где вместо N используется n, minus, 1. Однако цель данной статьи — объяснить вам основные принципы вычисления среднеквадратического отклонения вне зависимости от формулы, которую вы используете.

start text, С, О, end text, start subscript, start text, в, ы, б, о, р, к, и, end text, end subscript, equals, square root of, start fraction, sum, start subscript, end subscript, start superscript, end superscript, open vertical bar, x, minus, x, with, bar, on top, close vertical bar, squared, divided by, n, minus, 1, end fraction, end square root

Пошаговый разбор вычисления среднеквадратического отклонения.

В первую очередь нам понадобится набор данных. Давайте выберем не слишком большой набор, чтобы нам не пришлось иметь дело с огромным количеством точек. Вот хороший пример:

6, comma, 2, comma, 3, comma, 1

Этап 1. Находим start color #e07d10, mu, end color #e07d10 из square root of, start fraction, sum, start subscript, end subscript, start superscript, end superscript, open vertical bar, x, minus, start color #e07d10, mu, end color #e07d10, close vertical bar, squared, divided by, N, end fraction, end square root

На этом этапе мы находим среднее арифметическое набора данных, которое затем обозначаем буквой mu.

Этап 2. Находим start color #e07d10, open vertical bar, x, minus, mu, close vertical bar, squared, end color #e07d10 из square root of, start fraction, sum, start subscript, end subscript, start superscript, end superscript, start color #e07d10, open vertical bar, x, minus, mu, close vertical bar, squared, end color #e07d10, divided by, N, end fraction, end square root

На этом шаге мы находим разницу между каждым элементом из набора данных и средним арифметическим (то есть отклонение) и возводим в квадрат каждое из этих отклонений.

Например, первый элемент в наборе — 6, а среднее арифметическое — 3, значит, разница между ними равна 3. Возводим в квадрат и получаем 9.

Этап 3: Находим start color #e07d10, sum, open vertical bar, x, minus, mu, close vertical bar, squared, end color #e07d10 в square root of, start fraction, start color #e07d10, sum, start subscript, end subscript, start superscript, end superscript, open vertical bar, x, minus, mu, close vertical bar, squared, end color #e07d10, divided by, N, end fraction, end square root

Символ sum означает «сумма», то есть на этом этапе мы суммируем четыре числа, полученные на этапе 2.

Этап 4. Находим start color #e07d10, start fraction, sum, open vertical bar, x, minus, mu, close vertical bar, squared, divided by, N, end fraction, end color #e07d10 из square root of, start color #e07d10, start fraction, sum, start subscript, end subscript, start superscript, end superscript, open vertical bar, x, minus, mu, close vertical bar, squared, divided by, N, end fraction, end color #e07d10, end square root

На этом шаге мы делим результат, полученный из третьего этапа на N, на количество элементов в наборе.

Этап 5. Находим среднеквадратическое отклонение square root of, start fraction, sum, start subscript, end subscript, start superscript, end superscript, open vertical bar, x, minus, mu, close vertical bar, squared, divided by, N, end fraction, end square root

Почти закончили! Осталось извлечь квадратный корень из результата четвёртого этапа — и на этом всё.

Да! Мы это сделали! Мы успешно посчитали среднеквадратическое отклонение небольшого набора данных.

Подведём итоги

Мы разбили формулу на пять этапов:

Этап 1. Находим среднее арифметическое mu.

mu, equals, start fraction, 6, plus, 2, plus, 3, plus, 1, divided by, 4, end fraction, equals, start fraction, 12, divided by, 4, end fraction, equals, start color #11accd, 3, end color #11accd

Шаг 2: Находим квадрат расстояния от каждой точки данных до среднего арифметического open vertical bar, x, minus, mu, close vertical bar, squared.

x		open vertical bar, x, minus, mu, close vertical bar, squared
6		open vertical bar, 6, minus, start color #11accd, 3, end color #11accd, close vertical bar, squared, equals, 3, squared, equals, 9
2		open vertical bar, 2, minus, start color #11accd, 3, end color #11accd, close vertical bar, squared, equals, 1, squared, equals, 1
3		open vertical bar, 3, minus, start color #11accd, 3, end color #11accd, close vertical bar, squared, equals, 0, squared, equals, 0
1		open vertical bar, 1, minus, start color #11accd, 3, end color #11accd, close vertical bar, squared, equals, 2, squared, equals, 4

СО=∑∣x−μ∣2N=9+1+0+44=144 Суммируем квадраты расстояний (Этап 3).=3,5 Делим полученное число на количество элементов. (Этап 4).≈1,87 Извлечём квадратный корень (Этап 5).begin{aligned} text{СО} &= sqrt{dfrac{sumlimits_{}^{}{{lvert x-murvert^2}}}{N}}\\\\
&= sqrt{dfrac{9 + 1 + 0 + 4}{4}} \\\\
&= sqrt{dfrac{{14}}{4}} ~~~~~~~~small text {Суммируем квадраты расстояний (Этап 3).} \\\\
&= sqrt{{3{,}5}} ~~~~~~~~small text{Делим полученное число на количество элементов. (Этап 4).} \\\\
&approx 1{,}87 ~~~~~~~~small text{Извлечём квадратный корень (Этап 5).}
end{aligned}

Попробуйте сами

Давайте вспомним формулу:

start text, С, О, end text, equals, square root of, start fraction, sum, start subscript, end subscript, start superscript, end superscript, open vertical bar, x, minus, mu, close vertical bar, squared, divided by, N, end fraction, end square root

Источник

Евгений Николаевич Беляев

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Генеральная дисперсия

Пусть нам дана генеральная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:

Определение 1

Генеральная совокупность — совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.

Определение 2

Генеральная дисперсия — среднее арифметическое квадратов отклонений значений вариант генеральной совокупности от их среднего значения.

Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда генеральная дисперсия вычисляется по формуле:

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае генеральная дисперсия вычисляется по формуле:

С этим понятием также связано понятие генерального среднего квадратического отклонения.

Определение 3

Генеральное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:

[{sigma }_г=sqrt{D_г}]

Выборочная дисперсия

Пусть нам дана выборочная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:

Определение 4

Выборочная совокупность — часть отобранных объектов из генеральной совокупности.

Определение 5

Выборочная дисперсия — среднее арифметическое значений вариант выборочной совокупности.

«Дисперсия: генеральная, выборочная, исправленная» 👇

Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда выборочная дисперсия вычисляется по формуле:

Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае выборочная дисперсия вычисляется по формуле:

С этим понятием также связано понятие выборочного среднего квадратического отклонения.

Определение 6

Выборочное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:

[{sigma }_в=sqrt{D_в}]

Исправленная дисперсия

Для нахождения исправленной дисперсии $S^2$ необходимо умножить выборочную дисперсию на дробь $frac{n}{n-1}$, то есть

С этим понятием также связано понятие исправленного среднего квадратического отклонения, которое находится по формуле:

!!! В случае, когда значение вариант не являются дискретными, а представляют из себя интервалы, то в формулах для вычисления генеральной или выборочной дисперсий за значение $x_i$ принимается значение середины интервала, которому принадлежит $x_i.$

Пример задачи на нахождение дисперсии и среднего квадратического отклонения

Пример 1

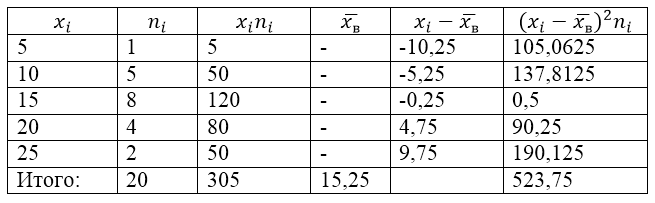
Выборочная совокупность задана следующей таблицей распределения:

Рисунок 1.

Найдем для нее выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение.

Решение:

Для решения этой задачи для начала сделаем расчетную таблицу:

Рисунок 2.

Величина $overline{x_в}$ (среднее выборочное) в таблице находится по формуле:

[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}]

То есть

[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}=frac{305}{20}=15,25]

Найдем выборочную дисперсию по формуле:

[D_в=frac{sumlimits^k_{i=1}{{{(x}_i-overline{x_в})}^2n_i}}{n}=frac{523,75}{20}=26,1875]

Выборочное среднее квадратическое отклонение:

[{sigma }_в=sqrt{D_в}approx 5,12]

Исправленная дисперсия:

[{S^2=frac{n}{n-1}D}_в=frac{20}{19}cdot 26,1875approx 27,57]

Исправленное среднее квадратическое отклонение:

[S=sqrt{S^2}approx 5,25]

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

В данной статье я расскажу о том, как найти среднеквадратическое отклонение. Этот материал крайне важен для полноценного понимания математики, поэтому репетитор по математике должен посвятить его изучению отдельный урок или даже несколько. В этой статье вы найдёте ссылку на подробный и понятный видеоурок, в котором рассказано о том, что такое среднеквадратическое отклонение и как его найти.

Среднеквадратическое отклонение дает возможность оценить разброс значений, полученных в результате измерения какого-то параметра. Обозначается символом (греческая буква «сигма»).

Формула для расчета довольно проста. Чтобы найти среднеквадратическое отклонение, нужно взять квадратный корень из дисперсии. Так что теперь вы должны спросить: “А что же такое дисперсия?”

Что такое дисперсия

Определение дисперсии звучит так. Дисперсия — это среднее арифметическое от квадратов отклонений значений от среднего.

Чтобы найти дисперсию последовательно проведите следующие вычисления:

Определите среднее (простое среднее арифметическое ряда значений).
Затем от каждого из значений отнимите среднее и возведите полученную разность в квадрат (получили квадрат разности).
Следующим шагом будет вычисление среднего арифметического полученных квадратов разностей (Почему именно квадратов вы сможете узнать ниже).

Рассмотрим на примере. Допустим, вы с друзьями решили измерить рост ваших собак (в миллиметрах). В результате измерений вы получили следующие данные измерений роста (в холке): 600 мм, 470 мм, 170 мм, 430 мм и 300 мм.

Порода собаки	Рост в миллиметрах
Ротвейлер	600
Бульдог	470
Такса	170
Пудель	430
Мопс	300

Вычислим среднее значение, дисперсию и среднеквадратическое отклонение.

Сперва найдём среднее значение. Как вы уже знаете, для этого нужно сложить все измеренные значения и поделить на количество измерений. Ход вычислений:

Среднее $=frac{600+470+170+430+300}{5} = 394$ мм.

Итак, среднее (среднеарифметическое) составляет 394 мм.

Теперь нужно определить отклонение роста каждой из собак от среднего:

$[ begin{array}{l} 1: 600-394 = 206 \ 2: 470-394 = 76 \ 3: 170-394 = -224\ 4: 430-394 = 36\ 5: 300-394 = -94 end{array} ]$

Наконец, чтобы вычислить дисперсию, каждую из полученных разностей возводим в квадрат, а затем находим среднее арифметическое от полученных результатов:

Дисперсия $= frac{206^2+76^2+(-224)^2+36^2+(-94)^2}{5} = 21704$ мм².

Таким образом, дисперсия составляет 21704 мм².

Как найти среднеквадратическое отклонение

Так как же теперь вычислить среднеквадратическое отклонение, зная дисперсию? Как мы помним, взять из нее квадратный корень. То есть среднеквадратическое отклонение равно:

мм (округлено до ближайшего целого значения в мм).

Применив данный метод, мы выяснили, что некоторые собаки (например, ротвейлеры) – очень большие собаки. Но есть и очень маленькие собаки (например, таксы, только говорить им этого не стоит).

Самое интересное, что среднеквадратическое отклонение несет в себе полезную информацию. Теперь мы можем показать, какие из полученных результатов измерения роста находятся в пределах интервала, который мы получим, если отложим от среднего (в обе стороны от него) среднеквадратическое отклонение.

То есть с помощью среднеквадратического отклонения мы получаем “стандартный” метод, который позволяет узнать, какое из значений является нормальным (среднестатистическим), а какое экстраординарно большим или, наоборот, малым.

Что такое стандартное отклонение

Но… все будет немного иначе, если мы будем анализировать выборку данных. В нашем примере мы рассматривали генеральную совокупность. То есть наши 5 собак были единственными в мире собаками, которые нас интересовали.

Но если данные являются выборкой (значениями, которые выбрали из большой генеральной совокупности), тогда вычисления нужно вести иначе.

Если есть значений, то:

Все остальные расчеты производятся аналогично, в том числе и определение среднего.

Например, если наших пять собак – только выборка из генеральной совокупности собак (всех собак на планете), мы должны делить на 4, а не на 5, а именно:

Дисперсия выборки = $frac{108520}{4}=27130$ мм².

При этом стандартное отклонение по выборке равно мм (округлено до ближайшего целого значения).

Можно сказать, что мы произвели некоторую “коррекцию” в случае, когда наши значения являются всего лишь небольшой выборкой.

Примечание. Почему именно квадраты разностей?

Но почему при вычислении дисперсии мы берём именно квадраты разностей? Допустим при измерении какого-то параметра, вы получили следующий набор значений: 4; 4; -4; -4. Если мы просто сложим абсолютные отклонения от среднего (разности) между собой … отрицательные значения взаимно уничтожатся с положительными:

$frac{4+4-4-4}{4}=0$ .

Получается, этот вариант бесполезен. Тогда, может, стоит попробовать абсолютные значения отклонений (то есть модули этих значений)?

$frac{4+4+|-4|+|-4|}{4} = frac{4+4+4+4}{4}=4$ .

На первый взгляд получается неплохо (полученная величина, кстати, называется средним абсолютным отклонением), но не во всех случаях. Попробуем другой пример. Пусть в результате измерения получился следующий набор значений: 7; 1; -6; -2. Тогда среднее абсолютное отклонение равно:

$frac{7+1+|-6|+|-2|}{4} = frac{7+1+6+2}{4}=4$ .

Вот это да! Снова получили результат 4, хотя разности имеют гораздо больший разброс.

А теперь посмотрим, что получится, если возвести разности в квадрат (и взять потом квадратный корень из их суммы).

Для первого примера получится:

$sqrt{frac{4^2+4^2+(-4)^2+(-4)^2}{4}}=4$ .

Для второго примера получится:

$sqrt{frac{7^2+1^2+(-6)^2+(-2)^2}{4}}=4.74$ .

Теперь – совсем другое дело! Среднеквадратическое отклонение получается тем большим, чем больший разброс имеют разности … к чему мы и стремились.

Фактически в данном методе использована та же идея, что и при вычислении расстояния между точками, только примененная иным способом.

И с математической точки зрения использование квадратов и квадратных корней дает больше пользы, чем мы могли бы получить на основании абсолютных значений отклонений, благодаря чему среднеквадратическое отклонение применимо и для других математических задач.

О том, как найти среднеквадратическое отклонение, вам рассказал репетитор по математике в Москве, Сергей Валерьевич

Источник

Представленную в табл. 1 совокупность
можно считать выборкой из генеральной
совокупности, то есть совокупности всех
изучаемых объектов. По этим данным можно
найти такое количественное значение
признака, которое позволяет получить
и надёжное представление об интересующем
нас параметре, то есть получить
статистическую оценку. Различают оценки
точечные и интервальные.

Точечной
называют статистическую оценку, которая
определяется одним числом. Для генеральной
средней точечной оценкой является
выборочная средняя, т.е.
;
для генерального среднего квадратического
отклонения такой оценкой является
выборочное среднее квадратическое
отклонение, т.е..
При этом следует помнить, что при
небольших объёмах выборки (n
< 60) следует умножить S_Х
на корректирующий множитель
.

Таким
образом, для нашей задачи точечная
оценка генеральной средней – это
выборочная средняя, то есть,
.Точечной
оценкой генерального среднего
квадратического отклонения будет
величина:S_Г
≈S_Х
≈ 11,9.

Интервальной
называют оценку, которая определяется
двумя числами ─ концами интервала,
покрывающего оцениваемый параметр.

Интервальную
оценку генеральной средней a
нормальной
совокупности можно найти по формуле:
,
гдеt
= t(p,n)
– аргумент функции Лапласа, при котором
Ф(t)
= p.
Значение t
находят по таблице приложения 5.

Интервальной
оценкой генерального среднего
квадратического отклонения S_Гнормально
распределённого признака Х
служит
доверительный интервал:

при
q
< 1,

0
< S_Г < S_Х
(1+q)
при q>1,

где
q=q(p;n)
находят по
таблице приложения 6.

Для
определения интервальной оценки
генеральной средней а
по заданным p
= 0,95 и
n
= 60 из таблицы
приложения 5 найдём
t
= t(0,95;60)
= 2. Теперь
рассчитаем предельную оценку выборки

и доверительный интервал для генеральной
средней из неравенства:

Тогда
45,5 – 3,2 < а
<45,5 + 3,2 или
42,3 < a
< 48,7.

Интервальные
оценки генерального среднего
квадратического отклонения S_Гвычисляются
следующим образом. По таблице приложения
6 найдём q
= q(p;n)
= q(0,95;60)
= 0,188.

Тогда из неравенства имеем:

11,9(1-0,188) < S_Г < 11,9(1+0,188)

или
9,7 < S_Г
< 14,1.

6)
Найдём теперь ошибки выборочных оценок.
Ошибка выборочной средней (стандартное
отклонение выборочной средней)
при нормальном законе распределения
определяется по формуле:.

Относительная
ошибка выборочного среднего находится
следующим образом:

Сопоставление
ошибки выборочного среднего с его
величиной даёт представление о точности
вычисления выборочного среднего
(точности опыта). Для рассматриваемой
задачи ошибка выборочной средней равна
.
Относительная ошибка выборочного
среднего (точность опыта):.

Ошибка
выборочного среднего квадратического
отклонения (стандарта) S_стпри
нормальном законе распределения
вычисляют по формуле:
.
Тогда относительная ошибка вычисления
стандарта равна:.
Ошибка выборочного среднего квадратического
отклонения.
Относительная ошибка вычисления
стандарта:.

7) Проведем анализ
вычисленных статистических параметров.

Полученные статистические характеристики
дают возможность сделать следующие
выводы:

Затраты
на животноводство по выбранным хозяйствам
в среднем составляют
=455
тыс. руб. на 100
голов. В большинстве хозяйств они
несколько больше: М₀
= 464 тыс. руб. При этом передовые хозяйства
затрачивают на животноводство
тыс. руб., а отстающие ─ в среднем только
потыс. руб. Наиболее отстающими являются
10 хозяйств, у которых затраты не превышают369
тыс. руб.
Проведённая
проверка согласия опытного и теоретического
распределения по критериям χ²
─ Пирсона
и
─
Смирнова подтвердила, что данный
признак Х
можно считать
подчиняющимся закону нормального
распределения. Это даёт основание при
вычислении интервальных оценок
параметров использовать формулы
нормального распределения.
Рассеяние
данных относительно выборочного
среднего характеризуется стандартным
отклонением S_x
=119 тыс. руб.
коэффициент вариации V%
= 26,2%
превосходит 20
%, что
свидетельствует о значительном разбросе
данных выборки Х — денежных затрат на
животноводство в различных хозяйствах.
Вычисленная
ошибка выборочного среднего
тыс. руб. даёт возможность определить
относительную ошибку найденного
выборочного среднего,
которая достаточно мала (менее 5%), а
также найти приточность оценки генеральной средней
(тыс. руб.) и установить с надёжностьюр
= 0,95 доверительный
интервал генеральной средней 423
< a
< 487 тыс.
руб., следовательно, можно с надёжностью
р = 95%
ожидать, что средние затраты на
животноводство в целом по области
(генеральная совокупность) будут
находиться в пределах от 423
тыс. руб. до 487
тыс. руб. на 100
голов, а среднее квадратическое
отклонение генеральной совокупности
─ в доверительном интервале: 97
< S_Г
< 141 тыс.
руб.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.

Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.

Стандартное отклонение обозначается буквой σ (греческая буква сигма).

Стандартное отклонение также называется:

среднеквадратическое отклонение,
среднее квадратическое отклонение,
среднеквадратичное отклонение,
квадратичное отклонение,
стандартный разброс.

Использование и интерпретация величины среднеквадратического отклонения

Стандартное отклонение используется:

в финансах в качестве меры волатильности,
в социологии в опросах общественного мнения — оно помогает в расчёте погрешности.

Пример:

Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.

	День 1	День 2	День 3	День 4
Пред.А	19	21	19	21
Пред.Б	15	26	15	24

В обеих компаниях среднее количество товара составляет 20 единиц:

А -> (19 + 21 + 19+ 21) / 4 = 20
Б -> (15 + 26 + 15+ 24) / 4 = 20

Однако, глядя на цифры, можно заметить:

в компании A количество товара всех четырёх дней очень близко находится к этому среднему значению 20 (колеблется лишь между 19 ед. и 21 ед.),
в компании Б существует большая разница со средним количеством товара (колеблется между 15 ед. и 26 ед.).

Если рассчитать стандартное отклонение каждой компании, оно покажет, что

стандартное отклонение компании A = 1,
стандартное отклонение компании Б ≈ 5.

Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).

Расчет среднеквадратичного (стандартного) отклонения

Формулы вычисления стандартного отклонения

Где:
σ — стандартное отклонение,
xi — величина отдельного значения выборки,
μ — среднее арифметическое выборки,
n — размер выборки.
Эта формула применяется, когда анализируются все значения выборки.

стандартное отклонение формула, среднее квадратичное отклонение формула, среднеквадратическое отклонение формула, среднее квадратическое отклонение формула

Где:
S — стандартное отклонение,
n — размер выборки,
xi — величина отдельного значения выборки,
xср — среднее арифметическое выборки.
Эта формула применяется, когда присутствует очень большой размер выборки, поэтому на анализ обычно берётся только её часть.
Единственная разница с предыдущей формулой: “n — 1” вместо “n”, и обозначение «xср» вместо «μ».

Разница между формулами S и σ («n» и «n–1»)

Состоит в том, что мы анализируем — всю выборку или только её часть:

только её часть – используется формула S (с «n–1»),
полностью все данные – используется формула σ (с «n»).

Как рассчитать стандартное отклонение?

Пример 1 (с σ)

Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.

	День 1	День 2	День 3	День 4
Пред.Б	15	26	15	24

Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:

Применяем эти шаги:

1. Найти среднее арифметическое выборки:

μ = (15 + 26 + 15+ 24) / 4 = 20

2. От каждого значения выборки отнять среднее арифметическое:

x1 — μ = 15 — 20 = -5

x2 — μ = 26 — 20 = 6

x3 — μ = 15 — 20 = -5

x4 — μ = 24 — 20 = 4

3. Каждую полученную разницу возвести в квадрат:

(x1 — μ)² = (-5)² = 25

(x2 — μ)² = 6² = 36

(x3 — μ)² = (-5)² = 25

(x4 — μ)² = 4² = 16

4. Сделать сумму полученных значений:

Σ (xi — μ)² = 25 + 36+ 25+ 16 = 102

5. Поделить на размер выборки (т.е. на n):

(Σ (xi — μ)²)/n = 102 / 4 = 25,5

6. Найти квадратный корень:

√((Σ (xi — μ)²)/n) = √ 25,5 ≈ 5,0498

Пример 2 (с S)

Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.

У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.

Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.

Яблоня 1	Яблоня 2	Яблоня 3	Яблоня 4	Яблоня 5	Яблоня 6
9	2	5	4	12	7

Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:

Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.

Применяем практически те же шаги:

1. Найти среднее арифметическое выборки:

Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5

2. От каждого значения выборки отнять среднее арифметическое:

X1 – Xср = 9 – 6,5 = 2,5

X2 – Xср = 2 – 6,5 = –4,5

X3 – Xср = 5 – 6,5 = –1,5

X4 – Xср = 4 – 6,5 = –2,5

X5 – Xср = 12 – 6,5 = 5,5

X6 – Xср = 7 – 6,5 = 0,5

3. Каждую полученную разницу возвести в квадрат:

(X1 – Xср)² = (2,5)² = 6,25

(X2 – Xср)² = (–4,5)² = 20,25

(X3 – Xср)² = (–1,5)² = 2,25

(X4 – Xср)² = (–2,5)² = 6,25

(X5 – Xср)² = 5,5² = 30,25

(X6 – Xср)² = 0,5² = 0,25

4. Сделать сумму полученных значений:

Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5

5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):

(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1

6. Найти квадратный корень:

S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193

Дисперсия и стандартное отклонение

Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).

Дисперсия — в статистике это «среднее квадратов отклонений от среднего». Чтобы её вычислить нужно:

Вычесть среднее значение из каждого числа
Возвести каждый результат в квадрат (так получатся квадраты разностей)
Найти среднее значение квадратов разностей.

Ещё расчёт дисперсии можно сделать по этой формуле:

Дисперсия и стандартное отклонение расчёт дисперсии формула

Где:
S² — выборочная дисперсия,
Xi — величина отдельного значения выборки,
Xср (может появляться как X̅) — среднее арифметическое выборки,
n — размер выборки.

Правило трёх сигм

Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.

Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:

одного среднеквадратического отклонения заключаются 68,26% значений (Xср ± 1σ или μ ± 1σ),
двух стандартных отклонений — 95,44% (Xср ± 2σ или μ ± 2σ),
трёх стандартных отклонений — 99,72% (Xср ± 3σ или μ ± 3σ).

Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.