Ответ:
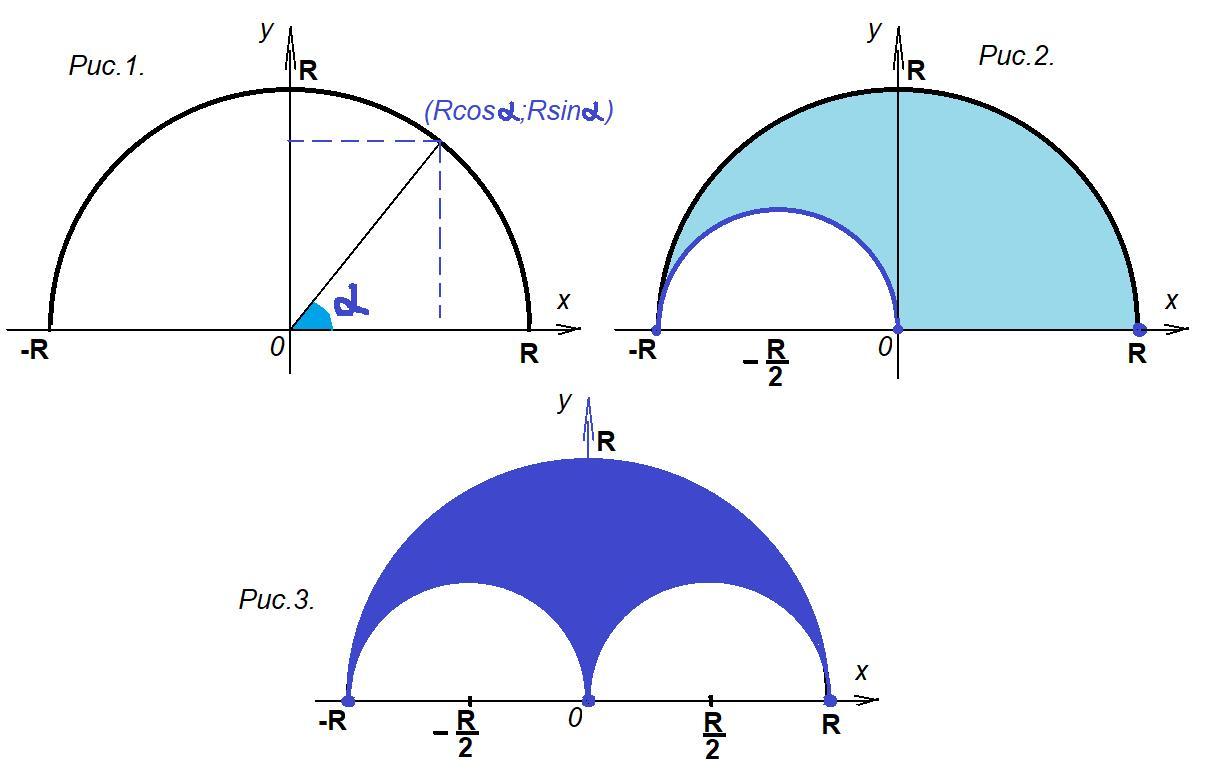
Геометрическое место середин отрезков, концы которых лежат на полуокружности, представлено в приложении на рис. 3.
Пошаговое объяснение:
Пусть дана полуокружность с радиусом R и центром в точке (рис. 1.).
Любую точку этой полуокружности можно представить в виде:
Максимальная длина отрезка, концы которого лежат на полуокружности, равна диаметру. Середина такого отрезка — это центр полуокружности. Геометрическое место середины отрезка-диаметра в системе координат — это точка
Минимальная длина отрезка, концы которого лежат на полуокружности, равна нулю, если концы отрезка совпадают. В этом случае середина отрезка совпадает с концами отрезка. Геометрическое место середин вырожденных отрезков — сама полуокружность.
Середины произвольных отрезков будут находиться в пределах полукруга, ограниченного заданной полуокружностью и осью Ох.
Координаты середины любого отрезка можно посчитать как среднее арифметическое координат концов отрезка:
Возьмём две точки полуокружности Одна точка произвольная, а вторая находится в первой четверти.
Для координат любых этих точек выполняются условия:
Тогда для координат середины такого отрезка выполняются неравенства:
Преобразуем неравенства:
В обоих неравенствах правые части неотрицательные, левые не меньше их, то есть тоже неотрицательные. Возведём в квадрат и сложим оба неравенства:
Это уравнение окружности с радиусом и центром в точке
Тогда точки, удовлетворяющие неравенству:, лежат либо на окружности, либо вне круга с радиусом
и центром в точке
Рис. 2.
Так как полуокружность симметрична относительно оси Оу, то в первой четверти можно вырезать точно такую же область, в которую середины отрезков попасть не могут. Эта ситуация соответствует условию, что один конец отрезка находится во второй четверти, а второй конец выбран произвольно. Таким образом, все возможные случаи расположения концов отрезков учтены.
На рис.3 синим цветом показано геометрическое место середин отрезков, концы которых лежат на полуокружности.
ГМТ пространства, задаваемые двумя скрещивающимися прямыми
Серединная плоскость скрещивающихся прямых. Найдем геометрическое место середин отрезков, концы каждого из которых принадлежат двум данным скрещивающимся прямым a и b
Решение 1. Пусть M — произвольная точка искомого множества, т.е. середина некоторого отрезка AB, A ?a, B ?b (рис. 5). Построим пару параллельных плоскостей a и b, содержащих соответственно прямые a и b. Проведем через точку M плоскость g, параллельную этим плоскостям. В плоскости г лежат середины всех отрезков с концами на a и b, в частности, и середины всех отрезков с концами на прямых a и b. Плоскость г называется серединной плоскостью скрещивающихся прямых.
Обратно, пусть точка M — произвольная точка серединной плоскости г. Прямая l пересечения плоскостей (M, a) и (M, b) пересекает каждую из прямых a и b. Следовательно, точка M принадлежит искомому ГМТ.
Итак, геометрическим местом середин отрезков, концы каждого из которых принадлежат двум скрещивающимся прямым, является серединная плоскость г этих прямых.
Решение 2 (методом преобразований). Фиксируем точку A прямой a. Гомотетия с центром A и коэффициентом 1/2 отображает прямую b на прямую b0 b (рис. 6), на которой лежат середины отрезков AB для любой точки B прямой b. Аналогично фиксируем точку B. Гомотетия с центром B и коэффициентом 1/2 отображает прямую a на прямую а0.Если перемещать одновременно точку A по прямой a, а точку B по прямой b, то объединение всех прямых a0 и b0 — образов прямых a и b при указанных гомотетиях есть серединная плоскость г, содержащая середины всех отрезков AB.
Метод геометрических мест точек
Одним из методов решения задач на построение является метод геометрических мест. Понятие геометрического места является одним из важнейших в геометрии. Термин «геометрическое место точек» был введен еще древнегреческим ученым и философом Аристотелем (384-222 гг. до новой эры), который представлял себе линию, как некоторое «место», где могут быть размещены точки. Понятие линии как следа движущей точки или совокупность точек, возникли значительно позже.
Геометрическим местом точек (сокращенно ГМТ), обладающих определенным свойством, называется множество всех точек, которые обладают этим свойством.
Сущность метода состоит в следующем. Пусть, решая задачу на построение, нам надо найти точку X , удовлетворяющую двум условиям. ГМТ, удовлетворяющих первому условию, есть некоторая фигура A, а ГМТ, удовлетворяющих второму условию, есть некоторая фигура B. Искомая точка X принадлежит A и B, т.е. является их точкой пересечения.
При решении задач этим методом надо знать основные геометрические места точек на плоскости:
1. ГМТ, равноудаленных от двух данных точек.
2. ГМТ, находящихся на данном расстоянии oт данной точки.
3. ГМТ, удаленных на расстояние d oт данной прямой.
4. ГМТ, равноудаленных от двух данных параллельных прямых.
5. ГМТ, равноудаленных от сторон угла.
6. ГМТ, из которых данный отрезок виден под данным углом.
Некоторые геометрические места точек, часто используемые
Рассмотрим построение основных ГМТ, перечисленных в предыдущем пункте.
1. Геометрическим местом точек, равноудаленных от двух данных
точек, является серединный перпендикуляр к отрезку с концами в этих
2. Геометрическим местом точек, находящихся на данном расстоянии
oт данной точки, является окружность с центром в данной точке и радиусом, равном данному отрезку.
3. Геометрическим местом точек, удаленных на расстояние d oт
данной прямой в выбранной полуплоскости, является прямая
параллельная данной и находящаяся на расстоянии d от нее.
А выбираем произвольно.
4. Геометрическим местом точек, равноудаленных от двух данных
параллельных прямых, является прямая, находящаяся на одинаковом
расстоянии от данных прямых (ось симметрии этих прямых).
5. Геометрическим местом точек, равноудаленных от сторон угла,
является биссектриса этого угла. (См. построение 4).
6. Геометрическим местом точек, из которых данный отрезок виден под
данным углом, является дуга окружности, опирающейся на этот отрезок.
I случай:
— данный угол,
АВ – данный отрезок.
Действительно, ∟АМВ, как угол, вписанный в окружность, измеряется
половиной малой дуги АВ, так как центральный угол ∟АОВ = 2α, то
При этом заметим, что центр окружности О и вершина М угла лежат по
одну сторону от данного отрезка
II случай:
1. О – середина АВ.
Полуокружность
(Любой угол, опирающийся на диаметр –
прямой).
III случай:
Действительно, ∟АОВ = 2( 90 0 – (α — 90 0 )) = 2(180 0 — α). Тогда большая дуга
АВ равна 360 0 – 2(180 0 — α) = 2α и угол АМВ, опирающийся на большую дугу АВ, измеряется половиной этой дуги, т.е. равен α.
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ В ПРОСТРАНСТВЕ
«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»
Сертификат и скидка на обучение каждому участнику
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ В ПРОСТРАНСТВЕ
Глава 1. Основные сведения о конструктивной геометрии в пространстве
1.1. Аксиомы конструктивной геометрии в пространстве
1.2. Задачи на построение в пространстве, разрешимость которых следует из аксиом
Глава 2. Решение задач на построения в пространстве
2.1. Скрещивающиеся прямые
2. 3 . Построения на изображениях
Актуальность работы. Геометрия в школе традиционно считается одним из сложных школьных предметов. Иногда, количества часов, отведенных на геометрию бывает недостаточно школьникам для полного и качественного усвоения материала. В связи с этим возникает недопонимание, отставание от тем и зазубривание материала с целью получения хорошей оценки. Таким образом теряется интерес к предмету.
Для достижения высокого интеллектуального развития уровня в геометрии необходимо: выработать у обучающихся желание к изучению и интерес к предмету; развить логическое мышление и пространственное воображение; самостоятельность в решении задач и доказательствах. Решить эту проблему можно разнообразив учебный процесс, внедряя различные современные ТСО (технические средства обучения).
Объект: процесс обучения геометрии обучающихся общеобразовательной школы.
Предмет: использование программы GeoGebra в процессе решения задач на геометрическое построение в пространстве.
1) Показать возможности и ценность использования программы GeoGebra в преподавании математики.
Глава 1.Основные сведения о конструктивной геометрии в пространстве
1.1. Аксиомы конструктивной геометрии в пространстве
Построения на плоскости выполняются с помощью чертежных
инструментов: циркуля и линейки. В отличие от этого, построения в
пространстве выполняют лишь мысленно, в уме. Чтобы было легче следить за ходом построения в пространстве, его сопровождают иллюстративным
рисунком. Стереометрические построения используются для доказательства
существования фигур, обладающих заданными свойствами. Аксиомы, используемые для стереометрических построений, можно разделить на две группы: 1) общие аксиомы конструктивной геометрии; 2) инструментальные аксиомы.
Общие аксиомы конструктивной геометрии используются при решении любой задачи на построение в любом пространстве (необязательно евклидовом). Общие аксиомы будем обозначать АО. Перейдем к их формулировке.
. Каждая из данных фигур построена.
. Если построены фигуры и , то построена и фигура , т.е. фигура, являющаяся их объединением.
. Если фигуры построены и их пересечение не пусто, то фигура построена. Вопрос о том, является ли пересечение фигур пустым множеством или нет, решается в каждом случае с помощью
соответствующих предложений математики.
. Если фигуры построены и их разность не является
пустым множеством, то фигура построена.
. Если фигура F построена, то можно построить точку, принадлежащую этой фигуре.
. Если фигура F построена, то можно построить точку, не принадлежащую этой фигуре F.
Из аксиом , следует существование произвольной прямой, произвольной плоскости.
Инструментальные аксиомы описывают возможности воображаемых
инструментов: сферографа и планиграфа. Будем обозначать инструментальные аксиомы АИ. Сформулируем эти аксиомы.
. Можно построить плоскость, если заданы три ее точки, не лежащие на одной прямой (аксиома планиграфа).
Можно построить сферу, если заданы центр и радиус (аксиома сферографа).
В любой построенной плоскости можно построить любую фигуру,
построение которой выполнимо циркулем и линейкой.
При решении задач на построение в пространстве кроме общих и
инструментальных аксиом используются аксиомы стереометрии, которые мы здесь не приводим, в тексте делаются ссылки на школьные учебники по геометрии под редакцией Л. С. Атанасяна [4,5].
Задача на построение в пространстве считается решенной, если она сводится к конечному числу построений, выполнимость которых гарантирована аксиомами.
Задача на построение в пространстве решается по обычной схеме: анализ, построение, доказательство, исследование.
1.2. Задачи на построение в пространстве, разрешимость которых следует из аксиом
Задача 1. Построить плоскость, проходящую через построенную прямую и построенную точку вне ее.
Обозначим построенную прямую а, построенную точку А .
1. Возьмем точки В и С, лежащие на прямой а.
2. Через точки А, В, С проведем плоскость (аксиома ). Построенная плоскость проходит через прямую а по следствию 2 из системы аксиом стереометрии.
Задача 2. Через данную точку провести прямую, параллельную данной прямой.
Обозначим данную точку А, данную прямую а. Проводим плоскость a через данные точку и прямую.
2. В этой плоскости a с помощью циркуля и линейки строим прямую ,
параллельную а ( ).
Задача 3. Через данную точку вне данной плоскости провести плоскость, параллельную данной плоскости.
Обозначим данную точку А, данную плоскость a .
1. В плоскости a проведем некоторую прямую а (сначала построим две
точки принадлежащие плоскости, а затем – прямую).
2. Проведем плоскость b через точку А и прямую а.
3. В плоскости b через точку А проведем прямую , параллельную а ( ). 4. В плоскости a построим прямую b.
5. Через точку А и прямую b проведем плоскость g .
6. В плоскости g через точку А проведем прямую , параллельную b.
7. Через прямые и проведем плоскость s .
Из параллельности прямых a и , b и следует параллельность плоскостей a и s . Построенная плоскость s единственная. Докажем это.
Предположим, что существует другая плоскость , которая проходит через точку А и параллельна плоскости a . Так как плоскости и b имеют общую точку А, то они пересекаются по прямой с, которая проходит через эту точку. Прямая с не имеет общих точек с прямой а, так как эти прямые лежат в плоскостях и a , не имеющих общих точек. Прямые а и с лежат в плоскости b , проходят через точку А и не имеют общих точек, следовательно, эти прямые параллельны, что противоречит аксиоме параллельных IX. Полученное противоречие доказывает единственность плоскости s .
Задача 4. Из данной точки, не принадлежащей данной прямой, опустить на эту прямую перпендикуляр.
1. Проведем плоскость a через данные прямую а и точку А.
2.В плоскости a из точки А опустим перпендикуляр на прямую а ( ).
Задача 5. Даны две скрещивающиеся прямые. Построить две параллельные плоскости, содержащие эти прямые.
1. Возьмем любую точку А на прямой а (аксиома ).
2. Через точку А проведем прямую , параллельную прямой b.
3. Проведем плоскость a через прямые а и .
Аналогично строим плоскость b , содержащую прямую b и параллельную прямой а. Плоскости a и b – искомые, так как они параллельны (а , b ) и каждая из них содержит одну из скрещивающихся прямых.
Докажем единственность этой пары параллельных плоскостей. Сначала докажем единственность плоскости a . Предположим, что существует другая плоскость , которая проходит через прямую а параллельна прямой b. Через прямые b и проведем плоскость g . Плоскости g и имеют общую точку А, поэтому они пересекаются по прямой с, которая проходит через эту точку.
В плоскости g имеем две разные прямые и с, которые проходят через одну точку А и параллельны прямой b. Это противоречие с аксиомой IX доказывает единственность плоскости a . Аналогично можно доказать единственность плоскости b .
Задача 6. Через данную вне прямой точку провести плоскость, перпендикулярную данной прямой.
Обозначим данную точку А, данную прямую l.
1. Через прямую l и точку А проведем плоскость b .
2. В плоскости b из точки А проведем перпендикуляр m к прямой l ( ).
3. Через произвольную точку В пространства (все пространство считается построенной фигурой, существование точки В гарантирует аксиома ) и прямую l проведем плоскость g .
4. В плоскости g из точки восстановим перпендикуляр n к прямой l.
5. Через прямые m и n проведем плоскость a . Плоскость a – искомая, так как m ^ l , n ^ l Þa ^ l. Докажем единственность плоскости a . Пусть существует плоскость ¹a , проходящая через точку А и перпендикулярная к прямой l. Так как плоскости и b имеют общую точку А, то по аксиоме они пересекаются по прямой , проходящей через точку А. Прямая l перпендикулярна к плоскости , поэтому прямая l перпендикулярна к прямой . Таким образом, в плоскости b через точку А проходят два различных перпендикуляра m и к прямой l, что противоречит аксиоме о параллельных прямых IX. Следовательно, a .
Задача 7. Через данную вне плоскости точку провести перпендикуляр к данной плоскости.
Обозначим данную точку М, данную плоскость a .
1. В плоскости a проведем произвольную прямую а.
2. Через точку М проведем плоскость b , перпендикулярную прямой а (основная задача 7).
3. .
4. В плоскости b из точки М опустим перпендикуляр с на прямую b. Прямая с перпендикулярна к плоскости a , так как прямая с перпендикулярна прямым а и b. Докажем единственность перпендикуляра с. Пусть через точку М проходит другой перпендикуляр к плоскости a . Через пересекающиеся прямые с и проведем плоскость. Обозначим N и основания перпендикуляров с и . Треугольник имеет два прямых угла, что противоречит аксиоме IX.
Глава 2. Решение задач на построения в пространстве
2.1. Скрещивающиеся прямые
Задача 1. Найдите геометрическое место середин отрезков, которые параллельны данной плоскости и концы которых лежат на двух данных
скрещивающихся прямых.
Пусть данные прямые и пересекают данную плоскость Π в точках P и Q (если Π или Π, то искомых отрезков нет). Проведём через
середину M отрезка PQ прямые и , параллельные прямым и соответственно. Пусть некоторая плоскость, параллельная плоскости Π, пересекает
прямые и в точках и , а прямые и — в точках и . Тогда
— искомый отрезок, причём его середина совпадает с серединой отрезка , так как — параллелограмм. Середины отрезков лежат на одной прямой, так как все эти отрезки параллельны друг другу.
Задача 2. Найдите геометрическое место середин отрезков данной длины, концы которых лежат на двух данных скрещивающихся перпендикулярных прямых.
Пусть k и m – данные прямые, расстояние между которыми равно h. Рассмотрим плоскость a , параллельную каждой из данных прямых и равноудаленную от них.
Середина любого отрезка KM с концами на данных прямых лежит в этой плоскости. Действительно, если K’ и M’ – ортогональные проекции точек K и M на плоскость a , а С – точка пересечения этой плоскости с прямой KM, то прямоугольные треугольники CKK’ и CMM’ равны по катету и острому углу, поэтому СK = СM, то есть С – середина отрезка KM. Заметим также, что утверждения “С – середина отрезка KM” и “С – середина отрезка K’M’ ” равносильны.
Пусть рассматриваемый отрезок KM имеет данную длину a. Рассмотрим прямые k’ и m’ – проекции прямых k и m на плоскость a и точку О их пересечения. Так как k || a и m || a , то k’ || k и m’ || m.
По условию , поэтому .
Кроме того, . Это означает, что точка С является серединой гипотезы K’M’ прямоугольного треугольника K’ОM’ , когда .
Таким образом, искомое ГМТ – множество точек плоскости a , находящихся от точки О на расстоянии , а это есть окружность с центром О и радиусом R.
Задача 1 . Нейти геометрическое место точек пространства, равноудаленных от двух данных точек.
Докажем, что искомое множество – плоскость, проходящая через середину отрезка, соединяющего эти точки, и перпендикулярная к нему. Обозначим эту плоскость через . Пусть точка М принадлежит плоскости . Тогда – общая сторона, . Отсюда АМ = МВ и точка М принадлежит к г.м.т.
Если точка N не принадлежит плоскости , то в отрезок С N – медиана. Так как CN не может быть высотой, то AN NB . Поэтому точка N не принадлежит г.м.т. Искомым г.м.т. будет плоскость .
Задача 2 . Найти геометрическое место точек пространства, равноудаленных от трех данных точек, не лежащих на одной прямой.
Докажем, что искомым множеством является перпендикуляр к плоскости этих точек, проходящий через центр окружности, описанной около треугольнике ABC .
Действительно, через точки А, В, С можно провести единственную плоскость , а в ней единственную окружность, проходящую через точки А, В, С. Пусть центр этой окружности – точка О. Тогда через эту точку проходит только одна прямая l , перпендикулярная плоскости . Проверим условия г.м.т. для этой прямой.
1)Пусть точка М принадлежит прямой l , тогда из равенства проекций АО = ОВ = ОС следует равенство наклонных АМ = BM = MC . Точка М удовлетворяет условиям г.м.т.
2)Если точка N не принадлежит прямой l , то ее ортогональная проекция точка на плоскость не совпадает с точкой О и поэтому проекции , , не могут быть равными.
Следовательно, не могут быть равными и наклонные AN , BN , CN . Точка М не может принадлежать к г.м.т.
Задача 3 . Найти множество точек пространства, равноудаленных от двух пересекающихся прямых.
Анализ искомого множества приводит к гипотезе, что это множество – две плоскости ( ), перпендикулярные плоскости данных прямых ( ) и проходящие через биссектрисы углов между этим прямыми. Проверим условия г.м.т. для этих плоскостей.
1) Пусть точка М принадлежит плоскости (или плоскости ), тогда ортогональная проекция точки М на плоскость (точка ) будет принадлежать прямой c , лежащей в плоскости . Прямая c будет содержать биссектрису угла между прямыми a и b . По свойству биссектрисы точка равноудалена от прямых a и b , то есть Так как по теореме о трех перпендикулярах , то М A = М B .
2) Если взять точку N, не принадлежащую ни плоскости , ни плоскости , то ее проекция (точка ) не будет принадлежать ни прямой с, ни прямой d . Поэтому, точка не будет равноудалена от прямых а и b . Нетрудно показать, что в этом случае и точка N не будет равноудаленной от прямых a и b .
Задача 4 . Найти геометрическое место точек пространства, равноудаленных от двух данных параллельных прямых.
Проведем через данные параллельные прямые a и b и плоскость . Построим в этой плоскости прямую c , равноудаленную от прямых a и b . Нетрудно доказать, что г.м.т. будет плоскость, проходящая через прямую c и перпендикулярная плоскости .
Задача 5 . Найти геометрическое место точек пространства, равноудаленных от двух скрещивающихся прямых.
Решим эту задачу методом координат. Рассмотрим две скрещивающиеся прямые a и b . Как известно, существует единственный общий перпендикуляр этих прямых АВ, длину которого обозначим через p . Выберем прямоугольную систему координат так, чтобы ее начало (точка О) совпало с серединой отрезка АВ, вектор был сонаправлен с , вектор параллелен прямой b и тройка векторов – правая. Тогда уравнение прямой b будет иметь вид:
Уравнение прямой a :
Пусть точка принадлежит искомому множеству, т.е. эта точка равноудалена от прямых a и b . Найдем расстояния и этой точки до прямых a и b соответственно. Расстояние от точки M до прямой b находится легко: .
Для нахождения расстояния от точки M до a воспользуемся следующей, известной из курса геометрии формулой. Если прямая l имеет направляющий вектор и проходит через точку , то расстояние от точки M ( x , y , z ) до l равно
Прямая a проходит через точку и имеет направляющий вектор с координатами , тогда
Записав равенство , получим уравнение
которое после преобразований примет вид
(1)
Для определения вида поверхности второго порядка, заданной уравнением (1), приведем это уравнение к каноническому виду. Повернем выбранную систему координат вокруг оси Oz на угол так, чтобы , тогда относительно новой системы координат O уравнение исследуемого множества точек примет вид
где
Уравнение (2) есть уравнение гиперболического параболоида. Можно показать и обратное, что всякая точка N , координаты которой относительно удовлетворяют уравнению (1), равноудалена от прямых а и b . Следовательно, множество точек, равноудаленных от двух скрещивающихся прямых – гиперболический параболоид
Задача 6 . Найти геометрическое место точек пространства, равноудаленных от данной точки плоскости F и данной плоскости .
Обозначим через P расстояние от точки F до плоскости . Воспользуемся методом координат для решения этой задачи. Пусть FK – перпендикуляр, проведенный из точки F на плоскость . Выберем прямоугольную систему координат так, чтобы точка О совпала о серединой отрезка KF , а , тогда точка , а плоскость задается уравнением
Пусть точка М ( x , у, z ) принадлежит искомому г.м.т. Тогда МF = М N , где N – основание перпендикуляра, проведенного ив точки М на плоскость . Очевидно, что .
Записав равенство MF = N М в координатной форме, получим
это выражение после соответствующих преобразований примет вид
Легко показать, что всякая точка, координаты которой удовлетворяют уравнению (З), принадлежит рассматриваемому множеству. Уравнение (З) будет уравнением этого множества. С другой стороны, уравнение (3) – уравнение параболоида вращения с осью вращения (осью О x ) и вершиной в точке О. Итак, исследуемое г.м.т. – параболоид вращения .
В пространстве кроме геометрических мест точек можно рассматривать геометрические места прямых. Для характеристики геометрических мест прямых напомним некоторые понятия.
Пучком прямых называется геометрическое место прямых плоскости, проходящих через одну точку. Эта точка называется центром пучка.
Пучком параллельных прямых называется геометрическое место прямых плоскости, параллельных между собой. Рассмотрим примеры геометрических мест прямых в пространстве .
1.Геометрическое место прямых, параллельных данной плоскости и проходящих через данную точку, есть пучок прямых с центром в данной точке. Плоскость пучка параллельна данной плоскости .
2. Геометрическим местом прямых, параллельных данной прямой l и пересекающих другую данную прямую m является: а) пучок прямых, параллельных прямой l и лежащих в плоскости, проходящей через m параллельно прямой l , если прямые l и m скрещиваются; б) пучок прямых, параллельных прямой l и лежащих в плоскости, образованной прямыми l и m , если прямые l и m пересекаются; в) пустое множество, если прямые m и l параллельны.
3. Геометрическое место прямых, проходящих через данную точку и наклоненных под данным углом к данной плоскости, состоит из прямых, содержащих образующие поверхности прямого кругового конуса с вершиной в данной точке и основанием, лежащим на данной плоскости.
4. Геометрическое место прямых, пересекающих данную окружность и параллельных данной прямой, не лежащей в плоскости окружности, состоит из прямых цилиндрической поверхности. Направляющей этой поверхности является данная окружность.
Задача 7. Найти геометрическое место прямых, проходящих через данную точку А и удаленных на данное расстояние от данной прямой a .
Из всех плоскостей, проходящих через точку А выберем те, которые отстоят на расстоянии d от прямой a . Для этого через точку А проведем плоскость , перпендикулярную прямой a . Пусть О – точка пересечения этой плоскости с прямой а. В плоскости построим окружность с центром в точке О и радиусом d . Проведем из точки А касательные к ней: b и c . Затем через точку А проведем прямую а. Рассмотрим плоскости, образованные прямыми и b (плоскость ), и c (плоскость ). Очевидно, что искомое г.м.т. – 2 пучка с центром в точке А и плоскостями и .
Заметим, что если расстояние от точки А до прямой a , равно d , то плоскости и совпадают и искомое множество – пучок прямых с центром в А, лежащий в совпавших плоскостях. Если расстояние от точки А до прямой a меньше d , то искомое геометрическое множество прямых будет пустым множеством.
Задача 1. Дано изображение проекции на некоторую плоскость куба с отмеченными точками P, Q, R на рёбрах , BC, .
Постройте на этом изображении сечение куба плоскостью PQR.
В процессе построения можно использовать то, что прямые, по которым некоторая плоскость пересекает пару параллельных плоскостей, параллельны.
Сначала через точку P проводим прямую, параллельную прямой RQ, и находим её точки пересечения с прямыми AD и . Эти точки соединяем с точками Q и R и получаем сечения граней ABCD и . На сечении одной из двух оставшихся граней уже построены две точки, и остаётся только соединить их.
Задача 2. Дано изображение проекции на некоторую плоскость куба с отмеченными точками P, Q и R на рёбрах , BC и . Постройте на этом изображении сечение куба плоскостью PQR.
Построим сначала точку M пересечения прямой PR и плоскости грани ABCD следующим образом. Проекцией точки P на плоскость грани ABCD является точка A, а проекцию R′ точки R на эту плоскость легко построить ( – параллелограмм). Искомая точка M является точкой пересечения прямых PR и AR′. Соединив точки M и Q, получим сечение грани ABCD. Дальнейшее построение проводится таким же способом, как и в задаче 1 пункта 2.5
Задача 3. а) Дано изображение проекции на некоторую плоскость трёхгранного угла Oabc, на гранях Obc и Oac которого отмечены точки A и B. Постройте на этом изображении точку пересечения прямой AB с плоскостью Oab. б) Дано изображение проекции на некоторую плоскость трёхгранного угла с тремя отмеченными на его гранях точками. Постройте на этом изображении сечение трёхгранного угла плоскостью, проходящей через отмеченные точки.
а) Пусть P – произвольная точка ребра c. Плоскость PAB пересекает рёбра a и b в тех же точках, в каких их пересекают прямые PB и PA соответственно. Обозначим эти точки и . Тогда искомая точка является точкой пересечения прямых и AB
б) Пусть на гранях Obc, Oac и Oab отмечены точки A, B и C. Воспользовавшись задачей (а), можно построить точку пересечения прямой AB с плоскостью Oab. Теперь на плоскости Oab известны две точки плоскости ABC: только что построенная точка и точка C. Соединив их, получим искомое сечение плоскости Oab. Дальнейшее построение очевидно.
Задача 4. Пусть – выпуклый шестигранник с четырёхугольными гранями. Дано изображение проекций на некоторую плоскость трёх его граней, сходящихся в вершине B (и тем самым – семи его вершин). Постройте изображение восьмой его вершины .
Построим сначала прямую пересечения плоскостей граней ABCD и . Этой прямой принадлежат точка P пересечения прямых AB и и точка Q пересечения прямых BC и . Пусть M – точка пересечения прямых DA и PQ. Тогда M – точка пересечения грани с прямой PQ, т. е. точка лежит на прямой . Аналогично если N – точка пересечения прямых CD и PQ, то точка лежит на прямой .
http://poisk-ru.ru/s5189t3.html
http://infourok.ru/geometricheskie-postroeniya-v-prostranstve-5478431.html
�������
������� �������������� ����� ������� ���� ��������, ���� �����
������� ����� �� ������ ������, � ������ ��������� � ������ ������,
�� ������� �� ���� ������.
���������
�������������� �������� � ������� ����� ������������.
�������
����� l — ������ ������, A — ������ �����, �� ������� �� ����
������, B — ��������� ����� ������ l, M — �������� ������� AB.
�����ģ� ����� ����� M ������ m, ������������ l. ���� C —
������������ ����� ������ l, � N — �������� AC, �� ������ m
�������� ����� ����� N, �.�.
MN || l �� ������� � ������� �����
������������, � ����� ����� M �������� ������ ���� ������,
������������ l.
����� ������ K — ������������ ����� ������ m, �������� �� M.
���� ������ AK ���������� ������ l � ����� D, �� K — �������� AD.
�������������, ���� ��� �� ���, ��, �������� �������� K1 ������� AD
� ������ M, ������� ������� ����� MK1 ������������ ABD. �����
MK1 || l. ������, ����� K1 ��������� � ������ K.
�����
������, ������������ ������.
��������� � ���������� �������������
| web-���� | |
| �������� | ������� ����� �� ��������� �.�.������� |
| URL | http://zadachi.mccme.ru |
| ������ | |
| ����� | 1899 |
Ответ:
Геометрическое место середин отрезков, концы которых лежат на полуокружности, представлено в приложении на рис. 3.
Пошаговое объяснение:
Пусть дана полуокружность с радиусом R и центром в точке (рис. 1.).
Любую точку этой полуокружности можно представить в виде:
Максимальная длина отрезка, концы которого лежат на полуокружности, равна диаметру. Середина такого отрезка — это центр полуокружности. Геометрическое место середины отрезка-диаметра в системе координат — это точка
Минимальная длина отрезка, концы которого лежат на полуокружности, равна нулю, если концы отрезка совпадают. В этом случае середина отрезка совпадает с концами отрезка. Геометрическое место середин вырожденных отрезков — сама полуокружность.
Середины произвольных отрезков будут находиться в пределах полукруга, ограниченного заданной полуокружностью и осью Ох.
Координаты середины любого отрезка можно посчитать как среднее арифметическое координат концов отрезка:
Возьмём две точки полуокружности Одна точка произвольная, а вторая находится в первой четверти.
Для координат любых этих точек выполняются условия:
Тогда для координат середины такого отрезка выполняются неравенства:
Преобразуем неравенства:
В обоих неравенствах правые части неотрицательные, левые не меньше их, то есть тоже неотрицательные. Возведём в квадрат и сложим оба неравенства:
Это уравнение окружности с радиусом и центром в точке
Тогда точки, удовлетворяющие неравенству:
, лежат либо на окружности, либо вне круга с радиусом
и центром в точке
Рис. 2.
Так как полуокружность симметрична относительно оси Оу, то в первой четверти можно вырезать точно такую же область, в которую середины отрезков попасть не могут. Эта ситуация соответствует условию, что один конец отрезка находится во второй четверти, а второй конец выбран произвольно. Таким образом, все возможные случаи расположения концов отрезков учтены.
На рис.3 синим цветом показано геометрическое место середин отрезков, концы которых лежат на полуокружности.

Дана полуокружность. Найдите геометрическое место середин отрезков, концы которых лежат на этой полуокружности
Светило науки — 1 ответ — 0 раз оказано помощи
Ответ:
Пошаговое объяснение:

Светило науки — 13455 ответов — 145139 раз оказано помощи
Ответ:
Пошаговое объяснение:
Если концами отрезка могут быть любые две точки на полуокружности, то серединой этого отрезка может быть любая точка внутри полукруга.
Иначе говоря: любая точка внутри полукруга есть середина какого-то отрезка, концы которого лежат на полуокружности.