При решении геометрических задач используется геометрический смысл модуля комплексного числа, его аргумента, геометрический смысл введенных алгебраических операций и пр. Приведем конкретные примеры.
Пример 1. Какое множество точек на плоскости (z) определяется условием
Решение. Имеем и, стало быть,
. По условию
или
. Последнее неравенство определяет множество точек в первом и третьем квадрантах, соответственно над и под гиперболой (см. рис.6).
Пример 2. Какое множество точек на плоскости (Z) определяется условием ?
Решение. Комплексное число изображается вектором, началом которого является точка –1+I и концом – точка z. Угол между этим вектором и осью Ox есть
, и он меняется в пределах от
до
. Следовательно, данное неравенство определяет угол между прямыми, выходящими из точки –1+ I и образующими с осью Ox углы в
и
(рис.7).
Пример 3. Какая кривая задается уравнением , где C и A – действительные положительные числа, причем A >C.
Решение. Модуль Есть расстояние между точками Z и – C;
— расстояние между точками Z и C. По условию сумма расстояний от точки Z до двух данных точек —C и C есть величина постоянная. Значит, точка Z лежит на эллипсе. Уравнение этого эллипса имеет вид

(рис.8).
Пример 4. Какая кривая определяется уравнением 
Решение. Имеем (см.(1.9)) 

— это окружность
(рис.9).
Пример 5. Написать в комплексной форме уравнение прямой .
Решение. Подставляя X и Y по формуле (1.9) в уравнение прямой, получим , или
. Обозначив
,
получим уравнение:
— уравнение прямой в комплексной форме.
Задачи для самостоятельного решения
1. Доказать следующие соотношения:
А) ; б)
; в)

.
2. Найти:
А) ; б)
; в)
; г)
; д)
.
3. Найти действительные решения уравнений:
А) ;
Б) , где A, B – заданные действительные числа,
;
В) .
4. Представить комплексное число 
5. Вычислить 
6. Выделить X и Y через U и V (X,…,V – действительные числа), если 
7. Найти все числа, удовлетворяющие условию .
8. Решить системы уравнений:
А)
В) 
9. Найти модуль и главное значение аргумента комплексного числа. Записать число в тригонометрической и показательной формах:
А) –2; б) 2I; в) ; г) –Z — I; д) 4-3I; е)
ж)
; з)
;
И)
.
10. Вычислить:
А) ; б)
; в)


Д) 
11. Найти все значения корней:
А) ; б)
; в)
; г)
; д)
; е)
;
Ж) 
; и)
; к)
; л)

.
12. Решить квадратные уравнения:
А) ; б)
;
В) .
13. Решить уравнения:
А); б)
; в)
;
Г) ; д)

14. Найти множества точек на плоскости (Z), определяемые заданными условиями:
А) 
; в)
; г)
;
Д) ; е)
; ж)

з) 
15. Какие линии определяются следующими уравнениями:
А) ; б)

;
Г) ; д)
; е)
; ж)
.
16. Написать в комплексной форме уравнение следующих линий:
А) координатных осей Ox и Oy; б) прямой Y = X; в) прямой ,
— действительные числа; г) гиперболы
; д) окружности
.
| < Предыдущая | Следующая > |
|---|
Множества на комплексной плоскости
Расположение точек на комплексной плоскости
Напомним известные из анализа функций двух действительных переменных основные геометрические понятия, связанные с расположением точек на плоскости. Определения будем давать в терминах комплексной плоскости, т.е. точка плоскости — это точка
комплексной плоскости.
1. Множество точек , удаленных от заданной точки
на расстояние, меньшее чем заданное число
, называется ε-окрестностью точки
, будем обозначать ее
. Используя понятие расстояния между точками плоскости
, определение можно записать в виде соотношения:
Очевидно, что геометрически — круг с центром в точке
и радиусом
.
2. Множество точек , удовлетворяющих неравенству
, образует проколотую окрестность точки
.
3. Точка называется внутренней точкой множества, если она принадлежит ему вместе с некоторой своей окрестностью, т.е. — внутренняя точка множества
, если
и
, что
.
4. Множество, состоящее только из внутренних точек (множество, все точки которого являются внутренними), называется открытым.
5. Точка называется граничной точкой множества, если в любой ее окрестности есть точки, принадлежащие множеству, и точки, не принадлежащие ему, т.е. — граничная точка множества
, если для
существуют точки
и
, то
, такие. что
.
Совокупность граничных точек множества образует границу множества.
Направление обхода границы называется положительным, если область, ограниченная контуром, при обходе расположена слева.
6. Множество, содержащее все свои граничные точки (множество вместе с границей), называется замкнутым. Оно обозначается , то есть
, где
— граница множества
.
7. Множество называется связным, если любые две его точки можно соединить непрерывной кривой, все точки которой принадлежат множеству.
8. Открытое, связное множество называется областью. Область с присоединенной границей — замкнутая обметь, и
.
9. Область (множество) называется односвязной, если для любой замкнутой кривой, принадлежащей области, точки множества, границей которого является кривая, также принадлежат области. В противном случае — область многосвязная.
10. Многосвязная область называется n-связной, если ее граница состоит из компонент. Порядок
связности многосвязной (n-связной) области определяется числом
связных компонент границы области.
На рис. 1.10 приведены геометрические примеры односвязных и многосвязных
областей. Обход границы области указан стрелкой.
11. Множество называется ограниченным, если существует круг с центром в начале координат, содержащий это множество, т.е. ограничено, если
, что
Кривые на комплексной плоскости
На множестве действительных чисел можно обычным образом определить функцию, которая принимает на этом множестве комплексные значения: любому соответствует
— комплекснозначная функция действительной переменной.
Например, — комплекснозначные функции, первые две определены для любого
, последняя — для любого
.
Для функции , так же как для действительной функции действительной переменной, вводится понятие предела в точке, а на его основе — понятия непрерывности, производной, интеграла.
Так как для любого значения из области определения число
является комплексным числом, то, записав его в алгебраической форме
, получим, что задание комплексной функции
действительной переменной на некотором множестве
равносильно заданию на этом множестве двух действительных функций
и
.
Используя соответствующие определения, нетрудно убедиться в справедливости следующих утверждений и формул:
1. Для непрерывности функции в точке
необходимо и достаточно, чтобы в этой точке были непрерывны функции
и
.
2. .
3. .
4. .
Уравнения кривых на комплексной плоскости
Одним из способов задания кривой на плоскости является параметрическое задание:
(1.18)
Будем рассматривать гладкие и кусочно-гладкие кривые.
Кривая называется гладкой на множестве , если функции
имеют на
непрерывные производные
. Геометрически гладкая кривая характеризуется существованием касательной к этой кривой в каждой точке, причем направление касательной изменяется непрерывно при движении точки по кривой.
Кривая называется кусочно-гладкой, если ее можно разбить на конечное число гладких кривых.
На рис. 1.11 изображены кривые, которые являются кусочно-гладкими на и гладкими на каждом из интервалов
и
.
Из определения функции , данного выше, следует, что геометрически её задание определяет кривую на плоскости (и обратно): по формуле (1.18) любому значению
соответствует точка
, то есть число
.
Следовательно, параметрическое задание кривой в форме (1.18) равносильно заданию . Равенство
(1.19)
называется уравнением кривой в параметрической форме.
Пример 1.26. Записать в параметрической форме уравнение окружности, центр которой находится в точке , а радиус равен
.
Решение
Используем известные параметрические уравнения окружности:
Отсюда получаем или
, где
— центр окружности. Используя формулу Эйлера, окончательно запишем уравнение окружности в параметрической форме:
(1.20)
Заметим, что если переписать (1.20) в виде , то получим равенство
, которое определяет окружность как геометрическое место точек плоскости (точек
), равноудаленных (на заданное расстояние
) от заданной точки
. Очевидно, уравнение (1.20) определяет гладкую кривую, что соответствует геометрическому виду этой кривой.
Уравнение плоской кривой, как известно, можно также записать в виде , т.е. соотношения, связывающего декартовы координаты
точек, принадлежащих этой линии; в частности,
— явное задание линии. Но так как пара
определяет комплексное число
, то, выразив
и
через
, можно записать соотношение в комплексной форме. Из
и
получаем
и
. Поэтому равенство
(1.21)
есть уравнение кривой на плоскости, записанное в комплексной форме. Используя тригонометрическую форму задания комплексного числа, можно получить и другие виды уравнений кривых на комплексной плоскости.
Пример 1.27. Записать в комплексной форме уравнения: а) прямой; б) окружности.
Решение
а) Общее уравнение прямой на плоскости имеет вид . Подставляя в это уравнение
и
, находим
, или
.
Введя обозначение , окончательно получим
— уравнение прямой в комплексной форме.
б) Используем уравнение окружности в общем виде . Подставляя в это уравнение
и
получаем
, или, обозначая
уравнение окружности в комплексной форме. Заметим, что при получаем задачу, рассмотренную в пункте «а».
Замечание 1.2. Утверждение, что уравнение прямой на плоскости является частным случаем уравнения окружности на комплексной плоскости имеет более глубокий смысл: прямые как геометрический образ являются частным случаем окружности (их можно рассматривать как окружности «бесконечного» радиуса, ). Обоснование этого можно получить, используя стереографическую проекцию — геометрическое изображение комплексных чисел (множества
) точками на сфере Римана.
Имеет место утверждение: окружности и прямые плоскости при стереографической проекции отображаются в окружности, причем образом окружности является окружность на сфере Римана, не проходящая через точку , а образом прямой — окружность, проходящая через
.
Для доказательства используем формулы связи координат точки плоскости и ее образа на сфере (см. рис. 1.12,а).
Если положить диаметр сферы равным единице и ввести систему координат
, направив по лучу
ось
, а плоскость
выбрав за плоскость
, где ось
, совпадает с
, а ось
— с
, то, используя коллинеарность векторов
и
, получим выражение координат точки
плоскости
через координаты ее образа
на сфере. Эти формулы имеют вид
.
Подставляем их в уравнение окружности и учитывая, что точка
лежит на сфере, т.е. ее координаты удовлетворяют уравнению
или
, после преобразований получаем уравнение плоскости
. Следовательно, образом окружности является линия пересечения сферы этой плоскостью, т.е. окружность на сфере. При
на плоскости имеем прямую с уравнением
; ее образом на сфере будет окружность
проходящая через точку , так как координаты точки
удовлетворяют этой системе.
Аналогично доказывается обратное утверждение: окружностям на сфере, не проходящим через точку , соответствуют окружности плоскости
, а окружностям, проходящим через
, — прямые.
Пример 1.28. Записать в комплексной форме уравнения: а) координатных осей; б) биссектрисы первого и третьего координатных углов.
Решение
Пример 1.29. Записать в комплексной форме уравнение:
а) дуги окружности единичного радиуса с центром в начале координат, расположенной в первой четверти;
б) биссектрисы первого координатного угла;
в) отрезка биссектрисы первого координатного угла, где
.
Решение
Пример 1.30. Определить вид кривой, заданной комплексным соотношением: a) ; б)
.
Решение
Пример 1.31. Определить вид кривой, заданной уравнением в комплексной форме:
а) ; б)
.
Решение
а) Используя правило деления , находим
. Получаем уравнение кривой в действительной форме:
, то есть
, или
.
Это уравнение окружности радиуса с центром в точке
.
б) Производим действия, как в предыдущем пункте:
В результате получено уравнение окружности радиуса с центром в точке
.
Области на комплексной плоскости
Будем рассматривать области, границы которых состоят из конечного числа кусочно-гладких кривых, в частности простых кривых, т.е. не имеющих точек самопересечения, а также отдельных изолированных точек.
Приведем аналитические выражения для областей простейшего вида, границами которых являются простейшие линии — прямые, окружности.
1. Круг радиуса с центром в точке
задается неравенством
. Это — открытое, связное множество, т.е. область. Область — ограниченная, односвязная; ее границей является окружность
(рис. 1.12,а). В частности, круг
есть окрестность точки
. Заметим, что неравенство
определяет замкнутую область, т.е. область вместе с границей.
2. Проколотая окрестность точки — круг с выброшенным центром задается неравенством
. Это двусвязная, ограниченная область, граница которой состоит из двух компонент — окружности
и точки
(рис. 1.12,б).
3. Окрестность бесконечно удаленной точки определяется как множество точек плоскости , образами которых на сфере Римана являются точки, принадлежащие окрестности точки
(см. рис. 1.12,а). Эта окрестность получается отсечением от сферы некоторой области плоскостью, перпендикулярной лучу
. Границей этой окрестности на сфере является окружность — пересечение сферы и плоскости. На плоскости
этой окружности соответствует также окружность, центр которой, очевидно, находится в точке
; ее уравнение
. Сферической окрестности точки
будет соответствовать часть плоскости, границей которой является окружность
и которая содержит бесконечно удаленную точку (образ точки
), эта область — внешность круга
(рис. 1.12,в).
4. Кольцо с центром в точке , радиус внешней окружности которого
и внутренней
, задается неравенством
(рис. 1.12,г). Это — ограниченная, двусвязная область, граница которой состоит из двух окружностей
и
.
5. Верхняя полуплоскость плоскости — множество точек, для которых
, т.е. в комплексной форме
(рис. 1.12,д); соответственно
— нижняя полуплоскость. Неравенство
определяет правую полуплоскость (рис. 1.12,е),
— левую полуплоскость. Это односвязные, неограниченные области.
Заметим, что на расширенной комплексной плоскости граница односвязной области состоит либо только из одной замкнутой кривой, либо её границей является единственная точка
(область
), или граница не содержит ни одной точки (сама расширенная плоскость
).
Замкнутая кривая на может быть неограниченной (кривая «проходит» через бесконечно удаленную точку). Например, на рис. 1.12,д границей односвязной области
является прямая
, которую рассматриваем на
как окружность радиуса
; её образом на сфере Римана является окружность (см. замечание 1.2).
Теорема Жордана
Утверждение 1.1. Простая замкнутая непрерывная кривая разбивает расширенную комплексную плоскость на две области.
Если граница — ограниченная кривая, то области называются внутренней и внешней; внутренняя — та из двух областей, которая не содержит бесконечно удаленную точку, внешняя — другая область. Так, на рис. 1.12,в область внешность круга; а множество
— внутренняя часть круга, или просто круг
Пример 1.32. Определить вид множеств, заданных соотношениями:
Решение
1) Искомым множеством является пересечение кольца и нижней полуплоскости — нижнее полукольцо (рис. 1.13,а). Это — ограниченная односвязная область.
2) Искомым множеством является пересечение круга и правой полуплоскости — правый полукруг (рис.1.13,б). Область ограниченная односвязная.
3) Определяем вид границы множеств — линий и
. Второе равенство определяет два луча
и
и, следовательно, мнимую ось. Чтобы определить вид другой линии, запишем уравнение в действительной форме, производя указанные действия с
Поэтому уравнение , то есть
, есть уравнение окружности
, а неравенство
— круг, который можно записав иначе
. Ответом является та же область, что и в предыдущем пункте (рис. 1.13,б).
Пример 1.33. Определить вид множеств, заданных неравенствами:
Решение
Для выяснения вида множества в каждом случае сначала определяем вид границы:
1) границей множества является линия , или
, то есть
. Она разбивает плоскость на две полуплоскости — верхнюю (содержит, например, точку
) и нижнюю (не содержит точку
). Условию задачи удовлетворяет верхняя полуплоскость (рис. 1.14,а). На рисунке указан обход границы и точки, принадлежащая множеству. Множество, очевидно, является односвязным и неограниченным;
2) граница области состоит из двух компонент — прямых , то есть
и
. Условие
определяет полосу на плоскости (условию удовлетворяет, например, точка
). На рис. 1.14,б указан обход границы. Множество является неограниченным односвязным;
3) граница области состоит из отрезков прямых и
. Контур прямоугольника, сторонами которого являются эти отрезки, разбивает плоскость МП два множества: внутреннюю часть и внешнюю. Условию задачи удовлетворяет, например, точка
, поэтому система
, описывает внутреннюю часть прямоугольника (рис. 1.14,в).
Пример 1.34. Записать в виде неравенств множества точек:
а) угла ; б) сектора
, если
.
Решение
Чтобы получить неравенства, определяющие эти множества, сначала составим уравнения, описывающие их границы:
а) границами множества являются лучи и
, уравнения которых i полярных координатах
и
, где
и
, то есть
и
. На комплексной плоскости уравнения этих лучей записываются в виде равенств
и
; область, ими ограниченная, — в виде неравенства
(рис. 1.15,д);
б) сектор геометрически можно рассматривать как пересечение двух множеств: угла
и круга радиуса 2 с центром в начале координат, т.е. множество точек сектора
может быть записано системой
. Это множество — ограниченная односвязная область (рис. 1.15,б).
Пример 1.35. Записать в виде неравенств множества, изображенные на рис. 1.16 (области заштрихованы, обход границ указан стрелками).
Решение
Как и в предыдущем примере, для каждого случая составим уравнение, описывающие границы множеств:
а) геометрически множество есть первый квадрант с разрезок (выброшенным лучом). Границами множества являются лучи и луч по биссектрисе от точки
в бесконечность. Уравнение этого луча можно писать в виде
.
Следовательно, множество, изображенное на рис. 1.16,а, можно описать соотношениями: для точек
, у которых
или
.
б) геометрически множество есть верхняя полуплоскость с разрезом по лучу от точки в бесконечность; уравнение луча:
Следовательно, множество, изображенное на рис. 1.16,б, можно описать соотношениями
в) на рис. 1.16,в изображена верхняя полуплоскость с «выброшенным» полукругом. Точки полукруга описываются системой
Следовательно, изображенное множество можно описать соотношениями
или
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Комплексные числа и многочлены
Скачиваний:
150
Добавлен:
18.04.2015
Размер:
527.62 Кб
Скачать
Для числа z = 1 a = 1, b = 0. Следовательно, ρ = 
|
(1.1) находим |
cos ϕ =1, |
Эта |
система имеет решение: ϕ = 0 . В итоге: |
||||||||||||||||||||||
|
sin ϕ = 0. |
|||||||||||||||||||||||||
|
1 =cos0 +isin 0 . |
|||||||||||||||||||||||||
|
Пример 15. Представить в тригонометрической форме число z = –i. |
|||||||||||||||||||||||||
|
Для него a = 0, b = –1. Следовательно, ρ = |
02 +(−1)2 =1 и система (1.1) |
||||||||||||||||||||||||
|
cosϕ = 0, |
ϕ = − |
π |
. Отсюда −i = cos(− |
π |
) +i sin(− |
π |
) . |
||||||||||||||||||
|
имеет вид: |
ϕ = −1 |
2 |
2 |
2 |
|||||||||||||||||||||
|
sin |
|||||||||||||||||||||||||
|
Пример 16. Представить в тригонометрической форме число z = –1. |
|||||||||||||||||||||||||
|
Для числа z = –1 a = –1, b = 0. Следовательно, ρ = |
(−1)2 +02 =1 и система |
||||||||||||||||||||||||
|
cosϕ |
= −1, |
ϕ = π. Получаем |
−1 = cos π+i sin π. |
||||||||||||||||||||||
|
(1.1) имеет вид |
ϕ = 0 |
||||||||||||||||||||||||
|
sin |
|||||||||||||||||||||||||
|
Пример 17. Представить в тригонометрической форме число z = 1 + i. |
|||||||||||||||||||||||||
|
Для него a = 1, b = 1. Следовательно, |
ρ = |
12 +12 = |
2 и по системе (1.1) |
||||||||||||||||||||||
|
1 |
|||||||||||||||||||||||||
|
cosϕ = |
2 |
, |
π |
. Значит, 1+i = |
2(cos |
π |
+i sin |
π |
) . |
||||||||||||||||
|
ϕ = |
4 |
4 |
|||||||||||||||||||||||
|
sin ϕ = |
1 |
4 |
|||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||
|
Пример 18. Представить в тригонометрической форме число z = –5 + 7i. |
|||||||||||||||||||||||||
|
Для него a = –5, b = 7. Следовательно, ρ = |
(−5)2 +72 = 74 |
и система |
|||||||||||||||||||||||
|
−5 |
, |
||||||||||||||||||||||||
|
cosϕ = |
74 |
||||||||||||||||||||||||
|
Решением этой системы будет |
|||||||||||||||||||||||||
|
(1.1) принимает вид |
|||||||||||||||||||||||||
|
sin ϕ = |
7 . |
||||||||||||||||||||||||
|
74 |
|||||||||||||||||||||||||
|
ϕ = π−arccos |
5 . Тогда |
||||||||||||||||||||||||
|
74 |
|||||||||||||||||||||||||
|
−5 +7i = |
74(cos(π−arccos |
5 |
) +i sin(π−arccos |
5 |
)). |
||||||||||||||||||||
|
74 |
74 |
||||||||||||||||||||||||
|
3.1.6. Умножение и деление комплексных чисел. Формула Муавра |
|||||||||||||||||||||||||
|
Пусть z = ρ1(cos ϕ+i sin ϕ); |
w = ρ2 (cos ψ +i sin ψ) . Тогда верны формулы: |
11
|
z w = ρ1 ρ2 (cos(ϕ+ψ) +isin(ϕ+ψ)) , |
|||||
|
z |
= |
ρ1 |
(cos(ϕ−ψ) +isin(ϕ−ψ)), |
(1.2) |
|
|
w |
|||||
|
ρ2 |
|||||
|
zn = ρn (cos nϕ+isin nϕ) . |
(1.3) |
Последняя формула называется формулой Муавра [1, с. 190]. Она верна для любого натурального n.
|
1+i |
3 |
20 |
|
|
Пример 19. Вычислить: |
1−i |
. |
|
Решение. Переведем числитель и знаменатель дроби из алгебраической
|
формы в тригонометрическую. |
||||||||||||||
|
Для числа z1 |
=1+i |
3 ρ = |
12 +( 3)2 = 2 , ϕ = arctg |
3 = |
π. |
|||||||||
|
1 |
3 |
|||||||||||||
|
Для числа |
z2 =1 −i |
ρ = 12 +(−1)2 = 2 , ϕ = arctg |
−1 |
= − |
π |
. Таким |
||||||||
|
π |
π |
1 |
4 |
|||||||||||
|
образом, |
z1 |
= |
2(cos |
3 |
+isin 3) |
=[поформуле(1.2)] = |
||||||||
|
z2 |
2(cos(− |
π |
π |
|||||||||||
|
4) +isin(− |
4)) |
=2(cos(127π) +isin(127π)).
Витоге:
|
20 |
2)20 |
(cos(7π 20) +i sin(7π 20)) = |
|||||||||||||||
|
z1 |
=[по формуле(1.3)] = ( |
||||||||||||||||
|
12 |
12 |
||||||||||||||||
|
z2 |
|||||||||||||||||
|
= 210 |
35π |
35π |
35π |
π |
|||||||||||||
|
(cos 3 +i sin 3 |
) =[так как |
3 |
=12π− |
3 |
] = |
||||||||||||
|
10 |
π |
π |
10 |
1 |
3 |
9 |
|||||||||||
|
= 2 |
(cos(− 3) +i sin(− |
3)) = 2 |
(2 − |
2 |
i) = 2 |
(1 |
− 3i). |
||||||||||
|
3.1.7. Задачи на построение областей на комплексной плоскости |
|||||||||||||||||
|
Пример 20. Изобразить на комплексной плоскости числа, модуль |
|||||||||||||||||
|
которых равен 1, т. е. |
z |
=1. |
|||||||||||||||
|
Решение. |
Запишем |
комплексное |
число |
в |
алгебраической |
форме |
|||||||||||
|
z = x + yi . По |
условию |
задачи |
интерес представляют те числа, |
модуль |
12
|
которых равен 1, т. |
е. |
x + yi |
=1. По определению модуля комплексного |
||
|
числа |
x2 + y2 =1. |
Возведя обе части равенства в квадрат, получим |
|||
|
x2 + y2 =1. Данное |
уравнение определяет на плоскости окружность с |
центром в точке с координатами (0; 0) и радиусом, равным 1.
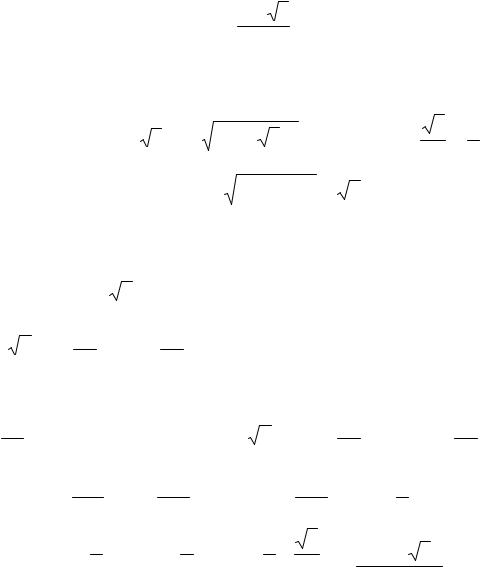
Пример 21. Найти геометрическое место точек, изображающих числа z, удовлетворяющие неравенству z −i ≤ 2.
Запишем комплексное число в общем виде z = x + yi . По условию задачи, интерес представляют те числа, модуль которых меньше или равен 2,
|
т. е. |
x + yi −i |
≤ 2. Сгруппируем под знаком модуля слагаемые, содержащие |
|||||
|
i : |
x +( y −1)i |
≤ 2 . По определению модуля комплексного числа: |
|||||
Данное уравнение определяет на плоскости круг с центром в точке с координатами (0; 1) и радиусом равным 2 (рис. 1.3).
Пример 22. Найти геометрическое место точек, изображающих числа z, удовлетворяющие неравенству Re z <1.
Re z – действительная часть числа z, неравенство можно записать как
|
x |
<1, или |
x <1 |
или −1 < x <1. Эта система определяет на плоскости |
|
|
x > −1 |
||||
полосу, ограниченную прямыми x = 1 и x = —1. Причем, обе прямые нарисованы на штрихами, так как сами прямые в искомую область не входят из-за строгого знака неравенства (рис. 1.4).
|
Y |
Y |
|||
|
3 |
||||
|
2 |
1 |
|||
|
1 |
—1 |
1 |
X |
|
|
—1 |
1 |
X |
—1 |
|
|
—1 |
||||
|
Рис. 1.3 |
Рис. 1.4 |
Пример 23. Найти геометрическое место точек, изображающих числа z,
z ≤ 2,
удовлетворяющие системе неравенств
Re z >1.
13
Как показано в примерах 20 и 21, неравенство z ≤ 2 определяет на
плоскости круг с центром в точке (0; 0) и радиусом, равным 2. Неравенство Re z >1, согласно примеру 22, определяет полуплоскость, ограниченную прямой x = 1 и находящуюся от нее справа. Так как неравенство Re z >1 строгое, то сама прямая x = 1 в область не входит и штрихами
пунктиром. Обе эти области изображены на рис. 1.5. Искомая область представляет собой пересечение двух данных областей (рис. 1.6).
|
Y |
Y |
|||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||
|
1 |
1 |
|||||||||||||||||||||
|
—2 |
—1 |
1 |
2 X |
—2 |
—1 |
1 |
2 X |
|||||||||||||||
|
—1 |
—1 |
|||||||||||||||||||||
|
—2 |
—2 |
|||||||||||||||||||||
|
Рис. 1.5 |
Рис. 1.6 |
|||||||||||||||||||||
|
Пример 24. Найти геометрическое место точек, изображающих числа z, |
||||||||||||||||||||||
|
Y |
удовлетворяющие системе неравенств |
|||||||||||||||||||||
|
2 |
z −1−i |
>1 |
||||||||||||||||||||
|
π. |
||||||||||||||||||||||
|
π |
||||||||||||||||||||||
|
1 |
≤ arg z ≤ |
|||||||||||||||||||||
|
− |
4 |
4 |
||||||||||||||||||||
|
—1 |
1 |
2 |
3 |
X |
Неравенство |
z −1−i |
>1 |
определяет |
||||||||||||||
|
—1 |
область вне круга с центром в точке (1; 1) |
и |
||||||||||||||||||||
|
—2 |
радиусом |
1. Так |
как |
неравенство |
строгое, |
то |
||||||||||||||||
|
сама окружность в |
область |
не |
входит |
и |
||||||||||||||||||
|
Рис. 1.7 |
изображена штрихами (рис. 1.7). |
14

|
Y |
Y |
||||
|
2 |
2 |
||||
|
1 |
1 |
||||
|
—1 |
1 2 |
3 X |
—1 |
1 2 |
3 X |
|
—1 |
—1 |
||||
|
—2 |
—2 |
||||
|
Рис. 1.8 |
Рис. 1.9 |
Двойное неравенство − π4 ≤ arg z ≤ π4 определяет на плоскости область, в
которую входят комплексные числа с аргументами в интервале от − π4 до π4 .
Эта область представляет собой угол (рис. 1.8).
Искомая область представляет собой пересечение двух данных областей
(рис. 1.9).
3.1.8.Извлечение корня из комплексных чисел в тригонометрической форме
Определения и утверждения к 3.1.8 можно найти в [1, с. 191-192]. Комплексное число w = n z называется корнем n-й степени из
комплексного числа z, если z = wn .
Утверждение. При любом натуральном n > 1 и любом комплексном z существует ровно n различных чисел wk , таких, что wn = z :
|
w = n ρ(cos ϕ+ 2πk |
+isin ϕ+ 2πk ), |
(1.4) |
|
|
k |
n |
n |
|
где k = 0, 1, 2, …, n – 1.
Пример 25. Вычислить 4 −1 .
Решение. Для того чтобы воспользоваться формулой (1.4), необходимо представить число, стоящее под знаком корня, в тригонометрической форме.
Для числа z = -1 найдем его модуль и аргумент: ρ = 
итоге −1 = cos π+isin π.
15
|
По формуле (1.4) w = 4 |
1(cos π+ 2πk |
+isin π+ 2πk ) . Тогда: |
|
k |
4 |
4 |
|
w |
= cos π+ 2π 0 +isin π+ 2π 0 = cos π +isin π = |
2 +i |
2 , |
||||||||||||||||||||||||||||||||||||||||||
|
0 |
4 |
4 |
4 |
4 |
2 |
2 |
|||||||||||||||||||||||||||||||||||||||
|
w |
= cos π+ 2π 1 +isin π+ 2π 1 = cos 3π +isin 3π = − |
2 +i |
2 , |
||||||||||||||||||||||||||||||||||||||||||
|
1 |
4 |
4 |
4 |
4 |
2 |
2 |
|||||||||||||||||||||||||||||||||||||||
|
w |
= cos π+ 2π 2 +isin π+ 2π 2 = cos 5π +isin 5π = − |
2 −i |
2 , |
||||||||||||||||||||||||||||||||||||||||||
|
2 |
4 |
4 |
4 |
4 |
2 |
2 |
|||||||||||||||||||||||||||||||||||||||
|
w |
= cos π+ 2π 3 +isin π+ 2π 3 = cos 7π +isin 7π = |
2 −i |
2. |
||||||||||||||||||||||||||||||||||||||||||
|
3 |
4 |
4 |
4 |
4 |
2 |
2 |
|||||||||||||||||||||||||||||||||||||||
|
Пример 26. Вычислить 5 −32i . |
|||||||||||||||||||||||||||||||||||||||||||||
|
Решение. Для числа z = −32i найдем его модуль ρ и аргумент ϕ: |
|||||||||||||||||||||||||||||||||||||||||||||
|
ρ = |
02 +322 |
= 32 , ϕ = − π, так как число z = −32i лежит на |
|||||||||||||||||||||||||||||||||||||||||||
|
2 |
−π |
−π |
|||||||||||||||||||||||||||||||||||||||||||
|
отрицательной части мнимой оси. В итоге z = −32i = 32(cos |
+i sin |
) . |
|||||||||||||||||||||||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||||||||||||||||||||||
|
−π + 2πk |
−π |
2 |
|||||||||||||||||||||||||||||||||||||||||||
|
+ 2πk |
|||||||||||||||||||||||||||||||||||||||||||||
|
По формуле (1.4) |
w = 5 32(cos |
2 |
+isin |
2 |
) , |
||||||||||||||||||||||||||||||||||||||||
|
k |
5 |
5 |
|||||||||||||||||||||||||||||||||||||||||||
|
где k = 0, 1, 2, 3, 4. Тогда: |
|||||||||||||||||||||||||||||||||||||||||||||
|
w |
= 2(cos |
−π |
+i sin |
−π |
), |
||||||||||||||||||||||||||||||||||||||||
|
0 |
10 |
10 |
|||||||||||||||||||||||||||||||||||||||||||
|
w |
= 2(cos 3π +i sin 3π), |
||||||||||||||||||||||||||||||||||||||||||||
|
1 |
10 |
10 |
|||||||||||||||||||||||||||||||||||||||||||
|
w |
= 2(cos 7π +i sin 7π), |
||||||||||||||||||||||||||||||||||||||||||||
|
2 |
10 |
10 |
|||||||||||||||||||||||||||||||||||||||||||
|
w |
= 2(cos |
11π |
+i sin |
11π |
) = 2(cos |
−9π |
+i sin |
−9π |
), |
||||||||||||||||||||||||||||||||||||
|
3 |
10 |
10 |
10 |
10 |
|||||||||||||||||||||||||||||||||||||||||
|
w |
= 2(cos15π |
+isin15π ) = 2(cos −π +isin −π ). |
|||||||||||||||||||||||||||||||||||||||||||
|
4 |
10 |
10 |
2 |
2 |
|||||||||||||||||||||||||||||||||||||||||
|
Для |
w |
и |
w |
аргументами |
будут |
−9π |
и |
−π |
, |
а |
не |
11π |
и |
15π |
|||||||||||||||||||||||||||||||
|
3 |
4 |
10 |
2 |
10 |
10 |
||||||||||||||||||||||||||||||||||||||||
соответственно, так как ϕ (−π; π].
16
|
Пример 27. Вычислить 3 − 2 + 2 |
3i . |
||||||||||||||||
|
Решение. Для числа |
z = −2 + 2 |
3i |
модуль ρ и аргумент ϕ есть: |
||||||||||||||
|
ρ = (−2)2 +(2 |
3)2 = 4 + |
124 = 16 = 4 |
, ϕ = |
2π |
|||||||||||||
|
. |
|||||||||||||||||
|
3 |
|||||||||||||||||
|
В итоге z = −2 + 2 3i = 4(cos |
2π |
+i sin |
2π |
) . По формуле (1.4) |
|||||||||||||
|
3 |
|||||||||||||||||
|
3 |
|||||||||||||||||
|
2π |
+2πk |
2π |
+2πk |
||||||||||||||
|
w |
= 3 4(cos |
3 |
+i sin |
3 |
), где k = 0, 1, 2. Тогда: |
||||||||||||
|
k |
3 |
3 |
|||||||||||||||
|
w |
= 3 4(cos 2π |
+isin 2π), |
|||||||||||||||
|
0 |
9 |
9 |
|||||||||||||||
|
w |
= 3 4(cos 2π |
+isin 2π), |
|||||||||||||||
|
0 |
9 |
9 |
|||||||||||||||
|
w |
= 3 4(cos 8π |
+isin 8π), |
|||||||||||||||
|
1 |
9 |
9 |
|||||||||||||||
|
w |
= 3 4(cos14π +isin14π) = 3 4(cos −4π +isin −4π). |
||||||||||||||||
|
2 |
9 |
9 |
9 |
9 |
|||||||||||||
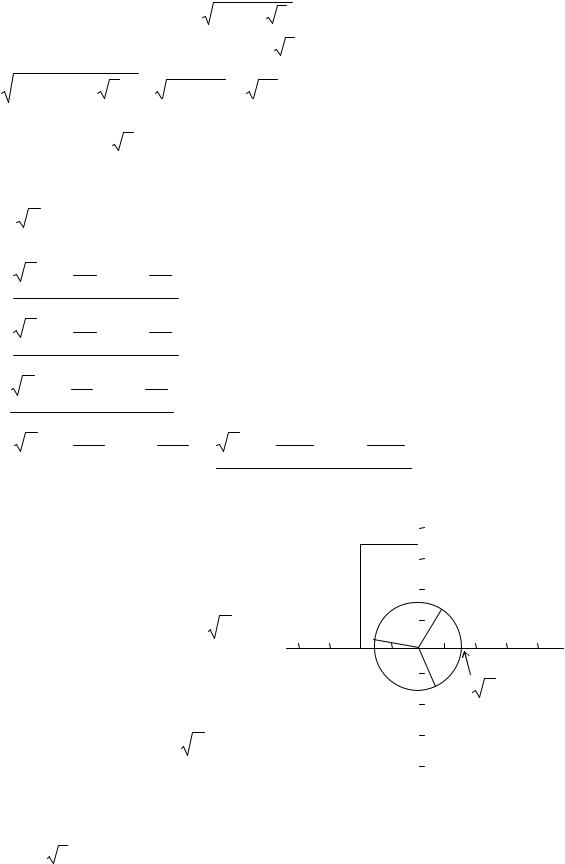
Из формулы (1.4) видно, что аргументы корней wk отличаются на одну и ту же
величину 2nπ , а модули всех
корней одинаковые и равны n ρ. Значит, на комплексной плоскости все wk лежат на окружности с центром в начале
|
координат |
и |
радиусом |
n ρ |
на |
|
одинаковом |
расстоянии |
друг |
от |
|
|
друга. |
Для |
примера |
27 |
|
|
изображения |
самого |
числа |
||
|
z = −2 + 2 |
3i |
и его корней w0 , |
w1 , |
|
Im z |
||
|
.z |
||
|
.w3 |
.w1 |
|
|
1 *2 3 4 Re z |
||
|
—4 —3 —2 —1 |
||
|
.w2 3 4 |
||
Рис. 1.10
w2 можно видеть на рис. 1.10.
17
2.МНОГОЧЛЕНЫ
2.1.Многочлены и действия над ними
Определения и утверждения к 2.1 можно найти в [1, с. 203-206].
Для действительной переменной x функция вида f (x) = axn , где a и x – действительные числа, а n – натуральное число или 0 (по-другому это можно записать как a R, n N {0}), называется одночленом с действительным коэффициентом.
Многочлен — это сумма одночленов, т.е. функция вида
|
g(x) = an xn + an−1xn−1 |
n |
|
+…+ a1x + a0 = ∑ai xi . |
|
|
i=0 |
При этом an называется старшим коэффициентом и an ≠ 0 , a0 — свободным членом, n — степенью многочлена.
Многочлен тождественно равен 0 тогда и только тогда, когда все его коэффициенты равны 0.
Если в записи многочлена нет какой-либо степени неизвестного, это значит, что коэффициент при этой степени равен 0.
На множестве многочленов определены следующие действия: 1. Сложение.
Пример 28. f (x) = 3x4 −7x2 + x −3; g(x) = 2x3 +5x2 +3x − 2 . Найти f (x) + g(x) .
f (x) + g(x) =3x4 + 2x3 +(−7 +5)x2 +(1+3)x +(−3 +(−2)) =
=3x4 + 2x3 −2x2 + 4x −5.
2.Умножение.
Пример 29. f (x) = 2x2 − x +1; g(x) = 3x −1. Найти f (x) g(x) . f (x) g(x) = (2x2 − x +1)(3x −1) =
=2x2 3x +(−x) 3x +1 3x + 2x2 (−1) +(−x) (−1) +1 (−1) =
=6x3 −3x2 +3x −2x2 + x −1 = 6x3 −5x2 + 4x −1.
|
3. Деление с остатком. |
|||||||
|
Разделить |
f (x) на |
g(x) |
— |
значит записать |
f (x) |
в виде |
|
|
f (x) = g(x)q(x) + r(x), |
или |
f (x) |
= q(x) + |
r(x) |
. Последняя |
запись |
|
|
g(x) |
g(x) |
||||||
18
аналогична записи для чисел: 173 = 5 + 23 , или 17 = 5 3 + 2.
Теорема (о делении с остатком) [1, с. 206]. Для любых многочленов
|
f (x) |
и g(x) ≠ 0 существуют, и притом единственные, |
многочлены q(x) и |
|
r(x) , такие, что |
||
|
f (x) = g(x) q(x) + r(x) . |
(2.1) |
|
|
При |
этом степень r(x) меньше степени g(x) , q(x) — |
неполное частное, |
|
r(x) |
— остаток. Разделить f (x) на g(x) — значит записать |
f (x) в виде (2.1). |
Для практического нахождения частного и остатка существует метод деления «уголком».
Пример 30. Выполнить «уголком» деление с остатком: f (x) = x3 −3x2 − x −1 на g(x) = x2 − 2x +1.
Решение. Запишем делимое f (x) и делитель g(x) как при делении многозначных чисел:
x3 −3x2 − x −1 x2 − 2x +1
Находим частное от деления старшего члена делимого на старший член
делителя ( x3 / x2 = x ) и записываем результат в графу частного: x3 −3x2 − x −1 x2 − 2x +1
x
Умножаем делитель на результат деления и записываем под делимым:
|
x3 −3x2 − x −1 x2 − 2x +1 |
|
|
x3 − 2x2 + x |
x |
Вычитаем из делимого результат умножения:
|
x3 −3x2 − x −1 |
x2 − 2x +1 |
||
|
x3 −2x2 + x |
x |
||
|
− x2 − 2x −1 |
Проверяем степень получившегося в результате вычитания многочлена. Если она меньше степени делителя, то процесс деления закончен, и полученный многочлен является остатком. В противном случае деление продолжается аналогично описанному ранее:
19

|
x3 −3x2 − x −1 x2 − 2x +1 |
|
|
x3 − 2x2 + x |
x — 1 |
−x2 − 2x −1
−x2 + 2x −1
—4x
Так как степень полученного многочлена меньше степени делителя, то процесс деления закончен. В результате: q(x) = x – 1– неполное частное, а
r(x) = –4x – остаток.
Ответ: x3 −3x2 − x −1 = (x2 −2x +1)(x −1) +(−4x) , или
|
x3 −3x2 − x −1 |
= x −1 |
− |
4x |
. |
||
|
x2 |
−2x +1 |
x2 |
−2x +1 |
|||
Пример 31. Выполнить деление с остатком: 3x5 +1 на x2 −1. Решение. Запишем делимое и делитель как при делении многозначных
чисел. Если в записи многочлена отсутствует одна или несколько степеней, то при записи, для удобства вычислений, следует на их места записать нули:
|
3x5 + 0x4 + 0x3 + 0x2 + 0x +1 |
x2 −1 |
|||
|
3x5 |
−3x3 |
3x3 +3x |
||
|
3x3 + 0x2 + 0x |
||||
|
3x3 |
−3x |
3x +1
Получившиеся в результате умножения многочлены удобнее записывать, располагая слагаемые в соответствии с их степенями. Так как степень полученного многочлена меньше степени делителя, то процесс деления
|
закончен. В результате: q(x) =3x3 +3x – неполное частное, а r(x) = 3x + 1 |
– |
|
|
остаток. |
||
|
Ответ: 3x5 +1 = (x2 −1)(3x3 +3x) + (3x +1) , или 3x5 +1 = 3x3 +3x + 3x +1 . |
||
|
x2 −1 |
x2 −1 |
|
|
Пример 32. Делится ли нацело многочлен |
x4 + 4x3 − 2x −8 на |
|
|
многочлен x3 − 2 ? |
Решение. Разделим один многочлен на другой «уголком».
20
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
Положим $%z=x+iy$%, где $%x,yinmathbb R$%. Тогда $%iz-1=-1-y+ix$%. Аргумент принимает значение $%pi/3$% для чисел первой координатной четверти, у которых отношение мнимой части к действительной равно $%sqrt3$%. Отсюда $%x > 0$%, $%x=-sqrt3(1+y)$%.
Рисуем график прямой $%y=-frac1{sqrt3}x-1$% для значений $%x > 0$%, что даёт открытый луч. Это и будет искомое ГМТ.







