Как найти гипотенузу в эксель - Исправление недочетов и поиск решений вместе с Examum.ru

Резюме

Чтобы вычислить самую длинную сторону (гипотенузу) прямоугольного треугольника в Excel, вы можете использовать формулу, основанную на теореме Пифагора, адаптированную для использования математических операторов и функций Excel. В показанном примере формула в D5, скопированная ниже, имеет следующий вид:

=SQRT(B5^2+C5^2)

который возвращает длину гипотенузы с учетом длины стороны a и стороны b, указанной в столбцах B и C соответственно.

Объяснение

Теорема Пифагора — ключевой принцип евклидовой геометрии. В нем говорится, что квадрат самой длинной стороны прямоугольного треугольника (гипотенуза) равен сумме квадратов двух других сторон. Теорема записывается в виде следующего уравнения:

а ² + Ь ² = с ²

Когда известны любые две стороны, это уравнение можно использовать для решения третьей стороны. Когда a и b известны, длину гипотенузы можно вычислить с помощью:

Когда известны b и c, длину стороны a можно рассчитать с помощью:

Когда a и c известны, длину стороны b можно рассчитать с помощью:

Чтобы перевести приведенное выше в синтаксис формулы Excel, используйте оператор возведения в степень (^) и функцию КОРЕНЬ, как показано ниже. Теорема Пифагора может быть записана как:

=a^2+b^2=c^2 // pythagorean theorem

Приведенные ниже формулы можно использовать для решения каждой из трех сторон:

c=SQRT(a^2+b^2) // hypotenuse a=SQRT(c^2-b^2) // side a b=SQRT(c^2-a^2) // side b

Вместо оператора возведения в степень вы также можете использовать функцию POWER следующим образом:

c=SQRT(POWER(a,2)+POWER(b,2)) a=SQRT(POWER(c,2)-POWER(b,2)) b=SQRT(POWER(c,2)-POWER(a,2))

Приведенные выше формулы являются примером вложения одной функции в другую.

Источник

Любой треугольник имеет шесть элементов: три стороны и три угла. На рисунке ниже показан прямоугольный треугольник, который имеет три угла (А, В и С), а также три стороны (гипотенузу, основание и высоту). Угол С всегда равен 90° (или π/2 радиан), поэтому, если известны два других элемента этого треугольника (исключая угол С), то с помощью определенных формул всегда можно вычислить остальные элементы.

Рабочую книгу, содержащую формулы расчета различных элементов прямоугольного треугольника по двум известным элементам, можно скачать с нашего сайта.
[lock]

скачать бесплатно

[/lock]

Рис. 1. Элементы прямоугольного треугольника

Вспомните, как выглядит теорема Пифагора: Высота^2+Основание^2=Гипотенуза^2. Если известны две стороны прямоугольного треугольника, всегда можно вычислить третью. Например, следующая формула вычисляет высоту прямоугольного треугольника по данным длин гипотенузы и основания: =КОРЕНЬ(Гипотенуза^2-Основание^2). В другой формуле, вычисляющей основание прямоугольного треугольника, используются
гипотенуза и высота: =КОРЕНЬ((Гипотенуза^2)-(Высота^2)). Для формулы расчета гипотенузы прямоугольного треугольника нужно задать основание и высоту: =КОРЕНЬ((Высота^2)+(Основание^2)).

Верны также приведенные ниже тригонометрические тождества:

SIN(А) = Высота/Гипотенуза
SIN(В) = Основание/Гипотенуза
COS(А) = Основание/Гипотенуза
COS(В) = Высота/Гипотенуза
TAN(А) = Высота/Гипотенуза

Все тригонометрические функции Excel подразумевают, что угол, являющийся аргументом функции, представлен в радианах. Для преобразования градусов в радианы используйте функцию РАДИАНЫ. Для обратного преобразования радиан в градусы примените функцию ГРАДУСЫ.

Если известны высота и основание, следующую формулу можно использовать для вычисления угла между гипотенузой и основанием (угол А): =ATAN(Высота/Основание). Формула, приведенная выше, возвращает значение угла в радианах. Для преобразования значения в градусы используйте следующую формулу: =ГРАДУСЫ(ATAN(Высота/Основание)). Если известны высота и основание, следующая формула может использоваться для вычисления угла между гипотенузой и высотой (угол В): =ПИ()/2-ATAN(Высота/Основание). Данная формула возвращает значение в радианах. Для преобразования значения в градусы используйте следующую формулу: =90-ГРАДУСЫ(ATAN(Высота/Основание).

На рис. 2 показана рабочая книга, которая содержит формулы для вычисления различных элементов прямоугольного треугольника.

Рис. 2. Данная рабочая книга пригодится для вычисления элементов прямоугольных треугольников

Источник

Основные
сведения

Одной из возможностей VBA
является создание новой функции MS
Excel,
которую впоследствии
можно использовать аналогично встроенным
функциям
(СУММ,
МАКС,
ЕСЛИ
и
др.).
Это
целесообразно
в
тех
случаях,
если
необходимой
функции
нет
в
стандартном
наборе
встроенных
функций
MS
Excel,
например формулы
Пифагора, а ей приходится часто
пользоваться.

Пример 1

Создадим пользовательскую
функцию, вычисляющую по формуле
Пифагора длину
гипотенузы прямоугольного
треугольника.

Для
этого:

Откроем
MS
Excel
и перейдем в редактор VB,
выполнив команду
Сервис

Макрос
Редактор
Visual
Basic
либо
нажав кнопку «Редактор
Visual
Basic»
на панели инструментов Visual
Basic.

В
новом
модуле
(Insert
Module)
через
команду
Insert
Procedure
зададим
имя
и
остальные
параметры
новой
функции
(рис.
11).
Нажмем
кнопку
«ОК».
В
окне кода между двумя
появившимися
строчками
напишем программный код
для
данной
функции, учитывая, что для
нахождения
длины гипотенузы по формуле
Пифагора
нужно знать значения двух
катетов:

Public Function Пифагор
(a As Single, b As
Single)
‘аргументы
а и b
вещественные

Пифагор
= Sqr(a ^ 2 + b ^
2)

End
Function

Закроем
редактор VB
и воспользуемся
нашей
функцией.
В
ячейки А1, В1 и С1 введем
соответственно
символы
а, b,
и с; в ячейки А2 и В2 –
значения

Рис.11.
Диалоговое
окно

Add Procedure

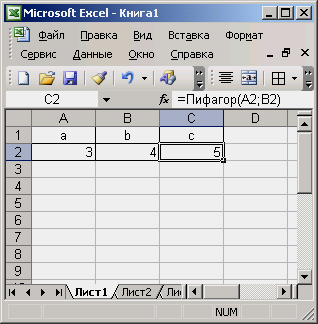
катетов (3 и 4), а в ячейку С2
вставим формулу, воспользовавшись
кнопкой

«fB_xB»
на
панели
инструментов
либо
командой
Вставка
Функция
и
выбрав
созданную функцию в категории «Определенные
пользователем»
диалогового окна Мастер
функций (рис.
12 и
13).

Рис.
12.
Диалоговое окно Мастер
функций Рис.
13. Результат
выполнения
функции

Добавим к вновь созданной
функции описание, поясняющее
ее
назначение.
Для этого выполним команду
Вид Макросы
Макросы
и, набрав
в поле
Имя
макроса
диалогового
окна
Макрос
название
данной
функции
(рис.
14),
введем описание,
нажав кнопку «Параметры»
(рис.
15).

Рис.14.
Диалоговое окно Макрос
Рис.15.
Диалоговое окно Параметры
макроса

Пример 2

Создадим функцию пользователя,
математически определенную
как

y
sin(x)e^²^xи
построим ее
график.

Для этого в редакторе VB
MS Excel в
новом модуле через команду
Insert

Procedure создадим
функцию с именем «Y»
и напишем для нее
программный
код:

Public
Function Y (x As
Single)

Y
= Sin(Application.Pi() * x) * Exp(-2 *
x)
End
Function

Здесь мы воспользовались
стандартной функцией Pi(),
которая возвращает
значение постоянной
(в
Excel – функция
пи()). Так
как она не является
внутренней функцией
VBA, то
ее необходимо записать в виде
Application.Pi().

Теперь проверим работу
созданной функции и построим ее
график:

Введем
в
ячейки
А1
и
В1
соответственно
«х»
и
«y»,
в
ячейки
А2
и
А3
–
значения х,
например -0,5 и -0,4 соответственно, и с
помощью маркера
заполнения
скопируем значения в ячейки
А4:А12.
В
ячейку
В2
вставим
формулу
«=Y(A2)»
и
также
с
помощью
маркера
заполнения
скопируем ее в ячейки В3:В12 (рис.
16).
Выделим
диапазон ячеек В2:В12 и с помощью Мастера
диаграмм
построим
график данной функции (рис.
16).

Рис.
16. Результат выполнения созданной
функции и ее
график

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

0 / 0 / 0

Регистрация: 03.11.2022

Сообщений: 11

Excel

08.12.2022, 18:48. Показов 748. Ответов 4

Добрый вечер друзья, помогите, пожалуйста, написать эту задачу в VBA

1.Даны длина катета, найти длину гипотенузы
2.Найти количество дней между датами.
3.Написать функцию, вставляющую подстрока в строку с заданной позицией.

за ранее благодарю

АЕ

ᴁ®

3116 / 1776 / 370

Регистрация: 13.12.2016

Сообщений: 6,078

Записей в блоге: 4

08.12.2022, 20:04

Сообщение было отмечено Medellin как решение

Решение

Medellin, обработку ошибок, проверки и красивости не делал. т.к. задание учебное.

Visual Basic

Public Sub med1()
Dim k1 As Double, k2
k1 = InputBox("Длина катета")
k2 = InputBox("Еще Длина катета")
x = Sqr(k1 * k1 + k2 * k2)
MsgBox "Длина гипотенузы = " & x, vbInformation
End Sub
 
Public Sub med2()
Dim k1 As Variant, k2
k1 = InputBox("Первая дата")
k2 = InputBox("Вторая дата")
x = DateDiff("d", k1, k2)
MsgBox "дней между датами = " & Abs(x), vbInformation
End Sub
 
Public Sub med3()
Dim k1 As Variant, k2, p
k1 = InputBox("Первая строка")
k2 = InputBox("Вторая строка")
p = InputBox("позиция")
x = Left(k1, p) & k2 & Right(k1, Len(k1) - p)
MsgBox "вставляющую подстрока в строку с заданной позицией = " & x, vbInformation
End Sub

Angry Old Man

1540 / 414 / 181

Регистрация: 26.03.2022

Сообщений: 775

08.12.2022, 20:41

Задание учебное, ввод данных во избежание ошибок и необходимости контроля правильности не делал. Если надо, можете разбить код на 3 отдельные процедуры.

Visual Basic

Option Explicit
Sub Medellin()
 
Const Cathet1 As Double = 5
Const Cathet2 As Double = 8.66
Dim Hypotenuse As Double
Hypotenuse = Sqr(Cathet1 ^ 2 + Cathet2 ^ 2)
MsgBox "Катет 1 =" + vbTab + vbTab + Format(Cathet1, "0.00") + vbCr + _
        "Катет 2 =" + vbTab + vbTab + Format(Cathet2, "0.00") + vbCr + _
        "Гипотенуза =" + vbTab + Format(Hypotenuse, "0.00"), 64, "Задача 1"
 
Const Date1 As Date = "28.02.2021"
Const Date2 As Date = "28.02.2022"
Dim Days As Long
Days = CLng(Date2 - Date1)
MsgBox "Дата 1 =" + vbTab + vbTab + CStr(Date1) + vbCr + _
        "Дата 2 =" + vbTab + vbTab + CStr(Date1) + vbCr + _
        "Дата2-Дата1(дней)=" + vbTab + CStr(Days), 64, "Задача 2"
 
Const Str1 As String = "1234567890"
Const Str2 As String = "abcdefgh"
Const N As Integer = 5
Dim NewStr As String
NewStr = InsertIn(Str1, Str2, N)
MsgBox "Строка1 =" + vbTab + """" + Str1 + """" + vbCr + _
        "Строка2 =" + vbTab + """" + Str2 + """" + vbCr + _
        "Новая строка =" + vbTab + """" + NewStr + """", 0, "Задача 3"
 
End Sub
 
Function InsertIn(s1 As String, s2 As String, i As Integer) As String
    InsertIn = Mid(s1, 1, i) + s2 + Mid(s1, i + 1)
End Function

0 / 0 / 0

Регистрация: 03.11.2022

Сообщений: 11

08.12.2022, 20:59

[ТС]

это получается нужно в UserForm прописать?…

ᴁ®

3116 / 1776 / 370

Регистрация: 13.12.2016

Сообщений: 6,078

Записей в блоге: 4

08.12.2022, 22:44

Сообщение от Medellin

это получается нужно в UserForm прописать?…

По крайней мере мой код никуда прописывать не надо. Сам спросит что вводить и даст ответ.
Ну а у коллеги код и спрашивать не будет. Он в коде все переменные определил для чего-то.
Когда просят для UserForm, то обычно говорят об этом. А я сделал именно то, что попросили, вплоть до грамматики.

IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604	08.12.2022, 22:44
5

Источник

теорема Пифагора

Объяснение

Когда известны b и c, длину стороны a можно рассчитать с помощью:

Когда a и c известны, длину стороны b можно рассчитать с помощью:

Приведенные ниже формулы можно использовать для решения каждой из трех сторон:

Вместо оператора возведения в степень вы также можете использовать функцию POWER следующим образом:

Приведенные выше формулы являются примером вложения одной функции в другую.

Как сделать таблицу пифагора в excel одной формулой

Создать таблицу умножения чисел от 1 до 9 (9 строк, 9 столбцов). В ячейке, соответствующей произведению 1*1, должна быть записана формула, которая затем должна быть скопирована во все остальные 80 ячеек. Решение в двух вариантах:

1)с использованием смешанных ссылок;

2)с использованием формулы массивов.

Метод 1. С использованием смешанных ссылок.

Составим таблицу. Введем по столбцам цифры от 1 до 9 и по строкам.
В ячейку В2 введем формулу: =$A2*Bкопируем эту ячейку во все остальные ячейки диапазона В2:J10. Получим таблицу умножения:

Метод 2. С использованием формулы массивов.

В ячейки В2:J2 введем цифры от1 до 9 и в ячейки А14:А22.
Выделим ячейки В14:J22 и введем формулу =B13:J13*A14:A22. Нажмем Ctrl+shift+Enter, чтобы формула вставилась как формула массива. Получим:

Excel: Абсолютные и относительные ссылки. Таблица Пифагора

Сегодняшняя статья для новичков. Помнится, не так давно на глаза попалась «экселевская» шутка, про то, что если ты не знаешь, чем $A$1 отличается от A1, то нам не о чем с тобой разговаривать. Но нам всегда есть о чём поговорить с нашими читателями и тем более о таком базовом вопросе, как абсолютные и относительные ссылки в Excel.

Итак, чем же эти ссылки отличаются одна от другой? Относительная ссылка в формуле вида A1 – это адресация на ячейку, которая удалена от ячейки с формулой на определённое расстояние. Поэтому, при протягивании формулы в сторону, она будет ссылаться на то же самое расстояние, а не на определённую ячейку. Например, если формулу протянуть вправо на одну ячейку, то она уже будет ссылаться не на A1, а на B1. Если вместо этого мы протянем формулу вниз, то ссылка окажется не на A1, а на A2. Таким образом, ссылки собьются и формула выдаст неправильный результат.

Если же мы вместо ссылки на ячейку A1, проставим $A$1, то куда бы мы не сдвигали формулу и на какое бы количество ячеек, формула всё равно будет ссылаться именно на ячейку A1. Сделать такую ссылку можно во время выбора ячейки в формуле, нажав клавишу F4.

Кроме жёсткой привязки к определённой ячейке может быть смешанная ссылка вида $A1 (фиксация столбца) или A$1 (фиксация строки). Это также достигается нажатием клавиши F4 два или три раза, пока знак $ не появится в нужном месте. Что это значит? При фиксации столбца $A1 во время сдвига формулы в сторону не будет происходить изменений. Ссылка будет изменяться только при движении по столбцу, то есть при протягивании формулы вверх или вниз. Соответственно, с учётом того, что ссылка идёт на ячейку A1, то при протягивании вверх, будет выдаваться ошибка #ССЫЛКА! (потому что выше A1 ячеек нет), а при протягивании формулы вниз, ссылка на ячейку примет вид $A2.

При создании ссылки вида A$1, будет зафиксирована строка, в результате, при протягивании формулы вверх или вниз, изменений в адресации ячейки не будет. При протягивании формулы влево будет выдаваться ошибка #ССЫЛКА! (слева от A1 нет ячеек), при протягивании формулы вправо, ссылка примет вид B$1 и выдаст значение из этой ячейки. Наглядным примером использования разной адресации ячеек служит таблица Пифагора. Если кто-то не помнит – это таблица умножения в шахматном виде, где перекрёстно перемножаются цифры из верхней строки (от 1 до 10) и из левого столбца (от 1 до 10).

Соответственно, мы получаем значения от 1 до 100. Если мы в ячейку B2 введём формулу =A2*B1 и протянем строки и столбцы, то формула будет считать неправильно, или, верней сказать, выдаст не те значения, которые нам нужны, так как, если вы помните, формула будет перемножать данные на определённом расстоянии от себя.

Если мы поставим формулу с жёсткой фиксацией (абсолютная адресация), то также не получим нужный результат. Формула просто скопирует одно и то же значение.

Лишь вводя смешанную адресацию, фиксируя левый столбец и верхнюю строку, мы получим правильный результат.

Наглядно ещё раз этот пример нам поможет проиллюстрировать короткое видео.

Рабочую книгу, содержащую формулы расчета различных элементов прямоугольного треугольника по двум известным элементам, можно скачать с нашего сайта.
[lock] скачать бесплатно [/lock]

Рис. 1. Элементы прямоугольного треугольника

Вспомните, как выглядит теорема Пифагора: Высота^2+Основание^2=Гипотенуза^2. Если известны две стороны прямоугольного треугольника, всегда можно вычислить третью. Например, следующая формула вычисляет высоту прямоугольного треугольника по данным длин гипотенузы и основания: =КОРЕНЬ(Гипотенуза^2-Основание^2) . В другой формуле, вычисляющей основание прямоугольного треугольника, используются
гипотенуза и высота: =КОРЕНЬ((Гипотенуза^2)-(Высота^2)) . Для формулы расчета гипотенузы прямоугольного треугольника нужно задать основание и высоту: =КОРЕНЬ((Высота^2)+(Основание^2)) .

Верны также приведенные ниже тригонометрические тождества:

SIN(А) = Высота/Гипотенуза
SIN(В) = Основание/Гипотенуза
COS(А) = Основание/Гипотенуза
COS(В) = Высота/Гипотенуза
TAN(А) = Высота/Гипотенуза

Если известны высота и основание, следующую формулу можно использовать для вычисления угла между гипотенузой и основанием (угол А): =ATAN(Высота/Основание) . Формула, приведенная выше, возвращает значение угла в радианах. Для преобразования значения в градусы используйте следующую формулу: =ГРАДУСЫ(ATAN(Высота/Основание)) . Если известны высота и основание, следующая формула может использоваться для вычисления угла между гипотенузой и высотой (угол В): =ПИ()/2-ATAN(Высота/Основание) . Данная формула возвращает значение в радианах. Для преобразования значения в градусы используйте следующую формулу: =90-ГРАДУСЫ(ATAN(Высота/Основание) .

Рис. 2. Данная рабочая книга пригодится для вычисления элементов прямоугольных треугольников

Источник