Как найти гистограмму пример

Гистограмма – очень полезный инструмент, с помощью которого можно сделать демонстрируемую информацию более наглядной и простой для восприятия. Это особенно актуально, когда время на изучение данных в таблице ограничено, и нужно в сжатые сроки сформировать целостное представление о них. Давайте посмотрим, каким образом можно построить гистограмму в Эксель.

Строим гистограмму

Для выполнения поставленной задачи в Excel можно воспользоваться разными методами:

• использовать инструменты на ленте программы;
• воспользоваться надстройкой “Пакет анализа”;
• применить условное форматирование.

Ниже мы подробнее остановимся на каждом из этих пунктов.

Метод 1: используем инструменты на ленте программы

Это, пожалуй, самый простой способ. И вот, как он реализуется:

1. Открываем (или создаем) таблицу. Выделяем любым удобным способом (например, с помощью зажатой левой кнопки мыши) ячейки, на базе которых планируется построить диаграмму.
2. Переходим во вкладку “Вставка”, в группе инструментов “Диаграммы” жмем кнопку “Вставить гистограмму”.
3. Раскроется перечень возможных вариантов:
   • гистограмма;
   • объемная гистограмма;
   • линейчатая;
   • объемная линейчатая.
4. После клика по нужному (понравившемуся) варианту, на листе появится гистограмма. В нашем случае мы выбрали самую простую.

Гистограмма с накоплением
До того, как приступить к созданию гистограммы с накоплением, проверяем, чтобы самая верхняя левая ячейка таблицы была пустой.
Затем делаем следующее:

1. Выполняем выделение таблицы, на базе которой планируем построить гистограмму. Переходим во вкладку “Вставка”, нажимаем кнопку “Вставить гистограмму” (группа “Диаграммы”) и в раскрывшемся перечне останавливаем на варианте – “Гистограмма с накоплением”.
2. Гистограмма вставлена, что и требовалось.

Примечание: в гистограммах с накоплением один столбец содержит сразу несколько значений. В нашем случае – это данные по всем четырем торговым точкам за конкретную дату.

Нормированная гистограмма с накоплением
В данном случае отображается (в процентном выражении) вклад каждого значения в общем количестве.

Метод 2: пользуемся надстройкой “Пакета “анализа”

Для начала нужно включить данный пакет.

1. Идем в меню “Файл”.
2. В перечне слева в самом низу щелкаем по пункту “Параметры”.
3. В открывшемся окне выбираем “Надстройки”. В правой части окна для параметра “Управление” ставим значение “Надстройки Excel”, после чего жмем кнопку “Перейти”.
4. В появившемся окошке ставим галочку напротив надстройки “Пакет анализа” и жмем OK.
5. Перейдя во вкладку “Данные” в группе инструментов “Анализ” нажимаем кнопку “Анализ данных”.
6. Откроется окошко, в котором нам нужен пункт “Гистограмма“, после выбора которого щелкаем OK.
7. Перед нами появится окно, в котором нужно выполнить настройки гистограммы:
   • в поле “Входной интервал” указываем диапазон ячеек, по которым нужно построить гистограмму. Сделать это можно вручную, прописав адреса с помощью клавиш на клавиатуре. Также мы можем выделить нужный диапазон ячеек в самой таблице, предварительно установив курсор в поле для ввода информации.
   • внизу окна ставим галочку напротив параметра “Вывод графика”.
   • в группе параметров вывода можно указать, куда следует вставить созданную гистограмму. Стандартное значение – на новом листе.
   • по готовности жмем кнопку OK.
8. Гистограмма сформирована и добавлена на отдельном листе, как мы и хотели.

Метод 3: выполняем условное форматирование с гистограммой

Получить гистограмму можно и с помощью условного форматирования ячеек. План действий следующий:

1. Для начала нужно выделить элементы, которые нужны для гистограммы.
2. Находясь в главной вкладке в группе “Стили” щелкаем по кнопке “Условное форматирование”. Откроется список, в котором выбираем “Гистограмму”. Раскроется еще один перечень, где нужно определиться с вариантами заливки – градиентная или сплошная.
3. В выделенных ячейках появились гистограммы, соответствующие их значениям. В нашем случае была выбрана сплошная заливка синим цветом.

Редактирование гистограммы

Вставленную на лист гистограмму можно изменить:

1. Корректируем или удаляем название. Для активации режима редактирования щелкаем по названию, после чего вокруг него появится рамка. Теперь кликаем в любом месте внутри рамки и мы можем приступать к редактированию.
2. Удаляем легенду (если она не нужна). Предварительно нужно ее выбрать. Первым кликом выделяем все легенды (если их несколько), вторым – конкретную легенду. Удалить легенду можно через контекстное меню, вызываемое щелчком правой кнопки мыши по ней или просто нажав клавишу Del на клавиатуре.
3. Меняем положение названия гистограммы и легенды. Для этого кликаем по выбранному объекту, чтобы выделить его. Затем наводим указатель мыши на любую из появившихся границ, и когда появится характерный символ в виде стрелок в четыре стороны, зажав левую кнопку мыши перетаскиваем объект в новое место.
4. Меняем размер и положение гистограммы. Чтобы изменить размер гистограммы, зажав левую кнопку мыши тянем за одну из точек, расположенных на рамке вокруг нее.Для изменения положения выполняем те же самые действия, что и в отношении названия или легенды.
5. Для более детальных настроек щелкаем по любой свободной части в области диаграммы (белые участки) и в открывшемся контекстном меню выбираем пункт “Формат области диаграммы”.Появится вспомогательное окно, в котором мы можем настроить:
   • заливку и границы;
   • добавить различные эффекты;
   • размеры и свойства;
   • параметры текста.
6. Настраиваем шкалы по осям X и Y. Щелкаем по подписям выбранной шкалы правой кнопкой мыши и в открывшемся контекстном меню выбираем “Формат оси”.Откроется окно, в котором мы можем выполнить соответствующие настройки.

Помимо вышеперечисленного, на ленте программы во вкладке “Конструктор”, в которой мы окажемся автоматическим после создания гистограммы, мы можем сменить стиль, выбрать один из экспресс-макетов и т.д.

Также, мы можем добавить новый элемент диаграммы, щелкнув на соответствующий значок в левом верхнем углу ленты и выбрав из списка нужный пункт.

Примечание: возможных настроек и параметров, которые можно задать для гистограммы достаточно много, и каждый пользователь сможет подобрать для себя оптимальный вариант. Мы описали лишь часть основных действий и инструментов, которые могут помочь в этом.

Заключение

Программа Excel позволяет построить различные гистограммы, которые помогают лучше и быстрее освоить информацию, особенно, когда ее слишком много, а времени, наоборот, мало. Выбор конкретного вида и метода построения диаграммы зависит от того, какие цели преследует пользователь, и каким он видит конечный результат.

Для
наглядности строят различные графики
статистического распределения, например,
гистограмму.

Гистограмма
частот — ступенчатая фигура, состоящая
из прямоугольников, основаниями которых
служат интервалы длиной h, а высота
которых равны отношению n_i/h, где
все наблюдаемые значения разбивают на
несколько интервалов длиною h и находят
значение n_i как сумму частот тех
вариант, которые попали в i-интервал.

Для
построения гистограммы частот на оси
абсцисс откладывают интервалы, а высота
каждого столбика равна n_i/h.

Площадь
i-прямоугольника равна = (n_i/h)
·
h , т. е.
сумме частот тех значений, которые
попали в этот i-интервал.

n_i/h
h

Площадь
всей гистограммы равна количеству
выборки n (сумме всех частот n_i)

Пример:
построить гистограмму частот распределения:
в 1м столбце указан интервал, а во 2м —
сумма частот вариант:

Строим
еще одну колонку, в которой укажем
высоту. Как написано выше, высота у нас
равна n_i/h,
и то, и другое нам известно. Интервал
(h) равен 3 (это можно проследить: 2-5=3,
8-5=3, 11-8=3 и т. д.). Итак, строим:

Посчитаем
сумму частот (это будет площадь
гистограммы):

складываем
все n_i =
9+10+25+6= 50

Строим
гистограмму:

8

,3

3,3

3

2

2
5 8 11 14

Ось х — интервалы.

Ось
у — высота (тот столбик, который мы
рассчитывали сами)

30. Свойства статистических оценок параметров распределения: несмещённость, эффективность, состоятельность.

Пусть
требуется изучить количественный
признак ГС. В распоряжении исследователя
имеется выборка объемом n
этого количественного признака

;

; … ;

Рассматривая
эти наблюдения как независимые случайные
величины

;

; … ;

можно сказать, что найти СТАТИСТИЧЕСКУЮ
ОЦЕНКУ НЕИЗВЕСТНОГО ПАРАМЕТРА это
значит найти функцию от наблюдаемых
значений, которая и дает приближенное
значение оцениваемого параметра.

Для
того, чтобы статистические оценки давали
хорошие приближения оцениваемых
параметров, они должны удовлетворять
некоторым требованиям.

Пусть


— статистическая оценка неизвестного
параметра

(«тета»)

1. ОПР
   – НЕСМЕЩЁННОЙ называют статистическую
   оценку
   
   математическое ожидание которой равно
   оцениваемому параметру при любом объеме
   выборки т.е.
   

   ОПР
   – СМЕЩЁННОЙ называют оценку, математическое
   ожидание которой не равно оцениваемому
   параметру.

Оценка
должна быть несмещенной.

1. ОПР
   – ЭФФЕКТИВНОЙ называют статистическую
   оценку, которая имеет наименьшую
   возможную дисперсию (при заданном
   объеме выборки n)

2. ОПР
   – СОСТОЯТЕЛЬНОЙ называют статистическую
   оценку, которая при
   
   стремится к оцениваемому параметру.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Была ли эта статья полезной?

Гистограмма и ящик с усами на пальцах

В этой заметке я хочу описать два типа графиков для одномерных данных, а именно

• гистограмма
• ящик с усами

Рассмотрим произвольную выборку вещественных чисел , будем обозначать порядковую статистику , такую что .

Гистограмма

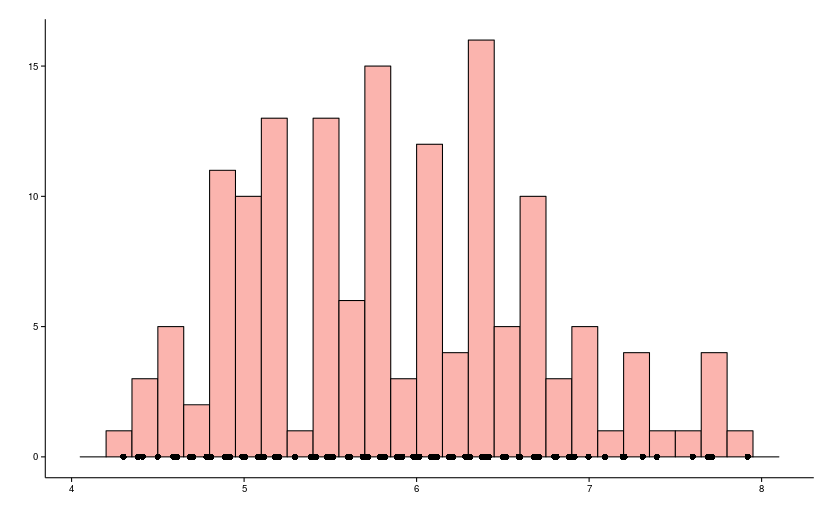
Скорее всего все поменять этот тип графика из школьной или университетской программы, который выглядит приблизительно так как на картинке.

Прежде всего необходимо помнить, что значения входной выборки располагаются по оси x, а по оси y располагается число раз, которое данное значение встретилось (назовем их отсчеты). Гистограмма позволяет огрубить и сделать набор данных более компактным, при этом не умаляя его специфичность.
Важными характеристиками гистограммы являются следующие:

• число столбцов (которые называются bins или bars)
• абсолютные или плотностные отсчеты по оси y
• как сгруппированы данные

Столбцы

В подавляющем большинстве случаев гистограмма определена на отрезке , где — исходная выборка, вспомогательные константы, округляющие до ближайших “читаемых” чисел, которые в каждом случае зависят от масштаба и, обычно, это делители десятки в масштабе исходных данных. Если вдруг стало интересно, как ставить отсечки в данных, то можно посмотреть ссылку: R (pretty).

Так же обычно гистограммы делят отрезок I на подотрезки равной длины и, вот, выбор числа отрезков является искусством, хотя можно привести несколько формул:

где — число столбцов, — размер исходной выборки, — оценка стандартного отклонения, — интерквартильное расстояние, которое еще встретится ниже.

Так же можно отметить несколько правил здравого смысла:

• хорошо чтобы в большинстве столбцов было больше одного исходного значения
• каждый столбец гистограммы требует хотя бы одного пикселя по ширине, и в целом ограничение “не более 200” столбцов достаточно распространено

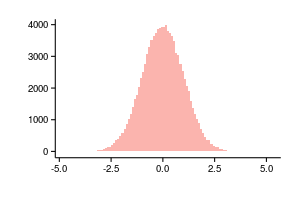
В противном случае, если число столбцов избыточно, а исходных данных мало, гистограмма будет напоминать штрих-код, как например на рисунке ниже.

Ось Y

Гистограммы бывают в абсолютных значениях, когда по оси y откладывается количество элементов исходной выборки попавших в каждый из интервалов, и в относительных, когда сумма столбцов нормируются на единицу, в этом случае гистограмма является оценкой плотности распределения и с точки зрения графика меняется лишь масштаб.

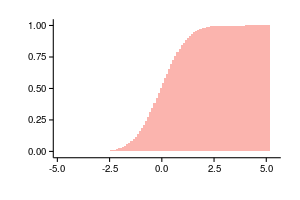
Так как обычная гистограмма является оценкой плотности, то мы можем суммировать столбцы и получить оценку функции вероятности следующим образом: . Два следующих графика построены по одним и тем же данным, слева не нормализованная гистограмма, справа аккумулированные значения нормализованной гистограммы.

Группировка данных

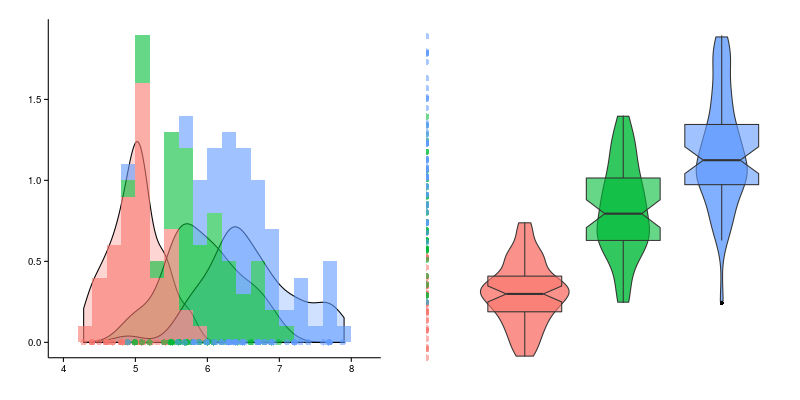
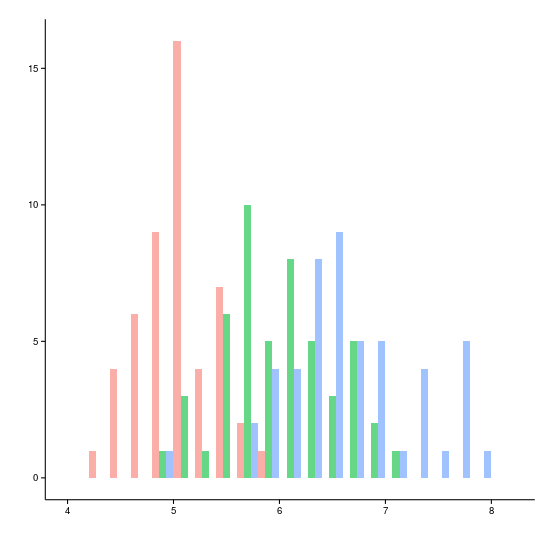
До сих пор был рассмотрен случай, когда у нас есть характеристика, на которую мы просто хотим взглянуть, обычно намного более интересно сравнивать поведение одной и той же характеристики для различных подгрупп. В таком случае гистограмма будет иметь следующий вид.

В данном случае, ширина каждого столбца для каждой группы уменьшается пропорционально числу групп и слегка сдвигаются друг относительно друга, в качестве альтернативы можно рассмотреть полупрозрачное перекрытие, которое будет выглядеть следующим образом для тех же данных.

В сухом остатке

Для отрисовки гистограммы необходимо определить

• Число столбцов
• Нужна ли нормализация и аккумулирование данных
• Способ отображения различных групп

Для отрисовки гистограммы для каждой группы требуется хранить следующие значения:

Диаграмма размаха

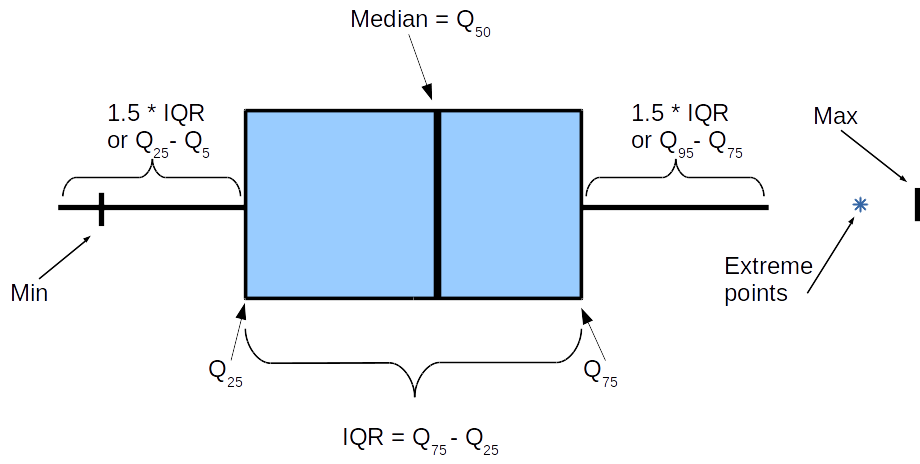
“Ящик с усами” не имеет официально устоявшегося названия, а называть его “ящиком с усами“ у меня язык не поворачивается, тем более когда ящиков несколько, а диаграмма размаха хоть и не очень частотное, но более благозвучное название. Приведем пример трех ящиков слева отображены соответствующие значения исходных данных (не являются частью диаграммы размаха). Прежде всего необходимо отметить, что в случае диаграмм размаха, исходная характеристика откладывается по оси Y, а ось X условна и представляет собой группирующую переменную.

Чтобы нарисовать ящик для одной группы про исходные данные необходимо знать всего три характеристики:

Иногда к “обязательному” набору добавляют следующие дополнительные:

Таким образом, ящик с усами в разрезе будет выглядеть следующим образом.

Некоторые моменты требуют пояснения. Ящик, то есть объект между и , практически везде ограничен этими значениями, а вот “усы” могут различаться и если вас действительно интересуют числа, необходимо уточнять, что имеется в виду в каждом отдельном случае. Самое важное это длина усов: исходим из того, что она .

Отметки минимума и максимума часто опускаются, экстремальные точки, то есть выходящие за пределы усов тоже опускаются либо рисуются точками или звездочками. В зависимости от структуры данных желание отрисовывать экстремальные значения может значительно увеличить объем данных для отрисовки диаграммы размаха.

Магическое число появилось в работе Тьюки Exploratory Data Analysis (1977) и причина его появления не очень ясна, но с тех времен ничего не менялось, многие инструменты предлагают его в качестве значения по умолчанию, но позволяют выставлять произвольное, вплоть до нуля, в этом случае, “усы” будут покрывать весь отрезок от минимального до максимального значений исходных данных.

Есть предположение, что возникло следующим образом. Ширина усов составляет , известно, что для симметричных распределений совпадает с абсолютным отклонением от медианы (MAD), которая в свою очередь, является оценкой дисперсии с коэффициентом . А значит, , мы получаем не безызвестные 3 сигмы влево, 3 сигмы вправо.
Иногда в качестве концов усов предлагается интервал , в таком случае очевидно, что всегда (если исходных данных больше 20) должны получаться точки, не попадающие внутрь интервала и поэтому их обычно игнорируют при таком подходе.

В сухом остатке

Для отрисовки “диаграммы размаха” необходимо определить:

• способ группировки данных
• длину усов
• нужно ли отмечать экстремальные значения

Для отрисовки “ящика с усами” для одной группы требуется всего 3 числа.