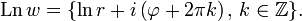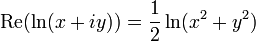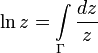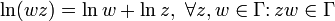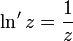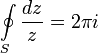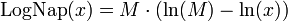Привет, сегодня поговорим про комплексный логарифм, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
комплексный логарифм , настоятельно рекомендую прочитать все из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного).
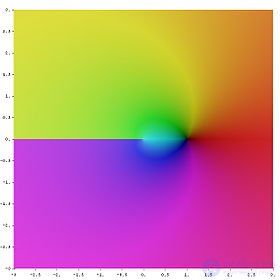
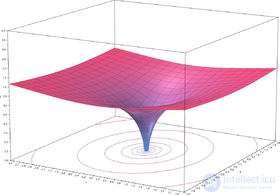
Наглядное представление функции натурального комплексного логарифма (главная ветвь). Аргумент значения функции обозначается цветом, а модуль — яркостью.
комплексный логарифм — аналитическая функция , получаемая распространением вещественного логарифма на всюкомплексную плоскость (кроме нуля). Существует несколько эквивалентных способов такого распространения. Данная функция имеет широкое применение в комплексном анализе. В отличие от вещественного случая, функция комплексного логарифма многозначна.
Содержание
- 1 Определение и свойства
- 2 Примеры значений комплексного логарифма
- 3 Комплексная логарифмическая функция и риманова поверхность
- 4 Аналитическое продолжение
- 5 Связь с обратными тригонометрическими и гиперболическими функциями
- 6 Исторический очерк
- 7 Литература
- 8 Примечания
Определение и свойства[править ]
Для комплексных чисел логарифм можно определить так же, как для вещественных, то есть как обращениепоказательной функции. На практике используется практически только натуральный комплексный логарифм, основание которого — число Эйлера 
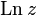
Другие, эквивалентные данному, варианты определения приведены ниже.
В поле комплексных чисел решение этого уравнения, в отличие от вещественного случая, не определено однозначно. Например, согласно тождеству Эйлера, 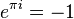
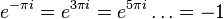
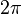
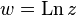
Комплексный нуль не имеет логарифма, поскольку комплексная экспонента не принимает нулевого значения. Ненулевое 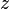
где
— произвольное целое число
Тогда 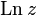
Здесь 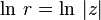
Вещественная часть комплексного логарифма
Из формулы видно, что у одного и только одного из значений мнимая часть находится в интервале 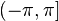
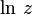
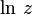
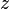
Из приведенной формулы также следует, что вещественная часть логарифма определяется следующим образом через компоненты аргумента:
На рисунке показано, что вещественная часть как функция компонентов центрально-симметрична и зависит только от расстояния до начала координат. Она получается вращением графика вещественного логарифма вокруг вертикальной оси. С приближением к нулю функция стремится к
Логарифм отрицательного числа находится по формуле[3]:
Примеры значений комплексного логарифма[править ]
Приведем главное значение логарифма (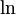
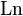
Следует быть осторожным при преобразованиях комплексных логарифмов, принимая во внимание, что они многозначны, и поэтому из равенства логарифмов каких-либо выражений не следует равенство этих выражений. Пример ошибочного рассуждения:
— явная ошибка.
Отметим, что слева стоит главное значение логарифма, а справа — значение из нижележащей ветви (
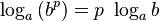
Комплексная логарифмическая функция и риманова поверхность[править ]
Риманова поверхность для комплексного логарифма
В комплексном анализе вместо рассмотрения многозначных функций на комплексной плоскости принято иное решение: рассматривать функцию как однозначную, но определенную не на плоскости, а на более сложном многообразии, которое называется римановой поверхностью[4]. Комплексная логарифмическая функция также относится к этой категории: ее образ (см. рисунок) состоит из бесконечного числа ветвей, закрученных в виде спирали. Эта поверхность непрерывна и односвязна. Единственный нуль у функции (первого порядка) получается при 
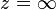
В силу односвязности риманова поверхность логарифма является универсальной накрывающей[6] для комплексной плоскости без точки 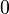
Аналитическое продолжение[править ]
Логарифм комплексного числа также может быть определен как аналитическое продолжение вещественного логарифма на всюкомплексную плоскость. Пусть кривая 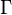
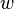
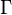
Если 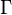
Главная ветвь логарифмической функции непрерывна и дифференцируема на всей комплексной плоскости, кроме отрицательной части вещественной оси, на которой мнимая часть скачком меняется на 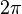
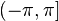
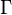
Из формулы аналитического продолжения следует, что на любой ветви логарифма[2]:
Для любой окружности 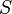
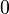
Интеграл берется в положительном направлении (против часовой стрелки). Это тождество лежит в основе теории вычетов.
Можно также определить аналитическое продолжение комплексного логарифма с помощью рядов, известных для вещественного случая:
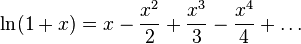 |
(Ряд 1) |
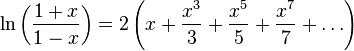 |
(Ряд 2) |
Однако из вида этих рядов следует, что в единице сумма ряда равна нулю, то есть ряд относится только к главной ветви многозначной функции комплексного логарифма. Радиус сходимости обоих рядов равен 1.
Связь с обратными тригонометрическими и гиперболическими функциями[править ]
Поскольку комплексные тригонометрические функции связаны с экспонентой (формула Эйлера), то комплексный логарифм как обратная к экспоненте функция связан собратными тригонометрическими функциями[7] [8]:
Гиперболические функции на комплексной плоскости можно рассматривать как тригонометрические функции мнимого аргумента, поэтому и здесь имеет место связь с логарифмом [8]:
— обратный гиперболический синус
— обратный гиперболический косинус
— обратный гиперболический тангенс
— обратный гиперболический котангенс
Исторический очерк[править ]
Первые попытки распространить логарифмы на комплексные числа предпринимали на рубеже XVII—XVIII веков Лейбниц и Иоганн Бернулли, однако создать целостную теорию им не удалось — в первую очередь по той причине, что тогда еще не было ясно определено само понятие логарифма[9]. Дискуссия по этому поводу велась сначала между Лейбницем и Бернулли, а в середине XVIII века — между Д’Аламбером и Эйлером. Бернулли и Д’Аламбер считали, что следует определить 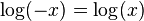
В XIX веке, с развитием комплексного анализа, исследование комплексного логарифма стимулировало новые открытия. Гаусс в 1811 году разработал полную теорию многозначности логарифмической функции[11], определяемой как интеграл от 
Разработка теории конформных отображений показала, что меркаторская проекция в картографии, возникшая еще до открытия логарифмов (1550), может быть описана как комплексный логарифм[12].
Литература[править ]
- Теория логарифмов
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973. — 720 с.
- Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. — М.: Наука, 1967. — 304 с.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — изд. 6-е. — М.: Наука, 1966. — 680 с.
- История логарифмов
- Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трех томах. — М.: Наука, 1972. — Т. III.
- Колмогоров А. Н., Юшкевич А. П. (ред.). Математика XIX века. Геометрия. Теория аналитических функций. — М.: Наука, 1981. — Т. II.
Напиши свое отношение про комплексный логарифм. Это меня вдохновит писать для тебя всё больше и больше интересного. Спасибо Надеюсь, что теперь ты понял что такое комплексный логарифм
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Комплексный анализ и операционное исчисление (теория функций комплексного переменного)
Элементарные функции комплексного переменного
Показательная функция комплексного переменного
В действительной области показательная функция вводится обычно в связи с обобщением понятия степени
. В комплексной области функцию требуется определить так, чтобы при
ее свойства совпадали с известными свойствами функции
. Одно из важнейших свойств функции
— представление ее рядом Тейлора: она является суммой сходящегося на всей числовой прямой ряда
.
Учитывая это, рассматриваем ряд и убеждаемся, что он абсолютно сходится при любом
, т.е. во всей комплексной плоскости
определена некоторая функция — сумма этого ряда. Так как при
имеем
, то вводим следующее определение: показательной функцией
в комплексной области называется функция, которая является суммой сходящегося во всей комплексной плоскости ряда
(2.3)
Из определения следует, что показательная функция определена во всей комплексной плоскости. В частности, при , где
— действительное число, имеем
. Используя свойства абсолютно сходящихся рядов (возможность перестановки и группировки членов ряда), ряд можно записать в виде алгебраической суммы двух рядов с действительными членами отделить действительную и мнимую части ряда:
Полученные ряды являются рядами Тейлора для функций и
. В результате имеем равенство
, или, обозначив
через
(2.4)
Формула (2.4) — формула Эйлера была использована для записи комплексного числа в показательной форме.
Функция обладает, очевидно, рядом свойств, справедливость которых установлена в действительной области, т.е. для
.
С другой стороны, в силу расширения множества, следует ожидать, что имеют место и другие свойства, аналога которых в действительной области нет.
К свойствам первой группы нужно отнести прежде всего формулу сложения:
(2.5)
Доказательство формулы сводится, согласно определению показательной функции, к доказательству справедливости при любых и
равенства
которое устанавливается путем перемножения абсолютно сходящихся рядов, записанных слева (см. пример 1.44).
Если в равенстве (2.5) положить — любое комплексное число, то, учитывая тождество
, можно записать
. Это равенство, справедливое при любых значениях
, означает, что функция
является периодической и ее период — чисто мнимое число
. Аналога этому свойству в действительной области нет, функция
— непериодическая.
Так же, как и в действительной области, показательная функция не обращается в нуль ни при каком значении аргумента. Действительно, если предположить противное, что существует
, при котором
, то из тождества
, где
— любое комплексное число, получили бы,
при любом
, что неверно. Однако это единственное исключение, т.е. нуль — единственное значение, которое не может принимать функция
. В отличие от
значение функции в комплексной области может быть отрицательным, например
. Вообще
может принимать любые значения в
, за исключением нуля. Это свойство доказывается просто, если в формуле (2.5) положить
и сравнить равенство
с показательной формой записи комплексного числа. В результате получим, что при фиксированном z , т.е. при фиксированных
и
, модуль числа
равен
, а аргумент равен
, т.е.
(2.6)
Отсюда получаем, что может принимать любые значения
, так как
— любое число.
Пример 2.13. Найти для чисел: а)
; б)
.
Решение
а) Находим модуль числа и аргумент
. После этого можно записать
, то есть
.
Можно записать решение иначе, используя формулу сложения (2.5) и формулу Эйлера (2.4):
Полому , а из показательной формы записи числа
находим
.
б) Представим число в виде произведения , а множитель
в показательной форме:
. Тогда
Поэтому имеем , или
, так как для
данного значения аргумента имеет место ограничение . После этого записываем
.
Пример 2.14. Найти , если
.
Решение
Применяя последовательно формулы (2.5),(2.6), находим
, то есть
.
Поэтому .
Пример 2.15. Показать, что функция является периодической и ее период — действительное число.
Решение
Нужно показать, что существует число такое, что
для любого
. Но из формулы (2.5) имеем
, поэтому число
должно быть таким, чтобы выполнялось равенство
, а это верно при
. Следовательно, период функции
— действительное число
.
Пример 2.16. Доказать, что функция является неоднолистной на множестве
. Найти область однолистности.
Решение
Неоднолистность функции следует из определения, так как существуют не равные значения аргумента, такие, что в них совпадают значения функции. Например, для и
получается
.
Чтобы определить область однолистности, запишем разность
или
.
Значения функции совпадают для тех и
, для которых выполняется равенство
, то есть
.
Однолистным отображение будет в любой области, принадлежащей горизонтальной полосе ширины , в частности полосе
или
(рис. 2.9).
Любая прямая , параллельная действительной оси отображается в луч
, так как из
получаем
. В частности, действительная ось
, то есть
, переходит в луч
— действительную положительную полуось, а прямая
, то есть
, — в луч
, геометрически это — та же действительная полуось
Для однозначности отображения на границе проведем разрез по лучу. При этом точкам прямой будут соответствовать точки нижнего «берега» оси
, а точкам прямой
точки верхнего «берега».
Такой же результат получим и для следующей полосы . Она отображается также в плоскость с разрезом
.
Вообще любая полоса с помощью функции
переходит в плоскость с разрезом по действительной положительной полуоси.
Нарушенную разрезом непрерывность отображения можно восстановить, построением римановой поверхности функции по такому же принципу как сделано для
.
Полученный результат (см. решение примера 2.16) запишем в виде утверждения: функция взаимно однозначно отображает:
1) любую полосу — в плоскость с разрезом по лучу
;
2) полосу в плоскость с разрезом по действительной отрицательной полуоси;
3) полосу во всю комплексную плоскость с разрезом по действительной положительной полуоси.
Тригонометрические и гиперболические комплексные функции
Функции вводятся аналогично показательной функции — как суммы соответствующих абсолютно сходящихся во всей комплексной плоскости рядов:
(2.7)
(2.8)
На основе этих функций определяются и другие тригонометрические и гиперболические:
Из определений следует, что функции являются четными, а остальные — нечетными.
Сравнивая формулы (2.7) и (2.8) с формулой (2.3) — определением функции , получаем следующие формулы, справедливые при любом
(2.9)
(2.10)
Формулы (2.9) и (2.10) — формулы Эйлера; они связывают тригонометрические и гиперболические функции с показательной. Формула (2.9) при , где
— действительная переменная, рассмотрена выше (см. формулу (2.4)).
Так как формулы (2.9) и (2.10) верны при любых значениях , то, заменяя
на
и учитывая, что
и
— нечетные, a
и
— четные функции, можем записать
Комбинируя эти формулы с (2.9) и (2.10), получаем представление тригонометрических и гиперболических функций через показательную:
(2.11)
(2.12)
Эти формулы позволяют использовать при исследовании гиперболических и тригонометрических функций в комплексной области свойства показательной функции и не обращаться к определениям (2.7),(2.8), т.е. не рассматривать более сложные операции — действия с рядами.
Так, с помощью (2.11) и (2.12) устанавливается справедливость таких формул сложения, как
и других формул, в частности формул тригонометрии.
Кроме того, что тригонометрические и гиперболические функции выражаются через , они еще и связаны между собой. Соответствующие формулы получаются из (2.11) и (2.12):
(2.13)
Отсюда, в частности, получаются такие формулы, как
Как и в действительной области, тригонометрические функции и
являются периодическими и их период равен
. Это следует из формул (2.11) (см. пример 2.15). А гиперболические функции, не будучи периодическими в действительной области, в комплексной области являются периодическими, их период, как и у функции
, — мнимое число
(это следует из рассмотрения равенств (2.12)).
Замечательным свойством, не имеющим аналога в действительной области, является свойство неограниченности (по модулю) функций и
. Эти функции могут принимать любые значения, в частности большие единицы. Например, для числа
по формуле (2.11) имеем:
.
Можно показать и в общем виде, что для любого числа найдется такое число
, что для всех
, удовлетворяющих условию
, выполняется неравенство
. Для доказательства следует использовать формулы (2.11).
Пример 2.17. Найти и
для чисел: а)
; б)
.
Решение
а) Используем формулу (2.13): , поэтому
, а так как
, то
и, следовательно,
.
б) Учитывая равенство , используем, как и выше, формулу (2.13):
Поэтому и, следовательно,
.
Пример 2.18. Найти , если a)
; б)
.
Решение
Для решения используем формулу сложения, обозначая , а также формулу (2.13).
а) Решим первый пример:
поэтому .
б) Решим второй пример:
поэтому .
Для решения можно использовать формулу сложения непосредственно для гиперболической функции:
Пример 2.19. Найти модуль и аргумент числа , если a)
; 6)
.
Решение
а) Используем определение функции и формулу (2.13):
поэтому .
б) Представим число в виде произведения двух чисел:
и найдем модуль и аргумент каждого. Для числа имеем
. Число
является действительным, причем отрицательным, так как
Поэтому . Окончательно, используя правило умножения комплексных чисел в тригонометрической форме, получаем
Пример 2.20. Найти мнимую часть числа , где
— тот корень уравнения
, который расположен в третьей четверти.
Решение
Корнями уравнения , или
, являются четыре комплексных числа, которые могут быть найдены по правилу извлечения корня из комплексного числа:
Для того чтобы отобрать корень, которому соответствует точка в третьей четверти, нужно взять . Искомым корнем будет число
, или в алгебраической форме
.
Вычислим теперь или, что то же,
. Можно перейти к показательной функции по формуле (2.12) или использовать формулу сложения для гиперболической функции и формулу (2.13):
Получаем ответ: .
Комплексный логарифм
Понятие функции, обратной показательной функции, как и в действительной области, связано с понятием логарифма числа.
Логарифмом комплексного числа называется число
такое, что справедливо равенство
; обозначается
. Таким образом,
.
Для нахождения логарифма числа , т.е. для нахождения действительной и мнимой частей числа
, запишем число
в показательной форме, и число
будем искать в алгебраической форме:
.
Тогда равенство или
есть равенство чисел, записанных в показательной форме, и из него находим
и
, а именно
, то есть
. Для искомого числа
получаем выражение:
, где
.
Из этого следует, что логарифм комплексного числа определяется неоднозначно; полученное выражение определяет множество значений логарифма данного числа ; обозначается
(2.14)
Для каждого фиксированного значения получаем определенное число — значение логарифма числа
; при
оно называется главным значением логарифма:
(2.15)
Пример 2.21. Найти — главные значения и
для следующих чисел:
а) ; б)
; в)
.
Решение
а) Находим модуль и аргумент числа . По формулам (2.14) и (2.15) получаем:
б) Для числа находим модуль и аргумент:
. Поэтому имеем результат:
в) Находим модуль и аргумент числа . Получаем ответ:
Пример 2.22. Найти модуль, аргумент, действительную и мнимую части числа .
Решение
Находим модуль и аргумент числа . По формуле (2.14) получаем
. Поэтому:
Точка расположена в первой четверти, так как
и
. Поэтому
Замечание 2.4. Введение понятия логарифма числа позволяет определить в комплексной области степень с любым комплексным показателем и показательную функцию с любым комплексным основанием
.
При и
, где
— натуральное число, степени
и
рассмотрены выше; при
и
, где
— целое число
, определение к также очевидно.
В общем случае при любом комплексном степень определяется формулой
(2.16)
Аналогично вводится функция с любым комплексным основанием
(2.17)
В силу бесконечной значности логарифма, каждому числу соответствует бесконечное множество значений степени
, определяемой по формуле (2.16), и бесконечное множество чисел, определяемых по формуле (2.17) при
. Среди этих множеств выделяются главные значения, которые соответствуют главным значениям логарифмов.
Пример 2.23. Показать, что выражение принимает только действительные значения.
Решение
Пример 2.24. Найти , где
— корень уравнения
, удовлетворяющий условию
.
Решение
Замечание 2.5. Введение понятия логарифма комплексного числа позволяет решать в комплексной области показательные уравнения. Простейшим таким уравнением является уравнение вида . Решение этого уравнения сводится к нахождению значений выражения
, то есть
.
Пример 2.25. Решить уравнения: a) ; б)
; в)
.
Решение
а) Из равенства по определению логарифма получаем
. Далее, учитывая равенства
, по формуле (2.14) находим
. Уравнение имеет бесчисленное множество решений, которые геометрически изображаются точками, расположенными на расстоянии
друг от друга на прямой
, параллельной мнимой оси. Среди решений есть действительное число
— точка на оси
.
б) Все решения уравнения получаются, как значения выражения , то есть
.
в) Из равенства получаем
. Находим модуль и аргумент числа
. Множество решений уравнения описывается равенством
В случаях «б» и «в» уравнения не имеют действительных решений, так как ни при каких значениях среди полученных множеств нет действительных чисел. Геометрически же соответствующие точки расположены на той же прямой
, что и в случае «а», на расстоянии
друг от друга; начальными значениями (при
) для них являются
и
. Решения уравнений «б» и «в» изображены на рис. 2.10 (по осям масштабы разные).
Пример 2.26. Найти из уравнения
.
Решение
Используя формулу (2.12), сведем задачу к решению показательного уравнения . Получим квадратное уравнение относительно функции
, корнями которого являются числа
. Далее нужно найти значения выражений
. Для этого используем формулу (2.14):
Получили два множества решений исходного уравнения:
Геометрически — это точки, лежащие на прямых
параллельных мнимой оси; расстояние между любыми соседними точками на каждой прямой равны ; начальные значения (при
):
или
и
(рис. 2.11).
Логарифмическая функция комплексного переменного
Логарифмическая функция вводится, как функция, обратная к показательной, т.е. как решение уравнения , значения функции при любом
определяются по формуле (2.14).
Функция, очевидно, многозначная и отображает плоскость на каждую из полос:
, или
.
В плоскости с разрезом по лучу возможно выделение однозначных ветвей, каждая из которых однозначно отображает эту плоскость на одну из полос
, в частности функция
— главное значение логарифмической функции отображает плоскость на полосу
(см. рис. 2.9). В плоскости с разрезом
также возможно выделение однозначных ветвей, каждая из которых однозначно отображает эту плоскость на одну из полос
, в частности функция
— главное значение логарифмической функции отображает плоскость на полосу
. Выделение ветви определяется заданием значения функции в одной из точек области.
Пример 2.27. Найти решение уравнения при условии
.
Решение
Обратные тригонометрические и гиперболические комплексные функции
Функции, обратные к тригонометрическим и гиперболическим функциям, определяются, как и в действительной области.
Например, обратным тригонометрическим синусом числа называется число
такое, что выполняется равенство
. Отображение обозначается, как и в действительной области,
.
Аналогично определяются и другие тригонометрические функции комплексного аргумента:
Из определений могут быть получены формулы для нахождения числа по заданному числу
.
Рассмотрим эту задачу на примере нахождения . По определению имеем
. Заменим
по формуле Эйлера (2.11), и из соотношения
или
, т.е. квадратного уравнения относительно
, находим
. Перед радикалом записан только знак плюс, так как в комплексной области
— двузначное выражение. Далее, используя определение логарифма, находим
Для каждого числа получаем бесконечное множество значений для
в силу двузначности
и бесконечной значности логарифма. Все это множество значений
обозначается
. Окончательный результат:
(2.18)
Формулы, аналогичные (2.18), могут быть получены и для других функций:
Все эти формулы, как и (2.18), дают бесконечнозначные выражения — определяют многозначные функции. Выделяя однозначную ветвь выражения , можно получить однозначные функции в каждом случае.
Большого практического значения эти формулы, как и (2.18), не имеют. Для нахождения значений обратных тригонометрических и обратных гиперболических функций можно использовать их определения и формулы связи тригонометрических и гиперболических функций с показательной функцией (формулы Эйлера (2.11)-(2.12)), т.е. применять метод, с помощью которого выведена формула (2.18). Этим методом решен пример 2.26, где найдено значение .
Замечание 2.6. Рассмотрим уравнения, содержащие тригонометрические и гиперболические функции. Простейшими из них являются уравнения:
Решение их, согласно определению, сводится к нахождению обратных тригонометрических и обратных гиперболических функций.
Пример 2.28. Решить уравнение .
Решение
Множество решений уравнения определяется выражением , или с помощью формулы (2.18):
. Выражение в скобках, в силу двузначности корня, записывается в виде
и
. Для каждого из этих чисел по сформулированному выше правилу находим логарифм:
а) для числа имеем
, поэтому
б) для числа имеем
, поэтому
Получаем два множества решений уравнения:
Геометрически — это множество точек, расположенных на расстоянии друг от друга на прямых, параллельных мнимой оси (рис. 2.12):
и
,
Действительных решений уравнение не имеет, так как ни при каком значении среди чисел
нет действительных. Это соответствует известному свойству функции
в действительной области
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Элементарные функции комплексного переменного.
Рассмотрим некоторые
элементарные функции комплексного
переменного, а именно, показательную
функцию
,
логарифмическую функцию
,
тригонометрические —
,
,
,
и,
обратные тригонометрические функции
,
,
,
,а
также гиперболические функции
,
,
,
и обратные к ним функции
,
,
,
).
1. Показательная функция комплексного переменного.
Показательная
функция
определяется как
или
(12)
Очевидны следующие
свойства функции
.
1)
;
2)
.
Так как
,
то показательная функция
— периодическая функция периода
.
Пример 24.
Найти значение функции
в точке
и указать координаты точки комплексной
плоскости, соответствующей найденному
значению.
Решение.
,
откуда координаты искомой точки
.●
2. Логарифмическая функция комплексного переменного.
Логарифмическая
функция
определяется как обратная к показательной.
Определение.
Натуральным логарифмом
(
)
комплексного числа
называется показатель степени
,
в которую необходимо возвести число
,
чтобы получить число
.
Пусть
,
,
где
.
Тогда
,
откуда
,
,
,
,
.
,
где
(13)
Определение.
Выражение
называется главным
значением натурального логарифма числа
.
Из формулы (13)
следует, что действительная часть
натурального логарифма определяется
однозначно, а мнимая часть содержит
неопределенное слагаемое, кратное
,
т. е. существует бесконечное множество
значений натурального логарифма любого
числа
,
отличного от нуля.
Логарифм нуля не
существует.
Пример 25.
Вычислить
и
.
Решение.
Найдем модуль и аргумент числа
.
.
Так
как действительная и мнимая части числа
отрицательны, то главное значение
аргумента равно
.
Тогда
—
главное
значение логарифма данного числа и
.●
Пример 26.
Вычислить
и
.
Решение.
Модуль числа
равен
,
а главное значение аргумента равно
,
следовательно,
,
.●
С помощью логарифма
может быть определена любая степень
комплексного числа.
Пример 27.
Вычислить
.
Решение.
,
где
.
Обратите внимание,
что
-действительные числа.●
3. Тригонометрические функции комплексного переменного.
Тригонометрические
функции синус и косинус определены
ранее (см. формулы (6)).
Определение.
Тригонометрическая функция синус
комплексного переменного определяется
как
,
где
,
(14)
функция косинус
как
,
где
, (15)
функция тангенс
как
,
где
, (16)
функция котангенс
как
,
где
. (17)
Пример 28.
Вычислить
.
Решение.
.●
Пример 29.
Вычислить
.
Пример
28.
Вычислить
.
Решение.
●
Пример 30.
Доказать, что
.
Решение.
.●
Замечание.
Для тригонометрических функций
комплексной переменной имеют место и
другие тождества, справедливые для
тригонометрических функций действительного
аргумента
(см. пример 31).
Пример 31.
Доказать, что
.
Решение.
.
Пример 32.
Решить уравнение
.
Решение.
,
откуда
,
и
.
Решая квадратное
относительно
,
имеем
или
,
откуда
и
.
Ответ:
Замечание.
Числа
при
имеют одинаковые мнимые части, поэтому
они лежат на прямой, параллельной
действительной оси и отстоящей от нее
на расстоянии
.●
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Множеством (областью) значений показательной функции
Такое значение аргумента единственное, так как если 
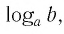
Таким образом, равенство 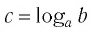
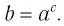
Определение:
Пусть 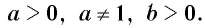
Приведем несколько примеров:
Нахождение логарифма числа называется логарифмированием.
Обозначим 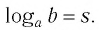
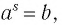
Это равенство называется основным логарифмическим тождеством.
Согласно этому тождеству, например, имеем: 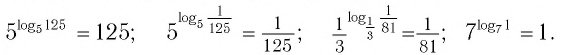
Например:
История логарифма
Логарифмы были изобретены в 1614 г. шотландским математиком Д. Непером (1550—1617) и независимо от него на 6 лет позднее швейцарским механиком и математиком И. Бюрги (1552—1632).
Оба исследователя хотели найти новое удобное средство арифметических вычислений, но их определения логарифма различны и у обоих не похожи на современные. Понимание логарифма как показателя степени с данным основанием впервые появилось в XVIII в. в работах английского математика В. Гардинера (1742). Широкому распространению этого определения логарифма более других содействовал Jl. Эйлер, который впервые применил в этой связи и термин «основание».
Термин «логарифм» принадлежит Неперу. Он возник из сочетания греческих слов логос — отношение и аритмос — число. Слово «логарифм», таким образом, означало «число отношения».
Пример:
а) Записать число 
б) Записать число -5 в виде логарифмов по основанию 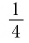
Решение:
а) По определению логарифма имеем:
б) По определению логарифма имеем:
Пример:
Между какими целыми числами находится число
Решение:
Пусть 
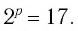
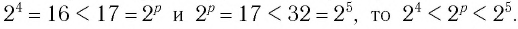
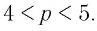
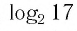
Ответ:
Пример:
Решить уравнение:
Решение:
а) Поскольку 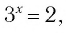
б)
Ответ:
Логарифмы по основанию 10 имеют особое название — десятичные логарифмы. Десятичный логарифм числа b обозначается 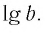
▲ Особое обозначение и название имеют не только десятичные логарифмы, но и логарифмы, основанием которых является число е:
Такие логарифмы называются натуральными.
Логарифмы по основанию е позволяют выражать математическую зависимость, которая характеризует многие биологические, химические, физические, социальные и другие процессы. По-видимому, этим объясняется и название «натуральные логарифмы», т. е. естественные (этот термин ввел в 1659 г. итальянский математик П. Менголи). Натуральные и десятичные логарифмы имели большое значение для облегчения вычислений в XVII—XX вв. до создания мощных современных вычислительных средств. Натуральные логарифмы имеют и большое теоретическое значение.▲
Основные свойства логарифмов
Теорема:
При любых положительных значениях b и с верно равенство:
Доказательство:
Докажем утверждение (1).
По основному логарифмическому тождеству
Таким образом, имеем:
Отсюда по следствию из п. 2.3 получаем равенство (1).
Докажем утверждение (2). Преобразуем левую часть равенства (2):
Заметим, что равенство (2) можно доказать тем же способом, что и равенство (1), — сделайте это самостоятельно.
Равенство (1) означает, что логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел.
Равенство (2) означает, что логарифм дроби с положительными. числителем и знаменателем равен разности логарифмов числителя и знаменателя.
Замечание. Равенства, доказанные в теореме 1 (как и другие равенства этого пункта), являются тождествами. Действительно, каждое из них превращается в верное числовое равенство при любых значениях a, b и с, для которых входящие в равенство выражения имеют смысл.
Теорема:
При любых значениях s и положительных значениях b верно равенство
Доказательство:
По основному логарифмическому тождеству
Таким образом, имеем
Отсюда по следствию из п. 2.3 получаем равенство (3).
Следствие 1. Если числа 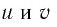
Следствие 2. При любом целом 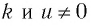
Пример №1
Найти значение выражения:
Решение:
Ответ:
Теорема:
При любых значениях 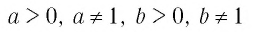
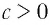
Доказательство:
Способ 1. По основному логарифмическому тождеству имеем
Прологарифмировав левую и правую части этого тождества по основанию а, получим
Применив тождество (3), имеем
Так как 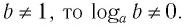
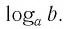
Способ 2. Пусть 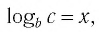
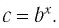
Откуда имеем
Итак,
Тождество (6) называется формулой перехода от логарифма по одному основанию к логарифму по другому основанию.
Обычно в таблицах, калькуляторах даются значения логарифмов по основанию 10, а когда нужно найти значение логарифма по другому основанию, пользуются формулой перехода от логарифма по одному основанию к логарифму по другому основанию.
Следствием из тождества (6) при основании а = с является формула
(убедитесь в этом самостоятельно).
Пример №2
Найти значение выражения, если
Решение:




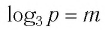
6)


Ответ:
Следствие 3. Имеют место тождества:
Тождества (8) и (9) можно доказать, используя уже доказанные тождества из этого пункта.
Пример №3
Упростить выражение
Решение:
Используя определение логарифма, представим числа 1 и 3 в виде логарифмов по основанию 2:
Ответ:
Развитие науки, прежде всего астрономии, уже в XVI в. привело к необходимости громоздких вычислений при умножении и делении многозначных чисел. Эти вычислительные проблемы были в некоторой степени решены с открытием логарифмов и созданием таблиц логарифмов.
Логарифмическая функция
Рассмотрим выражение 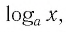
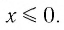
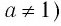
Определение:
Логарифмической функцией называется функция вида 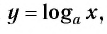
Область определения логарифмической функции — это естественная область определения выражения 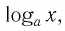
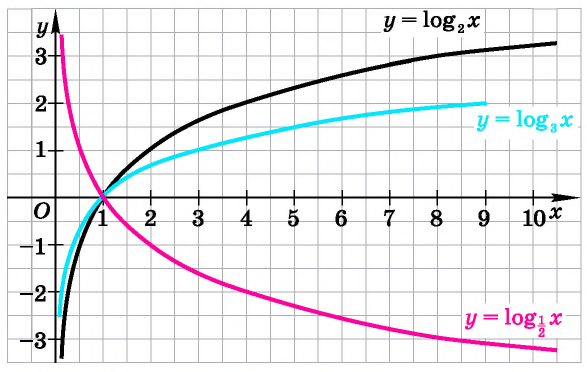
Графики некоторых логарифмических функций изображены на рисунке 34. Эти изображения (как и для графиков других функций) можно было получить, строя их по точкам. Отметим некоторые особенности изображенных графиков.
График функции 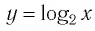
Когда значения аргумента х уменьшаются, т. е. приближаются к нулю, то график этой функции «приближается» к оси Оу и при этом «круто» опускается вниз. А когда значения аргумента х увеличиваются, то график «медленно» поднимается вверх (ем. рис. 34). Аналогично для любой функции 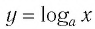
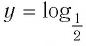
Заметим, что когда значения аргумента х уменьшаются, т. е. приближаются к нулю, то график этой функции «приближается» к оси Оу и при этом «круто» поднимается вверх. А когда значения аргумента х увеличиваются, то график «медленно» опускается вниз. Аналогично для любой функции 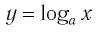
Теорема (о свойствах логарифмической функции 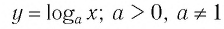
- Областью определения логарифмической функции является интервал
- Множеством (областью) значений логарифмической функции является множество R всех действительных чисел.
- Логарифмическая функция не имеет ни наименьшего, ни наибольшего значений.
- График логарифмической функции пересекается с осью абсцисс в точке (1; 0) и не пересекается с осью ординат.
- Значение аргумента х = 1 является нулем логарифмической функции.
- 6. При а > 1 логарифмическая функция принимает отрицательные значения на интервале (0; 1) и принимает положительные значения на интервале
И при 0 < а < 1 логарифмическая функция принимает отрицательные значения на интервале
и принимает положительные значения на интервале (0; 1).
- Логарифмическая функция не является ни четной, ни нечетной.
- При а > 1 логарифмическая функция возрастает на всей области определения. При 0 < а < 1 логарифмическая функция убывает на всей области определения.
- Логарифмическая функция не является периодической.
Изображение графика логарифмической функции позволяет наглядно представить эти свойства.
Множество (область) значений логарифмической функции — проекция ее графика на ось Оу, а на рисунках 35 и 36 видно, что эта проекция есть ось Оу. Это значит, что для любой точки 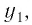
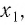
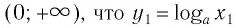
Множество (область) значений логарифмической функции — это множество всех действительных чисел, а в нем нет ни наименьшего числа, ни наибольшего (свойство 3).
График логарифмической функции проходит через точку (1; 0) и лежит в правой полуплоскости (свойства 4, 5).
При а > 1 график логарифмической функции лежит в IV координатном угле, когда 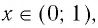
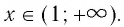
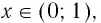
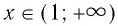
Область определения логарифмической функции — интервал 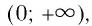
На рисунке 35 видно, что при а > 1 логарифмическая функция возрастает на области определения, а на рисунке 36 видно, что при 0 < а < 1 логарифмическая функция убывает на области определения (свойство 8).
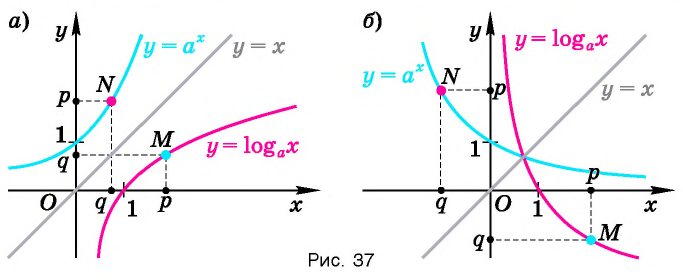
Пусть точка 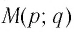
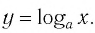
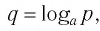
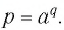
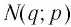
Заметим, что точки 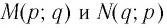
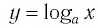
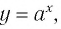
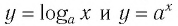
Последнее утверждение дает возможность, зная график функции 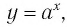
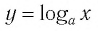
▲ Симметричность графиков функций 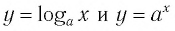
Функции 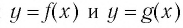
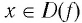
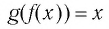
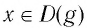
Покажем, что показательная и логарифмическая функции с одним, и тем же основанием а взаимно обратны.
Пусть 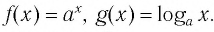
Для любого
Для любого
Покажем, что графики взаимно обратных функций 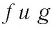
Пусть точка 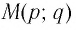
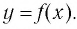
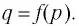
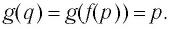
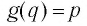
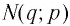
Таким образом, каждой точке М на графике функции 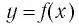
- Заказать решение задач по высшей математике
Логарифмы и их свойства
В предыдущем параграфе вы находили корни уравнения вида 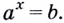
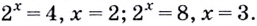
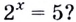
Для записи корней показательного уравнения используют понятие «логарифм» и соответствующий символ. Корнем уравнения 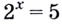
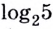
Рассмотрим общий случай-.
Пусть 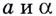
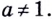
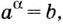
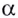
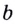
Логарифмом числа 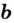
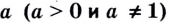
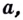
Логарифм числа 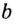
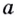
Примеры:
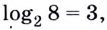
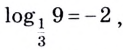
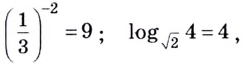
Основанием логарифма может быть произвольное положительное число, кроме единицы. Как известно, если 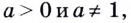
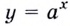
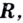
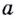
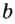
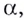
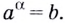
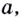
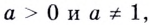
Полезно помнить, что для каждого
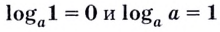
Нахождение логарифма числа называют логарифмированием. Эта операция обратная к операции возведения в степень с соответствующим основанием.
Согласно определению логарифма, если 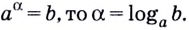
которое называют основным логарифмическим тождеством. Оно правильное для любых положительных
Например:
С помощью основного логарифмического тождества любое положительное число можно представить в виде степени, имеющей заданное основание.
Например:
Докажем ещё несколько важных свойств логарифмов (для положительных
1) По основному логарифмическому тождеству и основному свойству степени
Итак, 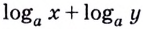
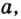
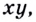
Эту формулу можно обобщить на три и более множителя:
Кратко говорят: логарифм произведения равен сумме логарифмов множителей.
2) Доказательство аналогичное предыдущему:
отсюда
Кратко говорят: логарифм частного равен разности логарифмов делимого и делителя.
3) Возведём обе части тождества 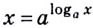
Итак,
Доказанные формулы можно использовать и справа налево, например:
В логарифмах переходить от одного основания к другому можно при помощи формулы перехода
где
Докажем эту формулу. Поскольку положительные числа 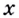
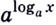
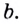
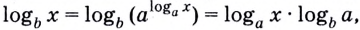
Обратите внимание! Как следствия из формулы перехода можно получить следующие формулы:
Докажите их самостоятельно.
Пример №4
Упростите выражение 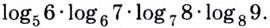
Решение:
Сведём все логарифмы к основанию 5. Имеем:
Особенно часто используют логарифмы по основаниям 10 и 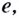
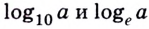
Рассмотренные в параграфе свойства логарифмов правиль-1 ные при условии, что переменные принимают положительные значения. С помощью модуля можно расширить использование некоторых формул. Например:
Для преобразования выражений, решения уравнений и неравенств используют и другие формулы, содержащие логарифмы:
Докажите их самостоятельно.
Пример №5
Вычислите:
Решение:
Пример №6
Решите уравнение:
Решение:
Пусть 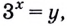
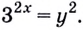
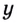
Получим: 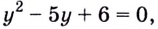
Поскольку 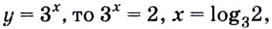
Ответ.
Пример №7
Найдите 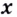
Решение:
Поскольку
Ответ.
Пример №8
Вычислите 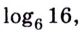
Решение:
Ответ.
- Корень из числа — нахождение и вычисление
- Теория множеств — виды, операции и примеры
- Числовые множества
- Вектор — определение и основные понятия
- Бесконечно убывающая геометрическая прогрессия
- Периодические дроби
- Степень с рациональным показателем
- Степень с действительным показателем
Рис. 1. Графики логарифмических функций
Логарифм числа b по основанию a определяется как показатель степени, в которую надо возвести число a, чтобы получить число b. Обозначение: 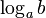
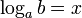
Пример: 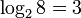
Содержание
- 1 Вещественный логарифм
- 1.1 Свойства
- 1.2 Натуральные логарифмы
- 1.3 Десятичные логарифмы
- 2 Комплексный логарифм
- 2.1 Многозначная функция
- 2.2 Аналитическое продолжение
- 2.3 Риманова поверхность
- 3 Исторический очерк
- 3.1 Вещественный логарифм
- 3.2 Комплексный логарифм
- 4 Логарифмические таблицы
- 5 См. также
- 6 Литература
Вещественный логарифм
Логарифм вещественного числа logab имеет смысл при 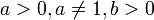
Наиболее широкое применение нашли следующие виды логарифмов.
Если рассматривать логарифмируемое число как переменную, мы получим логарифмическую функцию, например: 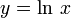
Свойства
Натуральные логарифмы
Для производной натурального логарифма справедлива простая формула:
По этой причине в математических исследованиях преимущественно используют именно натуральные логарифмы. Они нередко появляются при решении дифференциальных уравнений, исследовании статистических зависимостей (например, распределения простых чисел) и т. п.
При 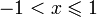
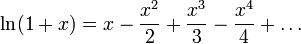 |
(1) |
В частности,
Формула (1) не имеет большой практической ценности из-за того, что ряд очень медленно сходится и значение x ограничено весьма узким диапазоном. Однако нетрудно получить из неё более удобную формулу:
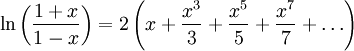 |
(2) |
Этот ряд сходится быстрее, а кроме того, левая часть формулы теперь может выразить логарифм любого положительного числа.
Связь с десятичным логарифмом: 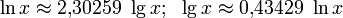
Десятичные логарифмы
Рис. 2. Логарифмическая шкала
Логарифмы по основанию 10 (обозначение: lg a) до изобретения калькуляторов широко применялись для вычислений. Неравномерная шкала десятичных логарифмов обычно наносится и на логарифмические линейки. Подобная шкала широко используется в различных областях науки, например:
- Физика — интенсивность звука (децибелы).
- Астрономия — шкала яркости звёзд.
- Химия — активность водородных ионов (pH).
- Сейсмология — шкала Рихтера.
- Теория музыки — нотная шкала, по отношению к частотам нотных звуков.
Логарифмическая шкала также широко применяется для выявления показателя степени в степенных зависимостях и коэффициента в показателе экспоненты. При этом график, построенный в логарифмическом масштабе по одной или двум осям, принимает вид прямой, более простой для исследования.
Комплексный логарифм
Многозначная функция
Для комплексных чисел логарифм определяется так же, как вещественный. Начнём с натурального логарифма, который обозначим 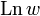
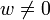
,
то логарифм 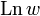
Здесь 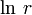

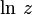
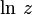
Из формулы следует:
- Вещественная часть логарифма определяется по формуле:
- Логарифм отрицательного числа находится по формуле:
Примеры (приведено главное значение логарифма):
Аналогично рассматриваются комплексные логарифмы с другим основанием. Следует, однако, быть осторожным при преобразованиях комплексных логарифмов, принимая во внимание, что они многозначны, и поэтому из равенства логарифмов каких-либо выражений не следует равенство этих выражений. Пример ошибочного рассуждения:
- iπ = ln( − 1) = ln(( − i)2) = 2ln( − i) = 2( − iπ / 2) = − iπ — явная нелепость.
Отметим, что слева стоит главное значение логарифма, а справа — значение из нижележащей ветви (k = − 1). Причина ошибки — неосторожное использования свойства 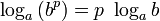
Аналитическое продолжение
Рис. 3. Комплексный логарифм (мнимая часть)
Логарифм комплексного числа также может быть определён как аналитическое продолжение вещественного логарифма на всю комплексную плоскость. В явном виде продолжение логарифма вдоль кривой Γ, не проходящей через 0, можно осуществить по формуле (соответствующую функцию также обозначаем ln)
При этом, если Γ — простая кривая (без самопересечений), то для чисел, лежащих на ней, логарифмические тождества можно применять без опасений, например
Из формулы аналитического продолжения следует, что на любой ветви логарифма
Для любой окружности S, охватывающей точку 0:
Интеграл берётся в положительном направлении (против часовой стрелки). Это тождество лежит в основе теории вычетов.
Риманова поверхность
Комплексная логарифмическая функция — пример римановой поверхности; её мнимая часть (рис. 3) состоит из бесконечного числа ветвей, закрученных наподобие спирали. Эта поверхность односвязна; её единственный нуль (первого порядка) получается при z = 1, особые точки: z = 0 и 
Риманова поверхность логарифма является универсальной накрывающей для комплексной плоскости без точки 0.
Исторический очерк
Вещественный логарифм
Потребность в сложных расчётах в XVI веке быстро росла, и значительная часть трудностей была связана с умножением и делением многозначных чисел. В конце века нескольким математикам, почти одновременно, пришла в голову идея: заменить трудоёмкое умножение на простое сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной. Тогда и деление автоматически заменяется на неизмеримо более простое и надёжное вычитание. Первым эту идею опубликовал в своей книге «Arithmetica integra» Михаэль Штифель, который, впрочем, не приложил серьёзных усилий для реализации своей идеи.
В 1614 году шотландский математик-любитель Джон Непер опубликовал на латинском языке сочинение под названием «Описание удивительной таблицы логарифмов». В нём было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1′. Термин логарифм, предложенный Непером, утвердился в науке.
Понятия функции тогда ещё не было, и Непер определил логарифм кинематически, сопоставив равномерное и логарифмически-замедленное движение. В современной записи модель Непера можно изобразить дифференциальным уравнением: dx/x = -dy/M, где M — масштабный множитель, введенный для того, чтобы значение получилось целым числом с нужным количеством знаков (десятичные дроби тогда ещё не нашли широкого применения). Непер взял M = 10000000.
Строго говоря, Непер табулировал не ту функцию, которая сейчас называется логарифмом. Если обозначить его функцию LogNap(x), то она связана с натуральным логарифмом следующим образом:
Очевидно, LogNap(M) = 0, то есть логарифм «полного синуса» есть нуль — этого и добивался Непер своим определением. LogNap(0) = ∞.
Основное свойство логарифма Непера: если величины образуют геометрическую прогрессию, то их логарифмы образуют прогрессию арифметическую. Однако правила логарифмирования для неперовой функции отличались от правил для современного логарифма.
Например, LogNap(ab) = LogNap(a) + LogNap(b) — LogNap(1).
К сожалению, все значения таблицы Непера содержали вычислительную ошибку после шестого знака. Однако это не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики, включая Кеплера.
В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов — незаменимый инструмент инженера.
Близкое к современному понимание логарифмирования — как операции, обратной возведению в степень — впервые появилось у Валлиса и Иоганна Бернулли, а окончательно было узаконено Эйлером в XVIII веке. В книге «Введение в анализ бесконечных» (1748) Эйлер дал современные определения как показательной, так и логарифмической функций, привёл разложение их в степенные ряды, особо отметил роль натурального логарифма.
Эйлеру принадлежит и заслуга распространения логарифмической функции на комплексную область.
Комплексный логарифм
Первые попытки распространить логарифмы на комплексные числа предпринимали на рубеже XVII—XVIII веков Лейбниц и Иоганн Бернулли, однако создать целостную теорию им не удалось — в первую очередь по той причине, что тогда ещё не было ясно определено само понятие логарифма. Дискуссия по этому поводу велась сначала между Лейбницем и Бернулли, а в середине XVIII века — между Даламбером и Эйлером. Бернулли и Даламбер считали, что следует определить log(-x) = log(x). Полная теория логарифмов отрицательных и комплексных чисел была опубликована Эйлером в 1747—1751 годах и по существу ничем не отличается от современной.
Хотя спор продолжался (Даламбер отстаивал свою точку зрения и подробно аргументировал её в статье своей «Энциклопедии» и в других трудах), однако точка зрения Эйлера быстро получила всеобщее признание.
Логарифмические таблицы
Логарифмические таблицы
Из свойств логарифма следует, что вместо трудоёмкого умножения многозначных чисел достаточно найти (по таблицам) и сложить их логарифмы, а потом по тем же таблицам выполнить потенцирование, то есть найти значение результата по его логарифму. Выполнение деления отличается только тем, что логарифмы вычитаются. Лаплас говорил, что изобретение логарифмов «продлило жизнь астрономов», многократно ускорив процесс вычислений.
При переносе десятичной запятой в числе на n разрядов значение десятичного логарифма этого числа изменяется на n. Например, lg8314,63 = lg8,31463 + 3. Отсюда следует, что достаточно составить таблицу десятичных логарифмов для чисел в диапазоне от 1 до 10.
Первые таблицы логарифмов опубликовал Джон Непер (1614), и они содержали только логарифмы тригонометрических функций, причём с ошибками. Независимо от него свои таблицы опубликовал Иост Бюрги, друг Кеплера (1620). В 1617 году оксфордский профессор математики Генри Бригс опубликовал таблицы, которые уже включали десятичные логарифмы самих чисел, от 1 до 1000, с 8 (позже — с 14) знаками. Но и в таблицах Бригса обнаружились ошибки. Первое безошибочное издание на основе таблиц Вега (1783) появилось только в 1857 году в Берлине (таблицы Бремивера).
В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого. В СССР выпускались несколько сборников таблиц логарифмов.
- Брадис В. М. Четырехзначные математические таблицы. 44-е издание, М., 1973.
Таблицы Брадиса (1921) использовались в учебных заведениях и в инженерных расчётах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты.
- Вега Г. Таблицы семизначных логарифмов, 4-е издание, М., 1971.
Профессиональный сборник для точных вычислений.
- Пятизначные таблицы натуральных значений тригонометрических величин, их логарифмов и логарифмов чисел, 6 изд., М.: Наука, 1972.
- Таблицы натуральных логарифмов, 2-е издание, в 2 томах, М.: Наука, 1971.
См. также
- Комплексное число
- Показательная функция
- Простаферетическая функция
- Системы счисления
- Еричная система счисления
Литература
- Выгодский М. Я. Справочник по элементарной математике. — М.: АСТ, 2003. — ISBN 5-17-009554-6
- История математики под редакцией А. П. Юшкевича в трёх томах, М.: Наука.
-
- Том 1 С древнейших времен до начала Нового времени. (1970)
- Том 2 Математика XVII столетия. (1970)
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, тома I, II. — М.: Наука, 1960.
Wikimedia Foundation.
2010.

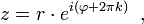 где
где 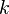 — произвольное целое число
— произвольное целое число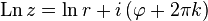
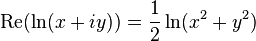
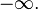

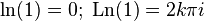

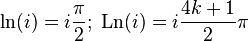
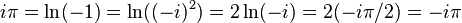 — явная ошибка.
— явная ошибка.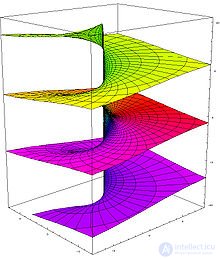
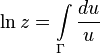
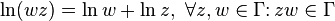
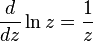
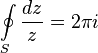
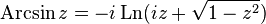
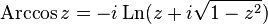
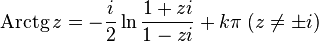

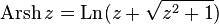 — обратный гиперболический синус
— обратный гиперболический синус 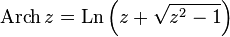 — обратный гиперболический косинус
— обратный гиперболический косинус 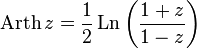 — обратный гиперболический тангенс
— обратный гиперболический тангенс 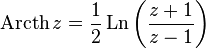 — обратный гиперболический котангенс
— обратный гиперболический котангенс 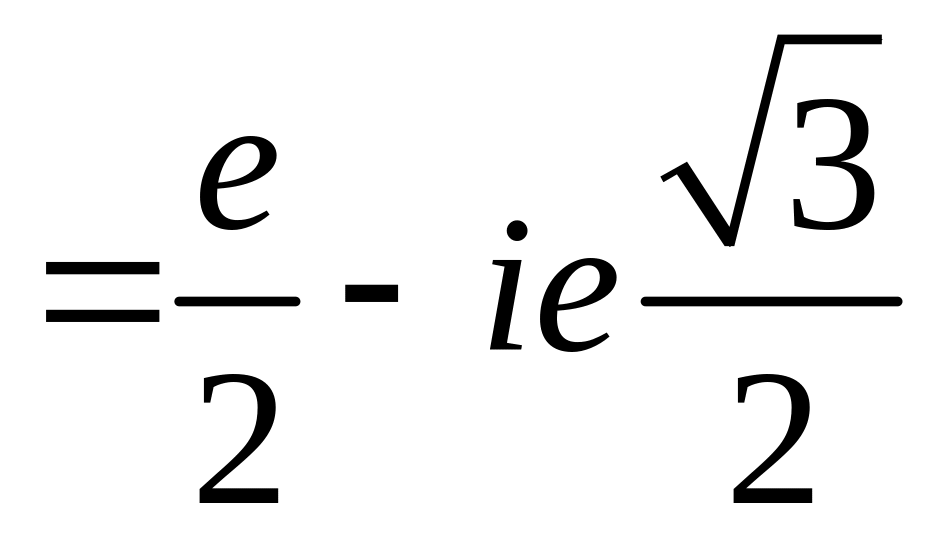
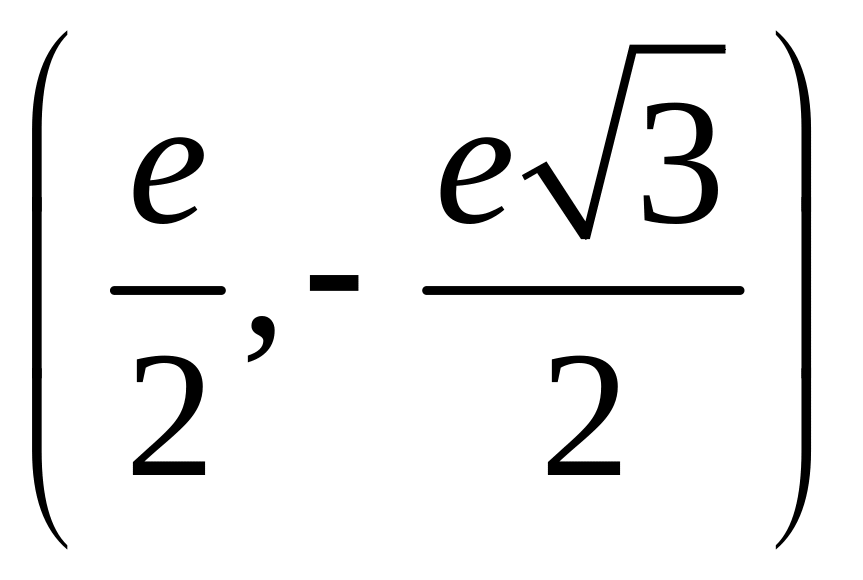
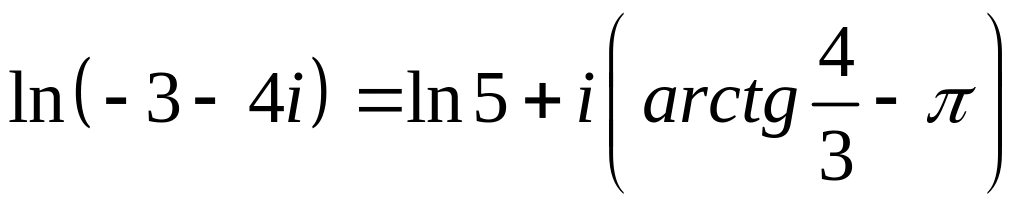
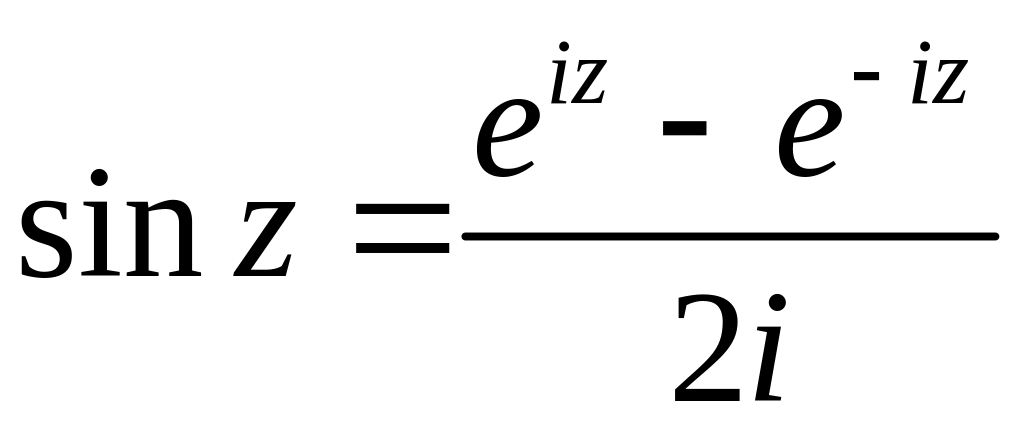
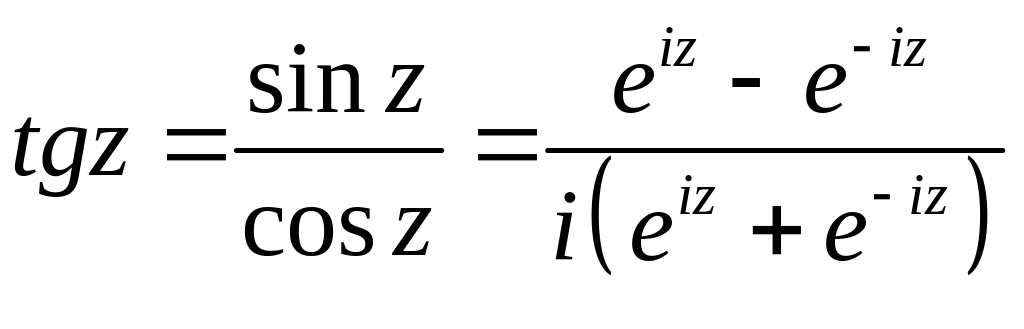
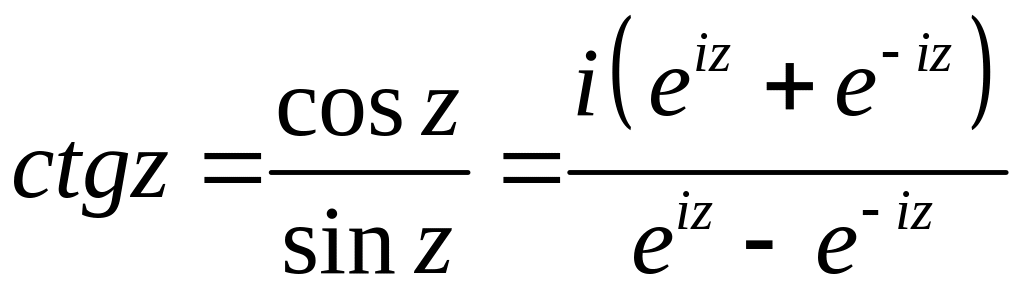
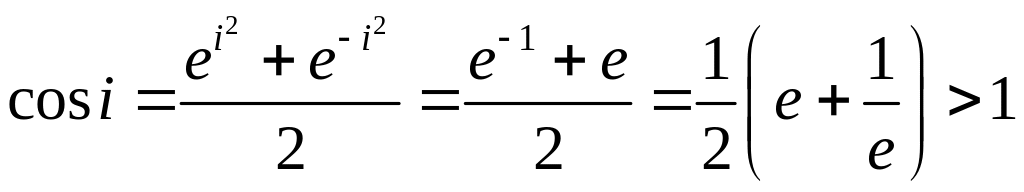
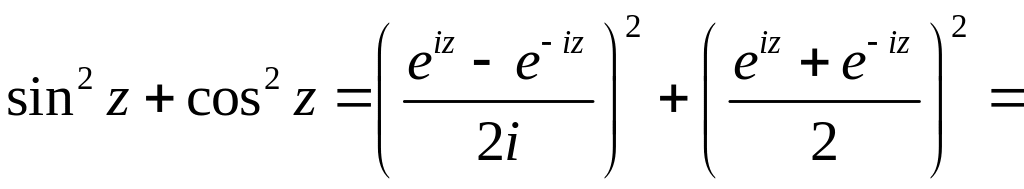
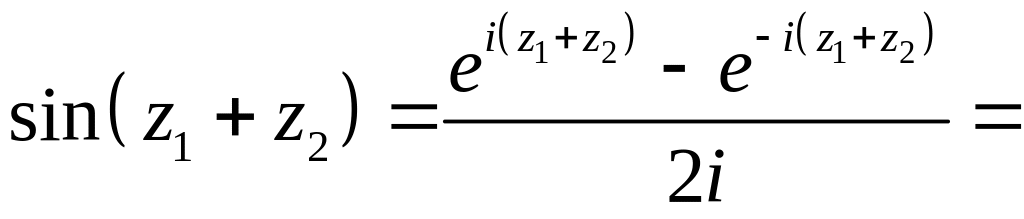
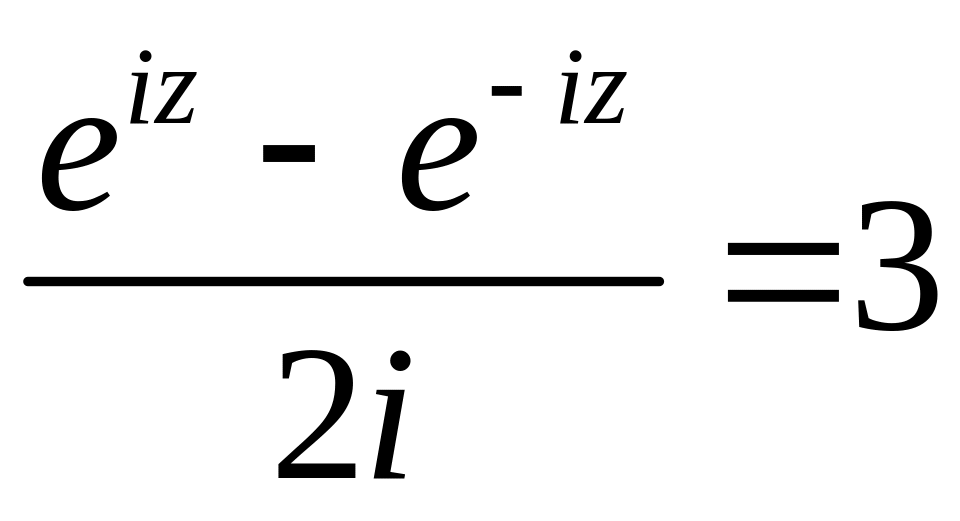

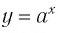
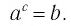
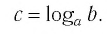
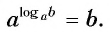
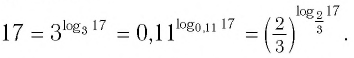
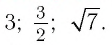
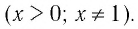
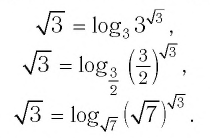
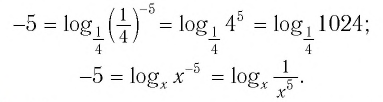
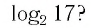
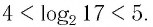
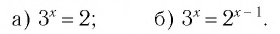
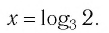
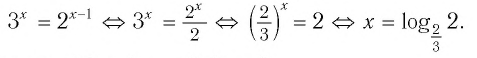
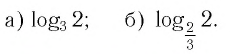
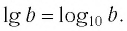
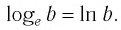
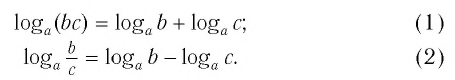
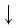
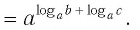
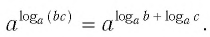
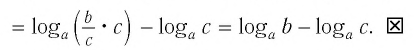

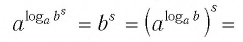
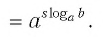
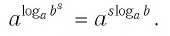

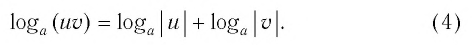
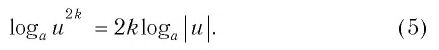
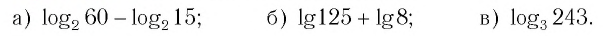
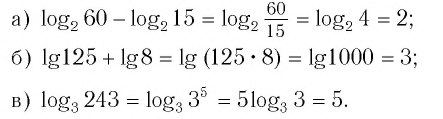
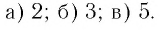

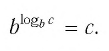
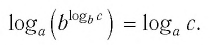
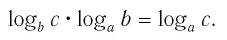

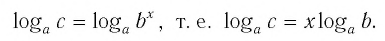
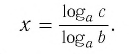
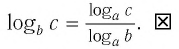

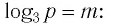
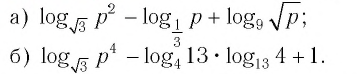
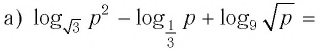
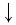
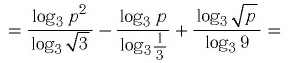
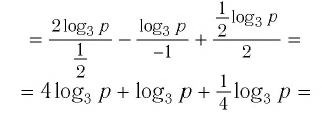
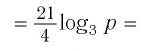
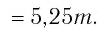
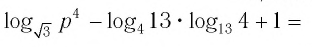
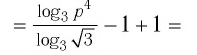
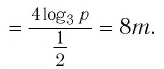
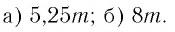

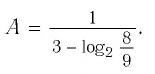
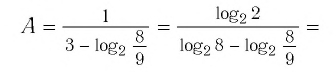
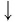
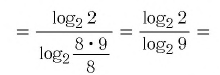
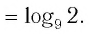
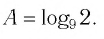
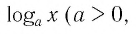
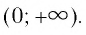
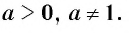
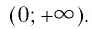
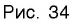
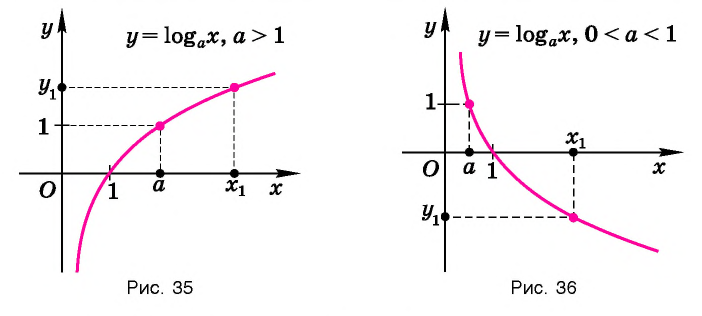
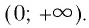
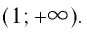 И при 0 < а < 1 логарифмическая функция принимает отрицательные значения на интервале
И при 0 < а < 1 логарифмическая функция принимает отрицательные значения на интервале 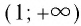 и принимает положительные значения на интервале (0; 1).
и принимает положительные значения на интервале (0; 1).
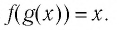
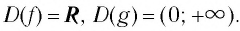
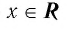
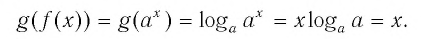
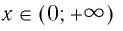
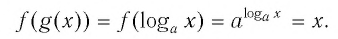
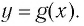
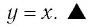
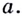
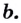
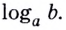
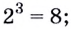
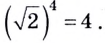
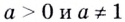
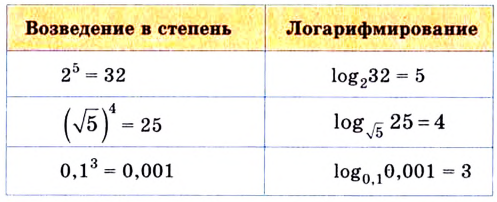
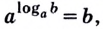
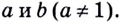
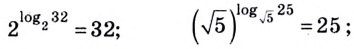
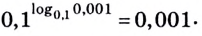
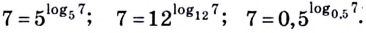
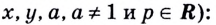
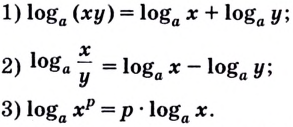
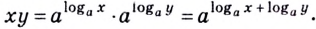
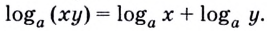
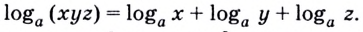
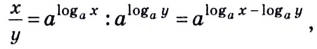
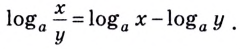
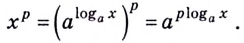
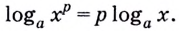
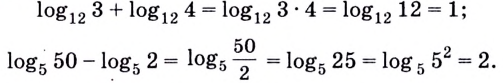
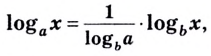
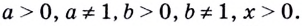
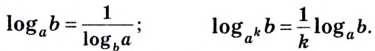
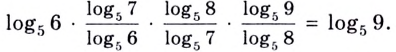
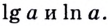
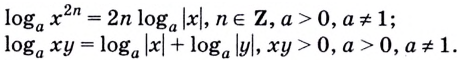
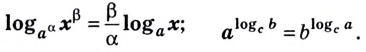
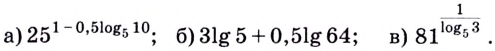
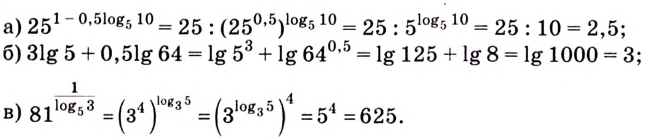
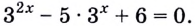
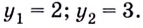
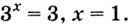
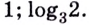
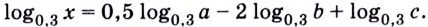
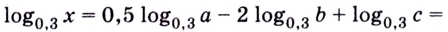
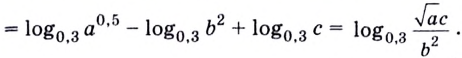
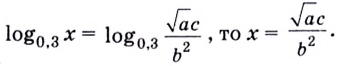
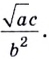
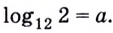
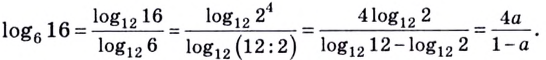
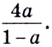

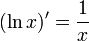
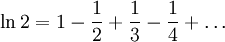
 ,
,