Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Главные направления аффинного преобразования плоскости
|
|
10/09/14 |
Здравствуйте. Подскажите, как решать задачи такого типа:
|
|
|
|
|
Brukvalub |
Re: Главные направления аффинного преобразования плоскости
|
||
01/03/06 |
Вы применили правильный подход, такой ход решения должен был привести к правильному результату.
|
||
|
|
|||
|
ИСН |
Re: Главные направления аффинного преобразования плоскости
|
||
18/05/06 |
Только прямые как-то не очень перпендикулярны.
|
||
|
|
|||
|
Viktor92 |
Re: Главные направления аффинного преобразования плоскости
|
|
10/09/14 |
Вы применили правильный подход, такой ход решения должен был привести к правильному результату. Спасибо, что-то я поначалу не довёл дело до конца, вот результат: направляющие векторы сингулярных направлений Только прямые как-то не очень перпендикулярны. Да, Вы правы, надо вот так:
|
|
|
|
Модераторы: Модераторы Математики, Супермодераторы
-
Образ прямой линии.
Начать изучение
-
Изменение площадей при аффинном преобразовании.
Начать изучение
-
Образы линий второго порядка.
Начать изучение
-
Разложение ортогонального преобразования.
Начать изучение
-
Разложение аффинного преобразования.
Начать изучение
Образ прямой линии.
Изучим геометрические свойства аффинных преобразований. Ниже (f) обозначает аффинное преобразование, записываемое в декартовой системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}) формулами
$$
x^{*}=a_{1}x+b_{1}y+c_{1}, y^{*}=a_{2}x+b_{2}y+c_{2}.label{ref1}
$$
при условии
$$
begin{vmatrix}
a_{1}& b_{1}\
a_{2}& b_{2}
end{vmatrix} neq 0.label{ref2}
$$
Рассмотрим на плоскости прямую линию с уравнением (boldsymbol{r}=boldsymbol{r}_{0}+boldsymbol{a}t) и найдем ее образ при преобразовании (f). (Под образом прямой понимается множество образов ее точек.) Радиус-вектор образа (M^{*}) произвольной точки (M) можно вычислить так:
$$
overrightarrow{OM^{*}}=overrightarrow{Of(O)}+foverrightarrow{(O)M^{*}}=boldsymbol{c}+f(boldsymbol{r}).nonumber
$$
Здесь (boldsymbol{c}) — постоянный вектор (overrightarrow{Of}(O)), а (boldsymbol{r}) — радиус-вектор точки (M). Согласно (11) §2 мы получаем
$$
overrightarrow{OM^{*}}=boldsymbol{c}+f(boldsymbol{r}_{0})+f(boldsymbol{a})t.label{ref3}
$$
Так как (f) — аффинное преобразование и (boldsymbol{a} neq boldsymbol{0}), то (boldsymbol{a}) перейдет в вектор (f(boldsymbol{a}) neq 0), и уравнение eqref{ref3} является уравнением прямой линии. Итак, образы всех точек прямой (boldsymbol{r}=boldsymbol{r}_{0}+boldsymbol{a}t) лежат на прямой eqref{ref3}.
Более того, преобразование (f) определяет взаимно однозначное отображение одной прямой на другую, так как при сделанном здесь выборе начальных точек и направляющих векторов точка (M^{*}) имеет на прямой eqref{ref3} то же значение параметра (t), что и точка (M) на исходной прямой. Отсюда мы получаем первое утверждение.
Утверждение 1.
При аффинном преобразовании:
- прямая линия переходит в прямую линию;
- отрезок переходит в отрезок;
- параллельные прямые переходят в параллельные.
Доказательство.
Для доказательства второго утверждения достаточно заметить, что отрезок прямой состоит из таких точек, у которых значения параметра удовлетворяют неравенству вида (t_{1} leq t leq t_{2}) Третье утверждение следует из того, что при аффинном преобразовании коллинеар-ные векторы переходят в коллинеарные.
Утверждение 2.
При аффинном преобразовании отношение длин параллельных отрезков не изменяется.
Доказательство.
Пусть отрезки (AB) и (CD) параллельны. Это значит, что существует такое число (lambda), что (overrightarrow{AB}=lambda overrightarrow{CD}). Образы векторов (overrightarrow{AB}) и (overrightarrow{CD}) связаны той же зависимостью (overrightarrow{A^{*}B^{*}}=lambda overrightarrow{C^{*}D^{*}}). Отсюда вытекает, что
$$
frac{|overrightarrow{AB}|}{|overrightarrow{CD}|}=frac{|overrightarrow{A^{*}B^{*}}|}{|overrightarrow{C^{*}D^{*}}|}=|lambda|.nonumber
$$
Следствие.
Если точка (C) делит отрезок (AB) в некотором отношении (lambda), то ее образ (C^{*}) делит образ (A^{*}B^{*}) отрезка (AB) в том же отношении (lambda).
Изменение площадей при аффинном преобразовании.
Для начала рассмотрим ориентированный параллелограмм. Выберем общую декартову систему координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}) и обозначим через ((p_{1}, p_{2})) и ((q_{1}, q_{2})) компоненты векторов (boldsymbol{p}) и (boldsymbol{q}), на которых он построен. Площадь параллелограмма мы можем вычислить, пользуясь формулой:
$$
S_{pm}=S_{pm} (boldsymbol{p}, boldsymbol{q})=(p_{1}q_{2}-p_{2}q_{1}) S_{pm} (boldsymbol{e}_{1}, boldsymbol{e}_{2}).nonumber
$$
Пусть аффинное преобразование (f) записывается в выбранной системе координат формулами eqref{ref1}. Из ранее доказанного утверждения следует, что векторы (f(boldsymbol{p})) и (f(boldsymbol{q})) имеют в базисе (f(boldsymbol{e}_{1}), f(boldsymbol{e}_{2})) те же компоненты ((p_{1}, p_{2})) и ((q_{1}, q_{2})), что и векторы (boldsymbol{p}) и (boldsymbol{q}) в базисе (boldsymbol{e}_{1}, boldsymbol{e}_{2}). Образ параллелограмма построен на векторах (f(boldsymbol{p})) и (f(boldsymbol{q})), и площадь его равна
$$
S_{pm}^{*}=S_{pm} (f(boldsymbol{p}), f(boldsymbol{q}))=(p_{1}q_{2}-p_{2}q_{1}) S_{pm} (f(boldsymbol{e}_{1}), f(boldsymbol{e}_{2})).nonumber
$$
Вычислим последний множитель. Как мы знаем из уже доказанного утверждения 7, координаты векторов (f(boldsymbol{e}_{1}), f(boldsymbol{e}_{2})) равны соответственно ((a_{1}, a_{2})) и ((b_{1}, b_{2})). Поэтому (S_{pm} (f(boldsymbol{e}_{1}), f(boldsymbol{e}_{2}))=(a_{1}b_{2}-a_{2}b_{1}) S_{pm} (boldsymbol{e}_{1}, boldsymbol{e}_{2})) и
$$
S_{pm}^{*}=(p_{1}q_{2}-p_{2}q_{1})(a_{1}b_{2}-a_{2}b_{1}) S_{pm} (boldsymbol{e}_{1}, boldsymbol{e}_{2}).nonumber
$$
Отсюда мы видим, что
$$
frac{S_{pm}^{*}}{S_{pm}}=begin{vmatrix}
a_{1}& b_{1}\
a_{2}& b_{2}
end{vmatrix}.label{ref4}
$$
Таким образом, отношение площади образа ориентированного параллелограмма к площади этого параллелограмма одинаково для всех параллелограммов и равно (a_{1}b_{2}-a_{2}b_{1}).
Отсюда следует, что данный детерминант не зависит от выбора системы координат, в которой записано преобразование, хотя он вычисляется по коэффициентам, зависящим от системы координат. Эта величина — инвариант, выражающий геометрическое свойство преобразования.
Из формулы eqref{ref4} видно, что отношение площади образа неориентированного параллелограмма к его площади равно
$$
S^{*}/S=|a_{1}b_{2}-a_{2}b_{1}|.label{ref5}
$$
Если (a_{1}b_{2}-a_{2}b_{1} > 0), то ориентации всех ориентированных параллелограммов сохраняются при преобразовании, а если (a_{1}b_{2}-a_{2}b_{1} < 0), то для каждого ориентированного параллелограмма ориентация образа противоположна его ориентации.
Займемся теперь площадями других фигур. Каждый треугольник может быть дополнен до параллелограмма, площадь которого равна удвоенной площади треугольника. Поэтому отношение площади образа треугольника к площади этого треугольника удовлетворяет равенству eqref{ref5}.
Каждый многоугольник может быть разбит на треугольники. Следовательно, формула eqref{ref5} справедлива и для произвольных многоугольников.
Мы не будем здесь касаться определения площади произвольной криволинейной фигуры. Скажем лишь, что в тех случаях, когда эта площадь определена, она равна пределу площадей некоторой последовательности многоугольников, вписанных в рассматриваемую фигуру. Из теории пределов известно следующее предположение: если последовательность (S_{n}) стремится к пределу (S), то последовательность (delta S_{n}), где (delta) постоянное, стремится к пределу (delta S). На основании этого предложения мы заключаем, что формула eqref{ref5} справедлива в самом общем случае.
В качестве примера найдем выражение площади эллипса через его полуоси. Ранее мы доказали, что эллипс с полуосями (a) и (b) может быть получен сжатием окружности радиуса (a) к прямой, проходящей через ее центр. Коэффициент сжатия равен (b/a). В одном из примеров мы получили координатную запись сжатия к прямой (x^{*}=x), (y^{*}=lambda y). Детерминант из коэффициентов в этих формулах равен (lambda), то есть в нашем случае (b/a). Таким образом, отношение площади эллипса к площади окружности равно (b/a), и эта площадь равна (S=(b/a)pi a^{2}). Окончательно имеем
$$
S=pi ab.nonumber
$$
Образы линий второго порядка.
Мы видели, что прямая линия переходит в прямую. Это частный случай следующего утверждения.
Утверждение 3.
Аффинное преобразование переводит алгебраическую линию в алгебраическую линию того же порядка.
Доказательство.
В самом деле, пусть линия (L) в декартовой системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}) имеет алгебраическое уравнение порядка (p). Мы уже доказали, что образы всех точек линии (L) при аффинном преобразовании (f) имеют в системе координат (f(O), f(boldsymbol{e}_{1}), f(boldsymbol{e}_{2})) те же координаты, что и их прообразы в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}). Следовательно, координаты образов в системе (f(O), f(boldsymbol{e}_{1}), f(boldsymbol{e}_{2})) связаны тем же алгебраическим уравнением порядка (p). Этого достаточно, чтобы сделать нужное нам заключение.
Из доказанного выше утверждения, в частности, следует, что линия второго порядка при аффинном преобразовании перейдет в линию второго порядка. Мы докажем более сильное утверждение. Как мы уже знаем, линии второго порядка можно разделить на семь классов. Мы увидим, что класс линии сохраняется при аффинном преобразовании. На этом основании классы линий, перечисленные в указанной теореме, называются аффинными классами. Итак, докажем новое утверждение.
Утверждение 4.
Линия второго порядка, принадлежащая к одному из аффинных классов, при любом аффинном преобразовании может перейти только в линию того же класса. Каждую линию второго порядка подходящим аффинным преобразованием можно перевести в любую другую линию того же аффинного класса.
Доказательство.
Линию мы назовем ограниченной, если она лежит внутри некоторого параллелограмма. Легко видеть, что при аффинном преобразовании ограниченная линия должна перейти в ограниченную, а неограниченная — в неограниченную.
- Эллипс — ограниченная линия второго порядка. Кроме эллипсов ограничены только линии, состоящие из одной точки, то есть пары мнимых пересекающихся прямых. Поскольку эллипс ограничен и состоит больше, чем из одной точки, он может перейти только в эллипс.
- Гипербола состоит из двух отдельных ветвей. Это свойство можно сформулировать так, что будет ясна его неизменность при аффинных преобразованиях. Именно, существует прямая линия, не пересекающая гиперболу, но пересекающая некоторые ее хорды.Из всех линий второго порядка только гиперболы и пары параллельных прямых обладают этим свойством. У гиперболы ветви не прямые линии, и потому при аффинном преобразовании она может перейти только в гиперболу.
- Парабола — неограниченная линия второго порядка, состоящая из одного непрямолинейного куска. Этим свойством не обладают никакие другие линии второго порядка, и потому парабола может перейти только в параболу.
- Если линия второго порядка представляет собой точку (пару мнимых пересекающихся прямых), прямую (пару совпавших прямых), пару пересекающихся или пару параллельных прямых, то из доказанных ранее свойств аффинных преобразований следует, что эта линия не может перейти в линию никакого другого класса.
Докажем вторую часть предложения. В уже доказанной нами теореме канонические уравнения линий второго порядка написаны в декартовой прямоугольной системе координат и содержат параметры (a, b, …) Если мы откажемся от ортонормированности базиса, то сможем произвести дальнейшие упрощения канонических уравнений и привести их к виду, не содержащему параметров. Например, замена координат (x’=x/a), (y’=y/b) переводит уравнение эллипса (x^{2}a^{2}+y^{2}b^{2}=1) в уравнение (x’^{2}+y’^{2}=1), каковы бы ни были (a) и (b). (Последнее уравнение не есть уравнение окружности, так как новая система координат не декартова прямоугольная.)
Читатель без труда покажет, что канонические уравнения линий второго порядка переходом к подходящей системе координат могут быть преобразованы в уравнения:
- (x^{2}+y^{2}=1);
- (x^{2}+y^{2}=0);
- (x^{2}-y^{2}=1);
- (x^{2}-y^{2}=0);
- (y^{2}=2x);
- (y^{2}-1=0);
- (y^{2}=0).
Такую систему координат мы назовем аффинной канонической системой координат.
Из ранее доказанного утверждения следует, что аффинное преобразование, которое совмещает аффинные канонические системы координат двух линий одного аффинного класса, совмещает и эти линии. Это заканчивает доказательство.
Разложение ортогонального преобразования.
Теорема 1.
Каждое ортогональное преобразование раскладывается в произведение параллельного переноса, поворота и, возможно, осевой симметрии.
Доказательство.
Пусть (f) — ортогональное преобразование и (vartriangle ABC) — равнобедренный прямоугольный треугольник с прямым углом (A). При преобразовании (f) он перейдет в равный ему треугольник (vartriangle A^{*}B^{*}C^{*}) с прямым углом при вершине (A^{*}). Теорема будет доказана, если, производя последовательно параллельный перенос (p), поворот (q) и (в случае необходимости) осевую симметрию (r), мы сможем совместить треугольники (ABC) и (A^{*}B^{*}C^{*}). Действительно, произведение (rqp) — аффинное преобразование так же, как и (f), а аффинное преобразование однозначно определяется образами трех точек, не лежащих на одной прямой. Поэтому (rqp) совпадает с (f).
Итак, переведем (A) и (A^{*}) параллельным переносом (p) на вектор (overrightarrow{AA^{*}}) (если (A=A^{*}), то (p) — тождественное преобразование). Затем поворотом (q) вокруг точки (A^{*}) совместим (p(B)) с (B^{*}) (возможно, и это преобразование окажется тождественным). Точка (q(p(C))) либо совпадает с (C^{*}), либо симметрична ей относительно прямой (A^{*}B^{*}). В первом случае цель уже достигнута, а во втором потребуется осевая симметрия относительно указанной прямой. Теорема доказана.
Следует иметь в виду, что полученное разложение ортогонального преобразования не однозначно. Более того, можно поворот или параллельный перенос разложить в произведение осевых симметрий, произведение параллельного переноса и поворота представить как один поворот и так далее. Мы не будем уточнять, как это сделать, а выясним следующее общее свойство всех таких разложений.
Утверждение 5.
При любом разложении ортогонального преобразования в произведение любого числа параллельных переносов, поворотов и осевых симметрий четность числа осевых симметрий, входящих в разложение, одна и та же.
Доказательство.
Для доказательства рассмотрим на плоскости произвольный базис и проследим за изменением его ориентации (направления кратчайшего поворота от (boldsymbol{e}_{1}) к (boldsymbol{e}_{2})) при осуществляемых преобразованиях. Заметим, что поворот и параллельный перенос не меняют ориентацию ни одного базиса, а осевая симметрия меняет ориентацию любого базиса. Поэтому, если данное ортогональное преобразование меняет ориентацию базиса, то в любое его разложение должно входить нечетное число осевых симметрий. Если же ориентация базиса не меняется, то число осевых симметрий, входящих в разложение, может быть только четным.
Определение.
Ортогональные преобразования, которые могут быть разложены в произведение параллельного переноса и поворота, называются ортогональными преобразованиями первого рода, а остальные — ортогональными преобразованиями второго рода.
Ортогональное преобразование в декартовой прямоугольной системе координат записывается формулами:
$$
begin{array}{cc}
& x^{*}=x cos varphi mp y sin varphi+c_{1},\
& y^{*}=x sin varphi pm y cos varphi+c_{2}.
end{array}.nonumber
$$
При верхних знаках коэффициентов у (y) в этих формулах детерминант, составленный из коэффициентов, равен +1, а при нижних знаках он равен —1. Отсюда и из формулы eqref{ref4} следует следующее утверждение.
Утверждение 6.
Ортогональное преобразование первого рода записывается в декартовой прямоугольной системе координат формулами
$$
begin{array}{cc}
& x^{*}=x cos varphi mp y sin varphi+c_{1},\
& y^{*}=x sin varphi pm y cos varphi+c_{2}.
end{array}.nonumber
$$
с верхними знаками у коэффициентов при (y), а ортогональное преобразование второго рода — с нижними знаками.
Разложение аффинного преобразования.
Мы видели, насколько аффинное преобразование может изменить плоскость: окружность может перейти в эллипс, правильный треугольник — в совершенно произвольный. Казалось бы, никакие углы при этом сохраниться не могут. Однако имеет место следующее утверждение
Утверждение 7.
Для каждого аффинного преобразования существуют две взаимно перпендикулярные прямые, которые переходят во взаимно перпендикулярные прямые.
Доказательство.
Для доказательства рассмотрим какую-либо окружность. При данном аффинном преобразовании она перейдет в эллипс. Каждая ось эллипса — множество середин хорд, параллельных другой оси. При аффинном преобразовании хорда перейдет в хорду, параллельность должна сохраниться, а середина отрезка переходит в середину его образа. Поэтому прообразы осей эллипса — отрезки, обладающие тем же свойством: каждый из них есть множество середин хорд окружности, параллельных другому отрезку. Такие отрезки непременно являются двумя взаимно перпендикулярными диаметрами окружности. Это то, что нам требовалось: существуют два взаимно перпендикулярных диаметра окружности, которые переходят во взаимно перпендикулярные отрезки — оси эллипса.
Стоит отметить один особый случай: окружность при аффинном преобразовании может перейти в окружность. В этом случае то же рассуждение проходит с любыми двумя взаимно перпендикулярными диаметрами окружности-образа. Очевидно, что при этом любые два взаимно перпендикулярных направления остаются перпендикулярными.
Определение.
Два взаимно перпендикулярных направления называются главными или синугулярными направлениями аффинного преобразования (f), если они переходят во взаимно перпендикулярные направления.
Теорема 2.
Каждое аффинное преобразование раскладывается в произведение ортогонального преобразования и двух сжатий к двум взаимно перпендикулярным прямым.
Доказательство.
Доказательство аналогично доказательству теоремы 1. Рассмотрим аффинное преобразование (f) и выберем равнобедренный прямоугольный треугольник (ABC) так, чтобы его катеты (AB) и (AC) были направлены вдоль главных направлений преобразования (f). Обозначим через (A^{*}), (B^{*}) и (C^{*}) образы его вершин. Сделаем такое ортогональное преобразование (g), при котором (g(A)=A^{*}), а точки (g(B)) и (g(C)) лежат соответственно на лучах (A^{*}B^{*}) и (A^{*}C^{*}). (Этого легко добиться, как и в теореме 1, параллельным переносом, поворотом и осевой симметрией.)
Пусть (lambda=|A^{*}B^{*}|/|A^{*}g(B)|), a (mu=|A^{*}C^{*}|/|A^{*}g(C)|). Тогда сжатие (p_{1}) к прямой (A^{*}C^{*}) в отношении (lambda) переведет (g(B)) в (p_{1}g(B)=B^{*}) и не сдвинет точек (A^{*}) и (g(C)). Аналогично, сжатие (p_{2}) к прямой (A^{*}B^{*}) переведет (g(C)) в (p_{2}g(C)=C^{*}) и не сдвинет точек прямой (A^{*}B^{*}).
Это означает, что произведение (p_{2}p_{1}g) переводит точки (A), (B) и (C) в точки (A^{*}), (B^{*}) и (C^{*}) так же, как и заданное нам преобразование (f). Согласно ранее доказанному утверждению имеем (p_{2}p_{1}g=f), как и требовалось.
Здравствуйте.
Имеется следующее задание: представить аффинное преобразование x*=2x+5y, y*=–11x+10y в виде произведения ортогонального преобразования и двух сжатий к двум взаимно перпендикулярным прямым.
Первое, что мне приходит в голову, – это найти главные направления: берем единичную окружность, под действием преобразования она перейдет в эллипс, уравнение которого в исходной системе координат мы можем найти. Затем ищем каноническую систему координат для эллипса (избавляемся от произведений xy), оси этой канонической системы координат перешли – почти то, что нужно, останется только найти прообраз этих осей.
Зная уравнения главных направлений, мы сможем повернуть окружность так, чтобы эти самые её диаметры встали нужным образом и, возможно, удастся как-нибудь подобрать коэффициенты сжатий.
В общем, первый вопрос: как можно проще решить эту задачу?
Второй вопрос: как проще найти главные направления преобразования?
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
Добавил:
Yanus
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Скачиваний:
59
Добавлен:
15.06.2014
Размер:
1.44 Mб
Скачать
Линейные
операторы, преобразующие плоскость
саму в себя (то есть линейные
операторы
вида
)
иимеющие
обратный,
играют важную с практической точки
зрения роль и потому выделяются в
специальный класс.
|
Определение 5.4.1. |
Линейный |
|
Теорема 5.4.1. |
Если |
|
Доказательство:
По Теорема |
|
Теорема 5.4.2. |
Каждое |
|
Доказательство:
Поскольку Теорема |
Для
выяснения геометрического смысла
числовых характеристик матрицы аффинного
преобразования переформулируем
определение 1.8.3. ориентации
пары неколлинеарных векторов
на плоскости, использовавшись операцией
векторного произведения.
|
Определение 5.4.2. |
Пусть |
Тогда
будет справедлива
|
Теорема |
1. |
|
2. |
|
Доказательство:
Рассмотрим |
|
|
|
Рисунок
По
то |
|
Наконец Теорема |
|
Теорема |
При |
|
Доказательство:
Пусть
тогда
А,
Сопоставляя Теорема |
Рассмотрим
теперь вопрос о том, что происходит с
различными геометрическими объектами
на плоскости при аффинном преобразовании.
|
Теорема |
При |
|
Доказательство:
Пусть
Предположим Теорема |
|
Теорема |
При |
|
Доказательство:
Предположим,
Рассмотрим
Однако
Если Теорема |
|
Теорема |
При |
|
|
Доказательство:
Пусть
|
M3 M2 M1
Рисунок |
|
Если
|
||
|
Аналогично Заметим,
Теорема |
Отметим
также, что из теоремы 5.4.7. непосредственно
вытекает, что при аффинном преобразовании
отрезок прямой переходит в отрезок.
|
Теорема |
При |
|
|
Доказательство:
Пусть M2
M1 M3 Рисунок |
|
|
Наконец
Теорема |
|
Теорема |
При |
|
|
Доказательство:
M2 O
Рисунок
Пусть
Пусть
После Теорема |
|
Теорема 5.4.10. |
Для
—
— |
|
Доказательство:
Рассмотрим
1.
2.
3.
4.
Рассмотрим
Из
Но, Теорема |
|
Замечание: |
изменение |
|
Теорема 5.4.11. |
Для |
|
Доказательство:
Рассмотрим
Потребуем,
были
а
Рассмотрим
1) 2) |
|
|
3) Теорема |

 , представить аффинное преобразование в виде композиции ортогонального преобразования
, представить аффинное преобразование в виде композиции ортогонального преобразования  и двух сжатий к взаимно перпендикулярным осям:
и двух сжатий к взаимно перпендикулярным осям: 

 , т.е.
, т.е.  ,
,  и
и  Потом применял само преобразование, где прямые должны перейти в другие перпендикулярные прямые,но к решению это не привело.
Потом применял само преобразование, где прямые должны перейти в другие перпендикулярные прямые,но к решению это не привело. и
и 


 .
.









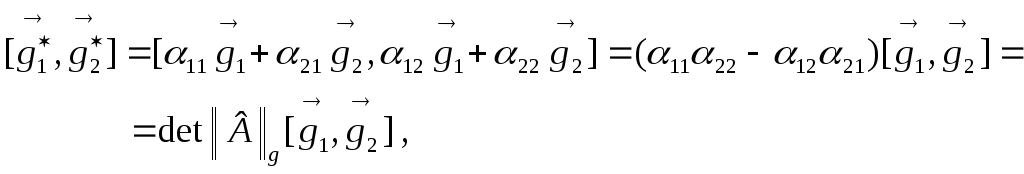
 ,
,
 ,
, ,
, .
. ,
,



 ,
,








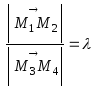 .
. — параллелограммы. (Рис. 5.4.3.). Следовательно,
— параллелограммы. (Рис. 5.4.3.). Следовательно,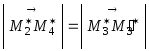 .
.
 .
.









 y
y .
.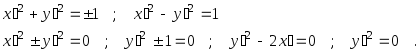 (5.4.1.)
(5.4.1.) ,
, при любом ненулевомU.
при любом ненулевомU.