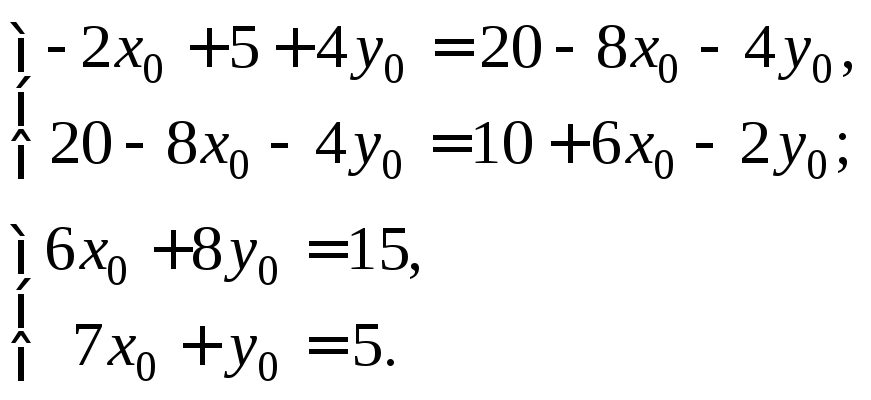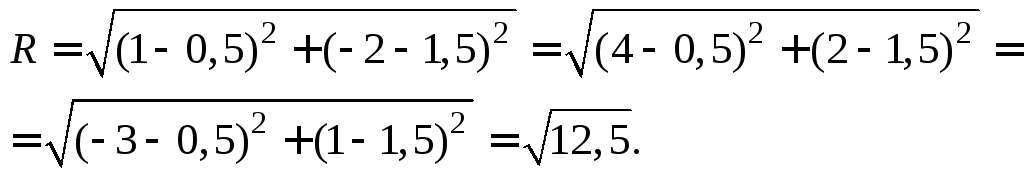Эллипс: определение, свойства, построение
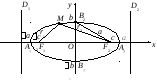
Эллипсом называется геометрическое место точек плоскости, сумма расстояний от каждой из которых до двух заданных точек , и
есть величина постоянная
, бо́льшая расстояния
между этими заданными точками (рис.3.36,а). Это геометрическое определение выражает фокальное свойство эллипса.
Фокальное свойство эллипса
Точки , и
называются фокусами эллипса, расстояние между ними
— фокусным расстоянием, середина
отрезка
— центром эллипса, число
— длиной большой оси эллипса (соответственно, число
— большой полуосью эллипса). Отрезки
и
, соединяющие произвольную точку
эллипса с его фокусами, называются фокальными радиусами точки
. Отрезок, соединяющий две точки эллипса, называется хордой эллипса.
Отношение называется эксцентриситетом эллипса. Из определения
следует, что
. При
, т.е. при
, фокусы
и
, а также центр
совпадают, и эллипс является окружностью радиуса
(рис.3.36,6).
Геометрическое определение эллипса, выражающее его фокальное свойство, эквивалентно его аналитическому определению — линии, задаваемой каноническим уравнением эллипса:
(3.49)
Действительно, введем прямоугольную систему координат (рис.3.36,в). Центр эллипса примем за начало системы координат; прямую, проходящую через фокусы (фокальную ось или первую ось эллипса), примем за ось абсцисс (положительное направление на ней от точки
к точке
); прямую, перпендикулярную фокальной оси и проходящую через центр эллипса (вторую ось эллипса), примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат
оказалась правой).
Составим уравнение эллипса, пользуясь его геометрическим определением, выражающим фокальное свойство. В выбранной системе координат определяем координаты фокусов . Для произвольной точки
, принадлежащей эллипсу, имеем:
Записывая это равенство в координатной форме, получаем:
Переносим второй радикал в правую часть, возводим обе части уравнения в квадрат и приводим подобные члены:
Разделив на 4, возводим обе части уравнения в квадрат:
Обозначив , получаем
. Разделив обе части на
, приходим к каноническому уравнению эллипса:
Следовательно, выбранная система координат является канонической.
Если фокусы эллипса совпадают, то эллипс представляет собой окружность (рис.3.36,6), поскольку . В этом случае канонической будет любая прямоугольная система координат с началом в точке
, a уравнение
является уравнением окружности с центром в точке
и радиусом, равным
.
Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.49), и только они, принадлежат геометрическому месту точек, называемому эллипсом. Другими словами, аналитическое определение эллипса эквивалентно его геометрическому определению, выражающему фокальное свойство эллипса.
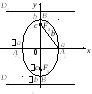
Директориальное свойство эллипса
Директрисами эллипса называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии от нее. При
, когда эллипс является окружностью, директрис нет (можно считать, что директрисы бесконечно удалены).
Эллипс с эксцентриситетом можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки
(фокуса) к расстоянию до заданной прямой
(директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету
(директориальное свойство эллипса). Здесь
и
— один из фокусов эллипса и одна из его директрис, расположенные по одну сторону от оси ординат канонической системы координат, т.е.
или
.
В самом деле, например, для фокуса и директрисы
(рис.3.37,6) условие
можно записать в координатной форме:
Избавляясь от иррациональности и заменяя , приходим к каноническому уравнению эллипса (3.49). Аналогичные рассуждения можно провести для фокуса
и директрисы
.
Уравнение эллипса в полярной системе координат
Уравнение эллипса в полярной системе координат (рис.3.37,в и 3.37(2)) имеет вид
где фокальный параметр эллипса.
В самом деле, выберем в качестве полюса полярной системы координат левый фокус эллипса, а в качестве полярной оси — луч
(рис.3.37,в). Тогда для произвольной точки
, согласно геометрическому определению (фокальному свойству) эллипса, имеем
. Выражаем расстояние между точками
и
(см. пункт 2 замечаний 2.8):
Следовательно, в координатной форме уравнение эллипса имеет вид
Уединяем радикал, возводим обе части уравнения в квадрат, делим на 4 и приводим подобные члены:
Выражаем полярный радиус и делаем замену
:
что и требовалось доказать.
Геометрический смысл коэффициентов в уравнении эллипса
Найдем точки пересечения эллипса (см. рис.3.37,а) с координатными осями (вершины зллипса). Подставляя в уравнение , находим точки пересечения эллипса с осью абсцисс (с фокальной осью):
. Следовательно, длина отрезка фокальной оси, заключенного внутри эллипса, равна
. Этот отрезок, как отмечено выше, называется большой осью эллипса, а число
— большой полуосью эллипса. Подставляя
, получаем
. Следовательно, длина отрезка второй оси эллипса, заключенного внутри эллипса, равна
. Этот отрезок называется малой осью эллипса, а число
— малой полуосью эллипса.
Действительно, , причем равенство
получается только в случае
, когда эллипс является окружностью. Отношение
называется коэффициентом сжатия эллипса.
Замечания 3.9
1. Прямые ограничивают на координатной плоскости основной прямоугольник, внутри которого находится эллипс (см. рис.3.37,а).
2. Эллипс можно определить, как геометрическое место точек, получаемое в результате сжатия окружности к ее диаметру.
Действительно, пусть в прямоугольной системе координат уравнение окружности имеет вид
. При сжатии к оси абсцисс с коэффициентом
координаты произвольной точки
, принадлежащей окружности, изменяются по закону
Подставляя в уравнение окружности и
, получаем уравнение для координат образа
точки
:
поскольку . Это каноническое уравнение эллипса.
3. Координатные оси (канонической системы координат) являются осями симметрии эллипса (называются главными осями эллипса), а его центр — центром симметрии.
Действительно, если точка принадлежит эллипсу
. то и точки
и
, симметричные точке
относительно координатных осей, также принадлежат тому же эллипсу.
4. Из уравнения эллипса в полярной системе координат (см. рис.3.37,в), выясняется геометрический смысл фокального параметра — это половина длины хорды эллипса, проходящей через его фокус перпендикулярно фокальной оси (
при
).
5. Эксцентриситет характеризует форму эллипса, а именно отличие эллипса от окружности. Чем больше
, тем эллипс более вытянут, а чем ближе
к нулю, тем ближе эллипс к окружности (рис.3.38,а). Действительно, учитывая, что
и
, получаем
где — коэффициент сжатия эллипса,
. Следовательно,
. Чем больше сжат эллипс по сравнению с окружностью, тем меньше коэффициент сжатия
и больше эксцентриситет. Для окружности
и
.
6. Уравнение при
определяет эллипс, фокусы которого расположены на оси
(рис.3.38,6). Это уравнение сводится к каноническому при помощи переименования координатных осей (3.38).
7. Уравнение определяет эллипс с центром в точке
, оси которого параллельны координатным осям (рис.3.38,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36).
При уравнение
описывает окружность радиуса
с центром в точке
.
Параметрическое уравнение эллипса
Параметрическое уравнение эллипса в канонической системе координат имеет вид
Действительно, подставляя эти выражения в уравнение (3.49), приходим к основному тригонометрическому тождеству .
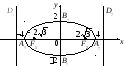
Пример 3.20. Изобразить эллипс в канонической системе координат
. Найти полуоси, фокусное расстояние, эксцентриситет, коэффициент сжатия, фокальный параметр, уравнения директрис.
Решение. Сравнивая заданное уравнение с каноническим, определяем полуоси: — большая полуось,
— малая полуось эллипса. Строим основной прямоугольник со сторонами
с центром в начале координат (рис.3.39). Учитывая симметричность эллипса, вписываем его в основной прямоугольник. При необходимости определяем координаты некоторых точек эллипса. Например, подставляя
в уравнение эллипса, получаем
Следовательно, точки с координатами — принадлежат эллипсу.
Вычисляем коэффициент сжатия ; фокусное расстояние
; эксцентриситет
; фокальный параметр
. Составляем уравнения директрис:
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Определение эллипсa
Определение.
Эллипс — это замкнутая плоская кривая, сумма расстояний от каждой точки которой до двух точек F1 и F2 равна постоянной величине. Точки F1 и F2 называют фокусами эллипса.
F1M1 + F2M1 = F1M2 + F2M2 = A1A2 = const
Элементы эллипсa
F1 и F2 — фокусы эллипсa
Оси эллипсa.
А1А2 = 2a — большая ось эллипса (проходит через фокусы эллипса)
B1B2 = 2b — малая ось эллипса (перпендикулярна большей оси эллипса и проходит через ее центр)
a — большая полуось эллипса
b — малая полуось эллипса
O — центр эллипса (точка пересечения большей и малой осей эллипса)
Вершины эллипсa A1, A2, B1, B2 — точки пересечения эллипсa с малой и большой осями эллипсa
Диаметр эллипсa — отрезок, соединяющий две точки эллипса и проходящий через его центр.
Фокальное расстояние c — половина длины отрезка, соединяющего фокусы эллипсa.
Эксцентриситет эллипсa e характеризует его растяженность и определяется отношением фокального расстояния c к большой полуоси a. Для эллипсa эксцентриситет всегда будет 0 < e < 1, для круга e = 0, для параболы e = 1, для гиперболы e > 1.
Фокальные радиусы эллипсa r1, r2 — расстояния от точки на эллипсе до фокусов.
Радиус эллипсa R — отрезок, соединяющий центр эллипсa О с точкой на эллипсе.
| R = | ab | = | b |
| √a2sin2φ + b2cos2φ | √1 — e2cos2φ |
где e — эксцентриситет эллипсa, φ — угол между радиусом и большой осью A1A2.
Фокальный параметр эллипсa p — отрезок который выходит из фокуса эллипсa и перпендикулярный большой полуоси:
Коэффициент сжатия эллипсa (эллиптичность) k — отношение длины малой полуоси к большой полуоси. Так как малая полуось эллипсa всегда меньше большей, то k < 1, для круга k = 1:
k = √1 — e2
где e — эксцентриситет.
Сжатие эллипсa (1 — k ) — величина, которая равная разности между единицей и эллиптичностью:
Директрисы эллипсa — две прямые перпендикулярные фокальной оси эллипса, и пересекающие ее на расстоянии
ae
от центра эллипса. Расстояние от фокуса до директрисы равно
pe
.
Основные свойства эллипсa
1. Угол между касательной к эллипсу и фокальным радиусом r1 равен углу между касательной и фокальным радиусом r2 (Рис. 2, точка М3).
2. Уравнение касательной к эллипсу в точке М с координатами (xM, yM):
3. Если эллипс пересекается двумя параллельными прямыми, то отрезок, соединяющий середины отрезков образовавшихся при пересечении прямых и эллипса, всегда будет проходить через центр эллипсa. (Это свойство дает возможность построением с помощью циркуля и линейки получить центр эллипса.)
4. Эволютой эллипсa есть астероида, что растянута вдоль короткой оси.
5. Если вписать эллипс с фокусами F1 и F2 у треугольник ∆ ABC, то будет выполнятся следующее соотношение:
| 1 = | F1A ∙ F2A | + | F1B ∙ F2B | + | F1C ∙ F2C |
| CA ∙ AB | AB ∙ BC | BC ∙ CA |
Уравнение эллипсa
Каноническое уравнение эллипсa:
Уравнение описывает эллипс в декартовой системе координат. Если центр эллипсa О в начале системы координат, а большая ось лежит на абсциссе, то эллипсa описывается уравнением:
Если центр эллипсa О смещен в точку с координатами (xo, yo), то уравнение:
| 1 = | (x — xo)2 | + | (y — yo)2 |
| a2 | b2 |
Параметрическое уравнение эллипсa:
| { | x = a cos α | де 0 ≤ α < 2π |
| y = b sin α |
Радиус круга вписанного в эллипс
Круг, вписан в эллипс касается только двух вершин эллипсa B1 и B2. Соответственно, радиус вписанного круга r будет равен длине малой полуоси эллипсa OB1:
r = b
Радиус круга описанного вокруг эллипсa
Круг, описан вокруг эллипсa касается только двух вершин эллипсa A1 и A2. Соответственно, радиус описанного круга R будет равен длине большой полуоси эллипсa OA1:
R = a
Площадь эллипсa
Формула определение площади эллипсa:
S = πab
Площадь сегмента эллипсa
Формула площади сегмента, что находится по левую сторону от хорды с координатами (x, y) и (x, -y):
| S = | πab | — | b | ( | x | √ | a2 — x2 + a2 ∙ arcsin | x | ) |
| 2 | a | a |
Периметр эллипсa
Найти точную формулу периметра эллипсa L очень тяжело. Ниже приведена формула приблизительной длины периметра. Максимальная погрешность этой формулы ~0,63 %:
| L ≈ 4 | πab + (a — b)2 |
| a + b |
Длина дуги эллипсa
Формулы определения длины дуги эллипсa:
1. Параметрическая формула определения длины дуги эллипсa через большую a и малую b полуоси:
| t2 | ||
| l = | ∫ | √a2sin2t + b2cos2t dt |
| t1 |
2. Параметрическая формула определения длины дуги эллипсa через большую полуось a и эксцентриситет e:
| t2 | ||
| l = | ∫ | √1 — e2cos2t dt, e < 1 |
| t1 |
Not to be confused with eclipse.
An ellipse (red) obtained as the intersection of a cone with an inclined plane.
Ellipses: examples with increasing eccentricity
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity 


An ellipse has a simple algebraic solution for its area, but only approximations for its perimeter (also known as circumference), for which integration is required to obtain an exact solution.
Analytically, the equation of a standard ellipse centered at the origin with width 

Assuming 


Ellipses are the closed type of conic section: a plane curve tracing the intersection of a cone with a plane (see figure). Ellipses have many similarities with the other two forms of conic sections, parabolas and hyperbolas, both of which are open and unbounded. An angled cross section of a cylinder is also an ellipse.
An ellipse may also be defined in terms of one focal point and a line outside the ellipse called the directrix: for all points on the ellipse, the ratio between the distance to the focus and the distance to the directrix is a constant. This constant ratio is the above-mentioned eccentricity:
Ellipses are common in physics, astronomy and engineering. For example, the orbit of each planet in the Solar System is approximately an ellipse with the Sun at one focus point (more precisely, the focus is the barycenter of the Sun–planet pair). The same is true for moons orbiting planets and all other systems of two astronomical bodies. The shapes of planets and stars are often well described by ellipsoids. A circle viewed from a side angle looks like an ellipse: that is, the ellipse is the image of a circle under parallel or perspective projection. The ellipse is also the simplest Lissajous figure formed when the horizontal and vertical motions are sinusoids with the same frequency: a similar effect leads to elliptical polarization of light in optics.
The name, ἔλλειψις (élleipsis, «omission»), was given by Apollonius of Perga in his Conics.
Definition as locus of points[edit]
Ellipse: definition by sum of distances to foci
Ellipse: definition by focus and circular directrix
An ellipse can be defined geometrically as a set or locus of points in the Euclidean plane:
- Given two fixed points
called the foci and a distance
which is greater than the distance between the foci, the ellipse is the set of points
such that the sum of the distances
is equal to
:
The midpoint 




The case 
The equation 
- If
is the circle with center
and radius
, then the distance of a point
to the circle
equals the distance to the focus
:


Using Dandelin spheres, one can prove that any section of a cone with a plane is an ellipse, assuming the plane does not contain the apex and has slope less than that of the lines on the cone.
In Cartesian coordinates[edit]
Shape parameters:
- a: semi-major axis,
- b: semi-minor axis,
- c: linear eccentricity,
- p: semi-latus rectum (usually
).
Standard equation[edit]
The standard form of an ellipse in Cartesian coordinates assumes that the origin is the center of the ellipse, the x-axis is the major axis, and:
- the foci are the points
,
- the major points are
.
For an arbitrary point 




Removing the radicals by suitable squarings and using 
or, solved for y:
The width and height parameters 




It follows from the equation that the ellipse is symmetric with respect to the coordinate axes and hence with respect to the origin.
Parameters[edit]
Principal axes[edit]
Throughout this article, the semi-major and semi-minor axes are denoted 


In principle, the canonical ellipse equation 





Linear eccentricity[edit]
This is the distance from the center to a focus: 
Eccentricity[edit]
The eccentricity can be expressed as:
assuming 

Semi-latus rectum[edit]
The length of the chord through one focus, perpendicular to the major axis, is called the latus rectum. One half of it is the semi-latus rectum 
[4]
The semi-latus rectum 
Tangent[edit]
An arbitrary line 


A vector parametric equation of the tangent is:
with
Proof:
Let 




There are then cases:
Then line
and the ellipse have only point
in common, and
is a tangent. The tangent direction has perpendicular vector
, so the tangent line has equation
for some
. Because
is on the tangent and the ellipse, one obtains
.
Then line
has a second point in common with the ellipse, and is a secant.
Using (1) one finds that 

If 



Shifted ellipse[edit]
If the standard ellipse is shifted to have center 
The axes are still parallel to the x- and y-axes.
General ellipse[edit]
In analytic geometry, the ellipse is defined as a quadric: the set of points 
provided 
To distinguish the degenerate cases from the non-degenerate case, let ∆ be the determinant
Then the ellipse is a non-degenerate real ellipse if and only if C∆ < 0. If C∆ > 0, we have an imaginary ellipse, and if ∆ = 0, we have a point ellipse.[7]: p.63
The general equation’s coefficients can be obtained from known semi-major axis 



These expressions can be derived from the canonical equation
by an affine transformation of the coordinates 
Conversely, the canonical form parameters can be obtained from the general form coefficients by the equations:[citation needed]
Parametric representation[edit]
The construction of points based on the parametric equation and the interpretation of parameter t, which is due to de la Hire
Ellipse points calculated by the rational representation with equal spaced parameters (
Standard parametric representation[edit]
Using trigonometric functions, a parametric representation of the standard ellipse 
The parameter t (called the eccentric anomaly in astronomy) is not the angle of 
Rational representation[edit]
With the substitution 
and the rational parametric equation of an ellipse
which covers any point of the ellipse 

For ![{displaystyle uin [0,,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c61b780db9ac550dd283876e16abe9c2cccdf8c3)


Alternately, if the parameter ![{displaystyle [u:v]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/297de5a93c52f13ef84add1d79d693fcda686176)

Then ![{textstyle [1:0]mapsto (-a,,0).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0da12e69b8138a30dcb6cfbeeb95bd63b890f2db)
Rational representations of conic sections are commonly used in computer-aided design (see Bezier curve).
Tangent slope as parameter[edit]
A parametric representation, which uses the slope 
can be obtained from the derivative of the standard representation 
With help of trigonometric formulae one obtains:
Replacing 

Here 



The equation of the tangent at point 



This description of the tangents of an ellipse is an essential tool for the determination of the orthoptic of an ellipse. The orthoptic article contains another proof, without differential calculus and trigonometric formulae.
General ellipse[edit]
Ellipse as an affine image of the unit circle
Another definition of an ellipse uses affine transformations:
- Any ellipse is an affine image of the unit circle with equation
.
- Parametric representation
An affine transformation of the Euclidean plane has the form 






Here 

- Vertices
The four vertices of the ellipse are 

(If 


At a vertex parameter 
Expanding and applying the identities 

- Area
From Apollonios theorem (see below) one obtains:
The area of an ellipse 
- Semiaxes
With the abbreviations

Solving this nonlinear system for 
- Implicit representation
Solving the parametric representation for 

.
Conversely: If the equation
with
of an ellipse centered at the origin is given, then the two vectors
point to two conjugate points and the tools developed above are applicable.
Example: For the ellipse with equation 
.
Whirls: nested, scaled and rotated ellipses. The spiral is not drawn: we see it as the locus of points where the ellipses are especially close to each other.
- Rotated Standard ellipse
For 

- Ellipse in space
The definition of an ellipse in this section gives a parametric representation of an arbitrary ellipse, even in space, if one allows 
Polar forms[edit]
Polar form relative to center[edit]
Polar coordinates centered at the center.
In polar coordinates, with the origin at the center of the ellipse and with the angular coordinate 
where 
Polar form relative to focus[edit]
Polar coordinates centered at focus.
If instead we use polar coordinates with the origin at one focus, with the angular coordinate 
where the sign in the denominator is negative if the reference direction 
In the slightly more general case of an ellipse with one focus at the origin and the other focus at angular coordinate 
The angle 

Eccentricity and the directrix property[edit]
Ellipse: directrix property
Each of the two lines parallel to the minor axis, and at a distance of 
- For an arbitrary point
of the ellipse, the quotient of the distance to one focus and to the corresponding directrix (see diagram) is equal to the eccentricity:
The proof for the pair 


The second case is proven analogously.
The converse is also true and can be used to define an ellipse (in a manner similar to the definition of a parabola):
- For any point
(focus), any line
(directrix) not through
, and any real number
with
the ellipse is the locus of points for which the quotient of the distances to the point and to the line is
that is:
The extension to 
(The choice 

Pencil of conics with a common vertex and common semi-latus rectum
- Proof
Let 

The directrix 



and
The substitution 
This is the equation of an ellipse (


If 


which is the equation of an ellipse with center 
the major/minor semi axis 
Construction of a directrix
- Construction of a directrix
Because of 







- General ellipse
If the focus is 

(The right side of the equation uses the Hesse normal form of a line to calculate the distance 
Focus-to-focus reflection property[edit]
Ellipse: the tangent bisects the supplementary angle of the angle between the lines to the foci.
Rays from one focus reflect off the ellipse to pass through the other focus.
An ellipse possesses the following property:
- The normal at a point
bisects the angle between the lines
.
- Proof
Because the tangent is perpendicular to the normal, the statement is true for the tangent and the supplementary angle of the angle between the lines to the foci (see diagram), too.
Let 














From the diagram and the triangle inequality one recognizes that 






- Application
The rays from one focus are reflected by the ellipse to the second focus. This property has optical and acoustic applications similar to the reflective property of a parabola (see whispering gallery).
Conjugate diameters[edit]
Definition of conjugate diameters[edit]
Orthogonal diameters of a circle with a square of tangents, midpoints of parallel chords and an affine image, which is an ellipse with conjugate diameters, a parallelogram of tangents and midpoints of chords.
A circle has the following property:
- The midpoints of parallel chords lie on a diameter.
An affine transformation preserves parallelism and midpoints of line segments, so this property is true for any ellipse. (Note that the parallel chords and the diameter are no longer orthogonal.)
- Definition
Two diameters 


From the diagram one finds:
- Two diameters
of an ellipse are conjugate whenever the tangents at
and
are parallel to
.
Conjugate diameters in an ellipse generalize orthogonal diameters in a circle.
In the parametric equation for a general ellipse given above,
any pair of points 

For the common parametric representation 

(signs: (+,+) or (-,-) )
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response («Math extension cannot connect to Restbase.») from server «http://localhost:6011/en.wikipedia.org/v1/»:): {displaystyle (x_2,y_2)=({color{red}{mp}} asin t,pm bcos t)quad }
(signs: (-,+) or (+,-) ) - are conjugate and
In case of a circle the last equation collapses to 
Theorem of Apollonios on conjugate diameters[edit]
For the alternative area formula
For an ellipse with semi-axes 
- Let
and
be halves of two conjugate diameters (see diagram) then
.
- The triangle
with sides
(see diagram) has the constant area
, which can be expressed by
, too.
is the altitude of point
and
the angle between the half diameters. Hence the area of the ellipse (see section metric properties) can be written as
.
- The parallelogram of tangents adjacent to the given conjugate diameters has the
- Proof
Let the ellipse be in the canonical form with parametric equation
.
The two points 

The area of the triangle generated by 
and from the diagram it can be seen that the area of the parallelogram is 8 times that of 
Orthogonal tangents[edit]
Ellipse with its orthoptic
For the ellipse 

This circle is called orthoptic or director circle of the ellipse (not to be confused with the circular directrix defined above).
Drawing ellipses[edit]
Central projection of circles (gate)
Ellipses appear in descriptive geometry as images (parallel or central projection) of circles. There exist various tools to draw an ellipse. Computers provide the fastest and most accurate method for drawing an ellipse. However, technical tools (ellipsographs) to draw an ellipse without a computer exist. The principle of ellipsographs were known to Greek mathematicians such as Archimedes and Proklos.
If there is no ellipsograph available, one can draw an ellipse using an approximation by the four osculating circles at the vertices.
For any method described below, knowledge of the axes and the semi-axes is necessary (or equivalently: the foci and the semi-major axis).
If this presumption is not fulfilled one has to know at least two conjugate diameters. With help of Rytz’s construction the axes and semi-axes can be retrieved.
de La Hire’s point construction[edit]
The following construction of single points of an ellipse is due to de La Hire.[11] It is based on the standard parametric representation 
- Draw the two circles centered at the center of the ellipse with radii
and the axes of the ellipse.
- Draw a line through the center, which intersects the two circles at point
and
, respectively.
- Draw a line through
that is parallel to the minor axis and a line through
that is parallel to the major axis. These lines meet at an ellipse point (see diagram).
- Repeat steps (2) and (3) with different lines through the center.
-
de La Hire’s method
-
Animation of the method
Ellipse: gardener’s method
Pins-and-string method[edit]
The characterization of an ellipse as the locus of points so that sum of the distances to the foci is constant leads to a method of drawing one using two drawing pins, a length of string, and a pencil. In this method, pins are pushed into the paper at two points, which become the ellipse’s foci. A string is tied at each end to the two pins; its length after tying is 
A similar method for drawing confocal ellipses with a closed string is due to the Irish bishop Charles Graves.
Paper strip methods[edit]
The two following methods rely on the parametric representation (see section parametric representation, above):
This representation can be modeled technically by two simple methods. In both cases center, the axes and semi axes 
- Method 1
The first method starts with
- a strip of paper of length
.
The point, where the semi axes meet is marked by 




A technical realization of the motion of the paper strip can be achieved by a Tusi couple (see animation). The device is able to draw any ellipse with a fixed sum 
-
Ellipse construction: paper strip method 1
-
Ellipses with Tusi couple. Two examples: red and cyan.
A variation of the paper strip method 1 uses the observation that the midpoint 






-
Variation of the paper strip method 1
-
Animation of the variation of the paper strip method 1
Ellipse construction: paper strip method 2
- Method 2
The second method starts with
- a strip of paper of length
.
One marks the point, which divides the strip into two substrips of length 



This method is the base for several ellipsographs (see section below).
Similar to the variation of the paper strip method 1 a variation of the paper strip method 2 can be established (see diagram) by cutting the part between the axes into halves.
-
-
Variation of the paper strip method 2
Most ellipsograph drafting instruments are based on the second paperstrip method.
Approximation of an ellipse with osculating circles
Approximation by osculating circles[edit]
From Metric properties below, one obtains:
The diagram shows an easy way to find the centers of curvature 


- mark the auxiliary point
and draw the line segment
- draw the line through
, which is perpendicular to the line
- the intersection points of this line with the axes are the centers of the osculating circles.
(proof: simple calculation.)
The centers for the remaining vertices are found by symmetry.
With help of a French curve one draws a curve, which has smooth contact to the osculating circles.
Steiner generation[edit]
Ellipse: Steiner generation
Ellipse: Steiner generation
The following method to construct single points of an ellipse relies on the Steiner generation of a conic section:
- Given two pencils
of lines at two points
(all lines containing
and
, respectively) and a projective but not perspective mapping
of
onto
, then the intersection points of corresponding lines form a non-degenerate projective conic section.
For the generation of points of the ellipse 













Steiner generation can also be defined for hyperbolas and parabolas. It is sometimes called a parallelogram method because one can use other points rather than the vertices, which starts with a parallelogram instead of a rectangle.
As hypotrochoid[edit]
An ellipse (in red) as a special case of the hypotrochoid with R = 2r
The ellipse is a special case of the hypotrochoid when 


Inscribed angles and three-point form[edit]
Circles[edit]
Circle: inscribed angle theorem
A circle with equation 


- For four points
(see diagram) the following statement is true:
- The four points are on a circle if and only if the angles at
and
are equal.
Usually one measures inscribed angles by a degree or radian θ, but here the following measurement is more convenient:
- In order to measure the angle between two lines with equations
one uses the quotient:
Inscribed angle theorem for circles[edit]
For four points 
- The four points are on a circle, if and only if the angles at
and
are equal. In terms of the angle measurement above, this means:
At first the measure is available only for chords not parallel to the y-axis, but the final formula works for any chord.
Three-point form of circle equation[edit]
- As a consequence, one obtains an equation for the circle determined by three non-colinear points
:
For example, for 
, which can be rearranged to
Using vectors, dot products and determinants this formula can be arranged more clearly, letting 
The center of the circle 
The radius is the distance between any of the three points and the center.
Ellipses[edit]
This section, we consider the family of ellipses defined by equations 

and to write the ellipse equation as:
where q is fixed and 


Inscribed angle theorem for an ellipse
Like a circle, such an ellipse is determined by three points not on a line.
For this family of ellipses, one introduces the following q-analog angle measure, which is not a function of the usual angle measure θ:[13][14]
- In order to measure an angle between two lines with equations
one uses the quotient:
Inscribed angle theorem for ellipses[edit]
- Given four points
, no three of them on a line (see diagram).
- The four points are on an ellipse with equation
if and only if the angles at
and
are equal in the sense of the measurement above—that is, if
At first the measure is available only for chords which are not parallel to the y-axis. But the final formula works for any chord. The proof follows from a straightforward calculation. For the direction of proof given that the points are on an ellipse, one can assume that the center of the ellipse is the origin.
Three-point form of ellipse equation[edit]
- A consequence, one obtains an equation for the ellipse determined by three non-colinear points
:
For example, for 

and after conversion
Analogously to the circle case, the equation can be written more clearly using vectors:
where 

Pole-polar relation[edit]
Ellipse: pole-polar relation
Any ellipse can be described in a suitable coordinate system by an equation 



- point
is mapped onto the line
, not through the center of the ellipse.
This relation between points and lines is a bijection.
The inverse function maps
Such a relation between points and lines generated by a conic is called pole-polar relation or polarity. The pole is the point; the polar the line.
By calculation one can confirm the following properties of the pole-polar relation of the ellipse:
- The intersection point of two polars is the pole of the line through their poles.
- The foci
and
, respectively, and the directrices
and
, respectively, belong to pairs of pole and polar. Because they are even polar pairs with respect to the circle
, the directrices can be constructed by compass and straightedge (see Inversive geometry).
Pole-polar relations exist for hyperbolas and parabolas as well.
Metric properties[edit]
All metric properties given below refer to an ellipse with equation
-
(1)
except for the section on the area enclosed by a tilted ellipse, where the generalized form of Eq.(1) will be given.
Area[edit]
The area 
-
(2)
where 









![{displaystyle xin [-a,a],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb19e5015712fa6f6c57d3f334266c73d7782434)

![[-a,a]](https://wikimedia.org/api/rest_v1/media/math/render/svg/50ccbcece37f9ec0a4c6d396be3a143a0b76d5c1)
The second integral is the area of a circle of radius 

An ellipse defined implicitly by 

The area can also be expressed in terms of eccentricity and the length of the semi-major axis as 
The area enclosed by a tilted ellipse is 
So far we have dealt with erect ellipses, whose major and minor axes are parallel to the 

-
(3)
where 



Circumference[edit]
Ellipses with same circumference
The circumference 
where again 


which is in general not an elementary function.
The circumference of the ellipse may be evaluated in terms of 
The exact infinite series is:
where 



Srinivasa Ramanujan gave two close approximations for the circumference in §16 of «Modular Equations and Approximations to 
and
where 


Arc length[edit]
More generally, the arc length of a portion of the circumference, as a function of the angle subtended (or x coordinates of any two points on the upper half of the ellipse), is given by an incomplete elliptic integral. The upper half of an ellipse is parameterized by
Then the arc length 


This is equivalent to
where 

Some lower and upper bounds on the circumference of the canonical ellipse 

Here the upper bound 

Curvature[edit]
The curvature is given by
radius of curvature at point 
Radius of curvature at the two vertices 
Radius of curvature at the two co-vertices 
In triangle geometry[edit]
Ellipses appear in triangle geometry as
- Steiner ellipse: ellipse through the vertices of the triangle with center at the centroid,
- inellipses: ellipses which touch the sides of a triangle. Special cases are the Steiner inellipse and the Mandart inellipse.
As plane sections of quadrics[edit]
Ellipses appear as plane sections of the following quadrics:
- Ellipsoid
- Elliptic cone
- Elliptic cylinder
- Hyperboloid of one sheet
- Hyperboloid of two sheets
-
Ellipsoid
-
Elliptic cone
-
Elliptic cylinder
-
Hyperboloid of one sheet
-
Hyperboloid of two sheets
Applications[edit]
Physics[edit]
Elliptical reflectors and acoustics[edit]
Wave pattern of a little droplet dropped into mercury in one focus of the ellipse
If the water’s surface is disturbed at one focus of an elliptical water tank, the circular waves of that disturbance, after reflecting off the walls, converge simultaneously to a single point: the second focus. This is a consequence of the total travel length being the same along any wall-bouncing path between the two foci.
Similarly, if a light source is placed at one focus of an elliptic mirror, all light rays on the plane of the ellipse are reflected to the second focus. Since no other smooth curve has such a property, it can be used as an alternative definition of an ellipse. (In the special case of a circle with a source at its center all light would be reflected back to the center.) If the ellipse is rotated along its major axis to produce an ellipsoidal mirror (specifically, a prolate spheroid), this property holds for all rays out of the source. Alternatively, a cylindrical mirror with elliptical cross-section can be used to focus light from a linear fluorescent lamp along a line of the paper; such mirrors are used in some document scanners.
Sound waves are reflected in a similar way, so in a large elliptical room a person standing at one focus can hear a person standing at the other focus remarkably well. The effect is even more evident under a vaulted roof shaped as a section of a prolate spheroid. Such a room is called a whisper chamber. The same effect can be demonstrated with two reflectors shaped like the end caps of such a spheroid, placed facing each other at the proper distance. Examples are the National Statuary Hall at the United States Capitol (where John Quincy Adams is said to have used this property for eavesdropping on political matters); the Mormon Tabernacle at Temple Square in Salt Lake City, Utah; at an exhibit on sound at the Museum of Science and Industry in Chicago; in front of the University of Illinois at Urbana–Champaign Foellinger Auditorium; and also at a side chamber of the Palace of Charles V, in the Alhambra.
Planetary orbits[edit]
In the 17th century, Johannes Kepler discovered that the orbits along which the planets travel around the Sun are ellipses with the Sun [approximately] at one focus, in his first law of planetary motion. Later, Isaac Newton explained this as a corollary of his law of universal gravitation.
More generally, in the gravitational two-body problem, if the two bodies are bound to each other (that is, the total energy is negative), their orbits are similar ellipses with the common barycenter being one of the foci of each ellipse. The other focus of either ellipse has no known physical significance. The orbit of either body in the reference frame of the other is also an ellipse, with the other body at the same focus.
Keplerian elliptical orbits are the result of any radially directed attraction force whose strength is inversely proportional to the square of the distance. Thus, in principle, the motion of two oppositely charged particles in empty space would also be an ellipse. (However, this conclusion ignores losses due to electromagnetic radiation and quantum effects, which become significant when the particles are moving at high speed.)
For elliptical orbits, useful relations involving the eccentricity 
where
Also, in terms of 




.
Harmonic oscillators[edit]
The general solution for a harmonic oscillator in two or more dimensions is also an ellipse. Such is the case, for instance, of a long pendulum that is free to move in two dimensions; of a mass attached to a fixed point by a perfectly elastic spring; or of any object that moves under influence of an attractive force that is directly proportional to its distance from a fixed attractor. Unlike Keplerian orbits, however, these «harmonic orbits» have the center of attraction at the geometric center of the ellipse, and have fairly simple equations of motion.
Phase visualization[edit]
In electronics, the relative phase of two sinusoidal signals can be compared by feeding them to the vertical and horizontal inputs of an oscilloscope. If the Lissajous figure display is an ellipse, rather than a straight line, the two signals are out of phase.
Elliptical gears[edit]
Two non-circular gears with the same elliptical outline, each pivoting around one focus and positioned at the proper angle, turn smoothly while maintaining contact at all times. Alternatively, they can be connected by a link chain or timing belt, or in the case of a bicycle the main chainring may be elliptical, or an ovoid similar to an ellipse in form. Such elliptical gears may be used in mechanical equipment to produce variable angular speed or torque from a constant rotation of the driving axle, or in the case of a bicycle to allow a varying crank rotation speed with inversely varying mechanical advantage.
Elliptical bicycle gears make it easier for the chain to slide off the cog when changing gears.[21]
An example gear application would be a device that winds thread onto a conical bobbin on a spinning machine. The bobbin would need to wind faster when the thread is near the apex than when it is near the base.[22]
Optics[edit]
- In a material that is optically anisotropic (birefringent), the refractive index depends on the direction of the light. The dependency can be described by an index ellipsoid. (If the material is optically isotropic, this ellipsoid is a sphere.)
- In lamp-pumped solid-state lasers, elliptical cylinder-shaped reflectors have been used to direct light from the pump lamp (coaxial with one ellipse focal axis) to the active medium rod (coaxial with the second focal axis).[23]
- In laser-plasma produced EUV light sources used in microchip lithography, EUV light is generated by plasma positioned in the primary focus of an ellipsoid mirror and is collected in the secondary focus at the input of the lithography machine.[24]
Statistics and finance[edit]
In statistics, a bivariate random vector 
Computer graphics[edit]
Drawing an ellipse as a graphics primitive is common in standard display libraries, such as the MacIntosh QuickDraw API, and Direct2D on Windows. Jack Bresenham at IBM is most famous for the invention of 2D drawing primitives, including line and circle drawing, using only fast integer operations such as addition and branch on carry bit. M. L. V. Pitteway extended Bresenham’s algorithm for lines to conics in 1967.[27] Another efficient generalization to draw ellipses was invented in 1984 by Jerry Van Aken.[28]
In 1970 Danny Cohen presented at the «Computer Graphics 1970» conference in England a linear algorithm for drawing ellipses and circles. In 1971, L. B. Smith published similar algorithms for all conic sections and proved them to have good properties.[29] These algorithms need only a few multiplications and additions to calculate each vector.
It is beneficial to use a parametric formulation in computer graphics because the density of points is greatest where there is the most curvature. Thus, the change in slope between each successive point is small, reducing the apparent «jaggedness» of the approximation.
- Drawing with Bézier paths
Composite Bézier curves may also be used to draw an ellipse to sufficient accuracy, since any ellipse may be construed as an affine transformation of a circle. The spline methods used to draw a circle may be used to draw an ellipse, since the constituent Bézier curves behave appropriately under such transformations.
Optimization theory[edit]
It is sometimes useful to find the minimum bounding ellipse on a set of points. The ellipsoid method is quite useful for solving this problem.
See also[edit]
- Cartesian oval, a generalization of the ellipse
- Circumconic and inconic
- Distance of closest approach of ellipses
- Ellipse fitting
- Elliptic coordinates, an orthogonal coordinate system based on families of ellipses and hyperbolae
- Elliptic partial differential equation
- Elliptical distribution, in statistics
- Elliptical dome
- Geodesics on an ellipsoid
- Great ellipse
- Kepler’s laws of planetary motion
- n-ellipse, a generalization of the ellipse for n foci
- Oval
- Spheroid, the ellipsoid obtained by rotating an ellipse about its major or minor axis
- Stadium (geometry), a two-dimensional geometric shape constructed of a rectangle with semicircles at a pair of opposite sides
- Steiner circumellipse, the unique ellipse circumscribing a triangle and sharing its centroid
- Superellipse, a generalization of an ellipse that can look more rectangular or more «pointy»
- True, eccentric, and mean anomaly
Notes[edit]
- ^ Apostol, Tom M.; Mnatsakanian, Mamikon A. (2012), New Horizons in Geometry, The Dolciani Mathematical Expositions #47, The Mathematical Association of America, p. 251, ISBN 978-0-88385-354-2
- ^ The German term for this circle is Leitkreis which can be translated as «Director circle», but that term has a different meaning in the English literature (see Director circle).
- ^ «Ellipse — from Wolfram MathWorld». Mathworld.wolfram.com. 2020-09-10. Retrieved 2020-09-10.
- ^ Protter & Morrey (1970, pp. 304, APP-28)
- ^ Larson, Ron; Hostetler, Robert P.; Falvo, David C. (2006). «Chapter 10». Precalculus with Limits. Cengage Learning. p. 767. ISBN 978-0-618-66089-6.
- ^ Young, Cynthia Y. (2010). «Chapter 9». Precalculus. John Wiley and Sons. p. 831. ISBN 978-0-471-75684-2.
- ^ a b Lawrence, J. Dennis, A Catalog of Special Plane Curves, Dover Publ., 1972.
- ^ K. Strubecker: Vorlesungen über Darstellende Geometrie, GÖTTINGEN,
VANDENHOECK & RUPRECHT, 1967, p. 26 - ^ Bronstein&Semendjajew: Taschenbuch der Mathematik, Verlag Harri Deutsch, 1979, ISBN 3871444928, p. 274.
- ^ Encyclopedia of Mathematics, Springer, URL: http://encyclopediaofmath.org/index.php?title=Apollonius_theorem&oldid=17516 .
- ^ K. Strubecker: Vorlesungen über Darstellende Geometrie. Vandenhoeck & Ruprecht, Göttingen 1967, S. 26.
- ^ J. van Mannen: Seventeenth century instruments for drawing conic sections. In: The Mathematical Gazette. Vol. 76, 1992, p. 222–230.
- ^ E. Hartmann: Lecture Note ‘Planar Circle Geometries’, an Introduction to Möbius-, Laguerre- and Minkowski Planes, p. 55
- ^ W. Benz, Vorlesungen über Geomerie der Algebren, Springer (1973)
- ^ Archimedes. (1897). The works of Archimedes. Heath, Thomas Little, Sir, 1861-1940. Mineola, N.Y.: Dover Publications. p. 115. ISBN 0-486-42084-1. OCLC 48876646.
- ^ Carlson, B. C. (2010), «Elliptic Integrals», in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
- ^ Ivory, J. (1798). «A new series for the rectification of the ellipsis». Transactions of the Royal Society of Edinburgh. 4 (2): 177–190. doi:10.1017/s0080456800030817. S2CID 251572677.
- ^ Bessel, F. W. (2010). «The calculation of longitude and latitude from geodesic measurements (1825)». Astron. Nachr. 331 (8): 852–861. arXiv:0908.1824. Bibcode:2010AN….331..852K. doi:10.1002/asna.201011352. S2CID 118760590. Englisch translation of Bessel, F. W. (1825). «Über die Berechnung der geographischen Längen und Breiten aus geodätischen Vermesssungen». Astron. Nachr. 4 (16): 241–254. arXiv:0908.1823. Bibcode:1825AN……4..241B. doi:10.1002/asna.18260041601. S2CID 118630614.
- ^ Ramanujan, Srinivasa (1914). «Modular Equations and Approximations to π». Quart. J. Pure App. Math. 45: 350–372. ISBN 9780821820766.
- ^ Jameson, G.J.O. (2014). «Inequalities for the perimeter of an ellipse». Mathematical Gazette. 98 (542): 227–234. doi:10.1017/S002555720000125X. S2CID 125063457.
- ^ David Drew.
«Elliptical Gears».
[1] - ^ Grant, George B. (1906). A treatise on gear wheels. Philadelphia Gear Works. p. 72.
- ^ Encyclopedia of Laser Physics and Technology — lamp-pumped lasers, arc lamps, flash lamps, high-power, Nd:YAG laser
- ^ «Cymer — EUV Plasma Chamber Detail Category Home Page». Archived from the original on 2013-05-17. Retrieved 2013-06-20.
- ^ Chamberlain, G. (February 1983). «A characterization of the distributions that imply mean—Variance utility functions». Journal of Economic Theory. 29 (1): 185–201. doi:10.1016/0022-0531(83)90129-1.
- ^ Owen, J.; Rabinovitch, R. (June 1983). «On the class of elliptical distributions and their applications to the theory of portfolio choice». Journal of Finance. 38 (3): 745–752. doi:10.1111/j.1540-6261.1983.tb02499.x. JSTOR 2328079.
- ^ Pitteway, M.L.V. (1967). «Algorithm for drawing ellipses or hyperbolae with a digital plotter». The Computer Journal. 10 (3): 282–9. doi:10.1093/comjnl/10.3.282.
- ^ Van Aken, J.R. (September 1984). «An Efficient Ellipse-Drawing Algorithm». IEEE Computer Graphics and Applications. 4 (9): 24–35. doi:10.1109/MCG.1984.275994. S2CID 18995215.
- ^ Smith, L.B. (1971). «Drawing ellipses, hyperbolae or parabolae with a fixed number of points». The Computer Journal. 14 (1): 81–86. doi:10.1093/comjnl/14.1.81.
References[edit]
- Besant, W.H. (1907). «Chapter III. The Ellipse». Conic Sections. London: George Bell and Sons. p. 50.
- Coxeter, H.S.M. (1969). Introduction to Geometry (2nd ed.). New York: Wiley. pp. 115–9.
- Meserve, Bruce E. (1983) [1959], Fundamental Concepts of Geometry, Dover Publications, ISBN 978-0-486-63415-9
- Miller, Charles D.; Lial, Margaret L.; Schneider, David I. (1990). Fundamentals of College Algebra (3rd ed.). Scott Foresman/Little. p. 381. ISBN 978-0-673-38638-0.
- Protter, Murray H.; Morrey, Charles B. Jr. (1970), College Calculus with Analytic Geometry (2nd ed.), Reading: Addison-Wesley, LCCN 76087042
External links[edit]
Кривые второго порядка. Эллипс: формулы и задачи
Понятие о кривых второго порядка
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:
,
где A, B, C, D, E, F — числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.
Эллипс, заданный каноническим уравнением
Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.
Фокусы обозначены как и на рисунке ниже.
Каноническое уравнение эллипса имеет вид:
,
где a и b (a > b) — длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.
Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат — в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат — малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b , то уравнение эллипса принимает вид . Это уравнение окружности радиуса a , а окружность — частный случай эллипса. Эллипс можно получить из окружности радиуса a , если сжать её в a/b раз вдоль оси Oy .
Пример 1. Проверить, является ли линия, заданная общим уравнением , эллипсом.
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия — эллипс.
Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось — это a = 5 , меньшая полуось — это b = 4 . Получаем каноническое уравнение эллипса:
.
Точки и , обозначенные зелёным на большей оси, где
,
называются фокусами.
называется эксцентриситетом эллипса.
Отношение b/a характеризует «сплюснутость» эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Решение. Делаем несложные умозаключения:
— если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,
— если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
Результат — каноническое уравнение эллипса:
.
Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет .
Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:
.
Вычисляем квадрат длины меньшей полуоси:
Составляем каноническое уравнение эллипса:
Пример 5. Определить фокусы эллипса, заданного каноническим уравнением .
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:
.
Получаем фокусы эллипса:
Решить задачи на эллипс самостоятельно, а затем посмотреть решение
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) расстояние между фокусами 30, а большая ось 34
2) малая ось 24, а один из фокусов находится в точке (-5; 0)
3) эксцентриситет , а один из фокусов находится в точке (6; 0)
Продолжаем решать задачи на эллипс вместе
Если — произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:
.
Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями
,
называются директрисами эллипса (на чертеже — красные линии по краям).
Из двух вышеприведённых уравнений следует, что для любой точки эллипса
,
где и — расстояния этой точки до директрис и .
Пример 7. Дан эллипс . Составить уравнение его директрис.
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. . Все данные для этого есть. Вычисляем:
.
Получаем уравнение директрис эллипса:
Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки , а директрисами являются прямые .
Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:
.
Теперь можем получить и квадрат длины меньшей полуоси:
Уравнение эллипса готово:
Пример 9. Проверить, находится ли точка на эллипсе . Если находится, найти расстояние от этой точки до фокусов эллипса.
Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:
.
Получили единицу, следовательно, точка находится на эллипсе.
Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e — эксцентриситет и числа «эр» с подстрочными индексами 1 и 2 — искомые расстояния. Получаем:
Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.
,
так как из исходного уравнения эллипса .
Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.
Эллипс — определение и вычисление с примерами решения
Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно Согласно определению эллипса имеем Из треугольников и по теореме Пифагора найдем
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим Раскроем разность квадратов Подставим найденное выражение в уравнение и сократим обе части равенства на 4, тогда оно перейдет в уравнение Вновь возведем обе части равенства в квадрат Раскрывая все скобки в правой части уравнения, получим Соберем не- известные в левой части, а все известные величины перенесем в правую часть уравнения, получим Введем обозначение для разности, стоящей в скобках Уравнение принимает вид Разделив все члены уравнения на получаем каноническое уравнение эллипса: Если то эллипс вытянут вдоль оси Ох, для противоположного неравенства — вдоль оси Оу (при этом фокусы тоже расположены на этой оси). Проанализируем полученное уравнение. Если точка М(х; у) принадлежит эллипсу, то ему принадлежат и точки следовательно, эллипс симметричен относительно координатных осей, которые в данном случае будут называться осями симметрии эллипса. Найдем координаты точек пересечения эллипса с декартовыми осями:
- т.е. точками пересечения эллипса с осью абсцисс будут точки
- т.е. точками пересечения эллипса с осью ординат будут точки (Рис. 30).
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если то параметр а называется большой, а параметр b — малой полуосями эллипса.
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству Кроме того, эта характеристика описывает форму эллипса. Для демонстрации этого факта рассмотрим квадрат отношения малой полуоси эллипса к большой полуоси
Если и эллипс вырождается в окружность. Если и эллипс вырождается в отрезок
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр Зная параметр с, можно вычислить малую полуось эллипса Следовательно, каноническое уравнение заданного эллипса имеет вид:
Пример:
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса а третья вершина — в центре окружности
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
Следовательно, большая полуось эллипса а малая полуось Так как то эллипс вытянут вдоль оси ординат Оу. Определим расположение фокусов данного эллипса Итак, Окружность: Выделим полные квадраты по переменным Следовательно, центр окружности находится в точке О(-5; 1).
Построим в декартовой системе координат треугольник Согласно школьной формуле площадь треугольника равна Высота а основание Следовательно, площадь треугольника равна:
Эллипс в высшей математике
где и —заданные положительные числа. Решая его относительно , получим:
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное по абсолютной величине меньше , подкоренное выражение положительно, корень имеет два значения. Каждому значению , удовлетворяющему неравенству соответствуют два значения , равных по абсолютной величине. Значит, геометрическое место точек, определяемое уравнением (2), симметрично относительно оси . Так же можно убедиться в том, что оно симметрично и относительно оси . Поэтому ограничимся рассмотрением только первой четверти.
При , при . Кроме того, заметим, что если увеличивается, то разность уменьшается; стало быть, точка будет перемещаться от точки вправо вниз и попадет в точку . Из соображений симметрии изучаемое геометрическое место точек будет иметь вид, изображенный на рис. 34.
Полученная линия называется эллипсом. Число является длиной отрезка , число —длиной отрезка . Числа и называются полуосями эллипса. Число эксцентриситетом.
Пример:
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом (рис. 35). В каждой из этих плоскостей возьмем систему координат, причем за ось примем прямую пересечения плоскостей, стало быть, ось будет общей для обеих систем. Оси ординат различны, начало координат общее для обеих систем. В плоскости возьмем окружность радиуса с центром в начале координат, ее уравнение .
Пусть точка лежит на этой окружности, тогда ее координаты удовлетворяют уравнению .
Обозначим проекцию точки на плоскость буквой , а координаты ее—через и . Опустим перпендикуляры из и на ось , это будут отрезки и . Треугольник прямоугольный, в нем , ,, следовательно, . Абсциссы точек и равны, т. е. . Подставим в уравнение значение , тогда cos
а это есть уравнение эллипса с полуосями и .
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей с коэффициентами деформации, равными
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам (х, у, z) с текущими координатами х, у, г, причем
Иными словами, линейные размеры сферы в направлении оси Ох уменьшаются в раз, если , и увеличиваются в раз, если и т. д.
Подставляя эти формулы в уравнение (1), будем иметь
где Уравнение (2) связывает текущие координаты точки М’ эллипсоида и, следовательно, является уравнением трехосного эллипсоида.
Величины называются полуосями эллипсоида; удвоенные величины называются осями эллипсоида и, очевидно, представляют линейные размеры его в направлениях деформации (в данном случае в направлениях осей координат).
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Кривые второго порядка в математике с примерами решения и образцами выполнения
1) всякая прямая в прямоугольной системе координат определяется уравнением первой степени относительно переменных и ;
2) всякое уравнение первой степени в прямоугольной системе координат определяет прямую и притом единственную.
Мы займемся изучением линий, определяемых уравнениями второй степени относительно текущих
координат и :
Такие линии называются линиями (кривыми) второго порядка. Коэффициенты уравнения (1) могут принимать различные действительные значения, исключая одновременное равенство и нулю (в противном случае уравнение (1) не будет уравнением второй степени).
Окружность и ее уравнения
Как известно, Окружностью называется множество всех точек плоскости, одинаково удаленных от данной точки, называемой центром.
Пусть дана окружность радиуса с центром в точке требуется составить ее уравнение.
Возьмем на данной окружности произвольную точку
(рис. 38). Имеем
удовлетворяют координаты произвольной точки окружности. Более того, этому уравнению не удовлетворяют координаты никакой точки, не лежащей на окружности, так как и . Следовательно, (I) есть уравнение окружности радиуса с центром в точке . Если центр окружности находится на оси , т. е. если , то уравнение (I) примет вид
Если центр окружности находится на оси т. е. если то уравнение (I) примет вид
Наконец, если центр окружности находится в начале координат, т. е. если , то уравнение (I) примет вид
Пример:
Составить уравнение окружности радиуса с центром в точке .
Решение:
Имеем: . Подставив эти значения в уравнение (I), найдем .
Из изложенного выше следует, что уравнение окружности является уравнением второй степени относительно переменных и , как бы она ни была расположена в плоскости . Уравнение окружности (I) является частным случаем общего уравнения второй степени с
переменными
В самом деле, раскрыв скобки в уравнении (1), получим
Справедливо следующее утверждение: если в уравнении (5) , то Уравнение (5) определяет окружность.
Действительно, разделив уравнение (5) почленно на , получим:
Дополним группы членов, стоящие в скобках, до полного квадрата:
Положим Так как, по условию, то можно положить
Получим
Если в уравнении то оно определяет точку (говорят также, что окружность вырождается в точку). Если же то уравнению (5) не удовлетворяет ни одна пара действительных чисел (говорят также, что уравнение (5) определяет «мнимую» окружность).
Пример:
Найти координаты центра и радиус окружности
Решение:
Сравнивая данное уравнение с уравнением (1), находим: . Следовательно, .
Пример:
Установить, какое из уравнений:
определяет окружность. Найти координаты центра и радиус каждой из них.
Решение:
Первое уравнение не определяет окружность, потому что . Во втором уравнении . Однако и оно не определяет окружность, потому что . В третьем уравнении условия выполняются. Для окончательного вывода преобразуем его так:
Это уравнение, а следовательно, и уравнение 3), определяет окружность с центром и радиусом .
В четвертом уравнении также выполняются условия Однако преобразовав его к виду
, устанавливаем, что оно не определяет никакой линии.
Эллипс и его каноническое уравнение
Определение:
Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек той же плоскости, называемых фокусами, есть величина постоянная, большая расстояния между фокусами.
Составим уравнение эллипса, фокусы и которого лежат на оси
и находятся на одинаковом расстоянии от
начала координат (рис. 39).
Обозначив , получим Пусть произвольная точка эллипса. Расстояния называются фокальными радиусами точки . Положим
тогда, согласно определению эллипса, — величина постоянная и По формуле расстояния между двумя точками находим:
Подставив найденные значения и в равенство (1), получим уравнение эллипса:
Преобразуем уравнение (3) следующим образом!
Имеем: положим
последнее уравнение примет вид
Так как координаты и любой точки эллипса удовлетворяют уравнению (3),то они удовлетворяют уравнению (5).
Покажем, что справедливо и обратное: если координаты точки удовлетворяют уравнению (5) то она принадлежит эллипсу.
Пусть — произвольная точка, координаты которой удовлетворяют уравнению (5). Так как из (5)
то откуда
Подставив (6) в соотношения (2) и проведя необходимые упрощения, получим
Но так как то
т. е. точка действительно принадлежит эллипсу.
Уравнение (5) называется каноническим уравнением
эллипса.
Исследование формы эллипса по его уравнению
Определим форму эллипса по его каноническому
уравнению
1. Координаты точки не удовлетворяют уравнению (1), поэтому эллипс, определяемый этим уравнением не проходит через начало координат.
Найдем точки пересечения эллипса с осями координат. Положив в уравнении (1) , найдем Следовательно, эллипс пересекает ось в точках . Положив в уравнении (1) , найдем точки пересечения эллипса с осью :
(рис.40).
3. Так как в уравнение (1) переменные и входят только в четных степенях, то эллипс симметричен относительно координатных осей, а следовательно, и относительно начала координат.
4. Определим область изменения переменных и . В предыдущем параграфе (см. (7)) мы уже показали, что
Аналогично, переписав уравнение эллипса (1) в виде
получим откуда или
Таким образом, все точки эллипса находятся внутри прямоугольника, ограниченного прямыми
(см. рис, 40).
5. Переписав уравнение (1) соответственно в вида
мы видим, что при возрастании от 0 до величина убывает от до 0, а при возрастании от 0 до величина убывает от до 0. Эллипс имеет форму, изображенную на рис. 41.
Точки пересечения эллипса с осями координат
называются вершинами эллипса. Отрезок называется
большой осью эллипса, а отрезок — малой осью. Оси являются осями симметрии эллипса, а точка — центром симметрии (или просто центром) эллипса.
Пример:
Определить длину осей и координаты фокусов эллипса
Решение:
Разделив обе части данного уравнения на 1176, приведем его к каноническому виду
Следовательно,
Пример:
Составить каноническое уравнение эллипса, если фокусное расстояние равно 10, а малая ось равна 6.
Решение:
Другие сведения об эллипсе
Мы рассмотрели эллипс, у которого Если же то уравнение
определяет эллипс, фокусы которого лежат на оси (рис. 42). В этом случае длина большой оси равна , а малой . Кроме того, связаны между собой равенством
Определение:
Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большой оси и обозначается буквой .
Если , то, по определению,
При имеем
Из формул (3) и (4) следует . При этом с
увеличением разности между полуосями и увеличивается соответствующим образом и эксцентриситет
эллипса, приближаясь к единице; при уменьшении разности между и уменьшается и эксцентриситет, приближаясь к нулю. Таким образом, по величине эксцентриситета можно судить о форме эллипса: чем больше эксцентриситет, тем более вытянут эллипс; чем меньше эксцентриситет, тем круглее эллипс. В частности, если и уравнение эллипса примет вид , которое определяет окружность с центром в начале координат. Таким образом, окружность можно рассматривать как частный случай эллипса, у которого полуоси равны между собой, а следовательно, эксцентриситет равен нулю.
Из рис. 43, на котором изображены эллипсы и окружность , хорошо видна зависимость формы эллипса от его эксцентриситета. В заключение поясним, как можно построить эллипс
Для этого на осях координат строим вершины эллипса . Затем из вершины (можно из ) радиусом, равным а, на большой оси делаем засечки (рис. 44). Это будут фокусы эллипса, потому что . Далее, берем нерастяжимую нить, длина которой равна , и закрепляем ее концы в найденных фокусах. Натягиваем нить
острием карандаша и описываем кривую, оставляя нить все время в натянутом состоянии.
Пример:
Составить каноническое уравнение эллипса, фокусы которого лежат на оси , если его большая ось равна 14 и
Решение. Так как фокусы лежат на оси , то По
формуле (2) находим:
Следовательно, искомое уравнение, будет
Гипербола и ее каноническое уравнение
Определение:
Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек той же плоскости, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Составим уравнение гиперболы, фокусы которой лежат на оси и находятся на одинаковом расстоянии от начала координат (рис. 45).
Обозначив получим , Пусть
— произвольная точка гиперболы.
Расстояния называются фокальными радиусами точки . Согласно определению гиперболы
где — величина постоянная и Подставив
в равенство (1), получим уравнение гиперболы
Уравнение (2) можно привести к более простому виду; для этого преобразуем его следующим образом:
Имеем: . Положим
тогда последнее равенство принимает вид
Так как координаты и любой точки гиперболы удовлетворяют уравнению (2), то они удовлетворяют и уравнению (4).
Как и в случае эллипса (см. конец § 2), можно показать, что справедливо и обратное: если координаты точки удовлетворяют уравнению (4), то она принадлежит гиперболе.
Уравнение (4) называется каноническим уравнением гиперболы.
Исследование формы гиперболы по ее уравнению
Определим форму гиперболы по ее каноническому уравнению
1. Координаты точки (0; 0) не удовлетворяют уравнению (1), поэтому гипербола, определяемая этим уравнением, не проходит через начало координат.
2. Найдем точки пересечения гиперболы с осями координат. Положив в уравнении (1) , найдем . Следовательно, гипербола пересекает ось в точках . Положив в уравнение (1) , получим , а это означает, что система
не имеет действительных решений. Следовательно, гипербола не пересекает ось .
3. Так как в уравнение (1) переменные и входят только в четных степенях, то гипербола симметрична относительно координатных осей, а следовательно, и относительно начала координат.
4. Определим область изменения переменных и ; для этого из уравнения. (1) находим:
Имеем: или ; из (3) следует, что — любое действительное число. Таким образом, все точки гиперболы расположены слева от прямой и справа от прямой
5. Из (2) следует также, что
Это означает, что гипербола состоит из двух ветвей, одна из которых расположена справа от прямой , а другая слева от прямой .
Гипербола имеет форму, изображенную на рис. 46.
Точки пересечения гиперболы с осью называются вершинами гиперболы. Отрезок Рис. 46.
соединяющий вершины гиперболы, называется действительной осью. Отрезок , , называется мнимой осью. Число называется действительной полуосью, число — мнимой полуосью. Оси являются осями симметрии гиперболы. Точка пересечения осей симметрии называется центром гиперболы. У гиперболы (1) фокусы всегда находятся на действительной оси.
Пример:
Составить уравнение гиперболы, вершины которой находятся в точках , а расстояние между фокусами равно 14.
Решение:
Имеем: . По формуле находим
Следовательно, искомое уравнение будет
Пример:
Составить каноническое уравнение гиперболы с фокусами на оси , если длина ее действительной оси равна 16 и гипербола проходит через точку .
Решение:
Имеем: . Положив в уравнении (1) , получим
Другие сведения о гиперболе
Асимптоты гиперболы
Определение:
Прямая называется
асимптотой кривой при , если
Аналогично определяется асимптота при . Докажем, что прямые
являются асимптотами гиперболы
при
Так как прямые (2) и гипербола (3) симметричны относительно координатных осей, то достаточно рассмотреть только те точки указанных линий, которые расположены в первой четверти (рис. 47). Напишем уравнения прямых (2) и гиперболы (3), соответствую*
щие первой четверти:
Положив найдем:
Следовательно, прямые (2) являются асимптотами гиперболы (3).
Отметим, что асимптоты (2) совпадают с диагоналям прямоугольника, стороны которого параллельны осям и и равны соответственно и , а его центр находится в начале координат. При этом ветви гиперболы расположены внутри вертикальных углов,
образуемых асимптотами, и приближаются сколь угодно близко к асимптотам (рис.48).
Пример:
Составить уравнение гиперболы, проходящей через точку и, имеющей асимптоты
Решение:
Из данных уравнений асимптот имеем:
Заменив в уравнении гиперболы переменные и координатами точки и его найденным значением, получим:
Следовательно, искомое уравнение будет
Эксцентриситет гиперболы
Определение:
Эксцентриситетом гиперболы называется отношение расстояния между фокусами
к длине действительной оси и обозначается буквой :
Из формулы (§ 5) имеем поэтому
Пример:
Найти эксцентриситет гиперболы .
Решение:
По формуле (5) находим
Равносторонняя гипербола
Гипербола называется равносторонней, если длины ее полуосей равны между собой, т. е. . В этом случае уравнение гиперболы принимает вид
Равносторонняя гипербола определяется одним пара*
метром и асимптотами являются биссектрисы координатных углов:
У всех равносторонних гипербол один и тот же эксцентриситет:
Так как асимптоты равносторонней гиперболы взаимно перпендикулярны, их можно принять за оси новой системы координат полученной в результате поворота осей старой системы вокруг начала координат на угол (рис.49).
Составим уравнение равносторонней гиперболы относительно новой системы координат . Для этого воспользуемся формулами
(4) § 3 гл. 2:
Положив , получим:
Учитывая равенство (6), получим
Уравнение (8) называется уравнением равносторонней гиперболы, отнесенной к своим асимптотам.
Из уравнения (8) следует, что переменные — величины обратно пропорциональные. Таким образом, равносторонняя гипербола, отнесенная к своим асимптотам, представляет собой график обратно пропорциональной зависимости.
Пример:
Составить каноническое уравнение
равносторонней гиперболы, проходящей через точку .
Решение:
Заменив в уравнении (6) переменные координатами точки , получим:
Следовательно, искомое уравнение будет
Парабола и ее каноническое уравнение
Определение:
Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и от данной прямой, не проходящей через данную точку и
называемой директрисой.
Составим уравнение параболы, фокус которой лежит на оси , а
директриса параллельна оси и удалена от нее на такое же расстояние, как и фокус от начала координат (рис.50).
Расстояние от фокуса до директрисы называется параметром параболы и обозначается через . Из рис. 50 видно, что следовательно, фокус имеет координаты , а уравнение директрисы имеет вид , или
Пусть — произвольная точка параболы. Соединим точки
и и проведем . Непосредственно из рис. 50 видно, что
а по формуле расстояния между двумя точками
согласно определению параболы
Уравнение (1) является искомым уравнением параболы. Для упрощения уравнения (1) преобразуем его следующим образом:
Последнее уравнение эквивалентно
Координаты точки параболы удовлетворяют уравнению (1), а следовательно, и уравнению (3).
Покажем, что справедливо и обратное: если координаты точки удовлетворяют уравнению (3), то она принадлежит параболе.
Но так как из (3) , и в левой части последнего уравнения можно оставить знак «плюс», т. е. оно является исходным уравнением параболы (1).
Уравнение (3) называется каноническим уравнением параболы.
Исследование формы параболы по ее уравнению
Определим форму параболы по ее каноническому уравнению
1. Координаты точки удовлетворяют уравнению (1), следовательно, парабола, определяемая этим уравнением, проходит через начало координат.
2. Так как в уравнение (1) переменная входит только в четной степени, то парабола симметрична относительно оси абсцисс.
Так как . Следовательно, парабола расположена справа от оси .
4. При возрастании абсциссы ордината изменяется от , т. е. точки параболы неограниченно удаляются как от оси , так и от оси .
Парабола имеет форму, изображенную на рис. 51.
Ось является осью симметрии параболы. Точка пересечения параболы с осью симметрии называется вершиной параболы. Отрезок называется фокальным радиусом точки .
5. Если фокус параболы лежит слева от оси , а директриса справа от нее, то ветви параболы расположены слева от оси (рис. 52, а). Уравнение такой параболы имеет вид
Координаты ее фокуса будут ; директриса определяется уравнением .
6. Если фокус параболы имеет координаты , а директриса задана уравнением , то ветви параболы направлены вверх (рис. 52,6), а ее уравнение имеет вид
7. Наконец, если фокус параболы имеет координаты а директриса задана уравнением , то ветви параболы направлены вниз (рис. 52, в), а ее уравнение имеет вид
Пример:
Дана парабола . Найти координаты ее фокуса и составить уравнение директрисы.
Решение:
Данная парабола симметрична относительно оси , ветви направлены вверх. Сравнивая данное уравнение с уравнением (3), находим:
Следовательно, фокус имеет координаты , а уравнение директрисы будет , или .
Пример:
Составить уравнение параболы с вершиной в начале координат, директриса которой задана уравнением .
Решение:
Из условия задачи следует, что парабола симметрична относительно оси и ветви расположены слева от оси , поэтому искомое уравнение имеет вид . Так как и, следовательно,
Параллельный перенос параболы
Пусть дана парабола с вершиной в точке , ось симметрии которой параллельна оси , а ветви направлены вверх (рис. 53).
Требуется составить ее уравнение. Сделаем параллельный перенос осей координат, поместив начало в точке . Относительно новой системы координат парабола определяется уравнением
Чтобы получить уравнение данной параболы относительно старой системы, воспользуемся формулами преобразования прямоугольных координат при параллельном переносе;
Подставив значения из формул (2) в уравнение (1), получим
Преобразуем это уравнение следующим образом:
С уравнением параболы вида (5) читатель хорошо знаком по школьному курсу.
Пример 1. Составить уравнение параболы с вершиной в точке и с фокусом в точке .
Решение. Вершина и фокус данной параболы лежат на прямой, параллельной оси (у них абсциссы одинаковы), ветви параболы направлены вверх (ордината фокуса больше ординаты вершины), расстояние фокуса от вершины равно
Заменив в уравнении (3) и координатами точки и его найденным значением, получим:
Пример:
Дано уравнение параболы
Привести его к каноническому виду.
Решение:
Разрешив данное уравнение относительно переменной , получим
Сравнивая это уравнение с уравнением (5), находим Из формул (4) имеем:
следовательно, Подставляем найденные значения в уравнение (3):
Положив получим т. е, каноническое уравнение данной параболы.
Уравнения кривых второго порядка как частные случаи общего уравнения второй степени с двумя переменными
Выше было установлено, что уравнение окружности есть частный случай общего уравнения второй степени с переменными и :
Покажем, что и канонические уравнения эллипса, гиперболы и параболы являются частными случаями уравнения (1). В самом деле:
1) при и уравнение (1) примет вид
т. е. определяет эллипс;
2) при и уравнение (1) примет вид
т. е. определяет гиперболу;
3) при и уравнение (1) примет вид т. е. определяет параболу.
Дополнение к кривым второго порядка
Пусть задана кривая, определяемая уравнением второй степени
где — действительные числа; и одновременно не равны нулю. Эта кривая называется кривой второго порядка.
Приведем еще одно определение кривой второго порядка.
Геометрическое место точек плоскости, для которых отношение их расстояний до заданной точки, называемой фокусом, и до заданной прямой, называемой директрисой, есть величина постоянная, равная , является кривой 2-го порядка с эксцентриситетом, равным . Если , то кривая второго порядка — эллипс; — парабола; — гипербола.
Эллипс
Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек и этой плоскости, называемых фокусами, есть величина постоянная, равная . Если фокусы совпадают, то эллипс представляет собой окружность.
Каноническое уравнение эллипса: .
Если , то эллипс расположен вдоль оси ; если , то эллипс расположен вдоль оси (рис. 9а, 9б).
Если , то, сделав замену , перейдем в «штрихованную» систему координат, в которой уравнение будет иметь канонический вид:
Декартова прямоугольная система координат, в которой уравнение эллипса имеет канонический вид, называется канонической.
Точки пересечения эллипса с осями координат называются вершинами эллипса. Расстояния от начала координат до вершин и называются соответственно большой и малой полуосями эллипса.
Центр симметрии эллипса, совпадающий с началом координат, называется центром эллипса.
Если — расстояние от начала координат канонической системы координат до фокусов, то .
Отношение называется эксцентриситетом эллипса.
Расстояние от произвольной точки , лежащей на эллипсе, до каждого из фокусов является линейной функцией от ее абсциссы, т.е. .
С эллипсом связаны две замечательные прямые, называемые его директрисами. Их уравнения в канонической системе имеют вид .
Гипербола
Гиперболой называется геометрическое место точек плоскости, для которых абсолютная величина разности расстояний до двух фиксированных точек и этой плоскости, называемых фокусами, есть величина постоянная, равная (рис. 10).
Декартова прямоугольная система координат, в которой уравнение гиперболы имеет канонический вид, называется канонической. Каноническое уравнение гиперболы:
Ось абсцисс канонической системы пересекает гиперболу в точках, называемых вершинами гиперболы. Ось ординат не пересекает гиперболу. и называются вещественной и мнимой полуосями гиперболы. Центр симметрии гиперболы, совпадающий с началом координат, называется центром гиперболы.
Если — расстояние от начала координат канонической системы координат до фокусов гиперболы, то .
Отношение называется эксцентриситетом гиперболы.
Расстояние от произвольной точки , лежащей на гиперболе, до каждого из фокусов равно .
Гипербола с равными полуосями называется равносторонней.
Прямые с уравнениями в канонической системе называются асимптотами гиперболы.
Прямые называют директрисами гиперболы в канонической системе координат.
Парабола
Параболой называется геометрическое место точек плоскости, для которых расстояние до некоторой фиксированной точки этой плоскости равно расстоянию до некоторой фиксированной прямой, также расположенной в рассматриваемой плоскости (рис. 11).
Указанная точка называется фокусом параболы, а фиксированная прямая — директрисой параболы.
Система координат, в которой парабола имеет канонический вид, называется канонической, а ось — осью параболы.
Каноническое уравнение параболы:
Парабола проходит через начало канонической системы координат. Эта точка называется вершиной параболы.
Фокус параболы имеет координаты .
Директрисой параболы называется прямая в канонической системе координат.
Расстояние от произвольной точки параболы до фокуса равно .
Пример задачи решаемой с применением кривых второго порядка
Линия задана уравнением в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от до и придавая значения через промежуток ; 2) найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс — с полярной осью, привести его к каноническому виду; 3) по уравнению в декартовой прямоугольной системе координат определить, какая это линия.
Решение:
1) Вычисляя значения с точностью до сотых при указанных значениях , получим таблицу:
Используя полученные табличные значения, построим кривую в полярной системе координат (рис. 17).
2) Используя формулы перехода
из полярной в декартовую систему координат, получим: .
Возведем левую и правую части в квадрат: Выделим полный квадрат и приведем к каноническому виду: , где
3) Это эллипс, смещенный на вдоль оси .
Ответ: эллипс , где
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Возможно вам будут полезны эти страницы:
Кривая второго порядка и её определение
Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением
Окружность и ее уравнение
Окружностью называется геометрическое место точек, одинаково удаленных от одной точки, называемой центром.
Пользуясь этим определением, выведем уравнение окружности. Пусть радиус ее равен r, а центр находится в точке
О1(а; b). Возьмем на окружности произвольную точку М(х; у) (рис. 27).
По формуле расстояния между двумя точками можем написать:
или, после возведения обеих частей равенства в квадрат,
Так как точка М нами взята произвольно, а радиус r — величина постоянная, то равенство (1) справедливо для всех точек окружности, т. е. координаты любой ее точки удовлетворяют этому равенству. А если так, то равенство (1) нужно рассматривать как уравнение окружности.
В уравнении (1) а и b — координаты центра окружности, а х и у — текущие координаты.
Если положить а = 0, то уравнение (1) обратится в следующее:
и будет определять окружность с центром на оси Оу (рис. 28).
При b = 0 уравнение (1) примет вид
и будет определять окружность с центром на оси Ох (рис. 29).
Наконец, при а = 0 и b = 0 уравнение (1) преобразуется в следующее:
и будет определять окружность с центром в начале координат (рис. 30).
Можно построить окружность, имея ее уравнение. Пусть, например, требуется построить окружность
Перепишем это уравнение в следующем виде:
сравнивая это уравнение с(1), видим, что координаты центра окружности суть (2; — 3) и радиус ее r = 3. Построив
точку О1(2;—3), опишем из нее радиусом, равным 3 единицам масштаба, искомую окружность (рис. 31).
Уравнение окружности как частный вид общего уравнения второй степени
Раскрыв скобки в уравнении (1) , можем написать:
Умножив все члены последнего равенства на А, получим:
тогда уравнение (1) окружности примет вид
Уравнение (2) является частным случаем общего уравнения второй степени с двумя переменными. В самом деле, сравним уравнение (2) с общим уравнением второй степени с двумя переменными, имеющим, как известно, следующий вид:
Мы видим, что уравнение (2) отличается от уравнения (3) только тем, что у первого коэффициенты при х2 и у2 одинаковы и отсутствует член, содержащий произведение ху.
Таким образом, окружность определяется общим уравнением второй степени с двумя переменными, если в нем коэффициенты при х2 и у2 равны между собой и отсутствует член с произведением ху.
Обратно, уравнение вида (2), вообще говоря, определяет окружность. Убедимся в этом на примере. Пусть дано уравнение
Перепишем его в следующем виде:
и преобразуем двучлены, стоящие в скобках, в полные квадраты суммы и разности, прибавив к первому 4, ко второму 16. Чтобы равенство при этом не нарушилось, увеличим и правую часть его на сумму 4+16. Получим:
Последнее равенство является уравнением окружности, имеющей радиус, равный 5, и центр в точке О1(-2; 4).
Бывают однако случаи, когда уравнение (2) при некоторых значениях коэффициентов не определяет окружности; например, уравнению
удовлетворяют координаты единственной точки (0; 0), а уравнению
не удовлетворяют координаты ни одной точки, так как сумма квадратов действительных чисел не может иметь отрицательного значения.
Пример:
и хорда Найти длину этой хорды.
Решение:
Так как концы хорды являются общими точками окружности и хорды, то их координаты удовлетворяют как уравнению первой, так и уравнению второй линии. Поэтому, чтобы найти эти координаты, нужно решить совместно уравнения окружности и хорды. Подставив значение
в уравнение окружности, получим:
Находим значение у:
Итак, концами хорды служат точки с координатами (4; 3) и (6; 1).
По формуле расстояния между двумя точками можем определить искомую длину хорды
Эллипс и его уравнение
Эллипсом называется геометрическое место точек, сумма расстояний каждой из которых от двух данных точек, называемых фокусами, есть величина постоянная (и болыиая, чем расстояние между фокусами).
Пусть, например, на эллипсе взяты точки М1, M2, M3, М4 и т. д. (рис. 32). Если фокусы обозначить через F и F1, то согласно данному определению можно написать:
Геометрическое место точек, обладающих вышеуказанным свойствам (1), и есть эллипс.
На основании определения эллипса составим его уравнение. Для этого выберем систему координат следующим образом. За ось Ох примем прямую, проходящую через фокусы F и F1, а за ось Оу — прямую перпендикулярную
к FF1 и проведенную через середину отрезка FF1 (рис. 33). Обозначим расстояние F1F между фокусами через 2с, тогда координаты фокусов будут:
Возьмем на эллипсе произвольную точку М(х;у). Обозначим постоянную величину суммы расстояний каждой точки от фокусов через 2а, тогда
По формуле расстояния между двумя точками найдем:
Теперь равенство (2) перепишется следующим образом:
и будет представлять уравнение эллипса в принятой системе координат.
Упростим уравнение (3). Для этого перенесем один из радикалов в правую часть уравнения:
Возведем обе части этого равенства в квадрат:
Приведем подобные члены:
Сократив на 4 и снова возведя в квадрат обе части равенства, получим:
Перенесем все члены, содержащие х и у, в левую часть равенства, остальные члены — в правую:
Но согласно определению эллипса
Из последнего неравенства следует, что а потому эту разность можно обозначить через Подставив это обозначение в равенство (4), найдем:
Наконец, разделим все члены последнего равенства на окончательно получим:
где х и у — текущие координаты точек эллипса, а
Уравнение (6) и есть простейший вид уравнения эллипса *).
*) Уравнение (6) получилось в результате двукратного возведения в квадрат уравнения (3), благодаря чему, вообще говоря, возможно появление посторонних корней. Можно показать, что уравнение (6) не имеет посторонних корней, т. е. любая точка, координаты которой удовлетворяют уравнению (6), лежит на эллипсе.
Исследование уравнения эллипса
Определим сначала у из уравнения (5) :
Из того же уравнения (5) найдем:
Рассмотрим теперь равенства (1) и (2).
I. Пусть
*) | х | означает, что х берется по абсолютной величине; таким образом, запись | х |
Тогда каждому значению у, как мы видим из равенства (2), отвечают два значения х равные по абсолютной величине, но с разными знаками. Отсюда следует, что каждому значению у соответствуют на эллипсе две точки, симметричные относительно оси Оу.
Из сказанного заключаем: эллипс симметричен относительно координатных осей.
II. Найдем точки пересечения эллипса с осью Ох. Пусть
тогда из равенства (2) имеем:
Отсюда следует: эллипс пересекает ось Ох в двух точках, координаты которых (а; 0) и (— а; 0) (точки А и А1 на рис. 34).
III. Найдем точки пересечения эллипса с осью Оу. Пусть
тогда из равенства (1) имеем:
Отсюда заключаем, что эллипс пересекает ось Оу в двух точках, координаты которых (0; b) и (0; —b) (точки В и В1 на рис. 35).
IV. Пусть х принимает такие значения, что
тогда выражение под корнем в равенстве (1) будет отрицательным, и, следовательно, у будет иметь мнимые значения. А это значит, что не существует точек эллипса, абсциссы которых удовлетворяют условию (3), т. е. эллипс расположен внутри полосы, заключенной между прямыми х = + а и х = — а (рис. 34, прямые КL и РQ).
Если же положить
то из равенства (2) получим для х мнимые значения. Это говорит о том, что точки, удовлетворяющие условию (4), на эллипсе не лежат, т. е. эллипс заключен между прямыми у = + b и у = — b (рис. 35, прямые РК и QL .
Из сказанного следует, что все точка эллипса лежат внутри прямоугольника, стороны которого параллельны координатным осям и имеют длины, равные 2а и 2b, а диагонали пересекаются в начале координат (рис. 36).
Эллипс имеет форму, показанную на рис. 37, Точки A,, A1, В и В1 называются вершинами эллипса, а точка О — его центром. Отрезок А1А = 2а называется его большой осью, а отрезок В1В = 2b — малой осью, Отрезки FМ и F1М носят название фокальных радиусов точки М.
Эксцентриситет эллипса
Эксцентриситетом эллипса называется отношение расстояния между его фокусами к длине большой оси, т. e.
Эксцентриситет обычно обозначают буквой е. Таким образом,
Но согласно формуле (7)
Поэтому для определения эксцентриситета может служить
Так как 0 а уравнение (6) представляет эллипс, фокусы которого лежат на оси Оу; в этом случае его большая ось равна 2 b , а малая 2 а . В соответствии с этим формула (7) и формулы (1) и (2) настоящей лекции примут такой вид:
Пример:
Определить длину его осей, координаты вершин и фокусов, а также величину эксцентриситета.
Решение:
Разделив обе части данного уравнения на 400, получим:
Итак, большая ось эллипса а малая
Координаты вершин его будут:
Чтобы найти координаты фокусов, нужно узнать величину
Из равенства (7) имеем:
Следовательно, координаты фокусов будут:
Наконец, по формуле (1) настоящей лекции находим:
Связь эллипса с окружностью
Положим, что полуоси эллипса равны между собой, т. е. а = b, тогда уравнение эллипса примет вид
Полученное уравнение, как известно, определяет окружность радиуса, равного а.
Посмотрим, чему будет равен эксцентриситет в этом случае; полагая в формуле (2)
Отсюда заключаем, что окружность есть частный случай эллипса, у которого полуоси равны между собой, а следовательно, эксцентриситет равен нулю.
Гипербола и ее уравнение
Гиперболой называется геометрическое место точек, разность расстояний каждой из которых от двух данных точек, называемых фокусами, есть величина постоянная (эта постоянная берется по абсолютному значению, причем она меньше расстояния между фокусами и не равна нулю).
Пусть, например, точки М1, М2, M3, М4 лежат на гиперболе, фокусы которой находятся в точках F и F1 (рис. 39). Тогда, согласно данному выше определению, можно написать:
Пользуясь определением гиперболы, выведем ее уравнение.
Примем за ось Ох прямую, проходящую через фокусы F и F1 (рис. 40), а за ось Оу — прямую, перпендикулярную к отрезку F1F и делящую его пополам.
Положим F1F = 2c тогда координаты фокусов будут
Возьмем на гиперболе произвольную точку М(х; у) и обозначим величину разности расстояний каждой точки от фокусов через 2а; тогда
По формуле расстояния между двумя точками найдем:
и, заменив в равенстве (2) F1М и FМ их выражениями, напишем:
Это и есть уравнение гиперболы относительно выбранной системы координат, так как оно согласно равенствам (1) справедливо для любой ее точки.
*) Знак + берется в случае, если F1М > FМ , и знак —, если F1М
Возведем обе части уравнения в квадрат:
Приведем подобные члены:
Сократив на 4, снова возведем в квадрат обе части уравнения; получим:
Перенесем в левую часть члены, содержащие х и у, а остальные члены в правую:
Согласно определению гиперболы
При условии (5) разность имеет только положительное значение, а потому ее можно обозначить через
Сделав это в равенстве (4), получим:
Разделив последнее равенство на найдем окончательно:
где х и у— текущие координаты точек гиперболы, а
Равенство (7) представляет собой простейший вид уравнения гиперболы *).
*) Как и в случае эллипса, можно показать, что уравнение (7) равносильно уравнению (3), т. е. не имеет посторонних корней.
Исследование уравнения гиперболы
Из уравнения (6) имеем:
Из этого же уравнения (6) находим:
Исследуем уравнения (1) и (2) для выяснения геометрической формы гиперболы.
I. Найдем точки пересечения гиперболы с осью Ох. Для этого полагаем, у = 0 и из уравнения (2) получаем:
Отсюда следует: гипербола пересекает ось Ох в двух точках, координаты которых (а; 0) и (— а; 0) (рис. 41, точки А и А1).
II. Положим в уравнении (1)
тогда у получит мнимое значение, а это значит, что на гиперболе нет точек, удовлетворяющих условию (3). Следовательно, в полосе между прямыми х = + а и х = — а (прямые KL и РQ на рис. 41) нет точек гиперболы
III. Пусть
тогда из равенства (1) найдем для каждого х два действительных значения у, равных по абсолютной величине, но с противоположными знаками. А это значит, что каждому значению х, удовлетворяющему неравенству (4), соответствуют на нашей кривой две точки, симметричные относительно оси Ох.
Следовательно, гипербола симметрична относительно оси Ох.
С другой стороны, для каждого значения у из равенства (2) найдем два действительных значения х, равных по абсолютной величине, но противоположных по знаку, т. е. каждому значению у на гиперболе соответствуют две точки, симметричные относительно оси Оу.
Следовательно, гипербола 1 симметрична относительно оси Оу.
IV. Если в уравнении (1) давать х значения, заключенные между +a и то величина у будет изменяться от 0 до : т. е. в этом случае каждому значению х соответствуют на кривой две точки, симметричные относительно оси Ох и отстоящие друг от друга тем дальше, чем больше величина абсциссы. Таким образом, можно сказать, что гипербола имеет бесконечную ветвь, расположенную справа от прямой х = с.
Если же давать х значения, заключенные между — а и , то у будет изменяться опять от 0 до а это значит, что, как в предыдущем случае, гипербола имеет бесконечную ветвь, но идущую влево от прямой х = — а. Итак, гипербола есть кривая, состоящая из двух ветвей, простирающихся в бесконечность.
Из всего изложенного следует, что гипербола
состоит из двух симметричных относительно оси Оу бесконечных ветвей, одна из которых расположена справа от
прямой х = + а, а другая слева от прямой х = — а. Каждая из этих ветвей симметрична относительно оси Ох (рис. 42).
Точки А(а; 0) и А1(- а; 0) называются вершинами гиперболы, а точка О (0; 0) — ее центром.
Отрезок АА1 = 2а носит название действительной или вещественной оси гиперболы в отличие от оси ВВ1 = 2b, называемой мнимой *).
*) Отрезок ВВ1 = 2b называется мнимой осью, так как на нем нет точек гиперболы.
Отрезки F1М и FМ — фокальные радиусы точки М.
Эксцентриситет гиперболы
Эксцентриситетом гиперболы называется отношение расстояния между фокусами к длине вещественной оси, т. е.
Эксцентриситет гиперболы, так же как и для эллипса, обозначается буквой е:
Но согласно равенству (8)
поэтому формулу (1) можно представить в следующем виде:
Так как для гиперболы с > а , то дробь
а потому эксцентриситет гиперболы больше единицы.
Асимптоты гиперболы
Построим на осях гиперболы
прямоугольник LQRS со сторонами, равными 2а и 2b и проведем его диагонали LR и QS продолжив их по обе стороны (рис. 43).
Прямая LR проходит через начало координат, поэтому ее уравнение будет:
Но угловой коэффициент
Заменив в уравнении (1) найденным его значением, получим уравнение прямой LR в следующем виде:
Прямая QS также определяется уравнением (1), но угловой коэффициент ее будет уже другой, а именно:
Таким образом, уравнение прямой QS будет:
Обычно уравнения (2) и (3) записывают следующим образом:
Между прямыми, представленными уравнениями (4), и гиперболой существует связь; выясним ее.
Решим совместно способом подстановки уравнения (4) и
уравнение гиперболы
что невозможно, так как
Таким образом, прямые (4) х2 уа
и гипербола не имеют общих точек, т. е. прямые (4) не пересекают гиперболу.
Возьмем на прямой LR и на гиперболе точки М и N, расположенные в первом координатном углу и имеющие одну и ту же абсциссу. Ординатой точки М служит РМ; обозначим ее через Y в отличие от ординаты точки N которую обозначим буквой у. Из уравнения (2) можно написать:
Из уравнения гиперболы имеем:
и посмотрим, как она будет изменяться при возрастании абсциссы. Для этого умножим и разделим правую часть последнего равенства на выражение
Пусть величина х в равенстве (5) бесконечно возрастает, тогда знаменатель дроби также бесконечно растет, а сама дробь уменьшается, приближаясь к нулю. Таким образом, гипотенуза NМ и, следовательно, катет NT в прямоугольном треугольнике МNТ стремится к нулю. Из сказанного делаем вывод: при неограниченном возрастании абсциссы х гипербола приближается к прямой LR как угодно близко, нигде ее не пересекая.
Так как прямые LR и QS, а также точки гиперболы симметричны относительно оси Ох, то можно сказать, что и часть гиперболы, расположенная в четвертом координатном углу, как угодно близко подходит к прямой QS , нигде ее не пересекая.
Вывод, сделанный для правой ветви гиперболы, справедлив и для ее левой ветви благодаря той же симметричности прямых (4) и гиперболы относительно координатных осей.
называются асимптотами гиперболы.
Из сказанного в настоящей лекции можно сделать заключение, что гипербола расположена всеми своими точками внутри вертикальных углов, образуемых асимптотами, и нигде не выходит за их границы. Этим обстоятельством можно воспользоваться для построения гиперболы в случае, если не требуется точного, а достаточно только приближенного ее изображения; для этого, нарисив асимптоты, нужно провести плавную кривую линию, постепенно приближая ее к асимптотам.
Пример:
Дана гипербола
Узнать, лежит ли точка A(2; 1,5) на какой-либо ее асимптоте.
Решение:
Из данного уравнения имеем:
Следовательно, уравнения асимптот будут:
Так как точка А лежит согласно условию в первом координатном углу, то она может принадлежать только асимптоте, определяемой уравнением
Подставив в него вместо х и у координаты точки А, получим тождество:
Значит, точка А лежит на указанной асимптоте гиперболы.
Равносторонняя гипербола
Если в уравнении гиперболы
положим а = b то это уравнение примет вид
Уравнение (1) определяет гиперболу, у которой полуоси равны между собой. Такая гипербола называется равносторонней. Уравнения асимптот в этом случае будут:
так как отношение
Как видно из уравнения (2), угловые коэффициенты асимптот равны + 1 и —1 . Если обозначить углы, образуемые асимптотами с положительным направлением оси Ох, соответственно через а и а1 (рис. 44), то
Следовательно, угол между асимптотами будет:
Отсюда заключаем: асимптоты равносторонней гиперболы взаимно перпендикулярны.
Уравнение равносторонней гиперболы, отнесенной к асимптотам
Так как асимптоты равносторонней гиперболы взаимно перпендикулярны, то их можно принять за оси прямоугольной системы координат и рассматривать гиперболу по отношению к этим новым осям. Выведем уравнение равносторонней гиперболы для этого случая.
Пусть дана равносторонняя гипербола. Тогда ее уравнение по отношению к координатным осям Ох и Оу (рис. 45)
выразится, как было пока-* у зано в , в виде
Взяв на гиперболе произвольную точку М (х; у) и построив ее координаты, будем иметь:
Примем теперь за оси координат асимптоты гиперболы: ОХ— за ось абсцисс, ОY — за ось ординат. Опустив перпендикуляр МС на новую ось абсцисс, найдем:
Выразим новые координаты X н Y точки М через старые х и у. Для этого из точки А проведем и
Обратим внимание на то, что в образовавшихся прямоугольных треугольниках АМВ и АОD
как углы, образованные взаимно перпендикулярными прямыми. Но
Из рисежа имеем:
Перемножив равенства (2) и (3) и приняв во внимание равенство (1), получим:
Положим для краткости
тогда равенство (4) перепишется так:
где m— постоянная величина.
Таково уравнение равносторонней гиперболы, если за оси координат принять ее асимптоты.
Как видно из уравнения (5), переменные X и Y — величины обратно пропорциональные, а потому можно сказать, что равносторонняя гипербола ху = m представляет собой график обратно пропорциональной зависимости между переменными величинами.
Парабола и ее простейшее уравнение
Параболой называется геометрическое место точек, каждая из которых одинаково удалена от точки, называемой фокусом, и от прямой, называемой директрисой <при условии, что фокус не лежит на директрисе).
Пусть точки М1 М2, М3, М4 лежат на параболе (рис. 46).
Если точка F изображает фокус, а прямая АВ— директрису, то согласно данному выше определению можем написать:
Выведем уравнение параболы, пользуясь ее определением. Для этого выберем систему координат, приняв за ось Ох прямую, проведенную через точку F (фокус) перпендикулярно к директрисе АВ, а за
ось Оу — прямую, проходящую через середину отрезка КF перпендикулярно к последнему (рис. 47). Обозначим
тогда координаты фокуса F будут
Возьмем на параболе произвольную точку М(x; у) расстояния ее от фокуса F и от директрисы АВ будут выражаться соответственно отрезками FМ и МN. Согласно определению параболы, можем написать:
Применяя формулу расстояния между двумя точками и приняв во внимание, что точка N имеет координаты , найдем:
Заменив FМ и МN в равенстве (1) их выражениями, получим:
Это и есть уравнение параболы относительно выбранной системы координат, так как оно справедливо для любой ее точки.
Упростим уравнение (2). Для этого возведем обе части его в квадрат:
Приведя подобные члены, получим простейшее уравнение параболы
*) Можно показать, что уравнение (3) равносильно уравнению (2). Величина р называется параметром параболы.
Исследование уравнения параболы
Из уравнения (3) найдем:
Исследуем уравнение (1) для выяснения геометрической формы нашей кривой, полагая р > 0.
I. Положим
Отсюда следует: парабола проходит через начало координат.
II. Если х 0, то у имеет два действительных значения, равных по абсолютной величине, но с разными знаками. Это значит, что каждому положительному значению х на параболе соответствуют две точки, расположенные симметрично относительно оси Ох.
Следовательно, парабола симметрична относительно оси Ох.
IV. Пусть х неограниченно возрастает, тогда и будет неограниченно расти, т. е. точки параболы с перемещением вправо от оси Оу неограниченно удаляются вверх и вниз от оси Ох.
Итак, парабола состоит из бесконечных ветвей.
Вышеизложенное позволяет представить параболу, как показано на рис. 48.
Точка О называется вершиной параболы, отрезок FМ — фокальным радиусом точки М параболы, а бесконечная прямая Ох является ее осью симметрии.
Если директрису параболы поместить справа от начала координат, то фокус и ветви ее расположатся как показано на рисеже 49.
При этом абсциссы точек параболы будут удовлетворять условию
а потому ее уравнение примет вид:
Парабола может быть симметрична и относительно оси Оу в этом случае фокус ее будет лежать па оси ординат, а директрисой будет прямая, параллельная оси Ох. Как видно при этом условии координатные оси поменяются ролями, и уравнение параболы примет вид
если ветви ее направлены вверх (рис. 50), и
если ветви направлены вниз (рис. 51).
Пример:
Найти координаты ее фокуса и написать уравнение директрисы.
Решение:
Данная парабола симметрична относительно оси Ох и расположена направо от оси Оу. Из уравнения находим:
Расстояние фокуса от начала координат равно , поэтому абсцисса фокуса будет Итак, фокус находится в точке
Директрисой служит прямая, параллельная оси Оу и отстоящая от последней на расстоянии Следовательно,
уравнение директрисы параболы будет х = — 3.
Пример:
Фокус параболы с вершиной в начале координат лежит в точке F(0; —4). Написать уравнение этой параболы.
Решение:
Согласно условию данная парабола симметрична относительно оси Оу, а ветви ее направлены вниз, поэтому искомое уравнение найдется из (3). Так как
и уравнение параболы будет:
Уравнение параболы со смещенной вершиной и осью, параллельной оси Оу
Возьмем уравнения параболы (2) и (3) и запишем их в следующем виде:
Положив в уравнении (1)
Уравнение (2) определяет параболу, ветви которой направлены вверх, если А > О, вниз, если А
Возьмем на параболе произвольную точку М(х; у). Опустив из нее перпендикуляр МР на ось Ох, будем иметь:
Проведем через О1 прямые О1Х и QY, параллельные координатным осям Ох и Оу, и положим временно, что прямые О1Х и О1Y служат осями новой системы координат. Обозначим координаты точки М в этой системе через X и Y, т. е.
Уравнение параболы в новой системе координат напишется следующим образом:
Чтобы найти ее уравнение относительно прежних осей Ох и Оу, нужно X и Y выразить через х и y. Так как
Подставив в уравнение (3) найденные значения X и Y, получим:
Упростим уравнение (4); для этого раскроем в нем скобки.
тогда уравнение (5) примет вид
Это—уравнение параболы с вершиной, лежащей в любой точке плоскости, и с осью симметрии, параллельной оси Оу.
Рассмотрим частные случаи.
Пусть абсцисса вершины параболы a = 0; тогда величина В в равенстве (6) также будет нулем и уравнение (8) примет следующий вид:
Полученное уравнение определяет параболу, у которой вершина лежит на оси Оу, являющейся в то же время и ее осью симметрии (рис. 53).
Положим, что одна из точек параболы (исключая ее вершину) лежит в начале координат; тогда координаты (0; 0) должны удовлетворять уравнению (8). Заменив в нем х и у нулями, найдем С=0. В этом случае уравнение (8) получит вид
и будет определять параболу, проходящую через начало координат (рис. 54).
Заметим, что и уравнение (2) можно рассматривать как частный случай уравнения (8). Действительно, положив в равенствах (6) и (7)
вследствие чего уравнение (8) преобразуется в следующее:
Из сказанного следует, что парабола, у которой ось симметрии параллельна оси Оу или совпадает с ней, определяется уравнением
при любых значениях А, В и С, кроме А = 0.
Убедимся на примере, что справедливо и обратное утверждение: всякое уравнение вида (8) определяет параболу с осью симметрии, параллельной оси Оу.
Пусть дано уравнение
Преобразуем его следующим образом:
тогда уравнение (10) примет вид:
Уравнение (11) имеет такой же вид, как и уравнение (2), поэтому оно, а следовательно, и уравнение (9) определяют параболу, у которой ось симметрии параллельна оси Оу.
Для построения параболы, определяемой уравнением вида (8), можно использовать обычный прием, применяемый для вычерчивания графиков функций, а именно: дав х ряд значений, вычислить значения у, а затем, построив точки по найденным координатам, провести через них плавную линию.
Пример:
Решение:
Прежде всего найдем абсциссы точек пересечения данной параболы с осью Ох; положив у = 0, получим:
Так как найденные точки симметричны относительно оси параболы, то вершина последней, находясь на этой оси, имеет 0 + 4 0
абсциссу, равную ордината же ее
Этих трех точек достаточно для приближенного изображения параболы.
Для более точного ее представления нужны дополнительные точки. Составим следующую таблицу:
Построив эти точки и прозедя через них плавную линию, получим искомую параболу (рис. 55).
Пример:
Решение:
мнимые, а потому ось Ох не пересекает данную параболу. В этом случае следует найти абсциссы точек пересечения параболы с прямой
(-1 — свободный член данного уравнения параболы)
Решая для этой цели систему уравнений
Полученные точки симметричны относительно оси параболы, поэтому абсцисса ее вершины равна ордината же ее
Присоединим к этим точкам несколько дополнительных точек. Составим таблицу:
Конические сечения
Окружность, эллипс, гипербола и парабола определяются, как мы установили в предыдущих лекциях уравнениями второй степени относительно текущих координат; поэтому их называют кривыми второго порядка. Они были известны еще древним грекам, которые изучали эти кривые, рассматривая их как результат сечения прямого кругового конуса плоскостью в следующих четырех случаях.
I. Секущая плоскость перпендикулярна к оси конуса; в сечении получается окружность (рис. 57).
II. Секущая плоскость образует с осью конуса угол, не равный 90°, и пересекает все его образующие по одну сторону от вершины S; в сечении получается эллипс (рис. 58).
III. Секущая плоскость параллельна какой-либо образующей конуса; при этом получается кривая, называемая параболой (рис. 59).
IV. Секущая плоскость пересекает обе полости конуса; при этом получаются две бесконечные ветви, образующие гиперболу (рис. 60).
Окружность, эллипс, гипербола и парабола называются коническими сечениями.
Конические сечения изучались в древности исключительно геометрическим путем, что представляло большие трудности, и только со времени Декарта, давшего метод координат, изучение их значительно упростилось.
Кривая второго порядка и её вычисление
Уравнение линии. Кривые второго порядка. Окружность. Эллипс. Гипербола. Парабола. Приведение к каноническому виду.
Уравнение линии в декартовых и полярных координатах
В лекции 3 было введено понятие неявной функции, задаваемой уравнением вида F(x,y) = 0.
Определение 6.1. Множество точек плоскости, координаты которых удовлетворяют некоторому уравнению
(6.1) F(x;y) = 0
называется линией (плоской кривой).
Не всякое уравнение определяет линию. Например, уравнение x² + y² = -1 не определяет никакой линии. Кроме того, линия может состоять из отдельных точек. Так, например, уравнению x² + y² = 0 удовлетворяет только начало координат.
Линия не обязательно является графиком функции. Так, например, уравнение x² + y² = 1 определяет окружность с центром в начале координат и радиуса 1 (т.к. d = = 1, расстояние от начала координат равно 1). Однако это не будет графиком функции у от х, т.к. каждому х, |x| ≤ 1, соответствует два значения у: у = ±, т.е. линия задается двумя функциями у = (верхняя полуокружность) и у = — (нижняя полуокружность).
Уравнение произвольной окружности с центром в точке M(a;b) и радиусом R будет иметь вид:
(6.2) (х — а)² + (у- b)² = R²,
т.к. окружность радиусом R есть геометрическое место точек плоскости, находящихся на расстоянии R от центра, т.е. в соответствии с формулой ( 6.2) d = = R.
В частности, окружность с центром в начале координат, радиусом R, описывается уравнением
x² + y² = R².
Пример 6.1. Какую линию описывает уравнение x² + y² = Rx?
Решение: Перенося Rx в левую часть и выделяя полный квадрат, получаем:
x² + y² = Rx ⇔ X2 — Rx + у² = 0 ⇔ x² — Rx + ⇔
(х — ) + y² = .
Ответ: данное уравнение описывает окружность с центром в точке M(;0) и радиусом .
Линия может определяться на плоскости уравнением как в декартовых, так и в полярных координатах: F(; r) = 0. Если при этом зависимость r от обладает тем свойством, что каждому значению из области определения соответствует единственное значение r, то данная линия будет графиком функции r от : r = f().
Пример 6.2. Построить график функции, заданной в полярных координатах уравнением r = 2 sin3, ∈ (—∞; ∞).
Решение: Составим таблицу некоторых значений этой функции:
| 0 | ||||||||
| r | 0 | 1 | 2 | 1 | 0 | -2 |
Рис. 70. График функции r = 2 sin 3 в декартовых координатах
Далее, пользуясь тем, что из вида графика функции r = 2 sin 3, приведенного в декартовых координатах на рис. 70, следует, что неотрицательные значения г повторяются на промежутках ∈ [0; ], ∈ [;π], ∈ [-;] и т. д.. Отсюда заключаем, что если в полярных координатах построить график в секторе ∈ [0; ], то в секторах ∈ [; π], ∈ [— ; ] и т. д. вид графика будет аналогичный, а в секторах ∈ (; ), ∈ ;0) и т.д. графика не будет, т.к. там r Рис. 71. График функции r = 2 sin 3 в полярных координатах
Такой график называют называют “трехлепестковая роза”.
Кривые второго порядка:
Определение 6.2. Кривой второго порядка называется линия, определяемая в декартовых координатах уравнением:
(6.3) Ax² + 2Bxy + Cy² + 2Dx + 2Ey + F = O.
Здесь коэффициенты — действительные числа и, по крайней мере, одно из чисел A₁B или C не равно нулю. Удобство таких обозначений для коэффициентов (2В, 2D, 2Е) станет ясно позже.
Всего существует три ’’реальных” кривых второго порядка: эллипс, (окружность — частный случай эллипса) гипербола и парабола, не считая такие линии, как ’’пара пересекающихся прямых” (ху = 0), «пара параллельных прямых” ((x — у)² — 4), ’’точка” ((x — 5)² + (у — 1)² = 0), ’’прямая” (х — 1)² = 0) и ’’мнимые кривые” (x² + y² + 5 = 0), которым не соответствует ни одна точка.
Окружность
Ранее было получено уравнение ( 6.2) окружности с центром в точке M(а; b), радиусом R. Это уравнение вида ( 6.3), т.е. окружность есть кривая второго порядка — можно показать, что уравнение (6.3), в котором A = C и B = O c помощью дополнения до полного квадрата каждой группы членов Ax² + 2Dx и By² + 2Еу приводится к виду (6.2), определяющему окружность радиуса R, или к виду: (х — а)² + (у — b)² = -R², не определяющему линию при R ≠ 0. Покажем это на примере.
Пример:
Показать, что уравнение 2x² + 2y² — 4x + 8y — 13 = 0 определяет окружность.
Решение: Поделив обе части на 2, получим уравнение в виде: x² + y² — 2x + 4y — 6,5 = 0 или, выделяя полный квадрат: (x² — 2х + 1) + (у² + 4y + 4) = 11,5 ⇔ (х — 1)² + (у + 2)² =11,5. Мы получим уравнение окружности с центром M(1; —2) и радиусом R = √11,5.
Пример:
Показать, что уравнение х² + у² + 6х — 6у + 22 = 0 не определяет никакой линии.
Решение:
Аналогично предыдущему, выделяя полный квадрат, получаем: х² + у² + 6х — 6у + 22 = 0 ⇔ (х² + 6х + 9) + (у² — 6у + 9) = — 4 ⇔ (x + 3)² + (y — 3)² =-4.
Эллипс
Определение:
Эллипсом называется множество всех точек плоскости, сумма расстояний каждой из которых от двух данных точек этой плоскости, называемых фокусами, равна постоянной величине.
Обозначим фокусы F₁ и F₁, расстояние между ними 2с, а сумму расстояний до них от точек эллипса через 2а (2а > 2с). Выберем декартову систему координат как показано на рис. 72. По определению эллипса: MF₁ + MF₂ = 2а. Пользуясь формулой (2.6) получаем:
Рис. 72. Фокусы эллипса и гиперболы
Обозначив b² = a² — с² > 0, получаем: b²x² + a²y² — a²b² или:
(6.4)
Уравнение ( 6.4) называется каноническим уравнением эллипса, а и b — полуосями, а — большая полуось, b — малая, т.к. b = Рис. 73. Эллипс
Так как 2а > 2с, то ε т.е. тем меньше эллипс вытянут вдоль фокальной оси Ох. В пределе, при ε → 0,a = b и получается окружность x² + у² = а² радиусом а При этом с = = 0, т.е. F₁ — F₂ = 0. Если эллипс расположен так, что центр его симметрии находится в точке P(x₀; y₀), а полуоси параллельны осям координат, то, перейдя к новым координатам X = х — х₀, У = у — у₀, начало которых совпадает с точкой Р, а оси параллельны исходным (см. п. 2.8), получим, что в новых координатах эллипс описывается каноническим уравнением Уравнение такого эллипса в старых координатах будет:
(6.5)
Гипербола
Определение 6.4. Гиперболой называется множество всех точек плоскости, модуль разности расстояний каждой из которых от двух данных точек этой плоскости, называемых фокусами, равен постоянной величине.
Обозначим фокусы F₁ и F₂, расстояние между ними 2с, а модуль разности расстояний до них от точек гиперболы через 2a (2c > 2a > 0). Выберем декартову систему координат, как показано на рис. 72. По определению гиперболы: MF₁ — MF₂ = ±2а. Пользуясь формулой (2.6), аналогично тому, как это было сделано для эллипса, получаем:
= ±2a ⇒ (а² — c²)x² + a²y² = a²(a² — с²). Обозначив b² = с² — a² > 0 (сравните с выводом формулы ( 6.4) для эллипса), получаем: -b²x² + a²y² = -b²a², или:
Уравнение (6.6) называется каноническим уравнением гиперболы, а и b — полуосями, а — действительной полуосью, b — мнимой. Так как х и у входят в уравнение только в четных степенях, гипербола симметрична относительно осей Ox и Оу. Выразив у из уравнения ( 6.6), получаем: , |x| ≥ а, что означает, что гипербола состоит из двух симметричных половин, верхней у = и нижней у = — . При х = а у = 0, при возрастании х от 0 до +∞, у для верхней части возрастает от 0 до +∞. C учетом симметрии, получаем линию, изображенную на рис. 74.
Точки пересечения гиперболы с осью Ox (фокальной осью) называются ее вершинами A₂(а;0), A₁(-a;0). C осью ординат гипербола не пересекается, поэтому фокальная ось называется действительной осью (а — действительная полуось), а перпендикулярная ей ось — мнимой осью (b — мнимая полуось). Можно показать, что при неограниченном возрастании абсциссы точка гиперболы неограниченно приближается к прямой у = (изображена на рис. 74 пунктиром). Такая прямая, к которой неограниченно приближается некоторая линия, называется асимптотой. Из соображений симметрии вытекает, что у гиперболы две асимптоты: у = и у =-, изображенные на рис. 74 пунктиром. Прямоугольник, с центром в начале координат, со сторонами 2а и 2b, параллельными осям, называется основным. Асимптоты являются его диагоналями.
Рис. 74. Гипербола
Отношение называется эксцентриситетом гиперболы. Т.к. 2α 1. Эксцентриситет определяет форму гиперболы: чем меньше е, тем более вытянут в направлении фокальной оси ее основной прямоугольник (= = — 1 = ε² — 1). Если а = b, гипербола называется равносторонней (равнобочной). Для нее х² — у² = а², асимптоты: у = х, у = —х, ε = = √2. Если центр гиперболы (центр ее симметрии) находится в точке P(x₀; y₀), a оси параллельны осям координат, то, применяя параллельный перенос координат (п. 2.8), аналогично тому, как это было сделано для эллипса, получим уравнение гиперболы:
(6.7)
Уравнение асимптот такой гиперболы будет: у — y₀ =
Парабола
Определение:
Параболой называется множество всех точек плоскости, равноудаленных от данной точки F, называемой фокусом, и данной прямой d, называемой директрисой (F ∉ d).
Обозначим расстояние от фокуса до директрисы р. Эта величина называется параметром параболы. Выберем декартову систему координат как показано на рис. 75.
По определению параболы MF=MN. Из рис. 75. ясно, что:
Рис. 75. Фокус и директриса параболы
Приравнивая, получаем:
(6.8) у² = 2рх
Уравнение ( 6.8) называется каноническим уравнением параболы. Т.к. у входит в уравнение в четной степени, парабола симметрична относительно оси Ох. Выразив у из уравнения, получаем: у = , х ≥ 0. При х =0 у = 0, при возрастании х от 0 до +∞ у для верхней части возрастает от 0 до +∞. C учетом симметрии получаем линию, изображенную на рис. 76.
Ось симметрии параболы называется фокальной осью (ось Ox на рис. 76), точка пересечения пораболы с ней называется вершиной пораболы (точка О на рис. 76). Если вершина параболы находится в точке P(x₀; у₀), фокальная ось параллельна и одинаково направлена с осью Ox и расстояние от директрисы до фокуса равно Р, то с помощью параллельного переноса осей координат нетрудно получить уравнение такой параболы:
(6.9) (y — y₀)² = 2p(x -х₀)
Пример:
Найти фокус, директрису, фокальную ось для параболы у= 4x².
Рис. 76. Парабола
Решение:
Как известно, осью симметрии параболы у = х² является ось Оу, а вершиной — точка О, поэтому фокальной осью будет ось Оу, вершиной — начало координат.
Для определения фокуса и директрисы запишем уравнение данной параболы в виде: x² = y, откуда 2р =; р =. Поэтому фокус имеет координаты F(0; ), а директриса — уравнение у = — (см. рис. 77).
Рис. 77. График параболы у = 4х²
Понятие о приведении общего уравнения второго порядка к каноническому виду
Если в общем уравнении кривой второго порядка ( 6.3)
Ax² + 2Bxy + Cy² + 2Dx + 2Ey +F = 0
коэффициент 2B ≠ 0, то методами, которые будут изложены позже (лекция 34) это уравнение преобразуется к виду, в котором отсутствует член с произведением координат (т.е. 2В — 0).
Для приведения к каноническому виду уравнения ( 6.3), в котором 2В = 0, необходимо дополнить члены, содержащие х и у, до полных квадратов.
Если при этом (В = 0) А = С, то получится окружность (пример 6.3), точка или мнимая окружность (пример 6.4).
Если при этом (В = 0) A ≠ C и A ∙ C > 0, то получится эллипс (пример 6.8) или мнимый эллипс.
Если при этом (В = 0) A ≠ C и A ∙ C Рис. 78. Гипербола
Пример:
Приведите к каноническому виду уравнение и определите вид кривой: x² — 6x — 4y + 29 = 0.
Решение:
Выделим полный квадрат: x² — 6x — 4y + 29 = 0 ⇔ x² — 6x + 9 = 4y — 20 ⇔ (x — 3)² = 4(у — 5). Сделав замену координат X =х — 3, Y = у — 5 мы получим каноническое уравнение параболы X² = 4Y с осью OY и параметром р = 2. Таким образом исходная парабола имела вершину A(3; 5) и ось х = 3 параллельную оси Oy (рис. 79).
Пример:
Приведите к каноническому виду уравнение и определите вид кривой: x² + 4y² + 2x — 24y + 21 =0.
Решение:
Выделив полный квадрат, получим уравнение: (x + 1)² + 4(у — 3)² = 16. Сделав замену координат: X = х + 1, Y = y — 3, получим каноническое уравнение эллипса: X² + AY² ⇔ = 1 с параметрами а = 4, b = 2. Таким образом, исходный эллипс имел центр A( —1;3) и полуоси а = 4, b = 2 (рис. 80).
Рис. 79. Решение примера 6.7 Рис. 80. Решение примера 6.8
Решение заданий на тему: Кривые второго порядка
Пример:
Составьте уравнение окружности, имеющей центр 0(2; —5) и радиус R = 4.
Решение:
В соответствии с формулой (6.2) искомое уравнение имеет вид: (х — 2)² + (у + 5)² = 16.
Ответ: (х — 2)² + (у + 5)² = 16.
Пример:
Составьте уравнение эллипса, зная, что сумма полуосей равна 8 и расстояние между фокусами равно 8.
Решение:
Из условия имеем: a + b = 8, 2c = 8. C учетом того, что b² = а² — с², находим с = 4, а = 5, b = 3. Искомое уравнение эллипса будет: .
Ответ:
Пример:
Составьте уравнение гиперболы, зная, что фокусы F₁(10;0) и F₂(-10; 0) и что гипербола проходит через точку M(12; 3√5)
Решение:
Из условия имеем: с = 10, |MF₁ — MF₂|= 2а ⇔ 2а = ⇔ а = 8. C учетом того, что b² = с² — а², находим а = 8, с = 10, b = 6. Искомое уравнение гиперболы будет: .
Ответ: .
Пример:
Составьте уравнение параболы, зная, что фокус имеет координаты (5;0), а ось ординат является директрисой.
Решение:
Поскольку расстояние от директрисы параболы до ее полюса равно параметру р, а вершина находится на середине, из условия следует, что р = 5 и вершина расположена в точке A(2,5;0). Таким образом, в новых координатах X = х — 2,5; У = у каноническое уравнение параболы будет: Y² = 10Х, а в старых координатах: у² = 10(х — 2,5).
Ответ: y² = 10x — 25.
Пример:
Приведите к каноническому виду уравнение x² + y² — 2х + 6у — 5 = 0, определите вид кривой и ее параметры.
Решение:
Выделим полный квадрат: х² — 2х + у² + 6у — 5 = 0 ⇔ x² — 2x + 1 + у² + 6у + 9 — 1 — 9 — 5 = 0 ⇔ (х — 1)² + (у + 3)² = 15
В соответствии с формулой (6.2) это есть уравнение окружности с центром в точке A(1; -3), радиусом √5.
Ответ: (х — 1)² + (у + 3)² = 15.
Пример:
Приведите к каноническому виду уравнение x² + 4у² + 4х — 16у — 8 = 0, определите вид кривой и ее параметры:
Решение:
Выделим полный квадрат: x² + 4х + 4у² — 16y -8 = 0 ⇔ x²+4x + 4 + 4y²- 16y + 16-4-16-8 = 0 ⇔ (x + 2)² + 4(y²-4у+ 4) -28 ⇔ (х + 2)² + 4(y — 2)² = 28 ⇔ = 1. Сделав замену координат: X = x +2, Y = у — 2, в новых координатах получим уравнение эллипса с полуосями а = √28 и b = √7. Таким образом, в старых координатах эллипс имеет центр A(—2; 2) и полуоси а = 2√7 и b = √7.
Ответ: = 1.
Пример:
Приведите к каноническому виду уравнение x² + 2y² + 8x — 4 = 0, определите вид кривой и ее параметры.
Решение:
Выделим полный квадрат:
x²+2y²+8x-4 = 0 ⇔ x²+8x+16+2y²-16-4 =0 ⇔ (x+4)²+2y2-20 = 0 ⇔ =1
Сделав замену координат X = х + 4, Y — у, убеждаемся, что эта кривая — эллипс, с полуосями a = 2√5 и b = √10 и центром A(-4;0).
Ответ: =1
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://www.evkova.org/ellips
http://lfirmal.com/krivyie-vtorogo-poryadka-ellips-giperbola-parabola/
Эллипсом
называется геометрическое место точек
плоскости, координаты которых удовлетворяют
уравнению
(9.7)
где
(9.8)
Уравнение (9.7)
называется
каноническим
уравнением эллипса.
Параметры эллипса
Точки F1(–c,
0) и F2(c,
0), где
называютсяфокусами
эллипса,
при этом величина 2c
определяет междуфокусное
расстояние.
Точки А1(–а,
0), А2(а,
0), В1(0,
–b),
B2(0,
b)
называются вершинами
эллипса
(рис. 9.2), при этом А1А2
= 2а
образует большую ось эллипса, а В1В2
– малую,
– центр эллипса.
Основные параметры
эллипса, характеризующие его форму:
ε
= с/a
– эксцентриситет
эллипса;
–фокальные
радиусы эллипса
(точка М
принадлежит эллипсу), причем r1
= a
+ εx,
r2
= a
– εx;
–директрисы
эллипса.
Рис. 9.2
Для эллипса
справедливо:
директрисы не пересекают границу и
внутреннюю область эллипса, а также
обладают свойством
Эксцентриситет
эллипса выражает его меру «сжатости».
Если b
> a
> 0, то
эллипс задается уравнением (9.7), для
которого вместо условия (9.8) выполняется
условие
.
(9.9)
Тогда 2а
– малая ось, 2b
– большая ось,
– фокусы (рис. 9.3). При этомr1
+ r2
= 2b,
ε
= c/b,
директрисы определяются уравнениями:
Рис. 9.3
При
условии
имеем (в виде частного случая эллипса)окружность
радиуса R
= a.
При этом с
= 0, а значит, ε = 0.
Точки эллипса
обладают характеристическим
свойством:
сумма расстояний от каждой из них до
фокусов есть величина постоянная, равная
2а
(рис. 9.2).
Для параметрического
задания эллипса
(формула (9.7)) в случаях выполнения условий
(9.8) и (9.9) в качестве параметра t
может быть взята величина угла между
радиус-вектором точки, лежащей на
эллипсе, и положительным направлением
оси Ox:
где
Если центр эллипса
с полуосями
находится в точке
то его уравнение имеет вид:
(9.10)
Пример 1.
Привести уравнение эллипса x2
+ 4y2
= 16 к каноническому виду и определить
его параметры. Изобразить эллипс.
Решение.
Разделим уравнение x2 + 4y2 = 16
на 16, после чего получим:
По виду полученного
уравнения заключаем, что это каноническое
уравнение эллипса (формула (9.7)), где а
= 4 – большая полуось, b
= 2 – малая полуось. Значит, вершинами
эллипса являются точки A1(–4, 0),
A2(4, 0),
B1(0, –2),
B2(0, 2).
Так как
– половина междуфокусного расстояния,
то точкиявляются фокусами эллипса. Вычислим
эксцентриситет:
Директрисы D1,
D2
описываются уравнениями:
Изображаем эллипс
(рис. 9.4).
Рис. 9.4
Пример 2.
Определить параметры эллипса
Решение.
Сравним данное уравнение с каноническим
уравнением эллипса
со смещенным центром. Находим центр
эллипсаС:
Большая полуось
малая полуось
прямые
– главные оси. Половина междуфокусного
расстоянияа значит, фокусы
Эксцентриситет
ДиректрисыD1
и D2
могут быть описаны с помощью уравнений:
(рис. 9.5).
Рис. 9.5
Пример 3.
Определить, какая кривая задается
уравнением, изобразить ее:
1) x2
+ y2
+ 4x
– 2y
+ 4 = 0; 2) x2
+ y2
+ 4x
– 2y
+ 6 = 0;
3) x2
+ 4y2
– 2x
+ 16y
+ 1 = 0; 4) x2
+ 4y2
– 2x
+ 16y
+ 17 = 0;
5)
Решение.
1) Приведем уравнение к каноническому
виду методом выделения полного квадрата
двучлена:
x2
+ y2
+ 4x
– 2y
+ 4 = 0;
(x2
+ 4x)
+ (y2
– 2y)
+ 4 = 0;
(x2
+ 4x
+ 4) – 4 + (y2
– 2y
+ 1) – 1 + 4 = 0;
(x
+ 2)2
+ (y
– 1)2
= 1.
Таким образом,
уравнение может быть приведено к виду
(x
+ 2)2
+ (y
– 1)2
= 1.
Это уравнение
окружности с центром в точке (–2, 1) и
радиусом R = 1
(рис. 9.6).
Рис. 9.6
2)
Выделяем полные квадраты двучленов в
левой части уравнения и получаем:
(x
+ 2)2
+ (y
– 1)2
= –1.
Это уравнение не
имеет смысла на множестве действительных
чисел, так как левая часть неотрицательна
при любых действительных значениях
переменных x
и y,
а правая – отрицательна. Поэтому говорят,
что это уравнение «мнимой окружности»
или оно задает пустое множество точек
плоскости.
3) Выделяем полные
квадраты:
x2
+ 4y2
– 2x
+ 16y
+ 1 = 0;
(x2
– 2x
+ 1) – 1 + 4(y2
+ 4y
+ 4) – 16 + 1 = 0;
(x
– 1)2
+ 4(y
+ 2)2
– 16 = 0;
(x
– 1)2
+ 4(y
+ 2)2
= 16.
Значит, уравнение
имеет вид:
или
Полученное
уравнение, а следовательно, и исходное
задают эллипс. Центр эллипса находится
в точке О1(1,
–2), главные оси задаются уравнениями
y
= –2, x
= 1, причем большая полуось а
= 4, малая полуось b
= 2 (рис. 9.7).
Рис. 9.7
4) После выделения
полных квадратов имеем:
(x
– 1)2
+ 4(y
+ 2)2
– 17 + 17 = 0 или (x
– 1)2
+ 4(y
+ 2)2
= 0.
Полученное уравнение
задает единственную точку плоскости с
координатами (1, –2).
5) Приведем уравнение
к каноническому виду:
Очевидно, оно
задает эллипс, центр которого находится
в точке
главные оси задаются уравнениями
причем большая полуось
малая полуось
(рис. 9.8).
Рис. 9.8
Пример 4.
Записать уравнение касательной к
окружности радиуса 2 с центром в
правом фокусе эллипса x2
+ 4y2
= 4 в точке пересечения с осью ординат.
Решение.
Уравнение эллипса приведем к каноническому
виду (9.7):
Значит,
и правый фокус –
Поэтому, искомое уравнение окружности
радиуса 2 имеет вид (рис. 9.9):
Окружность
пересекает ось ординат в точках,
координаты которых определяются из
системы уравнений:
Получаем:
Пусть это точки N
(0; –1) и М
(0; 1). Значит, можно построить две
касательные, обозначим их Т1
и Т2.
По известному свойству касательная
перпендикулярна радиусу, проведенному
в точку касания.
Пусть
Тогда
уравнение касательнойТ1
примет вид:
значит,
илиТ1:
Тогда уравнение
касательной Т2
примет вид:
значит,
илиТ2:
Рис. 9.9
Пример 5.
Записать уравнение окружности, проходящей
через точку М(1,
–2) и точки пересечения прямой x
– 7y
+ 10 = 0 с окружностью x2
+ y2
– 2x
+ 4y
– 20 = 0.
Решение.
Найдем точки пересечения прямой x
– 7y
+ 10 = 0 с окружностью x2
+ y2
– 2x
+ 4y
– 20 = 0, решив систему уравнений:
Выразим х
из первого уравнения системы:
x
= 7y
– 10.
Затем подставим
во второе:
(7y
– 10)2
+ y2
– 2(7y
– 10) + 4y
– 20 = 0.
Оно равносильно
уравнению
y2
– 3y
+ 2 = 0.
Используя формулы
корней квадратного уравнения, найдем
y1
= 1, y2
= 2, откуда x1
= –3, x2
= 4.
Итак, имеем три
точки, лежащие на окружности: M(1,
–2), M1(4,
2) и M2(–3,
1). Пусть О1(x0,
y0)
– центр окружности. Тогда
гдеR
– радиус окружности.
Найдем координаты
векторов:
Значит,
что равносильно
системе
Упрощаем ее:
Решая последнюю
систему, получаем ответ:
Таким образом,
центр окружности находится в точке
(0,5; 1,5), ее радиус
Тогда каноническое
уравнение искомой окружности имеет
вид:
Задания
Соседние файлы в папке Часть 2
- #
- #
- #
- #
- #
- #
- #
- #
- #






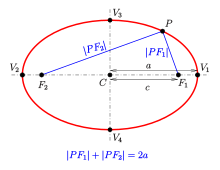
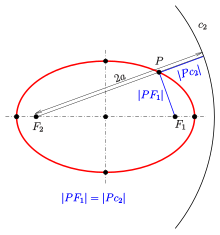




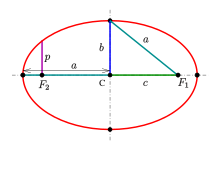




















![{displaystyle {begin{aligned}A&=a^{2}sin ^{2}theta +b^{2}cos ^{2}theta \[3mu]B&=2left(b^{2}-a^{2}right)sin theta cos theta \[3mu]C&=a^{2}cos ^{2}theta +b^{2}sin ^{2}theta \[3mu]D&=-2Ax_{circ }-By_{circ }\[3mu]E&=-Bx_{circ }-2Cy_{circ }\[3mu]F&=Ax_{circ }^{2}+Bx_{circ }y_{circ }+Cy_{circ }^{2}-a^{2}b^{2}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0229cbcba4d890d8b7ee7c0bec065a95a2b91229)


![{displaystyle {begin{aligned}a,b&={frac {-{sqrt {2{big (}AE^{2}+CD^{2}-BDE+(B^{2}-4AC)F{big )}{big (}(A+C)pm {sqrt {(A-C)^{2}+B^{2}}}{big )}}}}{B^{2}-4AC}}\x_{circ }&={frac {2CD-BE}{B^{2}-4AC}}\[5mu]y_{circ }&={frac {2AE-BD}{B^{2}-4AC}}\[5mu]theta &={begin{cases}operatorname {arccot} {dfrac {C-A-{sqrt {(A-C)^{2}+B^{2}}}}{B}}&{text{for }}Bneq 0\[5mu]0&{text{for }}B=0, A<C\[10mu]90^{circ }&{text{for }}B=0, A>C\end{cases}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c099e609531d008740862f621a7295d5015a2f9d)
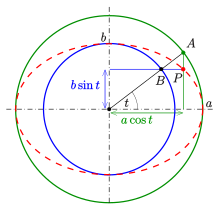



![{displaystyle {begin{aligned}x(u)&=a{frac {1-u^{2}}{1+u^{2}}}\[10mu]y(u)&=b{frac {2u}{1+u^{2}}}end{aligned}};,quad -infty <u<infty ;,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c86f5ffc504dac624df3b6ce483c47521615fd18)
![{displaystyle [u:v]mapsto left(a{frac {v^{2}-u^{2}}{v^{2}+u^{2}}},b{frac {2uv}{v^{2}+u^{2}}}right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa1c21205522d70966ce62b8e324b19ec4c90f41)





















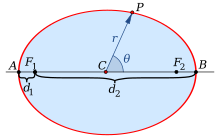

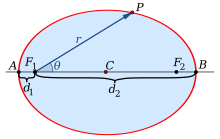


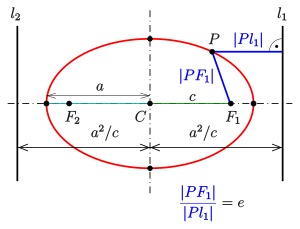











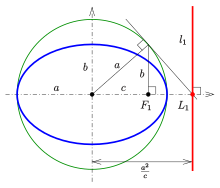

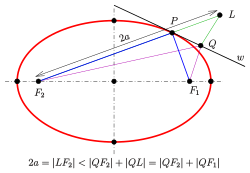
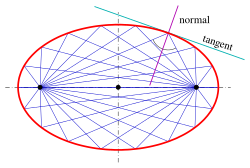
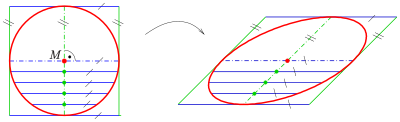





















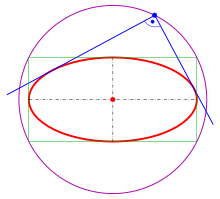

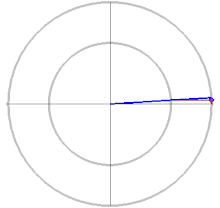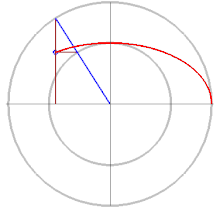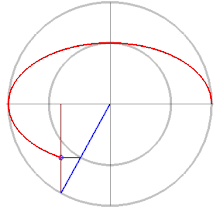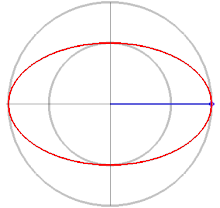
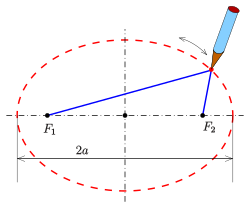









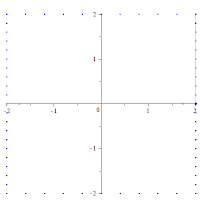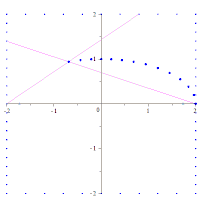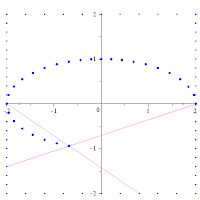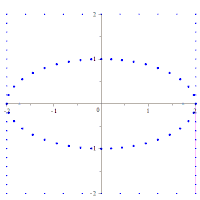






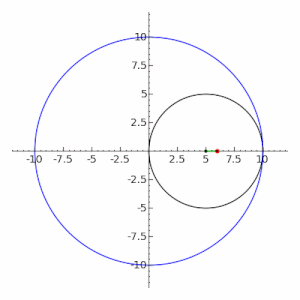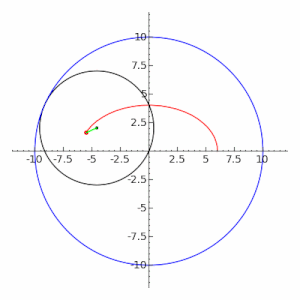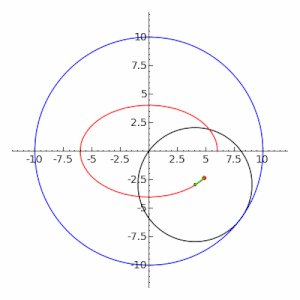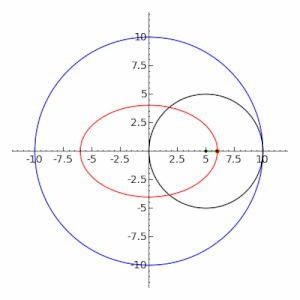
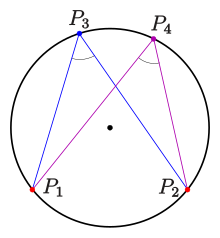
























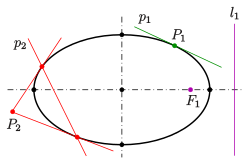










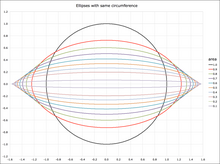


![{displaystyle {begin{aligned}C&=2pi aleft[{1-left({frac {1}{2}}right)^{2}e^{2}-left({frac {1cdot 3}{2cdot 4}}right)^{2}{frac {e^{4}}{3}}-left({frac {1cdot 3cdot 5}{2cdot 4cdot 6}}right)^{2}{frac {e^{6}}{5}}-cdots }right]\&=2pi aleft[1-sum _{n=1}^{infty }left({frac {(2n-1)!!}{(2n)!!}}right)^{2}{frac {e^{2n}}{2n-1}}right]\&=-2pi asum _{n=0}^{infty }left({frac {(2n-1)!!}{(2n)!!}}right)^{2}{frac {e^{2n}}{2n-1}},end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e202a234c19a28620ecf9c6d260eb21b1bd7aa0)
![{displaystyle {begin{aligned}C&=pi (a+b)sum _{n=0}^{infty }left({frac {(2n-3)!!}{2^{n}n!}}right)^{2}h^{n}\&=pi (a+b)left[1+{frac {h}{4}}+sum _{n=2}^{infty }left({frac {(2n-3)!!}{2^{n}n!}}right)^{2}h^{n}right]\&=pi (a+b)left[1+sum _{n=1}^{infty }left({frac {(2n-1)!!}{2^{n}n!}}right)^{2}{frac {h^{n}}{(2n-1)^{2}}}right].end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d29d8f31216e5d32400e99b04e75e242d987893)
![{displaystyle Capprox pi {biggl [}3(a+b)-{sqrt {(3a+b)(a+3b)}}{biggr ]}=pi {biggl [}3(a+b)-{sqrt {10ab+3left(a^{2}+b^{2}right)}}{biggr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86c8a7234c16af19a7338faafe61b4cf9a333f80)



![{displaystyle s=b left[;Eleft(z;{Biggl |};1-{frac {a^{2}}{b^{2}}}right);right]_{z = arccos {frac {x_{2}}{a}}}^{arccos {frac {x_{1}}{a}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7338c6c7bf9cc8e20da6c7da90eecd93f540416)






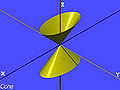




![{displaystyle {begin{aligned}a&={frac {r_{a}+r_{p}}{2}}\[2pt]b&={sqrt {r_{a}r_{p}}}\[2pt]ell &={frac {2}{{frac {1}{r_{a}}}+{frac {1}{r_{p}}}}}={frac {2r_{a}r_{p}}{r_{a}+r_{p}}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08835a73be73e7094f529d4eff42804930898271)