При подготовке к школе необходимо научить Вам своего ребёнка решать задачи. А чтобы Ваш ребёнок правильно, без ошибок и проблем решал задачи необходимо понять задачу, а для этого надо уметь находить ключевые слова в задаче.
Сегодня у нас тема: — Нахождение ключевых слов в задаче.
Почему некоторые дети не могут решать задачи по математике?
Потому что их еще до школы или в начальной школе не научили решать задачи с помощью ключевых слов. Хотя это вовсе и не трудно.
Мы с вами уже разбирали, вспомните.
Задача – это не скучное ненужное упражнение, а интересная жизненная ситуация.
И главное научиться различать части задачи:
— условие задачи;
— вопрос задачи;
— решение задачи;
— ответ задачи.
Допустим, Ваш ребенок уже нашел в задаче условие и вопрос, а решить все равно не может, соответственно и записать ответ тоже не может. Что же делать?
Необходимо еще раз прочитать условие задачи и найти ключевые слова. Найденные ключевые слова в задаче расставят все по своим местам и задача обязательно решится.
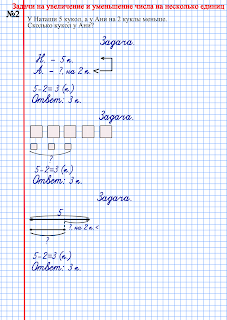
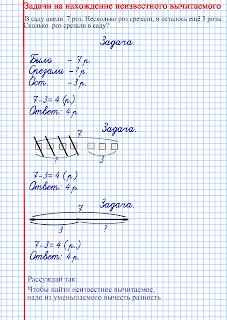
 Задача №1
Задача №1
У мальчика было 5 красных шаров. Мама ему купила еще 3 синих шара. Сколько шаров стало у мальчика?
Сделаем краткую запись задачи:
Было – 5 ш.
Купили – 3 ш.
Стало – ? ш.
Слова было, купили и стало – ключевые слова в задаче.
Теперь решаем задачу:
5 + 3 = 8 (ш.)
Ответ: 8 шаров стало у мальчика.
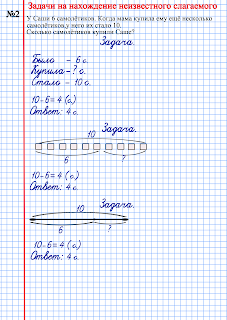
 Задача №2
Задача №2
В холодильнике было 5 яблок. Два яблока съели дети. Сколько яблок осталось в холодильнике?
Было – 5 яб.
Съели – 2 яб.
Осталось – ? яб.
5 – 2 = 3 (яб.)
Ответ: 3 яблока осталось в холодильнике.
Обратите внимание
Ответ пишем всё полностью из заданного вопроса задачи, заменяя слово сколько, полученным ответом при решении.
Решите самостоятельно:
Задача №3
В нашем саду росло (было) 6 яблонь. Мы посадили еще 2 яблони. Сколько яблонь стало в саду?
Задача №4
На полке стояло (было) 9 книг. Одну книгу взяла почитать Оля. Сколько книг осталось на полке?
В следующих задачах найдите ключевые слова и решите самостоятельно.
Задача №5
В коллекции папы было 7 монет. Он купил еще 2 монеты. Сколько монет стало у папы?
Задача №6
У бабушки было 6 клубков шерсти. Она уже извязала 2 клубка. Сколько клубков шерсти осталось у бабушки?
Задача №7
На стройке дома было 7 мешков цемента, но его не хватило, и поэтому привезли еще 2 мешка. Сколько всего цемента привезли на стройку дома?
Задача №8
В магазине было 5 мешков сахара. За день расфасовали и продали 2 мешка сахара. Сколько мешков сахара осталось в магазине?
Вот и все объяснение.
Подведем итог вышесказанного:
Чтобы задача решалась, необходимо научиться выделять ключевые слова в задаче. Ключевые слова, выделенные в задаче, позволят решить задачу правильно и без проблем.
Все ли понятно в моих объяснениях? Понятно ли Вашим детям? Напишите в комментариях.
Если что-то не понятно, задавайте вопросы. Присоединяйтесь ко мне в Skype, первая консультация бесплатная.
С уважением Ваш репетитор – Лидия Витальевна
ЧАСТИ ЛЮБОЙ ЗАДАЧИ ДЛЯ ЛЮБОГО КЛАССА
Компоненты
любой задачи:
УСЛОВИЕ – ВОПРОС – РЕШЕНИЕ – ОТВЕТ
Задание
Прочитай задачу и подчеркни УСЛОВИЕ – синей ручкой, ВОПРОС –
зелёной ручкой. ОПОРНЫЕ СЛОВА – обведи в овал простым карандашом.
Объяснение простых
задач
Например, в задаче:
В вазе 3 белых и 2 розовых гвоздики. Сколько всего гвоздик в
вазе?
————————————————- —————————————
ОПОРНЫЕ СЛОВА нужно уметь находить для нахождения главного в
задаче.
Опорные слова – это основа краткой записи.
В указанной задаче опорные слова:
Первое опорное слово – БЕЛЫХ (выделено жирным),
который сокращаем в первом классе Б., но, начиная со второго класса, БЕЛ.
Второе опорное слово – РОЗОВЫХ (выделено жирным),,
которое в первом классе сокращаем Р., но, начиная со второго класса, РОЗ.
Третье опорное слово всегда содержится в вопросе. В данной
задаче третье опорное слово – ВСЕГО, которое в краткой записи задачи
заменяется ФИГУРНОЙ СКОБКОЙ С ВОПРОСОМ ПОСЕРЕДИНЕ.
Б. – 3 г. ? г.
Р. – 2 г.
ПО РЕШЕНИЮ
ВСЕХ ВИДОВ СОСТАВНЫХ ЗАДАЧ.
ЦЕПОЧКА
РАССУЖДЕНИЙ
После нахождения опорных слов, составления краткой записи или
чертежа мы настоятельно рекомендуем ЛЮБУЮ задачу начинать решать С КОНЦА, то
есть с ВОПРОСА. Эта СИСТЕМАТИЧЕСКАЯ ЦЕПОЧКА РАССУЖДЕНИЙ приведет ребёнка к
правильному решению ЛЮБОЙ ЗАДАЧИ.
В приведённых ниже разборах задач ЦЕПОЧКА РАССУЖДЕНИЙ сначала идёт
после слов: Рассуждай так.
Потом ЦЕПОЧКА РАССУЖДЕНИЙ превращается в схему типа:
Осталось Ушло
Как составлялась эта схема? Была задача:
Во дворе
гуляли 16 ребят. Сначала домой ушли 6 девочек, а потом 3 мальчика. Сколько
ребят осталось во дворе?
Пошаговый
образец рассуждения вслух ребёнка
Решаем с конца, с вопроса.
— что спрашивается в задаче?
— сколько ребят осталось.
— значит, первое слово в цепочке пишем — осталось.
Осталось
— чтобы узнать, сколько осталось, надо знать, сколько БЫЛО и
сколько УШЛО. Сколько БЫЛО, мы знаем, сколько УШЛО – не знаем, значит, в
цепочке дописываем слово «ушло».
Осталось
Ушло
— так как в цепочке ДВА СЛОВА, то в задаче ДВА ДЕЙСТВИЯ.
РЕШАЕМ ЗАДАЧУ, РАСКРУЧИВАЕМ ЦЕПОЧКУ С КОНЦА.
— Первое слово с конца – УШЛО, значит, сначала узнаем,
сколько ребят УШЛО:
6 + 3 = 9 (р)
— Второе слово в цепочке – «осталось». Значит, вторым
действием мы отвечаем на главный вопрос задачи и узнаём, сколько ребят
осталось.
16 – 9 = 7 (р)
Почему так
важна такая ЦЕПОЧКА РАССУЖДЕНИЙ, которая пишется слева направо, а
раскручивается с конца, справа налево?
Почему
ЦЕПОЧКА РАССУЖДЕНИЙ НЕОБХОДИМА
при
решении КАЖДОЙ ЗАДАЧИ?
·
Потому что ТОЛЬКО при
ТАКОМ систематическом ПОДХОДЕ ваш ребёнок сможет решать ЛЮБУЮ ЗАДАЧУ в
начальной и средней школе, экономя вам лично время, силы и нервы.
·
Потому что это
развивает логику ребёнка
·
Потому что такая
ЦЕПОЧКА РАССУЖДЕНИЙ развивает ВСЕГО ребёнка по ВСЕМ НАПРАВЛЕНИЯМ.
ЗАДАЧИ
СПОСОБЫ РЕШЕНИЙ ВСЕХ ВИДОВ ЗАДАЧ
Компоненты любой задачи:
УСЛОВИЕ – ВОПРОС – РЕШЕНИЕ – ОТВЕТ
Задание
Прочитай задачу и подчеркни УСЛОВИЕ – синей ручкой, ВОПРОС – зелёной ручкой. ОПОРНЫЕ СЛОВА – обведи в овал простым карандашом.
Объяснение
Например, в задаче:
В вазе 3 белых и 2 розовых гвоздики. Сколько всего гвоздик в вазе?
————————————————- —————————————
ОПОРНЫЕ СЛОВА нужно уметь находить для нахождения главного в задаче.
Опорные слова – это основа краткой записи.
В указанной задаче опорные слова:
Первое опорное слово
– БЕЛЫХ (выделено жирным), который сокращаем в первом классе Б., но, начиная со второго класса, БЕЛ.
Второе опорное слово
– РОЗОВЫХ (выделено жирным),, которое в первом классе сокращаем Р., но, начиная со второго класса, РОЗ.
Третье опорное слово
всегда содержится в вопросе. В данной задаче
третье опорное слово
– ВСЕГО, которое в краткой записи задачи заменяется ФИГУРНОЙ СКОБКОЙ С ВОПРОСОМ ПОСЕРЕДИНЕ.
Потренируйся
Прочитай задачи и подчеркни УСЛОВИЕ – синей ручкой, ВОПРОС – зелёной ручкой. ОПОРНЫЕ СЛОВА – обведи в овал простым карандашом.
Здесь посмотри задачи для тренировки и скачай себе на компьютер.
Как записывать и решать простые задачи. Все типы задач. |
||
|
|
||
|
|
||
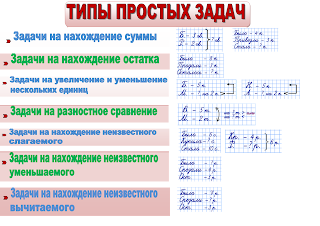
Все типы простых задач и способы записи условия задач |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
КАК РАБОТАТЬ С ЗАДАЧНИКОМ
|
|
|
|
|
|
|
Здесь можно посмотреть и скачать объяснение решения задач. |
КАК НАУЧИТЬСЯ РЕШАТЬ ТЕКСТОВЫЕ ЗАДАЧИ
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Чернышов С.В. 1
1МБОУ Гимназия №3
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
С простейшими текстовыми задачами учащиеся встречаются уже в первом классе. Переходя из класса в класс, ребята постепенно осваивают задачи на отношения «на …больше, на…меньше», «в…раз больше, в…раз меньше», причем заданных как в прямой, так и косвенной форме.
Новой ступенью развития умений решать текстовые задачи, является введение физической формулы равномерного движения: S=V*T. С помощью этой формулы можно решать несколько разновидностей задач: на прямую и обратную пропорциональные зависимости; такие процессы как «купля-продажа», «целое, разбитое на равные части», «работа», «площадь прямоугольника» и т.д.
Новый, очень серьёзный класс задач появляется при изучении процентов, обыкновенных и десятичных дробей. И начинается он с элементарных задач (процент или дробь от числа, число по его процентам или дроби) и заканчивается достаточно сложными для понимания и решения учащимися задачами на растворы, смеси, сплавы.
В курсе математики обязательно встречаются разного рода задачи, вот они и вызывают у многих затруднения. Все дело в том, что необходимо отработать и автоматизировать эти процессы. Чтобы получить правильный ответ на задачу, необходимо понять ее суть, поэтому тренироваться необходимо на простейших примерах для младшей школы.
Решение задач – это работа несколько необычная, а именно умственная работа. А чтобы научиться какой-либо работе, нужно предварительно хорошо изучить тот материал, над которым придется работать, те инструменты, с помощью которых выполняется эта работа.
Значит, для того, чтобы научиться решать задачи, надо разобраться в том, что собой они представляют, как они устроены, из каких основных частей они состоят, каковы инструменты, с помощью которых производится решение задач.
Итак, что же такое задача? Любая текстовая задача представляет собой описание какого-либо явления (ситуации, процесса). С этой точки зрения текстовая задача есть словесная модель явления (ситуации, процесса). И, как во всякой модели, в текстовой задаче описывается не все явление в целом, а лишь некоторые его стороны, главным образом, его количественные характеристики.
Любая текстовая задача состоит из двух частей – условия и требования (вопроса). В условии сообщаются сведения об объектах и некоторые числовые данные объекта, об известных и неизвестных значениях между ними. Требования задачи – это указание того, что нужно найти. Оно выражено предложением в повелительной или вопросительной форме.
Начинается работа над любой задачей с того, что:
1) Ученики самостоятельно знакомятся с условием задачи.
2) Далее один из учащихся читает задачу вслух. Ученик должен прочитать задачу так, чтобы условие задачи стало доступно каждому.
2) После четкого, разборчивого и выразительного чтения задачи учащихся должны рассказать о той ситуации, которая происходит в данной задаче.
3) Выделить главные слова, так как одним из важнейших этапов в работе над задачей является умение записать условие задачи в виде краткой записи.
4) Составить краткий план для записи решения задачи.
5) Выбрать модель задачи (рисунок, чертёж, таблица).
6) Спланировать способ решения.
7) Ответить на вопрос задачи.

Основная часть
2. 1 Классификация текстовых задач
Текстовые задачи делятся на группы, которые объединяет либо метод решения, либо количество действий, которые необходимо выполнить для решения задачи, либо схожий сюжет. Задачи можно классифицировать:
1. По числу действий, которые необходимо выполнить для решения задачи;
2. По соответствию числа данных и искомых;
3. По фабуле задачи;
4. По способам решения и др.
По числу действий:
простые;
составные задачи.
Задачу, для решения которой нужно выполнить одно арифметическое действие, называют простой.
Пример.Один кг яблок стоит 50 рублей. Сколько стоит один кг груш, если груши весят на 15, 5 рубля дороже?
Задачу, для которой нужно выполнить два или большее число действий, называют составной.
Пример. Ширина прямоугольника составляет 8/9 его длины. Найдите площадь и периметр прямоугольника, если его ширина равна 32 см.
Разделение задач на простые и составные не может быть проведено вполне строго. Например: задача на сложение нескольких слагаемых может быть решена одним действием сложения или несколькими действиями сложения, т.е. может быть причислена к простым или составным. Задачи на нахождение числа по его части могут решаться одним действием — делением на дробь, как задачи простые, или двумя действиями (деление на числитель дроби и умножением на ее знаменатель), т. е. могут быть отнесены к составным задачам.
Решение составной задачи сводится к разложению ее на простые задачи и к решению этих простых задач.
По соответствию числа данных и искомых;
определенные задачи;
неопределенные задачи;
Число условий должно соответствовать числу данных и искомых. Тогда задача имеет одно решение и является задачей определенной.
Пример. Два переплетчика должны переплести 384 книги. Один из них переплетает по пять книг в день и уже переплел 160 книг. Сколько книг в день должен переплетать другой переплетчик, чтобы закончить работу в один день с первым?
Если число условий в задаче недостаточно, то задача может иметь несколько решений и называется задачей неопределенной.
Пример. На складе было 392 банки вишневого, малинового и клубничного варенья. Банок с вишневым вареньем было в 3 раза больше, чем малинового. Какова масса вишневого варенья, если в каждой банке его 800 г?
По фабуле задачи:
«на движение»;
«на работу»;
«на смеси и сплавы»;
«на смешение и концентрацию»;
«на проценты»;
«на части»;
«на время»;
«на покупку и продажу» и т. п.
По способу решения задач:
задачи на тройное правило;
задачи на нахождение неизвестных по результатам действий;
задачи на пропорциональное деление;
задачи на исключение одного из неизвестных;
задачи на среднее арифметическое;
задачи на проценты и части;
задачи, решаемые с конца, или «обратным ходом».
При обучении математике в средних классах, кроме приведенной классификации задач по их месту при изучении нового материала используются классификации по другим основаниям:
По методам поиска решения — алгоритмические, типовые, эвристические;
По требованию задачи — на построение, вычисление, доказательство;
По трудности — легкие и трудные;
По сложности — простые и сложные;
По применению математических методов — уравнений, подобия, арифметический, алгебраический, графический, практический методы и т. д.
Все эти классификации позволяют рассматривать математические задачи под разными углами зрения и уточнять, совершенствовать методику работы с учащимися над задачей.
2.2 Методы и способы решения тестовых задач
Существуют различные методы решения текстовых задач:
арифметический,
алгебраический,
геометрический,
логический,
практический,
табличный,
комбинированный,
метод проб и ошибок.
В основе каждого метода лежат различные виды математических моделей.
При алгебраическом методе решения задачи составляются уравнения или неравенства, при геометрическом — строятся диаграммы или графики. Решение задачи логическим методом начинается с составления алгоритма.
Практически каждая задача в рамках выбранного метода допускает решение с помощью различных моделей. Используя алгебраический метод, ответ на требование одной и той же задачи можно получить, составив и решив совершенно разные уравнения; используя логический метод — построив разные алгоритмы. В этих случаях мы так же имеем дело с различными методами решения конкретной задачи, которые называют способы решения.
Арифметический метод. Решить задачу арифметическим методом — значит найти ответ на требование задачи посредством выполнения арифметических действий над числами. Одну и ту де задачу во многих случаях можно решить различными арифметическими способами.
Алгебраический метод. Решить задачу алгебраическим методом — это значит найти ответ на требование задачи, составив и решив уравнение или системы уравнений (или неравенств). Одну и ту же задачу можно так же решить различными алгебраическими способами.
Геометрический метод. Решить задачу геометрическим методом — значит найти ответ на требование задачи, используя геометрические построения или свойства геометрических фигур.
Логический метод. Решить задачу логическим методом — это значит найти ответ на требование задачи, как правило, не выполняя вычислений, а только используя логические рассуждения.
Практический метод. Решить задачу практическим методом — значит найти ответ на требования задачи, выполнив практические действия с предметами или их копиями (моделями, макетами).
Табличный методпозволяет видеть задачу целиком это- решение путем занесения содержания задачи в соответствующим образом организованную таблицу.
Комбинированный метод позволяет получить ответ на требование задачи более простым путем.
Метод проб и ошибок (самый примитивный), в нем ответ на вопрос задачи угадывается.
Методы решения могут быть разные, но способ решения, лежащий в их основе, может быть только один.
2.3 Практическая часть
В практической части научно-исследовательской работы для 5-го и 6-го классов были предложены следующие задачи:
Арифметический метод решения задачи. В этой задаче необходимо знать формулу: S=V*T.
Задача 1: Воробей за два часа пролетел 14 километров, а орел за три часа пролетел 210 километров. Во сколько раз скорость орла больше?
Условие
Воробей: 2ч – 14 км
в ? раз б
Орел: 3ч -210 км
Решение:
14 :2=7 (км/ч) — скорость воробья;
210 :3=70 (км/ч) — скорость орла;
70 :7=10 — во столько раз скорость орла превосходит скорость воробья.
Ответ: в 10 раз больше.
Задача 2.Найдем 12 % от 7000 рублей
1 способ: Найдем 1 %, а потом 12 %.
1) 7000:100 = 70(р.) – 1%
2) 70 * 12 = 840(р.) – 12%
2 способ: Перевод % в десятичную дробь
1) 12% = 0,12
2) 7000 * 0,12 = 840(р.)
Ответ: 840р.
Задача 3. Два мальчика выбежали одновременно навстречу друг другу по спортивной дорожке, длина которой 100 м. Они встретились через 10 с. Первый мальчик бежал со скоростью 4 м /с. С какой скоростью бежал второй мальчик?
План решения задачи:
І способ.
1.Найти путь, который пробежал первый мальчик до встречи.
2. Найти путь, который пробежал второй мальчик до встречи.
3. Найти скорость, с которой бежал второй мальчик.
II способ.
1. Найти скорость сближения.
2. Найти скорость, с которой бежал второй мальчик до встречи.
Задача 4.(2 уровень.) Цена книги понизилась на 15%. Найдите новую цену книги, если прежняя составляла 60 рублей?
Вот наглядный пример решения задачи на составление уравнения с использованием вспомогательной таблицы. Она значительно упрощает восприятие
Задача5. На первой полке книг в три раза больше, чем на второй. Если с первой полки убрать восемь книг, а на вторую поставить 32, то их станет поровну. Сколько книг было первоначально на каждой полке?
Условие
|
1 полка |
2 полка |
|
|
Было |
3х |
3х-8 |
|
Стало |
х |
х+32 |
Решение:
3х-8=х+32;
3х-х=32+8;
2х=40;
х=20
20 (книг) — было на второй полке;
20*3=60 (книг) — было на первой полке.
Ответ:60 книг;20книг.
Задача6. На солнышке грелось несколько кошек. У них вместе лап на 10 больше, чем ушей. Сколько кошек грелось на солнышке?
Решение.
1 способ.
|
Лапы |
Ушки |
|
|
1 кошка |
4х |
2х |
|
Кошки |
На 10 больше |
? |
Так как лап на 10 больше чем ушей.
Составим и решим уравнение:4х – 2х = 102х= 10 │: 2х = 5
Ответ: 5 кошек грелось на солнышке.
способ
1. На сколько лап больше чем ушей у одной кошки?4 – 2 = 2 (шт.)
2. Сколько кошек грелось на солнышке?10 : 2 = 5 (шт.)
Ответ: 5 кошек грелось на солнышке.
Задача7. В хозяйстве имеются куры и овцы. Сколько тех и других, если известно, что у них вместе 19 голов и 46 ног?
Составленное уравнение учащиеся решают самостоятельно, с последующей проверкой.
2х + 76 – 4х = 46-2х = -30 │: (-2)х= 1515 шт. – куры19 – 15 = 4 (шт.) – овцы
Ответ: 15 кур, 4 овцы
Логический метод.
Задача 8. Кто из учеников Саша, Сергей, Дима и Андрей играет, а кто не играет в шахматы, если известно следующее:
а) если Саша и Сергей играет, то Дима не играет;
б) если Сергей не играет, то играют Дима и Андрей;
в) Дима играет.
Решение:
Если Саша и Сережа играют, то Дима не играет.
Если играют Дима и Андрей, то Сережа не играет.
Так как Дима по условию играет в шахматы, значит – это Дима и Андрей играют в шахматы.
Ответ: в шахматы играют ученики Дима и Андрей, а Саша и Сергей – не играют.
Задача 9. Поют в хоре и занимаются танцами 82 ученика, занимаются танцами и художественной гимнастикой 32 ученика, а поют в хоре и занимаются художественной гимнастикой 78 учеников. Сколько учеников поют в хоре, занимаются танцами и художественной гимнастикой отдельно, если известно, что каждый ученик занимается только чем-то одним?
Решение:
1-й способ.
1) 82 32 + 78 = 192 (чел.) — удвоенное число учеников, поющих в хоре, занимающихся танцами и художественной гимнастикой;
2) 192 : 2 = 96 (чел.) — поют в хоре, занимаются танцами и художественной гимнастикой;
3) 96 – 32 = 64 (чел.) — поют в хоре;
4) 96 – 78 = 18 (чел.) — занимаются танцами;
5) 96 – 82 = 14 (чел.) — занимаются художественной гимнастикой.
2-й способ.
1) 82 – 32 = 50 (чел.) –на столько больше учеников поют в хоре, чем
занимаются художественной гимнастикой;
2) 50 + 78 = 128 (чел.) — удвоенное число учеников, поющих в хоре;
3) 128 : 2 = 64 (чел.) — поют в хоре;
4) 78 – 64 = 14 (чел.) — занимаются художественной гимнастикой;
5) 82 – 64 = 18 (чел.) — занимаются танцами.
Ответ: 64 ученика поют в хоре, 14 учеников занимаются художественной гимнастикой, 18 учеников занимаются танцами.
Среди учащихся 5 и 6 классов, в количестве 33 человек с предложенными задачами справилось 12 человек. Задачи на проценты в 5 классе учащиеся ещё не умеют решать. Обратились за помощью 8 учащихся, и потом они тоже справились с предложенными задачами.
Отсюда можно сделать вывод, что 37% успешно решили все задачи. Прибегнув к помощи, ещё 24% учащихся смогли справиться с данными задачами. Особые затруднения вызвали логические задачи.
Подводим итог: с задачами более простыми в целом ученики 5-го и 6-го классов справляются, но если добавляются немного больше элементов в рассуждениях, то справляются с такими заданиями не все.
Так же был проведён соц. Опрос среди учащихся 5-6 классов. Всем задавали вопрос: «Какие задачи легче решать: математические или логические?» В опросе участвовали 33 ученика. 25 учеников ответили – математические, 3 ученика – логические, 5 учеников – ни какие не могут решить.
Вывод: математические задачи легче решить 76-ти % опрошенных, логические – 10% и 14% не смогут решить никакую задачу.
Заключение
Для достижения цели данного исследования были выполнены следующие задачи:
1.Был произведен анализ некоторой методической и школьной литературы с точки зрения изучения методов решения задач в школе на уроках математики.
2.На основе изученного материла, были описаны методы и способы решения текстовых задач, в основной школе. С кратким описанием и приведением примеров.
3. В результате были описаны наиболее часто встречающиеся методы используемые в школьном курсе математики в 5 – 6 классах.
Таким образом, была достигнута цель данного исследования: описать методы и способы решения текстовой задачи в курсе изучения математики 5 – 6 классов.
Литература
1.Виленкин Н.Я. Математика: Учебник для 5 класса общеобразовательных учреждений// Н.Я.Виленкин, В.И. Жохов, А.С.Чесноков, С.И.Шварцбурд. – М.: Мнемозина: 1999-2004. – 384 с.
2.Виленкин Н.Я. Математика: Учебник для 6 класса общеобразовательных учреждений// Н.Я.Виленкин, В.И. Жохов, А.С.Чесноков, С.И.Шварцбурд. – М.: Мнемозина, 1999-2004. – 384 с.
3.Дорофеев Г.В. Математика 6 класс.-Просвещение,:2013.
4.Матвеева Г. Логические задачи // Математика. — 1999. № 25. — С. 4-8.
5. Фридман, Л.М. Как научиться решать задачи [Текст] : Кн. для учащихся ст. кл. средн. шк. / Л.М. Фридман, Е.Н. Турецкий.– 3-е изд., дораб.– М.: Просвещение, 1989.– 192 с.: ил.
6. Целищева, И. Как помочь каждому ученику самост-но решать текстовые задачи [Текст] / И. Целищева, С. Зайцева // Нач. шк.: еженед. прил. к газ. «Первое сентября».– 2001.– 00.05 (№ 18).– С. 2-5.
7. Шарыгин И.Ф. , Шевкин Е.А. Задачи на смекалку.-Москва,:Просвещение,1996.-65с.
Приложение
«ПАМЯТКА «КАК РЕШАТЬ ТЕКСТОВЫЕ ЗАДАЧИ»
1. Прочитай задачу и представь себе то, о чем в ней говорится.
2. Выдели условие и вопрос.
3. Запиши условие кратко или выполни чертёж.
4. Подумай можно ли сразу ответить на вопрос задачи. Если нет, то почему. Что надо узнать сначала, что потом?
5. Составь план решения.
6. Выполни решение.
7. Проверь решение и запиши ответ задачи.Примерный план ответа-рассуждения при решении задачи:
1.Арифметический метод.
Анализ задачи.
1. Известно, что … (расскажи условие задачи)
2. Надо узнать… (повтори вопрос)
3. Чтобы ответить на вопрос задачи, надо …
4. Сразу мы не можем ответить на вопрос задачи, так как не знаем…
5. Поэтому в первом действии мы узнаем …
6. Во втором действии мы ответим на вопрос задачи. Для этого … ( какое действие выполняем)
7. Ответ …
2. Алгебраический метод:
Одним из важнейших направлений улучшения качества обучения математике является совершенствование его практической составляющей. К средствам реализации этого направления можно отнести использование текстовых задач и метода уравнений. Действительно, решение текстовых задач с помощью уравнений иллюстрирует применение математики к исследованию явлений реальной действительности, обеспечивает реализацию общих принципов прикладной направленности курса математики. Поэтому необходимо уделять внимание решению текстовых алгебраических задач. Схема работы над задачей:1 этап – анализ и запись условия задачи. Выполнение чертежа, если он необходим.
Содержание данного этапа включает:
Установление объекта наблюдения (исследования);
Выделение процессов, подлежащих рассмотрению;
Выявление величин, входящих в каждый процесс;
Выяснение функциональной зависимости между величинами и составление формул этой зависимости;
Схематическая запись условия задачи с обозначение неизвестных величин;
2 этап – нахождение плана решения.
Выявление основания для составления уравнения или системы уравнений;
Составление уравнения или системы уравнений;
3 этап – осуществление плана решения задачи.
Решение уравнения или системы;
Исследование корней уравнения (системы) с целью установления решений задачи. Проверка расчетов и обоснований;
Запись ответа;
4 этап – анализ решения задачи.Комментирование решения задачи. Возвращение к решению задачи (ретроспективный подход) с целью уточнения идей и методов решения задачи, упрощение расчетов. Поиск более рациональных приёмов решения задачи.
Пример № 1.На середине пути между станциями А и В поезд был задержан на 10 минут. Чтобы прибыть вВ по расписанию, машинисту пришлось первоначальную скорость поезда увеличить на 12 км/ч. Найти первоначальную скорость поезда, если известно, что расстояние между А и В равно 120 км. 1 – Пусть Х км/ч — первоначальная скорость поезда (умение выделять величины и обозначать их буквами).2 – Найдем зависимость между зафиксированной величиной и другими, участвующими в задаче (умение формулировать зависимости между величинами и выражать посредством букв).ч – время прохождения поездом пути от А до середины;(х + 12) км/ч – скорость поезда от середины пути до В;ч – время прохождения второго участка пути; 3 – По условию задачи поезд прошел вторую часть пути на ч меньше, чем предполагалось по расписанию. Время прохождения поезда по расписанию от середины до конца пути — 60 км/ч, поезд из-за стоянки ч должен был увеличить первоначальную скорость на 12 км/ч , чтобы прибыть по расписанию, т.е. время, затраченное им на втором участке пути, равно ( + ) ч (умение выражать одну и ту же зависимость разными способами, умение составлять уравниваемые выражения). 4 – Составляем уравнениеРешив данное уравнение, получаем: х1 = 60, х2 = — 72. Условию задачи, отвечает х = 60. Таким образом первоначальная скорость поезда – 60 км/ч. (умение интерпретировать результат решения задачи на языке данной задачи).5 – Заметим, что словесная формулировка условия задачи довольно громоздка. В таких случаях осуществления анализа может помочь рисунок.На рисунок вынесены величины, содержащиеся в условии задачи (умение использовать графические модели условия задачи, осуществлять переход от одной модели к другой).
Памятка для лучшего усвоения решения задач с помощью уравнений.
Тщательно изучи условие задачи, если надо, сделай чертёж.
Выясни, о каких величинах идет речь в задаче.
Выбери любую из этих величин для правой части уравнения.
Установи, каким действием и над какими величинами её можно получить.
Выясни, какие из них известны, какие нет. Введи обозначение переменной.
Запиши уравнение.
Реши данное уравнение.
Сделай анализ уравнения.
20
Просмотров работы: 14541
Мы уже говорили о значимости понятного и реалистичного содержания задач в курсе арифметики в статьях «Какие задачи развивают ребёнка — лёгкие или трудные» и «Каким должно быть содержание задачи».
Второй важный фактор успешного обучения детей решению задач — сознательное усвоение ими условий задач. Ведь помимо образного представления реалий сюжета необходимо уловить числовые отношения, или математическую структуру задачи. Для этого классическая методика предлагает огромное количество форм работы. Давайте будем шаг за шагом осваивать эти приёмы.
1) Чтение, запись и повторение условия
В повседневной практике порой приходится наблюдать, как ребёнок слабо понимает текст условия из-за плохого чтения, особенно в первых двух классах. Процесс чтения условия задачи существенно отличается от чтения рассказов. Особые трудности для ребёнка представляет чередование в условии словесного текста с числами. Числа, как показывает опыт, читаются совсем иначе, чем слова. Объясняется это, главным образом, тем, что каждое число представляет собой особую комбинацию знаков — цифр, в то время как в словах знаки-буквы встречаются в своих специфических комбинациях. Вследствие этого ребёнок при чтении чисел делает больше фиксаций взгляда, а также больше регрессий (возвращений к просмотренному тексту), фиксации взгляда здесь более длительны, чем при чтении слова. При встрече числа в условии задачи ребёнок вынужден замедлять темп своего чтения.
Из сказанного видно, что чтение условия задач требует особых навыков. Поэтому нельзя полагаться на общие навыки чтения, которые приобретаются детьми на уроках словесности, а необходимо обучать их чтению текста математических задач как особому навыку.
Самый первый и простой приём, используемый учителем, — это чтение условия задачи не менее двух раз: при первом чтении ребёнок должен уловить общий смысл условия, а при вторичном — вникнуть в числовые данные.
Важный вопрос: кто должен читать условие — учитель или ученик? Наблюдения, а также исследования, которые проводились в данной области, показали, что дети лучше справляются с задачами, читаемыми учителем, чем с аналогичными задачами, условия которых они читают сами.
Следует ли из этого, что учитель должен всегда сам читать условие? Разумеется, нет. Конечная наша цель — развитие у детей умения самостоятельно, без посторонней помощи, решать задачи. Поэтому было бы вредно, если бы во всех случаях учитель сам читал условие. Вместо этого необходимо, начиная с I класса, приучать детей к чтению задач по учебнику.
Исходя из сказанного, наиболее правильным на первоначальных этапах обучения будет такой вариант: более сложные для понимания задачи правильнее читать учителю, причём более эффективно не читать, а рассказывать задачу наизусть, а на задачах более лёгких вырабатывать у детей навыки самостоятельного чтения и усвоения условия задачи.
2) Составление краткой записи
При работе над сложной задачей детям помогает запись её условия. Формы записи условия могут довольно разнообразными. Одна из них — краткая запись. Разберём её более подробно, так как краткая запись задачи — это настоящий бич современной начальной школы, сопоставимый по разрушительной силе со звуковыми транскрипциями и модулями-схемами.
Первый и самый важный момент: краткая запись не может и не должна быть самоцелью при обучении решению задач — это служебное подготовительное действие, которое нужно тогда и только тогда, когда задача настолько сложна, что ребёнок не может охватить её сюжет целиком. Краткая запись условия задачи должна способствовать пониманию, а не усложнять его; упрощать, а ни в коем случае не затруднять процесс решения задачи.
Итак, первоочередным условием использования краткой записи при усвоении условия задачи будем считать то, что задача настолько сложна, что ребёнок не может ухватить её сюжет целиком и нуждается в поэтапном (синтетическом) разборе задачи.
Выделение из текста условий числовых данных и их запись делает более ясным для учеников, что дано в задаче и что ищется. Такая запись помогает им лучше понять зависимость между величинами, о которых идёт речь в условии задачи.
Краткая запись условия может проводиться по-разному. Возьмём для примера задачу: «Конструктор, машинка и робот стоили 700 рублей. Конструктор стоил 130 рублей, машинка — в 2 раза больше, чем конструктор. Сколько стоил робот?»
Выписывая числовые данные из этого условия, можно расположить их в строчку, например:
3 игрушки — 700 руб.; конструктор — 130 руб., машинка — в 2 раза больше. Робот — ?
Можно расположить эти данные по-иному, схематически, примерно так:
Конструктор — 130 руб.
Машинка — в 2 раза больше.
3 игрушки — 700 руб.
Робот — ?
Легко видеть, что вторая форма записи делает условие более доходчивым для ребёнка, облегчает ему понимание зависимости между величинами. Целесообразно применять схематическую запись условия при решении трудных задач. Однако не нужно настаивать на каком-то однообразном, если не сказать однобоком, алгоритме краткой записи условия задачи. Подбирайте для каждой задачи наиболее понятную и удобную для целостного восприятия форму записи данных и искомых величин. Сделайте этот процесс творческим и интересным, а не «зубодробильным», как в современных методиках.
Очень полезно, чтобы учащиеся прибегали к краткой форме записи числовых данных при самостоятельном решении сложных задач, как в классе, так и дома. Пусть они выбирают свои приёмы записи, удобные для них. Это раскрепощает ребёнка перед задачей, побуждает его рассмотреть её с разных ракурсов, подталкивает мысль к нахождению путей решения, которых, как и форм краткой записи, может быть несколько. Чем свободнее и смелее ребёнок будет рассматривать и кратко записывать задачу по своему усмотрению, тем смелее и свободнее он решит её.
Однако следует ли всегда прибегать к схематической записи числовых данных задачи? Разумеется, нет, так как злоупотребление этой формой может привести к тому, что ученики не будут справляться с задачей при иной форме записи, в особенности же без записи условия.
А что делать, если ребёнок, только прочитав задачу, уже знает, как её решать? Ответ на этот вопрос однозначный — решай, моя умница!
3) Повторение, или пересказ условия
К сожалению, в современной общеобразовательной школе краткая запись стала единственной и безальтернативной формой работы с текстовыми задачами. Вводится она неоправданно рано и бесцельно усложняет решение простых и понятных ребёнку задач. Поэтому хочется обратить особое внимание наших читателей на другие формы работы над усвоением содержания задачи, в частности — на повторение, пересказ её условия.
Если вы начнёте практиковать пересказ задач, то убедитесь, что для формирования этого навыка также нужна практика. Обычно активно воспроизвести задачу могут немногие учащиеся, большая же часть детей воспринимает условие пассивно, на слух. Даже если вы дадите ребёнку прочитать задачу, которую он успешно решил несколько дней назад, и спросите его, может ли он её пересказать, скорее всего, он ответит утвердительно. Однако многие из тех детей, которые дают утвердительный ответ, всё же не могут повторить условие.
Здесь сказывается существенное различие между узнаванием и воспроизведением. Прочитав знакомое условие, ребёнок узнаёт его и чувствует уверенность, что может его повторить. При воспроизведении же оказывается, что он его не знает.
Наиболее часто дети затрудняются при пересказе середины и конца условия, в особенности же при пересказе главного вопроса. Иногда ученику требуется прочитать условие ранее решённой задачи несколько раз, пока он окажется в состоянии пересказать его.
Уметь пересказывать прочитанную задачу очень полезно, так как чаще всего бывает достаточно добиться хорошего пересказа условия, чтобы получить правильное решение задачи от ученика, который до этого не мог решить её.
Чтобы активизировать работу детей в процессе повторения задачи, можно рекомендовать им повторять условие прослушанной задачи сперва тихо или про себя и лишь после этого приступать к пересказу вслух. Таким образом, все учащиеся, а не только те, кого учитель вызывает для устного пересказа, будут повторять условие.
В том случае, когда дети сами читают условие, необходимо рекомендовать им читать задачу не менее двух раз, затем закрыть учебник и повторить условие тихо, про себя. При этом надо указать ученикам, что числовые данные можно не запоминать, главное — понять и усвоить содержание задачи. Следует предупреждать детей, что от них будет требоваться пересказ условия без книжки («Вы должны будете повторить задачу, не заглядывая в учебник. Числа запоминать не нужно»). По нашим наблюдениям, такие предупреждения заставляют детей читать условие внимательно и пересказывать его про себя, чтобы быть готовым к пересказу вслух.
Здесь уместно указать, что, как показали экспериментальные исследования, при чтении текста с необходимостью запомнить его читающий гораздо яснее представляет себе содержание читаемого. Вот что пишет по этому поводу проф. А. А. Смирнов:
«Под влиянием мнемонической направленности наглядные представления возникают чаще, чем в отсутствие её. Далее, при чтении в условиях мнемонической направленности образы чаще иллюстрируют само содержание текста, а не являются побочными, случайно связанными с тем, что говорится в тексте». «Пересказывая своими словами, — пишет в той же статье проф. Смирнов, — мы приспособляем воспринятое к самим себе, «ко всей системе нашей психической жизни», к нашему «образу мыслей». Мы действительно осваиваем текст».
Нередко дети приступают к решению заданной им задачи, не прочитав условия до конца, что оказывается причиной многих ошибочных решений. Внимательное чтение и пересказ условия могут способствовать заметному повышению правильности решений.
Следует рекомендовать детям, чтобы и при выполнении домашних заданий по арифметике они прочитывали условие заданной задачи не менее двух раз, повторяли его, не заглядывая в учебник, и лишь после правильного пересказа условия приступали к решению задачи.
Указанное требование не имеет ничего общего с требованием заучивать наизусть условие задаваемой задачи и знать его на память при проверке домашних задании на следующий день. Повторение условия про себя непосредственно перед решением задачи полезно, так как это способствует лучшему усвоению и пониманию детьми её содержания. Заучивание же условия задачи наизусть не имеет никакого смысла и зря обременяет память учащихся.
Особо следует остановиться на вопросе о том, как следует проводить повторение условия вслух.
Независимо от того, читает ли условие учитель или сами дети, нужно проверить, усвоили ли они условие (исключение должно допускаться лишь при вполне самостоятельном решении задач). В этих целях учитель может предложить вызываемым ученикам связно повторить условие либо ответить на отдельные частные вопросы, касающиеся содержания условия (повторение по вопросам учителя).
Как определить, какой способ уместнее в вашем конкретном случае? Здесь, как и всегда, опираемся на здравый смысл: когда решается новая, трудная задача, необходимость повторения условия и целиком, и по вопросам вполне оправдана; когда же решается сравнительно нетрудная задача, можно ограничиться тем, чтобы один-два ученика связно повторили условие, после чего можно переходить к её решению.
Однако и при такой форме работы возможен непродуктивный формальный подход, которого нужно стараться избегать. Порой при решении задачи обнаруживается, что ученик, правильно пересказавший условие, не представляет себе того, о чём он рассказывал. Очевидно, что при формальном усвоении словесного текста задачи ученик не всегда может правильно понять зависимость между величинами, о которых в ней идёт речь, и, как следствие, не может правильно решить задачу. Поэтому очень важно обращать внимание на то, чтобы дети ясно представляли себе содержание задачи, чтобы они видели в своём воображении то, о чём рассказывается в ней.
Д. Мартынов в своём пособии «Методика арифметики для начальной школы» говорит по этому поводу:
«Содержание задачи можно считать усвоенным лишь тогда, когда ученик достигнет до наглядного, как бы картинного представления между данными в задаче числами. Направить воображение ученика именно в эту сторону — дело учителя».
На значение отчётливого представления содержания задач указывает и проф. И. В. Арнольд, который пишет:
«Затруднения в использовании данных арифметических задач в большинстве случаев зависят от недостаточно отчётливого представления учащимися данных количественных взаимоотношений».
4) Понимание слов, входящих в состав условия
Прежде чем приступать к работе над задачей, учителю необходимо убедиться в том, что ребёнок понимает значение всех слов, входящих в состав условия. Тексты многих задач наших учебников содержат слова, недостаточно знакомые детям (а иногда и вовсе незнакомые им). Это затрудняет понимание смысла условия и, как следствие, понимание способа решения задачи.
Здесь внимание учителя должны привлекать не только особо трудные слова, с которыми дети редко встречаются, но и употребляемые более часто, которые, может быть, уже не раз встречались им, но о которых, как показывает целый ряд исследований, проведённых в этой области, у них нередко сформировываются неясные, а то и неверные представления.
Приведём для примера данные советского исследования этого вопроса.
Чтобы изучить доступность для учащихся III и IV классов словаря учебников по арифметике, из каждого сборника было выделено по 30 наиболее трудных слов.
Вот образцы слов, выделенных из учебника для III класса: «барка», «бетон», «домна», «ссыпной пункт», «кокс» и др. А вот образцы слов, выделенных из учебника для IV класса: «баржа», «зубчатое колесо», «зяблевая вспашка», «зольное удобрение», «мюльная машина», «шлюз» и др.
Перечисленные слова предложили соответственно учащимся третьих и четвёртых классов, при этом им дали задание — рядом с каждым словом написать, как они его понимают. Всего опросили 309 учащихся третьих классов и 438 учащихся четвёртых классов.
Полученные листки с ответами учащихся обработали так: по каждому слову был подсчитан процент полностью правильных, частично правильных, неправильных и отсутствующих ответов. Результаты обработки детских ответов показали, что многие из перечисленных выше слов малознакомы для школьников.
Приведём образцы детских ответов (правильных и неправильных) по отдельным словам.
Зяблевая вспашка:
«Вспашка, которую пашут под осень». «Это кто-нибудь вспашет и её замораживает». «Вспашка, у которой пахарь зябнет». «Зяблевая вспашка — это плохая работа». «Зяблевая вспашка называется вспашка бугристая, как будто озябший человек. Когда человек зябнет, то у него тело покрывается маленькими бугорками». «Это когда пашут и зябнут». «Зяблевая вспашка — это пашут зябликом». «Это он [видимо, зяблик] своим носом роет землю».
Чайная плантация:
«Поле, на котором возделывают чайные кусты». «Это большое поле, на котором растёт чай». «Это есть такая местность, где погружают чай». «Где прохожие пьют чай». «Посуда, из которой пьют чай». «Чайная плантация — небольшая лавочка». «Все чай пьют, все вместе». «Делают чайную посуду».
Более подробно результаты этого исследования изложены в статье «Изучение доступности словаря учебника» из журнала «Народный учитель» (1935).
Как видно из приведённых образцов, у некоторых учащихся превратные представления о словах, встречающихся в условиях задачи.
Оказывает ли наличие таких слов в условии влияние на правильность решения задачи? Чтобы проверить это, были составлены две пары задач, при этом задачи каждой пары были однородны по своей структуре, но различались между собой словарём: первая задача каждой пары содержала трудные слова, вторая задача была свободна от таких слов.
Вот первая пара задач:
1. «В районе 43 500 га посевной площади; 1/5 часть её — под яровыми. Средний урожай ярового поля — 1 700 кг с гектара. При переходе к зяблевой вспашке урожай яровых хлебов повысился на 170 кг с гектара. Сколько яровых хлебов собирает район при зяблевой вспашке?»
2. «В совхозе 23 400 га земли. 1/3 её засеяна пшеницей. Средний урожай пшеницы был 1 600 кг с гектара. На следующий год под пшеницу заняли столько же земли, как и раньше, но хорошо удобрили землю навозом, и урожай пшеницы повысился на 330 кг с гектара. Сколько пшеницы собрал совхоз с удобренной земли?»
А вот вторая пара задач:
1. «Два пассажирских поезда стоят один за другим. В одном — паровоз с тендером и 40 вагонов, в другом — паровоз с тендером и 45 вагонов. Длина вагона — 7 м, а паровоза с тендером — 23 м. Какой длины путь занимают оба поезда?»
2. «Два пассажирских поезда стоят один за другим. В одном — паровоз и 60 вагонов. В другом — паровоз и 76 вагонов. Длина вагона — 9 м, длина паровоза — 25 м. Какой длины путь занимают оба поезда?»
Опытная работа была проведена в трёх четвёртых классах. В каждом из этих классов сначала давались для самостоятельного решения две задачи в одной формулировке (вторая задача первой пары и первая задача второй пары), затем, ровно через шестидневку, в тот же час дня — две аналогичных задачи в другой формулировке (первая задача первой пары и вторая задача второй пары).
Из проведённого эксперимента стало очевидно, что наличие малопонятных слов в условии задачи оказывает отрицательное влияние на правильность её решения. Интересно, однако, отметить следующее: некоторые учащиеся из числа тех, которые обнаружили непонимание слов, входивших в состав контрольных задач, тем не менее, правильно решили их. Так, правильно решили задачу первой пары учащиеся, которые писали про зяблевую вспашку: «Это когда пашут и зябнут», «Это он своим носом роет землю» и др. Это значительно снижает ценность их работы, ибо образовательное значение решения задачи может в полной мере сказаться тогда, когда учащиеся правильно представляют себе, что такое посевная площадь, яровое поле, зяблевая вспашка. Лишь в этом случае они будут сознательно решать задачу и, кроме того, через посредство её решения уточнят свои знания о выгоде зяблевой вспашки, о которой идёт речь в условии.
Значит ли это, что сборники задач должны быть совершенно разгружены от трудных слов? Нет, ибо это могло бы привести к отрыву содержания задач от производственной и культурно-политической жизни взрослых. Тем самым решение задач потеряло бы в значительной мере своё воспитательно-образовательное значение. Речь должна идти не о разгрузке учебников от трудных слов, а лишь об исключении из них малоупотребительных слов с узко ограниченным применением в жизненной практике, при этом новые для учащихся слова должны вводиться в меру, с учётом уровня развития учащихся каждого класса. Нечего говорить о том, что значение каждого из таких слов должно подробно разъясняться детям.
Наши учебники в значительной части освобождены от слов, которые маловероятно встретятся в их жизни, однако нашей задачей было сохранить нравственный воспитательно-трудовой настрой учебника. В связи с этим у современных городских детей зачастую возникают трудности с пониманием некоторых слов задач. Обращайте на это особое внимание. Проводите краткие вводные беседы перед чтением текста задачи, содержащей понятия, малознакомые детям. Порой нам даже сложно предположить, что то или иное понятие (баржа, вагон пшеницы, экземпляр книги, железнодорожная ветка, лесной питомник, отрез ткани и т. п.) может вызвать затруднение у ребёнка.
5) Понимание жизненного смысла задачи
Когда мы убедились в том, что дети понимают значение отдельных слов, из которых состоит текст задачи, это ещё совершенно не означает того важного момента, что у ребёнка сложилось ясное представление о той жизненной среде (обстановке), из которой взята задача, что он понимает, кому и когда приходится решать такие задачи в жизни. Без этого трудно понять зависимость между величинами, о которых идёт речь в условии, и, как следствие, трудно правильно выбрать нужные действия.
При выборе тематики задач прежде всего следует соблюдать общедидактический принцип от близкого к далёкому, выбирая вначале задачи из близкого окружения детей и лишь постепенно переходя к менее знакомым для них областям жизни.
Для лучшего понимания условия, для активизации детского воображения возможно применять ещё целый ряд приёмов:
а) Вместо сжатой формулировки условия изложить его более полно — так, чтобы детям было легче представить себе жизненную обстановку, из которой взята задача, чтобы задача стала более понятной для них.
Приведём пример из школьной практики. Во II классе решали задачу:
«Чтобы оклеить комнату, достаточно иметь 6 кусков обоев по 14 м в каждом куске. Сколько кусков обоев пойдёт на эту комнату, если в каждом куске будет 12 м?»
При разборе задачи многие дети обнаружили непонимание способа её решения, непонимание зависимости между её величинами. Последнее, как это нетрудно было заметить, проистекало от непонимания ими жизненного смысла задачи.
Тогда учитель предложил ученикам условие задачи в новой редакции:
«Нужно оклеить комнату. Мастер велел купить 6 кусков обоев по 14 м в каждом. В магазине же оказались куски обоев длиною по 12 м каждый. Хозяйке нужно сосчитать, сколько таких кусков ей нужно купить?»
Далее учитель сказал: «Пусть каждый из вас представит себе, что он пошёл покупать обои для этой комнаты. Как бы вы стали решать задачу?»
И вот многие из тех учеников, которые до этого не знали, как решать задачу, стали более уверенно рассказывать её план и решение. Это явилось результатом того, что благодаря новой формулировке условия у детей возникло более ясное представление о жизненной обстановке, из которой взята задача, они поняли, зачем нужно было её решать (зачем нужно было узнавать количество кусков обоев по 12 м). Определённую роль здесь сыграло и то, что детей призвали поставить себя на место действующего лица — покупателя обоев, что сделало более активным их отношение к решаемой задаче.
Приведём ещё один пример. В IV классе решали задачу:
«Для осушения болота нужно вырыть канаву длиной в 1 080 м. Один землекоп может вырыть эту канаву за 40 дней, другой — за 60 дней. За сколько дней они выроют канаву, работая вместе?»
В беседе с учениками выяснили, для чего нужно было рыть канаву. Далее детям разъяснили содержание задачи примерно так:
«Для осушения болота нужно было вырыть канаву длиной в 1 080 м. Первый землекоп, которому предложили эту работу, был готов взяться за неё, но он сказал, что может вырыть канаву за 40 дней. Это оказалось слишком длинным сроком. Тогда обратились к другому землекопу. Но тот сказал, что он может вырыть канаву только за 60 дней. Этого срок был ещё длиннее. Чтобы канава была вырыта скорее, наняли обоих землекопов. В задаче спрашивается, за сколько дней оба землекопа выроют канаву, работая вместе».
Доведение до сознания учащихся жизненного смысла задачи помогло им лучше понять способ её решения.
При более полном изложении условия следует дополнять его лишь такими деталями, которые необходимы для лучшего понимания данных количественных отношений, так как излишние подробности могут отвлечь внимание детей от основной фабулы задачи и тем самым затруднить для них понимание зависимости между величинами.
Здесь уместно привести образцы задач из сборника Звягинцева и Бернашевского, в котором большинство задач изложено в форме рассказов:
«Костя помогает дедушке Савелию собирать в саду опавшие яблоки. Сегодня он собрал 22 спелых яблока и 13 зелёных. Сколько всего яблок собрал он?»
«Учительница рассказала ребятам, что ей пришлось однажды видеть в зверинце двух черепах: одну большую морскую весом 480 фунтов, а другую обыкновенную ручную весом 30 фунтов. Во сколько раз речная черепаха легче морской?»
В первой задаче, может быть, излишне указывать, как звали дедушку. Также можно было бы несколько короче изложить условие второй задачи. Но в целом введённые в эти задачи детали, не загромождая их основной фабулы, помогают детям легче представить содержание задачи, делают задачи более доходчивыми.
В то же время в этом сборнике много задач, условия которых чрезмерно загромождены излишними деталями. Приведём образцы таких задач:
«В жаркой стране Африке есть воробьи, которые целой стаей устраивают гнёздышки рядышком и выводят над ними общую крышу. Облюбовали эти воробьи большое высокое Дерево и устроили на нём под одной крышей 76 гнёзд. Потом прилетела к ним другая стайка, увеличила крышу и пристроила ещё 21 гнездо. Сколько всего гнёзд было под крышей?»
«Вывели воробьи птенцов и разлетелись. А когда настало время опять выводить птенцов, прилетели к тому же дереву сперва 38 пар воробьёв, потом — на 17 пар больше. Но поселились воробьи не в старых гнёздах, а свили и подвесили к ним новые гнёздышки, особое для каждой пары. Крыша же под гнёздами осталась прежняя. Сколько новых гнёзд устроили воробьи?»
Излишнее многословие, особенно во второй задаче, может затруднить детям решение, так как из-за обилия деталей они могут не понять данных количественных отношений.
Оживлению задач может способствовать введение в их условия прямой речи. Приведём образцы таких задач:
«Швее дали 15 м полотна и сказали: «Из 3 м сошьёте наволочки, а из остального полотна — 6 одинаковых простыней». Сколько метров полотна пошло на каждую простыню?»
«Мама выкопала в парнике 100 штук капустной рассады и говорит сыну: «На 4 маленьких грядках посадим по 10 штук, а остальные — на большой грядке». Сколько штук рассады мама хотела посадить на большой грядке?»
«Лиза рассказала своей подруге: «У меня было 70 см материи. Из 30 см я сшила своей кукле одеяльце, а из остальной материи — 2 одинаковых платьица». Сколько материи пошло на каждое платьице?»
Более полное изложение условий уместно, главным образом, в младших классах, особенно в первом, где умелое введение деталей в условие может способствовать усилению интереса детей к задаче, активизации их внимания.
б) Для того чтобы детям было легче понять, кому и при каких обстоятельствах приходится решать задачи, подобные данной, учитель после повторения условия проводит с детьми соответствующую беседу.
Приведём пример из школьной практики.
При решении в III классе задачи:
«Один каменщик укладывает 6 200 кирпичей за 5 дней, а другой — 7 350 кирпичей за 6 дней. Сколько кирпичей могут уложить оба каменщика за 25 дней?»
перед детьми поставили вопрос, кому из взрослых приходится решать такие задачи. Они ответили: инженерам, бригадирам. После этого был задан новый вопрос: зачем инженеру или бригадиру могло понадобиться вычислить, сколько кирпичей уложат оба каменщика за 25 дней. В беседе выяснили, что каменщики, возможно, были вновь приняты на работу, что каждого из них поставили на несколько дней на пробную кладку, чтобы выяснить, сколько кирпичей в среднем он может уложить за день. Затем их, может быть, поставили вместе работать, и нужно было сосчитать, сколько кирпичей они уложат за месяц вместе (за 25 рабочих дней).
в) В целях лучшего понимания детьми задачи иногда целесообразно проводить живое иллюстрирование условия, изображение его в лицах.
При решении в I классе задачи:
«2 мальчика пошли вместе на рыбалку и договорились делить пойманную рыбу поровну. Один мальчик поймал 7 рыб, а другой — 9. Сколько рыб досталось каждому мальчику?»
учитель после прочтения условия провёл с детьми беседу:
— Кто из вас когда-нибудь рыбачил (много мальчиков подняли руки)? Вот как много ребят удили рыбу! Двое из тех, кто удил рыбу, пойдут к доске. Вот вы двое встаньте у доски лицом к классу. Вы как бы будете теми мальчиками, о которых рассказывается в нашей задаче. Скажите, куда вы вместе пошли?
— Мы пошли на реку рыбачить.
— Сколько рыб ты поймал?
— Я поймал 7 рыб.
— А сколько рыб ты поймал?
— Я поймал 9 рыб.
— Как вы поделили между собою пойманную рыбу?
— Мы поделили её поровну.
— Что спрашивается в задаче?
— Сколько рыб получил каждый из нас.
В некоторых случаях полезно, чтобы дети, которые представляют действующих лиц задачи, изображали то, что делали последние. При решении задачи, в которой речь шла о собиравшей грибы девочке, вызванная ученица, держа в руках данную ей учительницей корзиночку, изображала в движениях то, о чём рассказывалось в задаче. Этот приём, как показывает опыт, активизирует внимание детей, помогает им более ясно представить содержание задачи.
Живое иллюстрирование условий применимо не только в первом, но иногда и в последующих классах. Приведём ещё пару примеров.
В III классе решали задачу:
«2 маляра вместе получили за свою работу 3 600 руб. Один из них работал 5 дней, а другой — 4 дня. Сколько рублей должен получить каждый маляр?»
При разборе задачи обнаружилось, что некоторые учащиеся не понимают способа её решения. Это выяснилось, когда дети стали предлагать неверный выбор действий для решения задачи (делить 3 600 на 5; 3 600 на 4 и т. п.). Тогда учитель в беседе с детьми выяснил, что маляры работали вместе, положим, вместе красили стены в школе. Один работал 5 дней, а другой — 4 дня. По окончании работы им выдали на двоих 3 600 руб., которые они должны были поделить между собой по количеству рабочих дней каждого. После этого учитель сказал учащимся: «Чтобы задача была вам понятнее, я вызову к доске двух учеников. Они как бы будут теми малярами, о которых рассказывается в задаче».
Затем вызванным ученикам были предложены следующие вопросы, на которые они отвечали:
— Сколько денег вы получили вместе за свою работу?
— Сколько дней ты работал?
— Сколько дней ты работал?
— Что вам нужно сосчитать?
Инсценирование условия оказалось в данном случае весьма эффективным и достаточным для осознанного решения задачи.
При решении в III классе задачи:
«Три парикмахера сообща купили 35 флаконов шампуня. Первый парикмахер дал на эту покупку 2 160 руб., второй — 1 620 руб., а третий — 2 520 руб. Сколько флаконов шампуня должен получить каждый парикмахер?»
в беседе выяснили, что парикмахеры, чтобы не ехать всем в магазин, могли послать туда одного человека закупить для них шампуни. Затем парикмахерам нужно было разделить между собой доставленные флаконы по количеству денег, которые каждый из них дал на эту покупку. После задача была инсценирована так же, как предыдущие.
Приведённые выше приёмы помогают детям яснее представить жизненное содержание задачи, обстоятельства, при которых приходится решать подобные вопросы в реальной жизни. Они содействуют активизации отношения учащихся к решению задач, как бы ставя их в положение действующих лиц, о которых рассказывается в задаче.
Само собой разумеется, эти приёмы уместны лишь тогда, когда дети без этого не понимают содержания задачи, её жизненного смысла, не могут самостоятельно решить задачу.
6) Применение наглядности
Лучшему усвоению условия задачи и, как следствие, лучшему пониманию способа её решения способствует применение наглядности. Здесь может быть использована как реальная наглядность, так и условная. Особенно уместно применение наглядности в младших классах. Применение наглядных пособий полезно при объяснении новых видов простых и составных задач и вообще во всех тех случаях, когда без этого детям трудно понять ход решения задачи.
Наглядные пособия должны подбираться с таким расчётом, чтобы они не освобождали ребёнка от мыслительной работы, а лишь облегчали ему процесс этой работы.
В качестве наглядных пособий при решении задач применим разного рода счётный материал, а также рисунки и чертежи.
Рисунки для иллюстрирования задач должны содержать, возможно, меньше деталей с тем, чтобы не отвлекать внимания от их математической стороны.
В наших учебниках встречаются следующие виды иллюстраций к задачам:
Когда вы даёте задачу для самостоятельного решения, очень полезно рекомендовать детям делать к ней рисунок или чертёж.
При частом применении наглядности во время классных и самостоятельных занятий дети, как показывает опыт, начинают прибегать к ней сами, без подсказки учителя. Этот навык чрезвычайно важен, особенно для решения нестандартных олимпиадных задач, так как они требуют хорошо развитого воображения и способности представить всю ситуацию, описанную в задаче.
Подробнее о методике обучения решению задач вы можете прочитать в пособии Г. Б. Поляка «Обучение решению задач в начальной школе».

 Задача №1
Задача №1 Задача №2
Задача №2