Определение 1. Функция называется Малой более высокого Порядка по сравнению с функцией
при
, если
и
и обозначается
.
Примеры. 1. при
, т. к.
. Заметим, что при
:
~
,
. Число
назы-вается Порядком малости функции
.
Определение 2. Функция называется Большой более высокого Порядка по сравнению с функцией
при
, если
и
.
2. при
, т. к.
.
Определение 3. Функция называется Главной частью функции
при
, если она представима при
в виде
.
При этом, функции и
называются Эквивалент-ными при
и обозначаются
~
.
Теорема 1. Для того чтобы функции и
были экви-валентными при
необходимо и достаточно, чтобы
=1.
Теорема 2. Следующие функции эквивалентными между собой при
~
~
~
~
~
.
Первые три соотношения следуют из 1-го замечательного предела и его следствий, а четвертое и пятое — из следствий 2-го замечательного предела.
Теорема 3. ~
при
.
Применим первый замечательный предел и формулу бинома Ньютона к тождеству
~
~
при
.
Выделение главной части функции значительно упрощает вычисление пределов.
Примеры.
1.
Поскольку ~
,
~
,
~
,
~ ~
,
~
, то
. Наконец,
~
,
~
при
, то
2.
Т. к. ~
,
~ 3
, то
.
3. 
Здесь нельзя использовать эквивалентные функции: ~
, т. к. получим неопределенность. Преобразуем основание степени
.
Тогда,

Замечание. Последний пример продемонстрировал, что методом выделения главной части функции следует обращаться осторожно. Может оказаться, что решающую роль играет не главная часть функции, а другие ее части.
| < Предыдущая | Следующая > |
|---|
Метод выделения главной части функции и его применение к вычислению пределов
Метод выделения главной части функции и его применение к вычислению пределов. Дадим функции. Если функция P всех x∈X может быть выражена в виде Р(х)= а (Х)+ О(а(Х)), Х> Х、 В свою очередь, функция a называется основной частью функции при x> x0. Образцы. 1. поскольку x ^8m x = x + o(x), функция 8m x из x ^равна X. 2. Пн (х)= apxn + … + а х + а apΦ, функция apnnn является главной частью многочлена РП (х) в Х>. потому что Pn (x)= apnn + o (xn) для x>^. 267. Функция P. учитывая X ^ K, основная часть x ^ x не определена однозначно. Согласно теореме 1, p-эквивалентная функция X> X0, a, является основной частью x> X0.
Однако, если вы запросите определенный тип основной детали, этот разумный выбор может гарантировать, что основная часть указанного типа определена однозначно.
Людмила Фирмаль
- Например, P = x + x2 + x3.С другой стороны, x2 + x3 = o (x) для x^, P = x + o (x) для x^ и xP = o (x + x2) для x^, поэтому、 P = х + Х2 + о (Х + Х2). В первом случае основную часть можно считать a = x. 2-й а = х + Х2. В частности, справедлива следующая Лемма. Лемма 5. X K, x∈K, x как предельная точка множества X. / Для функции P X ^ K для x ^ ^ x имеет основную часть вида a (X-x) Й, AΦ.Здесь A и V являются константами, которые определяются однозначно среди всех основных частей этой формы. Это справедливо только если A = A и V = ви. Я не уверен.
Понятие основной части функции полезно для изучения бесконечно малых и бесконечно малых чисел, оно используется при решении различных математических задач. analysis. In во многих случаях бесконечно сложная аналитическая форма в окрестности данной точки может быть заменена более простой (в некотором смысле) функцией с бесконечно малым высшим порядком. Например, P (x)=P (x) = A (x-x) d + o ((x-x) d), что является максимумом в случае x> x0, бесконечно малая бесконечность, бесконечно малая бесконечность (x), выше, чем (x-Xo) d, работает в окрестности Укажите на x как функцию, которая должна быть A (x-xo) d.
- В качестве примера мы покажем, как метод разделения основной части десятичной дроби применяется для расчета пределов function. In кроме того, широко используется полученное соотношение эквивалентности (8.26). Так что вам нужно найти предел(и таким образом доказать, что он существует). Используя вышеизложенное (см. отношения(8.26))、 Валентность 1N (1 + u)〜и u ^имеют 1n (1 + x + x)—x + x в x^, поэтому (см. теорему 1) 1n (1 + x + x)= = х + Х2 + о(Х + Х2).Однако o (x + x2)= o(x) (почему?) И быть X>x2 = o (x)、 Кроме того, агентство работает от 3 до 3 раз、 agszx 3х = 3х + о(Х3)= Х3 + о(Х). Также ясно, что это 5x = o (x).Из асимптотического уравнения получаем 8W 2x-2×8 Вт Х2 = Х2 + о (Х2)= 2х + о(Х).
Двадцать два от Х-Х a ^ 2 x = x2 + o (x2)= o (x), и(ex-1)5〜x5, аналогично、 (Пример-1) 5 = x5 + o(x5)= o(x). Все эти отношения справедливы для x^. Теперь у нас есть 1П(1 + х + х2)+ х3 ags81n-5×3 = = Х + О (х)+ 3х + о(Х) О (х)= 4х + о(Х)、 81n 2x + 1 ^ 2 x +(ex-1) 5 = 2x + o (x)+ o (x)= 2x + o (x), следовательно Однако по теореме 4 ^ + o (x)〜4x, а x ^2x + o (x) 2x Итак, предел искомого существует и равен 2. При вычислении пределов функции с использованием метода разделения основной части следует отметить, что если она не учитывается в разделе 8.3, то, в общем случае, заменить десятичную дробь эквивалентной не представляется возможным.
Метод расчета лимитов путем выделения основной части функции очень удобен, прост и в то же время очень популярен.
Людмила Фирмаль
- Например 。 S1P в Х-Х При нахождении предела формулы 11t p-это х<sup class=»reg»>®</sup>х Ошибочно замените функцию 81n x эквивалентной функцией x из x^. Естественный способ решения такой задачи описан в разделе 13.4. чтобы найти предел выражения в виде н (х) г (х), рекомендуется найти предел логарифма. Рассмотреть 1 / Х2 Хороший пример. Найти предел 11T сои 2x. равенства Некоторые сложности в работе приложения связаны с тем, что до сих пор не существует достаточно популярного способа выделения основной части функции. Эта проблема будет устранена в будущем (см.§ 13). Поскольку экспонента непрерывна, из(8.38).
Смотрите также:
Предмет математический анализ
Определение
порядка бесконечно малой.
Для
опред-я порядка малости бесконечной
ф-и, ее сравнивают со степенной ф-ей
вида:
g(x)
= (x-a)n,
(n>0) б.м.
при
x→a
g(x)
= xn,
(n>0)
б.м. при x→0
g(x)
=
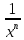
(n>0)
б.м. при x→∞.
Опред.:
пусть f(x)
и g(x)
= (x-a)n,
(n>0)
б.м. при x→a.
Если Ǝ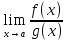
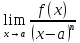
где С≠0-конечное число, f(x)
— б.м. при x→a
имеет порядок малости n.
Выделение
главной части бесконечно малых.
Опред.:
пусть f(x)
и g(x)=C(x-a)n
(где С≠0, n>0
– конечные числа) бесконечно малые при
x→a
такие, что Ǝ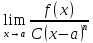
при x→a
имеет порядок малости n,
а величину C(x-a)n
назыв. глав. часть f(x)
при x→a.
Теорема
о выдел. глав. части б.м.
Если
C(x-a)n
– глав. часть б.м. f(x)
при x→a,
то f(x)
при x→a
представл. В виде f(x)
= C(x-a)n+0((x-a)n),
(x→a).
Док-во:
т.к. C(x-a)n
– глав. часть б.м. f(x)
при x→a,
то Ǝ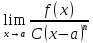
|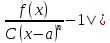
xϵE,
0<|x-a|<ƃ.
Т.к. ε-любое сколь угодно малое, то g(x)
=
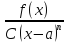
=>
g(x) * C(x-a)n
= f(x) – C(x-a)n
или
f(x) = C(x-a)n
+ + g(x) * C(x-a)n
= C(x-a)n+0((x-a)n),
(x→a).
________________________________________________________________________
22)Вывести таблицу эквивалентных б.М.
Эквивалентные
б.м. ф-и.
Пусть
f(x)
и g(x)
– б.м. одного порядка малости при x→a.
Если Ǝ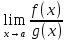
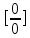
1, то их назыв. эквивалентными б.м.f(x)~g(x)
при x→a.
Теорема:
предел отношения двух б.м. не изменяется,
если каждую из них, или хотя бы одну
заменить эквивалентной б.м.
Док-во:
пусть f(x)~f*(x),
g(x)
~g*(x)
– б.м. при x→a.
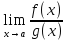
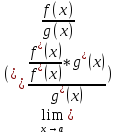
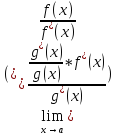
Таблица
эквивалентных б.м.
-
sinx~x,
при x→0 -
tgx~x,
при x→0 -
arctgx~x,
при x→0 -
arcsinx~x,
при
x→0 -
1-cosx~
x2,
при x→0 -
ax-1~x*lna,
при
x→0 -
ex-1~x,
при x→0 -
~
,
приx→0 -
ln(1+x)
~x,
при x→0 -
~
,
при x→0 -
~
,
при x→0 -
~
,
при x→0
________________________________________________________________________
23)Сравнение б.Б величин .
Опред.1:
пусть на мн-ве Е задана ф-я y=f(x),
a
– предельная точка мн-ва Е. ф-я f(x)
назыв. б.б при x→a,
если
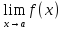
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,
0<|x-a|<ƃ):
|f(x)|>ε.
Опред.2:
пусть f(x)
и g(x)
– б.б. при x→a.
-
Если
Ǝ,
тоg(x)
имеет больший порядок роста, чем f(x)
при x→a -
Если
Ǝ,
тоf(x)
б.б. более высокого порядка роста при
x→a -
Если
Ǝ,
тоg(x)
и f(x)-б.б.
одного порядка роста при x→a.
Для
опред-я порядка роста ф-ю f(x)
сравнивают с ф-ей g(x):
g(x)
=
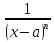
n>0
g(x)
=
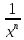
n>0
g(x)
= xn
– б.б. при x→∞,
n>0
Опред.3:
пусть f(x)
и g(x)=C(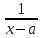
(С≠0б n>0)
– б.б. при x→a.
Если Ǝ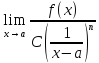
то ф-ю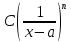
при x→a,
а число n
– порядком роста.
________________________________________________________________________
24)Запись
на языке (ε+
ƃ)
Определение пределов функции.
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,|x-a|<ƃ):
|f(x)-A|<ε.
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,|x-a|<ƃ):
A-ε<f(x)<A.
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,|x-a|<ƃ):
A <f(x)<A+ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,|x-a|<ƃ):
|f(x)|>
ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,|x-a|<ƃ):
f(x)<-ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,|x-a|<ƃ):
f(x)>ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,
a-
ƃ
<x<ƃ):
|f(x)-A|>ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,
a-
ƃ
<x<ƃ):
A-ε<f(x)<A
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,
a-
ƃ
<x<ƃ):
A <f(x)<A+ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,
a-
ƃ
<x<ƃ):
|f(x)|>ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,
a-
ƃ
<x<ƃ):
f(x)<-ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,
a-
ƃ
<x<ƃ):
f(x)>ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,
a <x<a+ƃ):
|f(x)-A|<ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,
a <x<a+ƃ):
A-ε<f(x)<A
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,
a <x<a+ƃ):
A <f(x)<A+ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,
a <x<a+ƃ):
|f(x)|>ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,
a <x<a+ƃ):
f(x)<-ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,
a <x<a+ƃ):
f(x)>ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,
|x|>ƃ):
|f(x)-A|<ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,
|x|>ƃ):
A-ε<f(x)<A
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,
|x|>ƃ):
A <f(x)<A+ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,
|x|>ƃ):
|f(x)|>ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,
|x|>ƃ):
f(x)<-ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,
|x|>ƃ):
f(x)>ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,x<-ƃ):
|f(x)-A|<ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,x<-ƃ):
A-ε<f(x)<A
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,x<-ƃ):
A <f(x)<A+ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,x<-ƃ):
|f(x)|>ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,x<-ƃ):
f(x)<-ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,x<-ƃ):
f(x)>ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,x>ƃ):
|f(x)-A|<ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,x>ƃ):
A-ε<f(x)<A
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,x>ƃ):
A <f(x)<A+ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,x>ƃ):
|f(x)|>ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,x>ƃ):
f(x)<-ε
(ε>0)(
Ǝƃ(ε)>0)(
xϵE,x>ƃ):
f(x)>ε
________________________________________________________________________
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
 Определение 1. Определение 1. |
|---|
|
Пусть |
| Замечание |
|
Вид главной части зависит от того, конечным или бесконечным 1) Если 2) Если |
 Определение 2. Определение 2. |
|---|
|
Пусть |
| Замечание. |
|
Пусть 1). если 2). если |
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
OMAAGAAD |
Заголовок сообщения: Выделить главный член функции
|
||
|
Добрый день, поомгите пожалуйста выделить главный член вида Cx^(alfa) Вложение: Комментарий к файлу: пример
|
||
| Вернуться к началу |
|
||
|
Prokop |
Заголовок сообщения: Re: Выделить главный член функции
|
|
Волнистая линия означает эквивалентность (предел отношения левой и правой части равен 1). [math]frac{1}{x}!left(4^{frac{1}{x}}-4^{frac{1}{x+1}}right)simfrac{1}{x}!left(1 — 4^{frac{-1}{(x+1)x}}right) sim frac{ln4}{x^3}[/math] Использовалась формула [math]a^alpha-1simalphaln{a}[/math], где [math]alpha[/math] — бесконечно малая величина
|
|
| Вернуться к началу |
|
| За это сообщение пользователю Prokop «Спасибо» сказали: OMAAGAAD |
|
|
OMAAGAAD |
Заголовок сообщения: Re: Выделить главный член функции
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Выделить главный член A ((α )^n)(x) б.м.(б.б.) функции
в форуме Пределы числовых последовательностей и функций, Исследования функций |
matan4635467325462 |
2 |
118 |
07 дек 2020, 21:33 |
|
Выделить главный член Aα^n(x) функции
в форуме Пределы числовых последовательностей и функций, Исследования функций |
Kurizer |
0 |
102 |
07 дек 2020, 18:59 |
|
Выделить главный член Aαn (x) б. м. (б. б.) функции
в форуме Пределы числовых последовательностей и функций, Исследования функций |
Zqquiet |
1 |
207 |
06 дек 2020, 11:54 |
|
Выделить главный член Aα^n (x) б. м. (б. б.) функции
в форуме Пределы числовых последовательностей и функций, Исследования функций |
SASHA PAHAN |
0 |
176 |
08 дек 2020, 17:37 |
|
Выделить главный член функции
в форуме Пределы числовых последовательностей и функций, Исследования функций |
Elphen Lied |
6 |
137 |
29 окт 2020, 13:17 |
|
Выделить главный член функции
в форуме Пределы числовых последовательностей и функций, Исследования функций |
czechcourier |
1 |
402 |
17 ноя 2015, 01:22 |
|
Выделить главный член
в форуме Пределы числовых последовательностей и функций, Исследования функций |
md_house |
1 |
777 |
24 дек 2017, 22:09 |
|
Главный член и порядок малости
в форуме Пределы числовых последовательностей и функций, Исследования функций |
md_house |
1 |
439 |
25 дек 2017, 15:49 |
|
Главный член и порядок малости
в форуме Пределы числовых последовательностей и функций, Исследования функций |
md_house |
1 |
235 |
18 дек 2017, 00:07 |
|
Выделить главную степенную часть функции
в форуме Пределы числовых последовательностей и функций, Исследования функций |
Oblomova |
6 |
374 |
16 дек 2020, 22:15 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 4 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB











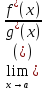
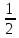 x2,
x2,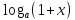 ~
~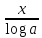 ,
,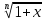 ~
~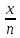 ,
,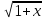 ~
~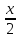 ,
,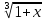 ~
~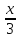 ,
,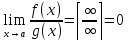 ,
,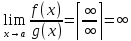 ,
,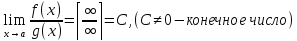 ,
,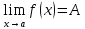
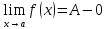
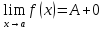
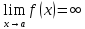
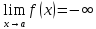
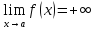
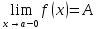
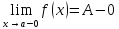
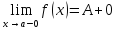
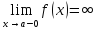
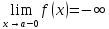
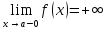
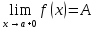

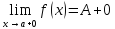
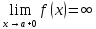
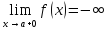
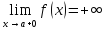
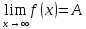
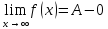
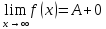
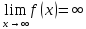
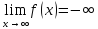
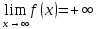
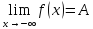
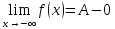
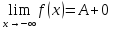
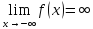
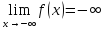
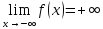
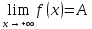
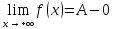
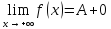
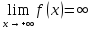
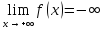
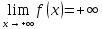
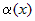 — простейшая б.м. в точке
— простейшая б.м. в точке 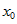 , а
, а 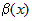 — другая б.м. в той же точке
— другая б.м. в той же точке 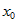 . Если
. Если 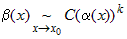 , где
, где 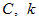 — постоянные числа,
— постоянные числа, 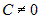 , то бесконечно малую
, то бесконечно малую 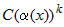 называют главной частью
называют главной частью 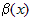 . Число
. Число 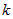 называют порядком функции
называют порядком функции 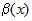 относительно
относительно 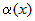 .
.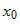 . Пусть
. Пусть 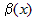 — б.м. в точке
— б.м. в точке 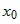 , то
, то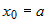 — конечное число, то главная часть функции
— конечное число, то главная часть функции 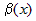 имеет вид
имеет вид 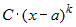 .
.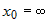 , то главная часть функции
, то главная часть функции 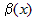 имеет вид
имеет вид 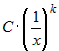 .
.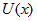 — простейшая бесконечно большая в точке
— простейшая бесконечно большая в точке 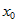 ,
, 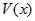 — другая бесконечно
— другая бесконечно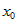 . Если
. Если 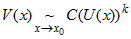 , где
, где 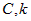 — постоянные числа,
— постоянные числа, 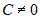 ,
, 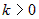 , то бесконечно большую
, то бесконечно большую 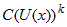 называют главной
называют главной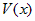 . Число
. Число 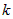 называют порядком функции
называют порядком функции 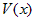 относительно
относительно 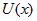 .
.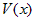 — б.б. в точке
— б.б. в точке 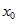 . Тогда:
. Тогда: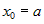 — конечное число, то главная часть функции
— конечное число, то главная часть функции 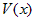 имеет вид
имеет вид 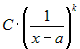 .
.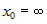 , то главная часть функции
, то главная часть функции 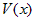 имеет вид
имеет вид 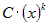 .
.


