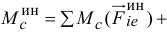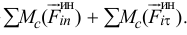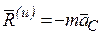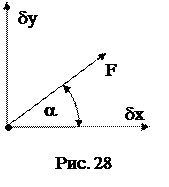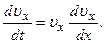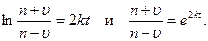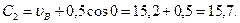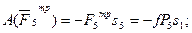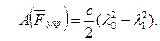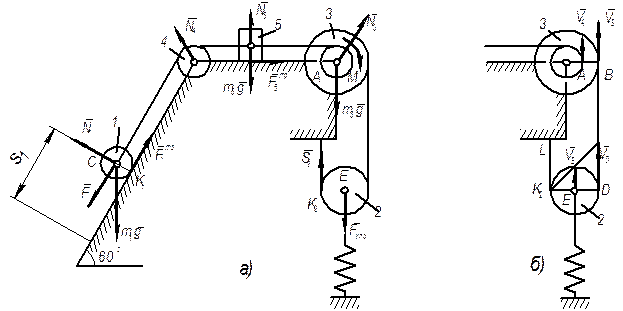Главный вектор и главный момент сил инерции
Система
сил инерции твёрдого тела можно заменить
одной силой, равной
и
приложенной в центре О, и парой с
моментом, равным
.
Главный вектор системы сил, как известно,
не зависит от центра приведения и может
быть вычислен заранее. Т.к.
,
то
(2)
Следовательно,
главный вектор сил инерции тела,
совершающего любое движение, равен
произведению массы тела на ускорение
его центра масс и направлен противоположно
этому ускорению.
Если
ускорение
разложить
на касательное и нормальное, то
вектор
разложиться
на составляющие
,
.
Главный
момент сил инерции найдём для некоторых
частных случаев:
1.
Поступательное движение. В
этом случае тело никакого вращения
вокруг центра масс С не имеет.
Отсюда заключаем, что
,
и равенство (1) даёт
.
Следовательно,
при поступательном движении силы
инерции твёрдого тела приводят к одной
равнодействующей, равной
и
проходящей через центр масс тела.
2.
Плоскопараллельное движение. Пусть
тело имеет плоскость симметрии и
движется параллельно ей. Вследствие
симметрии главный вектор и
результирующая пара сил инерции, так
же как и центр масс С тела, лежат
в плоскости симметрии.
Тогда,
помещая центр приведения в точке С,
получим из равенства (1)
.
С другой стороны
.
Отсюда заключаем, что
(3)
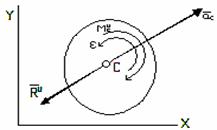
Таким
образом, в рассмотренном случае движение
системы сил инерции приводится к
результирующей силе, равной
[формула
(2)] и приложенной в центре масс С тела
(рис.32), и к лежащей в плоскости симметрии
тела паре, момент которой определяется
формулой (3). Знак минус в формуле
показывает, что направление
момента
противоположно
направлению углового ускорения тела.
3. Вращение
вокруг оси, проходящей через центр масс
тела. Пусть
опять тело имеет плоскость симметрии,
а ось вращения СZперпендикулярна
к этой плоскости и проходит через центр
масс тела. Тогда данный случай будет
частным случаем предыдущего. Но при
этом
, а
следовательно, и
.
Таким
образом, в рассмотренном случае система
сил инерции приводится к данной
паре, лежащей в плоскости, перпендикулярной
к оси вращения тела, и имеющей момент
.
При решение
задач по формулам (1) и (3) вычисляются
модули соответствующих величин, а
направление их указывают на чертеже.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Силы инерции твердого тела
Главный вектор сил инерции точек тела
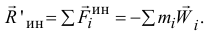
Но из определения радиуса-вектора центра масс
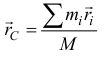
следует
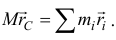
Взяв вторую производную по времени, получим
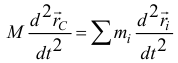
или
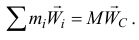
Поэтому главный вектор сил инерции точек тела при любом его движении
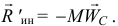
То есть модуль главного вектора равен произведению массы тела на ускорение его центра масс 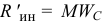
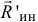
Прикладывается главный вектор к точке приведения, которую можно назначить в любом месте, то есть он не зависит от выбора этой точки.
С определением главного момента сил инерции возникает немало сложностей. Рассмотрим несколько частных случаев.
Твердое тело движется поступательно
При таком движении главный момент сил инерции можно не определять, а находить сразу равнодействующую этих сил. Как известно, она равна главному вектору
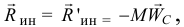
но имеет определенную точку приложения.
Поскольку при поступательном движении все точки тела имеют равные и параллельные векторы ускорений 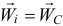
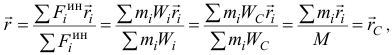
равен радиусу-вектору центра масс.
Следовательно, равнодействующая сил инерции точек тела при поступательном движении приложена к центру масс тела как к центру параллельных сил.
Твердое тело вращается вокруг неподвижной оси
Пусть тело вращается вокруг неподвижной оси 
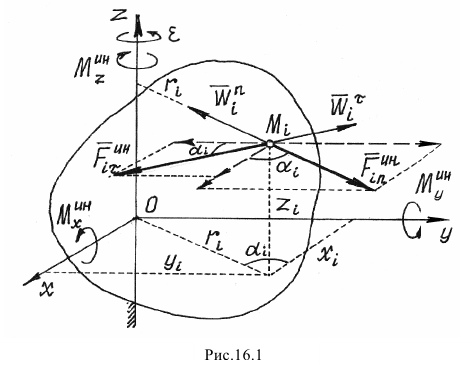
Проведем в теле, в какой-нибудь точке 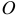

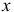

Определим касательное и нормальное ускорения некоторой точки 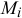

и соответствующие им силы инерции
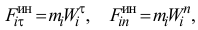
направленные противоположно ускорениям. Тогда главный момент сил инерции всех точек тела относительно оси
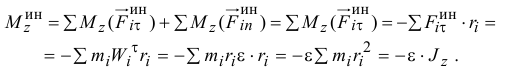
Итак, главный момент сил инерции точек тела относительно неподвижной оси вращения равен произведению момента инерции тела относительно этой оси на модуль углового ускорения
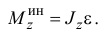
Направляется он в сторону, противоположную угловому ускорению.
Главный момент сил инерции точек тела относительно оси 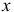
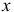
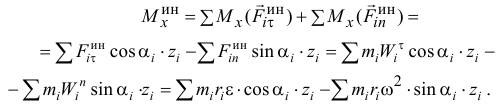
А так как
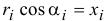
и
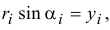
то
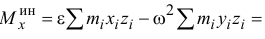
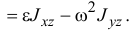
Итак, главный момент сил инерции относительно оси
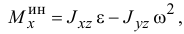
где 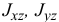
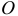
В частности, если тело имеет плоскость материальной симметрии, перпендикулярную оси вращения 

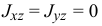
и тогда
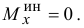
Осталось вычислить главный момент сил инерции относительно оси
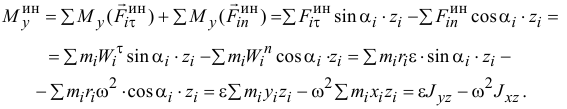
Следовательно, главный момент сил инерции точек тела относительно оси
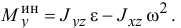
Опять, если тело имеет плоскость симметрии, перпендикулярную оси вращения, этот момент 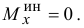
Примечания
а) Определив главные моменты сил инерции точек тела относительно взаимно перпендикулярных осей 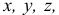
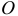
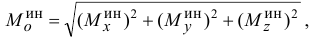
так как главные моменты относительно осей 
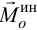
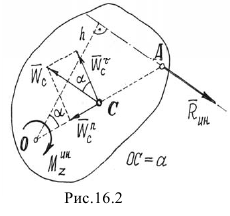
б) Если у тела имеется плоскость материальной симметрии, перпендикулярная оси вращения 
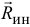
Она будет расположена в этой плоскости и равна главному вектору
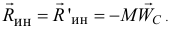
Центр масс также находится в этой плоскости.
На рис. 16.2 дано сечение тела плоскостью симметрии (точка 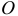

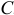
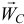
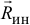
Легко находится расстояние 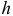

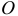
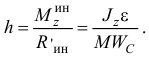
Но лучше найти расстояние 
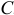
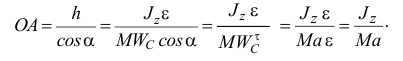
Это расстояние удобнее тем, что оно не зависит от закона вращения тела, определяется только его геометрией. Следовательно, в этом случае у тела имеется такая точка 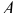
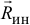
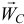
Тело совершает плоскопараллельное движение
При плоскопараллельном движении ускорение точки тела есть сумма трех ускорений: ускорения полюса, нормального ускорения и касательного ускорения точки при вращении вокруг полюса. Если полюс — центр масс 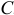
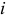
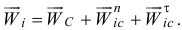
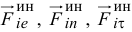

Тогда главный момент сил инерции точек тела относительно оси 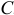
Но первая сумма равна нулю, так как по теореме Вариньона она равна моменту равнодействующей сил 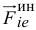
Вторая сумма также равна нулю, так как линии действия этих сил 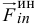
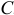
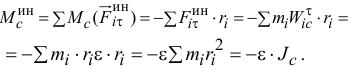
Итак, главный момент сил инерции точек тела при плоскопараллельном движении относительно центральной оси 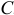
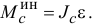
Направляется этот момент в сторону, противоположную направлению углового ускорения 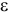
При желании можно найти равнодействующую сил инерции. Она будет равна главному вектору
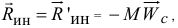
параллельна ему, а линия действия ее будет находиться на расстоянии
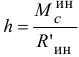
от центра масс, отложенном перпендикулярно 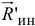
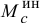
Принцип Даламбера удобно использовать при решении задач, в которых требуется определить неизвестные силы и иногда ускорение.
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
Определение сил инерции звеньев механизма
Важными качествами любой машины являются прочность, надежность и долговечность. Для определения конструктивных размеров и расчета элементов кинематических пар на прочность необходимо вычислить силы, действующие на каждое звено и кинематическую пару. Если при силовом расчете учитываются силы инерции, то расчет называют кинетостатичес- ким (в отличие от статического, при котором уравнения составляются без учета сил инерции).
Кинетостатический расчет основан на принципе Даламбера. Известно, что в общем случае все силы инерции звена, совершающего сложное плоское движение, могут быть сведены к главному вектор>’ сил инерции Ри и к паре сил инерции Ми, величины которых определяются по формулам
где т — масса звена, кг; as — ускорение центра масс (м/с 2 ); Js — момент инерции звена относительно оси, которая проходит через центр масс S звена, кг • м 2 (см. Раздел I); е — угловое ускорение звена, с 2 . Знак «минус» в формулах указывает на то, что сила Ри направлена противоположно ускорению й5, а момент инерции М„ — в сторону, обратную угловому ускорению.
Таким образом, инерционная нагрузка звена представляется одной инерционной силой Ри, приложенной в точке 5 и одним инерционным моментом Ми.
Частные случаи (рис. 9.3).
Поступательное движение звена. Инерционная нагрузка состоит только из одной инерционной силы Ри, определяемой формулой (9.4).
Неравномерное вращательное движение звена. Инерционная нагрузка состоит из силы инерции Ри и инерционного момента Ми, определяемых формулой (9.4). Модуль полного ускорения центра масс звена в этом случае равен
где а» и я5 т — нормальное (центростремительное) и касательное (тангенциальное) ускорения центра масс звена; со и е — угловая скорость и угловое ускорение звена; lAS — расстояние от центра масс 5 до оси А вращения звена.
Рис. 93. Частные случаи инерционной нагрузки звена
Равномерное вращательное движение звена. Инерционная нагрузка состоит только из силы инерции Ри звена, которая в этом случае направлена по радиусу противоположно направлению вектора центростремительного (нормального) ускорения центра масс звена. Это ускорение определяет центробежную силу инерции Ри = -mas ?—та» = -m 2 lAS. Произведение mlAS называется неуравновешенностью, или дисбалансом, и имеет размерность [гем].
Неравномерное вращательное движение звена при совпадении центра масс S звена с его осью вращения А (см. рис. 9.3). В этом случае инерционная нагрузка звена состоит только из инерционного момента Ми.
Равномерное вращательное движение звена при совпадении центра масс S звена с его центром вращения А (см. рис. 9.3, е). В этом случае lAS = 0 и Ри = О, и, так как е = 0 (равномерное вращение), то Ми = 0. В этом случае инерционная нагрузка звена равна нулю и оно называется уравновешенным (следует помнить, что рассматривается плоская система сил).
Пример: для кривошипно-ползунного механизма (рис. 9.4) найти инерционную нагрузку всех звеньев, если длины звеньев равны 1ЛВ = 0,020 м,
Рис. 9.4. Определение инерционной нагрузки звеньев кривошипно-ползунного
lBS = 0,060 м, /в5—з = 0,100 м; массы звеньев: кривошипа АВ тл = 10 кг, шатуна ВС т2 = 0,5 кг, ползуна 3 т3 = 0,40 кг; центральный момент инерции шатуна ВСJs = 0,0018 кгм 2 . Угловая скорость кривошипа АВ постоянна и равна со, = 200 с Задачу решить для положения механизма, когда угол 2 р, = 200 2 — 0,001 = 40 мс’ 2 /мм. Построение проводим в соответствии с равенством
На этом плане отрезок kb, изображающий вектор нормального ускорения точки В, будет равен АВ = kb = 74 мм.
Отрезок пЬ, изображающий на плане нормальное ускорение а’^в точки С во вращении звена ВС относительно точки В, найдется из равенства
где Ьс = 52 мм — отрезок (взятый из плана скоростей), изображающий скорость точки С в движении (вращении) звена ВС относительно точки В.
По правилу подобия находим точки s,, s2, s3 (концы векторов ускорений центров масс звеньев механизма кривошипа АВ, шатуна ВС и ползуна 3). Подсчитываем инерционную нагрузку для каждого механизма. Инерционные силы. Сила инерции кривошипа равна
приложена в центре масс кривошипа .V, и по направлению противоположна вектору ускорения aS< этого звена. Сила инерции шатуна равна
приложена в центре масс S2 и но направлению противоположна вектору ускорения as> этого звена. Сила инерции ползуна 3 равна
приложена в центре его масс (точке С, рис. 9.4) и по направлению противоположна вектору ас ускорения этого центра.
Инерционные моменты. Для кривошипа АВ инерционный момент Ми равен МиХ = 0, так как звено вращается равномерно.
Для шатуна ВС инерционный момент
Этот момент по направлению противоположен угловому ускорению звена ВС (см. рис. 9.4). Угловое ускорение звена ВС в нашем случае направлено против хода стрелки часов, в соответствии с направлением а Т св тангенциального ускорения точки С во вращении звена ВС относительно точки В.
Для ползуна 3 инерционный момент Мм3 = 0, так как звено движется поступательно.
Главный вектор и главный момент сил инерции
Находить значения главного вектора и главного момента сил инерции непосредственно по формулам (22.6) затруднительно, так как в общем случае будем иметь дело с множеством сил инерции всех материальных точек системы. Поэтому целесообразно получить выражения главного вектора и главного момента сил инерции через параметры, характеризующие в целом механическую систему и ее движение.
Подставив в первое из равенств (22.7) значение ZT 7 / из теоремы о движении центра масс Мас = ЕГ/ (см. § 17.3), найдем
т. е. главный вектор сил инерции механической системы направлен противоположно вектору ас, а модуль его равен произведению массы системы на ускорение ее центра масс.
Подставив теперь во второе из равенств (22.7) значение ‘Lni0(Fk e ) из теоремы моментов (см. § 18.2) dK0/dt = Y.m0(F?), найдем
т. е. главный момент сил инерции механической системы относительно некоего центра О направлен противоположно вектору производной по времени от кинетического момента системы относительно того же центра.
Аналогичным будет соотношение для моментов относительно оси. Так, относительно оси z будет
Таким образом, все силы инерции механической системы можно эквивалентно заменить двумя векторами: силой Я ф , приложенной в произвольно выбранном центре О, и парой сил с моментом, равным М ф .
Рассмотрим, как эти величины определяются для твердого тела.
Если тело совершает поступательное движение, то ускорения всех его точек одинаковы и равны ускорению ас центра масс С
тела (ак =ас). Следовательно, все силы инерции —ткак образуют систему параллельных сил, которая приводится к равнодействующей Я ф = -Мас, линия действия которой будет проходить через точку С (здесь полная аналогия с силами тяжести). Сумма моментов сил инерции относительно точки С будет равна нулю.
Для твердого тела, вращающегося вокруг неподвижной оси Oz, величину главного момента сил инерции относительно этой оси определим, подставив в формулу (22.11) значение Kz = Jzсо (см. § 18.1):
т. е. модуль M°Z = Jzs, а направление момента противоположно
направлению углового ускорения е (это следует учитывать при выполнении чертежей для расчета).
Следовательно, система сил инерции такого вращающегося тела приводится к приложенной в точке О силе Я ф , определяемой формулой (22.8), и к паре, момент которой определяется формулой (22.12).
В частном случае, когда тело вращается вокруг оси Cz, проходящей через его центр масс С, получим R ф = 0, так как ас = 0, и система сил инерции приводится лишь к одной паре с моментом
ф , определяемой формулой (22.8) и приложенной в центре масс С тела, и паре сил с моментом = — /Сге (ось Cz перпендикулярна плоскости движения).
Главный вектор и главный момент сил инерции
Определение: главным вектором сил инерции называется вектор, равный геометрической сумме векторов сил инерции. 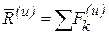
Просуммировав уравнения (51) с учетом того, что по свойствам внутренних сил (32) 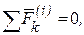
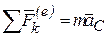
Определение: главным моментом сил инерции относительно точки О (оси), называется пара сил с моментом, равным геометрической сумме моментов сил инерции относительно той же точки (оси).
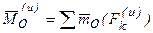
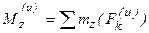
Поскольку система сил, определяемых уравнением (51) является уравновешенной, то для нее справедливо равенство:
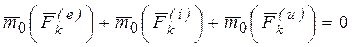
Просуммировав уравнения (52) с учетом того, что по свойствам внутренних сил (32) 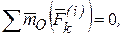
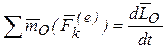
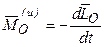
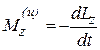
Приведение сил инерции для различных видов движения
В случае поступательного движения тела силы инерции, действующие на его точки, образуют систему параллельных сил, так как ускорения всех точек тела равны по величине и направлению, например, ускорению центра масс тела — 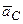
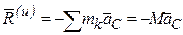
В случае вращательного движения тела, обладающего плоскостью материальной симметрии, вокруг оси, перпендикулярной этой плоскости и проходящей через центр масс тела, силы инерции могут быть приведены к паре сил с моментом, равным главному моменту сил инерции относительно оси вращения:
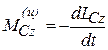
Учитывая, что: 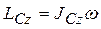
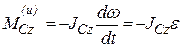
В случае когда ось вращения Oz не проходит через центр масс тела, силы инерции приводятся к силе 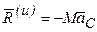
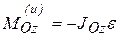
Приплоскомдвижении тела, имеющего плоскость симметрии и движущегося параллельно этой плоскости, силы инерции приводятся к силе, приложенной в центре масс тела и равной главному вектору сил инерции 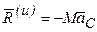
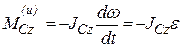
Принцип возможных перемещений
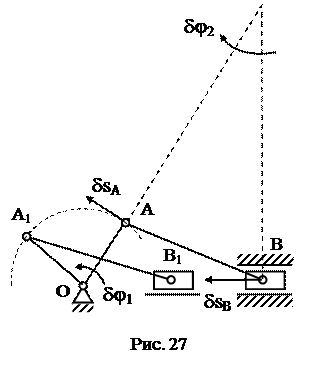
Определение: возможным называется бесконечно малое перемещение системы, которое допускают наложенные на нее связи. На рис. 27 показано возможное перемещение системы.
Направление возможных перемещений совпадает с направлением скоростей точек и угловых скоростей звеньев механизма. Перемещение из положения ОАВ в положение ОА1В1 не является возможным, так как оно конечное.
Определение: связь называется идеальной, если работа ее реакции на любом возможном перемещении равна нулю (например, гладкая поверхность).
Для равновесия системы с идеальными двухсторонними связями необходимо и достаточно, чтобы сумма работ активных сил, действующих на нее, на любом возможном перемещении равнялась нулю:
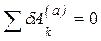
Общее уравнение динамики
Если к активным силам, действующим на систему с идеальными связями добавить силы инерции, то сумма работ этих сил на любом возможном перемещении будет равна нулю:
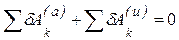
Общее уравнение динамики является суммой двух принципов: принципа Даламбера и принципа возможных перемещений. Действительно, если к неуравновешенной системе сил, действующей на механическую систему, добавить силы инерции, то согласно принципу Даламбера такая система сил будет уравновешенной и, следовательно, согласно принципу возможных перемещений
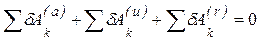
Но, поскольку связи, наложенные на систему, являются идеальными, то сумма работ их реакций на любом возможном перемещении равна нулю: 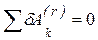
Уравнение Лагранжа II рода
Уравнение Лагранжа II рода имеет вид:
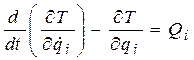
Здесь обозначено: T – кинетическая энергия системы; 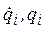
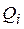
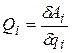
где 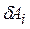
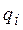
Например, для точки на рис. 28 обобщенные силы, соответствующие координатам x и y можно найти по формулам:
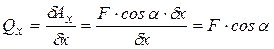
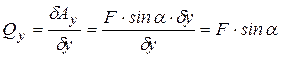
ЗАДАЧИ К КОНТРОЛЬНЫМ ЗАДАНИЯМ
Задача Д1
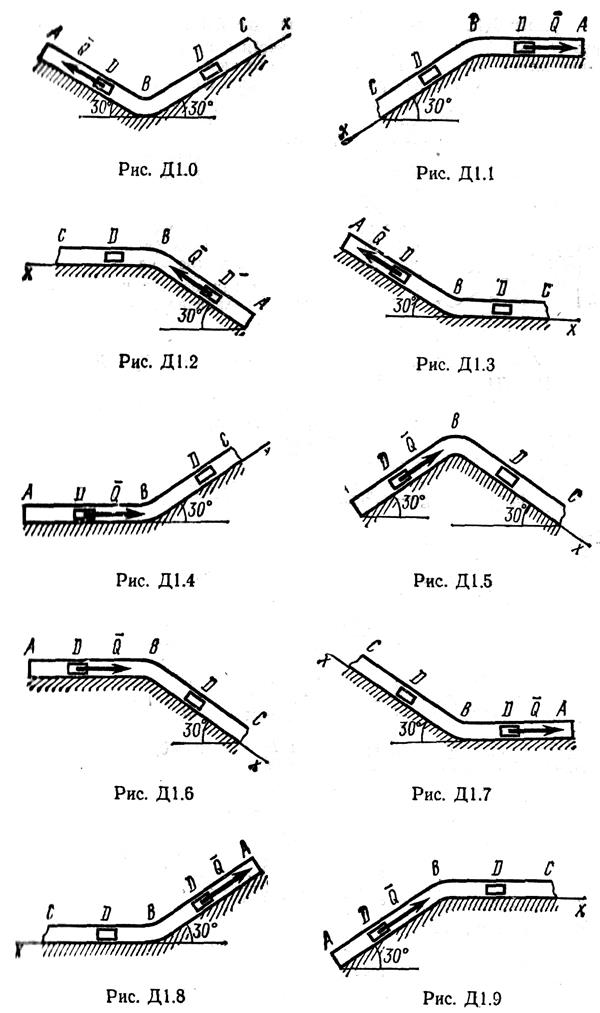
Груз D массой m, получив в точке А начальную скорость υ0, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0 – Д1.9, табл. Д1). На участке АВ, на груз кроме силы тяжести, действуют постоянная сила 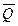
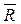
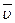
В точке В груз, не изменяя своей скорости, переходит на участок ВС трубы, где на него, кроме силы тяжести, действуют сила трения (коэффициент трения груза о трубу f = 0,2) и переменная сила 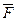
Указания.Задача Д1 – на интегрирование дифференциальных уравнений движения точки. (Решение основной задачи механики). Решение задачи разбивается на две части. Сначала нужно составить и проинтегрировать методом разделения переменных дифференциальное уравнение движения точки (груза) на участке AB, учтя начальные условия. Затем, зная время движения груза на участке АВ или длину этого участка, определить скорость груза в точке В. Эта скорость будет начальной для движения груза на участке ВС. После этого нужно составить и проинтегрировать дифференциальное уравнение движения груза на участке ВС тоже с учетом начальных условий, ведя отсчет времени от момента, когда груз находится в точке В, и полагая в этот момент t=0. При интегрировании уравнения движения на участке АВ в случае, когда задана длина l участка, целесообразно перейти к переменной х, учтя, что:
| Номер условия | m, кг | υ0, м/с | Q, H | R, H | l,м | t, c | Fx, H |
| 0,4υ | — | 2,5 | 2sin(4t) | ||||
| 2,4 | 0,8 υ 2 | 1,5 | — | 6t | |||
| 4,5 | 0,5 υ | — | 3sin(2t) | ||||
| 0,6 υ 2 | — | -3cos(2t) | |||||
| 1,6 | 0,4 υ | — | 4cos(4t) | ||||
| 0,5 υ 2 | — | -6sin(2t) | |||||
| 1,8 | 0,3 υ | — | 9t 2 | ||||
| 0,8 υ 2 | 2,5 | — | -8cos(4t) | ||||
| 0,5 υ | — | 2cos(2t) | |||||
| 4,8 | 0,2 υ 2 | — | -6sin(4t) |
Пример Д1. На вертикальном участке АВ трубы (рис. Д1) на груз D массой m действует сила тяжести и сила сопротивления 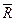
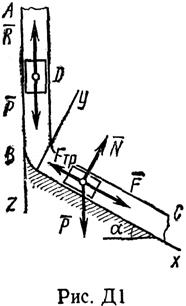
Определить: x=f(t) – закон движения груза на участке ВС.
Решение.1. Рассмотрим движение груза на участке АВ, считая груз материальной точкой. Изображаем груз (в произвольном положении) и действующие на него силы 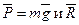
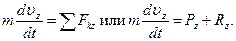
Далее находим Pz=P=mg, Rz=-R=-μυ 2 ; подчеркиваем, что в уравнении все переменные силы надо обязательно выразить через величины, от которых они зависят. Учтя еще, что υz=υ, получим
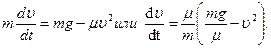
Введем для сокращения записей обозначение
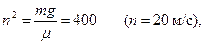
где при подсчете принято g≈ 10 м/с 2 . Тогда, разделяя в уравнении (2) переменные и взяв затем от обеих частей равенства интегралы, получим
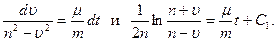
По начальным условиям при t = 0 υ=υ0=0, что дает С1=(1/2n)×ln1=0. Введя еще одно обозначение
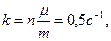
Отсюда находим, что
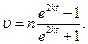
Полагая здесь t=t1=2 c и заменяя n и k их значениями (3) и (5), определим скорость υВ груза в точке В (число е=2,7):
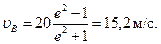
2. Рассмотрим движение груза на участке ВС; найденная скорость υВ будет для движения на этом участке начальной скоростью (υ0= υВ). Изображаем груз (в произвольном положении) и действующие на него силы 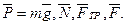
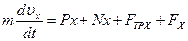
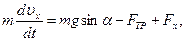
где FТР=fN. Для определения N составим уравнение в проекции на ось Вy. Так как ау=0, получим 0=N-mgcosα, откуда N=mgcosα. Следовательно, Fтр=fmgcosα; кроме того, Fx=16sin(4t) и управление (8) примет вид
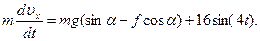
Разделив обе части равенства на m, вычислим
g(sinα – f cos α)=g(sin30˚-0,2cos30˚)=3,2; 16/m=2 и поставим эти значения в (9). Тогда получим
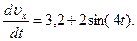
Умножая обе части уравнения (10) на dt и интегрируя, найдем
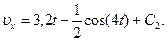
Будем теперь отсчитывать время от момента, когда груз находится в точке В, считая в этот момент t=0. Тогда при t=0 υ=υ0=υВ, где υВ дается равенством (7). Подставляя эти величины в (11), получим
При найденном значении С2 уравнение (11) дает
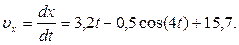
Умножая здесь обе части на dt и снова интегрируя, найдем
Так как при t=0 x=0, то C3=0 и окончательно искомый закон движения груза будет
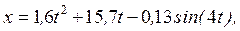
где x – в метрах, t – в секундах.
Задача Д4
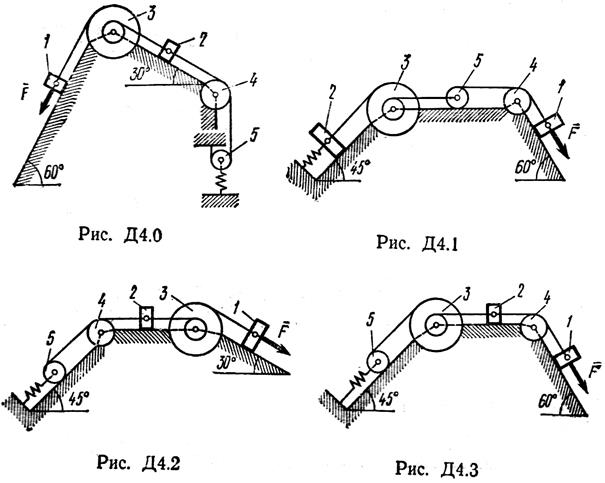
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3 = 0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д4.0 – Д4.9, табл. Д4); тело 5 считать сплошным однородным цилиндром, а массу блока 4 – равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υ2, υс5 – скорости грузов 1, 2 и центра масс тела 5 соответственно, ω3 и ω4 – угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 1), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2=0; остальные тела должны изображаться и тогда, когда их масса равна нулю.
Указания. Задача Д4 – на применение теоремы об изменении кинетической энергии системы. При решении задачи учесть, что кинетическая энергия Т системы равна сумме кинетических энергий всех входящих в систему тел; эту энергию нужно выразить через ту скорость (линейную или угловую), которую в задаче надо определить. При вычислении Т для установления зависимости между скоростями точек тела, движущегося плоскопараллельно, или между его угловой скоростью и скоростью центра масс воспользоваться мгновенным центром скоростей (кинематика). При вычислении работы надо все перемещения выразить через заданное перемещение s1, учтя, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями.
| Номер условия | m1, кг | m2, кг | m3, кг | m4, кг | m5, кг | с, Н/м | М, Н×м | F=f(s), H | Найти |
| 1,2 | 80(4+5s) | ω3 | |||||||
| 0,8 | 50(8+3s) | υ1 | |||||||
| 1,4 | 60(6+5s) | υ2 | |||||||
| 1,8 | 80(5+6s) | ω4 | |||||||
| 1,2 | 40(9+4s) | υ1 | |||||||
| 1,6 | 50(7+8s) | υС5 | |||||||
| 0,8 | 40(8+9s) | ω3 | |||||||
| 1,5 | 60(8+5s) | υ2 | |||||||
| 1,4 | 50(9+2s) | ω4 | |||||||
| 1,6 | 80(6+7s) | υС5 |
Пример Д4. Механическая система (рис. Д4, а) состоит из сплошного однородного цилиндрического катка 1, подвижного блока 2, ступенчатого шкива 3 с радиусами ступеней R3 и r3 и радиусом инерции относительно оси вращения ρ3, блока 4 и груза 5(коэффициент трения груза о плоскость равен f). Тела системы соединены нитями, намотанными на шкив 3. К центру Е блока 2 прикреплена пружина с коэффициентом жесткости с; ее начальная деформация равна нулю. Система приходит в движение из состояния покоя под действием силы F=f(s), зависящей от перемещения s точки ее приложения. На шкив 3 при движении действует постоянный момент М сил сопротивления.
Определить ω3 в тот момент времени, когда s=s1.
Решение.1. Рассмотрим движение неизменяемой механической системы, состоящей из весомых тел 1, 3, 5 и невесомых тел 2, 4, соединенных нитями. Изобразим действующие на систему внешние силы: активные 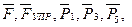
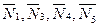
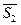
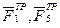
Для определения ω3 воспользуемся теоремой об изменении кинетической энергии:
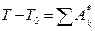
2. Определяем Т0 и Т. Так как в начальный момент система находилась в покое, то Т0=0. Величина Т равна сумме энергий всех тел системы:
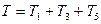
Учитывая, что тело 1 движется плоскопараллельно, тело 5 – поступательно, а тело 3 вращается вокруг неподвижной оси, получим
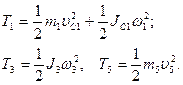
Все входящие сюда скорости надо выразить через искомую ω3. Для этого предварительно заметим, что υС1=υ5=υА, где А – любая точка обода радиуса r3 и что точка К1 – мгновенный центр скоростей катка 1, радиус которого обозначим r1. Тогда
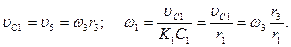
Кроме того, входящие в (3) моменты инерции имеют значения
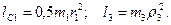
Подставив все величины (4) и (5) в равенства (3), а затем, используя равенство (2), получим окончательно
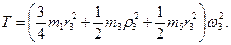
3. Теперь найдем сумму работ всех действующих внешних сил при том перемещении, которое будет иметь система, когда точка С1 пройдет путь s1. Введя обозначения: s5 – перемещение груза 5 (s5=s1), φ3 – угол поворота шкива 3, λ0 и λ1 – начальное и конечное удлинения пружины, получим
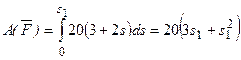
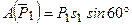
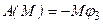
Работы остальных сил равны нулю, так как точки К1 и К2, где приложены силы 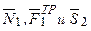
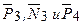
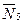
По условиям задачи λ0=0. Тогда λ1=sЕ, где sЕ – перемещение точки Е (конца пружины). Величины sE и φ3 надо выразить через заданное перемещение s1; для этого учтем, что зависимость между перемещениями здесь такая же, как и между соответствующими скоростями. Тогда, поскольку ω3=υА/r3=υC1 /r3 (равенство υС1=υА уже отмечалось), то и φ3=s1/r3.
Далее, из рисунка Д4, б видно, что υD=υB=ω3R3, а так как точка К2 является мгновенным центром скоростей для блока 2 (он как бы «катится по участку нити K2L), то υЕ=0,5υD=0,5ω3R3, следовательно, и λ1=sE=0,5φ3R3=0,5s1R3/r3. При найденных значениях φ3 и λ1 для суммы всех вычисленных работ получим
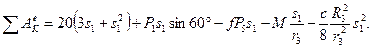
Подставляя выражения (6) и (7) в уравнение (1) и учитывая, что Т0=0, придем к равенству
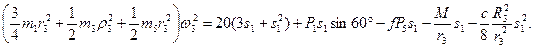
Из равенства (8), подставив в него числовые значения заданных величин, найдем искомую угловую скорость ω3. Ответ: ω3=8,1с -1 .
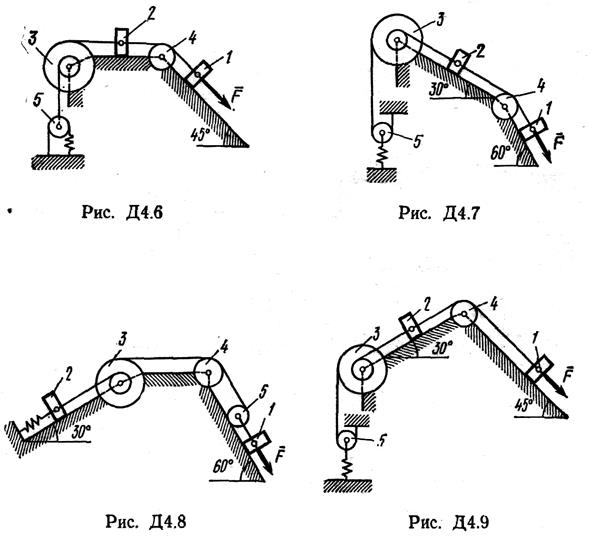
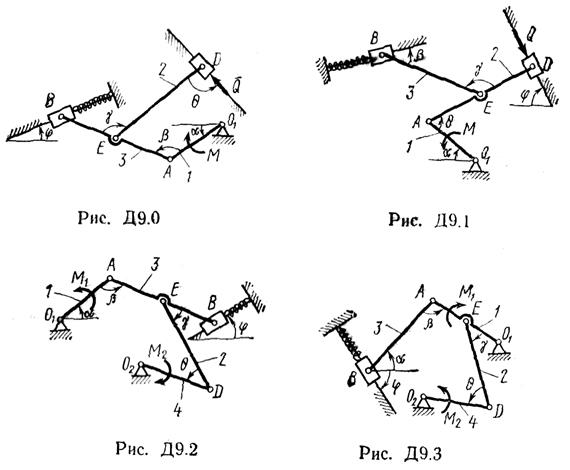
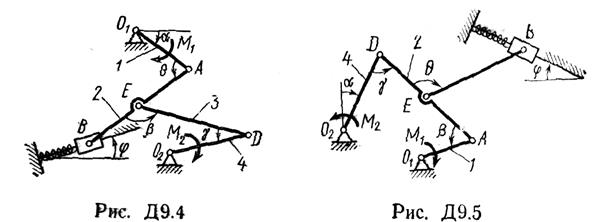
Задача Д9
Механизм, расположенный в горизонтальной плоскости, находится под действием приложенных сил в равновесии; положение равновесия определяется углами a, b, g, j, q (рис. Д9.0 – Д9.9, табл. Д9а и Д9б). Длины стержней механизма (кривошипов) равны: l1 = 0,4 м, l4 = 0,6 м (размеры l2 и l3 произвольны); точка Е находится в середине соответствующего стержня.
На ползун В механизма действует сила упругости пружины 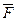
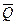
Определить, чему равна при равновесии деформация l пружины, и указать, растянута пружина или сжата. Значения всех заданных величин приведены в табл. Д9а для рис. Д9.0—Д9.4 и в табл. Д9б для рис. Д9.5—Д9.9, где Q выражено в ньютонах, а М, М1, М2 — в ньютон-метрах.
Построение чертежа начинать со стержня, направление которого определяется углом α; для большей наглядности ползун с направляющими и пружину изобразить так, как в примере Д9 (см. рис. Д9, а также рис. Д9.10б). Если на чертеже решаемого варианта задачи прикрепленный к ползуну В стержень окажется совмещенным с пружиной (как на рис. Д9.10а), то пружину следует считать прикрепленной к ползуну с другой стороны (как на рис. Д9.10б, где одновременно иначе изображены направляющие).
Указания. Задача Д9 — на определение условий равновесия механической системы с помощью принципа возможных перемещений. Механизм в рассматриваемой задаче имеет одну степень свободы, т. е. одно независимое возможное перемещение. Для решения задачи нужно сообщить механизму возможное перемещение, вычислить сумму элементарных работ всех действующих активных сил и пар на этом перемещении и приравнять ее к нулю. Все вошедшие в составленное уравнение возможные перемещения следует выразить через какое-нибудь одно.
Чтобы найти l, надо из полученного условия равновесия определить силу упругости F. На чертеже эту силу можно направить в любую сторону
(т. е. считать пружину или растянутой или сжатой); верно ли выбрано направление силы, укажет знак.
Таблица Д9а (к рис. Д9.0—Д9.4)
| Номер условия | Углы, град | с, Н/см | Для рис. 0—1 | Для рис.2 — 4 | ||||
| α | β | g | j | q | М, Н∙м | Q, Н | М1, Н∙м | M2, Н∙м |
Таблица Д9б (к рис. Д9.5—Д9.9)
| Номер условия | Углы, град | с, Н/см | М1, Н∙м | M2, Н∙м |
| α | β | g | j | q |
Пример Д9. Механизм (рис. Д9а), расположенный в горизонтальной плоскости, состоит из стержней 1, 2, 3 и ползунов B, D, соединенных друг с другом и с неподвижной опорой О1 шарнирами.
К ползуну В прикреплена пружина с коэффициентом жёсткости с, к ползуну D приложена сила 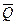
с= 125 Н/см, М = 150 Н×м, Q = 350 Н.
О п р е д е л и т ь: деформацию λ пружины при равновесии механизма.
Решение. 1. Строим положение механизма в соответствии с заданными углами (рис. Д9б); при этом согласно последнему из указаний к задаче Д9 прикрепляем пружину к ползуну с другой стороны (так, как если бы было β = 180°).
Для решения задачи воспользуемся принципом возможных перемещений, согласно которому
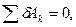
где δAk — элементарные работы активных сил на соответствующих возможных перемещениях.
Изображаем действующие на механизм активные силы: силу 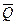
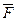
Неизвестную силу F найдем с помощью уравнения (1), а зная F и учитывая, что F = cλ, определим λ.
2. Чтобы составить уравнение (1), сообщим механизму возможное перемещение и введем следующие обозначения для перемещений звеньев, к которым приложены активные силы: δφ1 — поворот стержня 1 вокруг оси О1, δsD и δsB — перемещения ползунов (точек) D и В.
Из перемещений δφ1, δsD, δsB независимое от других — одно (у механизма одна степень свободы). Примем за независимое возможное перемещение δφ1 и установим, какими тогда будут δsD и δsB, выразив их через δφ1; при этом важно верно определить и направления δsD, δsB, так как иначе в уравнении (1) будут ошибки в знаках.
При расчетах учтем, что зависимость между возможными перемещениями здесь такая же, как между соответствующими скоростями звеньев механизма при его движении и воспользуемся известными из кинематики соотношениями (ход расчетов такой же, как в примере К3).
Сначала найдем и изобразим δsA (направление δsA определяется направлением δφ1); получим

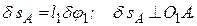
Теперь определим и изобразим δsD, учитывая, что проекции δsD и δsA на прямую АD должны быть равны друг другу (иметь одинаковые модули и знаки). Тогда
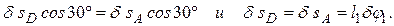
Чтобы определить δsB, найдем сначала δsE. Для этого построим мгновенный центр вращения (скоростей) С2 стержня 2 (на пересечении перпендикуляров к δsA и δsD, восстановленных из точек А и D) и покажем направление поворота стержня 2 вокруг С2, учтя направление δsA или δsD. Так как ÐС2АD = ÐC2DА = 60°, то DАС2D равносторонний и С2Е в нем высота, поскольку АЕ = ЕD. Тогда перемещение δsE, перпендикулярное С2Е, будет направлено по прямой ЕА (при изображении δsE учитываем направление поворота вокруг центра С2).
Воспользовавшись тем, что проекции δsE и δsA на прямую ЕА должны быть равны друг другу, получим (значение δsE можно найти и составив соответствующую пропорцию)
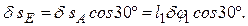
Наконец, из условия равенства проекций δsB и δsE на прямую ВЕ находим и изображаем δsB. Численно
3. Теперь составляем для механизма уравнение (1); получим
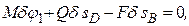
или, заменяя здесь δsD и δsB их значениями (3) и (5) и вынося одновременно δφ1 за скобки,
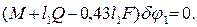
Так как δφ1¹0, то отсюда следует, что
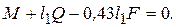
Из уравнения (8) находим значение F и определяем λ = F/с. Ответ: λ= 13,5 см. Знак указывает, что пружина, как и предполагалось, растянута.
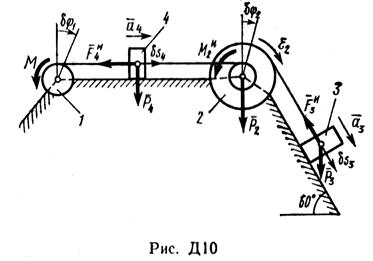
Задача Д10
Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3—6, прикрепленных к этим нитям, и невесомого блока (рис. Д10.0—Д10.9, табл. Д10). Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом М, приложенной к одному из шкивов. Радиусы ступеней шкива 1 равны:
R1 = 0,2 м, r1 = 0,1 м, а шкива 2 — R2 = 0,3 м, r2 = 0,15 м; их радиусы инерции относительно осей вращения равны соответственно ρ1=0,1 м и ρ2=0,2 м. Пренебрегая трением, определить ускорение груза, имеющего больший вес; веса Р1, . Р6 шкивов и грузов заданы в таблице в ньютонах. Грузы, веса которых равны нулю, на чертеже не изображать (шкивы 1, 2 изображать всегда как части системы).
Указания.Задача Д10 – на применение (к изучению движения системы) общего уравнения динамики (принципа Даламбера – Лагранжа). Ход решения задачи такой же, как в задаче Д9, только предварительно надо присоединить к действующим на систему силам соответствующие силы инерции. Учесть при этом, что для однородного тела, вращающегося вокруг своей оси симметрии (шкива), система сил инерции приводится к паре с моментом М и = Jzε , где Jz – момент инерции тела относительно оси вращения, ε – угловое ускорение тела; направление М и противоположно направлению ε.
| Номер условия | P1 | P2 | P3 | P4 | P5 | P6 | M, H×м |
| 0,9 | |||||||
| 1,2 | |||||||
| 0,6 | |||||||
| 1,8 | |||||||
| 1,2 | |||||||
| 0,9 | |||||||
| 1,8 | |||||||
| 0,6 | |||||||
| 0,9 | |||||||
| 1,2 |
источники:
http://studref.com/496104/matematika_himiya_fizik/glavnyy_vektor_glavnyy_moment_inertsii
http://zdamsam.ru/b12093.html
Содержание:
- Принцип Даламбера (метод кинетостатики)
- Принцип Даламбера для материальной точки
- Принцип Даламбера для механической системы
- Приведение сил инерции точек твердого тела к простейшему виду
- Порядок решения задач на применение принципа Даламбера
- Примеры решения задач на тему: Принцип Даламбера
- Приведение сил инерции точек твердого тела к простейшему виду
- Определение реакций связей плоского механизма с помощью принципа Даламбера
Принцип Даламбера (определение): если к действующей на тело активной силе и реакции связи приложить дополнительную силу инерции, то тело будет находиться в равновесии (сумма всех сил, действующих в системе, дополненная главным вектором инерции, равна нулю).
Принцип Даламбера (метод кинетостатики)
Принцип Даламбера — это один из основных принципов динамики, согласно которому, если к заданным силам, действующим на точки механической системы, и реакциям наложенных связей присоединить силы инерции, то получится уравновешенная система сил.
Принцип Даламбера для материальной точки
Рассмотрим материальную точку 







Добавим к силам 




а по модулю:
Сила, которая по модулю равна произведению массы точки на модуль ее ускорения и направлена противоположно ускорению, называется силой инерции.
Совокупность сил 


В этом состоит принцип Даламбера для материальной точки, значение которого состоит в том, что при его применении к задачам динамики уравнения движения состоят в форме хорошо известных уравнений равновесия.
При проектировании векторного равенства (12.1) на декартовы оси координат, получаем выражения для проекций силы инерции на эти оси:
Проецируя то же самое векторное равенство на естественные оси, получим проекции силы инерции на касательную, нормаль и бинормаль к траектории:
Составляющие силы инерции 

Принцип Даламбера для механической системы
Рассмотрим несвободную механическую систему, которая состоит из 

где 





Уравнение (12.5) показывает, что в любой момент времени геометрическая сумма равнодействующих заданных сил, реакций связей и силы инерции для каждой материальной точки несвободной механической системы равна нулю.
Это положение называется принципом Даламбера для несвободной механической системы .
Сложим все 
где 


Тогда:
Следовательно, в любой момент времени для всякой несвободной механической системы геометрическая сумма главных векторов заданных сил, реакций связей и сил инерции материальных точек системы равна нулю.
Проведем из произвольного неподвижного центра 




Сложим все 
или
Введем обозначение:






Тогда:
Из уравнения (12.10) следует: в каждый момент времени для всякой несвободной механической системы геометрическая сумма главных моментов заданных сил, реакций связей и сил инерции материальных точек системы относительно произвольного неподвижного центра равна нулю.
Если рассмотреть векторные уравнения (12.6) и (12.9) как условия равновесия произвольной пространственной системы сил, приложенных к твердому телу, то они эквивалентны шести алгебраическим уравнениям статики, а именно:
1) трем условиям равновесия в проекциях сил на оси 
2) трем условиям равновесия моментов сил относительно осей 


Приведение сил инерции точек твердого тела к простейшему виду
Как известно, систему сил можно привести к силе, равной главному вектору и к паре сил с моментом, равным главному моменту всех сил системы.
Приведение сил инерции точек твердого тела дает следующие результаты.
1. При поступательном движении тела силы инерции приводятся к равнодействующей, которая приложена в центре масс 

2. При вращении тела вокруг оси, проходящей через центр масс тела, силы инерции приводятся к одной пары, которая лежит в плоскости, перпендикулярной оси вращения тела и имеет момент (рис.12.2):
где 

Направление пары сил является противоположным направлению углового ускорения 
3. При плоском движении силы инерции приводятся к результирующей силы, которая равна 


Порядок решения задач на применение принципа Даламбера
Решение задач с помощью принципа Даламбера (метода кинетостатики) рекомендуется выполнять в такой последовательности:
Изобразить на рисунке активные силы, которые приложены к каждой материальной точке;
Изобразить реакции связей;
Добавить к активным силам и реакциям связей силы инерции материальных точек системы;
Выбрать систему координат;
Составить уравнения равновесия всех сил;
Решив составленную систему уравнений, определить величины, которые ищутся.
Примеры решения задач на тему: Принцип Даламбера
Задача №1
Автомобиль весом 


Определить давление автомобиля на мост в момент, когда он проезжает его середину (рис.12.4).
Решение. На автомобиль действуют активная сила тяжести 


Эти силы не уравновешивают друг друга, потому что автомобиль движется по криволинейной траектории с нормальным ускорением 




то система сил 


Поскольку все силы действуют вдоль одной прямой, которая совпадает с нормалью 

Отсюда
Давление 

Ответ:
Задача № 2
Груз 



Определить скорость груза 

Решение. На груз 




Подсчитаем силу инерции груза. Сила инерции 


Свяжем с точкой 







Согласно принципу Даламбера геометрическая сумма сил 


Спроектируем это векторное равенство на оси выбранной системы координат:
на ось 
на ось 
на ось 
Из второго уравнения определим натяжение нити 
Из первого уравнения находим скорость 
Ответ:
Задача № 3
Определить опорные реакции подпятника 








Решение. На кран действуют силы тяжести крана 


Для получения уравновешенной системы сил добавим силу инерции груза 
Сила инерции 
Перейдем, согласно методу кинетостатики, к составлению уравнений равновесия крана при наличии активных сил, реакций связей и силы инерции. Уравнения равновесия имеют вид:
Решая эти уравнения, находим неизвестные величины:
Ответ:
Задача № 4
Груз 








Определить реакции защемления.
Решение. На систему действуют внешние (активные) силы тяжести: груза 






Данная система сил не является уравновешенной.
Согласно принципу Даламбера, если к действующим активным силам и реакциям связей прибавить силы инерции, то новая система сил будет уравновешенной и к ней можно применить уравнение равновесия для определения опорных реакций.
Подсчитаем силы инерции. Сила инерции груза 

Силы инерции точек вращающегося барабана лебедки сводятся к паре сил с моментом 
где 

Угловое ускорение барабана 

Следовательно,
Направление момента 
Для определения реакций опоры 


Из первого уравнения находим реакцию 
Из второго уравнения определяем момент защемления 
Неизвестный момент пары сил 
или
Подставляя значение 
Ответ:
Задача № 5
Определить уравнение вынужденных колебаний электродвигателя весом 


Решение. Во время вращения вала электродвигателя груз весом 


По модулю
Проекция силы 

Таким образом, в вертикальном направлении на тело действует вынужденная сила, равная
и под действием которой балка будет совершать вынужденные колебания по закону:
где 


Вычислим частоту собственных колебаний 
Поскольку 

где
Итак,
Ответ:
Задача № 6
Полое полушарие с радиусом 


Определить высоту 

Решение. Изобразим шарик 



Применяя принцип Даламбера, приложим к шарику 


Тогда, по принципу Даламбера, данная система сил удовлетворяет условиям равновесия системы сходящихся сил:
Располагая, как показано на рисунке, координатные оси 

Из первого уравнения системы (2) находим нормальную реакцию 
где 
Подставляя полученное выражение для 
Поскольку
то
С рис.12.10 видно, что высота 
где
Таким образом, определив 

Из второго уравнения системы (2) находим величину 
Подставив значение 

Ответ:
Принцип Даламбера и механическая система
Принцип Даламбера позволяет решать задачи исследования динамики материальной системы методами статики, составлением уравнений равновесия, учитывая силы инерции точек системы.
Согласно принципу Даламбера главный вектор всех сил (внешних, внутренних, условно приложенных сил инерции точек) и главный момент их относительно любого неподвижного центра будут равны нулю
Учитывая что 
Таким образом, принцип Даламбера исключает внутренние силы и упрощает решение задач. Следует научиться находить главный вектор
и главный момент 
Приведение сил инерции точек твердого тела к простейшему виду
а) Твердое тело совершает поступательное движение (рис. 4.1).
Силы инерции приводятся к равнодействующей 



б) Твердое тело совершает вращение вокруг неподвижной оси, перпендикулярной к плоскости материальной симметрии (рис. 4.2).
При приведении сил инерции точек тела к центру ее вращения 
Сила равна главному вектору, направленному противоположно ускорению центра масс
где 
Модуль главного вектора равен
Момент пары сил равен главному моменту сил инерции относительно оси вращения, перпендикулярной к плоскости симметрии и по модулю равной
где 


Если твердое тело совершает вращение вокруг неподвижной оси, которая является главной центральной осью инерции (рис. 4.3), то 


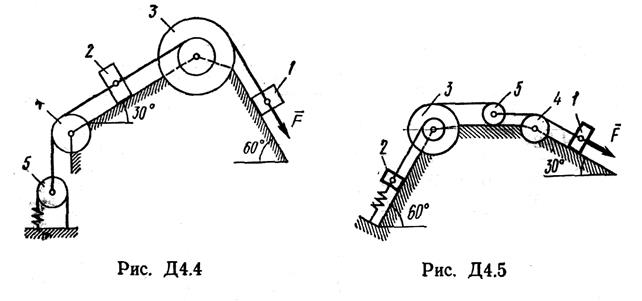
в) Тело совершает плоскопараллельное движение (рис. 4.4). Если твердое тело, имеющее плоскость материальной симметрии, движется параллельно этой плоскости, то силы инерции точек тела приводятся к силе, приложенной в центре масс и равной главному вектору сил
инерции 


Определение реакций связей плоского механизма с помощью принципа Даламбера
Пример с решением задачи 1
Рассмотрим макет плоского механизма (рис. 4.5), для которого известно:




Весом шатуна 


В начале выполнения работы, если ранее в предыдущих разделах не определялись кинематические характеристики механизма, требуется определить ускорение точки 

Для точек 

Ускорение точки 

Проектируя равенство (4.1) на ось 

Так как механизм строили в масштабе, все размеры 
На данную систему (плоский механизм) (рис. 4.6) действуют силы тяжести ведущего звена 


направляющих 

Эти составляющие направлены в противоположные стороны соответствующим ускорениям центра масс звена. Главный момент сил инерции относительно оси вращения 
Направляем его в сторону, противоположную направлению углового ускорения. Ползун 



Для полученной системы сил (см. рис. 4.6) составляем уравнения равновесия.
Решая систему уравнений, найдем из уравнения (4.2) 

Пример с решением задачи 2
В данном примере плоский механизм (рис. 4.7) включает в себя звенья, которые совершают вращательное движение 
В этом случае изменяется определение ускорений точек механизма.
Дано: 



Размеры звеньев замеряем на макете механизма.
Требуется определить реакции в осях 
Сначала определим ускорения 
По изученным ранее методам определения кинематических характеристик точек тел при различных видах движения определяем:
Переходим к определению ускорений:
или
Проектируем равенство (4.5) на ось 

откуда определяем 


Таким образом, определили необходимые ускорения, которые потребуются для определения приведенных сил инерции. Все размеры и углы берем с чертежа методом замера, так как механизм строится в масштабе.
Переходим к определению реакций в осях 

На данную систему (см. рис. 4.8) действуют силы тяжести 







Главный момент сил инерции относительно оси вращения 
Для второго звена соответственно имеем векторы 


Главные моменты сил инерции направлены в сторону, противоположную соответствующим угловым ускорениям (рис. 4.8). В результате получим расчетную схему произвольной плоской системы сил, содержащую четыре неизвестные реакции
Одной расчетной схемы недостаточно, так как для произвольной плоской системы можно составить лишь три уравнения равновесия. Поэтому, используя методику решения таких задач в статике, мы разъединяем систему на объекты равновесия и строим еще дополнительно две расчетные схемы (рис. 4.9,4.10).
Для определения четырех неизвестных 
Для объекта на рис. 4.8 составим два уравнения равновесия
Для объекта на рис. 4.9 составляем уравнение моментов всех сил относительно точки
Для объекта на рис. 4.10 составляем уравнение моментов всех сил относительно точки
Решаем систему четырех уравнений. Из уравнения (4.9) выразим 





Пример с решением задачи 3
На рис. 4.11 представлен плоский механизм, построенный в масштабе по макету, в котором к шатуну 





Найдем кинематические характеристики данного механизма:
Принимая точку 
Проектируя равенство (4.10) на ось 
Все размеры берем с чертежа (см. рис. 4.11). Далее показываем все силы (рис. 4.12), действующие на механизм: силы тяжести 



Рассмотрев два объекта равновесия (рис. 4.12; рис. 4.13), составим необходимые уравнения равновесия.
Для объекта на рис. 4.13 составим одно уравнение равновесия
Для объекта на рис. 4.12 составим три уравнения равновесия:
Для ролика отдельно найдем
Решая систему четырех уравнений, находим из уравнения (4.11) силу сцепления