Реализуем алгоритм поиска в глубину
Время на прочтение
5 мин
Количество просмотров 47K

В этом туториале описан алгоритм поиска в глубину (depth first search, DFS) с псевдокодом и примерами. Кроме того, расписаны способы реализации поиска в глубину в C, Java, Python и C++.
“Поиск в глубину” или “обход в глубину” — это рекурсивный алгоритм по поиску всех вершин графа или дерева. Обход подразумевает под собой посещение всех вершин графа.
Алгоритм поиска в глубину
Стандартная реализация поиска в глубину помещает каждую вершину (узел, node) графа в одну из двух категорий:
-
Пройденные (Visited).
-
Не пройденные (Not Visited).
Цель алгоритма состоит в том, чтобы пометить каждую вершину как “Пройденная”, избегая при этом циклов.
Алгоритм поиска в глубину работает следующим образом:
-
Начните с того, что поместите любую вершину графа на вершину стека.
-
Возьмите верхний элемент стека и добавьте его в список “Пройденных”.
-
Создайте список смежных вершин для этой вершины. Добавьте те вершины, которых нет в списке “Пройденных”, в верх стека.
-
Необходимо повторять шаги 2 и 3, пока стек не станет пустым.
Пример реализации поиска в глубину
Предлагаю рассмотреть на примере, как работает алгоритм поиска в глубину. Мы будем использовать неориентированный граф с пятью вершинами.
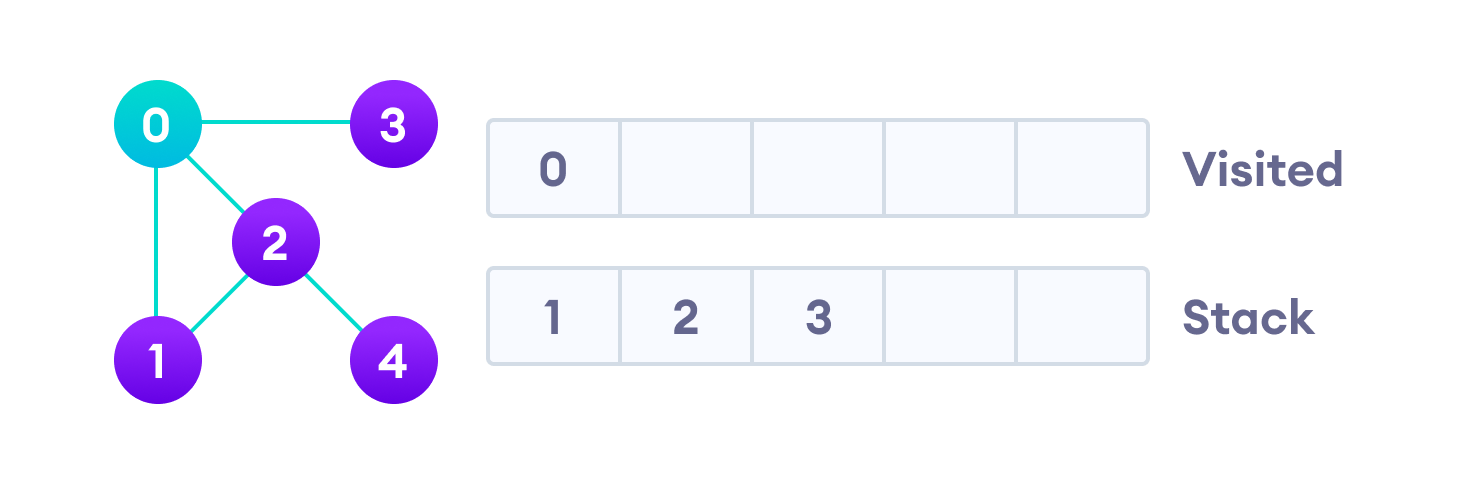
Начнем мы с вершины “0”. В первую очередь алгоритм поиска в глубину поместит ее саму в список “Пройденные” (на изображении “Visited”), а ее смежные вершины — в стек.
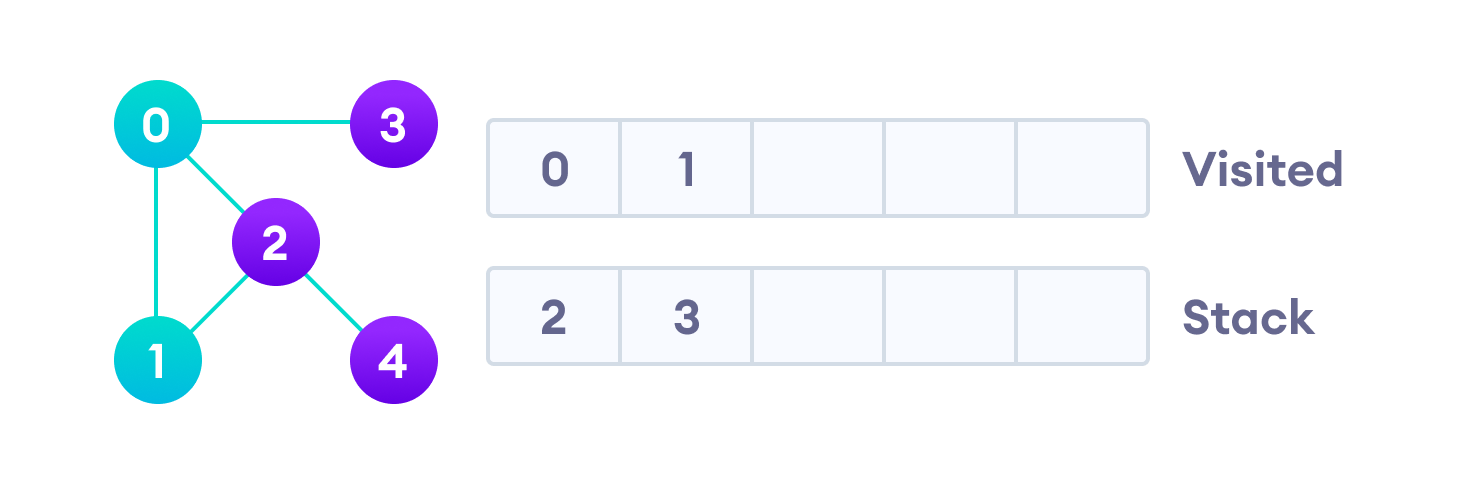
Затем мы берем следующий элемент сверху стека, т.е. к вершину “1”, и переходим к ее соседним вершинам. Поскольку вершина “0” уже пройдена, следующая вершина “2”.
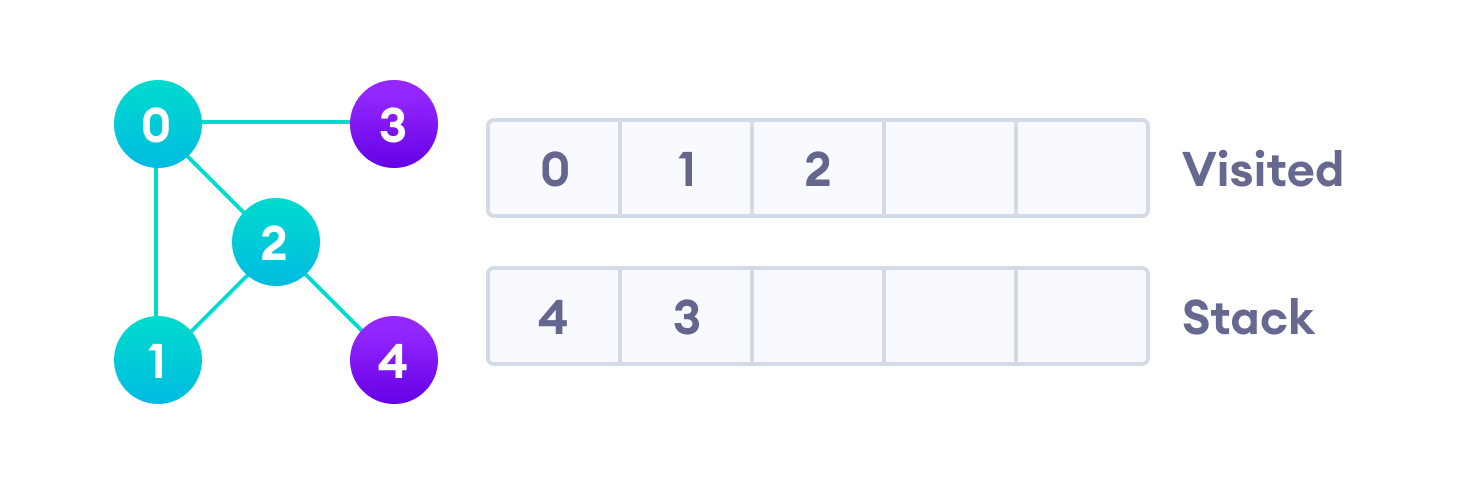
Вершина “2” смежна непройденной вершине “4”, следовательно мы добавляем ее наверх стека и проходим ее.
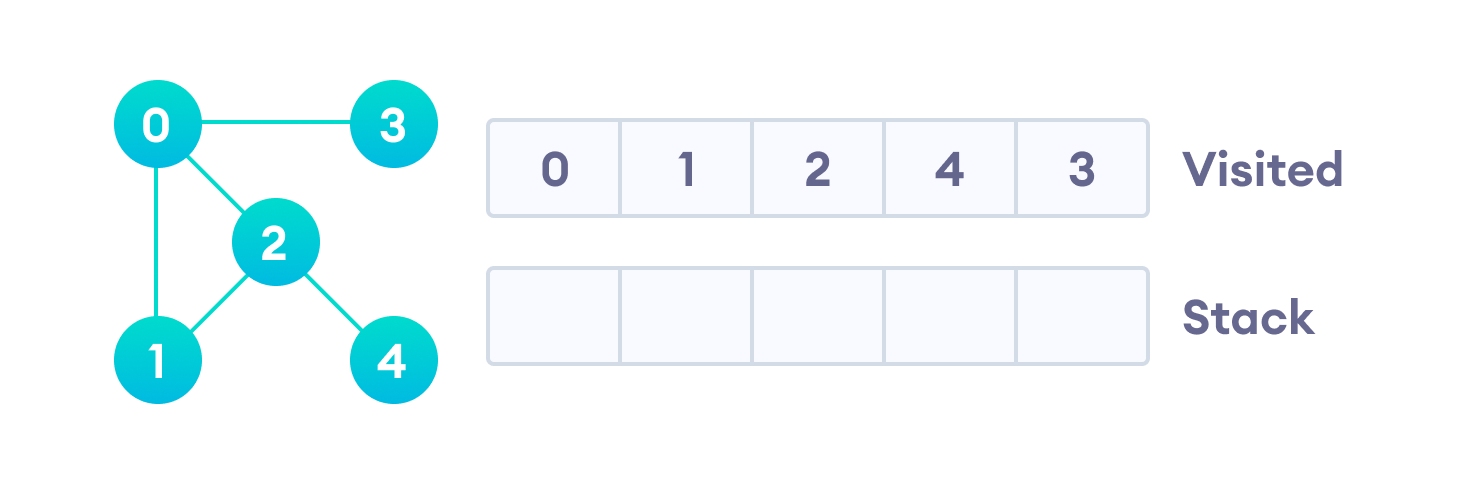
После того, как мы пройдем последний элемент (вершину “3”), в стеке не останется непройденных смежных вершин, и таким образом мы завершили обход графа в глубину.
Псевдокод поиска в глубину (рекурсивная реализация)
Ниже представлен псевдокод для алгоритма поиска в глубину. Обратите внимание, что в функции init() необходимо запускать функцию DFS на каждой вершине. Это связано с тем, что граф может иметь две разные несвязанные части, поэтому для того, чтобы убедиться, что мы покрываем каждую вершину, мы должны запускать алгоритм поиска в глубину на каждой вершине.
DFS(G, u)
u.visited = true
for each v ∈ G.Adj[u]
if v.visited == false
DFS(G,v)
init() {
For each u ∈ G
u.visited = false
For each u ∈ G
DFS(G, u)
}Реализация поиска в глубину на Python, Java и C/C++
Ниже приведены примеры реально кода алгоритма поиска в глубину. Код был упрощен, чтобы мы могли сфокусироваться на самом алгоритме, а не на других деталях.
# Алгоритм поиска в глубину на Python
# Алгоритм
def dfs(graph, start, visited=None):
if visited is None:
visited = set()
visited.add(start)
print(start)
for next in graph[start] - visited:
dfs(graph, next, visited)
return visited
graph = {'0': set(['1', '2']),
'1': set(['0', '3', '4']),
'2': set(['0']),
'3': set(['1']),
'4': set(['2', '3'])}
dfs(graph, '0')// Алгоритм поиска в глубину на Java
import java.util.*;
class Graph {
private LinkedList<Integer> adjLists[];
private boolean visited[];
// Создание графа
Graph(int vertices) {
adjLists = new LinkedList[vertices];
visited = new boolean[vertices];
for (int i = 0; i < vertices; i++)
adjLists[i] = new LinkedList<Integer>();
}
// Добавление ребер
void addEdge(int src, int dest) {
adjLists[src].add(dest);
}
// Алгоритм
void DFS(int vertex) {
visited[vertex] = true;
System.out.print(vertex + " ");
Iterator<Integer> ite = adjLists[vertex].listIterator();
while (ite.hasNext()) {
int adj = ite.next();
if (!visited[adj])
DFS(adj);
}
}
public static void main(String args[]) {
Graph g = new Graph(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 3);
System.out.println("Following is Depth First Traversal");
g.DFS(2);
}
}
// Алгоритм поиска в глубину на C
#include <stdio.h>
#include <stdlib.h>
struct node {
int vertex;
struct node* next;
};
struct node* createNode(int v);
struct Graph {
int numVertices;
int* visited;
// Нам нужен int** для хранения двумерного массива.
// Аналогично, нам нужна структура node** для хранения массива связанных списков.
struct node** adjLists;
};
// Алгоритм
void DFS(struct Graph* graph, int vertex) {
struct node* adjList = graph->adjLists[vertex];
struct node* temp = adjList;
graph->visited[vertex] = 1;
printf("Visited %d n", vertex);
while (temp != NULL) {
int connectedVertex = temp->vertex;
if (graph->visited[connectedVertex] == 0) {
DFS(graph, connectedVertex);
}
temp = temp->next;
}
}
// Создание вершины
struct node* createNode(int v) {
struct node* newNode = malloc(sizeof(struct node));
newNode->vertex = v;
newNode->next = NULL;
return newNode;
}
// Создание графа
struct Graph* createGraph(int vertices) {
struct Graph* graph = malloc(sizeof(struct Graph));
graph->numVertices = vertices;
graph->adjLists = malloc(vertices * sizeof(struct node*));
graph->visited = malloc(vertices * sizeof(int));
int i;
for (i = 0; i < vertices; i++) {
graph->adjLists[i] = NULL;
graph->visited[i] = 0;
}
return graph;
}
// Добавление ребра
void addEdge(struct Graph* graph, int src, int dest) {
// Проводим ребро от начальной вершины ребра графа к конечной вершине ребра графа
struct node* newNode = createNode(dest);
newNode->next = graph->adjLists[src];
graph->adjLists[src] = newNode;
// Проводим ребро из конечной вершины ребра графа в начальную вершину ребра графа
newNode = createNode(src);
newNode->next = graph->adjLists[dest];
graph->adjLists[dest] = newNode;
}
// Выводим граф
void printGraph(struct Graph* graph) {
int v;
for (v = 0; v < graph->numVertices; v++) {
struct node* temp = graph->adjLists[v];
printf("n Adjacency list of vertex %dn ", v);
while (temp) {
printf("%d -> ", temp->vertex);
temp = temp->next;
}
printf("n");
}
}
int main() {
struct Graph* graph = createGraph(4);
addEdge(graph, 0, 1);
addEdge(graph, 0, 2);
addEdge(graph, 1, 2);
addEdge(graph, 2, 3);
printGraph(graph);
DFS(graph, 2);
return 0;
}
// Алгоритм прохода в глубину в C++
#include <iostream>
#include <list>
using namespace std;
class Graph {
int numVertices;
list<int> *adjLists;
bool *visited;
public:
Graph(int V);
void addEdge(int src, int dest);
void DFS(int vertex);
};
// Инициализация графа
Graph::Graph(int vertices) {
numVertices = vertices;
adjLists = new list<int>[vertices];
visited = new bool[vertices];
}
// Добавление ребер
void Graph::addEdge(int src, int dest) {
adjLists[src].push_front(dest);
}
// Алгоритм
void Graph::DFS(int vertex) {
visited[vertex] = true;
list<int> adjList = adjLists[vertex];
cout << vertex << " ";
list<int>::iterator i;
for (i = adjList.begin(); i != adjList.end(); ++i)
if (!visited[*i])
DFS(*i);
}
int main() {
Graph g(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 3);
g.DFS(2);
return 0;
}Сложность алгоритма поиска в глубину
Временная сложность алгоритма поиска в глубину представлена в виде O(V + E), где V — количество вершин, а E — количество ребер.
Пространственная сложность алгоритма равна O(V).
Применения алгоритма
-
Для поиска пути.
-
Для проверки двудольности графа.
-
Для поиска сильно связанных компонентов графа.
-
Для обнаружения циклов в графе.
Приглашаем всех желающих на открытый урок в OTUS «Теория графов. Термины и определения. Основные алгоритмы», регистрация доступна по ссылке.
Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.
Обходы графов
В этой статье рассмотрены основные применения обхода в глубину: топологическая сортировка, нахождение компонент сильной связности, решение задачи 2-SAT, нахождение мостов и точек сочленения, а также построение эйлерова пути и цикла в графе.
Поиск в глубину
Поиском в глубину (англ. depth-first search, DFS) называется рекурсивный алгоритм обхода дерева или графа, начинающий в корневой вершине (в случае графа её может быть выбрана произвольная вершина) и рекурсивно обходящий весь граф, посещая каждую вершину ровно один раз.
const int maxn = 1e5;
bool used[maxn]; // тут будем отмечать посещенные вершины
void dfs(int v) {
used[v] = true;
for (int u : g[v])
if (!used[u])
dfs(v);
}Немного его модифицируем, а именно будем сохранять для каждой вершины, в какой момент мы в неё вошли и в какой вышли — соответствующие массивы будем называть (tin) и (tout).
Как их заполнить: заведем таймер, отвечающий за «время» на текущем состоянии обхода, и будем инкрементировать его каждый раз, когда заходим в новую вершину:
int tin[maxn], tout[maxn];
int t = 0;
void dfs(int v) {
tin[v] = t++;
for (int u : g[v])
if (!used[u])
dfs(u);
tout[v] = t; // иногда счетчик тут тоже увеличивают
}У этих массивов много полезных свойств:
- Вершина (u) является предком (v) (iff tin_v in [tin_u, tout_u)). Эту проверку можно делать за константу.
- Два полуинтервала — ([tin_v, tout_v)) и ([tin_u, tout_u)) — либо не пересекаются, либо один вложен в другой.
- В массиве (tin) есть все числа из промежутка от 0 до (n-1), причём у каждой вершины свой номер.
- Размер поддерева вершины (v) (включая саму вершину) равен (tout_v — tin_v).
- Если ввести нумерацию вершин, соответствующую (tin)-ам, то индексы любого поддерева всегда будут каким-то промежутком в этой нумерации.
Эти свойства часто бывают полезными в задачах на деревья.
Мосты и точки сочленения
Определение. Мостом называется ребро, при удалении которого связный неориентированный граф становится несвязным.
Определение. Точкой сочленения называется врешина, при удалении которой связный неориентированный граф становится несвязным.
Пример задачи, где их интересно искать: дана топология сети (компьютеры и физические соединения между ними) и требуется установить все единые точки отказа — узлы и связи, без которых будут существовать два узла, между которыми не будет пути.
Наивный алгоритм поочередного удаления каждого ребра ((u, v)) и проверки наличия пути (u leadsto v) потребует (O(m^2)) операций. Чтобы научиться находить мосты быстрее, сначала сформулируем несколько утверждений, связанных с обходом в глубину.
Запустим DFS из произвольной вершины. Введем новые виды рёбер:
-
Прямые рёбра — те, по которым были переходы в dfs.
-
Обратные рёбра — то, по которым не было переходов в dfs.
Заметим, что никакое обратное ребро ((u, v)) не может являться мостом: если его удалить, то всё равно будет существовать какой-то путь от (u) до (v), потому что подграф из прямых рёбер является связным деревом.
Значит, остается только проверить все прямые рёбра. Это уже немного лучше — такой алгоритм будет работать за (O(n m)).
Сооптимизировать его до линейного времени (до одного прохода dfs) поможет замечание о том, что обратные рёбра могут вести только «вверх» — к какому-то предку в дереве обхода графа, но не в другие «ветки» — иначе бы dfs увидел это ребро раньше, и оно было бы прямым, а не обратным.
Тогда, чтобы определить, является ли прямое ребро (v to u) мостом, мы можем воспользоваться следующим критерием: глубина (h_v) вершины (v) меньше, чем минимальная глубина всех вершин, соединенных обратным ребром с какой-либо вершиной из поддерева (u).
Для ясности, обозначим эту величину как (d_u), которую можно считать во время обхода по следующей формуле:
[
d_v = min begin{cases}
h_v, &\
d_u, &text{ребро } (v to u) text{ прямое} \
h_u, &text{ребро } (v to u) text{ обратное}
end{cases}
]
Если это условие ((h_v < d_u)) не выполняется, то существует какой-то путь из (u) в какого-то предка (v) или саму (v), не использующий ребро ((v, u)), а в противном случае — наоборот.
const int maxn = 1e5;
bool used[maxn];
int h[maxn], d[maxn];
void dfs(int v, int p = -1) {
used[u] = true;
d[v] = h[v] = (p == -1 ? 0 : h[p] + 1);
for (int u : g[v]) {
if (u != p) {
if (used[u]) // если рябро обратное
d[v] = min(d[v], h[u]);
else { // если рябро прямое
dfs(u, v);
d[v] = min(d[v], d[u]);
if (h[v] < d[v]) {
// ребро (v, u) -- мост
}
}
}
}
}Примечание. Более известен алгоритм, вместо глубин вершин использующий их (tin), но автор считает его чуть более сложным для понимания.
Точки сочленения
Задача поиска точек сочленения не сильно отличается от задачи поиска мостов.
Вершина (v) является точкой сочленения, когда из какого-то её ребёнка (u) нельзя дойти до её предка, не используя ребро ((v, u)). Для конкретного прямого ребра (v to u) этот факт можно проверить так: (h_v leq d_u) (теперь нам нам достаточно нестрогого неравенства, так как если из вершины можно добраться до нее самой, то она все равно будет точкой сочленения).
Используя этот факт, можно оставить алгоритм практически прежним — нужно проверить этот критерий для всех прямых рёбер (v to u):
void dfs(int v, int p = -1) {
used[u] = 1;
d[v] = h[v] = (p == -1 ? 0 : h[p] + 1);
int children = 0; // случай с корнем обработаем отдельно
for (int u : g[u]) {
if (u != p) {
if (used[u])
d[v] = min(d[v], h[u]);
else {
dfs(u, v);
d[v] = min(d[v], d[u]);
if (dp[v] >= tin[u] && p != -1) {
// u -- точка сочленения
}
children++;
}
}
}
if (p == -1 && children > 1) {
// v -- корень и точка сочленения
}
}Единственный крайний случай — это корень, так как в него мы по определению войдём раньше других вершин. Но фикс здесь очень простой — достаточно посмотреть, было ли у него более одной ветви в обходе (если корень удалить, то эти поддеревья станут несвязными между собой).
Топологическая сортировка
Задача топологической сортировки графа звучит так: дан ориентированный граф, нужно упорядочить его вершины в массиве так, чтобы все графа рёбра вели из более ранней вершины в более позднюю.
Это может быть полезно, например, при планировании выполнения связанных задач: вам нужно одеться, в правильном порядке надев шорты (1), штаны (2), ботинки (3), подвернуть штаны (4) — как хипстеры — и завязать шнурки (5).
Во-первых, сразу заметим, что граф с циклом топологически отсортировать не получится — как ни располагай цикл в массиве, все время идти вправо по ребрам цикла не получится.
Во-вторых, верно обратное. Если цикла нет, то его обязательно можно топологически отсортировать — сейчас покажем, как.
Заметим, что вершину, из которой не ведет ни одно ребро, можно всегда поставить последней, а такая вершина в ациклическом графе всегда есть (иначе можно было бы идти по обратным рёбрам бесконечно). Из этого сразу следует конструктивное доказательство: будем итеративно класть в массив вершину, из которой ничего не ведет, и убирать ее из графа. После этого процесса массив надо будет развернуть.
Этот алгоритм проще реализовать, обратив внимание на времена выхода вершин в dfs. Вершина, из которой мы выйдем первой — та, у которой нет новых исходящих ребер. Дальше мы будем выходить только из тех вершин, которые если имеют исходящие ребра, то только в те вершины, из которых мы уже вышли.
Следовательно, достаточно просто выписать вершины в порядке выхода из dfs, а затем полученный список развернуть, и мы получим какую-то из корректных топологических сортировок.
Компоненты сильной связности
Мы только что научились топологически сортировать ациклические графы. А что же делать с циклическими графами? В них тоже иногда требуется найти какую-то структуру.
Для этого можно ввести понятие сильной связности.
Определение. Две вершины ориентированного графа связаны сильно (англ. strongly connected), если существует путь из одной в другую и наоборот. Иными словами, они обе лежат в каком-то цикле.
Понятно, что такое отношение транзитивно: если (a) и (b) сильно связны, и (b) и (c) сильно связны, то (a) и (c) тоже сильно связны. Поэтому все вершины распадаются на компоненты сильной связности — такое разбиение вершин, что внутри одной компоненты все вершины сильно связаны, а между вершинами разных компонент сильной связности нет.
Самый простой пример сильно-связной компоненты — это цикл. Но это может быть и полный граф, или сложное пересечение нескольких циклов.
Часто рассматривают граф, составленный из самих компонент сильной связности, а не индивидуальных вершин. Очевидно, такой граф уже будет ациклическим, и с ним проще работать. Задачу о сжатии каждой компоненты сильной связности в одну вершину называют конденсацией графа, и её решение мы сейчас опишем.
Если мы знаем, какие вершины лежат в каждой компоненте сильной связности, то построить граф конденсации несложно: дальше нужно лишь провести некоторые манипуляции со списками смежности. Поэтому сразу сведем исходную задачу к нахождению самих компонент.
Лемма. Запустим dfs. Пусть (A) и (B) — две различные компоненты сильной связности, и пусть в графе конденсации между ними есть ребро (A to B). Тогда:
[
maxlimits_{a in A}(tout_a) > maxlimits_{bin B}(tout_b)
]
Доказательство. Рассмотрим два случая, в зависимости от того, в какую из компонент dfs зайдёт первым.
Пусть первой была достигнута компонента (A), то есть в какой-то момент времени dfs заходит в некоторую вершину (v) компоненты (A), и при этом все остальные вершины компонент (A) и (B) ещё не посещены. Но так как по условию в графе конденсаций есть ребро (A to B), то из вершины (v) будет достижима не только вся компонента (A), но и вся компонента (B). Это означает, что при запуске из вершины (v) обход в глубину пройдёт по всем вершинам компонент (A) и (B), а, значит, они станут потомками по отношению к (v) в дереве обхода, и для любой вершины (u in A cup B, u ne v) будет выполнено (tout_v] > tout_u), что и утверждалось.
Второй случай проще: из (B) по условию нельзя дойти до (A), а значит, если первой была достигнута (B), то dfs выйдет из всех её вершин ещё до того, как войти в (A).
Из этого факта следует первая часть решения. Отсортируем вершины по убыванию времени выхода (как бы сделаем топологическую сортировку, но на циклическом графе). Рассмотрим компоненту сильной связности первой вершины в сортировке. В эту компоненту точно не входят никакие рёбра из других компонент — иначе нарушилось бы условие леммы, ведь у первой вершины (tout) максимальный . Поэтому, если развернуть все рёбра в графе, то из этой вершины будет достижима своя компонента сильной связности (C^prime), и больше ничего — если в исходном графе не было рёбер из других компонент, то в транспонированном не будет ребер в другие компоненты.
После того, как мы сделали это с первой вершиной, мы можем пойти по топологически отсортированному списку дальше и делать то же самое с вершинами, для которых компоненту связности мы ещё не отметили.
vector<int> g[maxn], t[maxn];
vector<int> order;
bool used[maxn];
int component[maxn];
int cnt_components = 0;
// топологическая сортировка
void dfs1(int v) {
used[v] = true;
for (int u : g[v]) {
if (!used[u])
dfs1(u);
order.push_back(v);
}
// маркировка компонент сильной связности
void dfs2(int v) {
component[v] = cnt_components;
for (int u : t[v])
if (cnt_components[u] == 0)
dfs2(u);
}
// в содержательной части main:
// транспонируем граф
for (int v = 0; v < n; v++)
for (int u : g[v])
t[u].push_back(v);
// запускаем топологическую сортировку
for (int i = 0; i < n; i++)
if (!used[i])
dfs1(i);
// выделяем компоненты
reverse(order.begin(), order.end());
for (int v : order)
if (component[v] == 0)
dfs2(v);TL;DR:
-
Сортируем вершины в порядке убывания времени выхода.
-
Проходимся по массиву вершин в этом порядке, и для ещё непомеченных вершин запускаем dfs на транспонированном графе, помечающий все достижимые вершины номером новой компонентой связности.
После этого номера компонент связности будут топологически отсортированы.
2-SAT
Ликбез. Конъюнкция — это «правильный» термин для логического «И» (обозначается (wedge) или &). Конъюкция возвращает true тогда и только тогда, когда обе переменные true.
Ликбез. Дизъюнкция — это «правильный» термин для логического «ИЛИ» (обозначается (vee) или |). Дизъюнкция возвращает false тогда и только тогда, когда обе переменные false.
Рассмотрим конъюнкцию дизъюнктов, то есть «И» от «ИЛИ» от каких-то перемений или их отрицаний. Например, такое выражение:
(a | b) & (!c | d) & (!a | !b)Если буквами: (А ИЛИ B) И (НЕ C ИЛИ D) И (НЕ A ИЛИ НЕ B).
Можно показать, что любую логическую формулу можно представить в таком виде.
Задача satisfiability (SAT) заключается в том, чтобы найти такие значения переменных, при которых выражение становится истинным, или сказать, что такого набора значений нет. Для примера выше такими значениями являются a=1, b=0, c=0, d=1 (убедитесь, что каждая скобка стала true).
В случае произвольных формул эта задача быстро не решается. Мы же хотим решить её частный случай — когда у нас в каждой скобке ровно две переменные (2-SAT).
Казалось бы — причем тут графы? Заметим, что выражение (a , | , b) эквивалентно (!a rightarrow b ,| , !b rightarrow a). Здесь «(rightarrow)» означает импликацию («если (a) верно, то (b) тоже верно»). С помощью это подстановки приведем выражение к другому виду — импликативному.
Затем построим граф импликаций: для каждой переменной в графе будет по две вершины, (обозначим их через (x) и (!x)), а рёбра в этом графе будут соответствовать импликациям.
Заметим, что если для какой-то переменной (x) выполняется, что из (x) достижимо (!x), а из (!x) достижимо (x), то задача решения не имеет. Действительно: какое бы значение для переменной (x) мы бы ни выбрали, мы всегда придём к противоречию — что должно быть выбрано и обратное ему значение.
Оказывается, что это условие является не только достаточным, но и необходимым. Доказательством этого факта служит описанный ниже алгоритм.
Переформулируем данный критерий в терминах теории графов. Если из одной вершины достижима вторая и наоборот, то эти две вершины находятся в одной компоненте сильной связности. Тогда критерий существования решения звучит так: для того, чтобы задача 2-SAT имела решение, необходимо и достаточно, чтобы для любой переменной (x) вершины (x) и (!x) находились в разных компонентах сильной связности графа импликаций.
Пусть решение существует, и нам надо его найти. Заметим, что, несмотря на то, что решение существует, для некоторых переменных может выполняться, что из (x) достижимо (!x) или из (!x) достижимо (x) (но не одновременно). В таком случае выбор одного из значений переменной (x) будет приводить к противоречию, в то время как выбор другого — не будет. Научимся выбирать из двух значений то, которое не приводит к возникновению противоречий. Сразу заметим, что, выбрав какое-либо значение, мы должны запустить из него обход в глубину/ширину и пометить все значения, которые следуют из него, т.е. достижимы в графе импликаций. Соответственно, для уже помеченных вершин никакого выбора между (x) и (!x) делать не нужно, для них значение уже выбрано и зафиксировано. Нижеописанное правило применяется только к непомеченным ещё вершинам.
Утверждается следующее. Пусть (space{rm comp}[V]) обозначает номер компоненты сильной связности, которой принадлежит вершина (V), причём номера упорядочены в порядке топологической сортировки компонент сильной связности в графе компонентов (т.е. более ранним в порядке топологической сортировки соответствуют большие номера: если есть путь из (v) в (w), то (space{rm comp}[v] leq space{rm comp}[w])). Тогда, если (space{rm comp}[x] < space{rm comp}[!x]), то выбираем значение !x, иначе выбираем x.
Докажем, что при таком выборе значений мы не придём к противоречию. Пусть, для определённости, выбрана вершина (x) (случай, когда выбрана вершина (!x), доказывается также).
Во-первых, докажем, что из (x) не достижимо (!x). Действительно, так как номер компоненты сильной связности (space{rm comp}[x]) больше номера компоненты (space{rm comp}[!x]) , то это означает, что компонента связности, содержащая (x), расположена левее компоненты связности, содержащей (!x), и из первой никак не может быть достижима последняя.
Во-вторых, докажем, что из любой вершины (y), достижимой из (x) недостижима (!y). Докажем это от противного. Пусть из (x) достижимо (y), а из (y) достижимо (!y). Так как из (x) достижимо (y), то, по свойству графа импликаций, из (!y) будет достижимо (!x). Но, по предположению, из (y) достижимо (!y). Тогда мы получаем, что из (x) достижимо (!x), что противоречит условию, что и требовалось доказать.
Итак, мы построили алгоритм, который находит искомые значения переменных в предположении, что для любой переменной (x) вершины (x) и (!x) находятся в разных компонентах сильной связности. Выше показали корректность этого алгоритма. Следовательно, мы одновременно доказали указанный выше критерий существования решения.
Эйлеров цикл
Определение. Эйлеров путь — это путь в графе, проходящий через все его рёбра.
Определение. Эйлеров цикл — это эйлеров путь, являющийся циклом.
Для простоты в обоих случаях будем считать, что граф неориентированный.
Также существует понятие гамильтонова пути и цикла — они посещают все вершины по разу, а не рёбра. Нахождение гамильтонова цикла (задача коммивояжера, англ. travelling salesman problem) — одна из самых известных NP-полных задач, в то время как нахождение эйлерового цика решается за линейное время — и мы сейчас покажем, как.
Теорема. Эйлеров цикл существует тогда и только тогда, когда степени всех вершин чётны.
Доказательство. Необходимость показывается так: можно просто взять эйлеров цикл и ориентировать все его ребра в порядке обхода. Тогда из каждой вершины будет выходить столько же рёбер, сколько входить, а значит степень у всех вершин исходного неориентированного графа была четной.
Достаточность докажем конструктивно — предъявим алгоритм нахождения.
const int maxn = 1e5;
set<int> g[maxn];
void euler(int v) {
while (!g[v].empty()) {
u = *g[v].begin();
g[v].erase(g[v].begin());
dfs(u);
}
cout << v << " ";
}Если условие на четность степеней вершин выполняется, то этот алгоритм действительно выводит эйлеров цикл, то есть последовательность из ((m+1)) вершин, между соседними есть связи.
Следствие. Эйлеров путь существует тогда и только тогда, когда количество вершин с нечётными степенями не превосходит 2.
Кстати, аналогичная теорема есть и для ориентированного графа (можете сами попытаться сформулировать).
Доказать это можно например через лемму о рукопожатиях.
Как теперь мы будем решать задачу нахождения цикла в предположении, что он точно есть. Давайте запустимся из произвольной вершины, пройдем по любому ребру и удалим его.
void euler(int v){
stack >s;
s.push({v, -1});
while (!s.empty()) {
v = s.top().first;
int x = s.top().second;
for (int i = 0; i < g[v].size(); i++){
pair e = g[v][i];
if(!u[e.second]){
u[e.second]=1;
s.push(e);
break;
}
}
if (v == s.top().first) {
if (~x) {
p.push_back(x);
}
s.pop();
}
}
}Упражнение. Сформулируйте и докажите аналогичные утверждения для случая ориентированного графа.
- 1. Алгоритм DFS
- 2. Пример DFS
- 3. Псевдокод DFS (рекурсивная реализация)
- 4. Код DFS
- 5. DFS в C
- 6. Depth First Search (DFS) в C++
- 7. DFS Java код (Java code)
- 8. DFS в Python
Обход
означает посещение всех узлов графа.
«Обход в глубину» или «Поиск в глубину»
— это рекурсивный алгоритм поиска всех вершин графа или древовидной структуры данных. В этой статье, с помощью приведенных ниже примеров, вы узнаете: алгоритм DFS, псевдокод DFS и код алгоритма «поиска в глубину» с реализацией в программах на C ++, C, Java и Python.
Алгоритм DFS
Стандартная реализация DFS помещает каждую вершину графа в одну из двух категорий:
- Посещенные.
- Не посещенные.
Цель алгоритма
— пометить каждую вершину, как посещенную, избегая циклов.
Алгоритм DFS работает следующим образом:
- Начните с размещения любой вершины графа на вершине стека.
- Возьмите верхний элемент стека и добавьте его в список посещенных.
- Создайте список смежных узлов этой вершины. Добавьте те, которых нет в списке посещенных, в начало стека.
- Продолжайте повторять шаги 2 и 3, пока стек не станет пустым.
Пример DFS
Давайте посмотрим, как алгоритм «поиска в глубину» работает на примере. Мы используем неориентированный граф с 5 вершинами.
Мы начинаем с вершины 0, алгоритм DFS начинается с помещения его в список посещенных и размещения всех смежных вершин в стеке.
Затем мы посещаем элемент в верхней части стека, то есть 1, и переходим к смежным узлам. Так как 0 мы уже посетили, вместо этого посещаем 2.
У вершины 2 есть не посещенная смежная вершина 4, поэтому мы добавляем ее в верхнюю часть стека и посещаем.
После того, как мы посетим последний элемент 3, у него нет не посещенных смежных узлов. На этом мы завершим первый «обход в глубину» графа.
Псевдокод DFS (рекурсивная реализация)
Псевдокод для DFS показан ниже. Обратите внимание, что в функции
init()
мы запускаем функцию DFS на каждом узле. Это связано с тем, что граф может иметь две разные несвязанные части, поэтому, чтобы убедиться, что мы покрываем каждую вершину, мы также можем запустить алгоритм DFS на каждом узле.
DFS(G, u) u.visited = true for each v ∈ G.Adj[u] if v.visited == false DFS(G,v) init() { For each u ∈ G u.visited = false For each u ∈ G DFS(G, u) }Код DFS
Код для алгоритма «поиска в глубину» с примером показан ниже. Код был упрощен, поэтому мы можем сосредоточиться на алгоритме, а не на других деталях.
DFS в C
#include <stdio.h> #include <stdlib.h> struct node { int vertex; struct node* next; }; struct node* createNode(int v); struct Graph { int numVertices; int* visited; struct node** adjLists; // we need int** to store a two dimensional array. Similary, we need struct node** to store an array of Linked lists }; struct Graph* createGraph(int); void addEdge(struct Graph*, int, int); void printGraph(struct Graph*); void DFS(struct Graph*, int); int main() { struct Graph* graph = createGraph(4); addEdge(graph, 0, 1); addEdge(graph, 0, 2); addEdge(graph, 1, 2); addEdge(graph, 2, 3); printGraph(graph); DFS(graph, 2); return 0; } void DFS(struct Graph* graph, int vertex) { struct node* adjList = graph->adjLists[vertex]; struct node* temp = adjList; graph->visited[vertex] = 1; printf("Visited %d n", vertex); while(temp!=NULL) { int connectedVertex = temp->vertex; if(graph->visited[connectedVertex] == 0) { DFS(graph, connectedVertex); } temp = temp->next; } } struct node* createNode(int v) { struct node* newNode = malloc(sizeof(struct node)); newNode->vertex = v; newNode->next = NULL; return newNode; } struct Graph* createGraph(int vertices) { struct Graph* graph = malloc(sizeof(struct Graph)); graph->numVertices = vertices; graph->adjLists = malloc(vertices * sizeof(struct node*)); graph->visited = malloc(vertices * sizeof(int)); int i; for (i = 0; i < vertices; i++) { graph->adjLists[i] = NULL; graph->visited[i] = 0; } return graph; } void addEdge(struct Graph* graph, int src, int dest) { // Add edge from src to dest struct node* newNode = createNode(dest); newNode->next = graph->adjLists[src]; graph->adjLists[src] = newNode; // Add edge from dest to src newNode = createNode(src); newNode->next = graph->adjLists[dest]; graph->adjLists[dest] = newNode; } void printGraph(struct Graph* graph) { int v; for (v = 0; v < graph->numVertices; v++) { struct node* temp = graph->adjLists[v]; printf("n Adjacency list of vertex %dn ", v); while (temp) { printf("%d -> ", temp->vertex); temp = temp->next; } printf("n"); } }Depth First Search (DFS) в C++
#include <iostream> #include <list> using namespace std; class Graph { int numVertices; list *adjLists; bool *visited; public: Graph(int V); void addEdge(int src, int dest); void DFS(int vertex); }; Graph::Graph(int vertices) { numVertices = vertices; adjLists = new list[vertices]; visited = new bool[vertices]; } void Graph::addEdge(int src, int dest) { adjLists[src].push_front(dest); } void Graph::DFS(int vertex) { visited[vertex] = true; list adjList = adjLists[vertex]; cout << vertex << " "; list::iterator i; for(i = adjList.begin(); i != adjList.end(); ++i) if(!visited[*i]) DFS(*i); } int main() { Graph g(4); g.addEdge(0, 1); g.addEdge(0, 2); g.addEdge(1, 2); g.addEdge(2, 3); g.DFS(2); return 0; }DFS Java код (Java code)
import java.io.*; import java.util.*; class Graph { private int numVertices; private LinkedList<Integer> adjLists[]; private boolean visited[]; Graph(int vertices) { numVertices = vertices; adjLists = new LinkedList[vertices]; visited = new boolean[vertices]; for (int i = 0; i < vertices; i++) adjLists[i] = new LinkedList<Integer>(); } void addEdge(int src, int dest) { adjLists[src].add(dest); } void DFS(int vertex) { visited[vertex] = true; System.out.print(vertex + " "); Iterator ite = adjLists[vertex].listIterator(); while (ite.hasNext()) { int adj = ite.next(); if (!visited[adj]) DFS(adj); } } public static void main(String args[]) { Graph g = new Graph(4); g.addEdge(0, 1); g.addEdge(0, 2); g.addEdge(1, 2); g.addEdge(2, 3); System.out.println("Following is Depth First Traversal"); g.DFS(2); } }DFS в Python
def dfs(graph, start, visited=None): if visited is None: visited = set() visited.add(start) print(start) for next in graph[start] - visited: dfs(graph, next, visited) return visited graph = {'0': set(['1', '2']), '1': set(['0', '3', '4']), '2': set(['0']), '3': set(['1']), '4': set(['2', '3'])} dfs(graph, '0')
From Wikipedia, the free encyclopedia
|
Order in which the nodes are visited |
|
| Class | Search algorithm |
|---|---|
| Data structure | Graph |
| Worst-case performance |  for explicit graphs traversed without repetition, for explicit graphs traversed without repetition,  for implicit graphs with branching factor b searched to depth d for implicit graphs with branching factor b searched to depth d |
| Worst-case space complexity |  if entire graph is traversed without repetition, O(longest path length searched) = if entire graph is traversed without repetition, O(longest path length searched) =  for implicit graphs without elimination of duplicate nodes for implicit graphs without elimination of duplicate nodes |
Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking. Extra memory, usually a stack, is needed to keep track of the nodes discovered so far along a specified branch which helps in backtracking of the graph.
A version of depth-first search was investigated in the 19th century by French mathematician Charles Pierre Trémaux[1] as a strategy for solving mazes.[2][3]
Properties[edit]
The time and space analysis of DFS differs according to its application area. In theoretical computer science, DFS is typically used to traverse an entire graph, and takes time 



For applications of DFS in relation to specific domains, such as searching for solutions in artificial intelligence or web-crawling, the graph to be traversed is often either too large to visit in its entirety or infinite (DFS may suffer from non-termination). In such cases, search is only performed to a limited depth; due to limited resources, such as memory or disk space, one typically does not use data structures to keep track of the set of all previously visited vertices. When search is performed to a limited depth, the time is still linear in terms of the number of expanded vertices and edges (although this number is not the same as the size of the entire graph because some vertices may be searched more than once and others not at all) but the space complexity of this variant of DFS is only proportional to the depth limit, and as a result, is much smaller than the space needed for searching to the same depth using breadth-first search. For such applications, DFS also lends itself much better to heuristic methods for choosing a likely-looking branch. When an appropriate depth limit is not known a priori, iterative deepening depth-first search applies DFS repeatedly with a sequence of increasing limits. In the artificial intelligence mode of analysis, with a branching factor greater than one, iterative deepening increases the running time by only a constant factor over the case in which the correct depth limit is known due to the geometric growth of the number of nodes per level.
DFS may also be used to collect a sample of graph nodes. However, incomplete DFS, similarly to incomplete BFS, is biased towards nodes of high degree.
Example[edit]
Animated example of a depth-first search
For the following graph:

a depth-first search starting at the node A, assuming that the left edges in the shown graph are chosen before right edges, and assuming the search remembers previously visited nodes and will not repeat them (since this is a small graph), will visit the nodes in the following order: A, B, D, F, E, C, G. The edges traversed in this search form a Trémaux tree, a structure with important applications in graph theory.
Performing the same search without remembering previously visited nodes results in visiting the nodes in the order A, B, D, F, E, A, B, D, F, E, etc. forever, caught in the A, B, D, F, E cycle and never reaching C or G.
Iterative deepening is one technique to avoid this infinite loop and would reach all nodes.
Output of a depth-first search[edit]
The four types of edges defined by a spanning tree
The result of a depth-first search of a graph can be conveniently described in terms of a spanning tree of the vertices reached during the search. Based on this spanning tree, the edges of the original graph can be divided into three classes: forward edges, which point from a node of the tree to one of its descendants, back edges, which point from a node to one of its ancestors, and cross edges, which do neither. Sometimes tree edges, edges which belong to the spanning tree itself, are classified separately from forward edges. If the original graph is undirected then all of its edges are tree edges or back edges.
Vertex orderings[edit]
It is also possible to use depth-first search to linearly order the vertices of a graph or tree. There are four possible ways of doing this:
- A preordering is a list of the vertices in the order that they were first visited by the depth-first search algorithm. This is a compact and natural way of describing the progress of the search, as was done earlier in this article. A preordering of an expression tree is the expression in Polish notation.
- A postordering is a list of the vertices in the order that they were last visited by the algorithm. A postordering of an expression tree is the expression in reverse Polish notation.
- A reverse preordering is the reverse of a preordering, i.e. a list of the vertices in the opposite order of their first visit. Reverse preordering is not the same as postordering.
- A reverse postordering is the reverse of a postordering, i.e. a list of the vertices in the opposite order of their last visit. Reverse postordering is not the same as preordering.
For binary trees there is additionally in-ordering and reverse in-ordering.
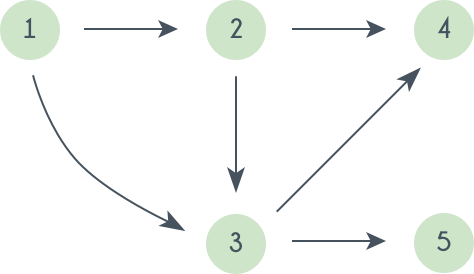
For example, when searching the directed graph below beginning at node A, the sequence of traversals is either A B D B A C A or A C D C A B A (choosing to first visit B or C from A is up to the algorithm). Note that repeat visits in the form of backtracking to a node, to check if it has still unvisited neighbors, are included here (even if it is found to have none). Thus the possible preorderings are A B D C and A C D B, while the possible postorderings are D B C A and D C B A, and the possible reverse postorderings are A C B D and A B C D.
Reverse postordering produces a topological sorting of any directed acyclic graph. This ordering is also useful in control-flow analysis as it often represents a natural linearization of the control flows. The graph above might represent the flow of control in the code fragment below, and it is natural to consider this code in the order A B C D or A C B D but not natural to use the order A B D C or A C D B.
if (A) then {
B
} else {
C
}
D
Pseudocode[edit]
Input:
Output:
A recursive implementation of DFS:[5]
procedure DFS(G, v) is
label v as discovered
for all directed edges from v to w that are in G.adjacentEdges(v) do
if vertex w is not labeled as discovered then
recursively call DFS(G, w)
A non-recursive implementation of DFS with worst-case space complexity 
procedure DFS_iterative(G, v) is
let S be a stack
S.push(v)
while S is not empty do
v = S.pop()
if v is not labeled as discovered then
label v as discovered
for all edges from v to w in G.adjacentEdges(v) do
S.push(w)
These two variations of DFS visit the neighbors of each vertex in the opposite order from each other: the first neighbor of v visited by the recursive variation is the first one in the list of adjacent edges, while in the iterative variation the first visited neighbor is the last one in the list of adjacent edges. The recursive implementation will visit the nodes from the example graph in the following order: A, B, D, F, E, C, G. The non-recursive implementation will visit the nodes as: A, E, F, B, D, C, G.
The non-recursive implementation is similar to breadth-first search but differs from it in two ways:
- it uses a stack instead of a queue, and
- it delays checking whether a vertex has been discovered until the vertex is popped from the stack rather than making this check before adding the vertex.
If G is a tree, replacing the queue of the breadth-first search algorithm with a stack will yield a depth-first search algorithm. For general graphs, replacing the stack of the iterative depth-first search implementation with a queue would also produce a breadth-first search algorithm, although a somewhat nonstandard one.[7]
Another possible implementation of iterative depth-first search uses a stack of iterators of the list of neighbors of a node, instead of a stack of nodes. This yields the same traversal as recursive DFS.[8]
procedure DFS_iterative(G, v) is
let S be a stack
label v as discovered
S.push(iterator of G.adjacentEdges(v))
while S is not empty do
if S.peek().hasNext() then
w = S.peek().next()
if w is not labeled as discovered then
label w as discovered
S.push(iterator of G.adjacentEdges(w))
else
S.pop()
Applications[edit]
Randomized algorithm similar to depth-first search used in generating a maze.
Algorithms that use depth-first search as a building block include:
- Finding connected components.
- Topological sorting.
- Finding 2-(edge or vertex)-connected components.
- Finding 3-(edge or vertex)-connected components.
- Finding the bridges of a graph.
- Generating words in order to plot the limit set of a group.
- Finding strongly connected components.
- Determining whether a species is closer to one species or another in a phylogenetic tree.
- Planarity testing.[9][10]
- Solving puzzles with only one solution, such as mazes. (DFS can be adapted to find all solutions to a maze by only including nodes on the current path in the visited set.)
- Maze generation may use a randomized DFS.
- Finding biconnectivity in graphs.
- Succession to the throne shared by the Commonwealth realms.[11]
Complexity[edit]
The computational complexity of DFS was investigated by John Reif. More precisely, given a graph 

A depth-first search ordering (not necessarily the lexicographic one), can be computed by a randomized parallel algorithm in the complexity class RNC.[14] As of 1997, it remained unknown whether a depth-first traversal could be constructed by a deterministic parallel algorithm, in the complexity class NC.[15]
See also[edit]
- Tree traversal (for details about pre-order, in-order and post-order depth-first traversal)
- Breadth-first search
- Iterative deepening depth-first search
- Search game
Notes[edit]
- ^ Charles Pierre Trémaux (1859–1882) École polytechnique of Paris (X:1876), French engineer of the telegraph
in Public conference, December 2, 2010 – by professor Jean Pelletier-Thibert in Académie de Macon (Burgundy – France) – (Abstract published in the Annals academic, March 2011 – ISSN 0980-6032) - ^ Even, Shimon (2011), Graph Algorithms (2nd ed.), Cambridge University Press, pp. 46–48, ISBN 978-0-521-73653-4.
- ^ Sedgewick, Robert (2002), Algorithms in C++: Graph Algorithms (3rd ed.), Pearson Education, ISBN 978-0-201-36118-6.
- ^ Cormen, Thomas H., Charles E. Leiserson, and Ronald L. Rivest. p.606
- ^ Goodrich and Tamassia; Cormen, Leiserson, Rivest, and Stein
- ^ Page 93, Algorithm Design, Kleinberg and Tardos
- ^ «Stack-based graph traversal ≠ depth first search». 11011110.github.io. Retrieved 2020-06-10.
- ^ Sedgewick, Robert (2010). Algorithms in Java. Addison-Wesley. ISBN 978-0-201-36121-6. OCLC 837386973.
- ^ Hopcroft, John; Tarjan, Robert E. (1974), «Efficient planarity testing» (PDF), Journal of the Association for Computing Machinery, 21 (4): 549–568, doi:10.1145/321850.321852, hdl:1813/6011, S2CID 6279825.
- ^ de Fraysseix, H.; Ossona de Mendez, P.; Rosenstiehl, P. (2006), «Trémaux Trees and Planarity», International Journal of Foundations of Computer Science, 17 (5): 1017–1030, arXiv:math/0610935, Bibcode:2006math…..10935D, doi:10.1142/S0129054106004248, S2CID 40107560.
- ^ Baccelli, Francois; Haji-Mirsadeghi, Mir-Omid; Khezeli, Ali (2018), «Eternal family trees and dynamics on unimodular random graphs», in Sobieczky, Florian (ed.), Unimodularity in Randomly Generated Graphs: AMS Special Session, October 8–9, 2016, Denver, Colorado, Contemporary Mathematics, vol. 719, Providence, Rhode Island: American Mathematical Society, pp. 85–127, arXiv:1608.05940, doi:10.1090/conm/719/14471, MR 3880014, S2CID 119173820; see Example 3.7, p. 93
- ^ Reif, John H. (1985). «Depth-first search is inherently sequential». Information Processing Letters. 20 (5): 229–234. doi:10.1016/0020-0190(85)90024-9.
- ^ Mehlhorn, Kurt; Sanders, Peter (2008). Algorithms and Data Structures: The Basic Toolbox (PDF). Springer. Archived (PDF) from the original on 2015-09-08.
- ^ Aggarwal, A.; Anderson, R. J. (1988), «A random NC algorithm for depth first search», Combinatorica, 8 (1): 1–12, doi:10.1007/BF02122548, MR 0951989, S2CID 29440871.
- ^ Karger, David R.; Motwani, Rajeev (1997), «An NC algorithm for minimum cuts», SIAM Journal on Computing, 26 (1): 255–272, CiteSeerX 10.1.1.33.1701, doi:10.1137/S0097539794273083, MR 1431256.
References[edit]
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 22.3: Depth-first search, pp. 540–549.
- Goodrich, Michael T.; Tamassia, Roberto (2001), Algorithm Design: Foundations, Analysis, and Internet Examples, Wiley, ISBN 0-471-38365-1
- Kleinberg, Jon; Tardos, Éva (2006), Algorithm Design, Addison Wesley, pp. 92–94
- Knuth, Donald E. (1997), The Art of Computer Programming Vol 1. 3rd ed, Boston: Addison-Wesley, ISBN 0-201-89683-4, OCLC 155842391
External links[edit]
- Open Data Structures — Section 12.3.2 — Depth-First-Search, Pat Morin
- C++ Boost Graph Library: Depth-First Search
- Depth-First Search Animation (for a directed graph)
- Depth First and Breadth First Search: Explanation and Code
- QuickGraph[permanent dead link], depth first search example for .Net
- Depth-first search algorithm illustrated explanation (Java and C++ implementations)
- YAGSBPL – A template-based C++ library for graph search and planning
Графы — определения, деревья, хранение и поиск в глубину
Основные определения
Формальное определение:
Графом $G$ называется пара множеств $G = (V, E$, где $V(G)$ — непустое конечное множество элементов, называемых вершинами графа, а $E$ — множество пар элементов из $V$ (необязательно различных), называемых ребрами графа. $E = {(u , v) | u, v in V}$ — множество ребер графа $G$, состоящее из пар вершин $(u, v)$. Ребро $(u, v)$ соединяет вершины $u$ и $v$.
Простое определение:
Граф — это набор вершин (точек) и соединяющих их отрезков (рёбер).
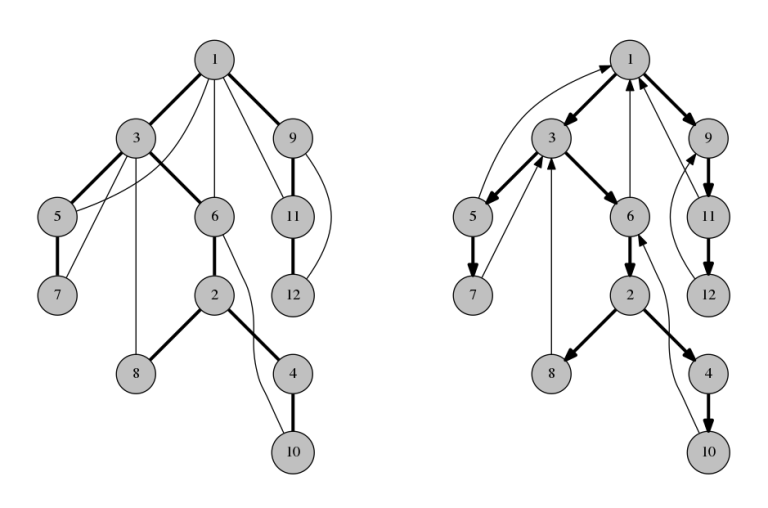
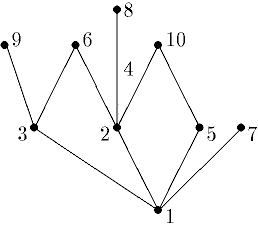
Две вершины, соединенные ребром, называют смежными вершинами. Обычно в задачах $N$ — количество вершин, а $M$ — ребер. Количество ребер, исходящее из вершины называют степенью вершины $d(v)$. Для вершины $a$ ребро $(a, b)$ называется инцидентным ей. На рисунке ниже вершине 8 инцидентно только ребро (4, 8), а вершине 10 ребра (2, 10) и (5, 10).
Теоретическое задание
Назовите степень 1-ой и 6-ой вершины и какие ребра инциденты им.
Если какие-то две вершины соединены более, чем одним ребром, то говорят, что граф содержит кратные ребра. Если ребро соединяет вершину саму с собой, то такое ребро называют петлей.
Простой граф не содержит петель и кратных ребер. Если не сказано ничего про наличие петель и кратных ребер, мы будем всегда считать, что граф простой.
Теоретическое задание
Сколько может быть рёбер в простом графе в $N$ вершинами?
Теоретическое задание
Найдите цикл размера 4 и петлю в этом непростом графе.
Также часто рассматривают ориентированные графы — это графы, у которых ребра имеют направление, а иначе граф – неориентированный.
Хранение графа в программе
Чаще всего в задачах по программмированию вершины графа — это числа от $0$ до $N-1$, чтобы удобно было обращаться к ним как к индексам в разных массивах.
Также чаще всего вам дают считать граф как просто список всех рёбер в нем (но не всегда, конечно). Как оптимально считать и сохранить граф? Есть 3 способа.
Для графа существуют несколько основных способов хранения:
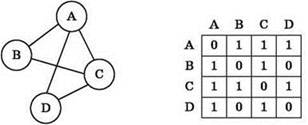
- Матрица смежности. Давайте хранить двумерную матрицу $A_{nn}$, где для данного графа G верно, что если $A_{ij}$ = 1, то две вершины $i$ и $j$ являются смежными, иначе вершины $i$ и $j$ смежными не являются.
Мы храним для каждой из $N$ вершин информацию, есть ли ребро в другие вершины, то есть суммарно мы храним $N^2$ ячеек, а следовательно асимптотика по памяти — $O(N^2)$.
- Список смежности. Давайте для каждой из $N$ вершин хранить все смежные с ней, для этого нам потребуется любая динамическая структура, например vector в с++.
// как сделать список по матрице
vector<vector<int> > g(n);
for (int i = 0; i < n; ++i){
for (int j = 0;j < n;++j){
cin >> a;
if (a) g[i].push_back(j);
}
}
// список по списку ребер
cin >> n >> m;
vector<vector<int> > g(n);
for (int i = 0; i < m; ++i){
cin >> v1 >> v2;
g[v1].push_back(v2);
g[v2].push_back(v1);
}
Здесь асимптотика по памяти и времени считывания — $O(N + M)$, так как мы храним для каждой вершины, куда есть ребра, то есть $2 M$ ребер, а также суммарно $N$ векторов.
Плотные графы, имеющие большое количество ребер следует хранить при помощи матрицы смежности, а разреженные графы, имеющие малое количество ребер, оптимальнее при помощи списка.
- Список рёбер. Иногда граф явно вообще не требуется, а хватает хранить просто список ребер, который нам дают на вход.
Заметьте, что все эти способы обощаются на случай ориентированных графов — при этом матрица смежности становится неориетированной: если есть ребро из вершины $i$ в вершину $j$, то сделаем $A_{ij} = 1$, а $A_{ji} = 0$, если только нет обратного ребра тоже. А в списке смежности в ориентированном случае при считывании ребра $(u, v)$ будем добавлять только $v$ в список соседей $u$, но не наоборот.
Практическое задание
Для окончательного закрепления темы советую решить первые 2 задачи.
Деревья
Дерево — это связный неориентированный граф без циклов.
Свойства дерева:
- У дерева с хотя бы 2 вершинами всегда есть висячая вершина — вершина степени 1.
Действительно, если начать из любой вершины идти по непосещенным ранее вершинам, то в какой-то момент мы прекратим это делать, ведь граф конечный. При этом если из этой вершины не может быть ребер в непосещенные вершины — ведь тогда прекращать рано, и не может быть ребер в посещенные ребра (помимо предыдущей) — ведь тогда есть цикл. А значит, есть ребро только в предыдущую вершину, значит степень равна 1.
- У дерева с хотя бы 2 вершинами всегда есть две висячие вершины.
Действительно, если предыдущий алгоритм начать из висячей вершины, то мы уткнемся в другую висячую вершину.
- У дерева с $N$ вершинами всегда ровно $N-1$ ребро.
Давайте отрезать от дерева его висячие вершины — при этом число вершин уменьшится на один, число ребер тоже уменьшится на один, а граф останется деревом. Раз граф остается деревом, у него все время будет висячая вершина, пока $N > 1$. В какой-то момент останется только одна вершина и ноль ребер. Раз мы отрезали столько же вершин, сколько ребер, и получили 1 вершину и 0 ребер, значит изначально вершин было ровно на одну больше.
- Между любыми двумя вершинами в дереве есть ровно один простой путь.
Действительно, если их два, то в графе есть цикл. Быть ноль их не может — ведь граф связный.
- Дерево — это минимальный по числу рёбер связный граф на $N$ вершинах.
Действительно, если есть связный граф, в котором меньше, чем $N-1$ ребро, то давайте уберем из его цикла ребро. Граф при этом остается связным, а число ребер уменьшается. Давайте повторять это, пока в какой-то момент циклов в графе не будет, а значит осталось дерево. Но мы уже доказали, что в дереве $N-1$ ребро, это противоречие, ведь у нас сначала было меньше ребер, а мы еще и удалили сколько-то.
DFS (Алгоритм обхода графа в глубину)
Обход в глубину — простой, но многофункциональный алгоритм обхода графа по ребрам. Самое главное, что он может — это проверить, какие вершины достижимы из данной.
При обходе графа мы используем вспомогательный массив used, в котором храним 1, если вершина была посещена или 0 иначе. В начале мы считаем, что все вершины не использовались, затем мы выбираем одну вершину, помечаем ее посещенной и запускаемся рекурсивно из всех ее соседей, тогда мы посетим все вершины, которые достижимы из данной, если же остались вершины с used = 0 значит они недостижимы.
Красивая визуализация: https://visualgo.net/en/dfsbfs
void dfs (int v) {
used[v] = 1;
for (auto to : g[v]) {
if (!used[to]) {
dfs(to);
}
}
}
Давайте оценим сложность алгоритма. Так как мы проверяем, что вершина еще не использовалась, то всего мы пройдет каждую вершину 1 раз, но при этом и ребро между двумя вершинами, мы рассматриваем только когда рассматривается один конец, то есть мы просмотрим каждое ребро не более одного раза, суммарно получаем оценку $O(N + M)$.
Практическое задание
Задачи 3-5 в контесте.
Поиск компонент связности графа
Путем в графе называется последовательность вершин $v_i in 𝑉$, $i = 1…k$ таких, что две последовательные вершины в пути соединены ребром, $k$ — длина пути. Граф называется связным, если для любых двух его вершин существует путь между ними. Граф всегда можно разбить на непересекающиеся связные подмножества (возможно одно), между которыми рёбер нет, они называются компонентами связности.
Поиск в глубину dfs будет обходить ту компоненту связности, из вершины которой, он был вызван. Поэтому для поиска компонент связности можно каждый раз вызываться из любой непосещенной вершины и тогда в результате мы посетим все вершины, а следовательно и найдем все компоненты связности.
for (int i = 0; i < n; ++i){
if (!used[i]) {
amount++;
dfs(i);
}
}
Практическое задание
На данную тему задачи 6 и 10 в контесте.
Остовное дерево
Остованым деревом в связном графе называется любое подмножество ребер, которое является деревом на всех вершинах. То есть любой способ выкинуть несколько ребер так, чтобы осталось дерево на N вершинах и N-1 ребро выделяет в графе остовное дерево.
Обход графа удобно использовать для выделения этого остовного дерева — если выделить каждое ребро, по которому мы прошли в обходе, то получится остовное дерево. Действительно, мы обойдем все вершины, и при этом никогда не пойдем в вершину, в которой уже были, поэтому циклов там не будет. Так что достаточно после прохода по любому ребру добавлять его в ответ.
Практическое задание
7 задача в контесте на выделение остовного дерева в графе.
Раскраска графа в два цвета
Корректной раскраской графа в два цвета назывется такая раскраска, что никакое ребро не соединяет две вершины одного цвета. Графы, которые можно так раскрасить, называют еще двудольными.
С помощью обхода графа легко проверить граф на двудольность и даже вывести цвет каждой вершины — достаточно выделить каждую.
Практическое задание
8 задача в контесте на раскраску графа в два цвета
Поиск циклов в графе
Циклом в графе $G$ называется ненулевой путь, ведущий из вершины $v$ в саму себя. Граф называют ацикличным, если в нем нет циклов.
В обычном dfs мы используем два цвета (1 — вершина посещена, 0 — не посещена), если же нам надо найти цикл, то давайте хранить 3 цвета:
- 0 — вершина не просмотрена
- 1 — мы входили DFS-ом в эту вершину, но еще не вышли (а значит из нее есть путь до текущей),
- 2 — мы входили DFS-ом в эту вершину
Заметим, что цикл будет тогда и только тогда, когда мы пытаемся войти в вершину с цветом 1.
void dfs (int v) {
used[v] = 1;
for (size_t i=0; i < g[v].size(); ++i) {
int to = g[v][i];
if (used[to] == 0){
p[to] = v;
dfs (to);
}
else if (used[to] == 1 && to != p[v]) {
cycle = true;
}
}
used[v] = 2;
}
В неориентированном графе также надо дополнительно рассмотреть случай, когда мы идем в предка — это циклом все-таки не считается, для этого нужно отдельно добавить второй аргумент prev, где хранить предыдущую вершину в dfs, и никогда не идти в неё.
Практическое задание
9 задача в контесте на поиск цикла в графе.
#Ссылка на контест
https://informatics.msk.ru/mod/statements/view3.php?id=33377