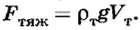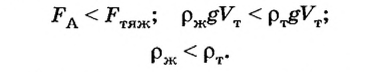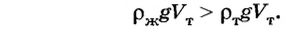На лесосплавных
предприятиях лесной промышленности
довольно часто приходится встречаться
с плавающими бревнами, бонами, пучками,
плотами, сплоточными машинами, патрульными
судами, буксирными катерами и др. Поэтому
важно знать законы плавания тел, уметь
определить их остойчивое и неостойчивое
положение на вод? при воздействии на
них грузов и других внешних сил.
Закон
Архимеда о силе, действующей на погруженное
в воду тело, был сформулирован Архимедом
за 250 лет до н. э. На основе закона
Архимеда были в последующем разработаны
вопросы теории корабля, изложенные
в трудах Эйлера, С. О. Макарова и А. Н.
Крылова. Закон Архимеда формулируется
следующим образом: на погруженное в
жидкость тело действует выталкивающая
сила, равная весу жидкости, вытесненной
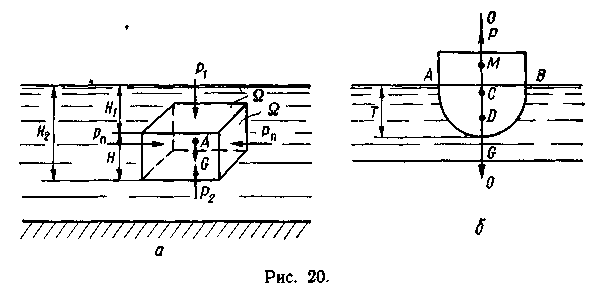
этим телом. Для доказательства этого
положения рассмотрим действующие на
погруженное в жидкость тело А
(рис.
20, а)
силы:
давление жидкости на тело сверху Р\
давление
жидкости на тело снизу Р2;
давление
жидкости на боковые стороны тела Рп.
Так
как на боковые стороны действуют равные,
но противоположно направленные силы,
то равнодействующая их равна нулю. Сила
веса G
погруженного
тела А
направлена
вниз
Давление
жидкости на тело А
сверху
будет Pi
= pgHiQ.
Давление
жидкости на тело снизу P2=pgH2Q.
Суммарное
давление жидкости на погруженное тело,
или выталкивающая сила, будет оавна
оазности сил Pi
и Р%,
а
именно:
(106)
где Н
—
высота тела, м; Q
— площадь верхней или нижней грани
тела, м2;
hi
—
глубина погружения в жидкость верхней
грани тела, м; Я2
— глубина погружения в жидкость нижней
грани тела, м.
Так
как Ни
представляет
собой объем V
погруженного
тела, то выталкивающая си»°
(107)
Следовательно,
подъемная, или выталкивающая, сила,
действующая на погруженное в жидкость
тело, равна весу жидкости, вытесненной
данным телом.
Величина выталкивающей
силы не зависит от глубины погружения
плавающего тела и будет постоянной при
погружении тела на различные глубины.
Закон Архимеда можно применять лишь
для тел, плавающих на поверхности
жидкости, точнее для погруженной в
жидкость части Плавающего тела, на
которую действует гидростатическое
давление.
10) Силы давления жидкости на плоские поверхности. Определение точки приложения.
Давление жидкости
на плоскую горизонтальную поверхность.
Гидростатический парадокс
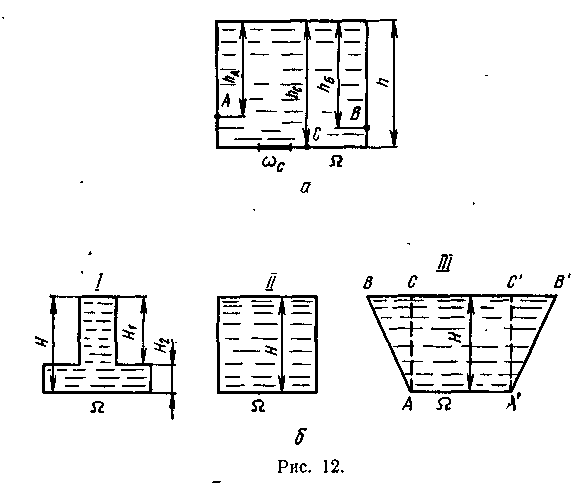
Имеем
сосуд (рис. 12, а) с глубиной воды h.
Давление
жидкости в какой-либо точке сосуда
зависит от глубины погружения этой
точки. Если взять точки А,
В и С, то
давления в них будут соответственно
равны
Сила
гидростатического давления на
горизонтальную площадку (Ос
Сила гидростатического
давления на все дно сосуда площадью
и может быть определена по Аоомуле —
(67)
Следовательно,
суммарная сила давления жидкости на
горизонтальную поверхность равна
весу столба жидкости/ расположенной
над рассматриваемой поверхностью.
На рис.
12, б
изображены
три сосуда различной формы. Площадь
дна Q
всех трех сосудов одинакова. Все сосуды
наполнены однородной жидкостью на
глубину Н.
На
рис. 12, б
Н=H1+H2.
Гидростатическое
давление на дно во всех сосудах будет
одинаковым и равным p
= pgH.
Суммарная
сила гидростатического давления на-
дно любого из трех показанных на рис.
12, б
сосудов
будет также одинаковой и равной P
= pxQ
= pgHQ.
Спрашивается,
откуда в сосуде I
берется
дополнительная сила по сравнению с
сосудом // и куда пропадает избыток веса
жидкости в сосуде /// по сравнению с
сосудом II.
Нет ли здесь противоречия с законами
физики? Законы гидравлики утверждают,
что давление жидкости не зависит от
формы сосуда, а зависит от
глубины
погружения площади-и ее размеров. В этом
и заключается гидростатический парадокс,
который может быть объяснен особым
свойством жидкости передавать внешнее
давление одинаковой величины по всем
направлениям (закон Паскаля). Например,
на дно сосуда /// действует суммарная
сила гидростатического давления P
= pgHQ.
Что
касается жидкости, находящейся в
объемах (АВС)Втл
(А’В’С’)В’, то
ее вес воспринимается наклонными
стенками, а не дном сосуда. Безусловно,
если сосуд /// будет стоять на столе, то
стол воспринимает вес всей жидкости,
находящейся в сосуде. Следовательно,
никакого противоречия между законами
физики и гидравлики не существует.
Суммарная сила гидростатического
давления на дно сосуда зависит от
плотности жидкости, глубины наполнения
сосуда и величины площади его дна и не
зависит от формы сосуда. тогда
(69)
где jq
t/dco
— статический момент площади относительно
оси х.
Как
известно, статический момент площади
равен произведению площади на
расстояние у0
от
центра его тяжести до рассматриваемой
оси. Следовательно,
На рис.
13 видно, что y0sna
= h0.
Тогда,
подставляя значение статического
момента в уравнение (69) и заменяя через
h0
получим
‘ (70)
При
ро—ра
на
щит будет действовать слева атмосферное
давление и справа давление со стороны
жидкости, направленные навстречу
друг к другу. Поэтому формула (70) для
этого случая будет иметь вид
(71)
Из
уравнения (71) видно, что суммарная сила
давления жидкости на плоскую поверхность
равна произведению площади смоченной
фигуры на давление в центре ее тяжести.
Нетрудно видеть также, что сила Р
состоит
из двух слагаемых! внешней силы суммарного
гидростатического давления рой и силы
избыточного давления pg/ioQ.
Первая сила приложена в центре тяжести
фигуры. Точка приложения второй силы
(центр давления) располагается ниже
центра тяжести.
3. Определение
местоположения центра давления
Центром давления
называют точку приложения равнодействующей
избыточного гидростатического давления.
Для установления размеров щитов,
затворов и других частей» сооружений
определяют не только величину, но и
точку приложения суммарной силы
гидростатического давления.
Для
определения центра давления Ц. Д.
обратимся вновь к рис. 13 и воспользуемся
известной теоремой теоретической
механики о том, что момент равнодействующей
силы равен сумме моментов составляющих
сил. На основании указанной теоремы
напишем уравнение моментов относительно
оси х,
полагая,
что координата центра давления равна
г/с-Тогда
(72)
Из.рисунка
видно,
что
Равнодействующая
сила
(73) В свою очередь
Но
интеграл §u&<s>y*
=
Ix
—
момент инерции смоченной площади
относительно оси х.
Тогда
pgsina^Q^^pgsin/,,
или
(74) и ордината центра
давления
(75) Момент инерции
/ж
может быть определен по формуле
(76)
гДе /о — момент
инерции смоченной фигуры, вычисленный
относительно оси, проходящей через
центр ее тяжести.
Подставим значение
/* в уравнение (75). После несложных
преобразований окончательно получим
(77)
Отсюда
следует, что
центр
давления всегда располагается ниже
центра тяжести фигуры на величину
/о/Йг/о, в случае, когда щит расположен
горизонтально, его центр давления
совпадает с центром тяжести.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Плавание тел
Условия плавания тел
Условия плавания тел следуют из закона Архимеда:
- Если выталкивающая сила больше, чем вес тела
, тело всплывает до тех пор, пока эти силы не уравновесятся.
- Если выталкивающая сила равна весу тела
, тело плавает в любой точке жидкости.
- Если выталкивающая сила меньше веса тела
, тело тонет.
Глубина погружения плавающего тела зависит от соотношения плотностей тела и жидкости. Если учесть, что и
, то тело будет плавать в жидкости, если
(здесь
и
— плотность и объем тела,
— плотность жидкости, а
— объем погруженной части тела).
Из полученного соотношения можно сделать важные выводы:
Плавания тел на границе нескольких сред
Если тело плавает на границе нескольких сред с плотностями то вес вытесненной жидкости, а, следовательно, и Архимедова сила в этом случае равны:
где — объем части тела, погруженной в первую среду,
— объем части тела, погруженной во вторую среду и т.д.
Плотность сухого дерева за счет полостей, наполненных воздухом, меньше плотности воды, и дерево может плавать на поверхности. Но железо и многие другие вещества значительно плотнее воды. Однако современные корабли сделаны из металла и перевозят различные грузы по воде. Как это возможно? Дело в том, что корпус корабля, который погружается в воду, делают объемным, а внутри этот корабль имеет большие полости, заполненные воздухом, что и уменьшает общую плотность корабля.
Глубина, на которую плавающий корабль погружается в воду, называется осадкой корабля. При полной загрузке корабль не должен опускаться ниже так называемой грузовой ватерлинии. Вес воды, вытесняемой судном при погружении до ватерлинии, называется водоизмещением судна. Он равен силе тяжести, действующей на судно с грузом. Грузоподъемность судна показывает вес груза, который перевозится судном. Грузоподъемность равна разности водоизмещения и веса незагруженного судна.
Плотность человеческого тела немного больше плотности воды. Однако, человек, когда у него в легких содержится некоторое количество воздуха, тоже может спокойно держаться на поверхности воды. Если же, находясь в воде, выдохнуть весь воздух из легких, то начнется медленное погружение на дно. Поэтому при плавании опасно наглотаться воды и впустить ее в легкие, именно это является наиболее частой причиной несчастных случаев на воде.
Примеры решения задач
ВЗ
Валентин Зворыкин
Плот перестанет погружаться в воду, когда сила Архимеда уравновесит силу тяжести плота, то есть в данном случае — его вес.
Сила Архимеда равна произведению плотности воды, ускорения свободного падения и объема погруженной части плота (то есть площади плота, умноженной на некую глубину h, которую и нужно найти), или Fa=ρ(воды) *g*S*h.
Сила тяжести плота, или просто-напросто его вес равны произведению массы всего плота на ускорение свободного падения, а так как масса равна плотности, умноженной на объем, то вес равен произведению плотности плота, его объема (произведение длины, ширины и высоты) и ускорения свободного падения, или Fт=P=ρ(плота) *abc*g=ρ(плота) *S*c*g.
Так как в конечном счете должны сравняться сила Архимеда и вес, то должны сравняться и произведения, которые их составляют: Fа=ρ(воды) *g*S*h=P=ρ(плота) *S*c*g. А дальше — простое уравнение:
ρ(воды) *g*S*h=ρ(плота) *S*c*g, делим и ту, и другую часть на S*g:
ρ(воды) *h=ρ(плота) *c, делим и ту, и другую часть на ρ(воды):
h=(ρ(плота) *c)/ρ(воды).
Подставляем числа: h=(ρ(плота) *c)/ρ(воды) =(800*0,4)/1000=320/1000=0,32м=32 сантиметра.
Содержание:
Условия плавания тел:
Вы уже знаете, что на погружённое в жидкость тело действуют две силы: сила тяжести
Под действием этих сил тело будет двигаться в сторону большей силы. При этом возможные следующие случаи:
- Если сила тяжести меньше архимедовой силы
то тело будет всплывать (рис. 144, а). На поверхности оно будет плавать, частично погрузившись на глубину, которой достаточно для возникновения архимедовой силы, уравновешивающей вес тела.
- Если сила тяжести равна архимедовой силе
, то тело будет находится в равновесии в любом месте жидкости (рис. 144 ,б).
- Если сила тяжести больше архимедовой силы
то тело утонет (рис. 144, в).
Рассмотренные условия плавания тел в каждом случае определяются соотношением между плотностями жидкости и погружённого тела.
- Если плотность тела меньше плотности жидкости
, то тело будет плавать на поверхности, частично погрузившись в воду.
- Если плотность тела равна плотности жидкости , то будет наблюдаться состояние безразличного (индифферентного) равновесия, когда тело может зависнуть на любой глубине (в водоёмах это представляет опасность для судоходства из-за возможного столкновения).
- Если плотность тела больше, чем плотность жидкости
, то тело будет тонуть.
Подводная лодка, опустившись на илистое дно, иногда с трудом может оторваться от него. Такое присасывание лодки ко дну возникает в том случае, когда лодка прижимается к грунту так, что между нею и грунтом нет воды. Значит, вода не давит на его нижнюю часть, т. е. не возникает выталкивающей силы.
Для выполнения подводных работ используют водолазные костюмы (рис. 145).
Они имеют массу до и более 50 кг, так как подошвы в них делают свинцовыми, чтобы увеличить вес водолаза и придать ему большую устойчивость во время — работы в воде. Как же может водолаз передвигаться в таком тяжёлом костюме? Благодаря значительному объёму костюма выталкивающая сила воды уравновешивает почти ведь его вес, поэтому водолаз может свободно передвигаться в воде.
Пользуясь аквалангом, изобретённым известным исследователем морских глубин французским учёным Жаком-Ивом Кусто, человек может долго находиться в воде и свободно плавать (рис. 146).
Для исследования морей и океанов на больших глубинах используют батисферы и батискафы. Батисфера (от греческих слов батис — глубокий и сфера) — это очень прочный стальной шар с иллюминаторами (окнами) из толстого стекла. Внутри шара находятся исследователи, поддерживающие связь с кораблём. Батисферу опускают на стальном тросе.
Батискаф (от греческих слов батис — глубокий; скафос — судно) отличается от батисферы тем, что он не удерживается на тросе, а имеет собственный двигатель и может свободно перемещаться на больших глубинах (до 11 км) в любых направлениях (рис. 147).
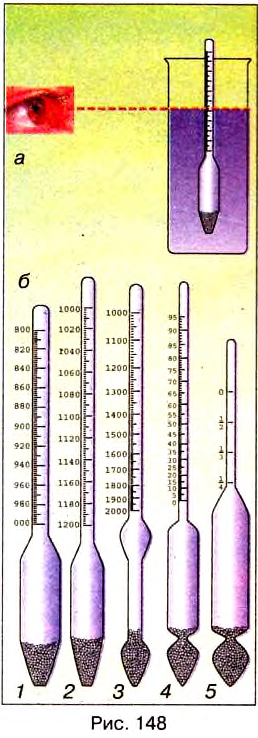
Тело, имеющее меньшую плотность, чем некоторые жидкости, по-разному погружается в них. Это явление используют в ареометрах (от греческих слов араиос — жидкий и метрео — измеряю) — приборах для измерения плотности жидкости по глубине их погружения. Любой ареометр — это стеклянный поплавок в виде трубки с делениями и грузом внизу (рис. 148, а). Он погружается в жидкость тем глубже, чем меньше плотность жидкости. В нижней части ареометра может быть термометр для измерения температуры исследуемой жидкости.
Ареометры имеют ещё и другое название; их називають денсиметрами (от латинских слов денсус — густой и метрео). Денсиметрами можно измерять плотности жидкостей от 0,7 до 2,0 На рисунке 148, б изображены денсиметры разных видов:
Плавающее тело своей подводной частью вытесняет воду. Вес этой воды равней силе тяжести, действующей на это тело. Это справедливо и для любого судна. Вес воды, которую вытесняет подводная часть судна, равен силе тяжести, действующей на судно с грузом.
Все суда погружаются в воду на определённую глубину, называемую осадкой. Максимально допустимую осадку обозначают на корпусе судна красной линией, называемую ватерлинией (от голландского слова ватер — вода). Кроме ватерлинии на судах делают и другие пометки, обозначающие уровни погружения судна в разных морях и океанах в зависимости от времени года (рис. 149).
Это связано с тем, что плотность воды в различных местах Мирового океана разная, кроме того, она ещё зависит и от температуры воды (летом плотность меньше, чем зимой).
Каждое судно имеет свое водоизмещение. Водоизмещение судна — это вес вытесненной судном воды, равный силе тяжести, действующей на судно с грузом при его погружении в воду.
Наибольшие суда используют для перевозки нефти, их называют танкерами. Водоизмещение таких судов достигает 5 ООО ООО ООО Н.
Свыше 200 лет отделяют нас от первых воздушных полётов человека. 5 мая 1783 г. — первая публичная демонстрация полёта оболочки, наполненной горячим воздухом. 21 ноября того же года французские изобретатели братья Жозеф и Этьенн Монгольфье осуществили первый полёт воздухоплавателей (рис. 150).
А через 10 дней французский физик Жак Шарль отправился в путешествие по воздушному океану на аэростате собственной конструкции, оболочка которого была наполнена водородом. Этот аэростат стал прообразом дирижаблей.
Для исследования верхних слоёв атмосферы на метеорологических станциях запускают небольшие, диаметром 1—2 м, воздушные шары-зонды (рис. 151). Они поднимаются на высоту до 35—40 км. К ним подвешивают приборы, посылающие по радио сигналы о высоте полёта, давлении, температуре воздуха. По направлению и скорости полёта шара можно определить направление и силу ветра на разных высотах. Сведения, получаемые с таких зондов, очень важны для прогнозирования погоды.
На рисунке 152 изображён управляемый летательный аппарат, который легче воздуха — дирижабль.
Этот аппарат приводят в движение винты, которые вращаются двигателями. Существенный недостаток аппаратов такого типа заключается в том, что их оболочка наполняется огнеопасным газом водородом. Воздушные шары, стратостаты, дирижабли, зонды поднимаются вверх за счёт того, что они наполнены газами, которые легче воздуха, и на них действует выталкивающая сила.
Кстати:
В июне 1893 г. канадский пароход «Порция» совершал рейс из порта Сент-Джон (Ньюфаундленд) в Нью-Брансвик. Мимо судна проплывали огромные ледяные горы — айсберги. Пассажиры захотели получше рассмотреть айсберг и уговорили капитана приблизиться к одному из них. «Порция» застопорила машины в 70 м от айсберга. Длина плавучей горы составляла почти 250 м, а высота — 60 м. Неожиданно ледяная глыба, искрящаяся на солнце, быстро отошла от парохода, и тотчас корпус судна содрогнулся от резкого толчка. Удивлённые матросы и пассажиры увидели, что пароход лежит на огромной льдине и с каждой секундой поднимается все выше и выше над поверхностью воды. Произошел невероятный случай! Известно, что время от времени айсберги переворачиваются. Пароход был подхвачен щелью в подводной части айсберга и оставался на вершине ледяной горы в течение нескольких минут. Потом айсберг пошатнулся и снова занял предыдущее положение, а судно благополучно оказалось в воде. Впрочем, не совсем благополучно: в его обшивке образовалась трещина, и «Порция» едва добралась до ближайшего порта.
- Заказать решение задач по физике
Условия плавания тел
Согласно закону Архимеда, на все тела, погруженные в жидкость, действуют выталкивающие силы, значение которых зависит от объемов этих тел и плотности жидкости. Таким образом, если тела имеют равные объемы, то и выталкивающие силы, действующие на них в данной жидкости, будут равными. Почему же тогда одни тела тонут в воде, а другие плавают?
Почему тела плавают или тонут
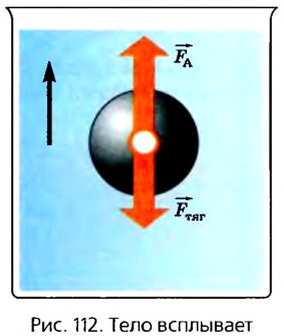
Для примера возьмем два шарика одинакового объема, но один металлический, а другой деревянный. Взвешивание их покажет, что вес деревянного шарика меньше веса металлического. Всплытие деревянного шарика, погруженного в жидкость, показывает, что равнодействующая силы тяжести и силы Архимеда направлена вверх, в направлении действия силы Архимеда. Таким образом, в этом случае сила Архимеда больше силы тяжести (рис. 112).
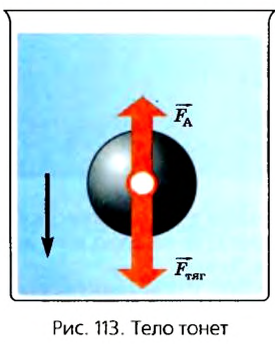
В случае с металлическим шариком равнодействующая направлена вниз, поскольку сила тяжести больше силы Архимеда (рис. 113).
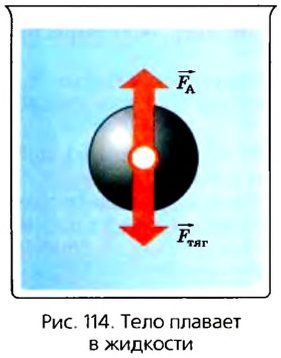
При равности сил Архимеда и тяжести, действующих на погруженное в жидкость тело, равнодействующая равна нулю (рис. 114). Следовательно, в этом случае погруженное в жидкость тело будет находиться в равновесии в любой точке жидкости.
Однако измерить силу тяжести или силу Архимеда во всех случаях невозможно или это неудобно. Поэтому предсказать поведение тела в жидкости можно не всегда. Чтобы найти выход, сделаем расчеты.
Когда тела тонут в жидкости
Тело тонет, если его средняя плотность больше плотности жидкости.
На каждое тело в жидкости действуют две силы: сила Архимеда 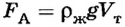
Для случая, когда тело тонет в данной жидкости:
Налитая в стакан с водой ртуть опускается на дно (рис. 115).
Подобным образом различные суда могут плавать по поверхности воды. Вес воды, вытесненной подводной частью судна, равен весу самого судна. Очевидно, что чем больший вес судна, тем больше глубина его погружения в воду.
Когда тела плавают в жидкости
Тело плавает, если его средняя плотность меньше плотности жидкости.
Если тело плавает, то
или
Отсюда
Налитое в стакан подсолнечное масло всплывает на поверхность воды, так как его плотность меньше плотности воды (рис. 116). Чтобы убедиться в этом, достаточно посмотреть в таблицу значений плотности на с. 53.
Плавание судов
Человек издавна мечтал о преодолении водного пространства. Сначала он приспосабливал для этого деревянные колоды, плоты, а затем начал строить деревянные лодки и корабли.
Для изготовления современных суден используют различные металлы. Из металла изготавливается корпус судна, его конструктивные элементы. Вместе с этим большой объем судна не заполнен металлом. Поэтому его средняя плотность меньше плотности воды.
При погружении нижней части судна в воду возникает сила Архимеда, равняющаяся весу вытесненной воды. При условиях плавания эта сила всегда равна весу судна. Если судно нагружают, его вес увеличивается, и оно начинает погружаться в воду. Чем глубже погружается судно, тем большей становится сила Архимеда. Когда она будет равной весу судна, оно прекращает погружаться. Глубину, на которую погружается судно в воду, называют осадкой судна.
Осадка судна зависит от его веса и массы груза, находящегося на судне. Увеличение массы груза приводит к увеличению осадки. Осадка уменьшается, когда судно переходит из реки в море, где плотность воды равна примерно 1030 кг/м3.
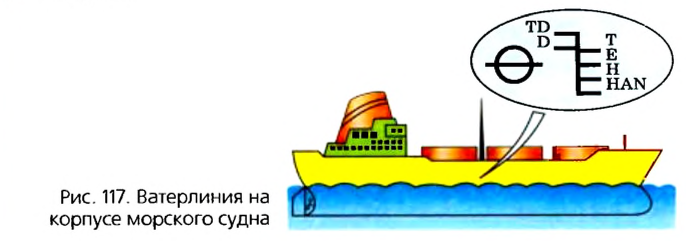
Осадка может изменяться только в определенных пределах, когда судно еще держится на поверхности воды. Чтобы контролировать осадку судна, на его борт наносят горизонтальную линию, которая получила название ватерлиния (от голландских слов water — вода и line — линия) (рис. 117). Значение силы Архимеда, когда судно погрузилось по ватерлинию, называют водотоннажностью судна.
Численно водотоннажность равна силе тяжести, действующей на судно с грузом. Самая большая водотоннажность у современных танкеров. Она достигает 5•106 кН и больше. Вместе с грузом масса этих суден 500 000 т и больше.
Если от водотоннажности вычесть вес судна, то получим вес груза, который это судно может перевезти. Это грузоподъемность судна.
Водный транспорт очень удобен и экономически выгоден. Перевозка грузов водным транспортом значительно дешевле, чем другими видами транспорта. Поэтому для дальнейшего его развития необходимо создавать более совершенные суда и одновременно заботиться о состоянии водных артерий страны, которым очень вредят промышленные выбросы и загрязнения (отходы) с судов.
Украина имеет развитый речной и морской флот. Самой большой судоходной рекой Украины является Днепр, фарватером которой плавают даже судна типа «река — море», которые выходят из реки в море, не перегружая груз.
- Гидростатическое взвешивание в физике
- Воздухоплавание в физике
- Машины и механизмы в физике
- Коэффициент полезного действия (КПД) механизмов
- Манометры в физике
- Барометры в физике
- Жидкостные насосы в физике
- Выталкивающая сила в физике

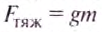
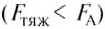 то тело будет всплывать (рис. 144, а). На поверхности оно будет плавать, частично погрузившись на глубину, которой достаточно для возникновения архимедовой силы, уравновешивающей вес тела.
то тело будет всплывать (рис. 144, а). На поверхности оно будет плавать, частично погрузившись на глубину, которой достаточно для возникновения архимедовой силы, уравновешивающей вес тела.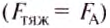 , то тело будет находится в равновесии в любом месте жидкости (рис. 144 ,б).
, то тело будет находится в равновесии в любом месте жидкости (рис. 144 ,б).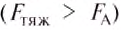 то тело утонет (рис. 144, в).
то тело утонет (рис. 144, в).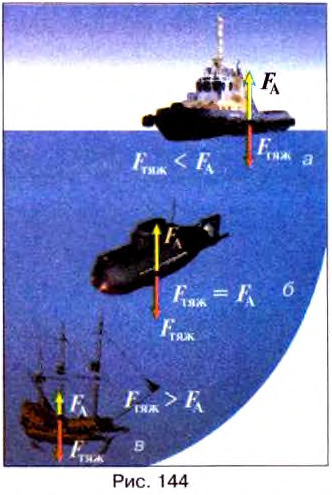
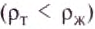 , то тело будет плавать на поверхности, частично погрузившись в воду.
, то тело будет плавать на поверхности, частично погрузившись в воду.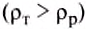 , то тело будет тонуть.
, то тело будет тонуть.