В этом посте мы подробно изучим подходы, как найти горизонтальную скорость снаряда
Мы можем найти горизонтальную составляющую скорости при движении снаряда, используя имеющиеся уравнения кинематики. Это дает точное значение скорости, но здесь горизонтальный путь считается расстоянием и делится на время. Формула, используемая для нахождения горизонтальной скорости снаряда:
- vfx2 = Vix2 + 2аxx
- vfx = Vix +xt
- vx = тележкаΘ
Теперь давайте посмотрим на различные подходы и проблемы, как найти горизонтальную скорость снаряда.
Как найти горизонтальную скорость снаряда?
Снарядное движение кого-либо или предмета рассматривается как горизонтальная скорость; его можно измерить, используя уравнения кинематики движения.
Одна из основных формул для нахождения горизонтальной скорости состоит в том, чтобы разделить горизонтальное расстояние, пройденное снарядом по рассматриваемой траектории, на затраченное время.

Теперь займемся изучением фактов движения снаряда.
Движение снаряда: концепция и факты
В физике движение снаряда — это тип двумерного движения, происходящего по параболической траектории.
Единственная сила, воздействующая на тело снаряда, — гравитация. Когда что-то брошено горизонтально вверх, гравитация притягивается к земле вертикально. Характер траектории движения имеет параболическую форму.

Снарядное движение любой частицы состоит из двух компонентов, так как это двумерное движение. Это горизонтальная x-компонента и вертикальная y-компонента.
Формула, используемая для измерения движения снаряда, выглядит следующим образом:
vfx = Vix +xt
vfx2 = Vix2 + 2аxx
Теперь пришло время узнать подробный подход к горизонтальной скорости.
Горизонтальная скорость снаряда: понимание и подход
В общем, движение снаряда происходит, когда объект обладает достаточной скоростью и имеет путь для движения.
Первоначально, когда любую частицу заставляют двигаться вверх, она сначала движется по горизонтальному пути; скорость, которой обладает частица, движущаяся по этой горизонтальной траектории, считается горизонтальной скоростью снаряда. Можно измерить его, взяв изменение положения или перемещение снаряда по горизонтали и время, необходимое для завершения этого движения.
Горизонтальное движение любого снаряда происходит в результате того, что движение частицы остается на траектории движения с постоянной скоростью.
Значение горизонтальной скорости снаряда можно рассчитать по приведенным ниже формулам:
vfx2 = Vix2 + 2аxx
vfx = Vix +xt
vx = Кос Θ
Теперь давайте подробно рассмотрим, как найти горизонтальную скорость снаряда с помощью формулы.
Подходы к нахождению горизонтальной скорости снаряда
Формула для измерения движения снаряда приведена ниже:
Используя это уравнение и из кинематики, мы можем рассмотреть уравнение для расчета горизонтальной скорости. Можно преобразовать уравнения, упомянутые выше, в горизонтальное движение, взяв только компоненты оси x, которые считаются горизонтальными компонентами любого движения снаряда. Позже мы можем поменять местами члены в уравнении, чтобы измерить требуемую горизонтальную скорость.
- х = vixт + 1/2аxt2
- vfx = Vix +xt
- vfx2 = Vix2 + 2аxx
В приведенных выше уравнениях
x относится к горизонтальному изменению положения
ax относится к горизонтальной составляющей изменения ускорения
vfx относится к конечной горизонтальной скорости
vix относится к начальной горизонтальной скорости
t относится ко времени, затраченному на преодоление пути.
Тета относится к углу траектории пути
Упомянутые выше формулы обычно используются, чтобы узнать, как найти горизонтальную скорость снаряда.
Задачи на определение горизонтальной скорости снаряда.
Ниже приведены некоторые задачи на определение горизонтальной скорости снаряда.
Проблема 1
Мяч из резины брошен вверх с начальной скоростью 40 м/с, причем вначале мяч летит под углом 25°. Найдите полную горизонтальную скорость мяча?
Решение: Сначала мы должны рассмотреть заданные значения.
Начальная скорость = Vi = 40 м / с
Θ = 25°
NВоспользуйтесь формулой, чтобы найти горизонтальную скорость,
Vx V =iCosΘ
V= (40) Cos(25°)
V = 36.24 м/с
Проблема 2
Сверху брошен камень с начальной скоростью 23 м/с под углом 5°. Найдите полную горизонтальную скорость мяча?
Решение: Сначала мы должны рассмотреть заданные значения.
Начальная скорость = Vi = 23 м / с
Θ = 5°
Теперь используйте формулу, чтобы найти горизонтальную скорость,
Vx V =iCosΘ
Vx = (23) Cos(5°)
Vx = 22.908 м / с
Пришло время узнать примеры того, как найти горизонтальную скорость снаряда.
Примеры горизонтальной скорости снаряда
Вещи, которые вы бросаете выше, упадут вниз из-за природы гравитации. Здесь движение двумерно и называется снарядом. Горизонтальный путь — это начальное движение, почти наблюдаемое в повседневной жизни. Вот несколько примеров горизонтальной скорости снаряда.
- Активация пушечного ядра вверх
- Игра в гольф
- Игра в метание молота
- Вода, падающая из трубы ПВХ
- Выстрел
- Запуск ракет
Активация пушечного ядра вверх
Мы вообще видели запуск пушечных ядер в любых клипах или аниме. Как только огнестрельное оружие системы зажжено, пушка перемещается вверх в горизонтальном движении, а затем движется вниз в нужное место. Здесь горизонтальное движение обладает горизонтальной скоростью, которая может быть измерена с помощью упомянутой выше формулы и является примером нахождения горизонтальной скорости снаряда. Здесь канонический шар — это снаряд.
Игра в гольф
Игра в гольф является одной из самых богатых международных игр, как только клюшка ударяет по мячу на поле. Он перемещается по горизонтальной траектории вверху и достигает требуемой позиции. Здесь происходит то, что скорость, которой обладает мяч для гольфа на горизонтальной траектории, считается горизонтальной скоростью. Ее можно измерить, используя формулу для нахождения горизонтальной скорости.
Игра в метание молота
Игра в метание молота считается одной из самых спортивных игр в мире. Даже в этой игре метание молота происходит по горизонтальной траектории; затем требуется кривая, чтобы достичь точки положения. Здесь молот действует как снаряд, и его скорость вдоль горизонтальной траектории может служить примером того, как найти горизонтальную скорость.
Вода, падающая из трубы ПВХ
В нашей повседневной жизни будет течь вода из трубы, и поток происходит от высокого давления к концу низкого давления, когда двигатель начинает работать после заполнения бака, избыточные водопады. Здесь мы должны заметить, что сначала поток будет горизонтальным, затем вертикальное движение происходит построение параболического пути. Горизонтальный поток воды будет иметь постоянную горизонтальную скорость. Мы можем использовать приведенные выше уравнения, чтобы найти значение его скорости.
Выстрел
Даже игра в толкание ядра чем-то похожа на метание копья и молота. Здесь дробовик будет выступать в роли снаряда. Как только игрок бросает мяч для толкания сверху, он движется по горизонтальной траектории и достигает места назначения. В этот момент мы можем измерить горизонтальное расстояние и время, чтобы получить горизонтальную скорость мяча для толкания ядра.
Запуск ракет
Вы наверняка видели запуски ракет на любых национальных каналах. Путь этой траектории движения будет иметь форму параболы. Запуск ракет требует больше энергии, и скорость будет еще выше, чем в любом другом случае движения. Сначала эти ракеты летят по горизонтальной траектории, а затем по кривой. Мы можем найти угол и скорость, используя формулы, упомянутые выше.
Вот несколько распространенных примеров того, как найти горизонтальную скорость снаряда.
Вертикальная скорость снаряда: понимание и подход
Вертикальная скорость снаряда — еще одна составляющая снарядного движения тела, противоположная горизонтальному движению.
Точно так же, когда мы вычисляем горизонтальную скорость снаряда, мы можем взять составляющую вдоль оси Y движения, чтобы узнать вертикальную скорость тела в движении снаряда. Скорость по вертикали не зависит от горизонтального направления.
Теперь дайте нам знать формулу, с помощью которой мы можем измерить вертикальную скорость снаряда.
Как найти конечную вертикальную скорость снаряда?
Формула, используемая для нахождения скорости вдоль вертикальной составляющей снаряда, имеет следующий вид:
vfy = Viy +yt
vix2 = Viy2 + 2аyy
Vy = Sin Θy
Итак, вот некоторые подходы, примеры и задачи, основанные на том, как найти горизонтальную скорость снаряда.
Узнать больше о Горизонтальное смещение
- Как найти горизонтальное смещение
Часто задаваемые вопросы | FAQs
Что вы подразумеваете под движением снаряда?
Движение снаряда является одним из важнейших двумерных движений.
В физической науке движение снаряда можно рассматривать как движение, на которое влияет только гравитационная сила. Характер движения снаряда — параболическая кривая. Особенность этого движения в том, что оно измеряет как горизонтальные, так и вертикальные компоненты.
Чем определяется горизонтальная скорость снаряда?
Горизонтальная скорость — это скорость любого снаряда по горизонтальной траектории.
Если какой-либо объект брошен в воздух под любым углом, отличным от 90 °, эта частица или объект движется по траектории траектории, делая характер кривой параболическим.
Наш калькулятор движения тела — это инструмент, который поможет вам проанализировать параболическое движение тела. Он может определить время полета, а также компоненты скорости, дальность полета и максимальную высоту полета. Продолжайте читать, если вы хотите понять, что такое движение тела, познакомьтесь с определением движения и определите вышеупомянутые значения с помощью уравнений движения тела.
Что такое движение тела (снаряда)? Определение движения снаряда
Представьте себе лучника, посылающего в воздух стрелу. Она начинает двигаться вверх и вперед при некотором наклоне к земле. Чем дальше она летит, тем медленнее она поднимается — и, наконец, она начинает снижаться, двигаясь теперь вниз и вперед и, наконец, снова ударяясь о землю. Если бы вы могли проследить ее путь, это была бы кривая, называемая траекторией в форме параболы. Любой объект, движущийся таким образом, движется как снаряд.
На снаряд действует только одна сила — сила тяжести. Сопротивление воздуха всегда не учитывается. Если вы начертите диаграмму свободного тела такого объекта, вам нужно будет нарисовать только один направленный вниз вектор и обозначить его «гравитация». Если бы на тело действовали какие-либо другие силы, то — по определению движения снаряда — это не был бы снаряд.
Калькулятор движения снаряда
Анализ движения снаряда
Движение снаряда довольно логично. Предположим, вы знаете начальную скорость объекта V, угол запуска α и начальную высоту h. Наш калькулятор движения снаряда выполняет следующие действия, чтобы найти все оставшиеся параметры:
1. Вычислите составляющие скорости.
- Скорость и ее горизонтальная и вертикальная составляющие
Горизонтальная составляющая скорости Vx равна V * cos (α).
Вертикальная составляющая скорости Vy равна V * sin (α).
Три вектора — V, Vx и Vy — образуют прямоугольный треугольник.
Если вертикальная составляющая скорости равна 0, то это случай горизонтального движения снаряда. Если дополнительно α = 90 °, то это случай свободного падения.
2. Запишите уравнения движения.
Расстояние
- Пройденное расстояние по горизонтали можно выразить как x = Vx * t, где t — время.
Вертикальное расстояние от земли описывается формулой y = h + Vy * t — g * t² / 2, где g — ускорение свободного падения.
Скорость
- Горизонтальная скорость равна Vx.
Вертикальную скорость можно выразить как Vy — g * t.
Ускорение
- Горизонтальное ускорение равно 0.
Вертикальное ускорение равно -g (потому что на снаряд действует только сила тяжести).
3.Рассчитайте время полета.
График движения снаряда: время полета
Полет заканчивается, когда снаряд попадает в землю. Можно сказать, что это происходит, когда вертикальное расстояние от земли равно 0. В случае, когда начальная высота равна 0, формулу можно записать как: Vy * t — g * t² / 2 = 0. Тогда из это уравнение, мы находим, что время полета
t = 2 * Vy / g = 2 * V * sin (α) / g.
Однако, если мы бросаем объект с некоторой возвышенности, тогда формула не так хорошо сокращается, как раньше, и мы получаем квадратное уравнение для решения: h + Vy * t — g * t² / 2 = 0. После решения этой задачи уравнение, получаем:
t = [V * sin (α) + √ ((V * sin (α)) ² + 2 * g * h)] / g
4. Рассчитайте дальность полета снаряда.
График движения снаряда: дальность
Дальность полета снаряда — это общее горизонтальное расстояние, пройденное за время полета. Опять же, если мы запускаем объект с земли (начальная высота = 0), то мы можем записать формулу как R = Vx * t = Vx * 2 * Vy / g. Его также можно преобразовать в форму: R = V² * sin (2α) / g
Ситуация усложняется для начального значения высоты, отличного от 0. Затем нам нужно заменить длинную формулу из предыдущего шага на t:
R = Vx * t = V * cos (α) * [V * sin (α) + √ (V * sin (α)) ² + 2 * g * h)] / g
5. Рассчитайте максимальную высоту.
График движения снаряда: максимальная высота
Когда снаряд достигает максимальной высоты, он перестает двигаться вверх и начинает падать. Это означает, что его вертикальная составляющая скорости изменяется с положительной на отрицательную, другими словами, она равна 0 на короткий момент времени t (Vy = 0).
Если Vy — g * t (Vy = 0) = 0, то мы можем переформулировать это уравнение к t (Vy = 0) = Vy / g.
Теперь мы просто находим расстояние по вертикали от земли в это время: hmax = Vy * t (vy = 0) — g * (t (Vy = 0)) ² / 2 = Vy² / (2 * g) = V² * sin (α) ² / (2 * г)
К счастью, в случае запуска снаряда с некоторой начальной высоты h нам нужно просто добавить это значение в окончательную формулу: hmax = h + V² * sin (α) ² / (2 * g)
Уравнения движения снаряда
Уфф, это было много вычислений! Подведем итог, чтобы сформировать наиболее важные уравнения движения снаряда:
Запуск объекта с земли (начальная высота h = 0)
- Составляющая горизонтальной скорости: Vx = V * cos (α)
Вертикальная составляющая скорости: Vy = V * sin (α)
Время полета: t = 2 * Vy / г
Дальность полета снаряда: R = 2 * Vx * Vy / g
Максимальная высота: hmax = Vy² / (2 * g)
Запуск объекта с некоторой высоты (начальная высота h> 0)
- Составляющая горизонтальной скорости: Vx = V * cos (α)
Вертикальная составляющая скорости: Vy = V * sin (α)
Время полета: t = [Vy + √ (Vy² + 2 * g * h)] / g
Дальность полета снаряда: R = Vx * [Vy + √ (Vy² + 2 * g * h)] / g
Максимальная высота: hmax = h + Vy² / (2 * g)
Использование нашего калькулятора движения снаряда наверняка сэкономит вам много времени. Он также может работать «наоборот». Например, введите время полета, расстояние и начальную высоту и смотрите, как он выполняет все вычисления за вас!
Часто задаваемые вопросы
Должен ли снаряд перемещаться горизонтально?
Нет, движение снаряда и его уравнения охватывают все движущиеся объекты, где единственной силой, действующей на них, является гравитация. Сюда входят объекты, которые подбрасываются прямо вверх, те, которые выбрасываются горизонтально, те, которые имеют горизонтальный и вертикальный компонент, и те, которые просто отбрасываются.
Как может снаряд упасть вокруг Земли?
На снаряд действует только одна сила — сила тяжести. Это означает, что объект в конечном итоге упадет на Землю. Но что делать, если объект движется по горизонтали так быстро, что к тому времени, как он достигает земли, земли уже нет? Это принцип, по которому работают спутники.
Как найти ускорение при движении снаряда?
На объект в метательном движении действует только одна сила — гравитация. Это означает, что любое изменение вертикальной скорости происходит из-за ускорения свободного падения, которое на Земле составляет 9,81 м / с2. В горизонтальном направлении скорость не изменяется, так как сопротивление воздуха считается незначительным, поэтому ускорение равно 0.
Какие факторы влияют на движение снаряда, выпущенного горизонтально?
Начальная скорость, начальная высота, с которой запускается снаряд, и сила тяжести будут влиять на снаряд, запущенный горизонтально. Сопротивление воздуха также будет иметь влияние в реальной жизни, но для большинства теоретических расчетов оно незначительно и поэтому игнорируется. Если у снаряда есть крылья, это также повлияет на его движение, так как он будет скользить.
Что такое снаряд?
Снаряд — это объект, который движется в воздухе и не имеет силы, действующей на него, кроме ускорения свободного падения (это означает, что он не может быть самоходным). Вы, наверное, можете вспомнить множество примеров: брошенный мяч или камень, стрела из лука. Даже Луна — это снаряд по отношению к Земле!
Каковы характеристики движения снаряда?
Свойства движения снаряда заключаются в том, что горизонтальная скорость объекта не изменяется, что его вертикальная скорость постоянно изменяется из-за силы тяжести, что форма его траектории будет параболой и что на объект не влияет сопротивление воздуха.
Кто первым и когда точно описал движение снаряда?
Галилей был первым человеком, который точно описал движение снаряда, разбив движение на горизонтальную и вертикальную составляющие и осознав, что график движения любого объекта всегда будет параболой. Он описал это в своей книге «О движении», опубликованной примерно в 1590-х годах.
Почему снаряд летит по кривой?
Объект следует параболе из-за того, что гравитация влияет на две его составляющие движения — горизонтальную и вертикальную. Горизонтальная составляющая вообще не подвержена влиянию силы тяжести, поэтому изменяется линейно. Однако вертикальная часть постоянно находится под действием силы тяжести, поэтому она будет увеличиваться в высоте, а затем уменьшаться, ускоряясь под действием силы тяжести.
Почему 45 градусов — оптимальный угол для снарядов?
Уравнение для расстояния, пройденного снарядом под действием силы тяжести, имеет вид sin (2θ) v2 / g, где θ — угол, v — начальная скорость, а g — ускорение свободного падения. Предполагая, что v2 / g постоянна, наибольшее расстояние будет, когда sin (2θ) будет максимальным, то есть когда 2θ = 90 градусов. Это означает θ = 45 градусов.
Как рассчитать движение снаряда
Когда объект запускается, он следует параболическому пути и движению, известному как движение снаряда. В этом посте мы рассмотрим параметры и способы их расчета. движение снаряда в подробном анализе.
Когда объект запускается и движется по симметричной параболической траектории, движение называется движением снаряда, а параболический путь объекта называется его траекторией. В этом случае объект перемещается одновременно по вертикали и горизонтали. В результате движение снаряда становится двумерным. При движении снаряда вам нужно только приложить силу в начале траектории; после этого на объект действует только сила тяжести.
Теперь давайте посмотрим, как рассчитать движение снаряда:
Предположим, вы стреляете пушечным ядром. Он начинает двигаться вверх и вперед, пока не достигнет максимальной высоты. С этого момента он будет продолжать двигаться вперед, но в нисходящем направлении. Он отслеживает этот изогнутый маршрут, известный как траектория, имеющая форму параболы. Любой объект, движущийся таким образом, называется движущимся снарядом. Поскольку траектория движения снаряда всегда параболическая, она представляется как:
у = ах + bx 2
Прежде чем достичь Земли, пушечное ядро во время своего путешествия пойдет по параболическому маршруту. скорость по оси X остается постоянной на протяжении всего движения, тогда как скорость по оси Y изменяется в зависимости от его положения. Только ускорение свободного падения 9.8 м / с 2 , управляет этим типом движения. Ускорение, направленное вниз, остается постоянным во время полета ядер.
Кинематические уравнения движения снаряда:
Формула начальной скорости:
Предположим, что начальная скорость равна u, а угол полета снаряда равен. У начальной скорости есть две составляющие: горизонтальная и вертикальная.
Горизонтальная составляющая начальной скорости ux и предоставлено:
ux = ты ᐧ потому что𝛳
Вертикальная составляющая начальной скорости равна uy и определяется выражением:
Время полета снаряда:
Время полета снаряда — это промежуток времени между запускаемым объектом и достижением земли. Величина стартовой скорости и угол полета снаряда определяют время полета, которое обозначается T.
Формула ускорения:
В горизонтальном направлении ускорение отсутствует, поскольку горизонтальная составляющая ускорения остается постоянной на протяжении всего движения. Единственное ускорение в вертикальном направлении происходит за счет силы тяжести.
Отрицательный знак означает ускорение вниз.
Формула скорости в момент времени t:
На протяжении всего движения горизонтальная составляющая скорости остается постоянной. Однако, поскольку вертикальное ускорение постоянно, вертикальная составляющая скорости изменяется линейно.
В результате скорость может быть рассчитана в любой момент времени t по следующей формуле:
vy = u ᐧ sin𝛳 — g ᐧ t
Используя теорему Пифагора, можно найти величину скорости.
Формула смещения в момент времени t:
В момент времени t смещение может быть определено как:
y = (u ᐧ sin𝛳) ᐧ t — ½ (gt 2 )
Формула параболической траектории:
Мы можем использовать уравнения смещения в направлениях x и y, чтобы вывести уравнение для параболической формы движения снаряда:
Формула дальности снаряда:
Общее горизонтальное расстояние, пройденное объектом за время полета, определяется как его дальность. Если объект запускается с земли (начальная высота = 0), формула выглядит следующим образом:
Согласно приведенному выше уравнению, максимальная дальность полета по горизонтали может быть получена при угле полета снаряда 𝛳 = 45 °. Rm представляет собой максимальный диапазон.
Формула максимальной высоты:
Когда вертикальная составляющая скорости равна нулю, vy = 0, максимальная высота может быть достигнута. Поскольку время полета — это полное время снаряда, для достижения максимальной высоты потребуется половина этого времени. Таким образом, время для достижения максимальной высоты составляет:
Таким образом, из уравнения перемещения максимальная высота может быть определена как:
Формула движения снаряда по горизонтали:
Горизонтальный снаряд Движение — это тип движения снаряда, при котором объект запускается горизонтально с возвышенной плоскости, а не с земли.
Угол запуска указывать не нужно, поскольку он параллелен земле (т. Е. Угол равен 0 °). В результате у нас есть только одна начальная составляющая скорости: Vx = V, тогда как Vy = 0.
В этом случае уравнения движения следующие:
Скорость горизонтального движения снаряда:
Горизонтальная скорость: vx = V
И вертикальная скорость: vx = -g ᐧ т
Расстояние, пройденное объектом при горизонтальном движении снаряда:
В этом случае горизонтальное расстояние рассчитывается следующим образом:
А расстояние по вертикали можно определить как:
y = — (g ᐧ t 2 ) / 2
Ускорение при горизонтальном движении снаряда:
Горизонтальное ускорение аx = 0, поскольку горизонтальная скорость постоянна.
Вертикальное ускорение аy = -г
Уравнение траектории горизонтального движения снаряда:
Уравнение траектории в этом случае может быть задано следующим образом:
Время полета при горизонтальном движении снаряда:
Время полета в этом случае может быть определено как:
Дальность полета снаряда при горизонтальном движении снаряда:
Дальность полета снаряда при горизонтальном движении снаряда составляет:
Поскольку мы запускаем объект с максимальной высоты, нам не нужно рассчитывать максимальную высоту в этом сценарии.
Давайте посмотрим на некоторые проблемы движения снаряда.
Проблема 1: Каким будет θmax, при котором расстояние от частицы до метателя всегда увеличивается до конца пути снова у земли?
Решение: Горизонтальное расстояние, пройденное объектом, называется его горизонтальным диапазоном и определяется по формуле:
Максимальная дальность полета может быть достигнута при угле выстрела 45 °.
Таким образом, для максимального угла Rm θmax = 45 °.
Задача 2: Если мяч брошен вертикально вверх со скоростью u, расстояние, пройденное за последние t секунд его всплытия, будет:
Решение: Поскольку мяч брошен вертикально, угол полета снаряда 𝛳 = 90 °.
Где Tm — время, необходимое объекту для достижения максимальной высоты.
Предположим, что h представляет собой расстояние, пройденное объектом за последние t секунд его подъема. Затем скорость в этот момент рассчитывается следующим образом:
Таким образом, расстояние, пройденное за последнюю t секунду, составляет:
3 задачи: Частица проецируется под углом 60 ° над горизонтом со скоростью 10 м / с. Через некоторое время скорость составит угол 30 ° от горизонтали. Скорость частицы в этот момент составляет?
Решение: Горизонтальная составляющая скорости определяется как:
vx = ты ᐧ потому что𝛳
Здесь в первом случае угол проекции составляет 60 °, а начальная скорость u = 10 м / с. Таким образом,
Теперь вертикальная составляющая скорости vy изменяется во время движения, но vx остается постоянным. Таким образом,
Где 𝛳2 = 30 °, а v — скорость, когда объект составляет угол 𝛳 = 30 ° с горизонтом.
Последние выпуски в области передовой науки и исследований
Уравнение траектории снаряда имеет вид
2017-10-05
Зенитное орудие может сообщить снаряду начальную скорость $v_<0>$ в любом направлении. Требуется найти зону поражения, т. е. границу, отделяющую цели, до которых снаряд из данного орудия может долететь, от недостижимых целей. Сопротивлением воздуха пренебречь.
рис.1
рис.2
Попробуем сначала выяснить, что можно сказать об этой границе, не решая задачи. Сам факт существования такой границы сомнений не вызывает, так что поставленный в задаче вопрос имеет смысл (кстати, начиная решать задачу, никогда не вредно подумать об этом). Попытаемся представить себе искомую границу. Очевидно, что она представляет собой некоторую поверхность. Если цель находится точно над орудием, то стрелять нужно вертикально вверх. Снаряд при этом поднимается на высоту $h = v_<0>^<2>/2g$, после чего начинает падать вниз, так что граница достижимых целей пересекает вертикаль в точке, находящейся на высоте $h$.
Если ограничиться целями, находящимися на горизонтальной плоскости, то очевидно, что граница представляет собой окружность, радиус которой равен максимальной дальности полета снаряда по горизонтали $s = v_<0>^<2>/g$ (напомним, что максимальная дальность полета по горизонтали достигается при угле возвышения ствола орудия $alpha = pi /4$). Эта окружность есть пересечение искомой поверхности с горизонтальной плоскостью (рис.). Вообще из симметрии можно сделать вывод, что искомая поверхность представляет собой поверхность вращения некоторой кривой вокруг вертикали, проходящей через орудие, и задача сводится к нахождению этой кривой. Отметим, что кривая есть огибающая всех возможных траекторий (рис. 2).
Приступим к решению задачи. Выберем систему координат: орудие расположим в начале координат, ось х направим горизонтально, ось $y$ — вертикально. Тогда зависимость координат снаряда от времени имеет вид
$x(t) = v_ <0>cos alpha t, y(t) = v_ <0>sin alpha t — frac><2>$.
Исключив из этих уравнений $t$, получим уравнение траектории снаряда $y=f(x)$:
$y = x tg alpha — frac><2v_<0>> (1 + tg^ <2>alpha)$. (1)
Это уравнение параболы. Коэффициенты при $x$ и $x^<2>$ зависят от угла $alpha$, т. е. при разных направлениях начальной скорости получаются различные траектории. Таким образом, данное уравнение описывает семейство траекторий при одних и тех же по модулю, но различных по направлению начальных скоростях $v_<0>$.
Но этому же уравнению можно придать и другой смысл. Будем теперь рассматривать х и у как координаты определенной цели, в которую попадает снаряд, двигаясь по некоторой траектории. Тогда при заданных координатах цели х и у уравнение (1) определяет угол, под которым нужно выпустить снаряд с начальной скоростью $v_<0>$ для того, чтобы он попал в эту цель. Решая это квадратное относительно $tg alpha$ уравнение, находим
Если уравнение имеет вещественное решение, т. е. дискриминант неотрицателен:
то в цель попасть можно. Если вещественных решений нет, т. е.
то в цель попасть нельзя. Это значит, что цель находится за пределами искомой границы. Координаты цели, расположенной на границе, должны удовлетворять соотношению $v_<0>^ <4>- g(gx^ <2>+ 2v_<0>^ <2>y) = 0$. Выражая отсюда у как функцию х, получаем уравнение границы в явном виде:
Это уравнение параболы с вершиной при $x = 0, y = v_<0>^<2>/2g$. Коэффициент при $x^<2>$ отрицателен, т. е. ветви параболы направлены вниз и пересекают горизонтальную ось в точках $x = pm v_<0>^<2>/g$ (рис. 2), Итак, полученная граница действительно проходит через точки, которые вначале были нами установлены из элементарных соображений.
Мы нашли сечение граничной поверхности вертикальной плоскостью, проходящей через начало координат. Вся поверхность может быть получена вращением этой параболы вокруг оси у.
В связи с приведенным решением сделаем еще несколько замечаний. Рассмотрим какую-либо точку, находящуюся ближе границы (например, точку А на рис. 2). Для такой точки подкоренное выражение в формуле (2) положительно, и, следовательно, через нее проходят две траектории (при заданном значении начальной скорости), соответствующие двум возможным значениям угла $alpha$.
В баллистике одна из этих траекторий называется настильной, а другая, касающаяся границы до попадания в цель,— навесной. Через каждую точку, принадлежащую границе, проходит лишь одна траектория. Отметим, что граница является огибающей для семейства траекторий при различных направлениях начальной скорости и фиксированном значении начальной скорости $v_<0>$.
Приведем другой возможный путь решения этой задачи, связанный с еще одной трактовкой уравнения (1). Рассмотрим цели, находящиеся на одной вертикали, отстоящей от орудия на расстояние $x$, и найдем на ней самую высокую точку, в которую еще может попасть снаряд. Эта точка, очевидно, принадлежит границе. Таким образом, задача сводится к нахождению максимума у, т. е. правой части уравнения (1), рассматриваемой как функция угла $alpha$. Правая часть есть квадратный трехчлен относительно $tg alpha$ и имеет максимум при $tg alpha = v_<0>^ <2>/ gx$. Соответствующее максимуму значение у получается подстановкой этого значения $tg alpha$ в уравнение (1):
что совпадает с полученным ранее уравнением границы (4).
ЭЛЕМЕНТЫ Траектории полета снаряда
Свободным полётом снаряда называется фаза его движения после выстрела до попадания в твёрдое препятствие (цель, грунт) или до дистанционного подрыва. В этом процессе на снаряд действуют только сила тяжести и силы, возникающие при движении тела в газообразной среде (атмосфере Земли). В общем случае в атмосфере Земли также могут существовать упорядоченные движения масс воздуха (ветер), которые оказывают определённое влияние на полёт снаряда.
Путь, описываемый центром тяжести снаряда в пространстве после вылета его из канала ствола, называется траекторией.
Принято считать за траекторию полёта снаряда кривую, которую при движении описывает его центр масс. Эта кривая также имеет название баллистической. В самом общем случае она не является ни прямой, ни параболической, ни даже плоской.
Основные элементами траектории (рис.1) являются:
1. Точка вылетаО — центр дульного среза орудия.
2. Горизонт орудия ОС— горизонтальная плоскость, проходящая через точку вылета.
3. Точка падения С — точка пересечения траектории с горизонтом орудия.
4. Точка встречи Ав — точка встречи снаряда с преградой.
5. Линия выстрела ОА — направление оси канала ствола наведенного орудия.
6. Линия бросания ОБ — направление оси канала ствола в момент вылета снаряда; из-за вибрации ствола в момент вылета снаряда, линия бросания не совпадает с линией выстрела.
7. Линия цели ОЦ — прямая, проходящая через точку вылета и цель,
8. Угол прицеливания α(альфа) — угол между линией цели ОЦ и линией выстрела ОА.
9. Угол места цели ε(эпсилон) — угол между горизонтом орудия ОС и линией цели ОЦ, угол места цели считается положительным, когда цель выше горизонта орудия, и отрицательным, когда цель ниже горизонта орудия.
10. Угол возвышения φ(фи) — угол между горизонтом орудия ОС и линией выстрела ОА.
11. Угол вылета γ(гамма) — угол между линией выстрела ОА и линией бросания ОБ.
12. Угол бросания θ0 (тета) — угол между горизонтом орудия ОС и линией бросания ОБ.
13. Угол падения θс (тета) — угол между горизонтом орудия ОС и касательной к траектории в точке падения.
14. Угол встречи μ(мю) — угол между касательной к траектории в точке встречи и плоскостью, касательной к поверхности цели (преграды) в той же точке; угол встречи может быть от 0 до 90°.
15. Вершина траектории S — точка траектории, превышение которой над горизонтом орудия ОС является наибольшим.
16. Высота траектории — вертикальное расстояние от горизонта орудия ОС до вершины траектории S.
17. Восходящая ветвьОS — отрезок траектории от точки вылета до вершины траектории.
18. Нисходящая ветвь SС — отрезок траектории от ее вершины до точки падения.
19. Дальность до цели ОЦ — расстояние по прямой от орудия до цели.
С увеличением угла возвышения увеличивается и дальность падения снаряда, однако увеличение дальности имеет предел. В безвоздушном пространстве наибольшая дальность получилась бы при угле возвышения 45°. При дальнейшем увеличении угла возвышения снаряд полетел бы выше, но дальность падения уменьшилась бы. То же происходит и при стрельбе в действительных условиях, но траектория снаряда имеет другую форму.
Мерой крутизны траектории является величина угла возвышения φ (фи). Траекторию с углом возвышения не более 20° принято называть отлогой, а траекторию с углом возвышения более 20°— крутой.
Стрельбу, при которой траектория получается отлогой, называют настильной. Стрельбу, при которой траектория получается крутой, называют навесной.
Навесную стрельбу при углах возвышения более 45° называют мортирной.
Траектория снаряда в воздухе значительно отличается от траектории в безвоздушном пространстве (рис.2).
В безвоздушном пространстве траектория снаряда симметрична относительно вершины траектории, а в действительных условиях траектория несимметрична, нисходящая ветвь траектории короче и круче восходящей; угол падения больше угла возвышения; вершина траектории находится ближе к точке падения.
| Восходящие Ветви |
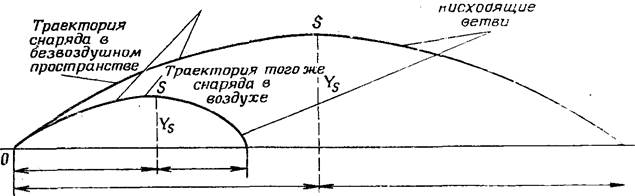 |
| Рис. 2. Траектория снаряда в безвоздушном пространстве и в воздухе |
Под действием силы сопротивления воздуха снаряд за каждую секунду проходит меньшее расстояние по направлению оси канала ствола, а понижается на ту же величину, что и в безвоздушном пространстве. В результате этого траектория в воздухе будет ниже и короче, чем в безвоздушном пространстве.
Угол бросания, отвечающий наибольшей дальности, при стрельбе в воздухе зависит от начальной скорости, массы и формы снаряда, а также от способа стабилизации снаряда на полете и может находиться в пределах от 28 до 55°.
При стрельбе из танков, БМП, противотанковых орудий и гранатометов и стрелкового оружия используются обычно настильные траектории. Чем меньше высота траектории и чем меньше угол падения, тем траектория более настильна.
Траектория в воздухе имеет следующие свойства:
§ траектория несимметрична, ее нисходящая ветвь короче и круче восходящей.
§ вершина траектории находится ближе к точке падения.
§ угол падения больше угла бросания.
У снаряда, движущегося в воздухе, окончательная скорость меньше начальной.
http://earthz.ru/solves/Zadacha-po-fizike-4147
http://helpiks.org/4-1510.html
Задания Д29 C2 № 4579
i
Прибор наблюдения обнаружил летящий снаряд и зафиксировал его горизонтальную координату и высоту
м над Землёй (см. рисунок). Через 3 с снаряд упал на Землю и взорвался на расстоянии
м от места его обнаружения. Чему равнялась начальная скорость
снаряда при вылете из пушки, если считать, что сопротивление воздуха пренебрежимо мало? Пушка и место взрыва находятся на одной горизонтали.
Спрятать решение
Решение.
Из закона сохранения энергии, начальная скорость снаряда равняется скорости, с которой снаряд ударился о землю.
Найдём горизонтальную скорость снаряда ():
Найдём вертикальную проекцию скорости снаряда в момент обнаружения:
Вертикальная проекция скорости в момент удара о Землю
Таким образом, начальная скорость снаряда равна
Ответ: примерно 800 м/с.
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Приведено полное решение, включающее следующие элементы:
I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: закон сохранения энергии или уравнение движения в поле силы тяжести); II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, и обозначений величин, используемых в условии задачи); III) проведены необходимые математические преобразования, приводящие к правильному ответу; IV) представлен правильный ответ |
3 |
| Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования. Но имеются следующие недостатки.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. ИЛИ В решении лишние записи, не входящие в решение (возможно, неверные), не отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т.п.). ИЛИ В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) преобразования/вычисления не доведены до конца. ИЛИ Отсутствует пункт IV, или в нём допущена ошибка |
2 |
| Представлены записи, соответствующие одному из следующих случаев.
Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения задачи, без каких-либо преобразований с их использованием, направленных на решение задачи, и ответа. ИЛИ В решении отсутствует ОДНА из исходных формул, необходимая для решения задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. ИЛИ В ОДНОЙ из исходных формул, необходимых для решения задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи |
1 |
| Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла | 0 |
| Максимальный балл | 3 |
Снаряд, летевший в
горизонтальном направлении со скоростью 20 м/с , разорвался на два осколка
массами 10 кг и 5 кг. Скорость меньшего осколка равна 20 м/с и направлена
вертикально вверх. Определите модуль и направление скорость движения большего
осколка.
Решение.
Материальными объектами
задачи являются: снаряд, два осколка, поверхность Земли, гравитационное поле
Земли и воздух. Снаряд и осколки примем за материальные точки.
Систему отсчета свяжем
с поверхностью Земли и будем считать ее инерциальной. Начало координат выберем
на поверхности Земли. Ось OX
направим горизонтально в направлении движения снаряда, ось OY – вертикально вверх.
В физическую систему
включим
снаряд и осколки. Земля и воздух по отношению к выделенной физической
системе являются внешними телами. Даже если не учитывать взаимодействие
физической системы с воздухом, она будет незамкнутой. Это обусловлено действием
на тела системы ничем не скомпенсированной силы тяжести.
Можно выделить два
состояния системы: начало взрыва и конец взрыва. Если учесть, что промежуток
времени между началом и концом взрыва небольшой, а внутренние силы, возникающие
при этом, велики по сравнению с силой тяжести, то выделенную физическую систему
можно считать практически замкнутой и описать законом сохранения импульса.
Начальный импульс
физической системы равен p1 = (m1 + m2)v , а ее конченый импульс – p2 = m1v1 + m2v2 .
Согласно закону сохранения
импульса: p
= p2 или
.
Если спроецировать
векторные величины на оси координат, получим
.
Откуда
.
Расчеты дают: v1 = 32 м/с, α = 19° . Таким образом, скорость большого осколка
равна 32 м/с и направлена вниз под углом α = 19° к горизонту.
Ответ: v1 = 32 м/с, α = 19° .
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.



