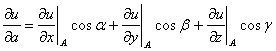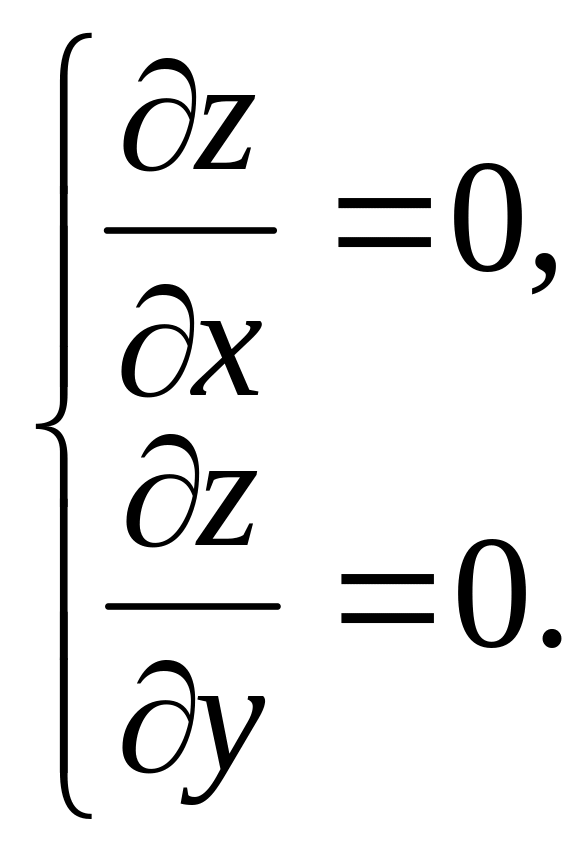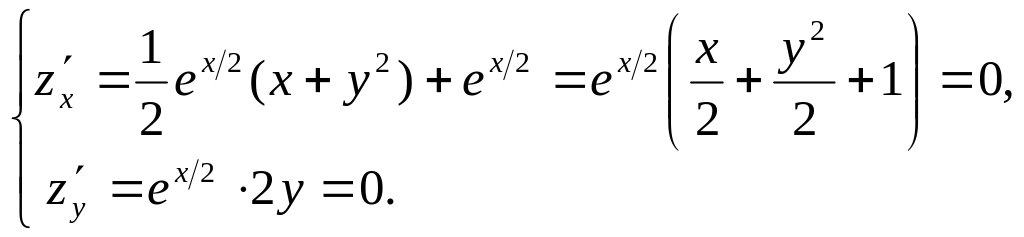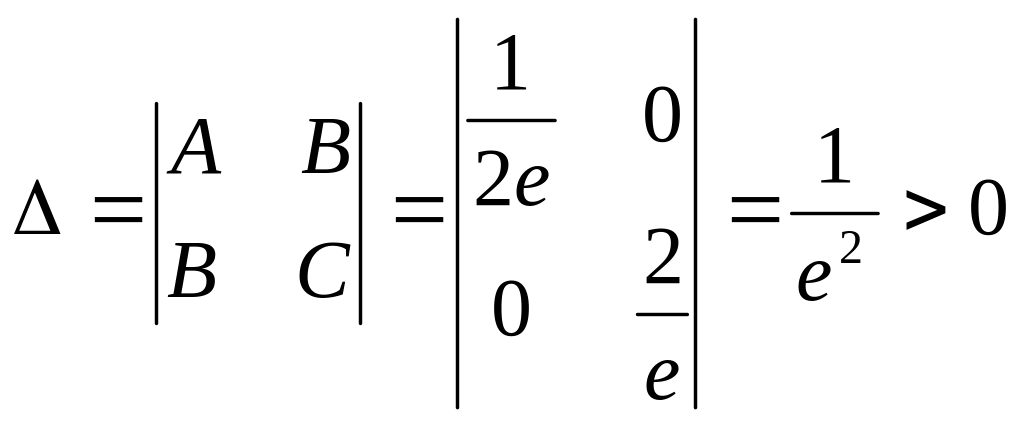Как найти градиент для функции

Градиент функции

Как найти?

Постановка задачи

Найти градиент функции $ f(x,y,z) $ в точке $ M(x_0,y_0,z_0) $

План решения

Градиент функции $ f(x,y,z) $ — это вектор, каждая координата которого является частной производной первого порядка этой функции:

$$ grad f = frac{partial f}{partial x} overline {i} + frac{partial f}{partial y} overline{j} + frac{partial f}{partial z} overline {k} $$

1. Берём частные производные первого порядка от функции $ f(x,y,z) $:
   $$ frac{partial f}{partial x}, frac{partial f}{partial y}, frac{partial f}{partial z} $$
2. Вычисляем полученные производные в точке $ M(x_0,y_0,z_0) $:
   $$ frac{partial f}{partial x} bigg |_{M(x_0,y_0,z_0)}, frac{partial f}{partial y} bigg |_{M(x_0,y_0,z_0)}, frac{partial f}{partial z} bigg |_{M(x_0,y_0,z_0)} $$
3. Подставляем, полученные данные в формулу градиента функции:
   $$ grad f bigg |_M = frac{partial f}{partial x} bigg |_M overline{i} + frac{partial f}{partial y} bigg |_M overline{j} + frac{partial f}{partial z} bigg |_M overline{k} $$

Примеры решений

Пример 1

Найти градиент функции $ u = x + ln (z^2+y^2) $ в точке $ M(2,1,1) $

Решение

Находим частные производные первого порядка функции трёх переменных: $$ frac{partial f}{partial x} = 1; frac{partial f}{partial y} = frac{2y}{z^2+y^2}; frac{partial f}{partial z} = frac{2z}{z^2+y^2} $$ Вычисляем значение производных в точке $ M(2,1,1) $: $$ frac{partial f}{partial x} bigg |_{M(2,1,1)} = 1 $$ $$ frac{partial f}{partial y} bigg |_{M(2,1,1)} = frac{2 cdot 1}{1^2+1^2} = frac{2}{2}=1 $$ $$ frac{partial f}{partial z} bigg |_{M(2,1,1)} = frac{2cdot 1}{1^2 + 1^2} = frac{2}{2}=1 $$ Подставляем в формулу градиента функции полученные данные: $$ grad f = 1 cdot overline{i} + 1 cdot overline{j} + 1 cdot overline{k} = overline{i}+overline{j}+overline{k} $$ Запишем ответ в координатной форме: $$ grad f = overline{i}+overline{j}+overline{k} = (1,1,1) $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ grad f = (1,1,1) $$

Пример 2

Найти градиент функции $ u = sin(x+2y)+2sqrt{xyz} $ в точке $ M bigg (frac{pi}{2},frac{3pi}{2},3 bigg ) $

Решение

Находим частные производные: $$ frac{partial f}{partial x} = cos(x+2y) + frac{yz}{sqrt{xyz}} $$ $$ frac{partial f}{partial y} = 2cos(x+2y) + frac{xz}{sqrt{xyz}} $$ $$ frac{partial f}{partial z} = frac{xy}{sqrt{xyz}} $$ Вычисляем значения производных в точке $ M bigg (frac{pi}{2},frac{3pi}{2},3 bigg ) $: $$ frac{partial f}{partial x} bigg |_{M(frac{pi}{2},frac{3pi}{2},3)} = cos(frac{pi}{2}+3pi)+ frac{frac{9pi}{2}}{sqrt{frac{9pi^2}{4}}} = cos frac{7pi}{2} + sqrt{9} = 3 $$ $$ frac{partial f}{partial y} bigg |_{M(frac{pi}{2},frac{3pi}{2},3)} = 2 cos(frac{pi}{2}+3pi) + frac{frac{3pi}{2}}{sqrt{frac{9pi^2}{4}}} = 2 cos frac{7pi}{2} + 1 = 2 cdot 0 + 1 = 1 $$ $$ frac{partial f}{partial y} bigg |_{M(frac{pi}{2},frac{3pi}{2},3)} = frac{frac{3pi^2}{4}}{sqrt{frac{9pi^2}{4}}} = sqrt{frac{pi^2}{4}} = frac{pi}{2} $$ Подставляем вычисленные недостающие данные в формулу и получаем: $$ grad f = 3 cdot overline{i}+ 1 cdot overline{j} + frac{pi}{2} cdot overline{k} = 3overline{i}+overline{j}+frac{pi}{2} overline{k} $$ Записываем ответ в координатной форме: $$ grad f = (3,1,frac{pi}{2}) $$

Ответ

$$ grad f = (3,1,frac{pi}{2}) $$

Градиент функции

Градиент — вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины u. Другими словами, направление градиента есть направление наибыстрейшего возрастания функции.

Назначение сервиса. Онлайн калькулятор используется для нахождения градиента функции нескольких переменных. (см. пример) При этом решаются следующие задачи:

• нахождение частных производных функции, запись формулы градиента, вычисление наибольшой скорости возрастания функции в указанной точке;
• вычисление градиента в точке A, нахождение производной в точке A по направлению вектора a;
• нахождение полного дифференциала функции.

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Решение со всеми исходными формулами сохраняется в формате Word.

Полный дифференциал для функции двух переменных: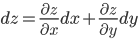

Полный дифференциал для функции трех переменных равен сумме частных дифференциалов: d f(x,y,z)=dxf(x,y,z)dx+dyf(x,y,z)dy+dzf(x,y,z)dz

Алгоритм нахождения градиента

1. Вычисление частных производных по формуле:

   

2. Вычисление частных производных в точке A.
3. Нахождение направляющих углов вектора a.
4. Вычисление производной в точке A по направлению вектора a по формуле;

   

5. Наибольшая скорость возрастания функции в указанной точке равна модулю градиента функции в этой точке.

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Частные производные функции нескольких
переменных, по своему смыслу, характеризуют
скорость изменения функции по направлениям
осей координат. Вполне естественно
выяснить с какой скоростью изменяется
функция в данной точке

в фиксированном направлении, задаваемом
вектором

.
Ответ на этот вопрос дает понятие
производной в точке

по
направлению вектора

.
Опуская точное определение такой
производной, которая естественно
является пределом отношения приращения
функции к приращению аргумента,
вычисленному в заданном направлении,
приведем формулы для её вычисления.

Для дифференцируемой функции трех
переменных

,
производная в направлении вектора

:

,
где

— направляющие косинусы вектора

,
которые вычисляются по формулам

,

,

и являются координатами единичного
вектора

того же направления:

.

Для дифференцируемой функции двух
переменных

формулы аналогичны, только будет
отсутствовать третья координата.

Определение. Градиентом функции

называется
вектор

,
координаты которого равны соответственно
частным производным

и

в точке

,
то есть

.

Для функции трех переменных

имеем

.

Используя определение градиента,
формулы для вычисления производной по
направлению можно записать в виде
скалярного произведения двух векторов:

или

Из этих формул, с учетом определения
скалярного произведения,

,
следуют основные свойства градиента:

• градиент
  это вектор, направленный в сторону
  максимального роста функции
  
  ,
  то есть производная по направлению в
  данной точке принимает максимальное
  значение в направлении её градиента
  в этой точке;

• модуль
  градиента равен максимальной производной
  по направлению.

• градиент
  перпендикулярен линии (поверхности)
  уровня функции;

Пример 1. Найти градиент функции

и
его модуль в точке

,
и вычислить производную по направлению
вектора

.

Решение.1)Вычисляем

.
Подставляя координаты точки

,
получим

.
Модуль, полученного вектора

.

2) Вычисляем единичный вектор заданного
направления

.
Производная по направлению равна

=

.

Пример 2. Найти вектор нормальный
к линиям уровня функции

.

Решение. Поскольку градиент функции
перпендикулярен линиям уровня этой
функции в произвольной точке, получим

,
значит, вектор

— нормальный вектор к линиям уровня

,
которые образовывают множество
параллельных прямых, перпендикулярных
вектору

.

7.7. Экстремум функции двух переменных

Определение. Точка

является точкой максимума (минимума)
функции

,
если существует окрестность этой точки
такая, что для всех точек

из
этой окрестности

(

).

Максимум или минимум, как и ранее,
называют экстремумом. Далее, в силу
простоты и наглядности, исследование
на экстремум проведем для функций двух
переменных

,
тем более, что идеи и последовательность
действий такие же, как и для функции
одной переменной.

Прежде всего, находим стационарные
точки, то есть точки в которых
обращаются в нуль обе частные производные
– необходимое условие экстремума,
то есть решаем систему уравнений:

Пусть, например, точка

является решением этой системы, то
есть – стационарная точка. Для
того, чтобы выяснить будет ли в этой
точке экстремум, используем следующие
достаточные условия существования
экстремума в стационарной точке.

1) Находим частные производные второго
порядка исследуемой функции и вычисляем
их значения в точке

,
обозначая:

;

;

.

2) Составим определитель

.

3) Если

,
то в точке

будет экстремум:

• максимум,
  если
  

• минимум,
  если
  

4) Если

,
то в точке

нет экстремума.

5) Если

,
то требуется дальнейшее исследование.

Пример. Исследовать на экстремум
функцию

Решение. 1) Ищем стационарные точки:

Из второго уравнения системы получим

,
подставляя это значение в первое
уравнение, после очевидных вычислений
имеем

.
Таким образом далее предстоит исследовать
единственную стационарную точку

.

2) Находим производные второго порядка
данной функции:

;

;

.

3) Вычисляем значения вторых производных
в стационарной точке:

;

;

.

4) Составляем определитель

,
т.к.

,
то в точке

есть экстремум, а так как

,
это минимум.

5) Находим

.

Замечание. Исследование на наибольшее
и наименьшее значение функции нескольких
переменных непрерывной в замкнутой
ограниченной области подобно исследованию
функции одной переменной на замкнутом
промежутке
.
Сначала ищутся критические точки внутри
области и вычисляются значения функции
в этих критических точках. Затем находят
наибольшее и наименьшее значения
функции на границе области. И в заключение,
из всех полученных значений выбирают
наибольшее и наименьшее, которые и
являются решением задачи.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Пусть F(x,y,z)F(x,y,z) – функция трех переменных, (x,y,z)(x,y,z) – декартовы координаты.

Градиентом функции F(x,y,z)F(x,y,z) называется векторное поле

∇F(x,y,z)=∂F∂xi+∂F∂yj+∂F∂zk,
nabla F(x,y,z)=frac{partial F}{partial x}mathbf{i}+frac{partial F}{partial y}mathbf{j}+frac{partial F}{partial z}mathbf{k},

где ∂F∂xfrac{partial F}{partial x}, ∂F∂yfrac{partial F}{partial y} и ∂F∂zfrac{partial F}{partial z} – частные производные функции F(x,y,z)F(x,y,z), а imathbf{i}, jmathbf{j} и kmathbf{k} – базис декартовой системы координат (x,y,z)(x,y,z).

Иногда градиент обозначается так: grad⁡F(x,y,z)operatorname{grad} F(x,y,z).

Градиент функции в данной точке показывает направление наибольшего роста функции.

Пример 1

Найти градиент функции F(x,y,z)=ln⁡(x2+y2+z2)F(x,y,z)=ln(x^2+y^2+z^2) в точке M(1,2,3)M(1,2,3).

Вычислим частные производные:
∂F∂x=∂∂xln⁡(x2+y2+z2)=2xx2+y2+z2,
frac{partial F}{partial x}=frac{partial }{partial x}ln(x^2+y^2+z^2)=frac{2x}{x^2+y^2+z^2},

∂F∂y=∂∂yln⁡(x2+y2+z2)=2yx2+y2+z2,
frac{partial F}{partial y}=frac{partial }{partial y}ln(x^2+y^2+z^2)=frac{2y}{x^2+y^2+z^2},

∂F∂z=∂∂zln⁡(x2+y2+z2)=2zx2+y2+z2.
frac{partial F}{partial z}=frac{partial }{partial z}ln(x^2+y^2+z^2)=frac{2z}{x^2+y^2+z^2}.

Градиент в точке M(1,2,3)M(1,2,3) (подставляем в формулы для частных производных значения x=1x=1, y=2y=2, z=3z=3):

∇F(M)=17  i+27  j+37  k=17  OM→.
nabla F(M)=frac{1}{7},,mathbf{i}+frac{2}{7},,mathbf{j}+frac{3}{7},,mathbf{k}=frac{1}{7},,overrightarrow{OM}.

Производная по направлению

Пусть FF – функция на плоскости или в пространстве.

Производной функции FF по направлению вектора amathbf{a} в точке MM называется число

∂F∂a(M)=1∥a∥ddεF(M+εa)∣ε=0,
frac{partial F}{partialmathbf{a}}(M)=frac{1}{|mathbf{a}|}left.frac{d}{dvarepsilon}Fleft(M+varepsilon mathbf{a}right)right|_{varepsilon=0},

если производная в правой части существует.

Пример 2

Найдем производную функции F(x,y,z)=x2y−y2z+z2xF(x,y,z)=x^2y-y^2z+z^2x по направлению вектора a=i−2j+2kmathbf{a}=mathbf{i}-2mathbf{j}+2mathbf{k} в точке M(−1,0,1)M(-1,0,1).

Вычисляем значение функции в точке M+εaM+varepsilon mathbf{a} с координатами (−1+ε,−2ε,1+2ε)(-1+varepsilon,-2varepsilon,1+2varepsilon):

F(M+εa)=(−1+ε)2(−2ε)−(−2ε)2(1+2ε)+(1+2ε)2(−1+ε)=−6ε3−5ε−1.
Fleft(M+varepsilon mathbf{a}right)=(-1+varepsilon)^2(-2varepsilon)-(-2varepsilon)^2(1+2varepsilon)+(1+2varepsilon)^2(-1+varepsilon)=-6{varepsilon^{3}}-5varepsilon-1.

Длина вектора amathbf{a}:

∥a∥=a12+a22+a32=12+(−2)2+22=9=3.
|mathbf{a}|=sqrt{a_1^2+a_2^2+a_3^2}=sqrt{1^2+(-2)^2+2^2}=sqrt{9}=3.

Производная по направлению:
∂F∂a(M)=1∥a∥ddεF(M+εa)∣ε=0=13ddε(−6ε3−5ε−1)∣ε=0=−53
frac{partial F}{partialmathbf{a}}(M)=frac{1}{|mathbf{a}|}left.frac{d}{dvarepsilon}Fleft(M+varepsilon mathbf{a}right)right|_{varepsilon=0}=frac{1}{3}left.frac{d}{dvarepsilon}left(-6{varepsilon^{3}}-5varepsilon-1right)right|_{varepsilon=0}=-frac{5}{3}

Выражение производной по направлению через градиент

Используя формулу Тейлора для функций нескольких переменных, легко получить выражение производной по направлению через градиент. Действительно, из равенства

F(M+εa)=F(M)+ε(∇F(M),a)+o(ε2)Fleft(M+varepsilon mathbf{a}right)=F(M)+varepsilonleft(nabla F(M),mathbf{a}right)+oleft(varepsilon^2right)

следует, что

ddεF(M+εa)∣ε=0=(∇F(M),a).
left.frac{d}{dvarepsilon}Fleft(M+varepsilon mathbf{a}right)right|_{varepsilon=0}=left(nabla F(M),mathbf{a}right).

Таким образом,

∂F∂a(M)=(∇F(M),a)∥a∥.
frac{partial F}{partialmathbf{a}}(M)=frac{left(nabla F(M),mathbf{a}right)}{|mathbf{a}|}.

Пример 2′2′

Найдем производную функции F(x,y,z)=x2y−y2z+z2xF(x,y,z)=x^2y-y^2z+z^2x по направлению вектора a=i−2j+2kmathbf{a}=mathbf{i}-2mathbf{j}+2mathbf{k} в точке M(−1,0,1)M(-1,0,1) используя градиент.

Частные производные:

∂F∂x(M)=2xy+z2∣(x,y,z)=(−1,0,1)=1,
frac{partial F}{partial x}(M)=left.2xy+z^2right|_{(x,y,z)=(-1,0,1)}=1,

∂F∂y(M)=x2−2yz∣(x,y,z)=(−1,0,1)=1,
frac{partial F}{partial y}(M)=left.x^2-2yzright|_{(x,y,z)=(-1,0,1)}=1,

∂F∂z(M)=−y2+2zx∣(x,y,z)=(−1,0,1)=−2.
frac{partial F}{partial z}(M)=left.-y^2+2zxright|_{(x,y,z)=(-1,0,1)}=-2.

Градиент:

∇F(M)=i+j−2k.
nabla F(M)=mathbf{i}+mathbf{j}-2mathbf{k}.

Скалярное произведение:

(∇F(M),a)=(i+j−2k,i−2j+2k)=1−2−4=−5.
left(nabla F(M),mathbf{a}right)=left(mathbf{i}+mathbf{j}-2mathbf{k},mathbf{i}-2mathbf{j}+2mathbf{k}right)=1-2-4=-5.

Производная по направлению:

∂F∂a(M)=(∇F(M),a)∥a∥=−53.
frac{partial F}{partialmathbf{a}}(M)=frac{left(nabla F(M),mathbf{a}right)}{|mathbf{a}|}=-frac{5}{3}.

Тест по теме “Градиент функции. Производная по направлению”

Рассмотрим функцию $z=f(x,y)$, которая определена в некоторой области в пространстве $Oxy$.

Для заданной функции определим вектор, для которого проекциями на оси координат являются значения частных производных заданной функции в некоторой точке $frac{partial z}{partial x} ;frac{partial z}{partial y} $.

«Градиент заданной функции» 👇

Рассмотрим функцию $w=f(x,y,z)$, которая определена в некоторой области в пространстве $Oxyz$.

Для заданной функции определим вектор, для которого проекциями на оси координат являются значения частных производных заданной функции в некоторой точке $frac{partial z}{partial x} ;frac{partial z}{partial y} $.

Перечислим некоторые свойства градиента:

• Производная заданной функции в заданной точке по направлению некоторого вектора $overrightarrow{s} $ имеет наибольшее значение, если направление данного вектора $overrightarrow{s} $ совпадает с направлением градиента. При этом данное наибольшее значение производной совпадает с длиной вектора градиента, т.е. $|overrightarrow{gradw} |$.

• Производная заданной функции по направлению вектора, который перпендикулярен к вектору градиента, т.е. $overrightarrow{gradw} $, равна 0. Так как $varphi =frac{pi }{2} $, то $cos varphi =0$; следовательно, $frac{partial w}{partial s} =|overrightarrow{gradw} |cdot cos varphi =0$.