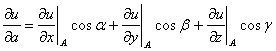Как найти градиент в точке онлайн калькулятор - Исправление недочетов и поиск решений вместе с Examum.ru

Градиент функции

Градиент — вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины u. Другими словами, направление градиента есть направление наибыстрейшего возрастания функции.

Назначение сервиса. Онлайн калькулятор используется для нахождения градиента функции нескольких переменных. (см. пример) При этом решаются следующие задачи:

нахождение частных производных функции, запись формулы градиента, вычисление наибольшой скорости возрастания функции в указанной точке;
вычисление градиента в точке A, нахождение производной в точке A по направлению вектора a;
нахождение полного дифференциала функции.

Шаг №1
Шаг №2
Видеоинструкция
Оформление Word

Решение со всеми исходными формулами сохраняется в формате Word.

Полный дифференциал для функции двух переменных: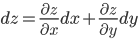

Полный дифференциал для функции трех переменных равен сумме частных дифференциалов: d f(x,y,z)=d_xf(x,y,z)dx+d_yf(x,y,z)dy+d_zf(x,y,z)dz

Алгоритм нахождения градиента

Вычисление частных производных по формуле:
Вычисление частных производных в точке A.
Нахождение направляющих углов вектора a.
Вычисление производной в точке A по направлению вектора a по формуле;
Наибольшая скорость возрастания функции в указанной точке равна модулю градиента функции в этой точке.

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Источник

Градиент функции — это вектор координатами которого являются частные производные этой функции по всем её переменным.

Градиент обозначается символом набла
. Выражение градиента некоторой функции

записывается следующим образом:

где
,
,
—
частные производные функции

по переменным
,
,

соответственно.

Вектор градиента указывает направление наискорейшего роста функции. Рассмотрим график функции
.

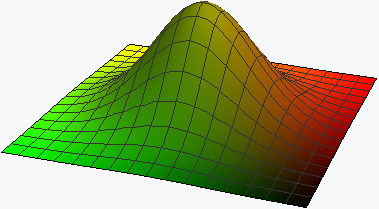
Эта функция достигает своего единственного максимума в точке
.
График градиентного поля данной функции имеет вид:

Из данного градика видно, что в каждой точке вектор градиента направлен в сторону наискорейшего роста функции, т.е. в точку
. При этом
модуль вектора
отражает скорость роста (крутизну подъёма) функции в этом направлении.

Задача
вычисления градиента
функции очень часто возникает при поиске
эстремумов функции
с использованием различных численных методов.

Наш онлайн калькулятор позволяет вычислить градиент практически любой функции как общем виде, так и в конкретной точке с описанием подробного хода решения на русском языке.

Источник

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	— twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{»}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Радианы}	mathrm{Степени}	square!	(	)	%	mathrm{очистить}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	—
pi	e	x^{square}	0	.	bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

градиент:3x^{2}yz+6xy^{2}z^{3}
градиент:sqrt{x^{2}+y^{2}},:at(2,2)
градиент:y^{2}z+2xz^{2},2xyz,xy^{2}+2x^{2}z
градиент:x^{2}+y^{2}+2xy,:at(1,2)
Показать больше

Описание

Шаг за шагом найти градиент функции в заданных точках

gradient-calculator

Блог-сообщения, имеющие отношение к Symbolab

Advanced Math Solutions – Ordinary Differential Equations Calculator, Exact Differential Equations

In the previous posts, we have covered three types of ordinary differential equations, (ODE). We have now reached…

Введите Задачу

Сохранить в блокнот!

Войти

Источник

Инструкции:

Используйте этот калькулятор градиента, чтобы вычислить вектор частных производных для многомерной функции, которую вы предоставляете, показывая все шаги. Пожалуйста, введите многопараметрическую функцию в форму ниже.

Калькулятор градиента

Этот калькулятор градиента с шагами поможет вам найти вектор градиента данной многомерной функции, которую вы предоставляете. Эта функция должна быть допустимой, дифференцируемой функцией с 2 или более переменными.

Предоставляемая вами функция должна сопровождаться полным определением имени переменной и функции, например f(x, y) = x^2 + y^2 или f(x,y,z) = xy+z*sin. (ху) и т. д.

Как только действительная функция с несколькими переменными предоставлена, все, что осталось сделать, это нажать кнопку «Рассчитать», чтобы получить все показанные шаги.

Градиенты представляют собой естественное расширение производных для ситуации с несколькими переменными, в которой скорость изменения лучше определяется вектором, чем числом.

Что такое градиент

Проще говоря, градиент — это вектор, содержащий все частные производные первого порядка функции многих переменных (f). Тогда для функции двух переменных (f(x, y)) ее градиент будет двумерным вектором (nabla f(x, y) = displaystyle left(frac{partial f}{partial x}, frac{partial f}{partial y}right)).

Точно так же для функции трех переменных (f(x, y, z) ее градиентом будет трехмерный вектор (nabla f(x, y, z) = displaystyle left(frac{partial f}{partial x}, frac{partial f}{partial y}, frac{partial f}{partial z}right)) и так далее.

Шаги для вычисления градиента

Шаг 1:

Определите функцию f, с которой вы хотите работать, и укажите количество задействованных переменных.
Шаг 2:

Найдите первый заказ

Частичная производная

по каждой из переменных
Шаг 3:

Создайте градиент как вектор, который содержит все частные производные первого порядка, найденные на шаге 2.

При желании вы можете упростить, если это возможно, после завершения шага 3. Затем с помощью градиента у вас есть версия того, что является производной для одномерной функции, в данном случае для многомерной функции.

Применение градиента

Так же, как и в случае одномерных функций при поиске критических точек нам нужно найти точки, в которых производная равна нулю, для многомерных функций нам нужно искать точки, в которых градиент равен нулю, чтобы найти критические точки.

Кроме того, эквивалент тестов второй производной представлен в виде правила Гессе для многомерных функций.

Советы и рекомендации

Помните, что

Градиент

определяется для многомерных функций с двумя или более переменными. Также имейте в виду, что градиент — это вектор, где каждый из компонентов — это функция. Точнее, каждый из его компонентов представляет собой

Частичная производная

первого порядка.

В качестве проверки своей работы не забывайте, что градиент — это вектор, размерность которого равна количеству независимых переменных, определенных в функции.

Пример: калькулятор градиента

Найдите градиент, связанный с функцией: (f(x,y,z)=x^2+y^2+z^2)

Отвечать:

Мы рассматриваем следующую многомерную функцию: (displaystyle f(x,y,z)=x^2+y^2+z^2), поэтому нам нужно вычислить ее градиент.

Дифференцирование по (x)

( displaystyle frac{partial }{partial x}left(x^2+y^2+z^2right))

By linearity, we know (frac{partial }{partial x}left( x^2+y^2+z^2 right) = frac{partial }{partial x}left(x^2right)+frac{partial }{partial x}left(y^2right)+frac{partial }{partial x}left(z^2right)), so plugging that in:

( displaystyle = ,,)

(displaystyle frac{partial }{partial x}left(x^2right)+frac{partial }{partial x}left(y^2right)+frac{partial }{partial x}left(z^2right))

Since the derivative of a constant with respect to (x) is 0, we get that:

( displaystyle = ,,)

(displaystyle frac{partial }{partial x}left(x^2right))

We can use the Power Rule for polynomial terms: (frac{partial }{partial x}left( x^2 right) = 2x)

( displaystyle = ,,)

(displaystyle 2x)

Дифференцирование по (y)

( displaystyle frac{partial }{partial y}left(x^2+y^2+z^2right))

By linearity, we know (frac{partial }{partial y}left( x^2+y^2+z^2 right) = frac{partial }{partial y}left(x^2right)+frac{partial }{partial y}left(y^2right)+frac{partial }{partial y}left(z^2right)), so plugging that in:

( displaystyle = ,,)

(displaystyle frac{partial }{partial y}left(x^2right)+frac{partial }{partial y}left(y^2right)+frac{partial }{partial y}left(z^2right))

Since the derivative of a constant with respect to (y) is 0, we find that:

( displaystyle = ,,)

(displaystyle frac{partial }{partial y}left(y^2right))

We use the Power Rule for polynomial terms: (frac{partial }{partial y}left( y^2 right) = 2y)

( displaystyle = ,,)

(displaystyle 2y)

Дифференцирование по (z)

( displaystyle frac{partial }{partial z}left(x^2+y^2+z^2right))

By linearity, we know (frac{partial }{partial z}left( x^2+y^2+z^2 right) = frac{partial }{partial z}left(x^2right)+frac{partial }{partial z}left(y^2right)+frac{partial }{partial z}left(z^2right)), so plugging that in:

( displaystyle = ,,)

(displaystyle frac{partial }{partial z}left(x^2right)+frac{partial }{partial z}left(y^2right)+frac{partial }{partial z}left(z^2right))

The derivative of a constant with respect to (z) is 0, so then:

( displaystyle = ,,)

(displaystyle frac{partial }{partial z}left(z^2right))

We use the Power Rule for polynomial terms: (frac{partial }{partial z}left( z^2 right) = 2z)

( displaystyle = ,,)

(displaystyle 2z)

Заключение:

Следовательно, можно сделать вывод, что градиент заданной функции (displaystyle f(x,y,z)=x^2+y^2+z^2 ) равен:

[ nabla f = left(2x,2y,2zright)]

Пример расчета градиента

Для следующей функции: (f(x, y) = xy) найдите ее градиент.

Отвечать:

Для этого примера у нас есть функция двух переменных x и y: (displaystyle f(x,y)=xy).

Во-первых, дифференцируя по x

( displaystyle frac{partial }{partial x}left(xyright))

Поскольку это постоянное время (x), мы сразу получаем: (frac{partial }{partial x}left( xy right) = y)

( displaystyle = ,,)

(displaystyle y)

Теперь продифференцируем по y

( displaystyle frac{partial }{partial y}left(xyright))

Поскольку это постоянное время (y), мы сразу получаем: (frac{partial }{partial y}left( xy right) = x)

( displaystyle = ,,)

(displaystyle x)

Заключение:

Непосредственно получаем, что градиент функции (displaystyle f(x,y)=xy ) равен:

[ nabla f = left(y, xright)]

Еще примеры градиентов

Вычислите соответствующий градиент ( f(x, y) = x^2 — y^2 — xy ).

Отвечать:

Наконец, в этом примере необходимо проанализировать следующую функцию: (displaystyle f(x,y)=x^2-y^2-xy). Поскольку это многомерная функция, имеет смысл вычислить ее градиент.

Шаг 2: Найдите производную относительно (x)

( displaystyle frac{partial }{partial x}left(x^2-xy-y^2right))

По линейности мы знаем (frac{partial }{partial x}left( x^2-xy-y^2 right) = frac{partial }{partial x}left(x^2right)-frac{partial }{partial x}left(xyright)-frac{partial }{partial x}left(y^2right)), поэтому подключаем это:

( displaystyle = ,,)

(displaystyle frac{partial }{partial x}left(x^2right)-frac{partial }{partial x}left(xyright)-frac{partial }{partial x}left(y^2right))

Производная константы по (x) равна 0, поэтому тогда:

( displaystyle = ,,)

(displaystyle frac{partial }{partial x}left(x^2right)-frac{partial }{partial x}left(xyright))

Поскольку это постоянное время (x), мы напрямую получаем: (frac{partial }{partial x}left( xy right) = y), и мы можем использовать правило степени для полиномиальных членов: (frac{partial }{partial x}left( x^2 right) = 2x)

( displaystyle = ,,)

(displaystyle 2x-y)

Шаг 2: Найдите производную относительно (y)

( displaystyle frac{partial }{partial y}left(x^2-xy-y^2right))

По линейности мы знаем (frac{partial }{partial y}left( x^2-xy-y^2 right) = frac{partial }{partial y}left(x^2right)-frac{partial }{partial y}left(xyright)-frac{partial }{partial y}left(y^2right)), поэтому подключаем это:

( displaystyle = ,,)

(displaystyle frac{partial }{partial y}left(x^2right)-frac{partial }{partial y}left(xyright)-frac{partial }{partial y}left(y^2right))

Мы используем степенное правило для полиномиальных членов: (frac{partial }{partial y}left( y^2 right) = 2y), и, поскольку это константа, умноженная на (y), мы напрямую получаем: (frac{partial }{partial y}left( xy right) = x)

( displaystyle = ,,)

(displaystyle frac{partial }{partial y}left(x^2right)-x-2y)

( displaystyle = ,,)

(displaystyle 0-x-2y)

Путем реорганизации/упрощения/расширения терминов, поддающихся

( displaystyle = ,,)

(displaystyle -x-2y)

Заключение:

Следовательно, можно сделать вывод, что градиент заданной функции (displaystyle f(x,y)=x^2-y^2-xy ) равен:

[ nabla f = left(2x-y,-x-2yright)]

Другие производные калькуляторы

Используя

производный калькулятор

определенно может облегчить вашу жизнь, поскольку позволит вам отслеживать все

Правила производных

Большинство из

правила дифференциации

используемые для одномерных функций, имеют эквивалент для многомерных функций. Таким образом,

Правило цепи

Правило Продукта

а также

правило квоты

также будет работать для многомерной функции, учитывая правильные размеры.

Источник

Find function gradient step by step

The calculator will find the gradient of the given function (at the given point if needed), with steps shown.

Enter a function:

Enter the order of variables and/or a point:

If you don’t need the order of variables, leave it empty.

If you want a specific order of variables, enter variables comma-separated, like `x,y,z`.

If you want the gradient at a specific point, for example, at `(1, 2, 3)`, enter it as `x,y,z=1,2,3`, or simply `1,2,3` if you want the order of variables to be detected automatically.

If the calculator did not compute something or you have identified an error, or you have a suggestion/feedback, please write it in the comments below.

Solution

Your input: find the gradient of $$$f=x^{3} + y^{5}$$$at $$$left(x,yright)=left(1,7right)$$$

To find the gradient of a function (which is a vector), differentiate the function with respect to each variable.

$$$nabla f = left(frac{partial f}{partial x},frac{partial f}{partial y}right)$$$

$$$frac{partial f}{partial x}=3 x^{2}$$$ (for steps, see derivative calculator)

$$$frac{partial f}{partial y}=5 y^{4}$$$ (for steps, see derivative calculator)

Finally, plug in the point:

$$$nabla f left(1,7right)=left(3,12005right)$$$

Answer

$$$nabla left(x^{3} + y^{5}right) left(x,yright)=left(3 x^{2},5 y^{4}right)$$$

$$$nabla left(x^{3} + y^{5}right)|_{left(x,yright)=left(1,7right)}=left(3,12005right)$$$

Источник