ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Наиболее простым и наглядным методом решения задачи линейного программирования (ЗЛП) является графический метод. Он основан на геометрической интерпретации задачи линейного программирования и применяется при решении ЗЛП с двумя неизвестными:
Будем рассматривать решение этой задачи на плоскости. Каждое неравенство системы функциональных ограничений геометрически определяет полуплоскость с граничной прямой апх, + + aj2х2 = bn i = 1, т. Условия неотрицательности определяют полуплоскости с граничными прямыми х <= 0, х2 = 0 соответственно. Если система совместна, то полуплоскости, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек; координаты каждой из этих точек являются решением данной системы. Совокупность этих точек называют многоугольником решений. Он может быть точкой, отрезком, лучом, ограниченным и неограниченным многоугольником.
Геометрически ЗЛП представляет собой отыскание такой угловой точки многоугольника решений, координаты которой доставляют максимальное (минимальное) значение линейной целевой функции, причем допустимыми решениями являются все точки многоугольника решений.
Линейное уравнение описывает множество точек, лежащих на одной прямой. Линейное неравенство описывает некоторую область на плоскости.
Определим, какую часть плоскости описывает неравенство 2х <+ Зх2 0, j = 1, п). Координаты любой точки, принадлежащей области определения, являются допустимым решением задачи.
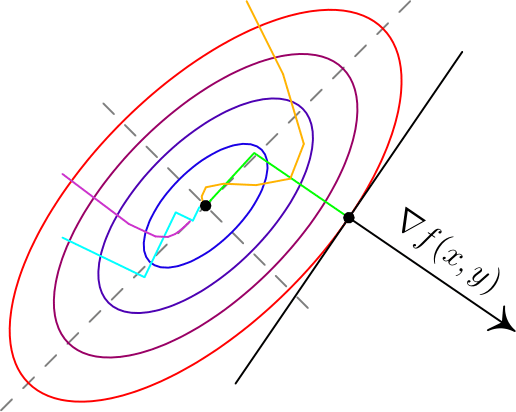
Для нахождения экстремального значения целевой функции при графическом решении ЗЛП используют вектор-градиент, координаты которого являются частными производными целевой функции:
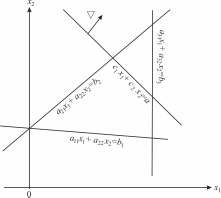
Этот вектор показывает направление наискорейшего изменения целевой функции. Прямая c[xl + с2х2 = f(x0), перпендикулярная вектору-градиенту, является линией уровня целевой функции (рис. 2.2.2). В любой точке линии уровня целевая функция принимает одно и то же значение. Приравняем целевую функцию постоянной величине а. Меняя значение а, получим семейство параллельных прямых, каждая из которых является линией уровня целевой функции.
Рис. 2.2.2. Вектор-градиент и линии уровня
Важное свойство линии уровня линейной функции состоит в том, что при параллельном смещении линии в одну сторону уровень только возрастает, а при смещении в д р у г у ю сторону — только убывает.
Графический метод решения ЗЛП состоит из четырех этапов:
- 1. Строится область допустимых решений (ОДР) ЗЛП.
- 2. Строится вектор-градиент целевой функции (ЦФ) с началом в точке х0 (0; 0): V = (с,, с2).
- 3. Линия уровня CjXj + с2х2 = а (а — постоянная величина) — прямая, перпендикулярная вектору-градиенту V, — передвигается в направлении вектора-градиента в случае максимизации целевой функции f(xv х2) до тех пор, пока не покинет пределов ОДР. При минимизации /(*,, х2) линия уровня перемещается в направлении, противоположном вектору-градиенту. Крайняя точка (или точки) ОДР при этом движении и является точкой максимума (минимума) f(xpjc2).
Если прямая, соответствующая линии уровня, при своем движении не покидает ОДР, то минимума (максимума) функции f(xр х2) не существует.
Если линия уровня целевой функции параллельна функциональному ограничению задачи, на котором достигается оптимальное значение ЦФ, то оптимальное значение ЦФ будет достигаться в любой точке этого ограничения, лежащей между двумя оптимальными угловыми точками, и, соответственно, любая из этих точек является оптимальным решением ЗЛП.
4. Определяются координаты точки максимума (минимума). Для этого достаточно решить систему уравнений прямых, дающих в пересечении точку максимума (минимума). Значение f(x<, х2), найденное в полученной точке, является максимальным (минимальным) значением целевой функции.
Возможные ситуации графического решения ЗЛП представлены в табл. 2.2.1.
Как построить вектор градиента целевой функции
Графический метод характеризуется простотой и наглядностью, однако он недостаточно точен и применим только для задач с не более чем тремя переменными. Последнее обусловлено тем, что человек, живущий в трехмерном пространстве, практически не способен представить себе визуально пространство более высокого порядка.
Метод основан на том, что каждое ограничение неравенство отсекает в n -мерном пространстве n -мерную полуплоскость (в данной курсовой работе это двухмерное пространство (плоскость) и простая полуплоскость). Совокупность этих полуплоскостей (если ограничения совместны) образует n -мерный многогранник допустимых решений. Оптимальное решение достигается в одной из вершин многогранника. Для определения этой вершины необходимо построить поверхность уровня целевой функции (в курсовом проекте линию уровня). Затем следует перемещать эту поверхность (линию) в направлении градиента до крайней точки области допустимых решений (ОДР).
Рассмотрим следующий простой пример решения задачи линейного программирования (ЗЛП) графическим методом.
Математическая модель: 2Х1+3Х2≤60;
3Х1+2Х2≤60;
4Х1+20Х2≤200;
Х1≥0; Х2≥0;
F=40Х1+30Х2→Мах.
Перейдем от неравенств к равенствам: 2Х1+3Х2=60;
3Х1+2Х2=60;
4Х1+20Х2=200.
Это уравнения прямых линий, которые могут быть легко построены по двум точкам:
для первого ограничения Х1=0; Х2=20;
Х2=0; Х1=30.
для второго ограничения Х1=0; Х2=30;
Х2=0; Х1=20.
для третьего ограничения Х1=0; Х2=10;
Х2=0; Х1=50.
Градиент целевой функции это вектор, характеризующий направление и скорость изменения функции (в данном случае целевой функции). Он определяется ее частными производными по каждой переменной:
Линия уровня целевой функции перпендикулярна градиенту.
Графическое решение данной задачи приведено на рисунке 6.1.
Рис. 6.1. Графическое решение задачи
Область допустимых решений (ОДР) в данном случае образуется четырехугольником ОВСД. Ни одна точка внутри его или на его границе не противоречит ни одному из ограничений. Оптимальное решение находится в одной из вершин четырехугольника. Для нахождения оптимального решения перемещаем линию уровня целевой функции в направлении градиента до крайней точки ОДР. Такой точкой является точка С с координатами: Х1=16; Х2=8. Значение целевой функции F=40×16+30×8=880. Очевидно, что это решение не отличается высокой точностью, что характерно для графического метода.
Из рисунка видно, что ресурсы второго и третьего видов использованы полностью, а ресурс первого вида оказался в избытке. Для количественной оценки этого избытка определим сначала расход данного ресурса: 2×16+3×8=56. Запас равен 60, тогда остаток составит 6056=4.
6.1.2. Симплексный метод решения
задач линейного программирования
В отличие от графического метода, симплексный метод абсолютно точен. Кроме того, он дает возможность для точной количественной оценки излишков имеющихся ресурсов, а применение двойственного симплекс-метода дает еще и большие возможности для технико-экономического анализа полученного решения с целью выработки обоснованных рекомендаций по улучшению условий функционирования системы.
Приведем задачу, рассмотренную в предыдущем разделе, к канонической форме: 2Х1+3Х2+Х3=60;
3Х1+2Х2+Х4=60;
4Х1+20Х2+Х5=200;
F-40Х1 -30Х2 =0.
Дополнительные переменные Х3, Х4 и Х5 равны разности между левой и правой частями ограничений и характеризуют недовыполнение данного ограничения (в данном случае излишний запас).
Задача решается в стандартных симплексных таблицах. Исходная таблица (см. табл. 6.1) заполняется коэффициентами модели.
| Базис | Х1 | Х2 | Х3 | Х4 | Х5 | а io | a io / a ip |
|---|---|---|---|---|---|---|---|
| Х3 | 2 | 3 | 1 | 0 | 0 | 60 | 20 |
| Х4 | 3 | 2 | 0 | 1 | 0 | 60 | 30 |
| Х5 | 4 | 20 | 0 | 0 | 1 | 200 | 10 |
| F | 4 | 3 | 0 | 0 | 0 | 0 |
Исходная таблица
Базисными переменными являются переменные, входящие только в одно уравнение, с коэффициентом +1. Базисным переменным соответствует единичный вектор-столбец. Базисные переменные равны свободным членам. Свободные переменные (переменные, не вошедшие в базис) равны нулю. Таким образом, Х1=0; Х2=0; Х3= 60; Х4= 60; Х5=200; F=0.
Данное решение является опорным, так как в столбце свободных членов нет отрицательных элементов.
В качестве разрешающего столбца выбирается любой столбец с отрицательной оценкой в строке целевой функции F. Выберем в данном случае в качестве разрешающего второй столбец. Для всех его элементов вычисляем симплексные отношения a io /a ip (отношение элемента столбца свободных членов к соответствующему элементу разрешающего столбца) и записываем их в последний столбец таблицы. Разрешающий элемент определяется минимальным симплексным отношением (в таблице он выделен жирным шрифтом). На месте разрешающего элемента ставится 1, а остальные элементы данного столбца равны нулю.
Остальные столбцы, соответствующие базисным переменным остаются без изменения. Столбец, соответствующий выводимой из базиса переменной, пересчитывается по общему правилу, описанному ниже. В данном случае Х2 вводится в базис вместо Х5 и столбец Х5 пересчитывается. Элементы разрешающей строки делятся на разрешающий элемент. Все остальные элементы таблицы пересчитываются по правилу прямоугольника. Пересчитываемый элемент образует с разрешающим элементом и соответствующими элементами разрешающей строки и столбца прямоугольник, изображенный на рисунке 6.2.
Рис. 6.2. Прямоугольник пересчета элементов симплексной таблицы
Пересчет производится по следующей формуле:
т.е. пересчитываемый элемент умножается на решающий элемент, минус элемент соответствующего разрешающего столбца, умноженный на соответствующий элемент разрешающей строки, и эта разность делится на разрешающий элемент. Или иначе: произведение элементов главной диагонали минус произведение элементов побочной диагонали, деленное на разрешающий элемент.
Например, пересчет элемента первого столбца первой строки:
| Базис | Х1 | Х2 | Х3 | Х4 | Х5 | а io | a io / a ip |
|---|---|---|---|---|---|---|---|
| Х3 | 1,4 | 0 | 1 | 0 | 0,15 | 30 | 21,4 |
| Х4 | 2,6 | 0 | 0 | 1 | 0,10 | 40 | 15,4 |
| Х2 | 0,2 | 1 | 0 | 0 | 0,05 | 10 | 50 |
| F | 3,4 | 0 | 0 | 0 | 0,150 | 300 |
Первая итерация расчета
Решение задачи на любой итерации читается следующим образом: базисные переменные равны свободным членам (предпоследний столбец в таблице) а свободные переменные (те, которые не входят в базис) равны нулю. В данном случае Х3 = 30; Х4 = 40; Х2 = 10; Х1 = Х5 = 0.
Или в краткой форме записи: Х1 = (0; 10; 30; 40; 0), F = 300.
Здесь значения переменных приводятся в порядке возрастания их индексов.
Технико-экономический анализ полученного решения
Выпускается десять единиц продукции второго вида (Х2 = 10). При этом ресурс второго вида останется в количестве тридцати единиц (Х3 = 30), ресурс первого вида останется в количестве сорока единиц (Х4 = 40), а ресурс третьего вида оказывается израсходованным полностью (Х5 = 0).
Проверка полученного решения: 2·0+3·10+30=60;
3·0+2·10+40=60;
4·0+20·10+0=200;
F=40·0+30·10=300.
Данное решение не является оптимальным, так как в строке целевой функции еще есть отрицательный элемент а 1F = 3,4.
Вторая и все последующие итерации выполняются аналогично.
| Базис | Х1 | Х2 | Х3 | Х4 | Х5 | а io | a io / a ip |
|---|---|---|---|---|---|---|---|
| Х3 | 0 | 0 | 1 | 0,54 | 0,1 | 8,5 | |
| Х1 | 1 | 0 | 0 | 0,38 | 0,04 | 15,4 | |
| Х2 | 0 | 1 | 0 | 0,74 | 0,17 | 6,9 | |
| F | 0 | 0 | 0 | 1,3 | 0,28 | 823 |
Вторая итерация расчета
Х2=(15,4; 6,9; 8,5; 0; 0) → F=823.
Это решение оптимально, так как в строке целевой функции нет отрицательных оценок.
Технико-экономический анализ полученного решения
При имеющихся ресурсах следует выпустить 15,4 единицы (Х1=15,4) продукции первого вида и 6,9 единицы продукции второго вида (Х2=6,9). При этом ресурсы первого вида остаются в количестве 8,5 единицы (Х3=8,5), а ресурсы второго и третьего вида израсходованы полностью (Х4=Х5=0). Прибыль составит 823 у.е.
Проверка: 2·15,4+3·6,9+8,5=60;
3·15,4+2·6,9+0=60;
4·15,4+20·6,9+0=200;
F=40·15,4+30·6,9=823.
Сравнение полученных результатов с результатами графического метода подтверждает, что графический метод при всей своей наглядности не отличается достаточной точностью.
© ФГОУ ВПО Красноярский государственный аграрный университет
Как построить вектор градиента целевой функции
ПРИМЕР ГРАФИЧЕСКОГО РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Построение градиента и определение оптимального плана
Обратимся к целевой функции. Ее градиент есть вектор (32; 27). Для решения задачи следует изобразить этот вектор в виде стрелки с началом в точке (0; 0) и концом в точке (32; 27).
Такая стрелка является короткой и поэтому плохо различимой на чертеже. Однако длина этой стрелки не играет никакой роли при решении задачи. Важно лишь ее направление. Если обе координаты точки (32; 27) умножить или разделить на одно и то же положительное число, то изменится лишь длина стрелки, но не ее направление. Поэтому на результате решения задачи это не скажется.
Удлиним стрелку до границы нашего рисунка ( Рис. 2.5 ).
Все линии уровня целевой функции параллельны друг другу и перпендикулярны градиенту. На Рис. 2.5 пунктиром изображены линии, соответствующие различным значениям целевой функции, начиная от 10000 и с шагом 16000. Разумеется, такие линии могут быть построены для любых значений целевой функции, они параллельны и все вместе покрывают координатную плоскость.
Градиент показывает направление роста целевой функции. Мы решаем задачу на максимум. Чем больше значение целевой функции, тем лучше. Однако при слишком больших значениях пунктирная линия уровня окажется за пределами области допустимых планов.
Рис. 2 . 6 . Построение оптимального плана
В своем крайнем положении линия уровня проходит через точку L . Таким образом, точка L является оптимальным планом задачи. Это единственная точка, принадлежащая одновременно области допустимых планов и линии уровня в ее крайнем положении. Следовательно, наша задача обладает единственным оптимальным планом.
Найдем координаты оптимального плана. Приближенно их можно определить по чертежу. Для точного расчета необходимо решить соответствующую систему уравнений. Точка L лежит на границе первого и четвертого ограничений. Составляем систему уравнений:
Решив эту систему, получаем компоненты оптимального плана: x 1 = 1250 и x 2 = 667. Таким образом, оптимальный план X*max равен:
.
Он предписывает выпустить 1250 кг Печенья и 667 (точнее, 666,667) кг Бисквитов.
Для определения оптимума следует подставить компоненты оптимального плана в целевую функцию задачи. Оптимум Z*max определяется равенством:
.
Таким образом, реализация выпущенной продукции даст выручку в размере 58000 руб. Задача решена. Теперь следует обратиться к экономическому содержанию задачи и проанализировать полученный результат.
Рассмотрим, для полноты картины, задачу, когда при той же системе ограничений и той же целевой функции требуется найти не максимальное, а минимальное ее значение. В этой ситуации все рассуждения, связанные с построением области допустимых планов и градиента полностью сохраняются. Однако для нахождения оптимального плана следует теперь смещать линию уровня до крайнего положения в направлении, противоположном градиенту. Оптимальным планам для задачи на минимум окажется точка О — начало координат. Оптимум будет равен 0.
http://www.kgau.ru/distance/fub_03/eldeshtein/logistika/kurs/06_01.html
http://ecocyb.narod.ru/217-220/s11.htm
4.
Оптимизационные
экономико-математические модели
4.1.
Общая задача оптимизации
В
экономике оптимизационные задачи
возникают в связи с многочисленностью
возможных вариантов функционирования
предприятия, когда возникают ситуации
выбора варианта, наилучшего по некоторому
правилу или критерию, характеризуемому
соответствующей целевой функцией
(например, иметь минимум затрат, максимум
продукции).
Отличительной
особенностью оптимизационных моделей
является наличие условия нахождения
оптимального решения (критерия
оптимальности), которое записывается
в виде функционала. Эти модели при
определенных исходных данных задачи
позволяют получить множество решений,
удовлетворяющих условиям задачи, и
обеспечивают выбор оптимального решения,
отвечающего критерию оптимальности.
В
общем виде математическая постановка
задачи математического программирования
состоит в определении наибольшего или
наименьшего значения целевой функции
при ограничениях
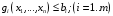
где
и
— заданные функции,
— некоторые заданные числа, а
— переменные, определяемые экономическое
содержание задачи.
Задачи
математического программирования
делятся на задачи линейного и нелинейного
программирования.
Если
все функции
и
линейные, то соответствующая задача
является задачей линейного
программирования (ЗЛП), в противном
случае перед нами задача нелинейного
программирования (ЗНП).
В
общем виде задача линейного программирования
ставится следующим образом: найти вектор
максимизирующий
линейную форму
141Equation Chapter 1 Section 4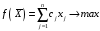
и
удовлетворяющий условиям
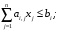
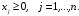
Линейная
функция (4.1) называется целевой функцией
задачи.
Условия
(4.2) называют функциональными, а (4.3) –
прямыми ограничениями задачи.
Вектор
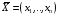
компоненты которого удовлетворяют
условиям (4.2 — 4.3), будем называть планом
или допустимым решением ЗЛП.
Все
допустимые решения образуют область
определения ЗЛП, или область допустимых
решений Допустимое решение, максимизирующие
целевую функцию (1), называют оптимальным
планом задачи
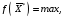
где
— оптимальное решение ЗЛП.
На
практике хорошо себя зарекомендовали
оптимизационные модели определение:
-
оптимальной
производственной программы; -
оптимального
смешения компонентов; -
оптимального
раскроя; -
оптимального
размещения предприятия некоторой
отрасли на определенной территории; -
формирования
оптимального портфеля ценных бумаг; -
транспортной
задачи.
Для
решения ЗЛП применяется метод
последовательно улучшения плана, или
симплекс-метод, который состоит из
двух вычислительных процедур:
симплекс-метода с естественным планом
и симплекс-метода с искусственным планом
(М-метод).
Выбор
конкретной вычислительной процедуры
осуществляется после приведения исходной
задачи к каноническому виду (КЗЛП) [13]:
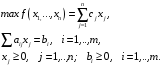
Будем
считать, что ЗПЛ записана в канонической
форме, если ее целевая функция
максимизируется, ограничения имеют вид
равенств с неотрицательной правой
частью и все переменные не отрицательные.
4.2. Графический
метод решения Задач линейного
программирования (ЗЛП)
Графический метод
решения ЗЛП является наиболее простым
и применяется для решения задач ЛП с
двумя переменными. Рассмотрим ЗЛП в
стандартной форме (4.1)-(4.3). Положим
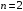
получим
(4.6)
при
условиях
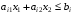
(4.7)
Система
неравенств (4.6) совместна (имеет хотя бы
одно решение). Каждое неравенство этой
системы графически определяет
полуплоскость, ограниченную прямой
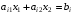
условия
не отрицательности определяют
полуплоскости с граничными прямыми
(рис. 4.1).
Рис.
4.1. Схема построения ОДР и вектора-градиента
Система совместна,
поэтому полуплоскости, как выпуклые
множества, пересекаясь, образуют общую
часть, которая является выпуклым
множеством, координаты каждой точки
которого удовлетворяют системе неравенств
(4.7). Совокупность этих точек называют
многоугольником решений. Он может
быть точкой, отрезком, лучом, ограниченным
и неограниченным многоугольником.
Таким образом,
геометрически решение ЗЛП представляет
собой отыскание такой точки многоугольника
решений, координаты которой доставляют
линейной функции цели.
Для нахождения
экстремального значения целевой функции
при графическом решении ЗЛП используют
вектор-градиент, координаты которого,
являются частными производными целевой
функции:
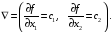
Этот вектор
показывает направление наискорейшего
изменения целевой функции. Прямая
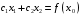
перпендикулярная вектору-градиенту,
является линией уровня целевой функции.
В любой точке
линии уровня целевая функция принимает
одно и тоже значение. Приравниваем
целевую функцию постоянной величине
«a». Меняя
значение «a»
получим семейство параллельных прямых,
каждая из которых является линией уровня
целевой функции (ЦФ).
Важное свойство
линии уровня ЦФ состоит в том, что при
параллельном смещении линии в одну
сторону уровень только возрастает, а
при смещении в другую сторону уровень
только убывает.
С геометрической
точки зрения в ЗЛП ищется такая угловая
точка или набор точек допустимого
множества решений, на котором достигается
самая верхняя (нижняя) линия уровня,
расположенная дальше (ближе) остальных
в направлении наискорейшего роста.
Графический
метод решения ЗЛП состоит из следующих
этапов:
-
строится
многоугольная ОДР ЗЛП; -
строится
вектор-градиент ЦФ в какой-нибудь точке
,
принадлежащей ОДР:
;
-
линии
уровня
(а – постоянная величина) – прямая,
перпендикулярная вектору-градиенту
,
– передвигается в направлении
этого вектора в случае максимизации
до тех пор, по не покинет ОДР. Предельная
точка (или точки) области при этом
движении является точкой максимума
;
-
для
нахождения координат точки максимума
достаточно решить два уравнения прямых,
получаемых из соответствующих ограничений
и дающих в пересечении точку максимума.
Значение
,
найденное в получаемой точке, является
максимальным.
При минимизации
(максимизации) функции
линия уровня перемещается в направлении,
противоположному вектору-градиенту.
Если прямая, соответствующая линии
уровня, при своем движении не покидает
ОДР, то минимум (максимум) функции
не существует.
Если линия уровня
параллельна какому-либо ограничению
задачи, то оптимальное значение ЦФ будет
двигаться в любой точке этого ограничения,
лежащей между двумя оптимальными
угловыми точками, и соответственно,
любая из этих точек является оптимальным
решением задачи.
Возможные ситуации
графического решения ЗЛП представлены
в табл. 4.1.
Таблица 4.1
Возможные ситуации
графического решения ЗЛП
|
№ |
Вид |
Вид |
|
1 |
Ограниченная |
Единственное |
|
Бесконечное |
||
|
2 |
Неограниченная |
ЦФ |
|
ЦФ |
||
|
Единственное |
||
|
Бесконечное |
||
|
3 |
Отрезок |
Единственное |
|
Бесконечное |
Рассмотрим
графическое решение задач линейного
программирования на следующем примере.
Пример 4.1.
Планирование
выпуска продукции пошивочного предприятия.
Намечается выпуск
костюмов двух видов – женских и мужских.
На женский костюм требуется 1 м шерсти,
2 м лавсана и 1 чел./день трудозатрат. На
мужской костюм – 3,5 м шерсти, 0,5 м лавсана
и 1 чел./день трудозатрат. Всего имеется
350 м шерсти, 240 м лавсана и 150 чел./дней
трудозатрат. Требуется определить,
сколько костюмов каждого вида необходимо
сшить, чтобы обеспечить максимальную
прибыль, если прибыль от реализации
женского костюма составляет 10 денежных
единиц, а от мужского – 20 денежных
единиц. При этом следует иметь в виду,
что необходимо сшить не менее 60 мужских
костюмов.
Экономико-математическая
модель задачи
Введем обозначения:
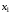
число женских костюмов;
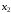
число мужских костюмов. Прибыль от
реализации женских костюмов составляет
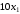
а от реализации мужских –
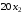
т.е. необходимо максимизировать целевую
функцию:
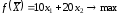
Ограничения задачи
имеют вид:
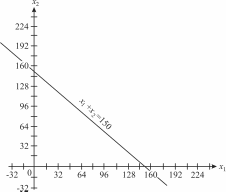
Первое ограничение
по труду

Прямая
проходит через точки
и
(рис. 4.2).
Второе ограничение
по лавсану
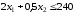
Прямая
проходит через точки
и

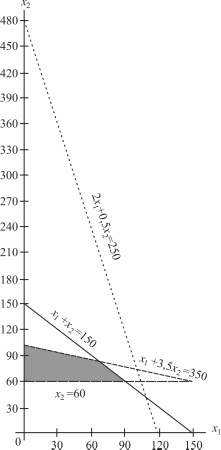
Третье ограничение по шерсти
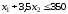
стоится аналогично. Добавим четвертое
ограничение по количеству мужских
костюмов
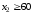
Решением этого неравенства является
полуплоскость, лежащая выше прямой
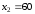
На рис. 4.3 заштрихована область допустимых
решений. Для определения направления
движения к оптимуму построим вектор
градиент

координаты которого являются частными
производными целевой функции, т.е.
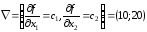
Чтобы построить
такой вектор, нужно соединить точку
с началом координат. При максимизации
целевой функции необходимо двигаться
в направлении вектора-градиента, а при
минимизации – в противоположном
направлении. Для удобства можно построить
вектор, пропорциональный вектору-градиенту.
Так, на рис. 4.4 изображен вектор-градиент
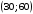
Рис.
4.2. Решением первого неравенства является
нижняя полуплоскость
Рис.
4.3. Заштрихована область допустимых
решений
Рис.
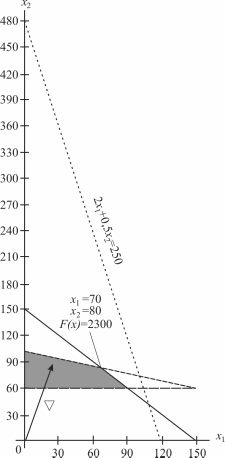
4.4. Максимум целевой функции достигается
в точке (70; 80)
В нашем случае
движение линии уровня будем осуществлять
до ее выхода из области допустимых
решений. В крайней, угловой, точке
достигается максимум целевой функции.
Для нахождения координат этой точки
достаточно решить систему из двух
уравнений прямых, получаемых из
соответствующих ограничений и дающих
в пересечении точку максимума:
Отсюда легко
записать решение исходной ЗЛП:
и достигается при
и
(рис. 4.4).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Для решения задач линейного программирования разработано множество методов, но наиболее популярными из них являются графический, симплексный и двойственный методы, которые мы и рассмотрим далее в нашей исследовательской работе.
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Возможно эта страница вам будет полезна:
Графический метод решения задач линейного программирования
Рассмотрим задачу линейного программирования в стандартной форме записи с двумя переменными
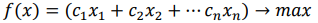
при условиях:
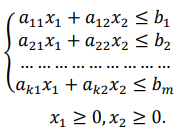
Необходимо найти вектор 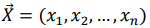
При решении, прежде всего, необходимо найти область допустимых решений системы неравенств (3.2). Рассмотрим декартову систему координат 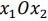
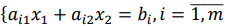
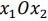
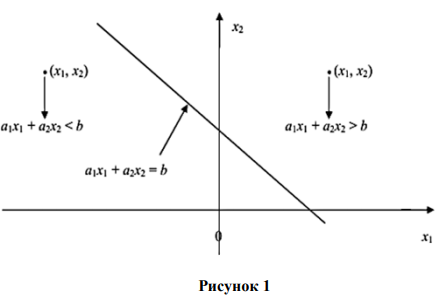
Чтобы определить, какую именно полуплоскость определяет данное неравенство, достаточно взять произвольную точку плоскости (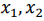
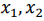
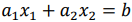
Для нахождения области допустимых решений строим граничные прямые полуплоскости, соответствующие всем неравенствам. Общая часть («пересечение») всех этих полуплоскостей будет решением системы неравенств данной задачи.
При нахождении области допустимых решений (ОДР) задачи линейного программирования может встретиться один из четырех случаев, рассмотренных в таблице 4:
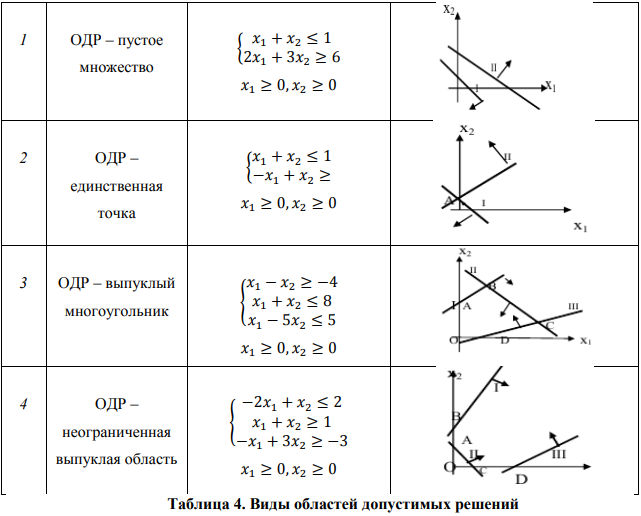
Рассмотренные примеры позволяют сделать вывод о том, что область допустимых решений системы неравенств может быть пустой, одной точкой, выпуклым многоугольником или неограниченной выпуклой областью.
Согласно теореме, описанной в предыдущем параграфе, оптимальное решение ЗЛП находится в одной из угловых точек многоугольника допустимых решений. Поэтому решение задачи с ограниченной целевой функцией и не слишком большим числом угловых точек может быть найдено перебором этих угловых точек.
Рассмотрим целевую функцию
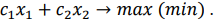
Уравнение
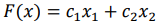
при фиксированном значении 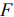
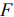
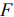
Для решения задачи необходимо среди точек области допустимых решений найти такую точку (точки), в которой целевая функция принимает максимальное значение.
Для этого построим вектор-градиент 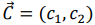
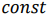
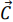
Линию уровня в направлении вектора 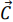
Таким образом, можно определить алгоритм геометрического (графического) решения задач линейного программирования:
- Записать уравнения прямых, соответствующих ограничениям, и построить их на плоскости
.
- Определить области, в которых выполняются ограничения задачи.
- Определить область допустимых решений задачи как область пересечения
полуплоскостей, соответствующих ограничениям задачи.
- Определить направление возрастания (убывания) целевой функции
- Определить граничную точку или точки области допустимых решений, в которых целевая функция принимает максимальное (минимальное) значение.
- Определить координаты найденной точки, решая систему уравнений, состоящую из уравнений прямых, на пересечении которых находится эта точка, или выявляя уравнение граничной прямой области допустимых решений, с которой совпадает линия уровня целевой функции.
Графический метод решения задачи линейного программирования состоит из двух этапов:
- Построение пространства допустимых решений, удовлетворяющих всем ограничениям модели.
- Поиск оптимального решения среди всех точек пространства допустимых решений.
Применение графического метода удобнее рассмотреть на конкретных примерах в двух постановках: для максимума и минимума целевой функции.
Примеры с решением
Пример решения задачи №1:
Задана стандартная математическая модель задачи с двумя неизвестными:
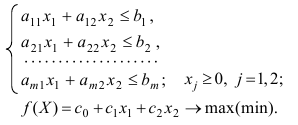
Нахождение решения этой модели на основе ее геометрической интерпретации включает следующие этапы.
- В плоскости
строят прямые, уравнения которых получаются в результате замены в ограничениях (2.1) модели знаков неравенств на знаки точных равенств.
- Находят полуплоскости, определенные каждым неравенством системы.
- Находят выпуклый многоугольник решений всей системы (2.1).
- Строят нормальный вектор целевой функции
, причем, начало вектора совмещают с началом координат и строят прямую
.
- Передвигают эту прямую в направлении вектора
, в результате либо находят вершину или отрезок, в которой целевая функция принимает наибольшее значение, либо устанавливают неограниченность сверху этой функции на множестве допустимых решений.
- Если функция ограничена, то определяют
, вычисляют значение функции в этой точке
.
При геометрической интерпретации задач ЛП могут встретиться случаи, изображенные на рис. 2.1. — 2.4.
Рис. 2.1. Задача ЛП имеет единственное решение 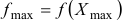
Рис. 2.2. Задача ЛП имеет бесчисленное множество решений, т.к. целевая функция достигает максимума на отрезке 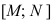
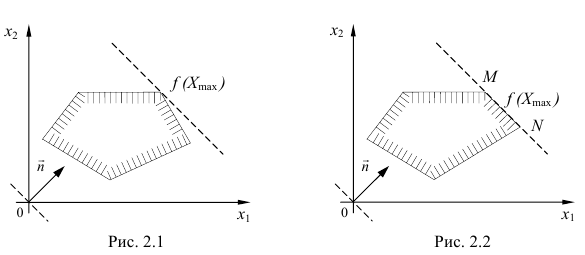
Рис. 2.3. Задача ЛП не имеет решения, т.к. функция неограниченна сверху.
Рис. 2.4. Задача ЛП не имеет решения, т.к. система (2.1) несовместна.
Пример решения задачи №2:
Для производства двух видов изделий 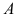
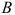
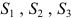
Прибыль от реализации одного изделия каждого вида равна 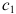
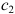
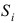
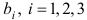
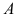
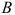
Решение. Обозначим через 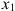
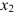
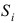
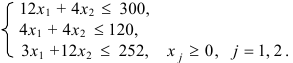
Переменные 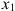
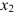
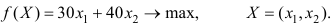
Итак, мы получили стандартную модель с двумя переменными.
Решим задачу линейного программирования геометрически, придерживаясь плана, приведенного ранее.
- Строим прямые
:

Обратимся к неравенствам (2.3). Отмстим те полуплоскости, которые им удовлетворяют. Учтем на чертеже и неотрицательность переменных 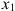
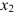
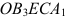
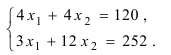
- Запишем окончательный ответ:
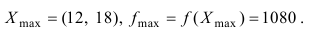
Наибольшая прибыль будет равна 1080 (у.е).
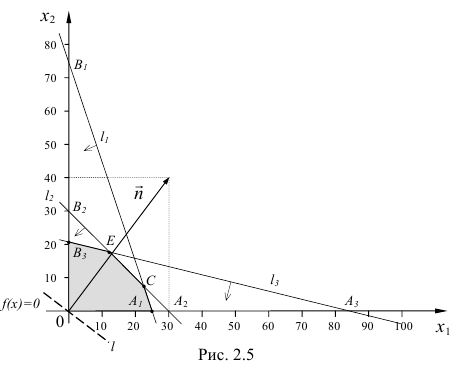
Пример решения задачи №3:
Минимизировать функцию
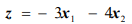
при ограничениях
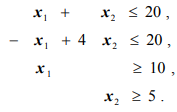
Допустимой областью, изображенной на рис. 1.2, является чегырехугольник 
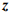
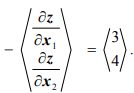
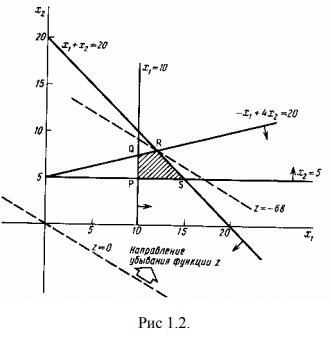
Минимальное значение функции 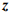
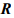
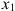
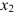
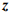
Иногда задача имеет более чем одно оптимальное решение.
Пример решения задачи №4:
Минимизировать функцию
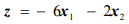
при ограничениях
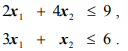
На рис. 1.3 чегырехугольник 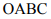
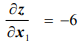
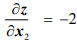
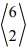
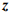
Любая точка на отрезке 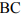
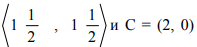
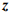
Любая точка на отрезке 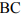
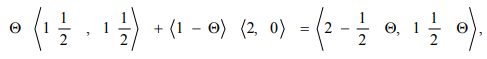
где
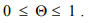
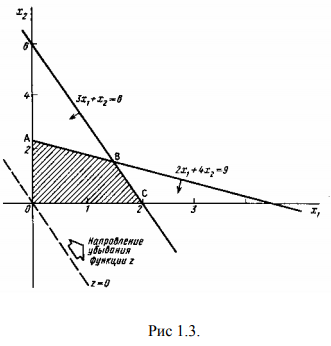
Для каждой такой точки значение функции 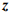
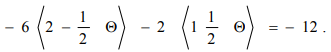
Функция 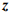
Иногда решение задачи не ограничено.
Пример решения задачи №5:
Максимизировать функцию
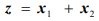
при ограничениях
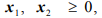
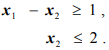
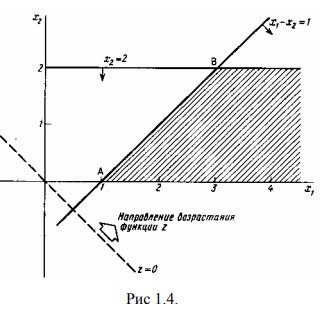
Допустимая область, изображенная на рис. 1.4, не ограничена в направлении, в котором функция 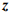
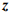
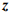
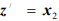
Разумеется, если бы задача состояла в минимизации функции 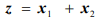
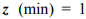
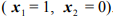
Иногда задача не имеет решения, поскольку допустимой области не существует.
Пример решения задачи №6:
Минимизировать функцию
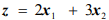
при ограничениях
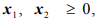
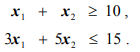
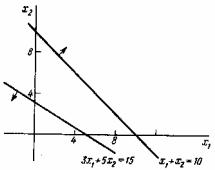
Ограничения задачи противоречивы, поэтому нет допустимых решений (рис. 1.5).
Уже из рассмотренных выше примеров можно вывести несколько характерных черт задач линейного программирования. Во-первых, допустимая область всегда является выпуклым многоугольником, даже в случае, когда она не ограничена. Во-вторых, оптимальное решение всегда достигается в вершинах допустимой области. В примере 2 и вершина 
Эти результаты могут быть обобщены. Сначала покажем, что задачи линейного программирования могут быть приведены к стандартной форме.
Пример решения задачи №7:
Найти максимум функции 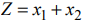
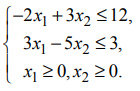
На рис. 3 изображены: неограниченная многогранная область решений данной системы ограничений-неравенств, линия уровня 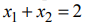
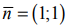
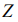
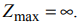
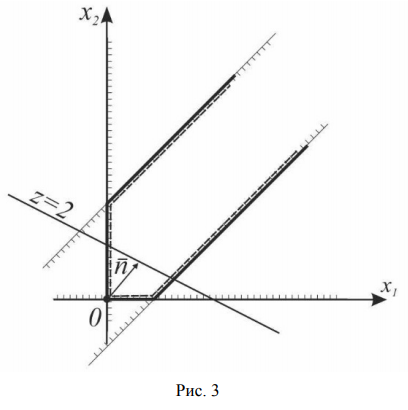
Пример решения задачи №8:
Найти максимум функции 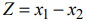
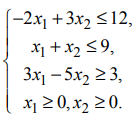
Изображенная на рис. 4 область не содержит ни одной общей точки, которая удовлетворяла бы всем неравенствам системы ограничений, т.е. система ограничений противоречива и не может содержать ни одного решения, в том числе и оптимального.
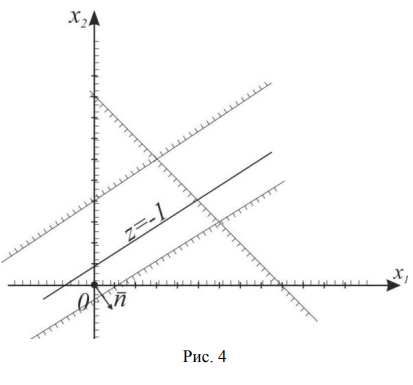
Пример решения задачи №9:
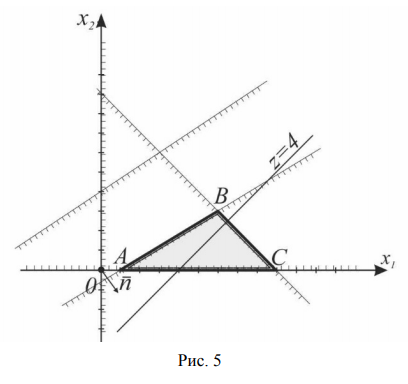
Найти максимум функции 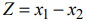
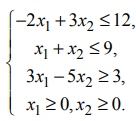
Всем неравенствам системы ограничений удовлетворяют точки треугольника 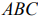
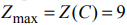
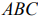
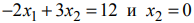
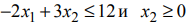
Пример решения задачи №10:
Найти минимум функции 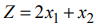
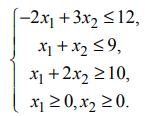
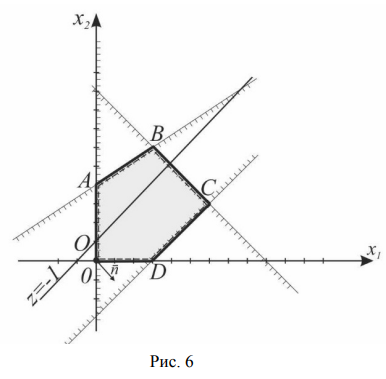
Областью решений данной системы ограничений является треугольник 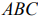
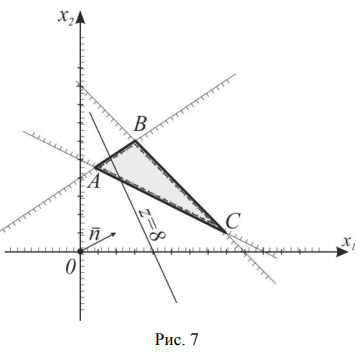
На рис. 7 также изображены исходная линия уровня 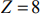
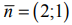
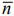
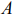
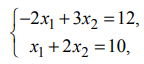
т.е.
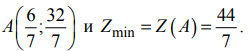
Опорнои прямой называется линия уровня, которая имеет хотя бы одну общую точку с областью допустимых решений и по отношению к которой эта область находится в одной из полуплоскостей.
Область допустимых решений любой задачи имеет не более двух опорных прямых, на одной из которых может находиться оптимальное решение.
На основании приведенных примеров и определения опорной прямой запишем этапы нахождения решения задачи линейного программирования с двумя переменными графическим методом:
- Изображаем область допустимых решений.
- Если область допустимых решений является пустым множеством, то задача не имеет решения ввиду несовместности системы ограничений.
- Если область допустимых решений является непустым множеством, то изображаем нормальный вектор
линий уровня и одну из линий уровня, имеющую общие точки с этой областью.
- Линию уровня перемещаем до опорной прямой в задаче на максимум в направлении нормали, в задаче на минимум — в противоположном направлении.
- Если при перемещении линии уровня по области допустимых решений в направлении, соответствующем приближению к максимуму (минимуму) целевой функции, линия уровня уходит в бесконечность, то
.
- Если задача линейного программирования имеет оптимальное решение, то для его нахождения решаем систему из уравнений прямых, ограничивающих область допустимых решений и имеющих общие точки с соответствующей опорой прямой. Если целевая функция достигает экстремума в двух угловых точках, то задача имеет бесконечное множество решений. Оптимальным решением является любая выпуклая линейная комбинация этих точек.
- Вычисляем значение целевой функции на оптимальном решении.
Графическим методом решаются задачи линейного программирования, записанные в каноническом виде и удовлетворяющие условию 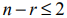
Возможно эти страницы вам будут полезны:
- Решение задач по математическому программированиюПримеры решения задач по математическому программированиюЗаказать работу по математическому программированиюПомощь по математическому программированиюЗадачи математического программированияЗадача линейного программированияРешение задач по линейному программированиюМетоды решения задач линейного программированияГрафический метод решения задач линейного программированияЗаказать работу по линейному программированиюПомощь по линейному программированиюКонтрольная работа по линейному программированиюЛинейное программирование в ExcelКурсовая работа по линейному программированию
Обзор градиентных методов в задачах математической оптимизации
Время на прочтение
11 мин
Количество просмотров 89K
Предисловие
В этой статье речь пойдет о методах решения задач математической оптимизации, основанных на использовании градиента функции. Основная цель — собрать в статье все наиболее важные идеи, которые так или иначе связаны с этим методом и его всевозможными модификациями.
UPD. В комментариях пишут, что на некоторых браузерах и в мобильном приложении формулы не отображаются. К сожалению, не знаю, как с этим бороться. Могу лишь сказать, что использовал макросы «inline» и «display» хабравского редактора. Если вдруг знаете, как это исправить — напишите в комментариях, пожалуйста.
Примечание от автора
На момент написания я защитил диссертацию, задача которой требовала от меня глубокое понимание теоретических основно методов математической оптимизации. Тем не менее, у меня до сих пор (как и у всех) расплываются глаза от страшных длинных формул, поэтому я потратил немалое время, чтобы вычленить ключевые идеи, которые бы характеризовали разные вариации градиентных методов. Моя личная цель — написать статью, содержащую минимальное количество информации, необходимое для более менее подробного понимания тематики. Но будьте готовы, без формул так или иначе не обойтись.
Постановка задачи
Прежде чем описывать метод, следует сначала описать задачу, а именно: «Даны множество
и функция
, требуется найти точку
, такую что
для всех
», что обычно записывается например вот так
В теории обычно предполагается, что
— дифференцируемая и выпуклая функция, а
— выпуклое множество (а еще лучше, если вообще
), это позволяет дать какие-то гарантии успешности применения градиентного спуска. На практике градиентный спуск успешно применяется даже когда у задачи нет ни одного из вышеперечисленных свойств (пример дальше в статье).
Немного математики
Допустим пока что нам нужно просто найти минимум одномерной функции
Еще в 17 веке Пьером Ферма был придуман критерий, который позволял решать простые задачи оптимизации, а именно, еcли — точка минимума
, то
где
— производная
. Этот критерий основан на линейном приближении
Чем ближе
к
, чем точнее это приближение. В правой части — выражение, которое при
может быть как больше
так и меньше — это основная суть критерия. В многомерном случае аналогично из линейного приближения
(здесь и далее
— стандартное скалярное произведение, форма записи обусловлена тем, что скалярное произведение — это то же самое, что матричное произведение вектор-строки на вектор-столбец) получается критерий
Величина
— градиент функции
в точке
. Также равенство градиента нулю означает равенство всех частных производных нулю, поэтому в многомерном случае можно получить этот критерий просто последовательно применив одномерный критерий по каждой переменной в отдельности.
Стоит отметить, что указанные условия являются необходимыми, но не достаточными, самый простой пример — 0 для
и

Этот критерий является достаточным в случае выпуклой функции, во многом из-за этого для выпуклых функций удалось получить так много результатов.
Квадратичные функции
Квадратичные функции в
— это функция вида
Для экономии места (да и чтобы меньше возиться с индексами) такую функцию обычно записывают в матричной форме:
где
,
,
— матрица, у которой на пересечении
строки и
столбца стоит величина
(
при этом получается симметричной — это важно). Далее. при упомянании квадратичной функции я буду иметь указанную выше функцию.
Зачем я об этом рассказываю? Дело в том, что квадратичные функции важны в оптимизации по двум причинам:
- Они тоже встречаются на практике, например при построении линейной регрессии методом наименьших квадратов
- Градиент квадратичной функции — линейная функция, в частности для функции выше
Или в матричной форме
Таким образом система
— линейная система. Системы, проще чем линейная, просто не существует. Мысль, к которой я старался подобраться — оптимизация квадратичной функции — самый простой класс задач оптимизации. С другой стороны, тот факт, что
— необходимые условия минимума дает возможность решать линейные системы через задачи оптимизации. Чуть позже я постараюсь вас убедить в том, что это имеет смысл.
Полезные свойства градиента
Хорошо, мы вроде бы выяснили, что если функция дифференцируема (у нее существуют производные по всем переменным), то в точке минимума градиент должен быть равен нулю. А вот несет ли градиент какую-нибудь полезную информацию в случае, когда он отличен от нуля?
Попробуем пока решить более простую задачу: дана точка , найти точку
такую, что
. Давайте возьмем точку рядом с
, опять же используя линейное приближение
. Если взять
,
то мы получим
Аналогично, если
, то
будет больше
(здесь и далее
). Опять же, так как мы использовали приближение, то эти соображения будут верны только для малых
. Подытоживая вышесказанное, если
, то градиент указывает направление наибольшего локального увеличения функции.
Вот два примера для двумерных функций. Такого рода картинки можно часто увидеть в демонстрациях градиентного спуска. Цветные линии — так называемые линии уровня, это множество точек, для которых функция принимает фиксированное значений, в моем случае это круги и эллипсы. Я обозначил синими линии уровня с более низким значением, красными — с более высоким.
Обратите внимание, что для поверхности, заданной уравнением вида
,
задает нормаль (в простонародии — перпендикуляр) к этой поверхности. Также обратите внимание, что хоть градиент и показывает в направлении наибольшего увеличения функции, нет никакой гарантии, что по направлению, обратному к градиенту, можно найти минимум (пример — левая картинка).
Градиентный спуск
До базового метода градиентного спуска остался лишь малый шажок: мы научились по точке
получать точку
с меньшим значением функции
. Что мешает нам повторить это несколько раз? По сути, это и есть градиентный спуск: строим последовательность
Величина
называется размером шага (в машинном обучении — скорость обучения). Пару слов по поводу выбора
: если
— очень маленькие, то последовательность медленно меняется, что делает алгоритм не очень эффективным; если же
очень большие, то линейное приближение становится плохим, а может даже и неверным. На практике размер шага часта подбирают эмпирически, в теории обычно предполагается липшицевость градиента, а именно, если
для всех
, то
гарантирует убывание
.
Анализ для квадратичных функций
Если
— симметричная обратимая матрица,
, то для квадратичной функции
точка
является точкой минимума (UPD. при условии, что этот минимум вообще существует —
не принимает сколько угодно близкие к
значения только если
положительно определена), а для метода градиентного спуска можно получить следующее
где
— единичная матрица, т.е.
для всех
. Если же
, то получится
Выражение слева — расстояние от приближения, полученного на шаге
градиентного спуска до точки минимума, справа — выражение вида
, которое сходится к нулю, если
(условие, которое я писал на
в предыдущем пункте как раз это гарантирует). Эта базовая оценка гарантирует, что градиентный спуск сходится.
Модификации градиентного спуска
Теперь хотелось бы рассказать немного про часто используемые модификации градиентного спуска, в первую очередь так называемые
Инерционные или ускоренные градиентные методы
Все методы такого класса выражаются в следующем виде
Последнее слагаемое характеризует эту самую «инерционность», алгоритм на каждом шаге старается двигаться против градиента, но при этом по инерции частично двигается в том же направлении, что и на предыдущей итерации. Такие методы обладают двумя важными свойствами:
- Они практически не усложняют обычный градиентный спуск в вычислительном плане.
- При аккуратном подборе
такие методы на порядок быстрее, чем обычный градиентный спуск даже с оптимально подобранным шагом.
Один из первых таких методов появился в середине 20 века и назывался метод тяжелого шарика, что передавало природу инерционности метода: в этом методе
не зависят от
и аккуратно подбираются в зависимости от целевой функции. Стоит отметить, что
может быть какой угодно, а
— обычно лишь чуть-чуть меньше единицы.
Метод тяжелого шарика — самый простой инерционный метод, но не самый первый. При этом, на мой взгляд, самый первый метод довольно важен для понимания сути этих методов.
Метод Чебышева
Да да, первый метод такого типа был придуман еще Чебышевым для решения систем линейных уравнений. В какой-то момент при анализе градиентного спуска было получено следующее равенство
где
— некоторый многочлен степени
. Почему бы не попробовать подобрать
таким образом, чтобы
было поменьше? Один уз универсальных многочленов, которые меньше всего отклоняются от нуля — многочлен Чебышева. Метод Чебышева по сути заключается в том, чтобы подобрать параметры спуска так, чтобы
был многочленом Чебышева. Есть правда одна небольшая проблема: для обычного градиентного спуска это просто невозможно. Однако для инерционных методов это оказывается возможным. В основном это происходит из-за того, что многочлены Чебышева удовлетворяют рекуррентному соотношению второго порядка
поэтому их невозможно построить для градиентного спуска, который вычисляет новое значение лишь по одному предыдущему, а для инерционных становится возможным за счет того, что используется два предыдущих значения. При этом оказывается, что сложность вычисления
не зависит ни от
, ни от размера пространства
.
Метод сопряженных градиентов
Еще один очень интересный и важный факт (следствие теоремы Гамильтона-Кэли): для любой квадратной матрицы размера
существует многочлен
степени не больше
, для которого
. Чем это интересно? Все дело в том же равенстве
Если бы мы могли подбирать размер шага в градиентном спуске так, чтобы получать именно этот обнуляющий многочлен, то градиентный спуск сходился бы за фиксированное число итерации не большее размерности
. Как уже выяснили — для градиентного спуска мы так делать не можем. К счастью, для инерционных методов — можем. Описание и обоснование метода довольно техническое, я ограничусь сутью:на каждой итерации выбираются параметры, дающие наилучший многочлен, который можно построить учитывая все сделанные до текущего шага измерения градиента. При этом
- Одна итерация градиентного спуска (без учета вычислений параметров) содежит одно умножение матрицы на вектор и 2-3 сложения векторов
- Вычисление параметров также требует 1-2 умножение матрицы на вектор, 2-3 скалярных умножения вектор на вектор и несколько сложений векторов.
Самое сложное в вычислительном плане — умножение Матрицы на вектор, обычно это делается за время
, однако для со специальной реализацией это можно сделать за
, где
— количество ненулевых элементов в
. Учитывая сходимость метода сопряженных градиентов не более, чем за
итерации получаем общую сложность алгоритма
, что во всех случаях не хуже
для метода Гаусса или Холесского, но намного лучше в случае, если
, что не так редко встречается.
Метод сопряженных градиентов хорошо работает и в случае, если
не является квадратичной функцией, но при этом уже не сходится за конечное число шагов и часто требует небольших дополнительных модификаций
Метод Нестерова
Для сообществ математической оптимизации и машинного обучения фамилия «Нестеров» уже давно стало нарицательной. В 80х годах прошлого века Ю.Е. Нестеров придумал интересный вариант инерционного метода, который имеет вид
при этом не предполагается какого-то сложного подсчета
как в методе сопряженных градиентов, в целом поведение метода похоже на метод тяжелого шарика, но при этом его сходимость обычно гораздо надежнее как в теории, так и на практике.
Стохастический градиентный спуск
Единственное формальное отличие от обычного градиентного спуска — использование вместо градиента функции
такой, что
(
— математическое ожидание по случайной величине
), таким образом стохастический градиентный спуск имеет вид
— это некоторый случайный параметр, на который мы не влияем, но при этом в среднем мы идем против градиента. В качестве примера рассмотрим функции
и
Если
принимает значения
равновероятно, то как раз в среднем
— это градиент
. Этот пример показателен еще и следующим: сложность вычисления градиента в
раз больше, чем сложность вычисления
. Это позволяет стохастическому градиентному спуску делать за одно и то же время в
раз больше итераций. Несмотря на то, что стохастический градиентный спуск обычно сходится медленней обычного, за счет такого большого увеличения числа итераций получается улучшить скорость сходимости на единицу времени. Насколько мне известно — на данный момент стохастический градиентный спуск является базовым методом обучения большинства нейронных сетей, реализован во всех основных библиотеках по ML: tensorflow, torch, caffe, CNTK, и т.д.
Стоит отметить, что идеи иннерционных методов применяются для стохастического градиентного спуска и на практике часто дают прирост, в теории же обычно считается, что асимптотическая скорость сходимости не меняется из-за того, что основная погрешность в стохастическом градиентном спуске обусловлена дисперсией
.
Субградиентный спуск
Эта вариация позволяет работать с недифференцируемыми функциями, её я опишу более подробно. Придется опять вспомнить линейное приближение — дело в том, что есть простая характеристика выпуклости через градиент, дифференцируемая функция выпукла тогда и только тогда, когда выполняется
для всех
. Оказывается, что выпуклая функция не обязаны быть дифференцируемой, но для любой точки
обязательно найдется такой вектор
, что
для всех
. Такой вектор
принято называть субградиентом
в точке
, множество всех субградиентов в точки
называют субдифференциалом
и обозначают
(несмотря на обозначение — не имеет ничего общего с частными производными). В одномерном случае
— это число, а вышеуказанное свойство просто означает, что график
лежит выше прямой, проходящей через
и имеющей тангенс угла наклона
(смотрите рисунки ниже). Отмечу, что субградиентов для одной точки может быть несколько, даже бесконечное число.

Вычислить хотя бы один субградиент для точки обычно не очень сложно, субградиентный спуск по сути использует субградиент вместо градиента. Оказывается — этого достаточно, в теории скорость сходимости при этом падает, однако например в нейронных сетях недифференцируемую функцию
любят использовать как раз из-за того, что с ней обучение проходит быстрее (это кстати пример невыпуклой недифференцируемой функции, в которой успешно применяется (суб)градиентный спуск. Сама по себе функция
выпукла, но многослойная нейронная сеть, содержащая
, невыпукла и недифференцируема). В качестве примера, для функции
субдифференциал вычисляется очень просто
Пожалуй, последняя важная вещь, которую стоит знать, — это то, что субградиентный спуск не сходится при постоянном размере шага. Это проще всего увидеть для указанной выше функции
. Даже отсутствие производной в одной точке ломает сходимость:
- Допустим мы начали из точки
.
- Шаг субградиентного спуска:
- Если
, то первые несколько шагов мы будет вычитать единицу, если
, то прибавлять. Так или иначе мы в какой-то момент окажемся на интервале
, из которого попадем в
, а дальше будем прыгать между двумя точками этих интервалов.
В теории для субградиентного спуска рекомендуется брать последовательность шагов
Где
обычно
или
. На практике я часто видел успешное применение шагов
, хоть и для таких шагов вообще говоря не будет сходимости.
Proximal методы
К сожалению я не знаю хорошего перевода для «proximal» в контексте оптимизации, поэтому просто так и буду называть этот метод. Proximal-методы появились как обобщение проективных градиентных методов. Идея очень простая: если есть функция
, представимая в виде суммы
, где
— дифференцируемая выпуклая функция, а
— выпуклая, для которой существует специальный proximal-оператор
(в этой статье ограничусь лишь примерами, описывать в общем виде не буду), то свойства сходимости градиентного спуска для
остаются и для градиентного спуска для
, если после каждой итерации применять этот proximal-оператор для текущей точки
, другими словами общий вид proximal-метода выглядит так:
Думаю, пока что совершенно непонятно, зачем это может понадобиться, особенно учитывая то, что я не объяснил, что такое proximal-оператор. Вот два примера:
— индикатор-функция выпуклого множества
, то есть
В этом случае
— это проекция на множество
, то есть «ближайшая к
точка множества
». Таким образом, мы ограничиваем градиентный спуск только на множество
, что позволяет решать задачи с ограничениями. К сожалению, вычисление проекции в общем случае может быть еще более сложной задачей, поэтому обычно такой метод применяется, если ограничения имеют простой вид, например так называемые box-ограничения: по каждой координате
—
-регуляризация. Такое слагаемое любят добавлять в задачи оптимизации в машинном обучении, чтобы избежать переобучения. Регуляризация такого вида еще и имеет тенденцию обнулять наименее значимые компоненты. Для такой функции proximal-оператор имеет вид (ниже описано выражение для одной координаты):
что довольно просто вычислить.
Заключение
На этом заканчиваются основные известные мне вариации градиентного метода. Пожалуй под конец я бы отметил, что все указанные модификации (кроме разве что метода сопряженных градиентов) могут легко взаимодействовать друг с другом. Я специально не стал включать в эту перечень метод Ньютона и квазиньютоновские методы (BFGS и прочие): они хоть и используют градиент, но при этом являются более сложными методами, требуют специфических дополнительных вычислений, которые обычно более вычислительно затратны, нежели вычисление градиента. Тем не менее, если этот текст будет востребован, я с удовольствием сделаю подобный обзор и по ним.
Использованная / рекомендованная литература
Boyd. S, Vandenberghe L. Convex Optimization
Shewchuk J. R. An Introduction to the Conjugate Gradient Method Without the Agonizing Pain
Bertsekas D. P. Convex Optimization Theory
Нестеров Ю. Е. Методы выпуклой оптимизации
Гасников А. В. Универсальный градиентный спуск

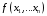
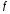
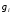
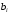
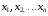
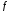
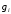
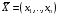
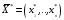
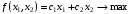
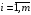
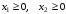
 ,
,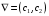 ;
;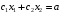
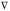 ,
,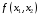
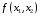 ;
;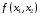 ,
,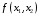
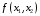
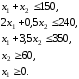
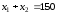
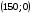
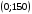
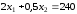
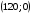
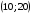
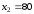

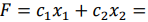
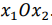 .
.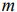 полуплоскостей, соответствующих ограничениям задачи.
полуплоскостей, соответствующих ограничениям задачи.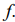
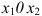 строят прямые, уравнения которых получаются в результате замены в ограничениях (2.1) модели знаков неравенств на знаки точных равенств.
строят прямые, уравнения которых получаются в результате замены в ограничениях (2.1) модели знаков неравенств на знаки точных равенств.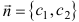 , причем, начало вектора совмещают с началом координат и строят прямую
, причем, начало вектора совмещают с началом координат и строят прямую 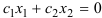 .
.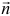 , в результате либо находят вершину или отрезок, в которой целевая функция принимает наибольшее значение, либо устанавливают неограниченность сверху этой функции на множестве допустимых решений.
, в результате либо находят вершину или отрезок, в которой целевая функция принимает наибольшее значение, либо устанавливают неограниченность сверху этой функции на множестве допустимых решений.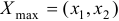 , вычисляют значение функции в этой точке
, вычисляют значение функции в этой точке 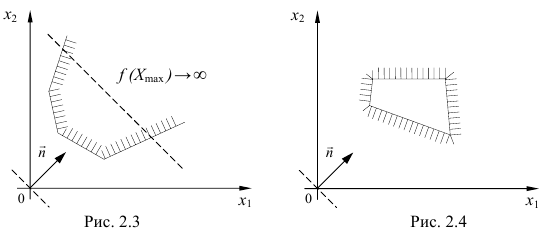

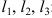 :
: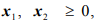
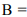
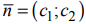 линий уровня и одну из линий уровня, имеющую общие точки с этой областью.
линий уровня и одну из линий уровня, имеющую общие точки с этой областью.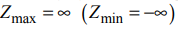 .
.