Обзор градиентных методов в задачах математической оптимизации
Время на прочтение
11 мин
Количество просмотров 89K
Предисловие
В этой статье речь пойдет о методах решения задач математической оптимизации, основанных на использовании градиента функции. Основная цель — собрать в статье все наиболее важные идеи, которые так или иначе связаны с этим методом и его всевозможными модификациями.
UPD. В комментариях пишут, что на некоторых браузерах и в мобильном приложении формулы не отображаются. К сожалению, не знаю, как с этим бороться. Могу лишь сказать, что использовал макросы «inline» и «display» хабравского редактора. Если вдруг знаете, как это исправить — напишите в комментариях, пожалуйста.
Примечание от автора
На момент написания я защитил диссертацию, задача которой требовала от меня глубокое понимание теоретических основно методов математической оптимизации. Тем не менее, у меня до сих пор (как и у всех) расплываются глаза от страшных длинных формул, поэтому я потратил немалое время, чтобы вычленить ключевые идеи, которые бы характеризовали разные вариации градиентных методов. Моя личная цель — написать статью, содержащую минимальное количество информации, необходимое для более менее подробного понимания тематики. Но будьте готовы, без формул так или иначе не обойтись.
Постановка задачи
Прежде чем описывать метод, следует сначала описать задачу, а именно: «Даны множество
и функция
, требуется найти точку
, такую что
для всех
», что обычно записывается например вот так
В теории обычно предполагается, что
— дифференцируемая и выпуклая функция, а
— выпуклое множество (а еще лучше, если вообще
), это позволяет дать какие-то гарантии успешности применения градиентного спуска. На практике градиентный спуск успешно применяется даже когда у задачи нет ни одного из вышеперечисленных свойств (пример дальше в статье).
Немного математики
Допустим пока что нам нужно просто найти минимум одномерной функции
Еще в 17 веке Пьером Ферма был придуман критерий, который позволял решать простые задачи оптимизации, а именно, еcли — точка минимума
, то
где
— производная
. Этот критерий основан на линейном приближении
Чем ближе
к
, чем точнее это приближение. В правой части — выражение, которое при
может быть как больше
так и меньше — это основная суть критерия. В многомерном случае аналогично из линейного приближения
(здесь и далее
— стандартное скалярное произведение, форма записи обусловлена тем, что скалярное произведение — это то же самое, что матричное произведение вектор-строки на вектор-столбец) получается критерий
Величина
— градиент функции
в точке
. Также равенство градиента нулю означает равенство всех частных производных нулю, поэтому в многомерном случае можно получить этот критерий просто последовательно применив одномерный критерий по каждой переменной в отдельности.
Стоит отметить, что указанные условия являются необходимыми, но не достаточными, самый простой пример — 0 для
и

Этот критерий является достаточным в случае выпуклой функции, во многом из-за этого для выпуклых функций удалось получить так много результатов.
Квадратичные функции
Квадратичные функции в
— это функция вида
Для экономии места (да и чтобы меньше возиться с индексами) такую функцию обычно записывают в матричной форме:
где
,
,
— матрица, у которой на пересечении
строки и
столбца стоит величина
(
при этом получается симметричной — это важно). Далее. при упомянании квадратичной функции я буду иметь указанную выше функцию.
Зачем я об этом рассказываю? Дело в том, что квадратичные функции важны в оптимизации по двум причинам:
- Они тоже встречаются на практике, например при построении линейной регрессии методом наименьших квадратов
- Градиент квадратичной функции — линейная функция, в частности для функции выше
Или в матричной форме
Таким образом система
— линейная система. Системы, проще чем линейная, просто не существует. Мысль, к которой я старался подобраться — оптимизация квадратичной функции — самый простой класс задач оптимизации. С другой стороны, тот факт, что
— необходимые условия минимума дает возможность решать линейные системы через задачи оптимизации. Чуть позже я постараюсь вас убедить в том, что это имеет смысл.
Полезные свойства градиента
Хорошо, мы вроде бы выяснили, что если функция дифференцируема (у нее существуют производные по всем переменным), то в точке минимума градиент должен быть равен нулю. А вот несет ли градиент какую-нибудь полезную информацию в случае, когда он отличен от нуля?
Попробуем пока решить более простую задачу: дана точка , найти точку
такую, что
. Давайте возьмем точку рядом с
, опять же используя линейное приближение
. Если взять
,
то мы получим
Аналогично, если
, то
будет больше
(здесь и далее
). Опять же, так как мы использовали приближение, то эти соображения будут верны только для малых
. Подытоживая вышесказанное, если
, то градиент указывает направление наибольшего локального увеличения функции.
Вот два примера для двумерных функций. Такого рода картинки можно часто увидеть в демонстрациях градиентного спуска. Цветные линии — так называемые линии уровня, это множество точек, для которых функция принимает фиксированное значений, в моем случае это круги и эллипсы. Я обозначил синими линии уровня с более низким значением, красными — с более высоким.
Обратите внимание, что для поверхности, заданной уравнением вида
,
задает нормаль (в простонародии — перпендикуляр) к этой поверхности. Также обратите внимание, что хоть градиент и показывает в направлении наибольшего увеличения функции, нет никакой гарантии, что по направлению, обратному к градиенту, можно найти минимум (пример — левая картинка).
Градиентный спуск
До базового метода градиентного спуска остался лишь малый шажок: мы научились по точке
получать точку
с меньшим значением функции
. Что мешает нам повторить это несколько раз? По сути, это и есть градиентный спуск: строим последовательность
Величина
называется размером шага (в машинном обучении — скорость обучения). Пару слов по поводу выбора
: если
— очень маленькие, то последовательность медленно меняется, что делает алгоритм не очень эффективным; если же
очень большие, то линейное приближение становится плохим, а может даже и неверным. На практике размер шага часта подбирают эмпирически, в теории обычно предполагается липшицевость градиента, а именно, если
для всех
, то
гарантирует убывание
.
Анализ для квадратичных функций
Если
— симметричная обратимая матрица,
, то для квадратичной функции
точка
является точкой минимума (UPD. при условии, что этот минимум вообще существует —
не принимает сколько угодно близкие к
значения только если
положительно определена), а для метода градиентного спуска можно получить следующее
где
— единичная матрица, т.е.
для всех
. Если же
, то получится
Выражение слева — расстояние от приближения, полученного на шаге
градиентного спуска до точки минимума, справа — выражение вида
, которое сходится к нулю, если
(условие, которое я писал на
в предыдущем пункте как раз это гарантирует). Эта базовая оценка гарантирует, что градиентный спуск сходится.
Модификации градиентного спуска
Теперь хотелось бы рассказать немного про часто используемые модификации градиентного спуска, в первую очередь так называемые
Инерционные или ускоренные градиентные методы
Все методы такого класса выражаются в следующем виде
Последнее слагаемое характеризует эту самую «инерционность», алгоритм на каждом шаге старается двигаться против градиента, но при этом по инерции частично двигается в том же направлении, что и на предыдущей итерации. Такие методы обладают двумя важными свойствами:
- Они практически не усложняют обычный градиентный спуск в вычислительном плане.
- При аккуратном подборе
такие методы на порядок быстрее, чем обычный градиентный спуск даже с оптимально подобранным шагом.
Один из первых таких методов появился в середине 20 века и назывался метод тяжелого шарика, что передавало природу инерционности метода: в этом методе
не зависят от
и аккуратно подбираются в зависимости от целевой функции. Стоит отметить, что
может быть какой угодно, а
— обычно лишь чуть-чуть меньше единицы.
Метод тяжелого шарика — самый простой инерционный метод, но не самый первый. При этом, на мой взгляд, самый первый метод довольно важен для понимания сути этих методов.
Метод Чебышева
Да да, первый метод такого типа был придуман еще Чебышевым для решения систем линейных уравнений. В какой-то момент при анализе градиентного спуска было получено следующее равенство
где
— некоторый многочлен степени
. Почему бы не попробовать подобрать
таким образом, чтобы
было поменьше? Один уз универсальных многочленов, которые меньше всего отклоняются от нуля — многочлен Чебышева. Метод Чебышева по сути заключается в том, чтобы подобрать параметры спуска так, чтобы
был многочленом Чебышева. Есть правда одна небольшая проблема: для обычного градиентного спуска это просто невозможно. Однако для инерционных методов это оказывается возможным. В основном это происходит из-за того, что многочлены Чебышева удовлетворяют рекуррентному соотношению второго порядка
поэтому их невозможно построить для градиентного спуска, который вычисляет новое значение лишь по одному предыдущему, а для инерционных становится возможным за счет того, что используется два предыдущих значения. При этом оказывается, что сложность вычисления
не зависит ни от
, ни от размера пространства
.
Метод сопряженных градиентов
Еще один очень интересный и важный факт (следствие теоремы Гамильтона-Кэли): для любой квадратной матрицы размера
существует многочлен
степени не больше
, для которого
. Чем это интересно? Все дело в том же равенстве
Если бы мы могли подбирать размер шага в градиентном спуске так, чтобы получать именно этот обнуляющий многочлен, то градиентный спуск сходился бы за фиксированное число итерации не большее размерности
. Как уже выяснили — для градиентного спуска мы так делать не можем. К счастью, для инерционных методов — можем. Описание и обоснование метода довольно техническое, я ограничусь сутью:на каждой итерации выбираются параметры, дающие наилучший многочлен, который можно построить учитывая все сделанные до текущего шага измерения градиента. При этом
- Одна итерация градиентного спуска (без учета вычислений параметров) содежит одно умножение матрицы на вектор и 2-3 сложения векторов
- Вычисление параметров также требует 1-2 умножение матрицы на вектор, 2-3 скалярных умножения вектор на вектор и несколько сложений векторов.
Самое сложное в вычислительном плане — умножение Матрицы на вектор, обычно это делается за время
, однако для со специальной реализацией это можно сделать за
, где
— количество ненулевых элементов в
. Учитывая сходимость метода сопряженных градиентов не более, чем за
итерации получаем общую сложность алгоритма
, что во всех случаях не хуже
для метода Гаусса или Холесского, но намного лучше в случае, если
, что не так редко встречается.
Метод сопряженных градиентов хорошо работает и в случае, если
не является квадратичной функцией, но при этом уже не сходится за конечное число шагов и часто требует небольших дополнительных модификаций
Метод Нестерова
Для сообществ математической оптимизации и машинного обучения фамилия «Нестеров» уже давно стало нарицательной. В 80х годах прошлого века Ю.Е. Нестеров придумал интересный вариант инерционного метода, который имеет вид
при этом не предполагается какого-то сложного подсчета
как в методе сопряженных градиентов, в целом поведение метода похоже на метод тяжелого шарика, но при этом его сходимость обычно гораздо надежнее как в теории, так и на практике.
Стохастический градиентный спуск
Единственное формальное отличие от обычного градиентного спуска — использование вместо градиента функции
такой, что
(
— математическое ожидание по случайной величине
), таким образом стохастический градиентный спуск имеет вид
— это некоторый случайный параметр, на который мы не влияем, но при этом в среднем мы идем против градиента. В качестве примера рассмотрим функции
и
Если
принимает значения
равновероятно, то как раз в среднем
— это градиент
. Этот пример показателен еще и следующим: сложность вычисления градиента в
раз больше, чем сложность вычисления
. Это позволяет стохастическому градиентному спуску делать за одно и то же время в
раз больше итераций. Несмотря на то, что стохастический градиентный спуск обычно сходится медленней обычного, за счет такого большого увеличения числа итераций получается улучшить скорость сходимости на единицу времени. Насколько мне известно — на данный момент стохастический градиентный спуск является базовым методом обучения большинства нейронных сетей, реализован во всех основных библиотеках по ML: tensorflow, torch, caffe, CNTK, и т.д.
Стоит отметить, что идеи иннерционных методов применяются для стохастического градиентного спуска и на практике часто дают прирост, в теории же обычно считается, что асимптотическая скорость сходимости не меняется из-за того, что основная погрешность в стохастическом градиентном спуске обусловлена дисперсией
.
Субградиентный спуск
Эта вариация позволяет работать с недифференцируемыми функциями, её я опишу более подробно. Придется опять вспомнить линейное приближение — дело в том, что есть простая характеристика выпуклости через градиент, дифференцируемая функция выпукла тогда и только тогда, когда выполняется
для всех
. Оказывается, что выпуклая функция не обязаны быть дифференцируемой, но для любой точки
обязательно найдется такой вектор
, что
для всех
. Такой вектор
принято называть субградиентом
в точке
, множество всех субградиентов в точки
называют субдифференциалом
и обозначают
(несмотря на обозначение — не имеет ничего общего с частными производными). В одномерном случае
— это число, а вышеуказанное свойство просто означает, что график
лежит выше прямой, проходящей через
и имеющей тангенс угла наклона
(смотрите рисунки ниже). Отмечу, что субградиентов для одной точки может быть несколько, даже бесконечное число.

Вычислить хотя бы один субградиент для точки обычно не очень сложно, субградиентный спуск по сути использует субградиент вместо градиента. Оказывается — этого достаточно, в теории скорость сходимости при этом падает, однако например в нейронных сетях недифференцируемую функцию
любят использовать как раз из-за того, что с ней обучение проходит быстрее (это кстати пример невыпуклой недифференцируемой функции, в которой успешно применяется (суб)градиентный спуск. Сама по себе функция
выпукла, но многослойная нейронная сеть, содержащая
, невыпукла и недифференцируема). В качестве примера, для функции
субдифференциал вычисляется очень просто
Пожалуй, последняя важная вещь, которую стоит знать, — это то, что субградиентный спуск не сходится при постоянном размере шага. Это проще всего увидеть для указанной выше функции
. Даже отсутствие производной в одной точке ломает сходимость:
- Допустим мы начали из точки
.
- Шаг субградиентного спуска:
- Если
, то первые несколько шагов мы будет вычитать единицу, если
, то прибавлять. Так или иначе мы в какой-то момент окажемся на интервале
, из которого попадем в
, а дальше будем прыгать между двумя точками этих интервалов.
В теории для субградиентного спуска рекомендуется брать последовательность шагов
Где
обычно
или
. На практике я часто видел успешное применение шагов
, хоть и для таких шагов вообще говоря не будет сходимости.
Proximal методы
К сожалению я не знаю хорошего перевода для «proximal» в контексте оптимизации, поэтому просто так и буду называть этот метод. Proximal-методы появились как обобщение проективных градиентных методов. Идея очень простая: если есть функция
, представимая в виде суммы
, где
— дифференцируемая выпуклая функция, а
— выпуклая, для которой существует специальный proximal-оператор
(в этой статье ограничусь лишь примерами, описывать в общем виде не буду), то свойства сходимости градиентного спуска для
остаются и для градиентного спуска для
, если после каждой итерации применять этот proximal-оператор для текущей точки
, другими словами общий вид proximal-метода выглядит так:
Думаю, пока что совершенно непонятно, зачем это может понадобиться, особенно учитывая то, что я не объяснил, что такое proximal-оператор. Вот два примера:
— индикатор-функция выпуклого множества
, то есть
В этом случае
— это проекция на множество
, то есть «ближайшая к
точка множества
». Таким образом, мы ограничиваем градиентный спуск только на множество
, что позволяет решать задачи с ограничениями. К сожалению, вычисление проекции в общем случае может быть еще более сложной задачей, поэтому обычно такой метод применяется, если ограничения имеют простой вид, например так называемые box-ограничения: по каждой координате
—
-регуляризация. Такое слагаемое любят добавлять в задачи оптимизации в машинном обучении, чтобы избежать переобучения. Регуляризация такого вида еще и имеет тенденцию обнулять наименее значимые компоненты. Для такой функции proximal-оператор имеет вид (ниже описано выражение для одной координаты):
что довольно просто вычислить.
Заключение
На этом заканчиваются основные известные мне вариации градиентного метода. Пожалуй под конец я бы отметил, что все указанные модификации (кроме разве что метода сопряженных градиентов) могут легко взаимодействовать друг с другом. Я специально не стал включать в эту перечень метод Ньютона и квазиньютоновские методы (BFGS и прочие): они хоть и используют градиент, но при этом являются более сложными методами, требуют специфических дополнительных вычислений, которые обычно более вычислительно затратны, нежели вычисление градиента. Тем не менее, если этот текст будет востребован, я с удовольствием сделаю подобный обзор и по ним.
Использованная / рекомендованная литература
Boyd. S, Vandenberghe L. Convex Optimization
Shewchuk J. R. An Introduction to the Conjugate Gradient Method Without the Agonizing Pain
Bertsekas D. P. Convex Optimization Theory
Нестеров Ю. Е. Методы выпуклой оптимизации
Гасников А. В. Универсальный градиентный спуск
Лекция 6.
Градиентные методы решения задач
нелинейного программирования.
Вопросы: 1. Общая характеристика
методов.
2. Метод градиента.
3. Метод наискорейшего спуска.
4. Метод Франка-Фулфа.
5. Метод штрафных функций.
1. Общая характеристика методов.
Градиентные методы представляют
собой приближенные (итерационные) методы
решения задачи нелинейного программирования
и позволяют решить практически любую
задачу. Однако при этом определяется
локальный экстремум. Поэтому целесообразно
применять эти методы для решения задач
выпуклого программирования, в которых
каждый локальный экстремум является и
глобальным. Процесс решения задачи
состоит в том, что, начиная с некоторой
точки х (начальной), осуществляется
последовательный переход в направлении
gradF(x), если
определяется точка максимума, и –gradF(x)
(антиградиента), если определяется точка
минимума, до точки, являющейся решением
задачи. При этом эта точка может оказаться
как внутри области допустимых значений,
так и на ее границе.
Градиентные методы можно разделить
на два класса (группы). К первой группе
относятся методы, в которых все исследуемые
точки принадлежат допустимой области.
К таким методам относятся: метод
градиента, наискорейшего спуска,
Франка-Вулфа и др. Ко второй группе
относятся методы, в которых исследуемые
точки могут и не принадлежать допустимой
области. Общим из таких методов является
метод штрафных функций. Все методы
штрафных функций отличаются друг от
друга способом определения «штрафа».
Основным понятием, используемым во
всех градиентных методах, является
понятие градиента функции, как направления
наискорейшего возрастания функции.
При определении решения градиентными
методами итерационный процесс продолжается
до тех пор, пока:
— либо grad F(x*) = 0, (точное решение);
— либо
(1)
где
— две последовательные точки,
—
малое число, характеризующее точность
решения.
2. Метод градиента.
Представим человека, стоящего на
склоне оврага, которому необходимо
спуститься вниз (на дно). Наиболее
естественным, кажется, направление в
сторону наибольшей крутизны спуска,
т.е. направление (-grad F(x)). Получаемая при
этом стратегия, называемая градиентным
методом, представляет собой
последовательность шагов, каждый из
которых содержит две операции:
а) определение направления наибольшей
крутизны спуска (подъема);
б) перемещение в выбранном направлении
на некоторый шаг.
Правильный выбор шага имеет существенное
значение. Чем шаг меньше, тем точнее
результат, но больше вычислений. Различные
модификации градиентного метода и
состоят в использовании различных
способов определения шага. Если на
каком-либо шаге значение F(x) не уменьшилось,
это означает, что точку минимума
«проскочили», в этом случае необходимо
вернуться к предыдущей точке и уменьшить
шаг, например, вдвое.
Схема решения.
1. Определение х0 = (х1,x2,…,xn),
принадлежащей допустимой области
и F(x0).
2. Определение grad F(x0) или
–grad F(x0).
3. Выбор шага h.
4. Определение следующей точки по формуле
x(k+1)
= x(k)
h grad F(x(k)),
«+» — если max,
«-» — если
min.
5. Определение F(x(k+1))
и :
— если
,
решение найдено;
— если нет, то переход к п. 2.
Замечание. Если grad F(x(k))
= 0, то решение будет точным.
Пример. F(x) = -6x1
+ 2x12
– 2x1x2
+ 2x22
min,
x1 + x2
2, x1
0, x2
0,
= 0,1.
3. Метод наискорейшего спуска.
В отличие от метода градиента, в
котором градиент определяют на каждом
шаге, в методе наискорейшего спуска
градиент находят в начальной точке и
движение в найденном направлении
продолжают одинаковыми шагами до тех
пор, пока значение функции уменьшается
(увеличивается). Если на каком-либо шаге
F(x) возросло
(уменьшилось), то движение в данном
направлении прекращается, последний
шаг снимается полностью или наполовину
и вычисляется новое значение градиента
и новое направление.
Схема решения.
1. Определение х0 = (х1,x2,…,xn),
принадлежащей допустимой области,
и F(x0), k = 0.
2. Определение grad F(x0) или
–grad F(x0).
3. Выбор шага h.
4. Определение следующей точки по формуле
x(k+1)
= x(k)
h grad F(x(k)),
«+» — если max,
«-» — если
min.
5. Определение F(x(k+1))
и :
— если
,
решение найдено;
— если нет:
а) при поиске min: — если F(x(k+1))
< F(x(k))
– переход к п. 4,
— если F(x(k+1))
> F(x(k))
– переход к п. 2;
б) при поиске max: —
если F(x(k+1))
> F(x(k))
– переход к п. 4;
— если F(x(k+1))
< F(x(k))
– переход к п. 2.
Замечания: 1. Если grad F(x(k))
= 0, то решение будет точным.
2. Преимуществом метода
наискорейшего спуска является его
простота и
сокращение расчетов, так
как grad F(x) вычисляется не во всех точках,
что
важно для задач большой
размерности.
3. Недостатком является то,
что шаги должны быть малыми, чтобы не
пропустить точку оптимума.
Пример. F(x) = 3x1
– 0,2x12
+ x2 —
0,2x22
max,
x1
+ x2
7, x1
0,
x1
+ 2x2
10, x2
0.
4. Метод Франка-Вулфа.
Метод используется для оптимизации
нелинейной целевой функции при линейных
ограничениях. В окрестности исследуемой
точки нелинейная целевая функция
заменяется линейной функцией и задача
сводится к последовательному решению
задач линейного программирования.
Схема решения.
1. Определение х0 = (х1,x2,…,xn),
принадлежащей допустимой области, и
F(x0), k = 0.
2. Определение grad F(x(k)).
3. Строят функцию
(min – «-»; max – «+»).
4. Определение max(min)
f(x) при
исходных ограничениях. Пусть это будет
точка z(k).
5. Определение шага вычислений x(k+1)
= x(k)
+
(k)(z(k)
– x(k)),
где
(k)
– шаг, коэффициент, 0
1.
(k)
выбирается так, чтобы значение функции
F(x) было max (min) в точке х(k+1).
Для этого решают уравнение
и
выбирают наименьший (наибольший) из
корней, но 0
1.
6. Определение F(x(k+1))
и проверяют необходимость дальнейших
вычислений:
— если
или grad F(x(k+1))
= 0, то решение найдено;
— если нет, то переход к п. 2.
Пример. F(x) = 4x1
+ 10x2
–x12
–x22
max,
x1
+x2
4, x1
0,
x2
2, x2
0.
5. Метод штрафных функций.
Пусть необходимо найти F(x1,
x2,…,xn)
max(min),
gi
(x1,
x2,…,xn)
bi, i
=
, xj
0, j =
.
Функции F и gi –
выпуклые или вогнутые.
Идея метода штрафных функций
заключается в поиске оптимального
значения новой целевой функции Q(x) = F(x)
+ H(x), которая является суммой исходной
целевой функции и некоторой функции
H(x), определяемой системой ограничений
и называемой штрафной функцией. Штрафные
функции строят таким образом, чтобы
обеспечить либо быстрое возвращение в
допустимую область, либо невозможность
выходы из нее. Метод штрафных функций
сводит задачу на условный экстремум к
решению последовательности задач на
безусловный экстремум, что проще.
Существует множество способов построения
штрафной функции. Наиболее часто она
имеет вид:
H(x) =
,
где
—
некоторые положительные Const.
Примечание:
— чем меньше
,
тем быстрее находится решение, однако,
точность снижается;
— начинают решение с малых
и увеличивают их на последующих шагах.
Используя штрафную функцию,
последовательно переходят от одной
точки к другой до тех пор, пока не получат
приемлемое решение.
Схема решения.
1. Определение начальную точку х0
= (х1,x2,…,xn),
F(x0) и k = 0.
2. Выбирают шаг вычислений h.
3. Определяют частные производные
и
.
4. Определяют координаты следующей точки
по формуле:
xj(k+1)

5. Если x(k+1)
Допустимой
области, проверяют:
а) если
—
решение найдено, если нет – переход к
п. 2.
б) если grad F(x(k+1))
= 0, то найдено точное решение.
Если x(k+1)
Допустимой области, задают новое значение
и
переходят к п. 4.
Пример. F(x) = – x12
– x22
max,
(x1
-5)2 + (x2
-5)2
8, x1
0, x2
0.
Соседние файлы в папке Модуль 2
- #
- #
- #
- #
Все курсы > Оптимизация > Занятие 2
На прошлом занятии мы познакомились с понятием производной и нашли минимум функции с одной переменной. При этом, мы отказались от использования второй переменной сдвига.
$$ y = w cdot x $$
Сегодня мы научимся находить минимум функции с двумя переменными w и b и построим полноценную модель простой линейной регрессии (Simple Linear Regression).
$$ y = w cdot x + b $$
Для этого мы напишем алгоритм, который называется методом градиентного спуска (gradient descent method). Однако перед этим мы возьмем более простую функцию и на ее примере изучим, как работает этот метод.
Градиент и метод градиентного спуска
Функция нескольких переменных
Возьмем вот такую функцию потерь.
$$ f(w_1, w_2) = w_1^2 + w_2^2 $$
График этой функции можно представить в трехмерном пространстве, где по осям w1 и w2 отложены веса исходной модели, а по оси f(w1, w2) — уровень потерь при заданных весах.
Откроем ноутбук к этому занятию⧉
Посмотрим на график этой функции.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
# установим размер графика fig = plt.figure(figsize = (12,10)) # создадим последовательность из 1000 точек в интервале от -5 до 5 # для осей w1 и w2 w1 = np.linspace(—5, 5, 1000) w2 = np.linspace(—5, 5, 1000) # создадим координатную плоскость из осей w1 и w2 w1, w2 = np.meshgrid(w1, w2) # пропишем функцию f = w1 ** 2 + w2 ** 2 # создадим трехмерное пространство ax = fig.add_subplot(projection = ‘3d’) # выведем график функции, alpha задает прозрачность ax.plot_surface(w1, w2, f, alpha = 0.4, cmap = ‘Blues’) # выведем точку A с координатами (3, 4, 25) и подпись к ней ax.scatter(3, 4, 25, c = ‘red’, marker = ‘^’, s = 100) ax.text(3, 3.5, 28, ‘A’, size = 25) # аналогично выведем точку B с координатами (0, 0, 0) ax.scatter(0, 0, 0, c = ‘red’, marker = ‘^’, s = 100) ax.text(0, —0.4, 4, ‘B’, size = 25) # укажем подписи к осям ax.set_xlabel(‘w1’, fontsize = 15) ax.set_ylabel(‘w2’, fontsize = 15) ax.set_zlabel(‘f(w1, w2)’, fontsize = 15) # выведем результат plt.show() |

Предположим мы начали с весов в точке A с координатами (3, 4, 25). Как нам спуститься в минимум функции в точке B (0, 0, 0)? Просто двигаться в направлении обратном производной мы не можем. Ведь единственной производной, которая бы описывала все изменения нашей функции, просто не существует.
Все дело в том, что если смотреть на нашу функцию «сверху» (то есть на график изолиний или линий уровня, contour lines), то в каждой точке у нас теперь два направления, по оси w1 и по оси w2.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
# установим размер графика fig, ax = plt.subplots(figsize = (10,10)) # создадим последовательность из 100 точек в интервале от -5 до 5 # для осей w1 и w2 w1 = np.linspace(—5.0, 5.0, 100) w2 = np.linspace(—5.0, 5.0, 100) # создадим координатную плоскость из осей w1 и w2 w1, w2 = np.meshgrid(w1, w2) # пропишем функцию C = w1 ** 2 + w2 ** 2 # построим изолинии (линии уровня) plt.contourf(w1, w2, C, cmap = ‘Blues’) # выведем точку А с координатами на плоскости (3, 4) ax.scatter(3, 4, c = ‘red’, marker = ‘^’, s = 200) ax.text(2.85, 4.3, ‘A’, size = 25) # и точку B с координатами (0, 0) ax.scatter(0, 0, c = ‘red’, marker = ‘^’, s = 200) ax.text(—0.15, 0.3, ‘B’, size = 25) # укажем подписи к осям ax.set_xlabel(‘w1’, fontsize = 15) ax.set_ylabel(‘w2’, fontsize = 15) # а также стрелки направления изменений вдоль w1 и w2 ax.arrow(2.7, 4, —2, 0, width = 0.1, head_length = 0.3) ax.arrow(3.005, 3.6, 0, —2, width = 0.1, head_length = 0.3) # создадим сетку в виде прерывистой черты plt.grid(linestyle = ‘—‘) # выведем результат plt.show() |

Как понять куда нам двигаться?
Частная производная
Если «заморозить» одну из переменных (то есть представить, что это константа), пусть это будет w2, мы можем найти производную по первой переменной w1.
$$ f_{w_1} = frac{partial f}{partial w_1} = 2w_1 $$
Такая производная называется частной (partial derivative), потому что она описывает изменение только в первой переменной w1.
Графически, мы как бы убираем переменную w2 (получается сечение, представленное параболой) и ищем производную функции, в которой есть только переменная w1.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
# зададим размер графика в дюймах plt.figure(figsize = (10, 8)) # объявим функцию параболы def f(x): return x ** 2 # объявим ее производную def der(x): return 2 * x # пропишем уравнение через point-slope form # y — y1 = m * (x — x1) —> y = m * (x — x1) + y1 def line(x, x1, y1): return der(x1) * (x — x1) + y1 # создадим последовательность координат x для параболы x = np.linspace(—4, 4, 100) # построим график параболы plt.plot(x, f(x)) # и заполним ее по умолчанию синим цветом с прозрачностью 0,5 plt.fill_between(x, f(x), 16, alpha = 0.5) # в цикле пройдемся по точкам -2, 0, 2 на оси х for x1 in range(—2, 3, 2): # рассчитаем соответствующие им координаты y y1 = f(x1) # определим пространство по оси x для касательных линий xrange = np.linspace(x1 — 3, x1 + 3, 9) # построим касательные линии plt.plot(xrange, line(xrange, x1, y1), ‘C1—‘, linewidth = 2) # и точки соприкосновения с графиком параболы plt.scatter(x1, y1, color = ‘C1’, s = 50) # укажем подписи к осям plt.xlabel(‘w1’, fontsize = 15) plt.ylabel(‘f(w1, w2)’, fontsize = 15) # выведем результат plt.show() |

Точно таким же образом мы поступаем со второй переменной w2. Мы замораживаем первую переменную w1 и вычисляем частную производную.
$$ f_{w_2} = frac{partial f}{partial w_2} = 2w_2 $$
Теперь, взяв точку на плоскости (w1, w2), мы будем точно знать скорость изменения функции f(w1, w2) в этой точке в каждом из направлений.
Например, возьмем ту же точку A с координатами w1 = 3, w2 = 4, скорость изменения функции в первом измерении будет равна 2 x 3 = 6, во втором 2 x 4 = 8.
Нотация анализа
Вы вероятно заметили, что мы использовали две нотации (записи) частной производной. С первой мы уже знакомы по предыдущему занятию, это нотация Лагранжа.
$$ f(w) rightarrow f'(w) $$
Вторую нотацию, нотацию Лейбница, удобнее использовать для записи частных производных.
$$ f(w_1, w_2) rightarrow frac{partial f}{partial w_1}, frac{partial f}{partial w_2} $$
Она позволяет сразу увидеть, по какой переменной происходит дифференцирование.
Напомню, что запись формул (и, в частности, производной) в текстовых ячейках ноутбуков с помощью LaTeX мы изучили, когда говорили про Jupyter Notebook.
Взятие частных производных
Пошагово рассмотрим, как мы пришли к результату (2w1, 2w2). Вначале найдем производную по первой переменой w1. Вторую переменную, w2, мы будем считать константой, то есть некоторым числом.
$$ frac{partial f}{partial w_1} (w_1^2 + w_2^2) $$
Первое, что бросается в глаза, это то, что у нас производная суммы, а она, как известно, равна сумме производных.
$$ frac{partial f}{partial w_1} (w_1^2 + w_2^2) = frac{partial f}{partial w_1} (w_1^2) + frac{partial f}{partial w_1} (w_2^2) $$
Производную первого слагаемого мы найдем по правилу производной степенной функции. Второе слагаемое мы решили считать константой, а производная константы равна нулю.
$$ frac{partial f}{partial w_1} (w_1^2) + frac{partial f}{partial w_1} (w_2^2) = 2w_1 + 0 = 2w_1 $$
Частная производная по второй переменной находится аналогично.
Использование SymPy
Функцию diff() библиотеки SymPy можно также использовать для взятия частных производных. Вначале импортируем функцию diff() и символы x и y (мы их используем вместо w1 и w2).
|
from sympy import diff from sympy.abc import x, y |
Напишем функцию, которую хотим дифференцировать.
После этого мы можем находить частные производные, передав в diff() функцию для дифференцирования, а затем либо первую, либо вторую переменную.
|
# найдем частную производную по первой переменной diff(f, x) |
|
# найдем частную производную по второй переменной diff(f, y) |
Градиент
Градиент (gradient) — есть не что иное, как совокупность частных производных по каждой из независимых переменных. Его можно назвать «полной производной».
Он обозначается через греческую букву набла ∇ или оператор Гамильтона.
$$ nabla f(w_1, w_2) = begin{bmatrix} frac{partial f}{partial w_1} \ frac{partial f}{partial w_1} end{bmatrix} = begin{bmatrix} 2w_1 \ 2w_2 end{bmatrix} $$
Еще раз посмотрим, чему равен градиент в точке (3, 4), но уже в новой записи.
$$ nabla f(3, 4) = begin{bmatrix} 2 cdot 3 \ 2 cdot 4 end{bmatrix} = begin{bmatrix} 6 \ 8 end{bmatrix} $$
Как вы видите, такая функция на входе принимает два числа, а на выходе выдает вектор, также состоящий из двух чисел. В этом случае говорят о вектор-функции (vector-valued function).
Метод градиентного спуска
Градиент, который мы только что нашли, показывает направление скорейшего подъема (возрастания) функции. Нам же, если мы хотим найти минимум функции, нужно двигаться вниз в направлении, обратном направлению градиента (еще говорят про направление антиградиента, negative gradient).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
# установим размер графика fig, ax = plt.subplots(figsize = (10,10)) # создадим последовательность из 100 точек в интервале от -10 до 10 # для осей w1 и w2 w1 = np.linspace(—10.0, 10.0, 100) w2 = np.linspace(—10.0, 10.0, 100) # создадим координатную плоскость из осей w1 и w2 w1, w2 = np.meshgrid(w1, w2) # пропишем функцию C = w1 ** 2 + w2 ** 2 # построим изолинии (линии уровня) plt.contourf(w1, w2, C, cmap = ‘Blues’) # выведем точку А с координатами на плоскости (3, 4) ax.scatter(3, 4, c = ‘red’, marker = ‘^’, s = 200) ax.text(2.5, 4.5, ‘A’, size = 25) # и точку B с координатами (0, 0) ax.scatter(0, 0, c = ‘red’, marker = ‘^’, s = 200) ax.text(—1, 0.3, ‘B’, size = 25) # укажем подписи к осям ax.set_xlabel(‘w1’, fontsize = 15) ax.set_ylabel(‘w2’, fontsize = 15) # а также стрелки направления изменений вдоль w1 и w2 ax.arrow(2.7, 4, —2, 0, width = 0.1, head_length = 0.3) ax.arrow(3, 3.5, 0, —2, width = 0.1, head_length = 0.3) # выведем вектор антиградиента с направлением (-6, -8) ax.arrow(3, 4, —6, —8, width = 0.05, head_length = 0.3) ax.text(—2.8, —4.5, ‘Антиградиент’, rotation = 53, size = 16) # создадим сетку в виде прерывистой черты plt.grid(linestyle = ‘—‘) # выведем результат plt.show() |

Если мы сдвинемся на −6 по оси w1 и на −8 по оси w2, то обязательно пройдем через минимум функции. При этом, если мы сдвинемся на всю величину градиента, то «перескочим» через минимум. Именно поэтому нам нужен коэффициент скорости обучения (learning rate).
Теперь мы готовы дать определение:
Метод градиентного спуска — это способ нахождения локального минимума функции в процессе движения в направлении антиградиента. Он был предложен Огюстеном Луи Коши еще в 1847 году.
Воспользуемся этим методом для нахождения минимума приведенной выше функции. Другими словами, проделаем путь из точки А в точку B.
Метод градиентного спуска на Питоне
Вначале объявим необходимые функции.
|
# пропишем функцию потерь def objective(w1, w2): return w1 ** 2 + w2 ** 2 # а также производную по первой def partial_1(w1): return 2.0 * w1 # и второй переменной def partial_2(w2): return 2.0 * w2 |
Зададим исходные параметры модели.
|
# пропишем изначальные веса w1, w2 = 3, 4 # количество итераций iter = 100 # и скорость обучения learning_rate = 0.05 |
Теперь создадим списки для учета обновления весов w1 и w2 и изменения уровня ошибки.
|
w1_list, w2_list, l_list = [], [], [] |
Найдем минимум функции потерь.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# в цикле с заданным количеством итераций for i in range(iter): # будем добавлять текущие веса в соответствующие списки w1_list.append(w1) w2_list.append(w2) # и рассчитывать и добавлять в список текущий уровень ошибки l_list.append(objective(w1, w2)) # также рассчитаем значение частных производных при текущих весах par_1 = partial_1(w1) par_2 = partial_2(w2) # будем обновлять веса в направлении, # обратном направлению градиента, умноженному на скорость обучения w1 = w1 — learning_rate * par_1 w2 = w2 — learning_rate * par_2 # выведем итоговые веса модели и значение функции потерь w1, w2, objective(w1, w2) |
|
(7.968419666276241e-05, 0.00010624559555034984, 1.7637697771638315e-08) |
Как мы видим, уже после ста итераций, как веса модели, так и уровень ошибки приблизились к нулю.
Разумеется, более сложные функции потерь потребуют большего количества итераций и более тонкой настройки коэффициента скорости обучения.
Остается посмотреть на графике, какой путь проделал наш алгоритм градиентного спуска.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
fig = plt.figure(figsize = (14,12)) w1 = np.linspace(—5, 5, 1000) w2 = np.linspace(—5, 5, 1000) w1, w2 = np.meshgrid(w1, w2) f = w1 ** 2 + w2 ** 2 ax = fig.add_subplot(projection = ‘3d’) ax.plot_surface(w1, w2, f, alpha = 0.4, cmap = ‘Blues’) ax.text(3, 3.5, 28, ‘A’, size = 25) ax.text(0, —0.4, 4, ‘B’, size = 25) ax.set_xlabel(‘w1’, fontsize = 15) ax.set_ylabel(‘w2’, fontsize = 15) ax.set_zlabel(‘f(w1, w2)’, fontsize = 15) # выведем путь алгоритма оптимизации ax.plot(w1_list, w2_list, l_list, ‘.-‘, c = ‘red’) plt.show() |
Промежуточные выводы
Давайте еще раз проговорим основные идеи пройденного материала.
- Градиент показывает скорость изменения многомерной функции по каждому из измерений (по каждой из переменных)
- Если «заморозить» все независимые переменные кроме одной и сделать срез, то наклон касательной к кривой среза будет значением частной производной по этому измерению.
- И самое важное для нас: градиент показывает направление скорейшего подъёма (возрастания) функции. Двигаясь в обратном направлении, мы придем к минимуму функции.
Простая линейная регрессия
А теперь давайте с нуля напишем нашу первую модель машинного обучения. Мы наконец-то приобрели для этого все необходимые знания. Наша модель будет по-прежнему иметь только один признак, но при этом будет учитываться не только наклон, но и сдвиг прямой.
$$ hat{y} = w cdot x + b $$
Данные и постановка задачи
Сегодня мы возьмем хорошо известные нам данные роста и обхвата шеи и сразу преобразуем их в массив Numpy.
|
X = np.array([1.48, 1.49, 1.49, 1.50, 1.51, 1.52, 1.52, 1.53, 1.53, 1.54, 1.55, 1.56, 1.57, 1.57, 1.58, 1.58, 1.59, 1.60, 1.61, 1.62, 1.63, 1.64, 1.65, 1.65, 1.66, 1.67, 1.67, 1.68, 1.68, 1.69, 1.70, 1.70, 1.71, 1.71, 1.71, 1.74, 1.75, 1.76, 1.77, 1.77, 1.78]) y = np.array([29.1, 30.0, 30.1, 30.2, 30.4, 30.6, 30.8, 30.9, 31.0, 30.6, 30.7, 30.9, 31.0, 31.2, 31.3, 32.0, 31.4, 31.9, 32.4, 32.8, 32.8, 33.3, 33.6, 33.0, 33.9, 33.8, 35.0, 34.5, 34.7, 34.6, 34.2, 34.8, 35.5, 36.0, 36.2, 36.3, 36.6, 36.8, 36.8, 37.0, 38.5]) |
Выведем эти данные на графике с помощью диаграммы рассеяния или точечной диаграммы.
|
# построим точечную диаграмму plt.figure(figsize = (10,6)) plt.scatter(X, y) # добавим подписи plt.xlabel(‘Рост, см’, fontsize = 16) plt.ylabel(‘Обхват шеи, см’, fontsize = 16) plt.title(‘Зависимость роста и окружности шеи у женщин в России’, fontsize = 18) plt.show() |
Как мы помним, нашей задачей является минимизация средней суммы квадрата расстояний между нашими данными и линией регрессии.
Также приведу формулу.
$$ MSE = frac {1}{n} sum^{n}_{i=1} (y_i-hat{y}_i) ^2 $$
Решение методом наименьшних квадратов
Прежде чем использовать алгоритм градиентного спуска найдем аналитическое решение с помощью метода наименьших квадратов (МНК, least squares method). Для уравнения с одной независимой переменной, напомню, используется следующая формула.
$$ w = frac {sum_{i = 1}^{n} (x_i-bar{x})(y_i-bar{y})} {sum_{i = 1}^{n} (x_i-bar{x})^2} $$
$$ b = bar{y}-wbar{x} $$
Собственная модель
Давайте вычислим наклон и сдвиг прямой с помощью этой формулы на Питоне.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# найдем среднее значение X и y X_mean = np.mean(X) y_mean = np.mean(y) # объявим переменные для числителя и знаменателя numerator, denominator = 0, 0 # в цикле пройдемся по данным for i in range(len(X)): # вычислим значения числителя и знаменателя по формуле выше numerator += (X[i] — X_mean) * (y[i] — y_mean) denominator += (X[i] — X_mean) ** 2 # найдем наклон и сдвиг w = numerator / denominator b = y_mean — w * X_mean w, b |
|
(26.861812005569753, -10.570936299787313) |
Также давайте реализуем этот алгоритм с помощью векторизованного кода.
|
w = np.sum((X — X_mean) * (y — y_mean)) / np.sum((X — X_mean) ** 2) b = y_mean — w * X_mean w, b |
|
(26.861812005569757, -10.57093629978732) |
Модель LinearRegression библиотеки sklearn
Надо сказать, что модель LinearRegression, которую мы использовали на вводном занятии по оптимизации и затем на занятии по линейной регрессии применяет именно МНК для минимизации MSE.
Давайте еще раз применим класс LinearRegression, чтобы убедиться в получении одинаковых результатов.
|
# из набора линейных моделей библиотеки sklearn импортируем линейную регрессию from sklearn.linear_model import LinearRegression # создадим объект этого класса и запишем в переменную model model = LinearRegression() # обучим модель (для X используем двумерный массив) model.fit(X.reshape(—1, 1), y) # выведем коэффициенты model.coef_, model.intercept_ |
|
(array([26.86181201]), -10.570936299787334) |
Как вы видите, результаты одинаковы. Теперь сделаем прогноз и рассчитаем среднеквадратическую ошибку.
|
# сделаем прогноз y_pred_least_squares = model.predict(X.reshape(—1, 1)) # импортируем модуль метрик from sklearn import metrics # выведем среднеквадратическую ошибку (MSE) metrics.mean_squared_error(y, y_pred_least_squares) |
Позднее мы сравним этот результат с аналогичным показателем алгоритма градиентного спуска.
МНК и метод градиентного спуска
Одна из причин использования алгоритма градиентного спуска вместо МНК заключается в том, что этот алгоритм менее требователен к вычислительным ресурсам при большом объеме (количество наблюдений) и размерности (количество признаков) данных.
Кроме того, метод градиентного спуска может применяться не только в задачах линейной регрессии, но и в других алгоритмах (например, в логистической регрессии, SVM или нейросетях).
Решение методом градиентного спуска
Модель линейной регрессии и функция потерь
Начнем с того, что объявим функцию линейной модели.
|
def regression(X, w, b): return w * X + b |
Теперь давайте немного модифицируем функцию потерь и найдем половину среднеквадратической ошибки (half MSE). Обозначим нашу функцию буквой J.
$$ J_{MSE} = frac{1}{2n} sum_{i=1}^{n} (y_i-(wx_i+b))^2 $$
Число два в знаменателе удачно сократится с двойкой, полученной при дифференцировании степенной функции. При этом точка минимума функции не изменится.
|
def objective(X, y, w, b, n): return np.sum((y — regression(X, w, b)) ** 2) / (2 * n) |
Дополнительно замечу, что использование именно среднеквадратической, то есть усредненной на количество наблюдений, ошибки (MSE) вместо «простой» суммы квадратов отклонений (Sum of Squared Errors, SSE)
$$ J_{SSE} = sum_{i=1} (y_i-(wx_i+b))^2 $$
может быть предпочтительнее, поскольку позволяет сравнивать результаты модели на выборках разных размеров.
Частные производные функции потерь
Найдем частные производные этой функции. Их будет две: одна по наклону (w), вторая по сдвигу (b). Начнем с наклона.
$$ frac{partial J}{partial w} left( frac{1}{2n} sum_{i=1}^{n} (y_i-(wx_i+b))^2 right) $$
Шаг 1. Вынесем число 1/2n за скобку по правилу умножения на число. В данном случае n, то есть количество наблюдений, превратится в число, как только мы применим формулу к набору данных.
$$ frac{partial J}{partial w} = frac{1}{2n} frac{partial J}{partial w} sum_{i=1}^{n} left( (y_i-(wx_i+b))^2 right) $$
Шаг 2. Теперь давайте для удобства перепишем выражение в векторизованной форме. Теперь x и y будут не отдельными числами, а векторами.
$$ frac{partial J}{partial w} = frac{1}{2n} frac{partial J}{partial w} left( (y-(wx+b)) ^2 right) $$
Шаг 3. Перед нами композиция из двух функций. Применим chain rule.
$$ frac{partial J}{partial w} = frac{1}{2n} cdot 2(y-(wx+b)) cdot frac{partial J}{partial w} (y-(wx+b)) $$
Шаг 4. К внутренней функции мы можем применить правило суммы и разности производных.
$$ frac{1}{2n} cdot 2(y-(wx+b)) cdot (0-(x+0)) $$
Замечу, что при дифференцировании внутренней функции, y превратился в ноль, потому что это константа. Одновременно переменную b мы «заморозили» и также решили считать константой.
Шаг 5. Упростим выражение.
$$ frac{partial J}{partial w} = frac{1}{cancel{2}n} cdot cancel{2}-x(y-(wx+b)) = frac{1}{n} cdot -x(y-(wx+b)) $$
Аналогично найдем частную производную по сдвигу.
$$ frac{partial J}{partial b} = frac{1}{n} cdot -(y-(wx+b)) $$
Здесь стоит уточнить лишь, что при нахождении производной внутренней функции мы «заморозили» переменную w.
$$ frac{partial J}{partial b} left( (y-(wx+b)) right) = 0-(0+1)$$
В невекторизованной форме производные выглядят следующим образом.
$$ frac{partial J}{partial w} = frac{1}{n} sum_{i=1}^{n} -x_i(y_i-(wx_i+b)) $$
$$ frac{partial J}{partial b} = frac{1}{n} sum_{i=1}^{n} -(y_i-(wx_i+b)) $$
Поменяв слагаемые в скобках местами и умножив на $-1$, частные производные можно записать и так.
$$ frac{partial J}{partial w} = frac{1}{n} sum_{i=1}^{n} ((wx_i+b)-y_i) cdot x_i $$
$$ frac{partial J}{partial b} = frac{1}{n} sum_{i=1}^{n} ((wx_i+b)-y_i) $$
Пропишем эти функции на Питоне.
|
def partial_w(X, y, w, b, n): return np.sum(—X * (y — (w * X + b))) / n def partial_b(X, y, w, b, n): return np.sum(—(y — (w * X + b))) / n |
Алгоритм градиентного спуска
Создадим функцию, которая будет на входе принимать данные, количество итераций и коэффициент скорости обучения, а на выходе выдавать веса модели и уровень ошибки.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# передадим функции данные, количество итераций и скорость обучения def gradient_descent(X, y, iter, learning_rate): # зададим изначальные веса w, b = 0, 0 # и количество наблюдений n = len(X) # создадим списки для записи весов модели и уровня ошибки w_list, b_list, l_list = [], [], [] # в цикле с заданным количеством итераций for i in range(iter): # добавим в списки текущие веса w_list.append(w) b_list.append(b) # и уровень ошибки l_list.append(objective(X, y, w, b, n)) # рассчитаем текущее значение частных производных par_1 = partial_w(X, y, w, b, n) par_2 = partial_b(X, y, w, b, n) # обновим веса в направлении антиградиента w = w — learning_rate * par_1 b = b — learning_rate * par_2 # выведем списки с уровнями ошибки и весами return w_list, b_list, l_list |
Обучение модели
Применим написанную выше функцию для обучения модели. Используем следующие гиперпараметры модели:
- количество итераций — 200 000
- коэффициент скорости обучения — 0,01
Напомню, что гиперпараметр — это параметр, который мы задаем до обучения модели.
|
# распакуем результат работы функции в три переменные w_list, b_list, l_list = gradient_descent(X, y, iter = 200000, learning_rate = 0.01) # и выведем последние достигнутые значения весов и уровня ошибки print(w_list[—1], b_list[—1], l_list[—1]) |
|
26.6917462520774 -10.293843835595917 0.1137823984153401 |
В целом, как мы видим, веса модели очень близки к результату, найденному с помощью метода наименьших квадратов. Теперь сделаем прогноз.
|
# передадим функции regression() наиболее оптимальные веса y_pred_gd = regression(X, w_list[—1], b_list[—1]) y_pred_gd[:5] |
|
array([29.20994062, 29.47685808, 29.47685808, 29.74377554, 30.01069301]) |
Посмотрим на результат на графике.
|
plt.figure(figsize = (10, 8)) plt.scatter(X, y) plt.plot(X, y_pred_gd, ‘r’) plt.show() |
Кроме того, мы можем посмотреть на то, как снижался уровень ошибки с каждой последующей итерацией.
Как мы видим, в первые итерации уровень ошибки снижался настолько стремительно, что последующие изменения практически незаметны. Давайте попробуем отбросить первые 150 наблюдений.
|
plt.figure(figsize = (8, 6)) plt.plot(l_list[150:]) plt.show() |
И все же кажется, что после 150000 итераций ошибка перестает снижаться и можно было бы обойтись меньшим количеством шагов. На самом деле это не так.
|
# отбросим первые 150 000 наблюдений plt.figure(figsize = (8, 6)) plt.plot(l_list[150000:]) plt.show() |
В целом подбор количества итераций и длины шага (коэффициента скорости обучения) довольно существенно влияют на качество обучения. Ближе к концу занятия мы рассмотрим этот момент более подробно.
Оценка качества модели
Оценим качество модели с помощью встроенной в sklearn метрики.
|
# рассчитаем MSE metrics.mean_squared_error(y, y_pred_gd) |
Результат очень близок к тому, который мы получили, используя МНК.
Визуализация шагов алгоритма оптимизации
Мы также как и раньше, можем посмотреть на путь, пройденный алгоритмом оптимизации.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
# создадим последовательности из 500 значений ww = np.linspace(—30, 30, 500) bb = np.linspace(—30, 30, 500) # сформируем координатную плоскость www, bbb = np.meshgrid(ww, bb) # а также матрицу из нулей для заполнения значениями функции J(w, b) JJ = np.zeros([len(ww), len(bb)]) # для каждой комбинации w и b for i in range(len(ww)): for j in range(len(bb)): # рассчитаем соответствующее прогнозное значение yy = www[i, j] * X + bbb[i, j] # и подставим его в функцию потерь (матрицу JJ) JJ[i, j] = 1 / (2 * len(X)) * np.sum((y — yy) ** 2) # зададим размер графика fig = plt.figure(figsize = (14,12)) # создидим трехмерное пространство ax = fig.add_subplot(projection = ‘3d’) # построим функцию потерь ax.plot_surface(www, bbb, JJ, alpha = 0.4, cmap = plt.cm.jet) # а также путь алгоритма оптимизации ax.plot(w_list, b_list, l_list, c = ‘red’) # для наглядности зададим более широкие, чем график # границы пространства ax.set_xlim(—40, 40) ax.set_ylim(—40, 40) plt.show() |
Мы также можем построить график изолиний («вид сверху»).
|
# для этого используем функцию plt.contour() fig, ax = plt.subplots(figsize = (10, 10)) ax.contour(www, bbb, JJ, 100, cmap = plt.cm.jet) ax.plot(w_list, b_list, c = ‘red’) plt.show() |
Как мы видим, алгоритм сначала двигался в одном направлении (очевидно, так ошибка снижалась наиболее стремительно), затем повернул на 90 градусов и продолжил движение.
Про выбор гиперпараметров модели
Давайте посмотрим, как поведет себя алгоритм при изменении гиперпараметров. Вначале попробуем тот же размер шага, но уменьшим количество итераций.
|
w_list_t1, b_list_t1, l_list_t1 = gradient_descent(X, y, iter = 10000, learning_rate = 0.01) w_list_t1[—1], b_list_t1[—1], l_list_t1[—1] |
|
(17.113947076094593, 5.311508333809235, 0.4836593999661288) |
Коэффициенты довольно сильно отличаются от найденных ранее значений. Посмотрим на графике изолиний, где остановился наш алгоритм.
|
fig, ax = plt.subplots(figsize = (10, 10)) ax.contour(www, bbb, JJ, 100, cmap = plt.cm.jet) ax.plot(w_list, b_list, c = ‘red’) # выведем точку, которой достиг новый алгоритм ax.scatter(w_list_t1[—1], b_list_t1[—1], s = 100, c = ‘blue’) plt.show() |
Как мы видим, алгоритм немного не дошел до оптимума. Теперь давайте попробуем уменьшить размер шага. Количество итераций вернем к прежнему значению.
|
w_list_t2, b_list_t2, l_list_t2 = gradient_descent(X, y, iter = 200000, learning_rate = 0.0001) w_list_t2[—1], b_list_t2[—1], l_list_t2[—1] |
|
(15.302448783526573, 8.263028645561734, 0.6339512457580667) |
|
fig, ax = plt.subplots(figsize = (10, 10)) ax.contour(www, bbb, JJ, 100, cmap = plt.cm.jet) ax.plot(w_list, b_list, c = ‘red’) ax.scatter(w_list_t2[—1], b_list_t2[—1], s = 100, c = ‘blue’) plt.show() |
В данном случае, так как мы делали слишком маленькие шаги, то продвинулись еще меньше.
Тема выбора гиперпараметров довольно сложна и выходит за рамки сегодняшнего занятия, однако уже на этих простых примерах видно, что один и тот же алгоритм при разных изначальных параметрах показывает совершенно разные результаты.
Подведем итог
В первой части занятия мы посмотрели как применить понятие производной к многомерной функции, познакомились с понятием градиента и методом градиентного спуска. Во второй части мы построили модель простой линейной регрессии и оптимизировали ее с помощью метода наименьших квадратов и алгоритма градиентного спуска.
Вопросы для закрепления
Вопрос. Что такое градиент?
Посмотреть правильный ответ
Ответ: градиент — это вектор, показывающий направление скорейшего подъема многомерной функции. Градиент состоит из частных производных по каждому из измерений (переменных) функции.
Вопрос. Какие гиперпараметры существенно влияют на качество оптимизации модели линейной регрессии?
Посмотреть правильный ответ
Ответ: количество итераций и коэффициент скорости обучения
Логичным продолжением будет построение модели многомерной или множественной линейной регрессии (multiple linear regression) с несколькими признаками. Однако прежде будет полезно еще раз в деталях изучить взаимосвязь переменных.
Ответы на вопросы
Вопрос. Почему если умножить функцию потерь на число, в частности на 1/2, точка ее минимума не изменится?
Ответ. Давайте посмотрим на график параболы и параболы, умноженной на 1/2.
Как мы видим, точка минимума не изменилась.
При этом обратите внимание на то, что изменился наклон (значение градиента). Эффект умножения функции потерь на число аналогичен измененению коэффициента скорости обучения (learning rate). Чем круче наклон, тем большие по размеру шаги мы будем делать.
Вопрос. Скажите, а как работает функция np.meshgrid()?
Ответ. Функция np.meshgrid() на входе принимает одномерные массивы и создает двумерный массив с привычной прямоугольной (декартовой) системой координат.
|
# создадим простые последовательности xvalues = np.array([0, 1, 2, 3, 4]) yvalues = np.array([0, 1, 2, 3, 4]) # сформируем координатную плоскость xx, yy = np.meshgrid(xvalues, yvalues) # выведем точки плоскости на графике plt.plot(xx, yy, marker = ‘.’, color = ‘r’, linestyle = ‘none’) plt.show() |
Обратите внимание, начало координат находится в левом нижнему углу.
Вопрос. Функция plt.fill_between() заполняет пространство между двумя функциями, но не очень понятно, какие параметры мы ей передаем.
Ответ. Функция np.fill_between(x, y1, y2 = 0) принимает три основных параметра: координаты по оси x, координаты по оси y (первая функция, y1) и координаты по оси y (вторая функция, y2) и заполняет пространство между y1 и y2. Параметр y2 не является обязательным. Если его не указывать, будет заполняться пространство между линией y1 и осью x (то есть функцией y = 0).
В конце ноутбука⧉ я привел два примера, когда параметр y2 не указывается, то есть равен 0, и когда y2 задает отличную от нуля функцию.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 января 2015;
проверки требуют 7 правок.
Градиентные методы — численные методы решения с помощью градиента задач, сводящихся к нахождению экстремумов функции.
Содержание
- 1 Постановка задачи решения системы уравнений в терминах методов оптимизации
- 2 Градиентные методы
- 2.1 Метод наискорейшего спуска (метод градиента)
- 2.1.1 Алгоритм
- 2.2 Метод покоординатного спуска (Гаусса—Зейделя)
- 2.2.1 Алгоритм
- 2.3 Метод сопряжённых градиентов
- 2.3.1 Алгоритм
- 2.1 Метод наискорейшего спуска (метод градиента)
- 3 Литература
- 4 Ссылки
- 5 См. также
Постановка задачи решения системы уравнений в терминах методов оптимизации[править | править вики-текст]
Задача решения системы уравнений:

с 


или какой-либо другой возрастающей функции от абсолютных величин 



Для решения этой задачи итерационными методами начинают с произвольных значений ![x_i^{[0]} (i = 1, 2, ..., n)](https://web.archive.org/web/20150906085958im_/https://upload.wikimedia.org/math/2/4/b/24b502645d57a21065029b59aa1f2734.png)
или покоординатно:
![x^{[j+1]}_i = x^{[j]}_i + lambda^{[j]}v^{[j]}_i ,quad i=1, 2, ldots,n,quad j = 0, 1, 2, ldots](https://web.archive.org/web/20150906085958im_/https://upload.wikimedia.org/math/0/b/1/0b1513e6f48293c1e7b7e9998cae2fe1.png)
которые сходятся к некоторому решению ![vec{x}^{[k]}](https://web.archive.org/web/20150906085958im_/https://upload.wikimedia.org/math/4/c/c/4ccdfc20582e8f5d06f279658421f5c5.png)

Различные методы отличаются выбором «направления» для очередного шага, то есть выбором отношений
![v^{[j]}_1: v^{[j]}_2: ldots :v^{[j]}_n](https://web.archive.org/web/20150906085958im_/https://upload.wikimedia.org/math/f/2/2/f225b0e2c36502971cea7a11e620b3c6.png)
Величина шага (расстояние, на которое надо передвинуться в заданном направлении в поисках экстремума) определяется значением параметра ![lambda^{[j]}](https://web.archive.org/web/20150906085958im_/https://upload.wikimedia.org/math/9/a/1/9a169478fa0488ba5525c558ab2c7b62.png)
![F(x^{[j+1]}_1, x^{[j+1]}_2, ldots, x^{[j+1]}_n )](https://web.archive.org/web/20150906085958im_/https://upload.wikimedia.org/math/4/7/4/474e913e9950516b05d42997961de759.png)
![lambda^{[j]}](https://web.archive.org/web/20150906085958im_/https://upload.wikimedia.org/math/9/a/1/9a169478fa0488ba5525c558ab2c7b62.png)
![lambda^{[j]}](https://web.archive.org/web/20150906085958im_/https://upload.wikimedia.org/math/9/a/1/9a169478fa0488ba5525c558ab2c7b62.png)

Градиентные методы[править | править вики-текст]
Основная идея методов заключается в том, чтобы идти в направлении наискорейшего спуска, а это направление задаётся антиградиентом 
где ![lambda^{[j]}](https://web.archive.org/web/20150906085958im_/https://upload.wikimedia.org/math/9/a/1/9a169478fa0488ba5525c558ab2c7b62.png)
- постоянной, в этом случае метод может расходиться;
- дробным шагом, то есть длина шага в процессе спуска делится на некое число;
- наискорейшим спуском:
Метод наискорейшего спуска (метод градиента)[править | править вики-текст]
Выбирают ![v^{[j]}_i = -frac{partial F}{partial x_i}](https://web.archive.org/web/20150906085958im_/https://upload.wikimedia.org/math/c/4/4/c4443a8be4dcaf84ec2500daa5a9d98e.png)
![x_i = x^{[j]}_i](https://web.archive.org/web/20150906085958im_/https://upload.wikimedia.org/math/1/9/7/19738e80edda66def17b91d288c05cc2.png)
![lambda^{[j]}](https://web.archive.org/web/20150906085958im_/https://upload.wikimedia.org/math/9/a/1/9a169478fa0488ba5525c558ab2c7b62.png)

Для аналитических функций 

![F(lambda^{[j]})](https://web.archive.org/web/20150906085958im_/https://upload.wikimedia.org/math/0/1/2/0124a3c8c52cafe2cb2053ea669b41cc.png)
![lambda^{[j]}=frac{sum_{k=1}^n(frac{partial F}{partial x_k})^2}{sum_{k=1}^nsum_{h=1}^nfrac{partial^2 F}{partial x_kdx_h}frac{partial F}{partial x_k}frac{partial F}{partial x_h}}](https://web.archive.org/web/20150906085958im_/https://upload.wikimedia.org/math/4/6/7/467d77cf79827242fb4ab65e337a15f5.png)
где все производные вычисляются при ![x_i = x^{[j]}_i](https://web.archive.org/web/20150906085958im_/https://upload.wikimedia.org/math/1/9/7/19738e80edda66def17b91d288c05cc2.png)
![F(lambda^{[j]})](https://web.archive.org/web/20150906085958im_/https://upload.wikimedia.org/math/0/1/2/0124a3c8c52cafe2cb2053ea669b41cc.png)
Алгоритм[править | править вики-текст]
- Задаются начальное приближение и точность расчёта
- Рассчитывают
, где
- Проверяют условие останова:
Метод покоординатного спуска (Гаусса—Зейделя)[править | править вики-текст]
Улучшает предыдущий метод за счёт того, что на очередной итерации спуск осуществляется постепенно вдоль каждой из координат, однако теперь необходимо вычислять новые 
Алгоритм[править | править вики-текст]
- Задаются начальное приближение и точность расчёта
- Рассчитывают
, где
- Проверяют условие остановки:
Метод сопряжённых градиентов[править | править вики-текст]
Метод сопряженных градиентов основывается на понятиях прямого метода многомерной оптимизации — метода сопряжённых направлений.
Применение метода к квадратичным функциям в 

Алгоритм[править | править вики-текст]
- Задаются начальным приближением и погрешностью:
- Рассчитывают начальное направление:
Литература[править | править вики-текст]
- Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. вузов. — М.: Высш. шк., 1986.
- Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М.: Мир, 1985.
- Коршунов Ю.М., Коршунов Ю.М. Математические основы кибернетики. — М.: Энергоатомиздат, 1972.
- Максимов Ю.А.,Филлиповская Е.А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
- Максимов Ю.А. Алгоритмы линейного и дискретного программирования. — М.: МИФИ, 1980.
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575-576.
Ссылки[править | править вики-текст]
- Интерполяционные формулы
- Математическое программирование
- Метод градиента
- Метод сопряжённых градиентов
- Прямые методы
- Формула Тейлора
См. также[править | править вики-текст]
- Численные методы
- Численное решение уравнений
- Метод Гаусса-Зейделя решения СЛАУ
| |
|
|---|---|
| Одномерные | Метод золотого сечения · Дихотомия · Метод парабол · Перебор по сетке · Метод Фибоначчи · Троичный поиск · Метод Пиявского · Метод Стронгина |
| Прямые методы | Метод Гаусса · Метод Нелдера — Мида · Метод Хука — Дживса · Метод конфигураций · Метод Розенброка |
| Первого порядка | Градиентный спуск · Метод Зойтендейка · Покоординатный спуск · Метод сопряжённых градиентов · Квазиньютоновские методы · Алгоритм Левенберга — Марквардта |
| Второго порядка | Метод Ньютона · Метод Ньютона — Рафсона · Алгоритм Бройдена — Флетчера — Гольдфарба — Шанно (BFGS) |
| Стохастические | Метод Монте-Карло · Имитация отжига · Эволюционные алгоритмы · Дифференциальная эволюция · Муравьиный алгоритм · Метод роя частиц · Алгоритм пчелиной колонии |
| Методы линейного программирования |
Симплекс-метод • Алгоритм Гомори · Метод эллипсоидов · Метод потенциалов |
| Методы нелинейного программирования |
Последовательное квадратичное программирование |

В математике, сопряженный градиент метод представляет собой алгоритм для численного решения конкретных систем линейных уравнений, а именно тех, матрица которых симметрична и положительно определенный. Метод сопряженных градиентов часто реализуется как итерационный алгоритм , применимый к разреженным системам, которые слишком велики, чтобы их можно было обрабатывать с помощью прямой реализации или других прямых методов, таких как Холецкого. разложение. Большие разреженные системы часто возникают при численном решении уравнений в частных производных или задач оптимизации.
Метод сопряженного градиента также может использоваться для решения задач безусловной оптимизации, таких как минимизация энергии. Он был в основном разработан Магнусом Хестенесом и Эдуардом Штифелем, которые запрограммировали его на Z4.
. Метод двусопряженных градиентов обеспечивает обобщение на несимметричные матрицы. Различные методы нелинейных сопряженных градиентов ищут минимум нелинейных уравнений.
Содержание
- 1 Описание проблемы, решаемой с помощью сопряженных градиентов
- 2 Как прямой метод
- 3 Как итерационный метод
- 3.1 Результирующий алгоритм
- 3.1.1 Вычисление альфа и бета
- 3.1.2 Пример кода в MATLAB / GNU Octave
- 3.2 Числовой пример
- 3.2.1 Решение
- 3.1 Результирующий алгоритм
- 4 Свойства сходимости
- 4.1 Теорема сходимости
- 5 Предварительно обусловленный метод сопряженного градиента
- 6 Гибкий метод предварительно обусловленного сопряженного градиента
- 6.1 Пример кода в MATLAB / GNU Octave
- 7 Vs. метод локально оптимального наискорейшего спуска
- 8 Вывод метода
- 9 Сопряженный градиент по нормальным уравнениям
- 10 См. также
- 11 Ссылки
- 12 Дополнительная литература
- 13 Внешние ссылки
Описание проблемы, решаемой с помощью сопряженных градиентов
Предположим, мы хотим решить систему линейных уравнений
- A x = b { displaystyle mathbf {A} mathbf {x} = mathbf {b}}
для вектора x, где известная матрица размера n × n A является симметричной (т. е. A= A), положительно-определенный (т.е. xAx>0 для всех ненулевых векторов x в R ) и real, и b тоже известен. Обозначим единственное решение этой системы как x ∗ { displaystyle mathbf {x} _ {*}}
Как прямой метод
Мы говорим, что два ненулевых вектора u и v являются сопряженными (относительно A ), если
- u TA v = 0. { displaystyle mathbf {u } ^ { mathsf {T}} mathbf {A} mathbf {v} = 0.}
Поскольку A симметрично и положительно определено, левая часть определяет внутренний продукт
- u TA v = ⟨u, v⟩ A: = ⟨A u, v⟩ = ⟨u, AT v⟩ = ⟨u, A v⟩. { displaystyle mathbf {u} ^ { mathsf {T}} mathbf {A} mathbf {v} = langle mathbf {u}, mathbf {v} rangle _ { mathbf {A}} : = langle mathbf {A} mathbf {u}, mathbf {v} rangle = langle mathbf {u}, mathbf {A} ^ { mathsf {T}} mathbf {v} rangle = langle mathbf {u}, mathbf {A} mathbf {v} rangle.}
Два вектора сопряжены тогда и только тогда, когда они ортогональны относительно этого внутреннего продукта. Сопряжение — это симметричное отношение: если u сопряжено с v, то v сопряжено с u . Предположим, что
- P = {p 1,…, pn} { displaystyle P = { mathbf {p} _ {1}, dots, mathbf {p} _ {n} }}
представляет собой набор из n взаимно сопряженных векторов (относительно A ). Тогда P образует базис для R n { displaystyle mathbb {R} ^ {n}}

- x ∗ = ∑ i = 1 n α ipi. { displaystyle mathbf {x} _ {*} = sum _ {i = 1} ^ {n} alpha _ {i} mathbf {p} _ {i}.}
На основе этого расширения мы вычислить:
- A x ∗ = ∑ i = 1 n α i A pi. { displaystyle mathbf {A} mathbf {x} _ {*} = sum _ {i = 1} ^ {n} alpha _ {i} mathbf {A} mathbf {p} _ {i}.}
Умножение слева на pk T { displaystyle mathbf {p} _ {k} ^ { mathsf {T}}}
- pk TA x ∗ = ∑ i = 1 n α ipk TA pi, { displaystyle mathbf {p} _ {k} ^ { mathsf {T}} mathbf {A} mathbf {x} _ {*} = sum _ {i = 1} ^ {n} alpha _ {i} mathbf {p} _ {k} ^ { mathsf {T}} mathbf {A} mathbf {p} _ {i},}
заменяя A x ∗ = б { displaystyle mathbf {Ax _ {*}} = mathbf {b}}

- pk T b = ∑ i = 1 N α я ⟨пк, пи⟩ A, { displaystyle mathbf {p} _ {k} ^ { mathsf {T}} mathbf {b} = sum _ {i = 1} ^ {n} alpha _ {i} left langle mathbf {p} _ {k}, mathbf {p} _ {i} right rangle _ { mathbf {A}},}
затем u T v знак равно ⟨U, v⟩ { displaystyle mathbf {u} ^ { mathsf {T}} mathbf {v} = langle mathbf {u}, mathbf {v} rangle}

- ⟨pk, b⟩ = α k ⟨pk, pk⟩ A, { displaystyle langle mathbf {p} _ {k}, mathbf. {b} rangle = alpha _ {k} langle mathbf {p} _ {k}, mathbf {p} _ {k} rangle _ { mathbf {A}},}
что подразумевает
- α k = ⟨pk, b⟩ ⟨pk, pk⟩ A. { displaystyle alpha _ {k} = { frac { langle mathbf {p} _ {k}, mathbf {b} rangle} { langle mathbf {p} _ {k}, mathbf { p} _ {k} rangle _ { mathbf {A}}}}.}
Это дает следующий метод решения уравнения Ax= b: найти последовательность из n сопряженных направлений, а затем вычислить коэффициенты α k.
Как итерационный метод
Если мы тщательно выберем сопряженные векторы pk, тогда нам, возможно, не понадобятся все они для получения хорошего приближения к решению x∗. Итак, мы хотим рассматривать метод сопряженных градиентов как итерационный метод. Это также позволяет нам приближенно решать системы, в которых n настолько велико, что прямой метод потребует слишком много времени.
Мы обозначаем начальное предположение для x∗как x0(мы можем предположить без ограничения общности, что x0= 0, в противном случае вместо этого рассмотрим систему Az= b− Ax0). Начиная с x0, мы ищем решение, и на каждой итерации нам нужна метрика, чтобы сказать нам, приблизились ли мы к решению x∗(которое нам неизвестно). Эта метрика происходит из того факта, что решение x∗также является единственным минимизатором следующей квадратичной функции
- f (x) = 1 2 x T A x — x T b, x ∈ R n. { Displaystyle е ( mathbf {x}) = { tfrac {1} {2}} mathbf {x} ^ { mathsf {T}} mathbf {A} mathbf {x} — mathbf {x } ^ { mathsf {T}} mathbf {b}, qquad mathbf {x} in mathbf {R} ^ {n} ,.}
Существование уникального минимизатора очевидно по его вторая производная задается симметричной положительно определенной матрицей
- ∇ 2 f (x) = A, { displaystyle nabla ^ {2} f ( mathbf {x}) = mathbf {A} ,,}
и что минимизатор (используйте Df (x ) = 0) решает исходную задачу, очевидно из его первой производной
- ∇ f (x) = A x — b. { displaystyle nabla f ( mathbf {x}) = mathbf {A} mathbf {x} — mathbf {b} ,.}
Это предлагает принять первый базисный вектор p0в качестве отрицательный градиент f на x= x0. Градиент f равен Ax− b. Начиная с первоначального предположения x0, это означает, что мы берем p0= b− Ax0. Другие векторы в базисе будут сопряжены с градиентом, отсюда и название метод сопряженного градиента. Обратите внимание, что p0также является остатком, предоставленным этим начальным шагом алгоритма.
Пусть rkбудет остатком на k-м шаге:
- r k = b — A x k. { displaystyle mathbf {r} _ {k} = mathbf {b} — mathbf {Ax} _ {k}.}
Как отмечалось выше, rk- это отрицательный градиент f в x= xk, поэтому метод градиентного спуска потребует перемещения в направлении rk. Здесь, однако, мы настаиваем на том, чтобы направления pkбыли сопряжены друг с другом. Практический способ обеспечить это — требовать, чтобы следующее направление поиска строилось из текущего остатка и всех предыдущих направлений поиска. Это дает следующее выражение:
- p k = r k — ∑ i < k p i T A r k p i T A p i p i {displaystyle mathbf {p} _{k}=mathbf {r} _{k}-sum _{i
(см. Рисунок в верхней части статьи, чтобы увидеть влияние ограничения сопряженности на сходимость). Следуя этому направлению, следующее оптимальное местоположение определяется как
- xk + 1 = xk + α kpk { displaystyle mathbf {x} _ {k + 1} = mathbf {x} _ {k} + alpha _ {k} mathbf {p} _ {k}}
с
- α k = pk T (b — A xk) pk TA pk = pk T rkpk TA pk, { displaystyle alpha _ {k} = { frac { mathbf {p} _ {k} ^ { mathsf {T}} ( mathbf {b} — mathbf {Ax} _ {k})} { mathbf {p} _ {k} ^ { mathsf {T}} mathbf {A} mathbf {p} _ {k}}} = { frac { mathbf {p} _ {k} ^ { mathsf {T}} mathbf {r } _ {k}} { mathbf {p} _ {k} ^ { mathsf {T}} mathbf {A} mathbf {p} _ {k}}},}
где следует последнее равенство из определения rk. Выражение для α k { displaystyle alpha _ {k}}
- е (х К + 1) = е (х К + α К п К) =: г (α К) г ‘(α К) =! 0 ⇒ α k = p k T (b — A x k) p k T A p k. { Displaystyle { begin {align} f ( mathbf {x} _ {k + 1}) = f ( mathbf {x} _ {k} + alpha _ {k} mathbf {p} _ { k}) =: g ( alpha _ {k}) \ g ‘( alpha _ {k}) { overset {!} {=}} 0 quad Rightarrow quad alpha _ {k} = { frac { mathbf {p} _ {k} ^ { mathsf {T}} ( mathbf {b} — mathbf {Ax} _ {k})} { mathbf {p} _ {k} ^ { mathsf {T}} mathbf {A} mathbf {p} _ {k}}} ,. end {align}}}
Результирующий алгоритм
Приведенный выше алгоритм дает наиболее прямое объяснение метода сопряженных градиентов. По-видимому, заявленный алгоритм требует хранения всех предыдущих направлений поиска и векторов остатков, а также множества операций умножения матрицы на вектор и, следовательно, может быть дорогостоящим в вычислительном отношении. Однако более тщательный анализ алгоритма показывает, что riортогонален rj, т.е. ri T rj = 0 { displaystyle mathbf {r} _ {i} ^ { mathsf {T}} mathbf {r} _ {j} = 0}

Ниже подробно описан алгоритм решения Ax= b, где A — действительная симметричная положительно определенная матрица. Входной вектор x0может быть приближенным начальным решением или 0 . Это другая формулировка точной процедуры, описанной выше.
- r 0: = b — A x 0, если r 0 достаточно мало, вернуть x 0 в качестве результата p 0: = r 0 k: = 0 повторить α k: = rk T rkpk TA pkxk + 1: = xk + α kpkrk + 1: = rk — α k A pk, если rk + 1 достаточно мало, то выйти из цикла β k: = rk + 1 T rk + 1 rk T rkpk + 1: = rk + 1 + β kpkk: = k + 1 end repeat return xk + 1 как результат { displaystyle { begin {align} mathbf {r} _ {0}: = mathbf {b} — mathbf {Ax} _ {0} { hbox {if}} mathbf {r} _ {0} { text {достаточно мал, тогда верните}} mathbf {x} _ {0} { text {в качестве результата}} \ mathbf {p} _ {0}: = mathbf {r} _ {0} \ k: = 0 \ { text {repeat}} \ qquad alpha _ {k}: = { frac { mathbf {r} _ {k} ^ { mathsf {T}} mathbf {r} _ {k}} { mathbf {p} _ {k} ^ { mathsf {T}} mathbf {Ap} _ {k}}} \ qquad mathbf {x} _ {k + 1}: = mathbf {x} _ {k} + alpha _ {k} mathbf {p} _ {k} \ qquad mathbf {r} _ {k + 1}: = mathbf {r} _ {k} — alpha _ {k} mathbf {Ap} _ {k} \ qquad { hbox {if}} mathbf {r} _ {k + 1} { text {достаточно мал, тогда выйдите из цикла}} \ qquad beta _ {k}: = { fra c { mathbf {r} _ {k + 1} ^ { mathsf {T}} mathbf {r} _ {k + 1}} { mathbf {r} _ {k} ^ { mathsf {T} } mathbf {r} _ {k}}} \ qquad mathbf {p} _ {k + 1}: = mathbf {r} _ {k + 1} + beta _ {k} mathbf {p} _ {k} \ qquad k: = k + 1 \ { text {end repeat}} \ { text {return}} mathbf {x} _ {k + 1} { text {в качестве результата}} end {align}}}
Это наиболее часто используемый алгоритм. Та же формула для β k также используется в методе Флетчера – Ривза нелинейного сопряженного градиента.
Вычисление альфа и бета
В алгоритме α k выбирается таким образом, чтобы rk + 1 { displaystyle mathbf {r} _ {k + 1}}
- α k = rk T rkrk TA pk = rk T rkpk TA pk { displaystyle alpha _ {k} = { frac { mathbf {r} _ {k} ^ { mathsf { T}} mathbf {r} _ {k}} { mathbf {r} _ {k} ^ { mathsf {T}} mathbf {A} mathbf {p} _ {k}}} = { гидроразрыв { mathbf {r} _ {k} ^ { mathsf {T}} mathbf {r} _ {k}} { mathbf {p} _ {k} ^ { mathsf {T}} mathbf { Ap} _ {k}}}}
так как rk + 1 = pk + 1 — β kpk { displaystyle mathbf {r} _ {k + 1} = mathbf {p} _ {k + 1} — mathbf { beta} _ {k} mathbf {p} _ {k}}

- β k = — rk + 1 TA pkpk TA pk { displaystyle beta _ {k} = — { frac { mathbf {r} _ {k + 1 } ^ { mathsf {T}} mathbf {A} mathbf {p} _ {k}} { mathbf {p} _ {k} ^ { mathsf {T}} mathbf {A} mathbf { p} _ {k}}}}
используя
- rk + 1 = rk — α k A pk { displaystyle mathbf {r} _ {k + 1} = mathbf {r} _ {k} — alpha _ {k} mathbf {A} mathbf {p} _ {k}}
и эквивалентно
A pk = 1 α k (rk — rk + 1), { displaystyle mathbf { A} mathbf {p} _ {k} = { frac {1} { alpha _ {k}}} ( mathbf {r} _ {k} — mathbf {r} _ {k + 1}),}
числитель β k переписывается как
- rk + 1 TA pk = 1 α krk + 1 T (rk — rk + 1) = — 1 α krk + 1 T rk + 1 { displaystyle mathbf {r} _ {k + 1} ^ { mathsf {T}} mathbf {A} mathbf {p} _ {k} = { frac {1} { alpha _ { k}}} mathbf {r} _ {k + 1} ^ { mathsf {T}} ( mathbf {r} _ {k} — mathbf {r} _ {k + 1}) = — { frac {1} { alpha _ {k}}} mathbf {r} _ {k + 1} ^ { mathsf {T}} mathbf {r} _ {k + 1}}
потому что rk + 1 { displaystyle mathbf {r} _ {k + 1}}
- pk TA pk = (rk + β k — 1 pk — 1) TA pk = 1 α krk T (rk — rk + 1) = 1 α krk T rk { displaystyle mathbf {p } _ {k} ^ { mathsf {T}} mathbf {A} mathbf {p} _ {k} = ( mathbf {r} _ {k} + beta _ {k-1} mathbf { p} _ {k-1}) ^ { mathsf {T}} mathbf {A} mathbf {p} _ {k} = { frac {1} { alpha _ {k}}} mathbf { r} _ {k} ^ { mathsf {T}} ( mathbf {r} _ {k} — mathbf {r} _ {k + 1}) = { frac {1} { alpha _ {k }}} mathbf {r} _ {k} ^ { mathsf {T}} mathbf {r} _ {k}}
с использованием того, что направления поиска pkсопряжены, и снова, что остатки ортогональны. Это дает β в алгоритме после отмены α k.
Пример кода в MATLAB / GNU Octave
function x = concgrad (A, b, x) r = b - A * x ; р = г; rsold = r '* r; для i = 1: длина (b) Ap = A * p; альфа = rsold / (p '* Ap); х = х + альфа * р; г = г - альфа * Ап; rsnew = r '* r; if sqrt (rsnew) < 1e-10 break end p = r + (rsnew / rsold) * p; rsold = rsnew; end end
Числовой пример
Рассмотрим линейную систему Ax= b, заданную как
- A x = [4 1 1 3] [x 1 x 2] = [1 2], { Displaystyle mathbf {A} mathbf {x} = { begin {bmatrix} 4 1 \ 1 3 end {bmatrix}} { begin {bmatrix} x_ {1} \ x_ {2} end {bmatrix} } = { begin {bmatrix} 1 \ 2 end {bmatrix}},}
мы выполним два шага метода сопряженных градиентов, начиная с первоначального предположения
- x 0 = [2 1] { displaystyle mathbf {x} _ {0} = { begin {bmatrix} 2 \ 1 end {bmatrix}}}
, чтобы найти приблизительное решение системы.
Решение
Для справки, точное решение:
- x = [1 11 7 11] ≈ [0,0909 0,6364] { displaystyle mathbf {x} = { begin {bmatrix } { frac {1} {11}} \\ { frac {7} {11}} end {bmatrix}} приблизительно { begin {bmatrix} 0,0909 \\ 0,6364 end {bmatrix} }}
Нашим первым шагом является вычисление остаточного вектора r0, связанного с x0. Этот остаток вычисляется по формуле r0= b- Ax0и в нашем случае равен
- r 0 = [1 2] — [4 1 1 3] [2 1] = [- 8 — 3] = p 0. { displaystyle mathbf {r} _ {0} = { begin {bmatrix} 1 \ 2 end {bmatrix}} — { begin {bmatrix} 4 1 \ 1 3 end {bmatrix}} { begin { bmatrix} 2 \ 1 end {bmatrix}} = { begin {bmatrix} -8 \ — 3 end {bmatrix}} = mathbf {p} _ {0}.}
Поскольку это на первой итерации мы будем использовать остаточный вектор r0в качестве начального направления поиска p0; способ выбора pkбудет меняться в дальнейших итерациях.
Теперь мы вычисляем скаляр α 0, используя соотношение
- α 0 = r 0 T r 0 p 0 TA p 0 = [- 8 — 3] [- 8 — 3 ] [- 8 — 3] [4 1 1 3] [- 8 — 3] = 73 331. { displaystyle alpha _ {0} = { frac { mathbf {r} _ {0} ^ { mathsf {T}} mathbf {r} _ {0}} { mathbf {p} _ {0 } ^ { mathsf {T}} mathbf {Ap} _ {0}}} = { frac {{ begin {bmatrix} -8 -3 end {bmatrix}} { begin {bmatrix} -8 -3 end {bmatrix}}} {{ begin {bmatrix} -8 -3 end {bmatrix}} { begin {bmatrix} 4 1 \ 1 3 end {bmatrix}} { begin {bmatrix} — 8 \ — 3 end {bmatrix}}}} = { frac {73} {331}}.}
Теперь мы можем вычислить x1по формуле
- x 1 = x 0 + α 0 p 0 = [2 1] + 73 331 [- 8 — 3] = [0,2356 0,3384]. { displaystyle mathbf {x} _ {1} = mathbf {x} _ {0} + alpha _ {0} mathbf {p} _ {0} = { begin {bmatrix} 2 \ 1 end {bmatrix}} + { frac {73} {331}} { begin {bmatrix} -8 \ — 3 end {bmatrix}} = { begin {bmatrix} 0,2356 \ 0,3384 end {bmatrix} }.}
Этим результатом завершается первая итерация, результатом которой является «улучшенное» приближенное решение системы, x1. Теперь мы можем продолжить и вычислить следующий вектор невязки r1, используя формулу
- r 1 = r 0 — α 0 A p 0 = [- 8 — 3] — 73 331 [4 1 1 3] [- 8 — 3] = [- 0,2810 0,7492]. { displaystyle mathbf {r} _ {1} = mathbf {r} _ {0} — alpha _ {0} mathbf {A} mathbf {p} _ {0} = { begin {bmatrix} -8 \ — 3 end {bmatrix}} — { frac {73} {331}} { begin {bmatrix} 4 1 \ 1 3 end {bmatrix}} { begin {bmatrix} -8 \ — 3 end {bmatrix}} = { begin {bmatrix} -0.2810 \ 0.7492 end {bmatrix}}.}
Наш следующий шаг в процессе — вычислить скаляр β 0, который в конечном итоге будет использоваться для определения следующего направления поиска p1.
- β 0 = r 1 T r 1 r 0 T r 0 = [- 0,2810 0,7492] [- 0,2810 0,7492] [- 8 — 3] [- 8 — 3] = 0,0088. { displaystyle beta _ {0} = { frac { mathbf {r} _ {1} ^ { mathsf {T}} mathbf {r} _ {1}} { mathbf {r} _ {0 } ^ { mathsf {T}} mathbf {r} _ {0}}} = { frac {{ begin {bmatrix} -0,2810 и 0,7492 end {bmatrix}} { begin {bmatrix} -0,2810 \ 0.7492 end {bmatrix}}} {{ begin {bmatrix} -8 -3 end {bmatrix}} { begin {bmatrix} -8 \ — 3 end {bmatrix}}}} = 0,0088. }
Теперь, используя этот скаляр β 0, мы можем вычислить следующее направление поиска p1, используя соотношение
- p 1 = r 1 + β 0 p 0 = [- 0,2810 0,7492] + 0,0088 [- 8 — 3] = [- 0,3511 0,7229]. { displaystyle mathbf {p} _ {1} = mathbf {r} _ {1} + beta _ {0} mathbf {p} _ {0} = { begin {bmatrix} -0,2810 \ 0,7492 end {bmatrix}} + 0.0088 { begin {bmatrix} -8 \ — 3 end {bmatrix}} = { begin {bmatrix} -0.3511 \ 0.7229 end {bmatrix}}.}
Мы теперь вычислите скаляр α 1, используя недавно полученный p1, используя тот же метод, который использовался для α 0.
- α 1 = r 1 T r 1 p 1 TA p 1 = [- 0,2810 0,7492] [- 0,2810 0,7492] [- 0,3511 0,7229] [4 1 1 3] [- 0,3511 0,7229] = 0,4122. { displaystyle alpha _ {1} = { frac { mathbf {r} _ {1} ^ { mathsf {T}} mathbf {r} _ {1}} { mathbf {p} _ {1 } ^ { mathsf {T}} mathbf {Ap} _ {1}}} = { frac {{ begin {bmatrix} -0,2810 и 0,7492 end {bmatrix}} { begin {bmatrix} -0,2810 \ 0.7492 end {bmatrix}}} {{ begin {bmatrix} -0.3511 0.7229 end {bmatrix}} { begin {bmatrix} 4 1 \ 1 3 end {bmatrix}} { begin {bmatrix} -0,3511 \ 0,7229 end {bmatrix}}}} = 0,4122.}
Наконец, мы находим x2, используя тот же метод, который использовался для нахождения x1.
- x 2 = x 1 + α 1 p 1 = [0,2356 0,3384] + 0,4122 [- 0,3511 0,7229] = [0,0909 0,6364]. { displaystyle mathbf {x} _ {2} = mathbf {x} _ {1} + alpha _ {1} mathbf {p} _ {1} = { begin {bmatrix} 0,2356 \ 0,3384 end {bmatrix}} + 0,4122 { begin {bmatrix} -0,3511 \ 0,7229 end {bmatrix}} = { begin {bmatrix} 0,0909 \ 0,6364 end {bmatrix}}.}
Результат, x2, является «лучшим» приближением к решению системы, чем x1и x0. Если бы в этом примере использовалась точная арифметика вместо ограниченной точности, то точное решение теоретически было бы достигнуто после n = 2 итераций (n — порядок системы).
Свойства сходимости
Теоретически метод сопряженных градиентов можно рассматривать как прямой метод, поскольку он дает точное решение после конечного числа итераций, которое не превышает размер матрицы, при отсутствии ошибки округления. Однако метод сопряженных градиентов неустойчив по отношению даже к небольшим возмущениям, например, большинство направлений на практике не являются сопряженными, и точное решение никогда не получается. К счастью, метод сопряженного градиента можно использовать как итерационный метод, поскольку он обеспечивает монотонно улучшающиеся приближения xk { displaystyle mathbf {x} _ {k}}



Если κ (A) { displaystyle kappa (A)}




Теорема сходимости
Определите подмножество многочленов как
- Π k ∗: = {p ∈ Π k: p (0) = 1}, { displaystyle Pi _ {k} ^ {*}: = left lbrace p in Pi _ {k} : p (0) = 1 right rbrace ,,}
где Π k { displaystyle Pi _ {k}}

Пусть (xk) k { displaystyle left ( mathbf {x} _ {k} right) _ {k}}


- ‖ e k ‖ A = min p ∈ Π k ∗ ‖ p (A) e 0 ‖ A ≤ min p ∈ Π k ∗ max λ ∈ σ (A) | p (λ) | ‖ Е 0 ‖ A ≤ 2 (κ (A) — 1 κ (A) + 1) к ‖ e 0 ‖ A, { displaystyle { begin {align} left | mathbf {e} _ {k} right | _ { mathbf {A}} = min _ {p in Pi _ {k} ^ {*}} left | p ( mathbf {A}) mathbf {e} _ {0} right | _ { mathbf {A}} \ leq min _ {p in Pi _ {k} ^ {*}} , max _ { lambda in sigma ( mathbf {A}) } | р ( лямбда) | left | mathbf {e} _ {0} right | _ { mathbf {A}} \ leq 2 left ({ frac {{ sqrt { kappa ( mathbf {A})}} — 1} {{ sqrt { kappa ( mathbf { A})}} + 1}} right) ^ {k} left | mathbf {e} _ {0} right | _ { mathbf {A}} ,, end {align}}}
где σ (A) { displaystyle сигма ( mathbf {A})}

Обратите внимание: важный предел, когда κ (A) { displaystyle kappa ( mathbf {A})}
- κ (A) — 1 κ (A) + 1 ≈ 1-2 κ (A) для κ (A) ≫ 1. { displaystyle { frac {{ sqrt { kappa ( mathbf {A})}} — 1} {{ sqrt { каппа ( mathbf {A})}} + 1}} приблизительно 1- { frac {2} { sqrt { kappa ( mathbf {A})}}} quad { text {for}} quad kappa ( mathbf {A}) gg 1 ,.}
Этот предел демонстрирует более высокую скорость сходимости по сравнению с итерационными методами Якоби или Гаусса — Зейделя, которые масштабируются как ≈ 1-2 κ (A) { displaystyle приблизительно 1 — { frac {2} { kappa ( mathbf {A})}}}
Метод сопряженного градиента с предварительным условием м
В большинстве случаев предварительное кондиционирование необходимо для обеспечения быстрая сходимость метода сопряженных градиентов. Предварительно предложенный метод сопряженного градиента имеет следующую форму:
- r 0: = b — A x 0 { displaystyle mathbf {r} _ {0}: = mathbf {b} — mathbf {Ax} _ {0} }
- z 0: = M — 1 r 0 { displaystyle mathbf {z} _ {0}: = mathbf {M} ^ {- 1} mathbf {r} _ {0}}
- п 0: знак равно Z 0 { Displaystyle mathbf {p} _ {0}: = mathbf {z} _ {0}}
- k: = 0 { displaystyle k: = 0 ,}
-
- α k: = rk T zkpk TA pk { displaystyle alpha _ {k}: = { frac { mathbf {r} _ {k} ^ { mathsf {T}} mathbf {z } _ {k}} { mathbf {p} _ {k} ^ { mathsf {T}} mathbf {Ap} _ {k}}}}
- xk + 1: = xk + α kpk { displaystyle mathbf {x} _ {k + 1}: = mathbf {x} _ {k} + alpha _ {k} mathbf {p} _ {k}}
- rk + 1: = rk — α К A pk { displaystyle mathbf {r} _ {k + 1}: = mathbf {r} _ {k} — alpha _ {k} mathbf {Ap} _ {k}}
- ifrk +1 достаточно мало, затем цикл выхода закончится, если
- zk + 1: = M — 1 rk + 1 { displaystyle mathbf {z} _ {k + 1}: = mathbf {M} ^ {- 1} mathbf {r} _ {k + 1}}
- β k: = rk + 1 T zk + 1 rk T zk { displaystyle beta _ {k}: = { frac { mathbf {r} _ {k + 1} ^ { mathsf {T}} mathbf {z} _ {k + 1}} { mathbf {r} _ {k} ^ { mathsf {T}} mathbf {z} _ {k}}}}
- pk + 1: = zk + 1 + β kpk { displaystyle mathbf {p} _ {k + 1}: = mathbf {z} _ {k +1} + beta _ {k} mathbf {p} _ {k}}
- k: = k + 1 { displaystyle k: = k + 1 ,}
- α k: = rk T zkpk TA pk { displaystyle alpha _ {k}: = { frac { mathbf {r} _ {k} ^ { mathsf {T}} mathbf {z } _ {k}} { mathbf {p} _ {k} ^ { mathsf {T}} mathbf {Ap} _ {k}}}}
- конец повторения
- результат: xk + 1
Приведенная выше формулировка эквивалентна применения метода сопряженных градиентов без предварительной обработки системы
- E — 1 A (E — 1) T x ^ = E — 1 b { Displaystyle mathbf {E} ^ {- 1} mathbf {A} ( mathbf {E} ^ {- 1}) ^ { mathsf {T}} mathbf { hat {x}} = mathbf {E} ^ {- 1} mathbf {b}}
где
- EET = M, x ^ = ET x. { Displaystyle mathbf {EE} ^ { mathsf {T}} = mathbf {M}, qquad mathbf { hat {x}} = mathbf {E} ^ { mathsf {T}} mathbf {x}.}
Матрица предобуславливателя M должна быть симметричной положительно определенной и фиксированной, т. е. не может изменяться от итерации к итерации. Если какое-либо из этих предположений о предобуславливателе нарушается, метод вызванного сопряженного градиента может стать непредсказуемым.
Примером обычно используемого предобуславливателя является неполная факторизация Холецкого.
Гибкий метод сопряженного градиента с предварительным условием
В приложениях, требующихся численного решения, предварительные кондиционеры используются, что может привести к предварительной обработке чисел, изменяющейся между итерациями. Даже если предобуславливатель является симметричным положительно определенным фактом каждой итерации, тот, который он может изменить, делает приведенные выше аргументы недействительными и практическими тестами приводит к значительному замедлению сходимости алгоритма, представленного выше. По формуле Полака — Рибьера
- β k: = rk + 1 T (zk + 1 — zk) rk T zk { displaystyle beta _ {k}: = { frac { mathbf { r} _ {k + 1} ^ { mathsf {T}} left ( mathbf {z} _ {k + 1} — mathbf {z} _ {k} right)} { mathbf {r} _ {k} ^ { mathsf {T}} mathbf {z} _ {k}}}}
вместо формулы Флетчера — Ривза
- β k: = rk + 1 T zk + 1 рк T zk { displaystyle beta _ {k}: = { frac { mathbf {r} _ {k + 1} ^ { mathsf {T}} mathbf {z} _ {k +1} } { mathbf {r} _ {k} ^ { mathsf {T}} mathbf {z} _ {k}}}}
может улучшить сходимость в случае. Эту версию метода вызванного сопряженного градиента можно назвать гибким, . Также показано, что гибкая версия является устойчивой, даже если предобуславливатель не является симметричным положительно определенным (SPD).
Реализация гибкой версии требует хранения дополнительного события. Для фиксированного предварительного кондиционера SPD rk + 1 T zk = 0, { displaystyle mathbf {r} _ {k + 1} ^ { mathsf {T}} mathbf {z} _ {k} = 0, }
Математическое объяснение поведения лучшей сходимости с формулой Полака — Рибьера заключается в том, что метод локально оптимален в этом случае, в частности, он не сходится медленнее, чем метод локально оптимального наискорейшего спуска.
Пример кода в MATLAB / GNU Octave
function [x, k] = cgp (x0, A, C, b, mit, stol, bbA, bbC)% Синопсис:% x0: начальная точка% A: Матрица A системы Ax = b% C: матрица предварительной подготовки может быть левой или правой% mit: максимальное количество итераций% stol: допускаются нормы остатка% bbA: черный ящик, вычисляет который выполняет матрица-вектор для A * u% bbC: черный ящик который вычисляет:% для левого предобуславливателя: ha = C ra% для правого предобуславливателя: ha = C * ra% x: Предполагаемая точка решения% k: количество выполненных итераций %% Пример:% tic; [x, t] = cgp (x0, S, speye (1), b, 3000, 10 ^ -8, @ (Z, o) Z * o, @ (Z, o) o); toc% Истекшее время составляет 0,550190 секунд. %% Ссылка:% Métodos iterativos tipo Krylov para sistema lineales% B. Molina y M. Raydan - {{ISBN | 908-261-078-X}}, если nargin < 8, error('Not enough input arguments. Try help.'); end; if isempty(A), error('Input matrix A must not be empty.'); end; if isempty(C), error('Input preconditioner matrix C must not be empty.'); end; x = x0; ha = 0; hp = 0; hpp = 0; ra = 0; rp = 0; rpp = 0; u = 0; k = 0; ra = b - bbA(A, x0); % <--- ra = b - A * x0; while norm(ra, inf)>stol ha = bbC (C, ra); % <--- ha = C ra; k = k + 1; if (k == mit), warning('GCP:MAXIT', 'mit reached, no conversion.'); return; end; hpp = hp; rpp = rp; hp = ha; rp = ra; t = rp' * hp; if k == 1 u = hp; else u = hp + (t / (rpp' * hpp)) * u; end; Au = bbA(A, u); % <--- Au = A * u; a = t / (u' * Au); x = x + a * u; ra = rp - a * Au; end;
Против. локально используемый метод наискорейшего спуска
Как в исходном, так и в стимулированном методе сопряженного градиента нужно установить β k: = 0 { displaystyle beta _ {k}: = 0}
Вывод метода
Метод сопряженного градиента может быть получен с нескольких точек зрения, включая специализацию метода сопряженного направления для оптимизации и вариативного метода Арнольди / Итерация Ланцоша для задач с величиной . Несмотря на различия в подходах, эти выводы общую тему — доказательство ортогональности остатков и сопряженности поиска поиска. Эти два свойства имеют решающее значение для разработки известной лаконичной формулировки метода.
Метод сопряженного градиента также может быть получен с использованием теории оптимального управления. В этом подходе метод сопряженных градиентов оказывается оптимальным контроллером обратной,
u = k (x, v): = — γ a ∇ f (x) — γ bv { displaystyle u = k (x, v): = — gamma _ {a} nabla f (x) — gamma _ {b} v}

x ˙ = v, v ˙ = u { displaystyle { dot {x}} = v, quad { dot {v}} = u}

γ a { displaystyle gamma _ {a}}

γ b { displaystyle gamma _ {b}}

Сопряженный градиент в обычных уравнениях
Метод сопряженного градиента может применяться к произвольным n матрица -by-m, применяя ее к нормальным уравнениям AAи вектору правой части Ab, поскольку AAявляется симметричной положительно-полуопределенной матрицей для любого A . Результатом является сопряженный градиент нормальных уравнений (CGNR).
- AAx= Ab
В качестве итеративного метода нет необходимости явно формировать AAв памяти, а только выполнять умножения матрица-вектор и транспонировать матрицу-вектор. Следовательно, CGNR особенно полезен, когда A — это разреженная матрица, поскольку эти операции обычно чрезвычайно эффективны. Однако обратная сторона формирования нормальных уравнений состоит в том, что число условия κ(AA) равно κ (A ), поэтому скорость сходимости CGNR может быть медленной, а качество приближенного решение может быть чувствительным к ошибкам округления. Поиск хорошего прекондиционера часто является важной частью использования метода CGNR.
Было предложено несколько алгоритмов (например, CGLS, LSQR). Алгоритм LSQR предположительно имеет лучшую числовую стабильность, когда A плохо обусловлен, т. Е. A имеет большое число условия.
См. Также
Ссылки
Дополнительная литература
- Atkinson, Kendell A. (1988). «Раздел 8.9». Введение в численный анализ (2-е изд.). Джон Уайли и сыновья. ISBN 978-0-471-50023-0.
- Авриэль, Мардохей (2003). Нелинейное программирование: анализ и методы. Dover Publishing. ISBN 978-0-486-43227-4.
- Golub, Gene H.; Ван Лоан, Чарльз Ф. (1996-10-15). «Глава 10». Матричные вычисления (3-е изд.). Издательство Университета Джона Хопкинса. ISBN 978-0-8018-5414-9.
- Саад, Юсеф (01.04.2003). «Глава 6». Итерационные методы для разреженных линейных систем (2-е изд.). СИАМ. ISBN 978-0-89871-534-7.

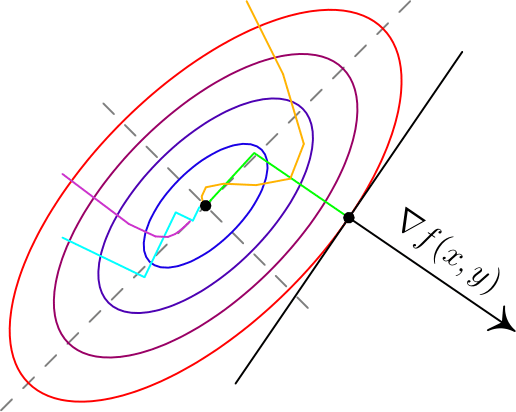






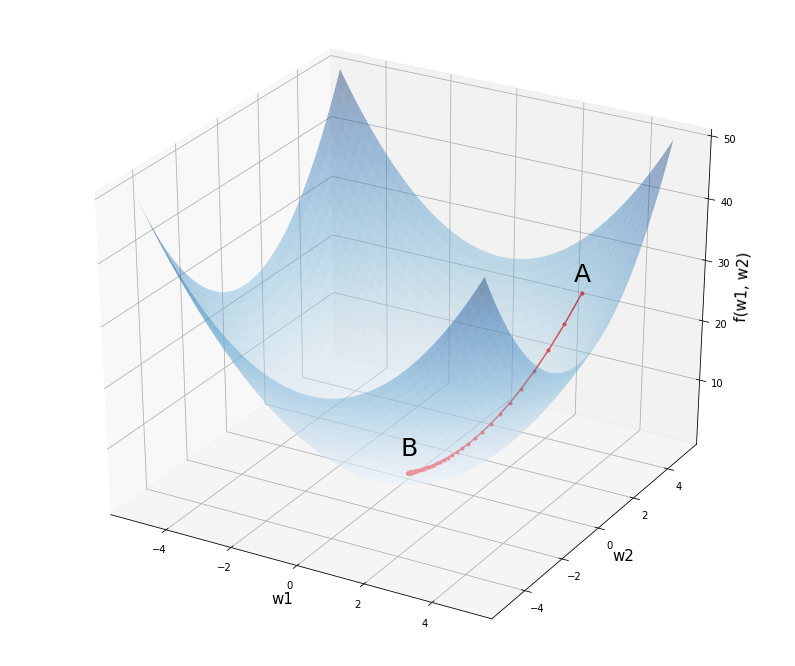

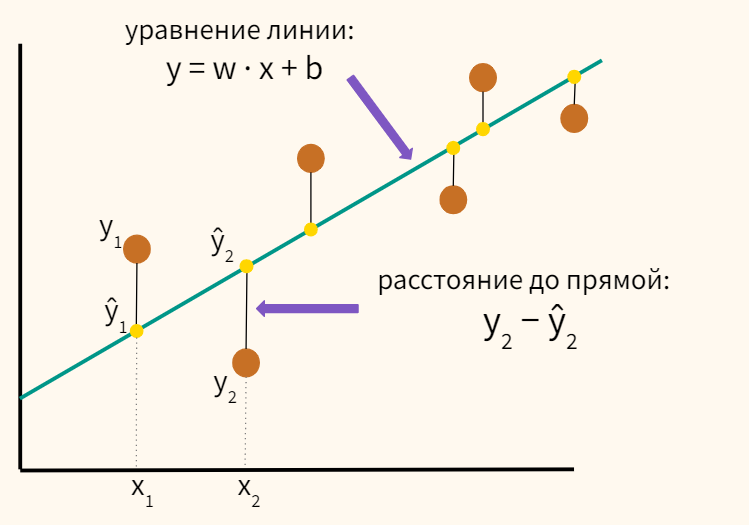







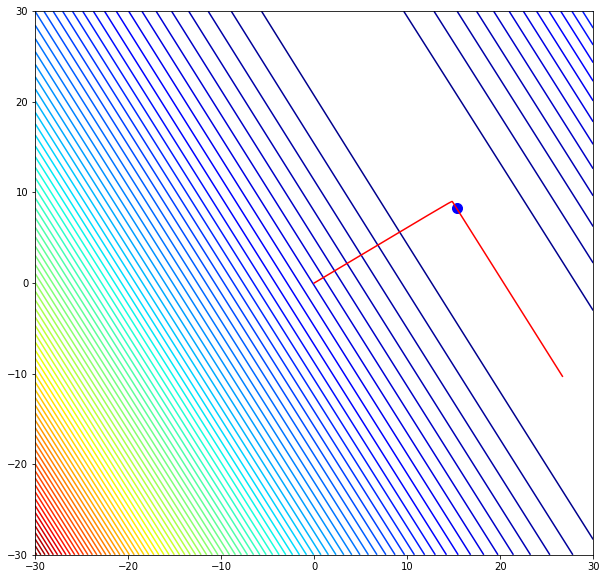



![vec{x}^{[j+1]}=vec{x}^{[j]}+lambda^{[j]} vec{v}^{[j]}](https://web.archive.org/web/20150906085958im_/https://upload.wikimedia.org/math/6/f/8/6f83562e28b2cd8410eccaccd6a3d4de.png)
![overrightarrow{x}^{[j+1]}=overrightarrow{x}^{[j]}-lambda^{[j]}nabla F(overrightarrow{x}^{[j]})](https://web.archive.org/web/20150906085958im_/https://upload.wikimedia.org/math/d/1/7/d179f1d86aaedbced2f7e49a1af9bc4d.png)
![lambda^{[j]}=mathrm{argmin}_{lambda} ,F(vec{x}^{[j]}-lambda^{[j]}nabla F(vec{x}^{[j]}))](https://web.archive.org/web/20150906085958im_/https://upload.wikimedia.org/math/6/e/5/6e5c92778e76ef3da1fcc4561a403344.png)


![left{begin{array}{lcr}
vec{x}^{[j]}_1 & = & vec{x}^{[j]}_0-lambda^{[j]}_1frac{partial F(vec{x}^{[j]}_0)}{partial x_1}vec{e}_1 \
ldots & & \
vec{x}^{[j]}_n & = & vec{x}^{[j]}_{n-1}-lambda^{[j]}_nfrac{partial F(vec{x}^{[j]}_{n-1})}{partial x_n}vec{e}_n
end{array} right.](https://web.archive.org/web/20150906085958im_/https://upload.wikimedia.org/math/3/7/9/3793adb81cf70ddd17d1abe493d243f0.png) , где
, где ![lambda^{[j]}_i=mathrm{argmin}_{lambda} ,Fleft( vec{x}^{[j]}_{i-1}-lambda^{[j]}frac{partial F(vec{x}^{[j]}_{i-1})}{partial x_{i-1}} vec{e}_i right)](https://web.archive.org/web/20150906085958im_/https://upload.wikimedia.org/math/1/2/d/12d7a5a72da318ba61ea75225b9be412.png)
























































