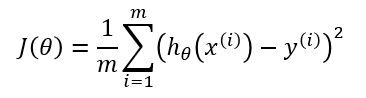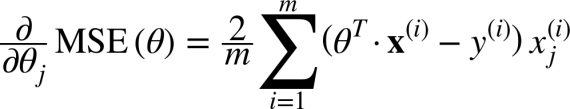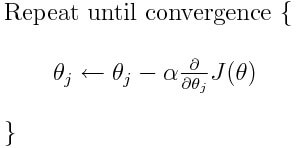Время на прочтение
8 мин
Количество просмотров 125K
Часть 1 — линейная регрессия
В первой части я забыл упомянуть, что если случайно сгенерированные данные не по душе, то можно взять любой подходящий пример отсюда. Можно почувствовать себя ботаником, виноделом, продавцом. И все это не вставая со стула. В наличии множество наборов данных и одно условие — при публикации указывать откуда взял данные, чтобы другие смогли воспроизвести результаты.
Градиентный спуск
В прошлой части был показан пример вычисления параметров линейной регрессии с помощью метода наименьших квадратов. Параметры были найдены аналитически — 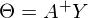
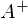
Проблема заключается в том, что вычисление псевдообратной матрицы очень затратно: 2 умножения по 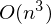
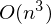
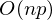
Не будем отходить от линейной регрессии и МНК и обозначим функцию потерь 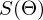
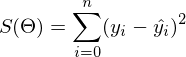
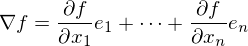
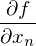
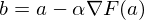
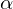
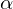
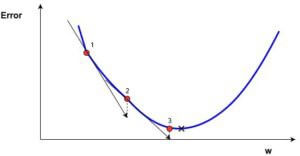
Метод очень прост и интуитивен, возьмем простой двумерный пример для демонстрации:
Необходимо минимизировать функцию вида 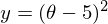
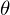
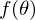
1) Необходима производная по 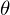
2) Установим начальное значение 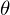
3) Установим размер шага — попробуем несколько значений — 0.1, 0.9, 1.2, чтобы посмотреть как этот выбор повлияет на сходимость.
4) 25 раз подряд выполним указанную выше формулу: 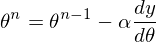
Код крайне прост. Исключая определение функций, весь алгоритм уместился в 3 строки:
simple_gd_console.py
STEP_COUNT = 25
STEP_SIZE = 0.1 # Скорость обучения
def func(x):
return (x - 5) ** 2
def func_derivative(x):
return 2 * (x - 5)
previous_x, current_x = 0, 0
for i in range(STEP_COUNT):
current_x = previous_x - STEP_SIZE * func_derivative(previous_x)
previous_x = current_x
print("After", STEP_COUNT, "steps theta=", format(current_x, ".6f"), "function value=", format(func(current_x), ".6f"))
Весь процесс можно визуализировать примерно так (синяя точка — значение на предыдущем шаге, красная — текущее):
Или же для шага другого размера:
При значении, равном 1.2, метод расходится, каждый шаг опускаясь не ниже, а наоборот выше, устремляясь в бесконечность. Шаг в простой реализации подбирается вручную и его размер зависит от данных — на каких-нибудь ненормализованных значениях с большим градиентом и 0.0001 может приводить к расхождению.
Код для генерации гифок
import matplotlib.pyplot as plt
import matplotlib.animation as anim
import numpy as np
STEP_COUNT = 25
STEP_SIZE = 0.1 # Скорость обучения
X = [i for i in np.linspace(0, 10, 10000)]
def func(x):
return (x - 5) ** 2
def bad_func(x):
return (x - 5) ** 2 + 50 * np.sin(x) + 50
Y = [func(x) for x in X]
def func_derivative(x):
return 2 * (x - 5)
def bad_func_derivative(x):
return 2 * (x + 25 * np.cos(x) - 5)
# Какая-то жажа и первый кадр пропускается
skip_first = True
def draw_gradient_points(num, points, line, cost_caption, step_caption, theta_caption):
global previous_x, skip_first, ax
if skip_first:
skip_first = False
return points, line
current_x = previous_x - STEP_SIZE * func_derivative(previous_x)
step_caption.set_text("Step: " + str(num))
cost_caption.set_text("Func value=" + format(func(current_x), ".3f"))
theta_caption.set_text("$\theta$=" + format(current_x, ".3f"))
print("Step:", num, "Previous:", previous_x, "Current", current_x)
points[0].set_data(previous_x, func(previous_x))
points[1].set_data(current_x, func(current_x))
# points.set_data([previous_x, current_x], [func(previous_x), func(current_x)])
line.set_data([previous_x, current_x], [func(previous_x), func(current_x)])
if np.abs(func(previous_x) - func(current_x)) < 0.5:
ax.axis([4, 6, 0, 1])
if np.abs(func(previous_x) - func(current_x)) < 0.1:
ax.axis([4.5, 5.5, 0, 0.5])
if np.abs(func(previous_x) - func(current_x)) < 0.01:
ax.axis([4.9, 5.1, 0, 0.08])
previous_x = current_x
return points, line
previous_x = 0
fig, ax = plt.subplots()
p = ax.get_position()
ax.set_position([p.x0 + 0.1, p.y0, p.width * 0.9, p.height])
ax.set_xlabel("$\theta$", fontsize=18)
ax.set_ylabel("$f(\theta)$", fontsize=18)
ax.plot(X, Y, '-r', linewidth=2.0)
ax.axvline(5, color='black', linestyle='--')
start_point, = ax.plot([], 'bo', markersize=10.0)
end_point, = ax.plot([], 'ro')
rate_capt = ax.text(-0.3, 1.05, "Rate: " + str(STEP_SIZE), fontsize=18, transform=ax.transAxes)
step_caption = ax.text(-0.3, 1, "Step: ", fontsize=16, transform=ax.transAxes)
cost_caption = ax.text(-0.3, 0.95, "Func value: ", fontsize=12, transform=ax.transAxes)
theta_caption = ax.text(-0.3, 0.9, "$\theta$=", fontsize=12, transform=ax.transAxes)
points = (start_point, end_point)
line, = ax.plot([], 'g--')
gradient_anim = anim.FuncAnimation(fig, draw_gradient_points, frames=STEP_COUNT,
fargs=(points, line, cost_caption, step_caption, theta_caption),
interval=1500)
# Для того, чтобы получить гифку необходимо установить ImageMagick
# Можно получить .mp4 файл без всяких magick-shmagick
gradient_anim.save("images/animation.gif", writer="imagemagick")
Вот еще пример с «плохой» функцией. В первой анимации метод также расходится и будет долго блуждать по холмам из-за слишком высокого шага. Во втором случае был найден локальный минимум и варьируя значение скорости не получится заставить метод найти минимум глобальный. Этот факт является одним недостатков метода — он может найти глобальный минимум только если функция выпуклая и гладкая. Или если повезет с начальными значениями.
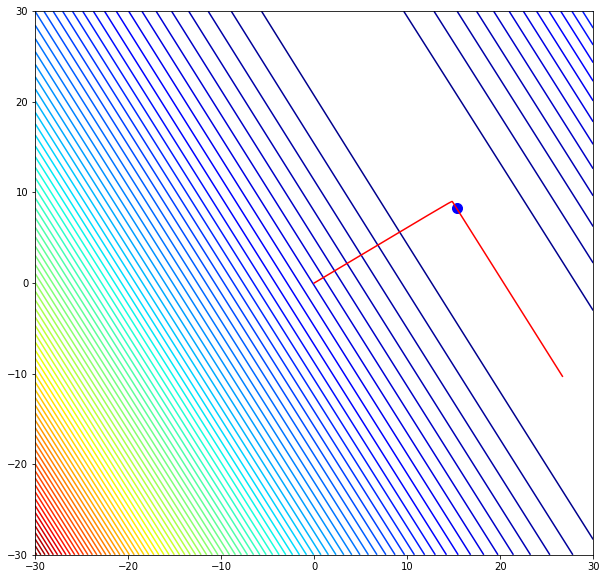
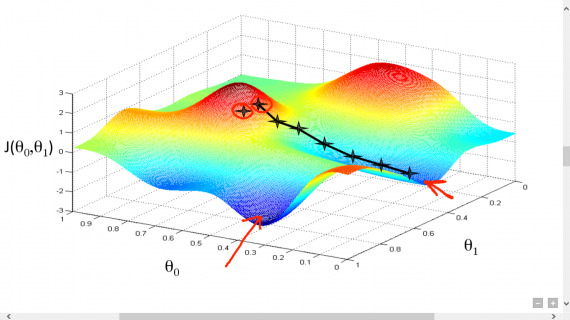
Также возможно рассмотреть работу алгоритма на трехмерном графике. Часто рисуют только изолинии какой-то фигуры. Я взял простой параболоид вращения: 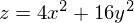
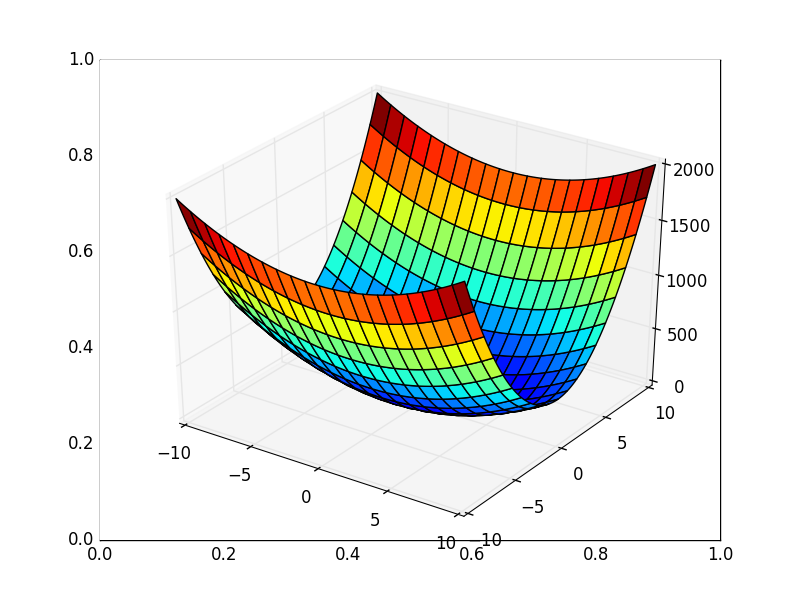
Contour plot
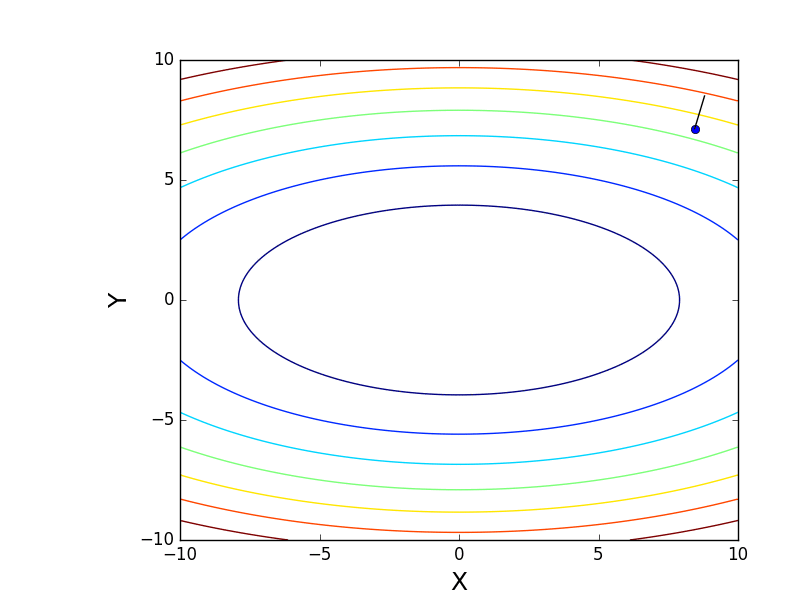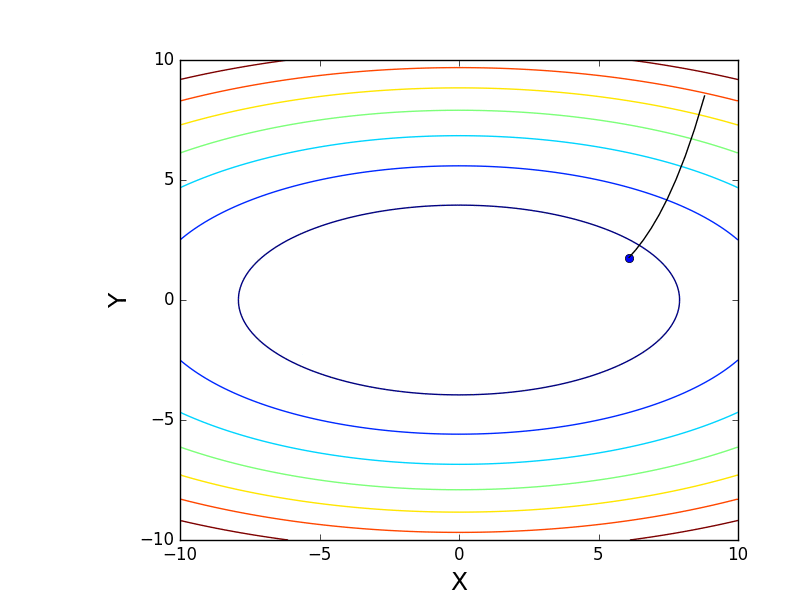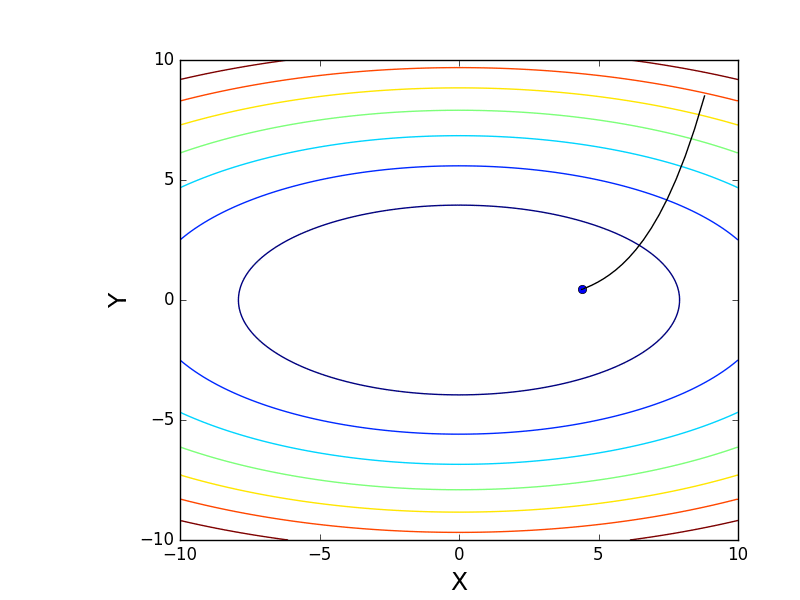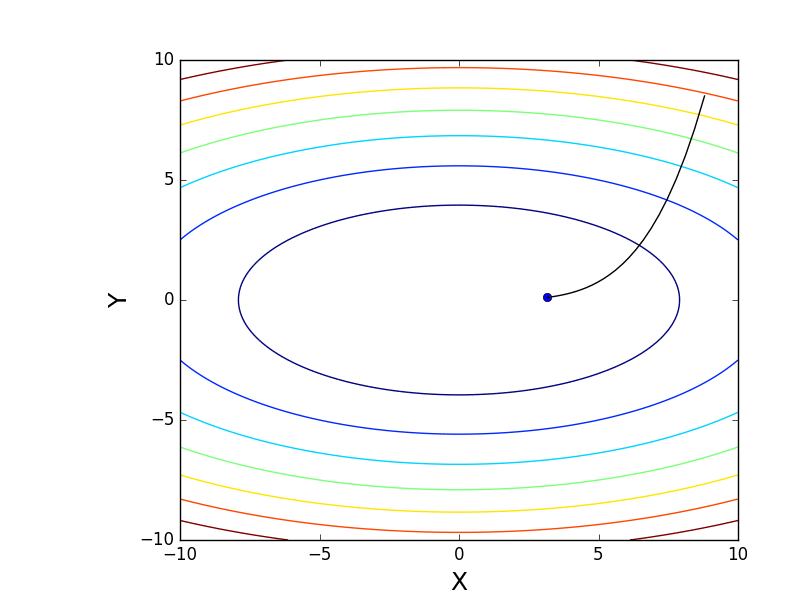
Генерация графика с изолиниями
import matplotlib.pyplot as plt
import matplotlib.animation as anim
import numpy as np
STEP_COUNT = 25
STEP_SIZE = 0.005 # Скорость обучения
X = np.array([i for i in np.linspace(-10, 10, 1000)])
Y = np.array([i for i in np.linspace(-10, 10, 1000)])
def func(X, Y):
return 4 * (X ** 2) + 16 * (Y ** 2)
def dx(x):
return 8 * x
def dy(y):
return 32 * y
# Какая-то жажа и первый кадр пропускается
skip_first = True
def draw_gradient_points(num, point, line):
global previous_x, previous_y, skip_first, ax
if skip_first:
skip_first = False
return point
current_x = previous_x - STEP_SIZE * dx(previous_x)
current_y = previous_y - STEP_SIZE * dy(previous_y)
print("Step:", num, "CurX:", current_x, "CurY", current_y, "Fun:", func(current_x, current_y))
point.set_data([current_x], [current_y])
# Blah-blah
new_x = list(line.get_xdata()) + [previous_x, current_x]
new_y = list(line.get_ydata()) + [previous_y, current_y]
line.set_xdata(new_x)
line.set_ydata(new_y)
previous_x = current_x
previous_y = current_y
return point
previous_x, previous_y = 8.8, 8.5
fig, ax = plt.subplots()
p = ax.get_position()
ax.set_position([p.x0 + 0.1, p.y0, p.width * 0.9, p.height])
ax.set_xlabel("X", fontsize=18)
ax.set_ylabel("Y", fontsize=18)
X, Y = np.meshgrid(X, Y)
plt.contour(X, Y, func(X, Y))
point, = plt.plot([8.8], [8.5], 'bo')
line, = plt.plot([], color='black')
gradient_anim = anim.FuncAnimation(fig, draw_gradient_points, frames=STEP_COUNT,
fargs=(point, line),
interval=1500)
# Для того, чтобы получить гифку необходимо установить ImageMagick
# Можно получить .mp4 файл без всяких magick-shmagick
gradient_anim.save("images/contour_plot.gif", writer="imagemagick")
Также обратите внимание, что все линии градиента, направлены перпендикулярно изолиниям. Это означает, что двигаясь в сторону антиградиента, не получится за один шаг сразу же прыгнуть в минимум — градиент указывает совсем не туда.
После графического пояснения, найдем формулу для вычисления неизвестных параметров 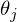
Если бы количество элементов в тестовой выборке было равно единице, то формулу можно было бы так и оставить и считать. В случае, когда в наличии n элементов алгоритм выглядит так:
Повторять v раз
{
для каждого j одновременно.
}, где n — количество элементов в обучающей выборке, v — количество итераций
Требование одновременности означает, что производная должна быть вычислена со старыми значениями theta, не стоит вычислять сначала отдельно первый параметр, затем второй и т.д., потому что после изменения первого параметра отдельно, производная также изменит свое значение. Псевдокод одновременного изменения:
for i in train_samples:
new_theta[1] = old_theta[1] + a * derivative(old_theta)
new_theta[2] = old_theta[2] + a * derivative(old_theta)
old_theta = new_theta
Если вычислять значения параметров по одиночке, то это уже будет не градиентный спуск. Допустим, у нас трехмерная фигура и если вычислять параметры один за одним, то можно представить этот процесс как движение только по одной координате за раз — один шажок по x координате, затем шажок по y координате и т.д. ступеньками, вместо движения в сторону вектора антиградиента.
Приведенный выше вариант алгоритма называют пакетный градиентный спуск. Количество повторений можно заменить на фразу «Повторять, пока не сойдется». Эта фраза означает, что параметры будут корректироваться до тех пор, пока предыдущее и текущее значения функции стоимости не сравняются. Это значит, что локальный или глобальный минимум найден и дальше алгоритм не пойдет. На практике равенства достичь невозможно и вводится предел сходимости 

while abs(S_current - S_previous) >= Epsilon:
# do something
Так как пост неожиданно растянулся, я бы хотел его на этом завершить — в следующей части я продолжу разбор градиентного спуска для линейной регрессии с МНК.
Продолжение.
Для запуска примеров необходимы: numpy, matplotlib.
Для запуска примеров, создающих анимации необходим ImageMagick.
Материалы, использованные в статье — github.com/m9psy/neural_network_habr_guide
Введение
Зачастую задачи машинного обучения формулируются таким образом, что «веса» модели, которую мы строим, возникают, как решение оптимизационной задачи. В качестве VIP-примера рассмотрим задачу линейной регрессии:
$$
Vert y — Xw Vert_2^2 to min_w,
$$
По сути, мы получили чистейшую задачу квадратичной оптимизации. В чем особенность конкретно этой задачи? Она выпуклая.
Для интересующихся определением.
Функция $f colon mathbb{R}^d to mathbb{R}$ является (нестрого) выпуклой (вниз), если для любых $x_1,x_2 in mathbb{R}^d$ верно, что
$$
forall t in [0,1] : f(tx_1 + (1-t)x_2) leq t f(x_1) + (1-t) f(x_2).
$$
Чтобы запомнить, в какую сторону неравенство, всегда полезно рисовать следующую картинку с графическим определением выпуклой функции.
Эквивалентное определение, если функция достаточно гладкая – гессиан неотрицательно определен в любой точке, то есть в каждой точке функция хорошо приближается параболоидом ветвями вверх. Отсюда по критерию минимальности второго порядка автоматически следует, что всякая точка локального оптимума является точкой локального минимума, то есть локальных максимумов и сёдел в выпуклом мире попросту не существует.
Важное свойство выпуклых функций – локальный минимум автоматически является глобальным (но не обязательно единственным!). Это позволяет избегать уродливых ситуаций, которые с теоретической точки зрения могут встретиться в невыпуклом случае, например, вот такой:
Теорема (No free lunch theorem) Пусть $A$ – алгоритм оптимизации, использующий локальную информацию (все производные в точке). Тогда существует такая невыпуклая функция $f colon [0,1]^d to [0,1]$, что для нахождения глобального минимума на квадрате $[0,1]^d$ с точностью $frac{1}{m}$ требуется совершить хотя бы $m^d$ шагов.
Для интересующихся доказательствами.
Будем строить наш контрпример, пользуясь принципом сопротивляющегося оракула (или рассуждениями с противником, кому как привычнее называть).
Разделим нашу область на подкубики размера $1/m times ldots times 1/m$. Зададим функцию следующим образом – она будет тождественно равна $1$ на всех кубиках, кроме одного, в середине которого будет точка с значением $0$ (мы не специфицируем, как значение будет гладко «снижаться» до $0$; можно построить кусочно-линейную функцию, а потом сгладить её).
А именно поставим ноль в тот кубик, который наш алгоритм оптимизации $A$ посетит последним. Так как кубиков у нас $m^d$, то алгоритм должен всегда совершить как минимум $m^d$ шагов, попробовав все кубики. Итого у нас следующая картинка ($m=3, d=2$):
Отметим дополнительно, что полученный контрпример можно сделать какой угодно гладкости (но не аналитическим).
Мы видим, что в общем случае без выпуклости нас ожидает полное разочарование. Ничего лучше перебора по сетке придумать в принципе невозможно. В выпуклом случае же существуют алгоритмы, которые находят глобальный минимум за разумное время.
Встречаются ли в жизни функции невыпуклые? Повсеместно! Например, функция потерь при обучении нейронных сетей, как правило, не является выпуклой. Но отсюда не следует, что любой алгоритм их оптимизации будет обязательно неэффективным: ведь «контрпример» из теоремы довольно специфичен. И, как мы увидим, оптимизировать невыпуклые функции очень даже возможно.
Найти глобальный минимум невыпуклой функции – очень трудная задача, но зачастую нам хватает локального, который является, в частности, стационарной точкой: такой, в которой производная равна нулю. Все теоретические результаты в случае невыпуклых задач, как правило, касаются поиска таких точек, и алгоритмы тоже направлены на их отыскание.
Этим объясняется и то, что большинство алгоритмов оптимизации, придуманных для выпуклого случая, дословно перешли в невыпуклый. Теоретическая причина в следующем: в выпуклом случае поиск стационарной точки и поиск минимума – буквально одна и та же задача, поэтому то, что хорошо ищет минимум в выпуклом случае, ожидаемо будет хорошо искать стационарные точки в невыпуклом. Практическая же причина в том, что оптимизаторы в библиотеках никогда не спрашивают, выпуклую ли им функцию подают на вход, а просто работают и работают хорошо.
Внимательный читатель мог возразить на моменте подмены задачи: подождите-ка, мы ведь хотим сделать функцию как можно меньше, а не стационарную точку искать какую-то непонятную. Доказать в невыпуклом случае тут, к сожалению, ничего невозможно, но на практике мы снова используем алгоритмы изначально для выпуклой оптимизации. Почему?
Причина номер 1: сойтись в локальный минимум лучше, чем никуда. Об этом речь уже шла.
Причина номер 2: в окрестности локального минимума функция становится выпуклой, и там мы сможем быстро сойтись.
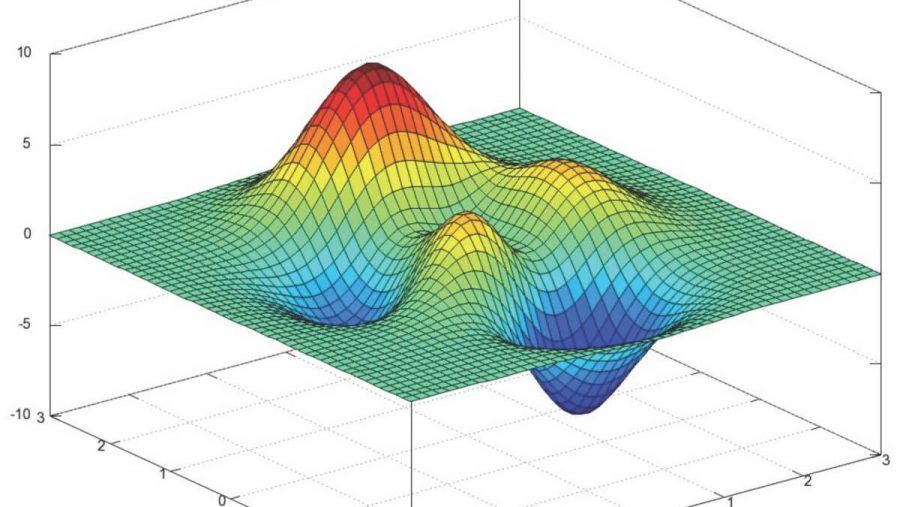
Причина номер 3: иногда невыпуклая функция является в некотором смысле «зашумленной» версией выпуклой или похожей на выпуклую. Например, посмотрите на эту картинку (функция Леви):
У этой функции огромное количество локальных минимумов, но «глобально» она кажется выпуклой. Что-то отдаленно похожее наблюдается и в случае нейронных сетей. Нашей задачей становится не скатиться в маленький локальный минимум, который всегда рядом с нами, а в большую-большую ложбину, где значение функции минимально и в некотором смысле стабильно.
Причина номер 4: оказывается, что градиентные методы весьма часто сходятся именно к локальным минимумам.
Сразу отметим важную разницу между выпуклой и невыпуклой задачами: в выпуклом случае работа алгоритма оптимизации не очень существенно зависит от начальной точки, поскольку мы всегда скатимся в точку оптимума. В невыпуклом же случае правильно выбранная точка старта – это уже половина успеха.
Теперь перейдём к разбору важнейших алгоритмов оптимизации.
Градиентный спуск (GD)
Опишем самый простой метод, который только можно придумать – градиентный спуск. Для того, чтобы его определить, вспомним заклинание из любого курса матанализа: «градиент – это направление наискорейшего локального возрастания функции», тогда антиградиент – это направление наискорейшего локального убывания.
Для интересующихся формализмом.
Воспользуемся формулой Тейлора для $Vert h Vert = 1$ (направления спуска):
$$
f(x + alpha h) = f(x) + alpha langle nabla f(x), h rangle + o(alpha).
$$
Мы хотим уменьшить значение функции, то есть
$$
f(x) + alpha langle nabla f(x), h rangle + o(alpha) < f(x).
$$
При $alpha to 0$ имеем $langle nabla f(x), Delta x rangle leq 0$. Более того, мы хотим наискорешйшего убывания, поэтому это скалярное произведение хочется минимизировать. Сделаем это при помощи неравенства Коши-Буняковского:
$$
langle nabla f(x), h rangle geq — Vert nabla f(x) Vert_2 Vert h Vert_2 = Vert nabla f(x) Vert_2.
$$
Равенство в неравенстве Коши-Буняковского достигается при пропорциональности аргументов, то есть
$$
h = — frac{nabla f(x)}{Vert nabla f(x) Vert_2}.
$$
$$tag*{$blacksquare$}$$
Тогда пусть $x_0$ – начальная точка градиентного спуска. Тогда каждую следующую точку мы выбираем следующим образом:
$$
x_{k+1} = x_k — alpha nabla f(x_k),
$$
где $alpha$ – это размер шага (он же learning rate). Общий алгоритм градиентного спуска пишется крайне просто и элегантно:
x = normal(0, 1) # можно пробовать и другие виды инициализации
repeat S times: # другой вариант: while abs(err) > tolerance
h = grad_f(x) # вычисляем направление спуска
x -= alpha * h # обновляем значение в точке
Эту схему в приложении к линейной регрессии можно найти в главе про линейные модели.
После всего этого начинаются тонкости:
- А как вычислять градиент?
- А как выбрать размер шага?
- А есть ли какие-то теоретические оценки сходимости?
Начнем разбирать вопросы постепенно. Для вычисления градиентов современный человек может использовать инструменты автоматического дифференцирования. Идейно, это вариация на тему алгоритма обратного распространения ошибки (backpropagation), ведь как правило человек задает функции, составленные из элементарных при помощи умножений/делений/сложений/композиций. Такой метод реализован во всех общих фреймворках для нейронных сетей (Tensorflow, PyTorch, Jax).
Но, вообще говоря, возникает некоторая тонкость. Например, расмотрим задачу линейной регрессии. Запишем её следующим образом:
$$
f(w) = frac{1}{N} sum_{i=1}^N (w^top x_i — y_i)^2.
$$
Видим, что слагаемых суммарно $N$ – размер выборки. При $N$ порядка $10^6$ и $d$ (это количество признаков) порядка $10^4$ вычисление градиента за $O(Nd)$ становится жутким мучением. Но если от $d$ избавиться без дополнительных предположений (например, о разреженности) нельзя, то с зависимостью от $N$ в каком-то смысле удастся разделаться при помощи метода стохастического градиентного спуска.
Хранение градиентов тоже доставит нам проблемы. У градиента столько же компонент, сколько параметров у модели, и если мы имеем дело с глубокой нейросетью, это даст значительные затраты дополнительной памяти. Хуже того, метод обратного распространения ошибки устроен так, что нам приходится помнить все промежуточные представления для вычисления градиентов. Поэтому вычислить градиент целиком невозможно ни для какой нормальной нейросети, и от этой беды тоже приходится спасаться с помощью стохастического градиентного спуска.
Теперь перейдем к размеру шага. Теория говорит о том, что если функция гладкая, то можно брать достаточно маленький размер шага, где под достаточно маленьким подразумевается $alpha leq frac1L$, где $L$ – некоторая константа, которая зависит от гладкости задачи (так называемая константа Липшица). Вычисление этой константы может быть задачей сложнее, чем изначальная задача оптимизации, поэтому этот вариант нам не годится. Более того, эта оценка крайне пессимистична – мы ведь хотим размер шага как можно больше, чтобы уменьшить функцию как можно больше, а тут мы будем изменять все очень мало.
Существует так называемый метод наискорейшего спуска: выбираем размер шага так, чтобы как можно сильнее уменьшить функцию:
$$
alpha_k = argmin_{alpha geq 0} f(x_k — alpha nabla f(x_k)).
$$
Одномерная оптимизация является не сильно сложной задачей, поэтому теоретически мы можем её совершать (например, методом бинарного/тернарного поиска или золотого сечения), можно этот шаг также совершать неточно. Но сразу стоит заметить, что это можно делать, только если функция $f$ вычислима более-менее точно за разумное время, в случае линейной регрессии это уже не так (не говоря уже о нейронных сетях).
Также есть всевозможные правила Армихо/Гольдштейна/Вульфа и прочее и прочее, разработанные в давние 60-е, и для их проверки требуется снова вычислять значения функции в точке. Желающие могут посмотреть на эти условия на википедии. Про более хитрые вариации выбора шагов мы поговорим позже, но сразу стоит сказать, что эта задача довольно сложная.
По поводу теории: сначала скажем что-то про выпуклый случай.
В максимально общем выпуклом случае без дополнительных предположений оценки для градиентного спуска крайне и крайне пессимистичные: чтобы достичь качества $varepsilon$, то есть
$$vert f(x_k) — f(x^*) vertleq varepsilon $$
достаточно сделаеть $O(R^2/varepsilon^2)$ шагов, где $R^2$ — это расстояние от $x_0$ до $x^*$. Выглядит очень плохо: ведь чтобы достичь точности $10^{-2}$, необходимо сделать порядка $10^4$ шагов градиентного спуска. Но на практике такого не происходит, потому что на самом деле верны разные предположения, дающие более приятные свойства. Для контраста, укажем оценку в случае гладкой и сильно выпуклой в точке оптимума функции: за $k$ шагов будет достигнута точность
$$
Oleft( minleft{R^2 exp
left(-frac{k}{4kappa}right), frac{R^2}{k} right}right),
$$
где $kappa$ – это так называемое число обусловленности задачи. По сути, это число измеряет, насколько линии уровня функции вытянуты в окрестности оптимума.
Морали две:
- Скорость сходимости градиентного спуска сильно зависит от обусловленности задачи;
- Также она зависит от выбора хорошей точки старта, ведь везде входит расстояние от точки старта до оптимума.
В качестве ссылки на доказательство укажем на работу Себастиана Стича, где оно довольно простое и общее.
В невыпуклом же случае все куда хуже с точки зрения теории: требуется порядка $O(1/varepsilon^2)$ шагов в худшем случае даже для гладкой функции, где $varepsilon$ – желаемая точность уменьшения нормы градиента.
Стохастический градиентный спуск (SGD)
Теперь мы попробуем сэкономить в случае регрессии и подобных ей задач. Будем рассматривать функционалы вида
$$
f(x) = sum_{i=1}^N mathcal{L}(x, y_i),
$$
где сумма проходится по всем объектам выборки (которых может быть очень много). Теперь сделаем следующий трюк: заметим, что это усреднение – это по сути взятие матожидания. Таким образом, мы говорим, что наша функция выглядит как
$$
f(x) = mathbb{E}[mathcal{L}(x, xi)],
$$
где $xi$ равномерно распределена по обучающей выборке. Задачи такого вида возникают не только в машинном обучении; иногда встречаются и просто задачи стохастического программирования, где происходит минимизация матожидания по неизвестному (или слишком сложному) распределению.
Для функционалов такого вида мы также можем посчитать градиент, он будет выглядеть довольно ожидаемо:
$$
nabla f(x) = mathbb{E} nabla mathcal{L}(x, xi).
$$
Будем считать, что вычисление матожидания напрямую невозможно.
Новый взгляд из статистики дает возможность воспользоваться классическим трюком: давайте подменим матожидание на его несмещенную Монте-Карло оценку. Получается то, что можно назвать стохастическим градиентом:
$$
tilde nabla f(x) = frac{1}{B} sum_{i=1}^B nabla mathcal{L}(x, xi_i).
$$
Говоря инженерным языком, мы подменили вычисление градиента по всей выборке вычислением по случайной подвыборке. Подвыборку $xi_1,ldots,xi_B$ часто называют (мини)батчем, а число $B$ – размерном батча.
По-хорошему, наука предписывает нам каждый раз независимо генерировать батчи, но это трудно с вычислительной точки зрения. Вместо этого воспользуемся следующим приёмом: сначала перемешаем нашу выборку (чтобы внести дополнительную случайность), а затем будем рассматривать последовательно блоки по $B$ элементов выборки. Когда мы просмотрели всю выборку – перемешиваем еще раз и повторяем проход. Очередной прогон по обучающей выборке называется эпохой. И, хотя, казалось бы, независимо генерировать батчи лучше, чем перемешивать лишь между эпохами, есть несколько результатов, демонстрирующих обратное: одна работа и вторая (более новая); главное условие успеха – правильно изменяющийся размер шага.
Получаем следующий алгоритм, называемый стохастическим градиентным спуском (stochastic gradient descent, SGD):
x = normal(0, 1) # инициализация
repeat E times: # цикл по количеству эпох
for i = 0; i <= N; i += B:
batch = data[i:i+B]
h = grad_loss(batch).mean() # вычисляем оценку градиента как среднее по батчу
x -= alpha * h
Дополнительное удобство такого подхода – возможность работы с внешней памятью, ведь выборка может быть настолько большой, что она помещается только на жёсткий диск. Сразу отметим, что в таком случае $B$ стоит выбирать достаточно большим: обращение к данным с диска всегда медленнее, чем к данным из оперативной памяти, так что лучше бы сразу забирать оттуда побольше.
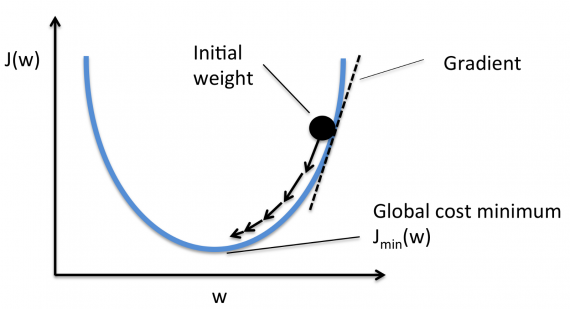
Поскольку стохастические градиенты являются лишь оценками истинных градиентов, SGD может быть довольно шумным:
Поэтому если вы обучаете глубокую нейросеть и у вас в память влезает лишь батч размером с 2-4 картинки, модель, возможно, ничего хорошего не сможет выучить. Аппроксимация градиента и поведение SGD может стать лучше с ростом размера батча $B$ – и обычно его действительно хочется подрастить, но парадоксальным образом слишком большие батчи могут порой испортить дело (об этом дальше в этой главе!).
Теоретический анализ
Теперь перейдем к теоретической стороне вопроса. Сходимость SGD обеспечивается несмещенностью стохастического градиента. Несмотря на то, что во время итераций копится шум, суммарно он зачастую оказывается довольно мал.
Теперь приведем оценки. Сначала, по традиции, в выпуклом случае. Для выпуклой функции потерь за $k$ шагов будет достигнута точность порядка
$$
Oleft( minleft{R^2 exp
left(-frac{k}{4kappa} right)+ frac{sigma^2}{mu k}, frac{R^2}{k} + frac{sigma^2 R}{sqrt{k}} right}right),
$$
где $sigma^2$ – это дисперсия стохградиента, а $mu$ – константа сильной выпуклости, показывающая, насколько функция является «не плоской» в окрестности точки оптимума. Доказательство в том же препринте С. Стича.
Мораль в следующем: дисперсия стохастического градиента, вычисленного по батчу размера $B$ равна $sigma_0^2/B$, где $sigma_0^2$ – это дисперсия одного градиента. То есть увеличение размера батча помогает и с теоретической точки зрения.
В невыпуклом случае оценка сходимости SGD просто катастрофически плохая: требуется $O(1/varepsilon^4)$ шагов для того, чтобы сделать норму градиента меньше $varepsilon$. В теории есть всевозможные дополнительные способы снижения дисперсии с лучшими теоретическими оценками (Stochastic Variance Reduced Gradient (SVRGD), Spider, etc), но на практике они активно не используются.
Использование дополнительной информации о функции
Методы второго порядка
Основной раздел.
Постараемся усовершенствовать метод стохастического градиентного спуска. Сначала заметим, что мы используем явно не всю информацию об оптимизируемой функции.
Вернемся к нашему VIP-примеру линейной регресии с $ell_2$ регуляризацией:
$$
Vert y — Xw Vert_2^2 + lambda Vert w Vert_2^2 to min_w.
$$
Эта функция достаточно гладкая, и может быть неплохой идеей использовать её старшие производные для ускорения сходимости алгоритма. В наиболее чистом виде этой философии следует метод Ньютона и подобные ему; о них вы можете прочитать в соответствующем разделе. Отметим, что все такие методы, как правило, довольно дорогие (исключая L-BFGS), и при большом размере задачи и выборки ничего лучше вариаций SGD не придумали.
Проксимальные методы
Основной раздел.
К сожалению, не всегда функции такие красивые и гладкие. Для примера рассмотрим Lasso-регресию:
$$
Vert y — Xw Vert_2^2 + lambda Vert w Vert_1 to min_w.
$$
Второе, не гладкое слагаемое резко ломает все свойства этой задачи: теоретически оценки для градиентного спуска становятся гораздо хуже (и на практике тоже). С другой стороны, регуляризационное слагаемое устроено очень просто, и эту дополнительную структурную особенность можно и нужно эксплуатировать. Методы решения задачи вида
$$
f(x) + h(x) to min_x,
$$
где $h$ – простая функция (в некотором смысле), а $f$ – гладкая, называются методами композитной оптимизации. Глубже погрузиться в них можно в соответствующем разделе, посвященном проксимальным методам.
Использование информации о предыдущих шагах
Следующая претензия к методу градиентного спуска – мы не используем информацию о предыдущих шагах, хотя, кажется, там может храниться что-то полезное.
Метод инерции, momentum
Начнем с физической аналогии. Представим себе мячик, который катится с горы. В данном случае гора – это график функции потерь в пространстве параметров нашей модели, а мячик – её текущее значение. Реальный мячик не застрянет перед небольшой кочкой, так как у него есть некоторая масса и уже накопленный импульс – некоторое время он способен двигаться даже вверх по склону. Аналогичный прием может быть использован и в градиентной оптимизации. В англоязычной литературе он называется Momentum.
С математической точки зрения, мы добавляем к градиентному шагу еще одно слагаемое:
$$
x_{k+1} = x_k — alpha_k nabla f(x_k) + color{red}{beta_k (x_k — x_{k-1})}.
$$
Сразу заметим, что мы немного усугубили ситуацию с подбором шага, ведь теперь нужно подбирать не только $alpha_k$, но и $beta_k$. Для обычного, не стохастического градиентного спуска мы можем адаптировать метод наискорейшего и получить метод тяжелого шарика:
$$
(alpha_k, beta_k) = argmin_{alpha,beta} f(x_k — alpha nabla f(x_k) + beta (x_k — x_{k-1})).
$$
Но, увы, для SGD это работать не будет.
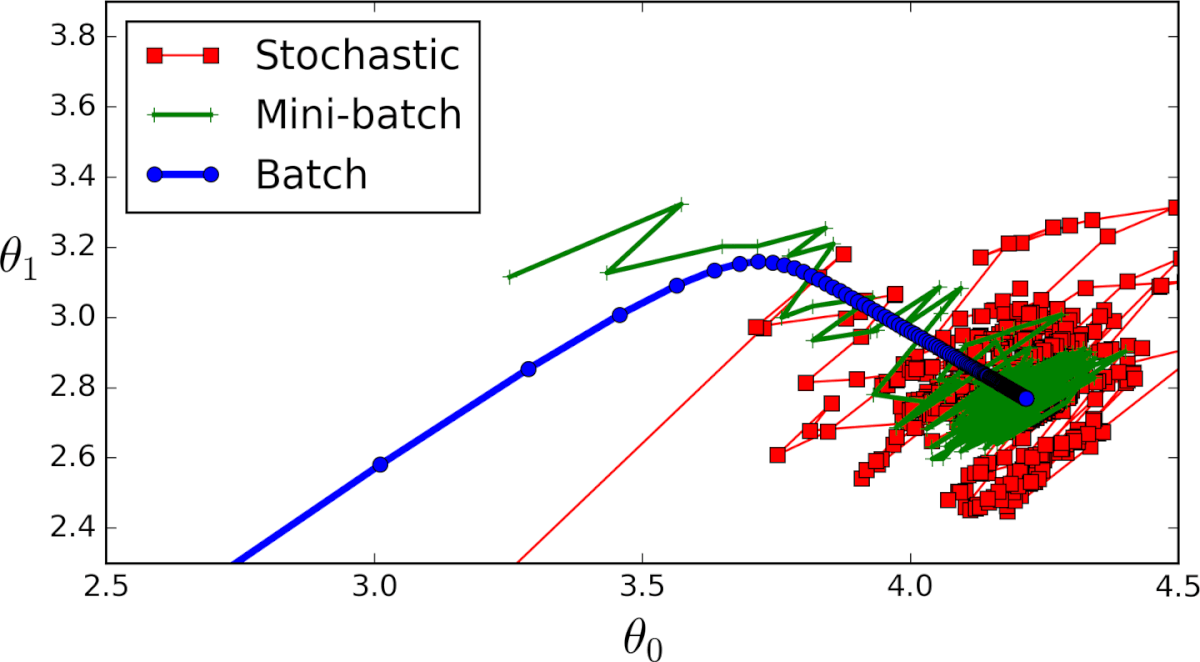
Выгода в невыпуклом случае от метода инерции довольно понятна – мы будем пропускать паразитные локальные минимумы и седла и продолжать движение вниз. Но выгода есть также и в выпуклом случае. Рассмотрим плохо обусловленную квадратичную задачу, для которой линии уровня оптимизируемой функции будут очень вытянутыми эллипсами, и запустим на SGD с инерционным слагаемым и без него. Направление градиента будет иметь существенную вертикальную компоненту, а добавление инерции как раз «погасит» паразитное направление. Получаем следующую картинку:
Также удобно бывает представить метод моментума в виде двух параллельных итерационных процессов:
$$begin{align}
v_{k+1} &= beta_k v_k — alpha_k nabla f(x_k)
x_{k+1} &= x_k + v_{k+1}.
end{align}
$$
Accelerated Gradient Descent (Nesterov Momentum)
Рассмотрим некоторую дополнительную модификацию, которая была предложена в качестве оптимального метода первого порядка для решения выпуклых оптимизационных задач.
Можно доказать, что в сильно выпуклом и гладком случае найти минимум с точностью $varepsilon$ нельзя быстрее, чем за
$$
Omegaleft( R^2expleft(-frac{k}{sqrt{kappa}}right) right)
$$
итераций, где $kappa$ – число обусловленности задачи. Напомним, что для обычного градиентного спуска в экспоненте у нас был не корень из $kappa$, а просто $kappa$, то есть, градиентный спуск справляется с плохой обусловленностью задачи хуже, чем мог бы.
В 1983 году Ю.Нестеровым был предложен алгоритм, имеющий оптимальную по порядку оценку. Для этого модифицируем немного моментум и будем считать градиент не в текущей точке, а как бы в точке, в которую мы бы пошли, следуя импульсу:
$$begin{align}
v_{k+1} &= beta_k v_k — alpha_k nabla f(color{red}{x_k + beta_k v_k})
x_{k+1} &= x_k + v_{k+1}
end{align}
$$
Сравним с обычным momentum:
Комментарий: иногда упоминается, что Nesterov Momentum «заглядывает в будущее» и исправляет ошибки на данном шаге оптимизации. Конечно, никто не заглядывает в будущее в буквальном смысле.
В работе Нестерова были предложены конкретные (и довольно магические) константы для импульса, которые получаются из некоторой еще более магической последовательности. Мы приводить их не будем, поскольку мы в первую очередь заинтересованы невыпуклым случаем.
Nesterov Momentum позволяет значительно повысить устойчивость и скорость сходимости в некоторых случаях. Но, конечно, он не является серебряной пулей в задачах оптимизации, хотя в выпуклом мире и является теоретически неулучшаемым.
Также отметим, что ускоренный метод может напрямую примениться к проксимальному градиентному спуску. В частности, применение ускоренного метода к проксимальному алгоритму решения $ell_1$ регрессии (ISTA) называется FISTA (Fast ISTA).
Общие выводы:
- Добавление momentum к градиентному спуску позволяет повысить его устойчивость и избегать маленьких локальных минимумов/максимумов;
- В выпуклом случае добавление моментного слагаемого позволяет доказуемо улучшить асимптотику и уменьшить зависимость от плохой обусловленности задачи.
- Идея ускорения применяется к любым около-градиентным методам, в том числе и к проксимальным, позволяя получить, например, ускоренный метод для $ell_1$-регрессии.
Адаптивный подбор размера шага
Выше мы попытались эксплуатировать свойства градиентного спуска. Теперь же пришел момент взяться за больной вопрос: как подбирать размер шага? Он максимально остро встаёт в случае SGD: ведь посчитать значение функции потерь в точке очень дорого, так что методы в духе наискорейшего спуска нам не помогут!
Нужно действовать несколько хитрее.
Adagrad
Рассмотрим первый алгоритм, который является адаптацией стохастического градиентного спуска. Впервые он предложен в статье в JMLR 2011 года, но она написана в очень широкой общности, так что читать её достаточно сложно.
Зафиксируем $alpha$ – исходный learning rate. Затем напишем следующую формулу обновления:
$$begin{align}
G_{k+1} &= G_k + (nabla f(x_k))^2
x_{k+1} &= x_k — frac{alpha}{sqrt{G_{k+1} + varepsilon}} nabla f(x_k).
end{align}
$$
Возведение в квадрат и деления векторов покомпонентные. По сути, мы добавляем некоторую квазиньютоновость и начинаем динамически подбирать размер шага для каждой координаты по отдельности. Наш размера шага для фиксированной координаты – это какая-то изначальная константа $alpha$ (learning rate), деленная на корень из суммы квадратов координат градиентов плюс дополнительный параметр сглаживания $varepsilon$, предотвращающий деление на ноль. Добавка $varepsilon$ на практике оставляется дефолтными 1e-8 и не изменяется.
Идея следующая: если мы вышли на плато по какой-то координате и соответствующая компонента градиента начала затухать, то нам нельзя уменьшать размер шага слишком сильно, поскольку мы рискуем на этом плато остаться, но в то же время уменьшать надо, потому что это плато может содержать оптимум. Если же градиент долгое время довольно большой, то это может быть знаком, что нам нужно уменьшить размер шага, чтобы не пропустить оптимум. Поэтому мы стараемся компенсировать слишком большие или слишком маленькие координаты градиента.
Но довольно часто получается так, что размер шага уменьшается слишком быстро и для решения этой проблемы придумали другой алгоритм.
RMSProp
Модифицируем слегка предыдущую идею: будем не просто складывать нормы градиентов, а усреднять их в скользящем режиме:
$$begin{align}
G_{k+1} &= gamma G_k + (1 — gamma)(nabla f(x_k))^2
end{align}
$$
$$begin{align}
x_{k+1} &= x_k — frac{alpha}{sqrt{G_{k+1} + varepsilon}} nabla f(x_k).
end{align}
$$
Такой выбор позволяет все еще учитывать историю градиентов, но при этом размер шага уменьшается не так быстро.
Общие выводы:
- Благодаря адаптивному подбору шага в современных оптимизаторах не нужно подбирать последовательность $alpha_k$ размеров всех шагов, а достаточно выбрать всего одно число – learning rate $alpha$, всё остальное сделает за вас сам алгоритм. Но learning rate все еще нужно выбирать крайне аккуратно: алгоритм может либо преждевременно выйти на плато, либо вовсе разойтись. Пример приведен на иллюстрации ниже.
Объединяем все вместе…
Adam
Теперь покажем гвоздь нашей программы: алгоритм Adam, который считается решением по умолчанию и практически серебряной пулей в задачах стохастической оптимизации.
Название Adam = ADAptive Momentum намекает на то, что мы объединим идеи двух последних разделов в один алгоритм. Приведем его алгоритм, он будет немного отличаться от оригинальной статьи отсутствием коррекций смещения (bias correction), но идея останется той же самой:
$$begin{align}
v_{k+1} &= beta_1 v_k + (1 — beta_1) nabla f(x_k)
end{align}
$$
$$begin{align}
G_{k+1} &= beta_2 G_k + (1 — beta_2)(nabla f(x_k))^2
end{align}
$$
$$begin{align}
x_{k+1} &= x_k — frac{alpha}{sqrt{G_{k+1} + varepsilon}} v_{k+1}.
end{align}
$$
Как правило, в этом алгоритме подбирают лишь один гиперпараметр $alpha$ – learning rate. Остальные же: $beta_1$, $beta_2$ и $varepsilon$ – оставляют стандартными и равными 0.9, 0.99 и 1e-8 соответственно. Подбор $alpha$ составляет главное искусство.
Зачастую, при начале работы с реальными данными начинают со значения learning rate равного 3e-4. История данного значения достаточно забавна: в 2016 году Андрей Карпатый (Andrej Karpathy) опубликовал шутливый пост в Twitter.
После чего сообщество подхватило эту идею (до такой степени, что иногда число 3e-4 называют Karpathy constant).
Обращаем ваше внимание, что при работе с учебными данными зачастую полезно выбирать более высокий (на 1-2 порядка) начальный learning rate (например, при классификации MNIST, Fashion MNIST, CIFAR или при обучении языковой модели на примере поэзии выбранного поэта).
Также стоит помнить, что Adam требует хранения как параметров модели, так и градиентов, накопленного импульса и нормировочных констант (cache). Т.е. достижение более быстрой (с точки зрения количества итераций/объема рассмотренных данных) сходимости требует больших объемов памяти. Кроме того, если вы решите продолжить обучение модели, остановленное на некоторой точке, необходимо восстановить из чекпоинта не только веса модели, но и накопленные параметры Adam. В противном случае оптимизатор начнёт сбор всех своих статистик с нуля, что может сильно сказаться на качестве дообучения. То же самое касается вообще всех описанных выше методов, так как каждый из них накапливает какие-то статистики во время обучения.
Интересный факт: Adam расходится на одномерном контрпримере, что совершенно не мешает использовать его для обучения нейронных сетей. Этот факт отлично демонстрирует, насколько расходятся теория и практика в машинном обучении. В той же работе предложено исправление этого недоразумения, но его активно не применяют и продолжают пользоваться «неправильным» Adamом потому что он быстрее сходится на практике.
AdamW
А теперь давайте добавим $ell_2$-регуляризацию неявным образом, напрямую в оптимизатор и минуя адаптивный размер шага:
$$begin{align}
v_{k+1} &= beta_1 v_k + (1 — beta_1) nabla f(x_k)
end{align}
$$
$$begin{align}
G_{k+1} &= beta_2 G_k + (1 — beta_2)(nabla f(x_k))^2
end{align}
$$
$$begin{align}
x_{k+1} &= x_k — left( frac{alpha}{sqrt{G_{k+1} + varepsilon}} v_{k+1} color{red}{ + lambda x_{k}} right).
end{align}
$$
Это сделано для того, чтобы эффект $ell_2$-регуляризации не затухал со временем и обобщающая способность модели была выше. Оставим ссылку на одну заметку про этот эффект. Отметим, впрочем, что этот алгоритм особо не используется.
Практические аспекты
Расписания
Часто learning rate понижают итеративно: каждые условные 5 эпох (LRScheduler в Pytorch) или же при выходе функции потерь на плато. При этом лосс нередко ведет себя следующим схематичным образом:
Помимо этого используют другие варианты «расписаний» для learning rate. Из часто применяемых неочевидных лайфхаков: сначала сделать warmup, то есть увеличивать learning rate, а затем начать постепенно понижать. Использовалось в известной статье про трансформеры. В ней предложили следующую формулу:
$$
lr = d^{-0.5}_{rm{model}} cdot min(step_ num^{-0.5}, step_ num cdot warmup_ steps^{-1.5}).
$$
По сути, первые $warmup_ steps$ шагов происходит линейный рост размера шага, а затем он начинает уменьшаться как $1/sqrt{t}$, где $t$ — число итераций.
Есть и вариант с косинусом из отдельной библиотеки для трансформеров.
В этой же библиотеке можно также почерпнуть идею рестартов: с какого-то момента мы снова включаем warmup, увеличивая размер шага.
Большие батчи
Представим ситуацию, что мы хотим обучить свою нейронную на нескольких GPU. Одно из решений выглядит следующим образом: загружаем на каждую видеокарту нейронную сеть и свой отдельный батч, вычисляем стохастические градиенты, а затем усредняем их по всем видеокартам и делаем шаг. Что плохого может быть в этом?
По факту, эта схема в некотором смысле эквивалентна работе с одним очень большим батчем. Хорошо же, нет разве?
На самом деле существует так называемый generalization gap: использование большого размера батча может приводить к худшей обобщающей способности итоговой модели. О причине этого эффекта можно поспекулировать, базируясь на текущих знаниях о ландшафтах функций потерь при обучении нейронных сетей.
Больший размер батча приводит к тому, что оптимизатор лучше «видит» ландшафт функции потерь для конкретной выборки и может скатиться в маленькие «узкие» паразитные локальные минимумы, которые не имеют обобщающий способности — при небольшом шевелении этого ландшафта (distributional shift c тренировочной на тестовую выборку) значение функции потерь резко подскакивает. В свою очередь, широкие локальные минимумы дают модель с лучшей обобщающей способностью. Эту идею можно увидеть на следующей картинке:
Иными словами, большие батчи могут приводить к переобучению, но это можно исправить правильным динамическим подбором learning rate, как будет продемонстрировано далее. Сразу отметим, что совсем маленькие батчи – это тоже плохо, с ними ничего не получится выучить, так как каждая итерация SGD знает слишком мало о ландшафте функции потерь.
LARS
Мы рассмотрим нестандартный оптимизатор для обучения нейронных сетей, которого нет в Pytorch по умолчанию, но который много где используется: Layer-wise Adaptive Rate Scaling (LARS). Он позволяет эффективно использовать большие размеры батчей, что очень важно при вычислении на нескольких GPU.
Основная идея заключена в названии – нужно подбирать размер шага не один для всей сети или каждого нейрона, а отдельный для каждого слоя по правилу, похожему на RMSProp. По сравнению с оригинальным RMSProp подбор learning rate для каждого слоя дает большую стабильность обучения.
Теперь рассмотрим формулу пересчета: пусть $w_l$ – это веса слоя $l$, $l < L$. Параметры алгоритма: базовый learning rate $eta$ (на который запускается расписание), коэффициент инерции $m$, коэффециент затухания весов $beta$ (как в AdamW).
for l in range(L): # Цикл по слоям
g_l = stochgrad(w_prev)[l] # Вычисляем стохградиент из батча для текущего слоя
lr = eta * norm(w[l]) / (norm(g_l) + beta * norm(w[l])) # Вычислеяем learning rate для текущего слоя
v[l] = m * v[l] + lr * (g_l + beta * w[l]) # Обновляем momentum
w[l] -= v[l] # Делаем градиентный шаг по всему слою сразу
w_prev = w # Обновляем веса
LAMB
Этот оптимизатор введен в статье Large Batch Optimization For Deep Learning и является идейным продолжателем LARS, более приближенным к Adam, чем к обычному RMSProp. Его параметры – это параметры Adam $eta, beta_1, beta_2, varepsilon$, которые беруется как в Adam, а также параметр $lambda$, который отвечает за затухание весов ($beta$ в LARS).
for l in range(L): # Цикл по слоям
g_l = stochgrad(w_prev)[l] # Вычисляем стохградиент из батча для текущего слоя
m[l] = beta_1 * m[l] + (1 - beta_1) * g_l # Вычисляем моментум
v[l] = beta_2 * v[l] + (1 - beta_2) * g_l # Вычисляем новый размер шага
m[l] /= (1 - beta_1**t) # Шаг для уменьшения смещения из Adam
v[l] /= (1 - beta_2**t)
r[l] = m[l] / sqrt(v[l] + eps) # Нормируем моментум как предписывает Adam
lr = eta * norm(w[l]) / norm(r[l] + llambda * w[l]) # Как в LARS
w[l] = w[l] - lr * (r[l] + llambda * w[l]) # Делаем шаг по моментуму
w_prev = w # Обновляем веса
Усреднение
Теперь снова заглянем в теорию: на самом деле, все хорошие теоретические оценки для SGD проявляются, когда берётся усреднение по точкам.
Этот эффект при обучении нейронных сетей был исследован в статье про алгоритм SWA. Суть очень проста: давайте усреднять веса модели по каждой $c$-й итерации; можно считать, что по эпохам. В итоге, веса финальной модели являются усреднением весов моделей, имевщих место в конце каждой эпохи.
В результате такого усреднения сильно повышается обобщающая способность модели: мы чаще попадаем в те самые широкие локальные минимумы, о которых мы говорили в разделе про большие батчи. Вдохновляющая картинка из статьи прилагается:
На второй и третьей картинке изображено сравнение SGD и SWA при обучении нейронной сети (Preactivation ResNet-164 on CIFAR-100) при одной и той же инициализации.
На первой же картинке изображено, как идеологически должен работать SWA. Также мы видим тут демонстрацию эффекта концентрации меры: после обучения стохастический градиентный спуск становится случайным блужданием по области в окрестности локального минимума. Если, например, предположить, что итоговая точка – это нормальное распределение с центром в реальном минимуме в размерности $d > 10^6$, то все эти точки с большой вероятности будут находиться в окрестности сферы радиуса $sqrt{d}$. Интуитивную демонстрацию многомерного нормального распределения можно увидеть на следующей картинке из книги Р.Вершинина «High-Dimensional Probability» (слева в размерности 2, справа в большой размерности):
Поэтому, чтобы вычислить центральную точку этой гауссианы, усреднение просто необходимо, по такому же принципу работает и SWA.
Предобуславливание
Теперь мы снова обратимся к теории: скорость сходимости градиентного спуска (даже ускоренного) очень сильно зависит от числа обусловленности задачи. Разумной идеей будет попытаться использовать какие-то сведения о задаче и улучшить этот показатель, тем самым ускорив сходимость.
В теории, здесь могут помочь техники предобуславливания. Но, к сожалению, попытки наивно воплотить эту идею приводят к чему-то, похожему на метод Ньютона, в котором нужно хранить большую-большую матрицу для обучения больших моделей. Способ обойти эту проблему рассмотрели в статье о методе Shampoo, который использует то, что веса нейронной сети зачастую удобно представлять как матрицу или даже многомерный тензор. Таким образом, Shampoo можно рассматривать как многомерный аналог AdaGrad.
In mathematics, gradient descent (also often called steepest descent) is a first-order iterative optimization algorithm for finding a local minimum of a differentiable function. The idea is to take repeated steps in the opposite direction of the gradient (or approximate gradient) of the function at the current point, because this is the direction of steepest descent. Conversely, stepping in the direction of the gradient will lead to a local maximum of that function; the procedure is then known as gradient ascent.
It is particularly useful in machine learning for minimizing the cost or loss function.[1] Gradient descent should not be confused with local search algorithms, although all are iterative methods for optimization.
Gradient descent is generally attributed to Augustin-Louis Cauchy, who first suggested it in 1847.[2] Jacques Hadamard independently proposed a similar method in 1907.[3][4] Its convergence properties for non-linear optimization problems were first studied by Haskell Curry in 1944,[5] with the method becoming increasingly well-studied and used in the following decades.[6][7]
A simple extension of gradient descent, stochastic gradient descent, serves as the most basic algorithm used for training most deep networks today.
Description[edit]
Illustration of gradient descent on a series of level sets
Gradient descent is based on the observation that if the multi-variable function 





for a small enough step size or learning rate 






We have a monotonic sequence
so, hopefully, the sequence 





convergence to a local minimum can be guaranteed. When the function 
This process is illustrated in the adjacent picture. Here, 


An analogy for understanding gradient descent[edit]
The basic intuition behind gradient descent can be illustrated by a hypothetical scenario. A person is stuck in the mountains and is trying to get down (i.e., trying to find the global minimum). There is heavy fog such that visibility is extremely low. Therefore, the path down the mountain is not visible, so they must use local information to find the minimum. They can use the method of gradient descent, which involves looking at the steepness of the hill at their current position, then proceeding in the direction with the steepest descent (i.e., downhill). If they were trying to find the top of the mountain (i.e., the maximum), then they would proceed in the direction of steepest ascent (i.e., uphill). Using this method, they would eventually find their way down the mountain or possibly get stuck in some hole (i.e., local minimum or saddle point), like a mountain lake. However, assume also that the steepness of the hill is not immediately obvious with simple observation, but rather it requires a sophisticated instrument to measure, which the person happens to have at the moment. It takes quite some time to measure the steepness of the hill with the instrument, thus they should minimize their use of the instrument if they wanted to get down the mountain before sunset. The difficulty then is choosing the frequency at which they should measure the steepness of the hill so not to go off track.
In this analogy, the person represents the algorithm, and the path taken down the mountain represents the sequence of parameter settings that the algorithm will explore. The steepness of the hill represents the slope of the function at that point. The instrument used to measure steepness is differentiation. The direction they choose to travel in aligns with the gradient of the function at that point. The amount of time they travel before taking another measurement is the step size.
Choosing the step size and descent direction[edit]
Since using a step size 


To reason about this mathematically, consider a direction 

.
Finding good settings of 






-
(1)
This inequality implies that the amount by which we can be sure the function 
In principle inequality (1) could be optimized over 


Usually by following one of the recipes above, convergence to a local minimum can be guaranteed. When the function 
Solution of a linear system[edit]
Gradient descent can be used to solve a system of linear equations
reformulated as a quadratic minimization problem.
If the system matrix 
so that
For a general real matrix 
In traditional linear least squares for real 

The line search minimization, finding the locally optimal step size 

For example, for real symmetric and positive-definite matrix 
To avoid multiplying by 
we note that 

The method is rarely used for solving linear equations, with the conjugate gradient method being one of the most popular alternatives. The number of gradient descent iterations is commonly proportional to the spectral condition number 


Solution of a non-linear system[edit]
Gradient descent can also be used to solve a system of nonlinear equations. Below is an example that shows how to use the gradient descent to solve for three unknown variables, x1, x2, and x3. This example shows one iteration of the gradient descent.
Consider the nonlinear system of equations
Let us introduce the associated function
where
One might now define the objective function
which we will attempt to minimize. As an initial guess, let us use
We know that
where the Jacobian matrix 
We calculate:
Thus
and
An animation showing the first 83 iterations of gradient descent applied to this example. Surfaces are isosurfaces of 

Now, a suitable 
This can be done with any of a variety of line search algorithms. One might also simply guess 
Evaluating the objective function at this value, yields
The decrease from 
is a sizable decrease in the objective function. Further steps would reduce its value further until an approximate solution to the system was found.
[edit]
Gradient descent works in spaces of any number of dimensions, even in infinite-dimensional ones. In the latter case, the search space is typically a function space, and one calculates the Fréchet derivative of the functional to be minimized to determine the descent direction.[7]
That gradient descent works in any number of dimensions (finite number at least) can be seen as a consequence of the Cauchy-Schwarz inequality. That article proves that the magnitude of the inner (dot) product of two vectors of any dimension is maximized when they are colinear. In the case of gradient descent, that would be when the vector of independent variable adjustments is proportional to the gradient vector of partial derivatives.
The gradient descent can take many iterations to compute a local minimum with a required accuracy, if the curvature in different directions is very different for the given function. For such functions, preconditioning, which changes the geometry of the space to shape the function level sets like concentric circles, cures the slow convergence. Constructing and applying preconditioning can be computationally expensive, however.
The gradient descent can be combined with a line search, finding the locally optimal step size 

Methods based on Newton’s method and inversion of the Hessian using conjugate gradient techniques can be better alternatives.[15][16] Generally, such methods converge in fewer iterations, but the cost of each iteration is higher. An example is the BFGS method which consists in calculating on every step a matrix by which the gradient vector is multiplied to go into a «better» direction, combined with a more sophisticated line search algorithm, to find the «best» value of 
While it is sometimes possible to substitute gradient descent for a local search algorithm, gradient descent is not in the same family: although it is an iterative method for local optimization, it relies on an objective function’s gradient rather than an explicit exploration of a solution space.
Gradient descent can be viewed as applying Euler’s method for solving ordinary differential equations 



It can be shown that there is a correspondence between neuroevolution and gradient descent.[18]
Modifications[edit]
Gradient descent can converge to a local minimum and slow down in a neighborhood of a saddle point. Even for unconstrained quadratic minimization, gradient descent develops a zig-zag pattern of subsequent iterates as iterations progress, resulting in slow convergence. Multiple modifications of gradient descent have been proposed to address these deficiencies.
Fast gradient methods[edit]
Yurii Nesterov has proposed[19] a simple modification that enables faster convergence for convex problems and has been since further generalized. For unconstrained smooth problems the method is called the fast gradient method (FGM) or the accelerated gradient method (AGM). Specifically, if the differentiable function 






For constrained or non-smooth problems, Nesterov’s FGM is called the fast proximal gradient method (FPGM), an acceleration of the proximal gradient method.
Momentum or heavy ball method[edit]
Trying to break the zig-zag pattern of gradient descent, the momentum or heavy ball method uses a momentum term in analogy to a heavy ball sliding on the surface of values of the function being minimized,[6] or to mass movement in Newtonian dynamics through a viscous medium in a conservative force field.[24] Gradient descent with momentum remembers the solution update at each iteration, and determines the next update as a linear combination of the gradient and the previous update. For unconstrained quadratic minimization, a theoretical convergence rate bound of the heavy ball method is asymptotically the same as that for the optimal conjugate gradient method.[6]
This technique is used in stochastic gradient descent and as an extension to the backpropagation algorithms used to train artificial neural networks.[25][26] In the direction of updating, stochastic gradient descent adds a stochastic property. The weights can be used to calculate the derivatives.
Extensions[edit]
Gradient descent can be extended to handle constraints by including a projection onto the set of constraints. This method is only feasible when the projection is efficiently computable on a computer. Under suitable assumptions, this method converges. This method is a specific case of the forward-backward algorithm for monotone inclusions (which includes convex programming and variational inequalities).[27]
Gradient descent is a special case of mirror descent using the squared Euclidean distance as the given Bregman divergence.[28]
See also[edit]
- Backtracking line search
- Conjugate gradient method
- Stochastic gradient descent
- Rprop
- Delta rule
- Wolfe conditions
- Preconditioning
- Broyden–Fletcher–Goldfarb–Shanno algorithm
- Davidon–Fletcher–Powell formula
- Nelder–Mead method
- Gauss–Newton algorithm
- Hill climbing
- Quantum annealing
- Continuous Local Search
References[edit]
- ^ «Gradient descent intuition | Stanford University — KeepNotes».
- ^ Lemaréchal, C. (2012). «Cauchy and the Gradient Method» (PDF). Doc Math Extra: 251–254.
- ^ Hadamard, Jacques (1908). «Mémoire sur le problème d’analyse relatif à l’équilibre des plaques élastiques encastrées». Mémoires présentés par divers savants éstrangers à l’Académie des Sciences de l’Institut de France. 33.
- ^ Courant, R. (1943). «Variational methods for the solution of problems of equilibrium and vibrations». Bulletin of the American Mathematical Society. 49 (1): 1–23. doi:10.1090/S0002-9904-1943-07818-4.
- ^ Curry, Haskell B. (1944). «The Method of Steepest Descent for Non-linear Minimization Problems». Quart. Appl. Math. 2 (3): 258–261. doi:10.1090/qam/10667.
- ^ a b c d e Polyak, Boris (1987). Introduction to Optimization.
- ^ a b Akilov, G. P.; Kantorovich, L. V. (1982). Functional Analysis (2nd ed.). Pergamon Press. ISBN 0-08-023036-9.
- ^ Barzilai, Jonathan; Borwein, Jonathan M. (1988). «Two-Point Step Size Gradient Methods». IMA Journal of Numerical Analysis. 8 (1): 141–148. doi:10.1093/imanum/8.1.141.
- ^ Fletcher, R. (2005). «On the Barzilai–Borwein Method». In Qi, L.; Teo, K.; Yang, X. (eds.). Optimization and Control with Applications. Applied Optimization. Vol. 96. Boston: Springer. pp. 235–256. ISBN 0-387-24254-6.
- ^ Wolfe, Philip (April 1969). «Convergence Conditions for Ascent Methods». SIAM Review. 11 (2): 226–235. doi:10.1137/1011036.
- ^ Bernstein, Jeremy; Vahdat, Arash; Yue, Yisong; Liu, Ming-Yu (2020-06-12). «On the distance between two neural networks and the stability of learning». arXiv:2002.03432 [cs.LG].
- ^ Haykin, Simon S. Adaptive filter theory. Pearson Education India, 2008. — p. 108-142, 217-242
- ^ Saad, Yousef (2003). Iterative methods for sparse linear systems (2nd ed.). Philadelphia, Pa.: Society for Industrial and Applied Mathematics. pp. 195. ISBN 978-0-89871-534-7.
- ^ a b Bouwmeester, Henricus; Dougherty, Andrew; Knyazev, Andrew V. (2015). «Nonsymmetric Preconditioning for Conjugate Gradient and Steepest Descent Methods». Procedia Computer Science. 51: 276–285. doi:10.1016/j.procs.2015.05.241.
- ^ Press, W. H.; Teukolsky, S. A.; Vetterling, W. T.; Flannery, B. P. (1992). Numerical Recipes in C: The Art of Scientific Computing (2nd ed.). New York: Cambridge University Press. ISBN 0-521-43108-5.
- ^ Strutz, T. (2016). Data Fitting and Uncertainty: A Practical Introduction to Weighted Least Squares and Beyond (2nd ed.). Springer Vieweg. ISBN 978-3-658-11455-8.
- ^ Ross, I.M. (July 2019). «An optimal control theory for nonlinear optimization». Journal of Computational and Applied Mathematics. 354: 39–51. doi:10.1016/j.cam.2018.12.044. S2CID 127649426.
- ^ Whitelam, Stephen; Selin, Viktor; Park, Sang-Won; Tamblyn, Isaac (2 November 2021). «Correspondence between neuroevolution and gradient descent». Nature Communications. 12 (1): 6317. arXiv:2008.06643. Bibcode:2021NatCo..12.6317W. doi:10.1038/s41467-021-26568-2. PMC 8563972. PMID 34728632.
- ^ Nesterov, Yurii (2004). Introductory Lectures on Convex Optimization : A Basic Course. Springer. ISBN 1-4020-7553-7.
- ^ Vandenberghe, Lieven (2019). «Fast Gradient Methods» (PDF). Lecture notes for EE236C at UCLA.
- ^ Walkington, Noel J. (2023). «Nesterov’s Method for Convex Optimization». SIAM Review. 65 (2): 539–562. doi:10.1137/21M1390037. ISSN 0036-1445.
- ^ Kim, D.; Fessler, J. A. (2016). «Optimized First-order Methods for Smooth Convex Minimization». Math. Prog. 151 (1–2): 81–107. arXiv:1406.5468. doi:10.1007/s10107-015-0949-3. PMC 5067109. PMID 27765996. S2CID 207055414.
- ^ Drori, Yoel (2017). «The Exact Information-based Complexity of Smooth Convex Minimization». Journal of Complexity. 39: 1–16. arXiv:1606.01424. doi:10.1016/j.jco.2016.11.001. S2CID 205861966.
- ^ Qian, Ning (January 1999). «On the momentum term in gradient descent learning algorithms». Neural Networks. 12 (1): 145–151. CiteSeerX 10.1.1.57.5612. doi:10.1016/S0893-6080(98)00116-6. PMID 12662723. S2CID 2783597.
- ^ «Momentum and Learning Rate Adaptation». Willamette University. Retrieved 17 October 2014.
- ^ Geoffrey Hinton; Nitish Srivastava; Kevin Swersky. «The momentum method». Coursera. Retrieved 2 October 2018. Part of a lecture series for the Coursera online course Neural Networks for Machine Learning Archived 2016-12-31 at the Wayback Machine.
- ^ Combettes, P. L.; Pesquet, J.-C. (2011). «Proximal splitting methods in signal processing». In Bauschke, H. H.; Burachik, R. S.; Combettes, P. L.; Elser, V.; Luke, D. R.; Wolkowicz, H. (eds.). Fixed-Point Algorithms for Inverse Problems in Science and Engineering. New York: Springer. pp. 185–212. arXiv:0912.3522. ISBN 978-1-4419-9568-1.
- ^ «Mirror descent algorithm».
Further reading[edit]
- Boyd, Stephen; Vandenberghe, Lieven (2004). «Unconstrained Minimization» (PDF). Convex Optimization. New York: Cambridge University Press. pp. 457–520. ISBN 0-521-83378-7.
- Chong, Edwin K. P.; Żak, Stanislaw H. (2013). «Gradient Methods». An Introduction to Optimization (Fourth ed.). Hoboken: Wiley. pp. 131–160. ISBN 978-1-118-27901-4.
- Himmelblau, David M. (1972). «Unconstrained Minimization Procedures Using Derivatives». Applied Nonlinear Programming. New York: McGraw-Hill. pp. 63–132. ISBN 0-07-028921-2.
External links[edit]
- Using gradient descent in C++, Boost, Ublas for linear regression
- Series of Khan Academy videos discusses gradient ascent
- Online book teaching gradient descent in deep neural network context
- Archived at Ghostarchive and the Wayback Machine: «Gradient Descent, How Neural Networks Learn». 3Blue1Brown. October 16, 2017 – via YouTube.
- Handbook of Convergence Theorems for (Stochastic) Gradient Methods
Все курсы > Оптимизация > Занятие 2
На прошлом занятии мы познакомились с понятием производной и нашли минимум функции с одной переменной. При этом, мы отказались от использования второй переменной сдвига.
$$ y = w cdot x $$
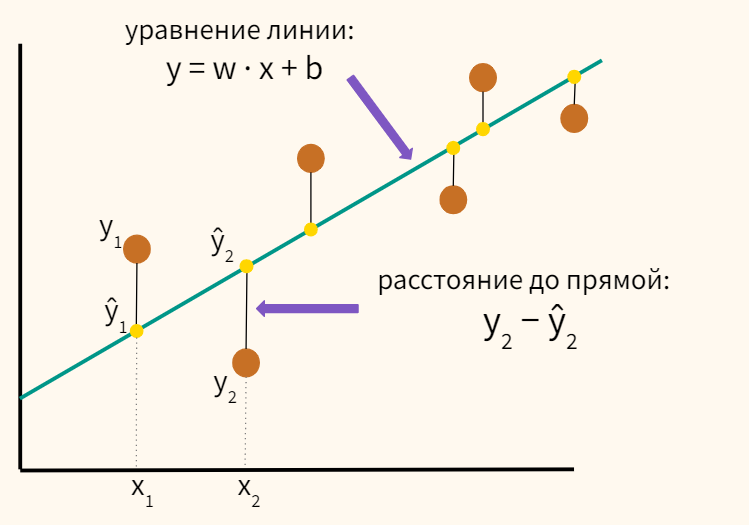
Сегодня мы научимся находить минимум функции с двумя переменными w и b и построим полноценную модель простой линейной регрессии (Simple Linear Regression).
$$ y = w cdot x + b $$
Для этого мы напишем алгоритм, который называется методом градиентного спуска (gradient descent method). Однако перед этим мы возьмем более простую функцию и на ее примере изучим, как работает этот метод.
Градиент и метод градиентного спуска
Функция нескольких переменных
Возьмем вот такую функцию потерь.
$$ f(w_1, w_2) = w_1^2 + w_2^2 $$
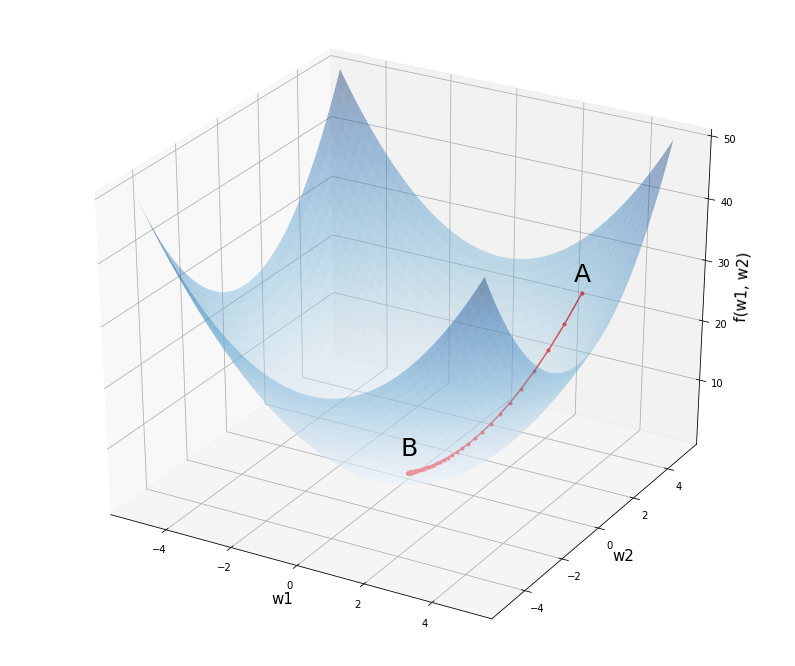
График этой функции можно представить в трехмерном пространстве, где по осям w1 и w2 отложены веса исходной модели, а по оси f(w1, w2) — уровень потерь при заданных весах.
Откроем ноутбук к этому занятию⧉
Посмотрим на график этой функции.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
# установим размер графика fig = plt.figure(figsize = (12,10)) # создадим последовательность из 1000 точек в интервале от -5 до 5 # для осей w1 и w2 w1 = np.linspace(—5, 5, 1000) w2 = np.linspace(—5, 5, 1000) # создадим координатную плоскость из осей w1 и w2 w1, w2 = np.meshgrid(w1, w2) # пропишем функцию f = w1 ** 2 + w2 ** 2 # создадим трехмерное пространство ax = fig.add_subplot(projection = ‘3d’) # выведем график функции, alpha задает прозрачность ax.plot_surface(w1, w2, f, alpha = 0.4, cmap = ‘Blues’) # выведем точку A с координатами (3, 4, 25) и подпись к ней ax.scatter(3, 4, 25, c = ‘red’, marker = ‘^’, s = 100) ax.text(3, 3.5, 28, ‘A’, size = 25) # аналогично выведем точку B с координатами (0, 0, 0) ax.scatter(0, 0, 0, c = ‘red’, marker = ‘^’, s = 100) ax.text(0, —0.4, 4, ‘B’, size = 25) # укажем подписи к осям ax.set_xlabel(‘w1’, fontsize = 15) ax.set_ylabel(‘w2’, fontsize = 15) ax.set_zlabel(‘f(w1, w2)’, fontsize = 15) # выведем результат plt.show() |

Предположим мы начали с весов в точке A с координатами (3, 4, 25). Как нам спуститься в минимум функции в точке B (0, 0, 0)? Просто двигаться в направлении обратном производной мы не можем. Ведь единственной производной, которая бы описывала все изменения нашей функции, просто не существует.
Все дело в том, что если смотреть на нашу функцию «сверху» (то есть на график изолиний или линий уровня, contour lines), то в каждой точке у нас теперь два направления, по оси w1 и по оси w2.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
# установим размер графика fig, ax = plt.subplots(figsize = (10,10)) # создадим последовательность из 100 точек в интервале от -5 до 5 # для осей w1 и w2 w1 = np.linspace(—5.0, 5.0, 100) w2 = np.linspace(—5.0, 5.0, 100) # создадим координатную плоскость из осей w1 и w2 w1, w2 = np.meshgrid(w1, w2) # пропишем функцию C = w1 ** 2 + w2 ** 2 # построим изолинии (линии уровня) plt.contourf(w1, w2, C, cmap = ‘Blues’) # выведем точку А с координатами на плоскости (3, 4) ax.scatter(3, 4, c = ‘red’, marker = ‘^’, s = 200) ax.text(2.85, 4.3, ‘A’, size = 25) # и точку B с координатами (0, 0) ax.scatter(0, 0, c = ‘red’, marker = ‘^’, s = 200) ax.text(—0.15, 0.3, ‘B’, size = 25) # укажем подписи к осям ax.set_xlabel(‘w1’, fontsize = 15) ax.set_ylabel(‘w2’, fontsize = 15) # а также стрелки направления изменений вдоль w1 и w2 ax.arrow(2.7, 4, —2, 0, width = 0.1, head_length = 0.3) ax.arrow(3.005, 3.6, 0, —2, width = 0.1, head_length = 0.3) # создадим сетку в виде прерывистой черты plt.grid(linestyle = ‘—‘) # выведем результат plt.show() |

Как понять куда нам двигаться?
Частная производная
Если «заморозить» одну из переменных (то есть представить, что это константа), пусть это будет w2, мы можем найти производную по первой переменной w1.
$$ f_{w_1} = frac{partial f}{partial w_1} = 2w_1 $$
Такая производная называется частной (partial derivative), потому что она описывает изменение только в первой переменной w1.
Графически, мы как бы убираем переменную w2 (получается сечение, представленное параболой) и ищем производную функции, в которой есть только переменная w1.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
# зададим размер графика в дюймах plt.figure(figsize = (10, 8)) # объявим функцию параболы def f(x): return x ** 2 # объявим ее производную def der(x): return 2 * x # пропишем уравнение через point-slope form # y — y1 = m * (x — x1) —> y = m * (x — x1) + y1 def line(x, x1, y1): return der(x1) * (x — x1) + y1 # создадим последовательность координат x для параболы x = np.linspace(—4, 4, 100) # построим график параболы plt.plot(x, f(x)) # и заполним ее по умолчанию синим цветом с прозрачностью 0,5 plt.fill_between(x, f(x), 16, alpha = 0.5) # в цикле пройдемся по точкам -2, 0, 2 на оси х for x1 in range(—2, 3, 2): # рассчитаем соответствующие им координаты y y1 = f(x1) # определим пространство по оси x для касательных линий xrange = np.linspace(x1 — 3, x1 + 3, 9) # построим касательные линии plt.plot(xrange, line(xrange, x1, y1), ‘C1—‘, linewidth = 2) # и точки соприкосновения с графиком параболы plt.scatter(x1, y1, color = ‘C1’, s = 50) # укажем подписи к осям plt.xlabel(‘w1’, fontsize = 15) plt.ylabel(‘f(w1, w2)’, fontsize = 15) # выведем результат plt.show() |

Точно таким же образом мы поступаем со второй переменной w2. Мы замораживаем первую переменную w1 и вычисляем частную производную.
$$ f_{w_2} = frac{partial f}{partial w_2} = 2w_2 $$
Теперь, взяв точку на плоскости (w1, w2), мы будем точно знать скорость изменения функции f(w1, w2) в этой точке в каждом из направлений.
Например, возьмем ту же точку A с координатами w1 = 3, w2 = 4, скорость изменения функции в первом измерении будет равна 2 x 3 = 6, во втором 2 x 4 = 8.
Нотация анализа
Вы вероятно заметили, что мы использовали две нотации (записи) частной производной. С первой мы уже знакомы по предыдущему занятию, это нотация Лагранжа.
$$ f(w) rightarrow f'(w) $$
Вторую нотацию, нотацию Лейбница, удобнее использовать для записи частных производных.
$$ f(w_1, w_2) rightarrow frac{partial f}{partial w_1}, frac{partial f}{partial w_2} $$
Она позволяет сразу увидеть, по какой переменной происходит дифференцирование.
Напомню, что запись формул (и, в частности, производной) в текстовых ячейках ноутбуков с помощью LaTeX мы изучили, когда говорили про Jupyter Notebook.
Взятие частных производных
Пошагово рассмотрим, как мы пришли к результату (2w1, 2w2). Вначале найдем производную по первой переменой w1. Вторую переменную, w2, мы будем считать константой, то есть некоторым числом.
$$ frac{partial f}{partial w_1} (w_1^2 + w_2^2) $$
Первое, что бросается в глаза, это то, что у нас производная суммы, а она, как известно, равна сумме производных.
$$ frac{partial f}{partial w_1} (w_1^2 + w_2^2) = frac{partial f}{partial w_1} (w_1^2) + frac{partial f}{partial w_1} (w_2^2) $$
Производную первого слагаемого мы найдем по правилу производной степенной функции. Второе слагаемое мы решили считать константой, а производная константы равна нулю.
$$ frac{partial f}{partial w_1} (w_1^2) + frac{partial f}{partial w_1} (w_2^2) = 2w_1 + 0 = 2w_1 $$
Частная производная по второй переменной находится аналогично.
Использование SymPy
Функцию diff() библиотеки SymPy можно также использовать для взятия частных производных. Вначале импортируем функцию diff() и символы x и y (мы их используем вместо w1 и w2).
|
from sympy import diff from sympy.abc import x, y |
Напишем функцию, которую хотим дифференцировать.
После этого мы можем находить частные производные, передав в diff() функцию для дифференцирования, а затем либо первую, либо вторую переменную.
|
# найдем частную производную по первой переменной diff(f, x) |
|
# найдем частную производную по второй переменной diff(f, y) |
Градиент
Градиент (gradient) — есть не что иное, как совокупность частных производных по каждой из независимых переменных. Его можно назвать «полной производной».
Он обозначается через греческую букву набла ∇ или оператор Гамильтона.
$$ nabla f(w_1, w_2) = begin{bmatrix} frac{partial f}{partial w_1} \ frac{partial f}{partial w_1} end{bmatrix} = begin{bmatrix} 2w_1 \ 2w_2 end{bmatrix} $$
Еще раз посмотрим, чему равен градиент в точке (3, 4), но уже в новой записи.
$$ nabla f(3, 4) = begin{bmatrix} 2 cdot 3 \ 2 cdot 4 end{bmatrix} = begin{bmatrix} 6 \ 8 end{bmatrix} $$
Как вы видите, такая функция на входе принимает два числа, а на выходе выдает вектор, также состоящий из двух чисел. В этом случае говорят о вектор-функции (vector-valued function).
Метод градиентного спуска
Градиент, который мы только что нашли, показывает направление скорейшего подъема (возрастания) функции. Нам же, если мы хотим найти минимум функции, нужно двигаться вниз в направлении, обратном направлению градиента (еще говорят про направление антиградиента, negative gradient).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
# установим размер графика fig, ax = plt.subplots(figsize = (10,10)) # создадим последовательность из 100 точек в интервале от -10 до 10 # для осей w1 и w2 w1 = np.linspace(—10.0, 10.0, 100) w2 = np.linspace(—10.0, 10.0, 100) # создадим координатную плоскость из осей w1 и w2 w1, w2 = np.meshgrid(w1, w2) # пропишем функцию C = w1 ** 2 + w2 ** 2 # построим изолинии (линии уровня) plt.contourf(w1, w2, C, cmap = ‘Blues’) # выведем точку А с координатами на плоскости (3, 4) ax.scatter(3, 4, c = ‘red’, marker = ‘^’, s = 200) ax.text(2.5, 4.5, ‘A’, size = 25) # и точку B с координатами (0, 0) ax.scatter(0, 0, c = ‘red’, marker = ‘^’, s = 200) ax.text(—1, 0.3, ‘B’, size = 25) # укажем подписи к осям ax.set_xlabel(‘w1’, fontsize = 15) ax.set_ylabel(‘w2’, fontsize = 15) # а также стрелки направления изменений вдоль w1 и w2 ax.arrow(2.7, 4, —2, 0, width = 0.1, head_length = 0.3) ax.arrow(3, 3.5, 0, —2, width = 0.1, head_length = 0.3) # выведем вектор антиградиента с направлением (-6, -8) ax.arrow(3, 4, —6, —8, width = 0.05, head_length = 0.3) ax.text(—2.8, —4.5, ‘Антиградиент’, rotation = 53, size = 16) # создадим сетку в виде прерывистой черты plt.grid(linestyle = ‘—‘) # выведем результат plt.show() |

Если мы сдвинемся на −6 по оси w1 и на −8 по оси w2, то обязательно пройдем через минимум функции. При этом, если мы сдвинемся на всю величину градиента, то «перескочим» через минимум. Именно поэтому нам нужен коэффициент скорости обучения (learning rate).
Теперь мы готовы дать определение:
Метод градиентного спуска — это способ нахождения локального минимума функции в процессе движения в направлении антиградиента. Он был предложен Огюстеном Луи Коши еще в 1847 году.
Воспользуемся этим методом для нахождения минимума приведенной выше функции. Другими словами, проделаем путь из точки А в точку B.
Метод градиентного спуска на Питоне
Вначале объявим необходимые функции.
|
# пропишем функцию потерь def objective(w1, w2): return w1 ** 2 + w2 ** 2 # а также производную по первой def partial_1(w1): return 2.0 * w1 # и второй переменной def partial_2(w2): return 2.0 * w2 |
Зададим исходные параметры модели.
|
# пропишем изначальные веса w1, w2 = 3, 4 # количество итераций iter = 100 # и скорость обучения learning_rate = 0.05 |
Теперь создадим списки для учета обновления весов w1 и w2 и изменения уровня ошибки.
|
w1_list, w2_list, l_list = [], [], [] |
Найдем минимум функции потерь.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# в цикле с заданным количеством итераций for i in range(iter): # будем добавлять текущие веса в соответствующие списки w1_list.append(w1) w2_list.append(w2) # и рассчитывать и добавлять в список текущий уровень ошибки l_list.append(objective(w1, w2)) # также рассчитаем значение частных производных при текущих весах par_1 = partial_1(w1) par_2 = partial_2(w2) # будем обновлять веса в направлении, # обратном направлению градиента, умноженному на скорость обучения w1 = w1 — learning_rate * par_1 w2 = w2 — learning_rate * par_2 # выведем итоговые веса модели и значение функции потерь w1, w2, objective(w1, w2) |
|
(7.968419666276241e-05, 0.00010624559555034984, 1.7637697771638315e-08) |
Как мы видим, уже после ста итераций, как веса модели, так и уровень ошибки приблизились к нулю.
Разумеется, более сложные функции потерь потребуют большего количества итераций и более тонкой настройки коэффициента скорости обучения.
Остается посмотреть на графике, какой путь проделал наш алгоритм градиентного спуска.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
fig = plt.figure(figsize = (14,12)) w1 = np.linspace(—5, 5, 1000) w2 = np.linspace(—5, 5, 1000) w1, w2 = np.meshgrid(w1, w2) f = w1 ** 2 + w2 ** 2 ax = fig.add_subplot(projection = ‘3d’) ax.plot_surface(w1, w2, f, alpha = 0.4, cmap = ‘Blues’) ax.text(3, 3.5, 28, ‘A’, size = 25) ax.text(0, —0.4, 4, ‘B’, size = 25) ax.set_xlabel(‘w1’, fontsize = 15) ax.set_ylabel(‘w2’, fontsize = 15) ax.set_zlabel(‘f(w1, w2)’, fontsize = 15) # выведем путь алгоритма оптимизации ax.plot(w1_list, w2_list, l_list, ‘.-‘, c = ‘red’) plt.show() |
Промежуточные выводы
Давайте еще раз проговорим основные идеи пройденного материала.
- Градиент показывает скорость изменения многомерной функции по каждому из измерений (по каждой из переменных)
- Если «заморозить» все независимые переменные кроме одной и сделать срез, то наклон касательной к кривой среза будет значением частной производной по этому измерению.
- И самое важное для нас: градиент показывает направление скорейшего подъёма (возрастания) функции. Двигаясь в обратном направлении, мы придем к минимуму функции.
Простая линейная регрессия
А теперь давайте с нуля напишем нашу первую модель машинного обучения. Мы наконец-то приобрели для этого все необходимые знания. Наша модель будет по-прежнему иметь только один признак, но при этом будет учитываться не только наклон, но и сдвиг прямой.
$$ hat{y} = w cdot x + b $$
Данные и постановка задачи
Сегодня мы возьмем хорошо известные нам данные роста и обхвата шеи и сразу преобразуем их в массив Numpy.
|
X = np.array([1.48, 1.49, 1.49, 1.50, 1.51, 1.52, 1.52, 1.53, 1.53, 1.54, 1.55, 1.56, 1.57, 1.57, 1.58, 1.58, 1.59, 1.60, 1.61, 1.62, 1.63, 1.64, 1.65, 1.65, 1.66, 1.67, 1.67, 1.68, 1.68, 1.69, 1.70, 1.70, 1.71, 1.71, 1.71, 1.74, 1.75, 1.76, 1.77, 1.77, 1.78]) y = np.array([29.1, 30.0, 30.1, 30.2, 30.4, 30.6, 30.8, 30.9, 31.0, 30.6, 30.7, 30.9, 31.0, 31.2, 31.3, 32.0, 31.4, 31.9, 32.4, 32.8, 32.8, 33.3, 33.6, 33.0, 33.9, 33.8, 35.0, 34.5, 34.7, 34.6, 34.2, 34.8, 35.5, 36.0, 36.2, 36.3, 36.6, 36.8, 36.8, 37.0, 38.5]) |
Выведем эти данные на графике с помощью диаграммы рассеяния или точечной диаграммы.
|
# построим точечную диаграмму plt.figure(figsize = (10,6)) plt.scatter(X, y) # добавим подписи plt.xlabel(‘Рост, см’, fontsize = 16) plt.ylabel(‘Обхват шеи, см’, fontsize = 16) plt.title(‘Зависимость роста и окружности шеи у женщин в России’, fontsize = 18) plt.show() |
Как мы помним, нашей задачей является минимизация средней суммы квадрата расстояний между нашими данными и линией регрессии.
Также приведу формулу.
$$ MSE = frac {1}{n} sum^{n}_{i=1} (y_i-hat{y}_i) ^2 $$
Решение методом наименьшних квадратов
Прежде чем использовать алгоритм градиентного спуска найдем аналитическое решение с помощью метода наименьших квадратов (МНК, least squares method). Для уравнения с одной независимой переменной, напомню, используется следующая формула.
$$ w = frac {sum_{i = 1}^{n} (x_i-bar{x})(y_i-bar{y})} {sum_{i = 1}^{n} (x_i-bar{x})^2} $$
$$ b = bar{y}-wbar{x} $$
Собственная модель
Давайте вычислим наклон и сдвиг прямой с помощью этой формулы на Питоне.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# найдем среднее значение X и y X_mean = np.mean(X) y_mean = np.mean(y) # объявим переменные для числителя и знаменателя numerator, denominator = 0, 0 # в цикле пройдемся по данным for i in range(len(X)): # вычислим значения числителя и знаменателя по формуле выше numerator += (X[i] — X_mean) * (y[i] — y_mean) denominator += (X[i] — X_mean) ** 2 # найдем наклон и сдвиг w = numerator / denominator b = y_mean — w * X_mean w, b |
|
(26.861812005569753, -10.570936299787313) |
Также давайте реализуем этот алгоритм с помощью векторизованного кода.
|
w = np.sum((X — X_mean) * (y — y_mean)) / np.sum((X — X_mean) ** 2) b = y_mean — w * X_mean w, b |
|
(26.861812005569757, -10.57093629978732) |
Модель LinearRegression библиотеки sklearn
Надо сказать, что модель LinearRegression, которую мы использовали на вводном занятии по оптимизации и затем на занятии по линейной регрессии применяет именно МНК для минимизации MSE.
Давайте еще раз применим класс LinearRegression, чтобы убедиться в получении одинаковых результатов.
|
# из набора линейных моделей библиотеки sklearn импортируем линейную регрессию from sklearn.linear_model import LinearRegression # создадим объект этого класса и запишем в переменную model model = LinearRegression() # обучим модель (для X используем двумерный массив) model.fit(X.reshape(—1, 1), y) # выведем коэффициенты model.coef_, model.intercept_ |
|
(array([26.86181201]), -10.570936299787334) |
Как вы видите, результаты одинаковы. Теперь сделаем прогноз и рассчитаем среднеквадратическую ошибку.
|
# сделаем прогноз y_pred_least_squares = model.predict(X.reshape(—1, 1)) # импортируем модуль метрик from sklearn import metrics # выведем среднеквадратическую ошибку (MSE) metrics.mean_squared_error(y, y_pred_least_squares) |
Позднее мы сравним этот результат с аналогичным показателем алгоритма градиентного спуска.
МНК и метод градиентного спуска
Одна из причин использования алгоритма градиентного спуска вместо МНК заключается в том, что этот алгоритм менее требователен к вычислительным ресурсам при большом объеме (количество наблюдений) и размерности (количество признаков) данных.
Кроме того, метод градиентного спуска может применяться не только в задачах линейной регрессии, но и в других алгоритмах (например, в логистической регрессии, SVM или нейросетях).
Решение методом градиентного спуска
Модель линейной регрессии и функция потерь
Начнем с того, что объявим функцию линейной модели.
|
def regression(X, w, b): return w * X + b |
Теперь давайте немного модифицируем функцию потерь и найдем половину среднеквадратической ошибки (half MSE). Обозначим нашу функцию буквой J.
$$ J_{MSE} = frac{1}{2n} sum_{i=1}^{n} (y_i-(wx_i+b))^2 $$
Число два в знаменателе удачно сократится с двойкой, полученной при дифференцировании степенной функции. При этом точка минимума функции не изменится.
|
def objective(X, y, w, b, n): return np.sum((y — regression(X, w, b)) ** 2) / (2 * n) |
Дополнительно замечу, что использование именно среднеквадратической, то есть усредненной на количество наблюдений, ошибки (MSE) вместо «простой» суммы квадратов отклонений (Sum of Squared Errors, SSE)
$$ J_{SSE} = sum_{i=1} (y_i-(wx_i+b))^2 $$
может быть предпочтительнее, поскольку позволяет сравнивать результаты модели на выборках разных размеров.
Частные производные функции потерь
Найдем частные производные этой функции. Их будет две: одна по наклону (w), вторая по сдвигу (b). Начнем с наклона.
$$ frac{partial J}{partial w} left( frac{1}{2n} sum_{i=1}^{n} (y_i-(wx_i+b))^2 right) $$
Шаг 1. Вынесем число 1/2n за скобку по правилу умножения на число. В данном случае n, то есть количество наблюдений, превратится в число, как только мы применим формулу к набору данных.
$$ frac{partial J}{partial w} = frac{1}{2n} frac{partial J}{partial w} sum_{i=1}^{n} left( (y_i-(wx_i+b))^2 right) $$
Шаг 2. Теперь давайте для удобства перепишем выражение в векторизованной форме. Теперь x и y будут не отдельными числами, а векторами.
$$ frac{partial J}{partial w} = frac{1}{2n} frac{partial J}{partial w} left( (y-(wx+b)) ^2 right) $$
Шаг 3. Перед нами композиция из двух функций. Применим chain rule.
$$ frac{partial J}{partial w} = frac{1}{2n} cdot 2(y-(wx+b)) cdot frac{partial J}{partial w} (y-(wx+b)) $$
Шаг 4. К внутренней функции мы можем применить правило суммы и разности производных.
$$ frac{1}{2n} cdot 2(y-(wx+b)) cdot (0-(x+0)) $$
Замечу, что при дифференцировании внутренней функции, y превратился в ноль, потому что это константа. Одновременно переменную b мы «заморозили» и также решили считать константой.
Шаг 5. Упростим выражение.
$$ frac{partial J}{partial w} = frac{1}{cancel{2}n} cdot cancel{2}-x(y-(wx+b)) = frac{1}{n} cdot -x(y-(wx+b)) $$
Аналогично найдем частную производную по сдвигу.
$$ frac{partial J}{partial b} = frac{1}{n} cdot -(y-(wx+b)) $$
Здесь стоит уточнить лишь, что при нахождении производной внутренней функции мы «заморозили» переменную w.
$$ frac{partial J}{partial b} left( (y-(wx+b)) right) = 0-(0+1)$$
В невекторизованной форме производные выглядят следующим образом.
$$ frac{partial J}{partial w} = frac{1}{n} sum_{i=1}^{n} -x_i(y_i-(wx_i+b)) $$
$$ frac{partial J}{partial b} = frac{1}{n} sum_{i=1}^{n} -(y_i-(wx_i+b)) $$
Поменяв слагаемые в скобках местами и умножив на $-1$, частные производные можно записать и так.
$$ frac{partial J}{partial w} = frac{1}{n} sum_{i=1}^{n} ((wx_i+b)-y_i) cdot x_i $$
$$ frac{partial J}{partial b} = frac{1}{n} sum_{i=1}^{n} ((wx_i+b)-y_i) $$
Пропишем эти функции на Питоне.
|
def partial_w(X, y, w, b, n): return np.sum(—X * (y — (w * X + b))) / n def partial_b(X, y, w, b, n): return np.sum(—(y — (w * X + b))) / n |
Алгоритм градиентного спуска
Создадим функцию, которая будет на входе принимать данные, количество итераций и коэффициент скорости обучения, а на выходе выдавать веса модели и уровень ошибки.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# передадим функции данные, количество итераций и скорость обучения def gradient_descent(X, y, iter, learning_rate): # зададим изначальные веса w, b = 0, 0 # и количество наблюдений n = len(X) # создадим списки для записи весов модели и уровня ошибки w_list, b_list, l_list = [], [], [] # в цикле с заданным количеством итераций for i in range(iter): # добавим в списки текущие веса w_list.append(w) b_list.append(b) # и уровень ошибки l_list.append(objective(X, y, w, b, n)) # рассчитаем текущее значение частных производных par_1 = partial_w(X, y, w, b, n) par_2 = partial_b(X, y, w, b, n) # обновим веса в направлении антиградиента w = w — learning_rate * par_1 b = b — learning_rate * par_2 # выведем списки с уровнями ошибки и весами return w_list, b_list, l_list |
Обучение модели
Применим написанную выше функцию для обучения модели. Используем следующие гиперпараметры модели:
- количество итераций — 200 000
- коэффициент скорости обучения — 0,01
Напомню, что гиперпараметр — это параметр, который мы задаем до обучения модели.
|
# распакуем результат работы функции в три переменные w_list, b_list, l_list = gradient_descent(X, y, iter = 200000, learning_rate = 0.01) # и выведем последние достигнутые значения весов и уровня ошибки print(w_list[—1], b_list[—1], l_list[—1]) |
|
26.6917462520774 -10.293843835595917 0.1137823984153401 |
В целом, как мы видим, веса модели очень близки к результату, найденному с помощью метода наименьших квадратов. Теперь сделаем прогноз.
|
# передадим функции regression() наиболее оптимальные веса y_pred_gd = regression(X, w_list[—1], b_list[—1]) y_pred_gd[:5] |
|
array([29.20994062, 29.47685808, 29.47685808, 29.74377554, 30.01069301]) |
Посмотрим на результат на графике.
|
plt.figure(figsize = (10, 8)) plt.scatter(X, y) plt.plot(X, y_pred_gd, ‘r’) plt.show() |
Кроме того, мы можем посмотреть на то, как снижался уровень ошибки с каждой последующей итерацией.
Как мы видим, в первые итерации уровень ошибки снижался настолько стремительно, что последующие изменения практически незаметны. Давайте попробуем отбросить первые 150 наблюдений.
|
plt.figure(figsize = (8, 6)) plt.plot(l_list[150:]) plt.show() |
И все же кажется, что после 150000 итераций ошибка перестает снижаться и можно было бы обойтись меньшим количеством шагов. На самом деле это не так.
|
# отбросим первые 150 000 наблюдений plt.figure(figsize = (8, 6)) plt.plot(l_list[150000:]) plt.show() |
В целом подбор количества итераций и длины шага (коэффициента скорости обучения) довольно существенно влияют на качество обучения. Ближе к концу занятия мы рассмотрим этот момент более подробно.
Оценка качества модели
Оценим качество модели с помощью встроенной в sklearn метрики.
|
# рассчитаем MSE metrics.mean_squared_error(y, y_pred_gd) |
Результат очень близок к тому, который мы получили, используя МНК.
Визуализация шагов алгоритма оптимизации
Мы также как и раньше, можем посмотреть на путь, пройденный алгоритмом оптимизации.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
# создадим последовательности из 500 значений ww = np.linspace(—30, 30, 500) bb = np.linspace(—30, 30, 500) # сформируем координатную плоскость www, bbb = np.meshgrid(ww, bb) # а также матрицу из нулей для заполнения значениями функции J(w, b) JJ = np.zeros([len(ww), len(bb)]) # для каждой комбинации w и b for i in range(len(ww)): for j in range(len(bb)): # рассчитаем соответствующее прогнозное значение yy = www[i, j] * X + bbb[i, j] # и подставим его в функцию потерь (матрицу JJ) JJ[i, j] = 1 / (2 * len(X)) * np.sum((y — yy) ** 2) # зададим размер графика fig = plt.figure(figsize = (14,12)) # создидим трехмерное пространство ax = fig.add_subplot(projection = ‘3d’) # построим функцию потерь ax.plot_surface(www, bbb, JJ, alpha = 0.4, cmap = plt.cm.jet) # а также путь алгоритма оптимизации ax.plot(w_list, b_list, l_list, c = ‘red’) # для наглядности зададим более широкие, чем график # границы пространства ax.set_xlim(—40, 40) ax.set_ylim(—40, 40) plt.show() |
Мы также можем построить график изолиний («вид сверху»).
|
# для этого используем функцию plt.contour() fig, ax = plt.subplots(figsize = (10, 10)) ax.contour(www, bbb, JJ, 100, cmap = plt.cm.jet) ax.plot(w_list, b_list, c = ‘red’) plt.show() |
Как мы видим, алгоритм сначала двигался в одном направлении (очевидно, так ошибка снижалась наиболее стремительно), затем повернул на 90 градусов и продолжил движение.
Про выбор гиперпараметров модели
Давайте посмотрим, как поведет себя алгоритм при изменении гиперпараметров. Вначале попробуем тот же размер шага, но уменьшим количество итераций.
|
w_list_t1, b_list_t1, l_list_t1 = gradient_descent(X, y, iter = 10000, learning_rate = 0.01) w_list_t1[—1], b_list_t1[—1], l_list_t1[—1] |
|
(17.113947076094593, 5.311508333809235, 0.4836593999661288) |
Коэффициенты довольно сильно отличаются от найденных ранее значений. Посмотрим на графике изолиний, где остановился наш алгоритм.
|
fig, ax = plt.subplots(figsize = (10, 10)) ax.contour(www, bbb, JJ, 100, cmap = plt.cm.jet) ax.plot(w_list, b_list, c = ‘red’) # выведем точку, которой достиг новый алгоритм ax.scatter(w_list_t1[—1], b_list_t1[—1], s = 100, c = ‘blue’) plt.show() |
Как мы видим, алгоритм немного не дошел до оптимума. Теперь давайте попробуем уменьшить размер шага. Количество итераций вернем к прежнему значению.
|
w_list_t2, b_list_t2, l_list_t2 = gradient_descent(X, y, iter = 200000, learning_rate = 0.0001) w_list_t2[—1], b_list_t2[—1], l_list_t2[—1] |
|
(15.302448783526573, 8.263028645561734, 0.6339512457580667) |
|
fig, ax = plt.subplots(figsize = (10, 10)) ax.contour(www, bbb, JJ, 100, cmap = plt.cm.jet) ax.plot(w_list, b_list, c = ‘red’) ax.scatter(w_list_t2[—1], b_list_t2[—1], s = 100, c = ‘blue’) plt.show() |
В данном случае, так как мы делали слишком маленькие шаги, то продвинулись еще меньше.
Тема выбора гиперпараметров довольно сложна и выходит за рамки сегодняшнего занятия, однако уже на этих простых примерах видно, что один и тот же алгоритм при разных изначальных параметрах показывает совершенно разные результаты.
Подведем итог
В первой части занятия мы посмотрели как применить понятие производной к многомерной функции, познакомились с понятием градиента и методом градиентного спуска. Во второй части мы построили модель простой линейной регрессии и оптимизировали ее с помощью метода наименьших квадратов и алгоритма градиентного спуска.
Вопросы для закрепления
Вопрос. Что такое градиент?
Посмотреть правильный ответ
Ответ: градиент — это вектор, показывающий направление скорейшего подъема многомерной функции. Градиент состоит из частных производных по каждому из измерений (переменных) функции.
Вопрос. Какие гиперпараметры существенно влияют на качество оптимизации модели линейной регрессии?
Посмотреть правильный ответ
Ответ: количество итераций и коэффициент скорости обучения
Логичным продолжением будет построение модели многомерной или множественной линейной регрессии (multiple linear regression) с несколькими признаками. Однако прежде будет полезно еще раз в деталях изучить взаимосвязь переменных.
Ответы на вопросы
Вопрос. Почему если умножить функцию потерь на число, в частности на 1/2, точка ее минимума не изменится?
Ответ. Давайте посмотрим на график параболы и параболы, умноженной на 1/2.
Как мы видим, точка минимума не изменилась.
При этом обратите внимание на то, что изменился наклон (значение градиента). Эффект умножения функции потерь на число аналогичен измененению коэффициента скорости обучения (learning rate). Чем круче наклон, тем большие по размеру шаги мы будем делать.
Вопрос. Скажите, а как работает функция np.meshgrid()?
Ответ. Функция np.meshgrid() на входе принимает одномерные массивы и создает двумерный массив с привычной прямоугольной (декартовой) системой координат.
|
# создадим простые последовательности xvalues = np.array([0, 1, 2, 3, 4]) yvalues = np.array([0, 1, 2, 3, 4]) # сформируем координатную плоскость xx, yy = np.meshgrid(xvalues, yvalues) # выведем точки плоскости на графике plt.plot(xx, yy, marker = ‘.’, color = ‘r’, linestyle = ‘none’) plt.show() |
Обратите внимание, начало координат находится в левом нижнему углу.
Вопрос. Функция plt.fill_between() заполняет пространство между двумя функциями, но не очень понятно, какие параметры мы ей передаем.
Ответ. Функция np.fill_between(x, y1, y2 = 0) принимает три основных параметра: координаты по оси x, координаты по оси y (первая функция, y1) и координаты по оси y (вторая функция, y2) и заполняет пространство между y1 и y2. Параметр y2 не является обязательным. Если его не указывать, будет заполняться пространство между линией y1 и осью x (то есть функцией y = 0).
В конце ноутбука⧉ я привел два примера, когда параметр y2 не указывается, то есть равен 0, и когда y2 задает отличную от нуля функцию.
Градиентный спуск — самый используемый алгоритм обучения нейронных сетей, он применяется почти в каждой модели машинного обучения. Метод градиентного спуска с некоторой модификацией широко используется для обучения персептрона и глубоких нейронных сетей, и известен как метод обратного распространения ошибки.
В этом посте вы найдете объяснение градиентного спуска с небольшим количеством математики. Краткое содержание:
- Смысл ГС — объяснение всего алгоритма;
- Различные вариации алгоритма;
- Реализация кода: написание кода на языке Python.
Что такое градиентный спуск
Градиентный спуск — метод нахождения минимального значения функции потерь (существует множество видов этой функции). Минимизация любой функции означает поиск самой глубокой впадины в этой функции. Имейте в виду, что функция используется, чтобы контролировать ошибку в прогнозах модели машинного обучения. Поиск минимума означает получение наименьшей возможной ошибки или повышение точности модели. Мы увеличиваем точность, перебирая набор учебных данных при настройке параметров нашей модели (весов и смещений).
Итак, градиентный спуск нужен для минимизации функции потерь.
Суть алгоритма – процесс получения наименьшего значения ошибки. Аналогично это можно рассматривать как спуск во впадину в попытке найти золото на дне ущелья (самое низкое значение ошибки).
В дальнейшем, чтобы найти самую низкую ошибку (глубочайшую впадину) в функции потерь (по отношению к одному весу), нужно настроить параметры модели. Как мы их настраиваем? В этом поможет математический анализ. Благодаря анализу мы знаем, что наклон графика функции – производная от функции по переменной. Это наклон всегда указывает на ближайшую впадину!
На рисунке мы видим график функции потерь (названный «Ошибка» с символом «J») с одним весом. Теперь, если мы вычислим наклон (обозначим это dJ/dw) функции потерь относительно одного веса, то получим направление, в котором нужно двигаться, чтобы достичь локальных минимумов. Давайте пока представим, что наша модель имеет только один вес.
- Функция потерь
Важно: когда мы перебираем все учебные данные, мы продолжаем добавлять значения dJ/dw для каждого веса. Так как потери зависят от примера обучения, dJ/dw также продолжает меняться. Затем делим собранные значения на количество примеров обучения для получения среднего. Потом мы используем это среднее значение (каждого веса) для настройки каждого веса.
Также обратите внимание: Функция потерь предназначена для отслеживания ошибки с каждым примером обучениям, в то время как производная функции относительного одного веса – это то, куда нужно сместить вес, чтобы минимизировать ее для этого примера обучения. Вы можете создавать модели даже без применения функции потерь. Но вам придется использовать производную относительно каждого веса (dJ/dw).
Теперь, когда мы определили направление, в котором нужно подтолкнуть вес, нам нужно понять, как это сделать. Тут мы используем коэффициент скорости обучения, его называют гипер-параметром. Гипер-параметр – значение, требуемое вашей моделью, о котором мы действительно имеем очень смутное представление. Обычно эти значения могут быть изучены методом проб и ошибок. Здесь не так: одно подходит для всех гипер-параметров. Коэффициент скорости обучения можно рассматривать как «шаг в правильном направлении», где направление происходит от dJ/dw.
Это была функция потерь построенная на один вес. В реальной модели мы делаем всё перечисленное выше для всех весов, перебирая все примеры обучения. Даже в относительно небольшой модели машинного обучения у вас будет более чем 1 или 2 веса. Это затрудняет визуализацию, поскольку график будет обладать размерами, которые разум не может себе представить.
Подробнее о градиентах
Кроме функции потерь градиентный спуск также требует градиент, который является dJ/dw (производная функции потерь относительно одного веса, выполненная для всех весов). dJ/dw зависит от вашего выбора функции потерь. Наиболее распространена функция потерь среднеквадратичной ошибки.
Производная этой функции относительно любого веса (эта формула показывает вычисление градиента для линейной регрессии):
Это – вся математика в ГС. Глядя на это можно сказать, что по сути, ГС не содержит много математики. Единственная математика, которую он содержит в себе – умножение и деление, до которых мы доберемся. Это означает, что ваш выбор функции повлияет на вычисление градиента каждого веса.
Коэффициент скорости обучения
Всё, о чём написано выше, есть в учебнике. Вы можете открыть любую книгу о градиентном спуске, там будет написано то же самое. Формулы градиентов для каждой функции потерь можно найти в интернете, не зная как вывести их самостоятельно.
Однако проблема у большинства моделей возникает с коэффициентом скорости обучения. Давайте взглянем на обновленное выражение для каждого веса (j лежит в диапазоне от 0 до количества весов, а Theta-j это j-й вес в векторе весов, k лежит в диапазоне от 0 до количества смещений, где B-k — это k-е смещение в векторе смещений). Здесь alpha – коэффициент скорости обучения. Из этого можно сказать, что мы вычисляем dJ/dTheta-j ( градиент веса Theta-j), и затем шаг размера alpha в этом направлении. Следовательно, мы спускаемся по градиенту. Чтобы обновить смещение, замените Theta-j на B-k.
Если этот размера шага alpha слишком велик, мы преодолеем минимум: то есть промахнемся мимо минимума. Если alpha слишком мала, мы используем слишком много итераций, чтобы добраться до минимума. Итак, alpha должна быть подходящей.
Использование градиентного спуска
Что ж, вот и всё. Это всё, что нужно знать про градиентный спуск. Давайте подытожим всё в псевдокоде.
Примечание: Весы здесь представлены в векторах. В более крупных моделях они, наверное, будут матрицами.
От i = 0 до «количество примеров обучения»
1. Вычислите градиент функции потерь для i-го примера обучения по каждому весу и смещению. Теперь у вас есть вектор, который полон градиентами для каждого веса и переменной, содержащей градиент смещения.
2. Добавьте градиенты весов, вычисленные для отдельного аккумулятивного вектора, который после того, как вы выполнили итерацию по каждому учебному примеру, должен содержать сумму градиентов каждого веса за несколько итераций.
3. Подобно ситуации с весами, добавьте градиент смещения к аккумулятивной переменной.
Теперь, ПОСЛЕ перебирания всех примеров обучения, выполните следующие действия:
1. Поделите аккумулятивные переменные весов и смещения на количество примеров обучения. Это даст нам средние градиенты для всех весов и средний градиент для смещения. Будем называть их обновленными аккумуляторами (ОА).
2. Затем, используя приведенную ниже формулу, обновите все веса и смещение. Вместо dJ / dTheta-j вы будете подставлять ОА (обновленный аккумулятор) для весов и ОА для смещения. Проделайте то же самое для смещения.
Это была только одна итерация градиентного спуска.
Повторите этот процесс от начала до конца для некоторого количества итераций. Это означает, что для 1-й итерации ГС вы перебираете все примеры обучения, вычисляете градиенты, потом обновляете веса и смещения. Затем вы проделываете это для некоторого количества итераций ГС.
Различные типы градиентного спуска
Существует 3 варианта градиентного спуска:
1. Мini-batch: тут, вместо поочерёдного перебора всех примеров обучения и произведения необходимых вычислений для каждого из них, мы производим вычисления для n примеров обучения сразу. Этот выбор подходит для очень больших наборов данных.
2. Стохастический градиентный спуск: в этом случае вместо перебора и использования всего набора примеров обучения мы применяем подход “используй только один”. Здесь нужно отметить несколько моментов:
- Набор примеров обучения необходимо перемешать перед каждым его проходом в ГС, чтобы перебирать их каждый раз в случайном порядке.
- Поскольку каждый раз используется только один пример обучения, то ваш путь к локальному минимуму будет очень неоптимальным;
- С каждой итерацией ГС вам нужно перемешать набор обучения и выбрать случайный пример обучения;
- Поскольку вы используете только один пример обучения, ваш путь к локальным минимумам будет очень шумным.
3. Серия ГС: это то, о чем написано в предыдущих разделах. Цикл на каждом примере обучения.
Пример кода на python
Применимо к cерии ГС, так будет выглядеть блок учебного кода на Python.
def train(X, y, W, B, alpha, max_iters):
'''
Performs GD on all training examples,
X: Training data set,
y: Labels for training data,
W: Weights vector,
B: Bias variable,
alpha: The learning rate,
max_iters: Maximum GD iterations.
'''
dW = 0 # Weights gradient accumulator
dB = 0 # Bias gradient accumulator
m = X.shape[0] # No. of training examples
for i in range(max_iters):
dW = 0 # Reseting the accumulators
dB = 0
for j in range(m):
# 1. Iterate over all examples,
# 2. Compute gradients of the weights and biases in w_grad and b_grad,
# 3. Update dW by adding w_grad and dB by adding b_grad,
W = W - alpha * (dW / m) # Update the weights
B = B - alpha * (dB / m) # Update the bias return W, B # Return the updated weights and bias.Вот и всё. Теперь вы должны хорошо понимать, что такое метод градиентного спуска.

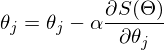
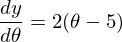
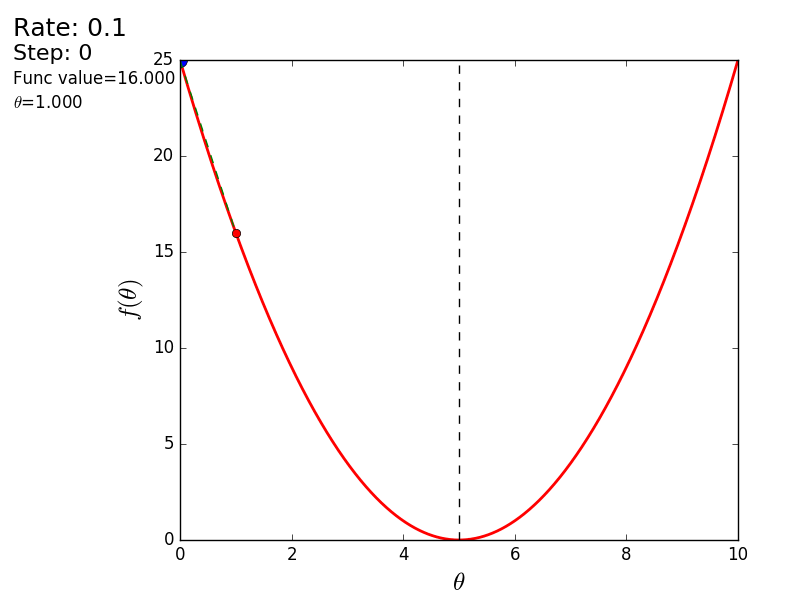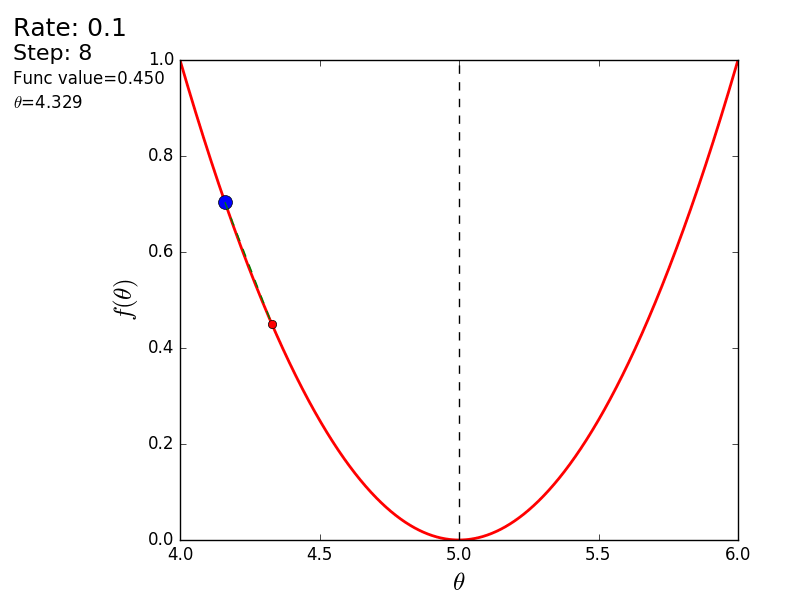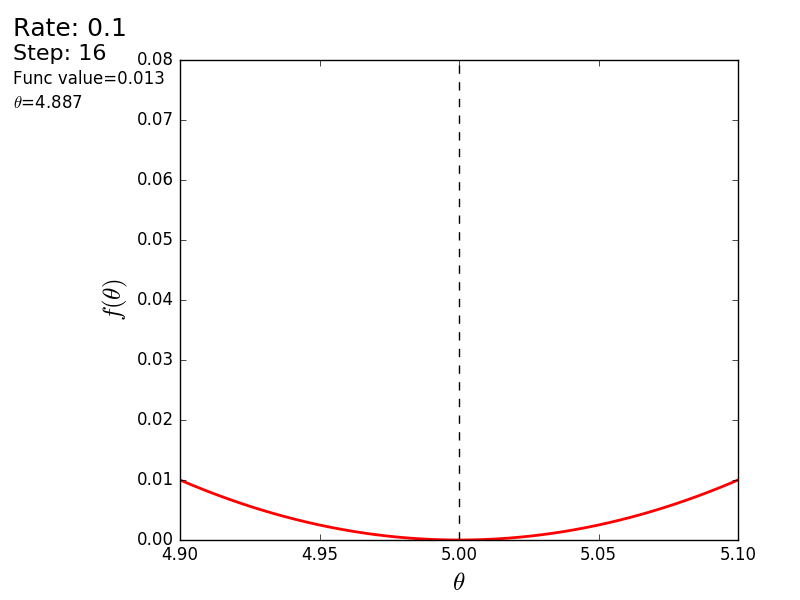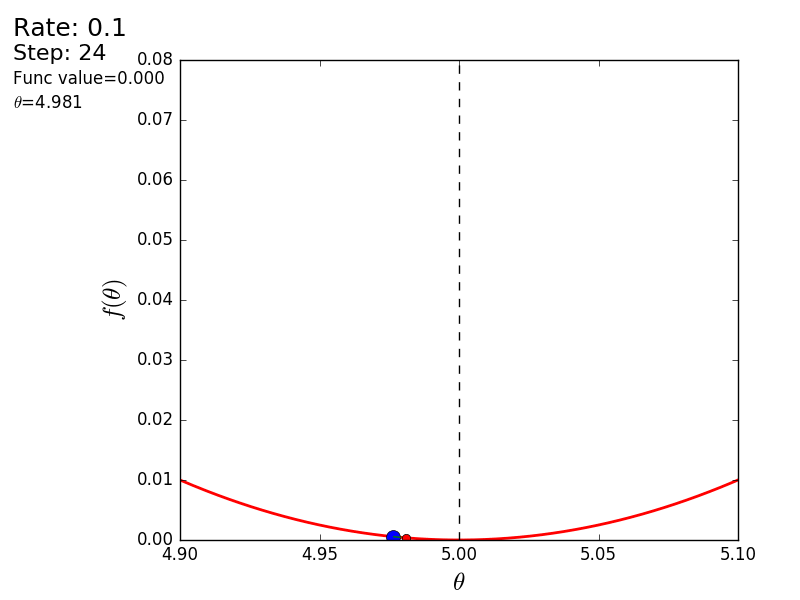
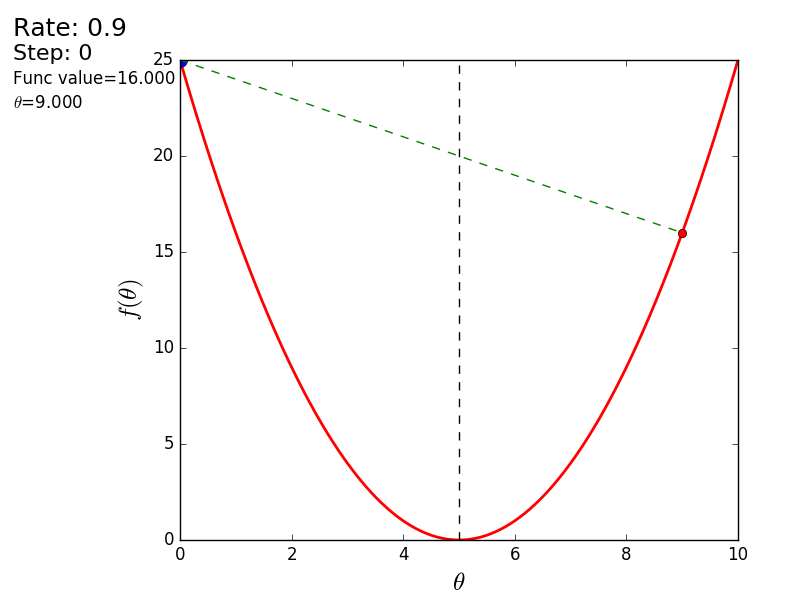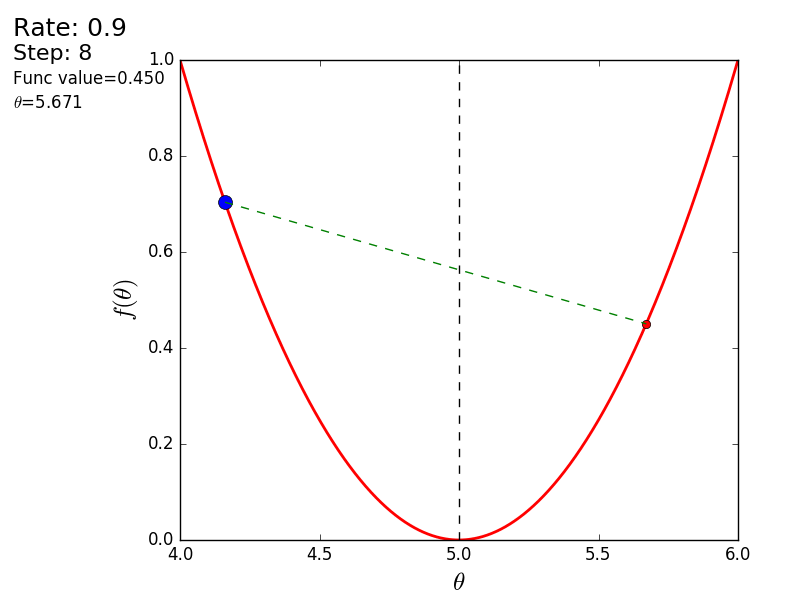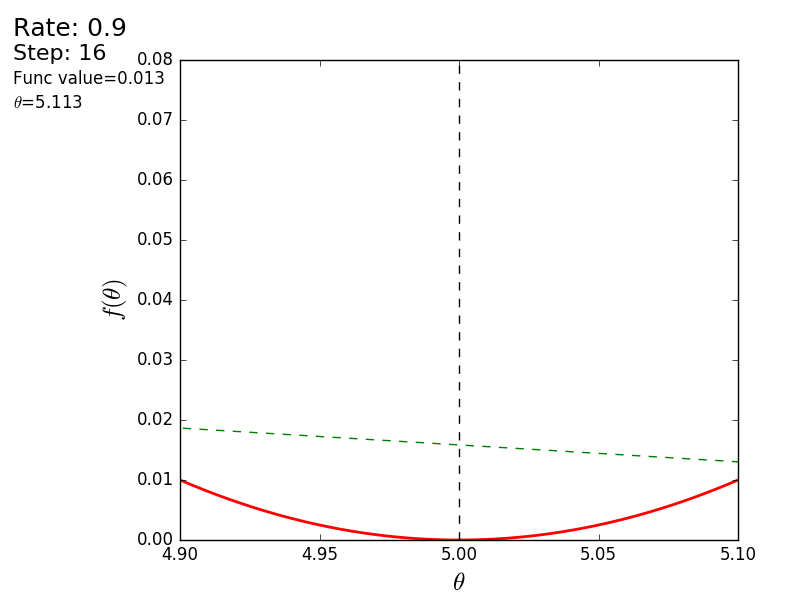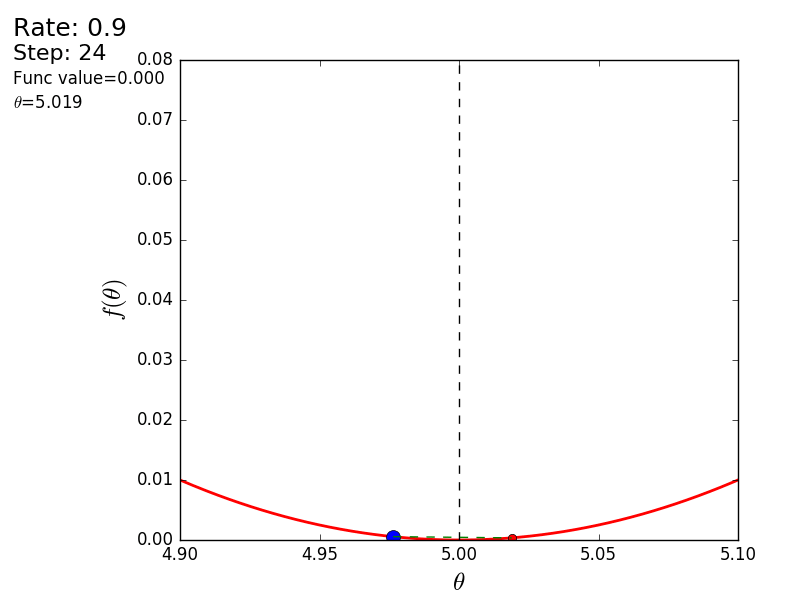
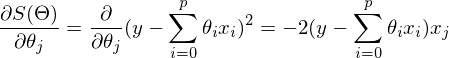
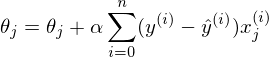
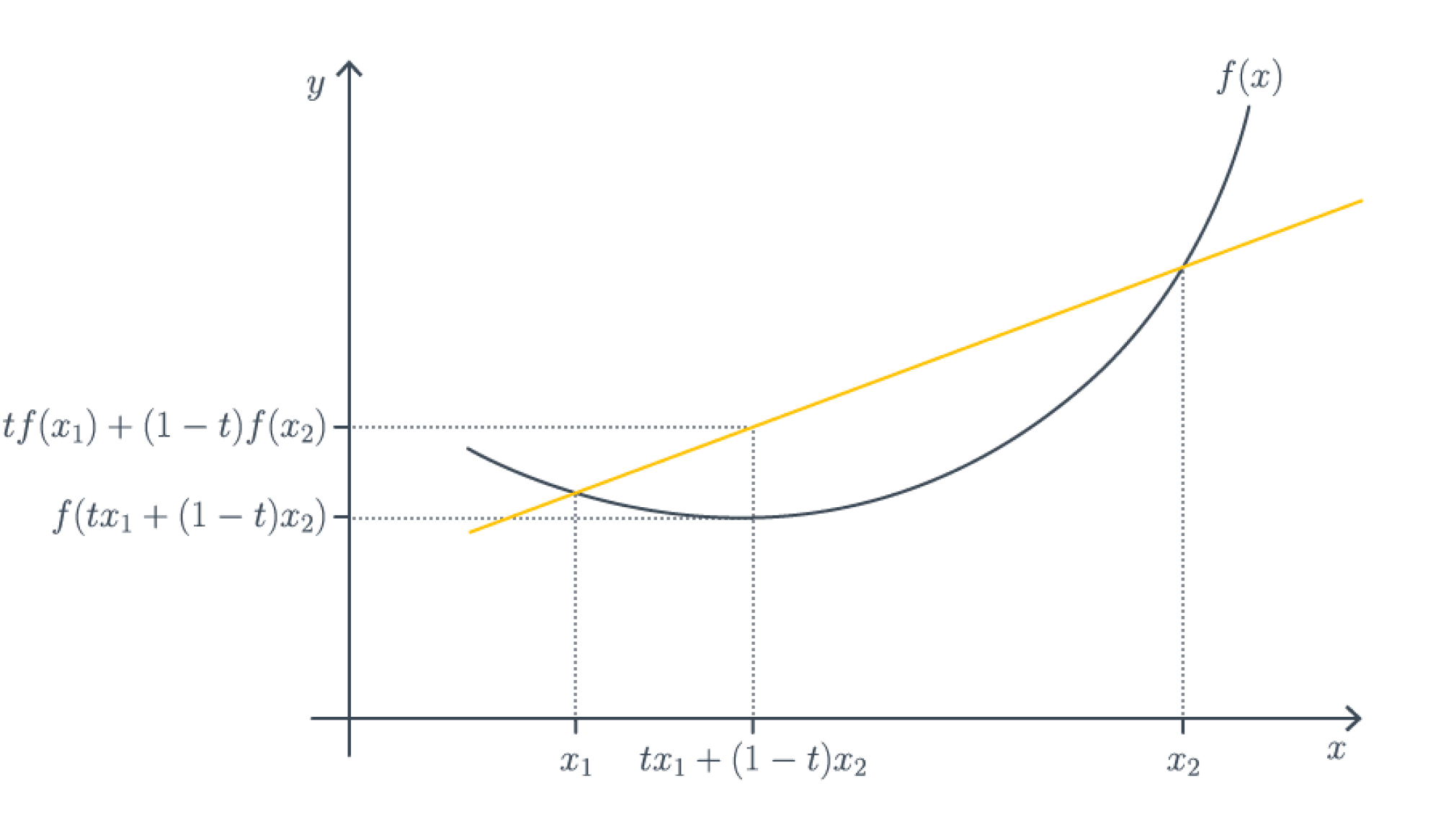
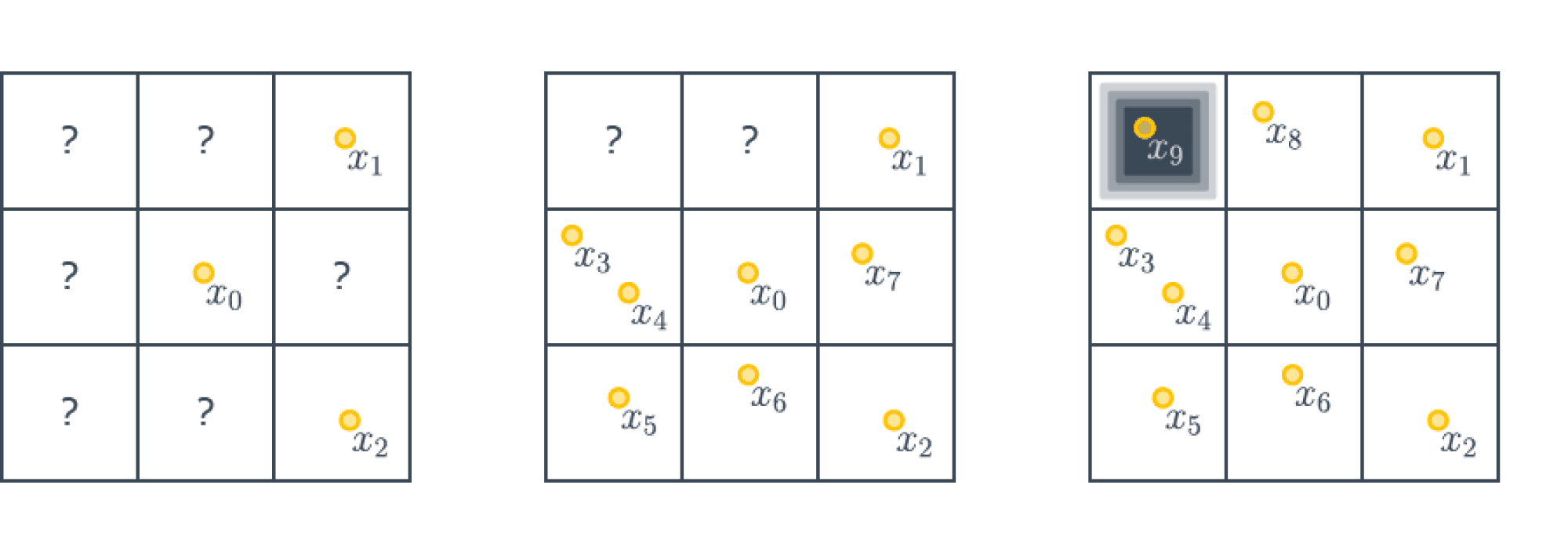
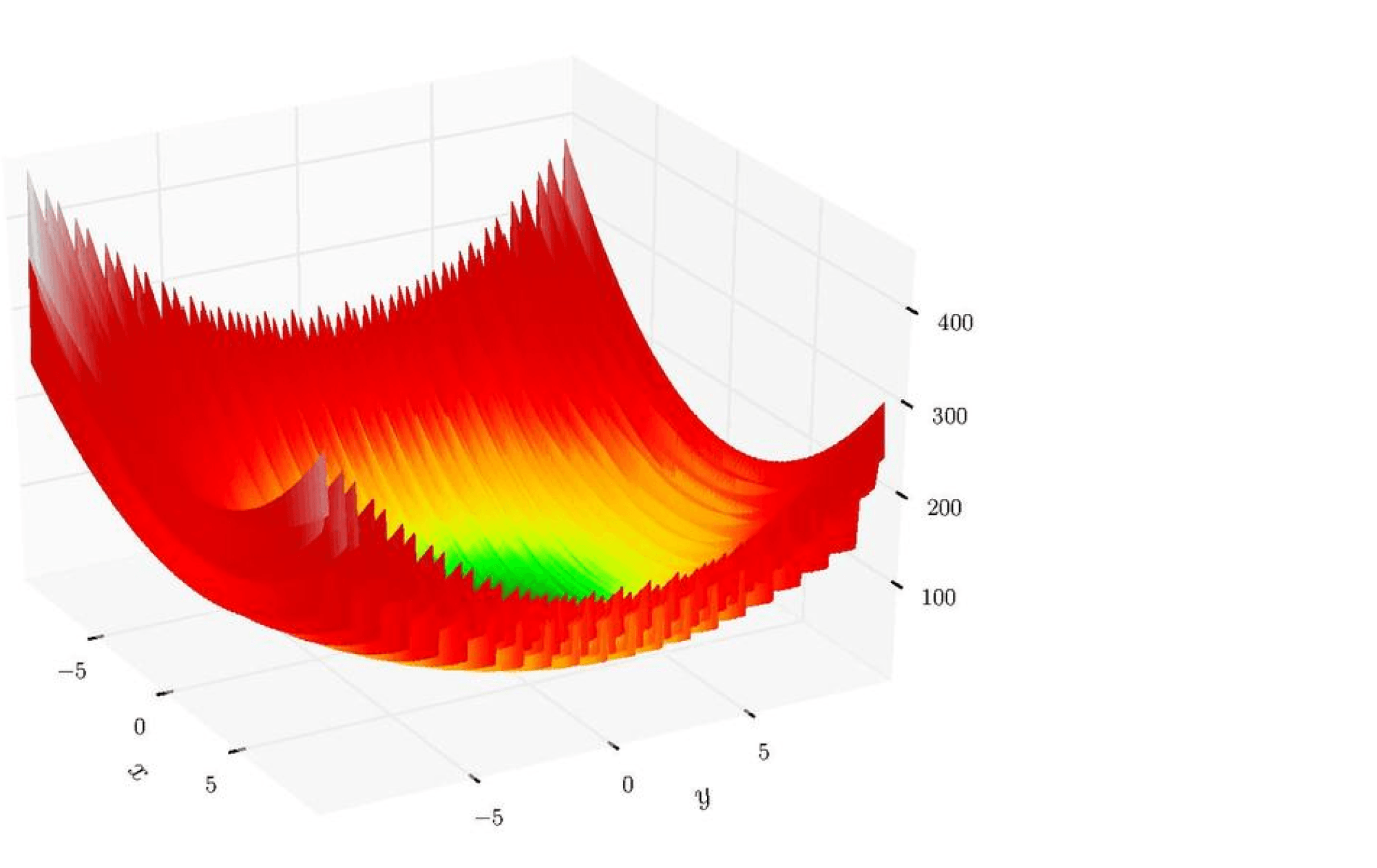
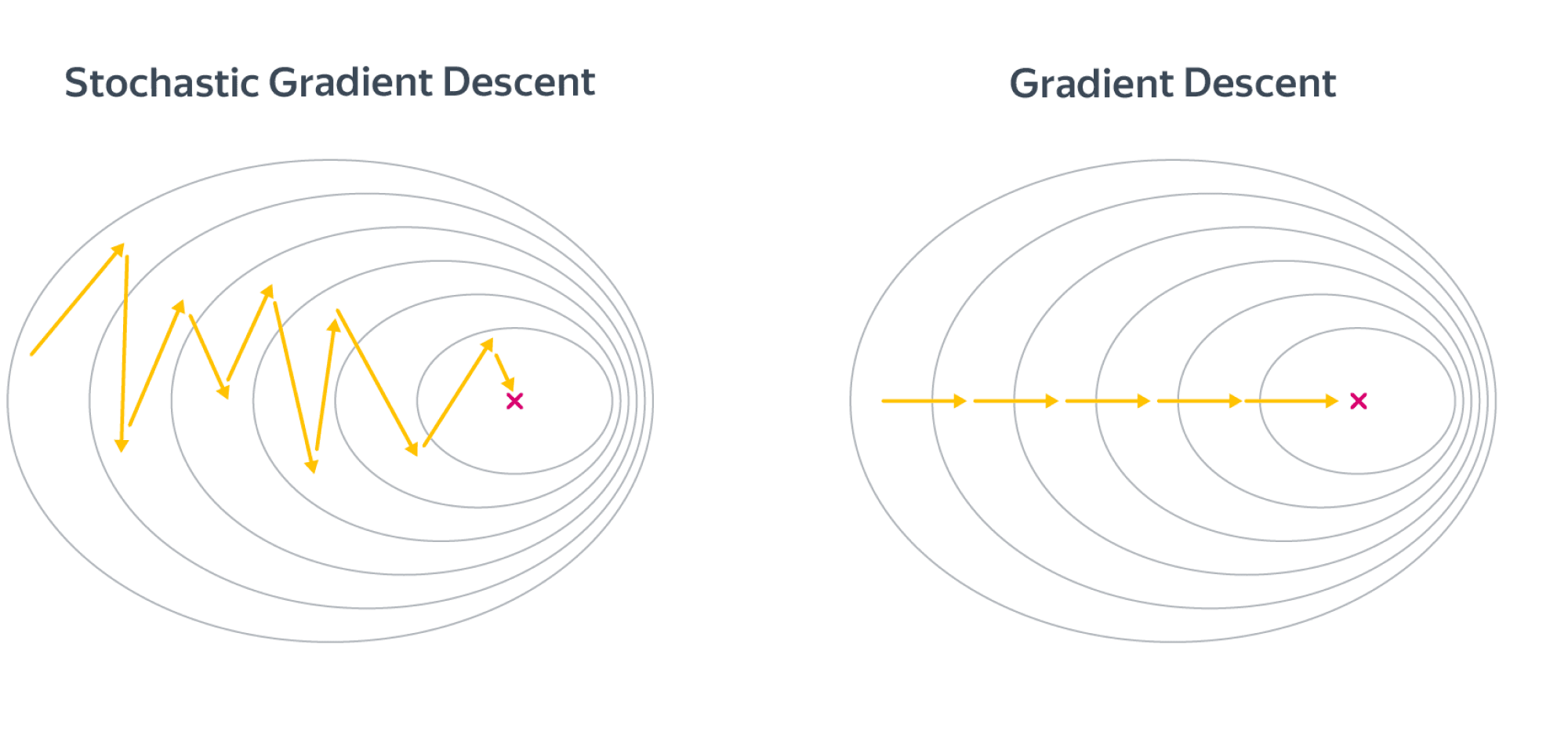
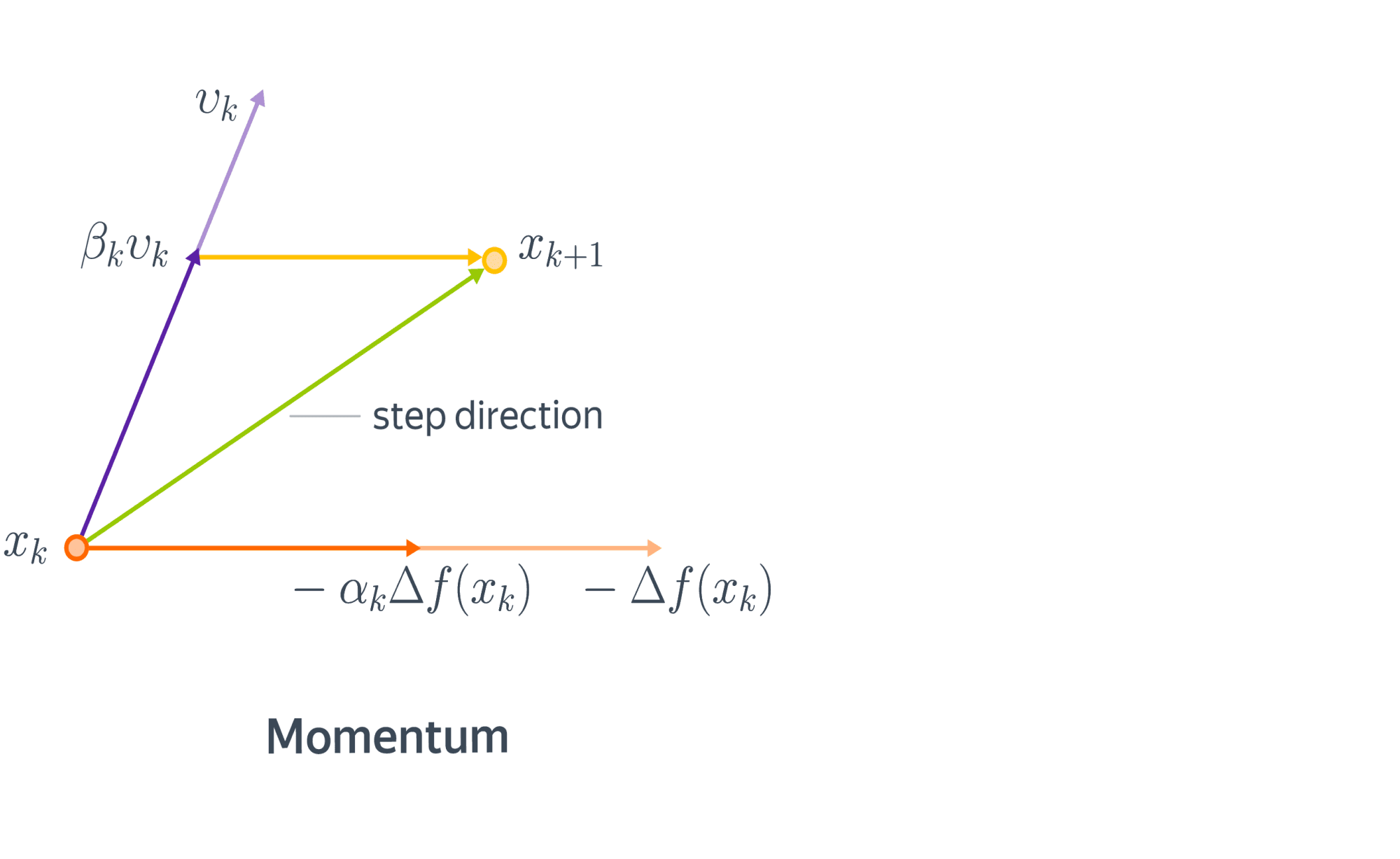
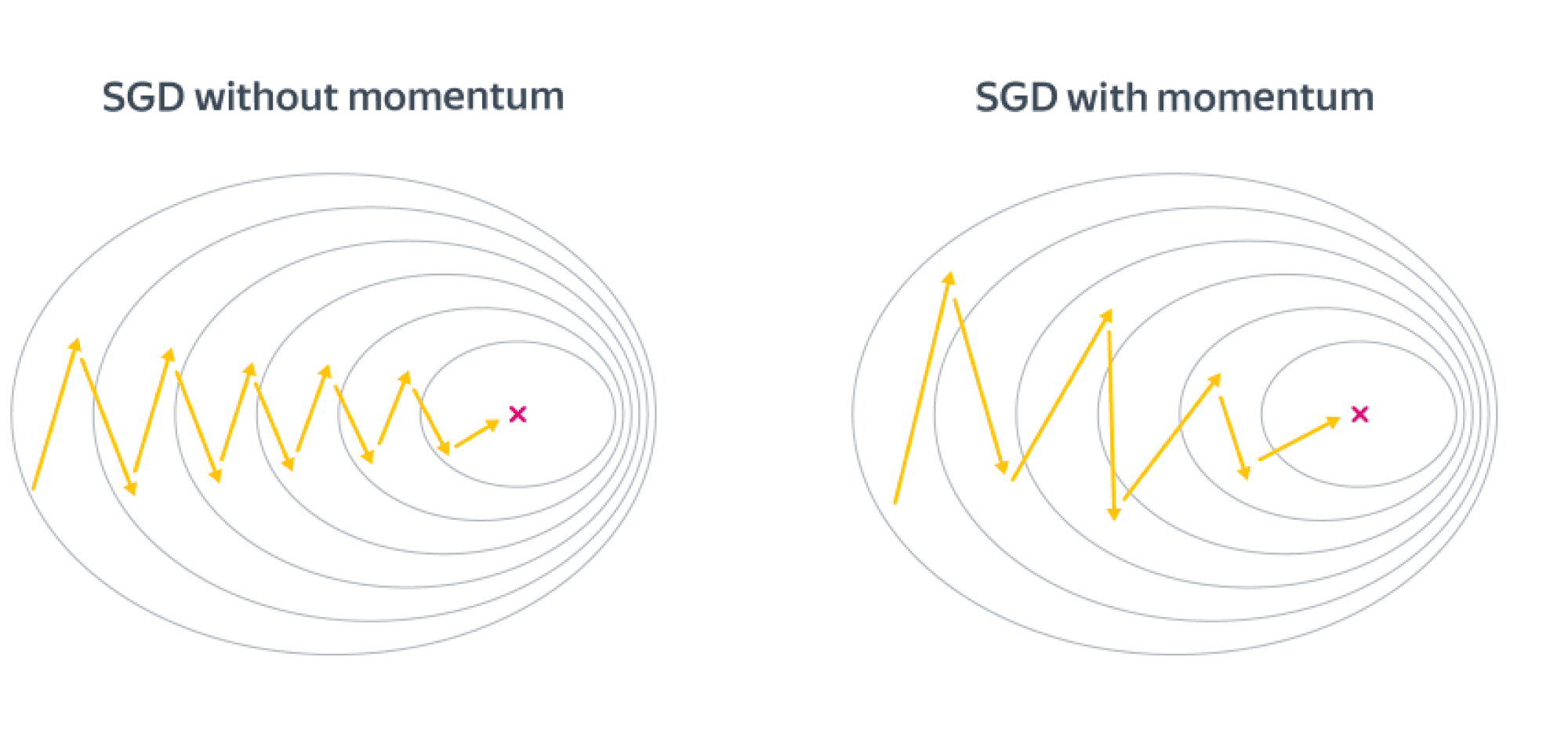
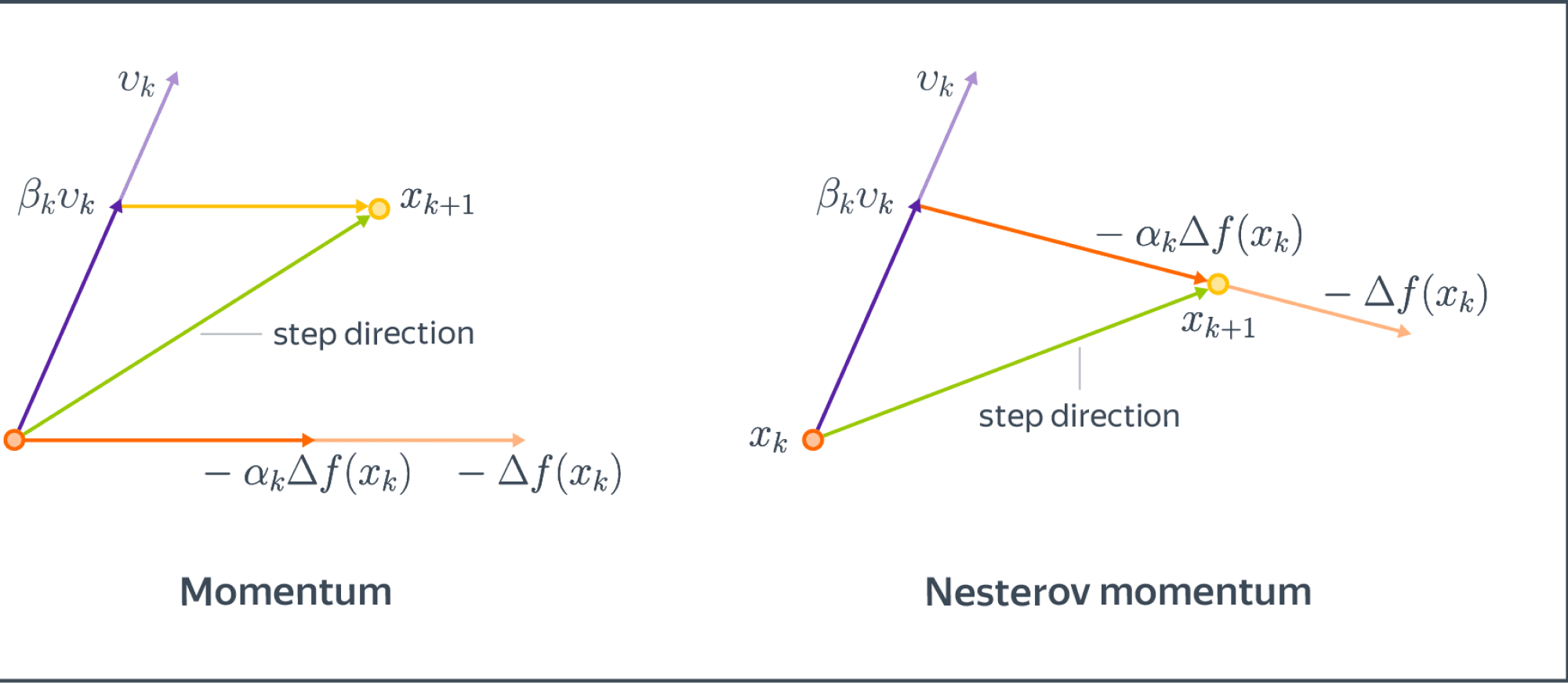
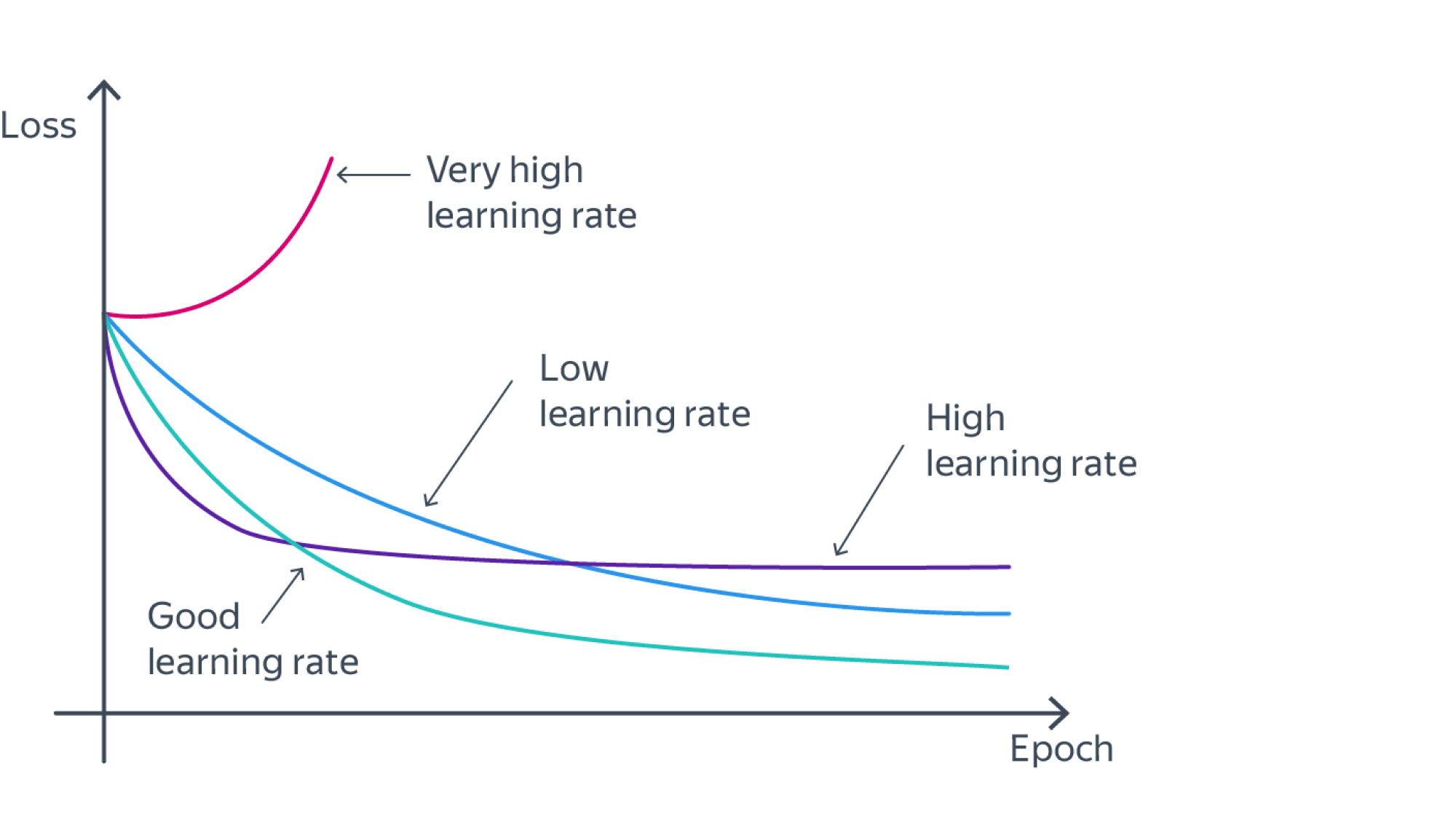

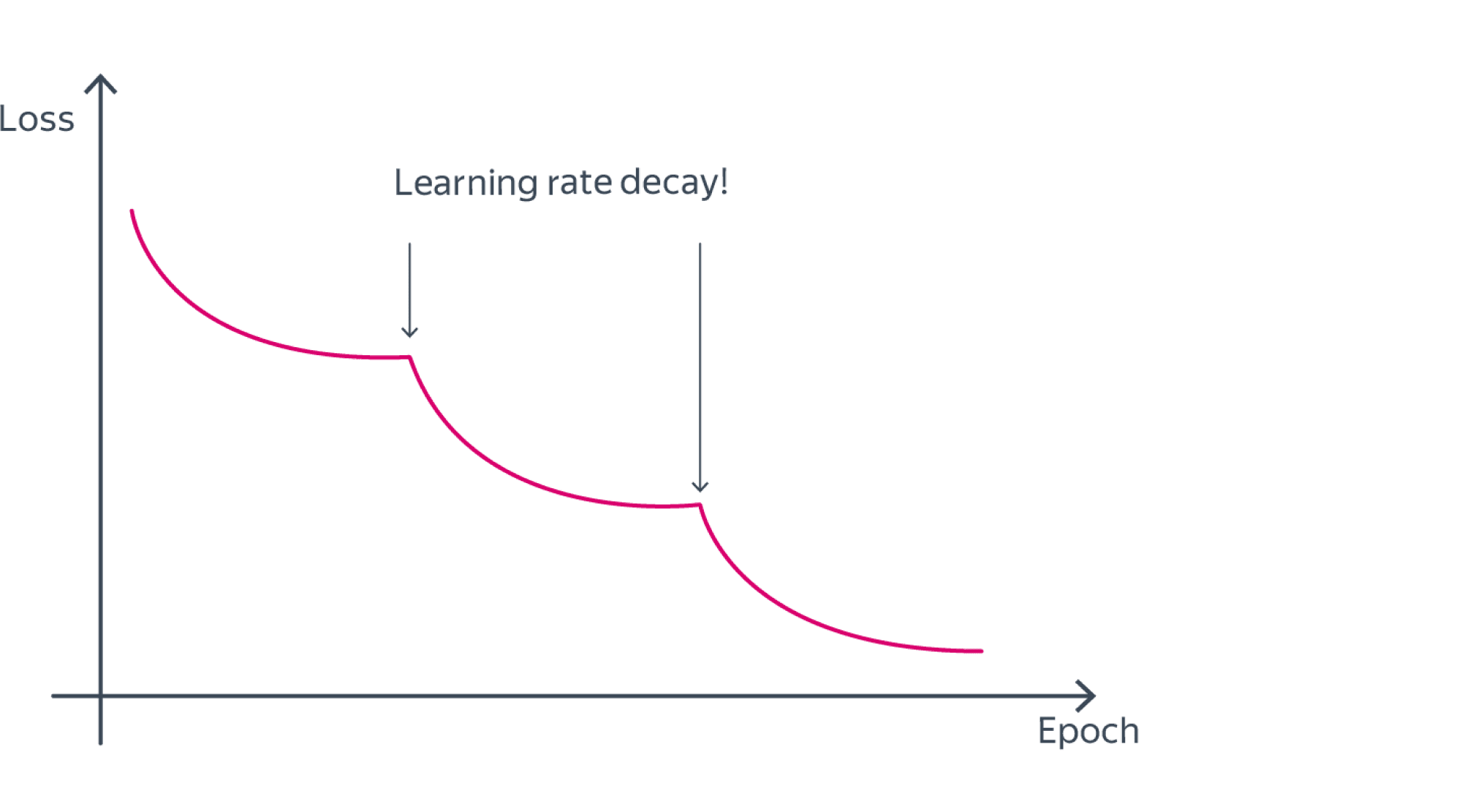
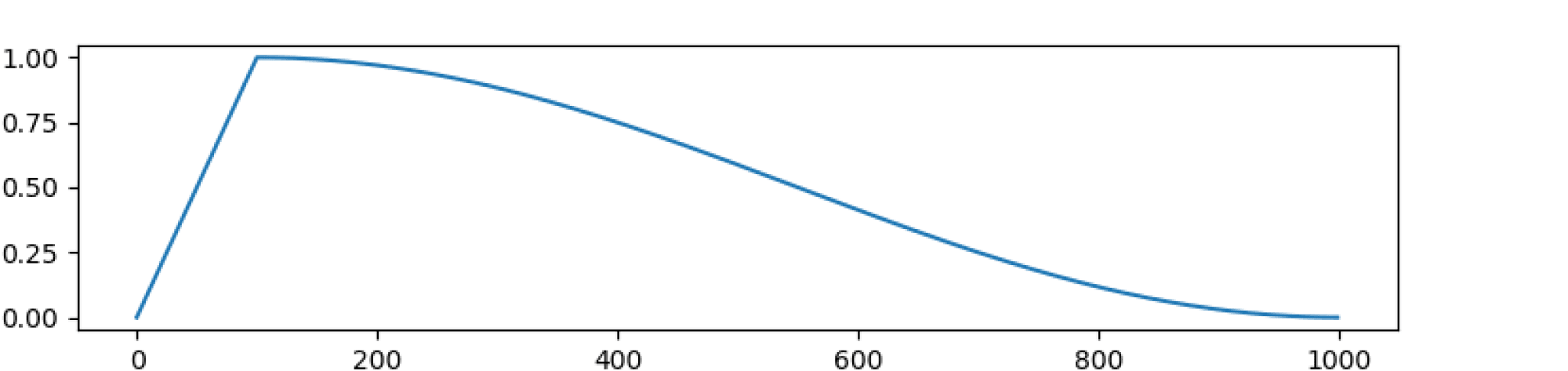
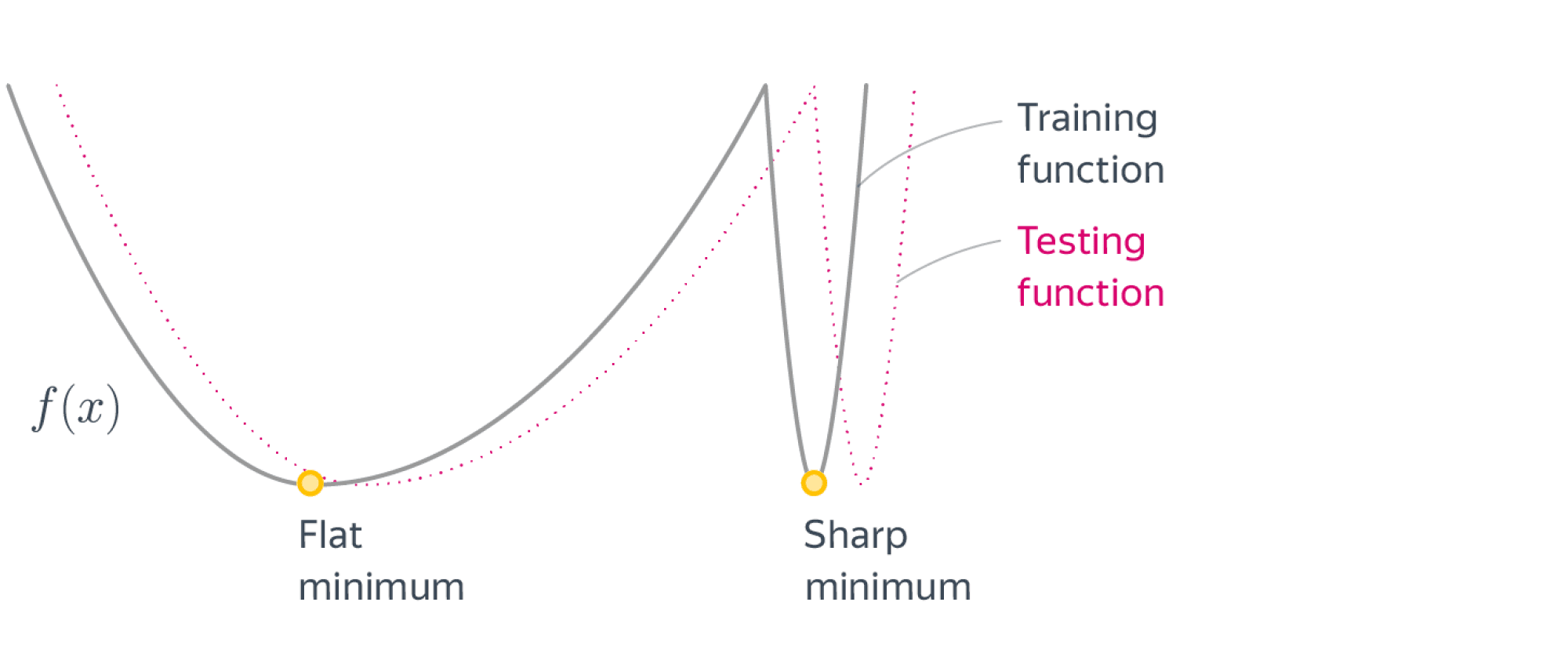
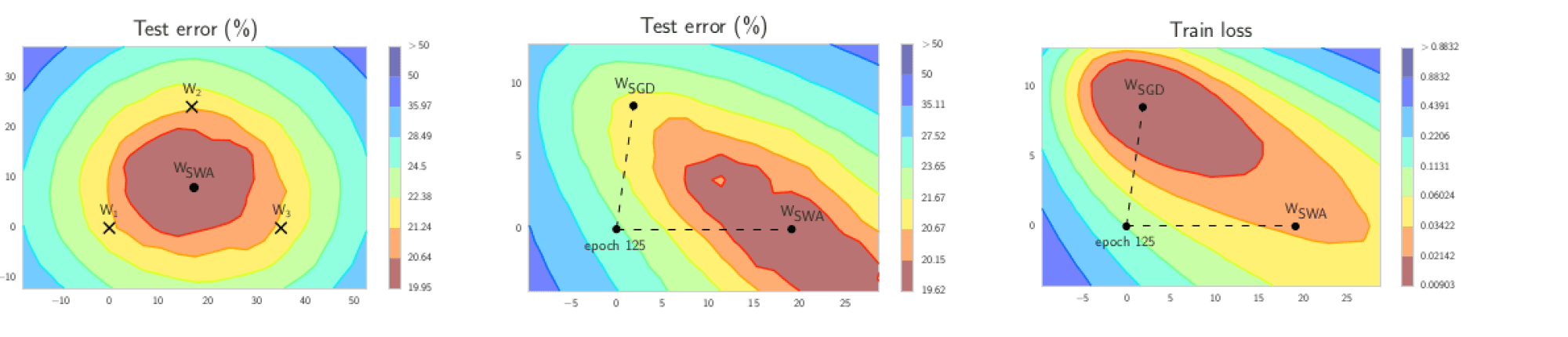





![{displaystyle gamma _{n}={frac {left|left(mathbf {x} _{n}-mathbf {x} _{n-1}right)^{T}left[nabla F(mathbf {x} _{n})-nabla F(mathbf {x} _{n-1})right]right|}{left|nabla F(mathbf {x} _{n})-nabla F(mathbf {x} _{n-1})right|^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4bd0be3d2e50d47f18b4aeae8643e00ff7dd2e9)


![{displaystyle F(mathbf {a} _{n+1})leq F(mathbf {a} _{n})-gamma _{n}|nabla F(mathbf {a} _{n})|_{2}|mathbf {p} _{n}|_{2}left[cos theta _{n}-max _{tin [0,1]}{frac {|nabla F(mathbf {a} _{n}-tgamma _{n}mathbf {p} _{n})-nabla F(mathbf {a} _{n})|_{2}}{|nabla F(mathbf {a} _{n})|_{2}}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1433794e842e36580db8fa219ae5ca650010d6d6)











![{displaystyle {begin{aligned}F(mathbf {x} )&={frac {1}{2}}G^{mathrm {T} }(mathbf {x} )G(mathbf {x} )\&={frac {1}{2}}left[left(3x_{1}-cos(x_{2}x_{3})-{frac {3}{2}}right)^{2}+left(4x_{1}^{2}-625x_{2}^{2}+2x_{2}-1right)^{2}+right.\&{}qquad left.left(exp(-x_{1}x_{2})+20x_{3}+{frac {10pi -3}{3}}right)^{2}right],end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/837d796ffc4f2135bfef2fdd0c94d5c0db358f1d)