Часовая и минутная стрелка онлайн.Угол между ними.
| Час и минута разделенные пробелом |
| Угол между стрелками (градусы) |
Обратимся опять к школьным задачам и задачам на сообразительность. Одной из таких задач является узнать, какой угол образуют между собой минутная и часовая стрелка на механических часах в 16 часов 38 минут, или одна из вариаций — сколько времени будет после начала первых суток, когда часовая и минутная стрелка будут образовывать угол в 70 градусов.
Или в самом общем виде «найдите угол между часовой и минутной стрелкой»(с)
Самый простой вопрос, на который много людей умудряются давать неправильный ответ. Какой угол между часовой и минутной стрелкой на часах в 15 часов 15 минут?
Ответ ноль градусов не является правильным ответом 
Давайте разбираться.
Минутная стрелка за 60 минут совершает полный оборот по циферблату, то есть совершит оборот на 360 градусов. За это же самое время (60 минут) часовая стрелка пройдет путь всего одну двенадцатую часть от окружности, то есть сдвинется на 360/12 = 30 градусов
Давайте считать подробно, какой же угол проходит каждая стрелка от 0 часов и нуля минут?
Насчет минутной все очень просто. Составляем пропорцию минуты относятся к пройденному углу как полный оборот(60 минут) к 360 градусам.
Таким образом пройденный угол минутной стрелкой составит минуты/60*360 = минуты*6
Как результат вывод каждая пройденная минута смещает минутную стрелку на 6 градусов
Отлично! Теперь что насчет часовой. А принцип тот же самый, только надо время (часы и минуты) привести к долям часа.
Например 2 часа 30 минут — это 2.5 часа ( 2 часа и его половинка), 8 часов и 15 минут — это 8.25 ( 8 часов и одна четвертинка часа), 11 часов 45 минут — это 11 часов и три четвертинки часа то есть 8.75)
А дальше все просто такая же пропорция: Час(в виде долей часа) относится пройденному углу как 12 часов ( за 12 часов ведь часовая стрелка опишет весь циферблат) к 360 градусам.
Таким образом пройденный угол часовой стрелкой составит часы( в долях часа)*360.12 = часы*30
И как следствие вывод каждая пройденный час смещает часовую стрелку на 30 градусов
Теперь очень легко посчитать угол между стрелками вычислив разницу между углом минутной и часовой стрелки
угол между стрелками = (час+(минуты /60))*30 -минуты*6
где час+(минуты /60) — это положение часовой стрелки
Таким образом ответ к задаче: какой же угол составят стрелки когда на часах 15 часов 15 минут, будет следующим:
15 часов 15 минут это равноценно положению стрелок в 3 часа и 15 минут и таким образом угол составит (3+15/60)*30-15*6=7.5 градуса
В принцие можно считать и так 15.25*30-15*6=367.5 градуса, просто отсюда убираете полные обороты (360 градусов) и получаем тот же самый результат в 7.5 градуса.
Если же у вас есть потребность перевести время в текст то пожалуйста ознаомтесь с материалом Время (часы, минуты, секунды) прописью, а кому часто приходится работать с временными отрезками, складывать минуты и часы, высчитывая простой или наработку на отказ то стоит перейти сюда Суммирование временных отрезков
По углу между стрелками определить время
| Угол, между минутной и часовой стрелкой |
| Время на циферблате когда будет заданный угол |
Это задача сложнее, так как мы решать будем в общем виде, то есть определять все пары (час и минута) когда они будут образовывать заданный угол.
Итак, напомним. Если время выражено в виде HH:MM (час:минута) то угол между стрелками выражается формулой
((HH+cfrac{MM}{60})30-6MM)
Теперь, если обозначим угол буквой U и перевести все в альтернативный вид, то получим следующую формулу
(U=30HH-cfrac{11MM}{2})
Или избавшись от знаменателя, получаем основную формулу связывающая угол между двумя стрелками, и позициями этих стрелок на циферблате.
(2U=60HH-11MM)
заметьте, что угол может быть и отрицательным, то есть в пределах часа у нас может два раза встречаться один и тот же угол, например угол в 7.5 градуса может быть и в 15 часов 15 минут и 15 часов и 17.72727272 минут
Если нам, как в первой задаче был задан угол, то получаем уравнение с двумя переменными. В принципе оно не решается, если не принять условие что час и минута могут быть только целыми числами.
При таком условии мы получаем классическое диофантово уравнение. Решение которого очень простое. Рассматривать мы их пока не будем, а приведем сразу окончательные формулы
где k — произвольное целое число.
Результат часов естественно берем по модулю 24, а результат минут по модулю 60
Посчитаем все варианты когда часовая и минутная стрелка совпадают? То есть когда угол между ними равен 0 градусов.
Как минимум мы знаем две таких точки 0 часов и 0 минут и 12 часов дня 0 минут. А остальные??
Создадим таблицу, положений стрелок когда угол между ними ноль градусов
| k | Часовая стрелка | Минутная стрелка | Пояснения |
|---|---|---|---|
| 0 | 0 | 0 | то есть ровно полночь |
| 1 | 11 | 60 | то есть 12 часов |
| 2 | 22 | 0 | ОШИБКА!! |
Упс! на третьей строке у нас ошибка в 10 часов никак стрелки не совпадают.Это можно убедится взглянув на циферблат. В чём же дело?? Вроде все правильно считали.
А все дело в том, что в промежутке между 10 и 11 часами, для того что бы минутная и часовая стрелка совпадала, минутная стрелка должна находится где то в дробной части какой то минуты.
Это легко проверить по формуле 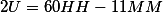
получим, что минутная стрелка будет находится между(!!) делениями 54 и 55 ( совсем точно на позиции 54.545454 минут).
Именно поэтому наши последние формулы не сработали, так как мы подразумевали что часы и минуты числа целые(!).
Задачи, которые встречаются на ЕГЭ
Мы рассмотрим задачи, решения которых есть в интернете, но пойдем другим путем. Возможно это облегчить той части школьников, которые ищут простой и необременительный способ решать задачи.
Ведь чем больше разных вариантов решения задач тем лучше.
Итак, мы знаем только одну формулу 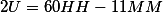
Часы со стрелками показывают 1 час 35 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?
Рассуждения «решателей» на других интернет-ресурсах меня немного утомили и запутали . Вот для таких «утомленных» как я, мы решаем эту задачу по другому.
Определим когда в первом (1) часу минутная и часовая стрелка совпадет (угол 0 градусов)? Подставляем в уравнение изветные числа и получаем
(MM=cfrac{60}{11}=5.45454545)
то есть в 1 час и почти в 5.5 минут. это раньше чем 1 час 35 минут? Да! Отлично, значит этот час мы не учитываем в дальнейших расчетах.
Нам надо найти 10-ое совпадение минутной и часовой стрелки, начинаем анализировать:
в первый раз часовая стрелка будет в 2 часа и сколько то минут,
во второй раз в 3 часа и сколько минут
…
в восьмой раз в 9 часов и сколько то минут
в девятый раз в 10 часов и сколько то минут
в девятый раз в 11 часов и сколько то минут
Теперь осталось найти где будет находится минутная стрелка в 11 часов, так что бы стрелки совпадали
(MM=cfrac{660}{11}=60)
А теперь умножает 10 раз оборота( а это каждый час) на 60 (перведя в минуты) получим 600 минут. и высчитываем разницу между 60 минутами и 35 минутами ( которые были заданы)
Окончательный ответ получили 625 минут.
Что и требовалось доказать. Не надо никаких уравнений, пропорций, ни какая из стрелок с какой скоростью двигалась. Всё это мишура. Достаточно знать одну формулу.
Более интересная и сложная задача звучит так. В 8 часов вечера, угол между часовой и минутной стрелкой составялет 31 градуса . Сколько будет показывать время стрелки, после того как минутная и часовая стрелка образуют прямой угол 5 раз?
Итак в нашей формуле опять известны два из трех параметров 8 и 31 градус. Определяем миунтную стрелку по формуле получим 38 минут.
Когда ближайшее время когда стрелки будут образовывать прямой (90 градусов) угол?
(MM=cfrac{480-180}{11}=27.272727)
(MM=cfrac{480+180}{11}=60)
То есть в 8 часов 27.27272727 минут это первый прямой угол в этом часе и в 8 часов и 60 минут это второй угол в этом часе.
Первый прямой угол уже прошел относительно заданного времени, поэтому его не считаем.
Первый 90 градусов в 8 часов 60 минут ( можно сказать что ровно в 9-00) — раз
в 9 часов и сколько то минут — это два
в 10 часов и сколько минут — это три
еще раз в 10 и сколько минут — это 4-ре, так совпадений в 10 часу два
и в 11 часов и сколько минут это пять.
то есть нам надо посчитать в 11 часу два положения минутной стрелки когда угол равен +90 и -90 градусов. Какое время из этих раньше наступит то и является правильным ответом
Еще проще если мы воспользуемся ботом. Введем 90 градусов и получим следующую таблицу
| Время на циферблате когда будет заданный угол | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
то есть в 11 часо 10.90 минут будет как раз пятый раз когда между часовой и минутной стрелкой вновь образуется прямой угол.
Надеемся данный разбор, поможет Вам как формулировать задачи для учеников, так и легко решать подобные тесты на сообразительность и в ЕГЭ.
Удачи в расчетах!
|
Онлайн калькулятор находит какой угол образует минутная и часовая стрелка часов, калькулятор вычисляет наименьший угол между стрелками, для определения наибольшего угла необходимо от 360 градусов отнять наименьший угол.
Отметка 12 часов — это 0°
1 час — 360°:12 = 30° (градусы часовой стрелки)
1 минута — 360°:60 = 6° (градусы минутной стрелки)
Каждую минуту часовая стрелка смещается на 30°:60 = 0.5°
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
This problem is known as Clock angle problem where we need to find angle between hands of an analog clock at a given time.
Examples:
Input: h = 12:00 m = 30.00 Output: 165 degree Input: h = 3.00 m = 30.00 Output: 75 degree
The idea is to take 12:00 (h = 12, m = 0) as a reference. Following are detailed steps.
1. Calculate the angle made by hour hand with respect to 12:00 in h hours and m minutes.
2. Calculate the angle made by minute hand with respect to 12:00 in h hours and m minutes.
3. The difference between the two angles is the angle between the two hands.
How to calculate the two angles with respect to 12:00?
The minute hand moves 360 degrees in 60 minute(or 6 degrees in one minute) and hour hand moves 360 degrees in 12 hours(or 0.5 degrees in 1 minute). In h hours and m minutes, the minute hand would move (h*60 + m)*6 and hour hand would move (h*60 + m)*0.5.
C++
#include <bits/stdc++.h>
using namespace std;
int min(int x, int y)
{
return (x < y)? x: y;
}
int calcAngle(double h, double m)
{
if (h <0 || m < 0 || h >12 || m > 60)
printf("Wrong input");
if (h == 12) h = 0;
if (m == 60)
{
m = 0;
h += 1;
if(h>12)
h = h-12;
}
float hour_angle = 0.5 * (h * 60 + m);
float minute_angle = 6 * m;
float angle = abs(hour_angle - minute_angle);
angle = min(360 - angle, angle);
return angle;
}
int main()
{
cout << calcAngle(9, 60) << endl;
cout << calcAngle(3, 30) << endl;
return 0;
}
C
#include <stdio.h>
#include <stdlib.h>
int min(int x, int y) { return (x < y)? x: y; }
int calcAngle(double h, double m)
{
if (h <0 || m < 0 || h >12 || m > 60)
printf("Wrong input");
if (h == 12) h = 0;
if (m == 60)
{
m = 0;
h += 1;
if(h>12)
h = h-12;
}
int hour_angle = 0.5 * (h*60 + m);
int minute_angle = 6*m;
int angle = abs(hour_angle - minute_angle);
angle = min(360-angle, angle);
return angle;
}
int main()
{
printf("%d n", calcAngle(9, 60));
printf("%d n", calcAngle(3, 30));
return 0;
}
Java
import java.io.*;
class GFG
{
static int calcAngle(double h, double m)
{
if (h <0 || m < 0 || h >12 || m > 60)
System.out.println("Wrong input");
if (h == 12)
h = 0;
if (m == 60)
{
m = 0;
h += 1;
if(h>12)
h = h-12;
}
int hour_angle = (int)(0.5 * (h*60 + m));
int minute_angle = (int)(6*m);
int angle = Math.abs(hour_angle - minute_angle);
angle = Math.min(360-angle, angle);
return angle;
}
public static void main (String[] args)
{
System.out.println(calcAngle(9, 60)+" degree");
System.out.println(calcAngle(3, 30)+" degree");
}
}
Python3
def calcAngle(h,m):
if (h < 0 or m < 0 or h > 12 or m > 60):
print('Wrong input')
if (h == 12):
h = 0
if (m == 60):
m = 0
h += 1;
if(h>12):
h = h-12;
hour_angle = 0.5 * (h * 60 + m)
minute_angle = 6 * m
angle = abs(hour_angle - minute_angle)
angle = min(360 - angle, angle)
return angle
h = 9
m = 60
print('Angle ', calcAngle(h,m))
C#
using System;
class GFG {
static int calcAngle(double h, double m)
{
if (h < 0 || m < 0 ||
h > 12 || m > 60)
Console.Write("Wrong input");
if (h == 12)
h = 0;
if (m == 60)
{
m = 0;
h += 1;
if(h>12)
h = h-12;
}
int hour_angle = (int)(0.5 * (h * 60 + m));
int minute_angle = (int)(6 * m);
int angle = Math.Abs(hour_angle - minute_angle);
angle = Math.Min(360 - angle, angle);
return angle;
}
public static void Main ()
{
Console.WriteLine(calcAngle(9, 60));
Console.Write(calcAngle(3, 30));
}
}
PHP
<?php
function mintwo($x, $y)
{
return ($x < $y) ?
$x : $y;
}
function calcAngle($h, $m)
{
if ($h <0 || $m < 0 ||
$h >12 || $m > 60)
echo "Wrong input";
if ($h == 12) $h = 0;
if ($m == 60) {
$m = 0;
$h += 1;
if($h>12)
$h = $h-12;
}
$hour_angle = 0.5 *
($h * 60 + $m);
$minute_angle = 6 * $m;
$angle = abs($hour_angle -
$minute_angle);
$angle = min(360 - $angle,
$angle);
return $angle;
}
echo calcAngle(9, 60), "n";
echo calcAngle(3, 30), "n";
?>
Javascript
<script>
function min(x, y)
{
return (x < y)? x: y;
}
function calcAngle(h, m)
{
if (h <0 || m < 0 || h >12 || m > 60)
document.write("Wrong input");
if (h == 12) h = 0;
if (m == 60)
{
m = 0;
h += 1;
if(h>12)
h = h-12;
}
let hour_angle = 0.5 * (h * 60 + m);
let minute_angle = 6 * m;
let angle = Math.abs(hour_angle - minute_angle);
angle = min(360 - angle, angle);
return angle;
}
document.write(calcAngle(9, 60) + "<br>");
document.write(calcAngle(3, 30) + "<br>");
</script>
Time Complexity: O(1)
Auxiliary Space: O(1)
Exercise: Find all times when hour and minute hands get superimposed.
This article is contributed by Ashish Bansal. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above
Last Updated :
14 Jan, 2022
Like Article
Save Article
Можно решить задачу двумя способами.
Первый вариант.
На часовом циферблате полный оборот, это 360°.
И они разделены на 12 частей.
Делим 360:12=30°.
30 градусов приходятся на каждые 5 минут.
25 минут это 5 × 30= 150°.
Можно и по-другому.
Второй способ решения.
360 градусов- это 60 минут.
360:60=6° на одно деление, на 1 минуту.
По условиям задачи, делений 25, поэтому далее умножаем.
6×25=150°
Ответ. На 25 минут циферблата часов приходится 150° из 360°. Столько проходит часовая стрелка за 25 минут.
Проблема угла часов: задано время в hh:mm формате в 24-часовом формате, рассчитайте меньший угол между часовой и минутной стрелками в аналоговых часах.
Например,
Input: 5:30
Output: 15°
Input: 21:00
Output: 90°
Input: 12:00
Output: 0°
Please note that hh:60 should be considered as (hh+1):0
Потренируйтесь в этой проблеме
Идея состоит в том, чтобы учитывать скорость изменения угла в градусах в минуту. Часовая стрелка 12-часовых аналоговых часов поворачивается 360° за 12 часов, а минутная стрелка вращается через 360° через 60 минут. Итак, мы можем вычислить угол в градусах часовой стрелки минутной стрелки отдельно и вернуть их разницу по следующей формуле:
Degree(hh) = H×(360/12) + (M×360)/(12×60)
Degree(mm) = M×(360/60)
Здесь, H это час, и M это минуты после часа. Угол должен быть в градусах и измеряться по часовой стрелке от положения часов на 12 часов. Если угол больше 180°, возьмите его разницу с 360.
Ниже приведена программа на C++, Java и Python, которая демонстрирует это:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
#include <iostream> using namespace std; // Функция для вычисления угла между часовой и минутной стрелками int findAngle(int hh, int mm) { // обработка 24-часовой записи hh = hh % 12; // найти положение часовой стрелки int h = (hh * 360) / 12 + (mm * 360) / (12 * 60); // найти положение минутной стрелки int m = (mm * 360) / (60); // вычисляем разницу углов int angle = abs(h — m); // считаем меньший угол и возвращаем его if (angle > 180) { angle = 360 — angle; } return angle; } // Проблема угла часов int main() { int hh = 5; int mm = 30; cout << findAngle(hh, mm); return 0; } |
Скачать Выполнить код
результат:
15
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
class Main { // Функция для вычисления угла между часовой и минутной стрелками public static int findAngle(int hh, int mm) { // обработка 24-часовой записи hh = hh % 12; // найти положение часовой стрелки int h = (hh * 360) / 12 + (mm * 360) / (12 * 60); // найти положение минутной стрелки int m = (mm * 360) / (60); // вычисляем разницу углов int angle = Math.abs(h — m); // считаем меньший угол и возвращаем его if (angle > 180) { angle = 360 — angle; } return angle; } // Проблема угла часов public static void main(String[] args) { int hh = 5; int mm = 30; System.out.println(findAngle(hh, mm)); } } |
Скачать Выполнить код
результат:
15
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# Функция для вычисления угла между часовой и минутной стрелками def findAngle(hh, mm): # обрабатывает 24-часовую запись hh = hh % 12 # найти положение часовой стрелки h = (hh * 360) // 12 + (mm * 360) // (12 * 60) # найти положение минутной стрелки m = (mm * 360) // (60) # рассчитать разницу углов angle = abs(h — m) # считает меньший угол и возвращает его if angle > 180: angle = 360 — angle return angle # Проблема с углом синхронизации if __name__ == ‘__main__’: hh = 5 mm = 30 print(findAngle(hh, mm)) |
Скачать Выполнить код
результат:
15
Использованная литература: Проблема угла наклона часов — Википедия
Спасибо за чтение.
Пожалуйста, используйте наш онлайн-компилятор размещать код в комментариях, используя C, C++, Java, Python, JavaScript, C#, PHP и многие другие популярные языки программирования.
Как мы? Порекомендуйте нас своим друзьям и помогите нам расти. Удачного кодирования 

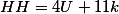
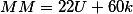
mod24)
mod60)
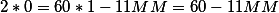
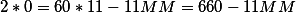
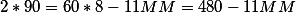
=60*8-11MM=480-11MM)