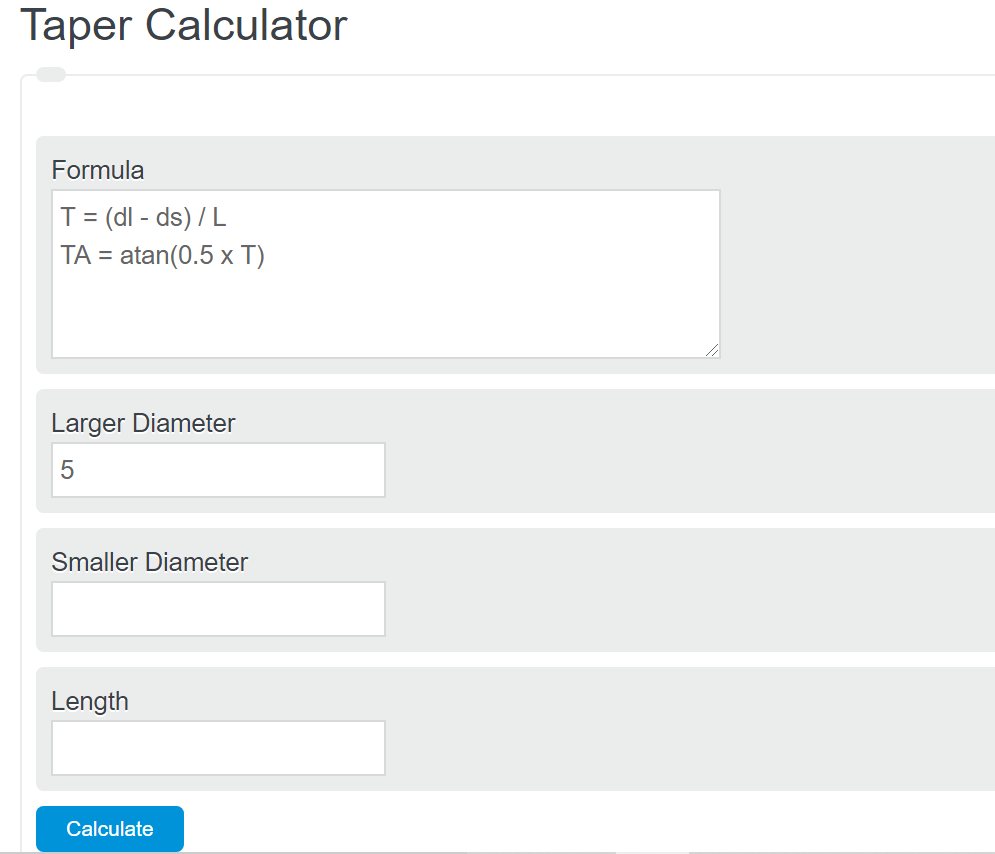
Enter the larger diameter, smaller diameter, and length of taper into the calculator. The calculator will evaluate and display the total taper and taper angle. This calculator can also determine any of the variables in the below formulas if the other values are known.
- Inscribe Angle Calculator
- Reference Angle Calculator
- Angle of Depression Calculator
Taper Angle Formula
The following equations are used to calculate the overall taper and taper angle.
T = (dl – ds) / L
TA = atan(0.5 x T)
- Where T is the taper
- dl is the larger diameter
- ds is the smaller diameter
- TA is the taper angle
- L is the length
To calculate the taper length, subtract the smaller diameter from the larger diameter, then divide by the overall length.
Taper Definition
A taper is typically referred to as a section of a pipe that reduces in overall diameter over a certain length. That reduction in size is the taper, and the rate at which it reduces over the length is considered the taper angle.
Taper Example
How to calculate a taper?
The first step in determining a taper is to determine the larger diameter of the section of a pipe.
For this example problem, the larger diameter is found to be 10 inches.
Next, the small diameter of the taper must be measured.
In this case, the small diameter is found to be 5 inches.
Next, determine the total length of the section from the small diameter to the larger diameter.
In this problem, the total length is found to be 3 inches.
Finally, calculate the taper using the formula above:
T = (dl – ds) / L
T = (10-5) / 3
T = 1.667 inches of taper
FAQ
What is a taper?
A taper is a section of a pipe that reduces in diameter over its length.

Конусность — это отношение разности диаметров к длине(высоте) конуса. Например,
конусноть 1:10 означает, что D — d = 1, а L(h) = 10. А конусноть 7:24 означает, что D — d = 7, а L(h) = 24.

Конус — геометрическое тело, которое получается путем вращением прямой линии (образующей конуса),
расположенной под углом к оси вращения.
Конусность измерить нельзя. Измеряют угол, который соответсвует конкретной конусности. Например,
угол конусности 1 : 10 будет равен 5° 43′ 29.3″ (5 градусам 43 минутам 29.3 секундам). 1 угол содержит 60 минут, а 1 минута содержит 60 секунд.
На производстве углы измеряют инструментом, который называется угломер.
С помощью калькулятора на данной странице вы сможете рассчитать любую конусность.
Часто это бывает нужно, когда на чертеже не хватает размеров, а чертеж не в векторном формате.
Так же, например, необходима бывает индентификация конусности на существующем изделии (штифт, инструмент и др.).
Нормальные конусности представлены в ГОСТ 8593-81.
Инструментальные конусности представлены в ГОСТ 25557-2006. Среди инструментальных конусов
выделяются конуса Морзе. В российских стандартах обозначаются КМ0-КМ7 (КМ7 не рекомендован к применению). В немецких стандартах
МК0-МК7. В английских стандартах МТ0-МТ7.
При расчете используются следующие буквенные обозначения:
- D — наибольшее основание конуса;
- d — наименьшее основание конуса;
- L — длина конуса;
- α — угол конуса;
- α/2- угол уклона.
| Конусность | Угол конуса | Угол уклона |
|---|---|---|
| 1 : 500 | 0° 6′ 52.5″ | 0° 3′ 25.25″ |
| 1 : 200 | 0° 17′ 11.3″ | 0° 8′ 35.65″ |
| 1 : 100 | 0° 34′ 22.6″ | 0° 17′ 11.3″ |
| 1 : 50 | 1° 8′ 45.2″ | 0° 34′ 22.6″ |
| 1 : 30 | 1° 54′ 34.9″ | 0° 57′ 17.45″ |
| 1 : 20 | 2° 51′ 51.1″ | 1° 25′ 55.55″ |
| 1 : 15 | 3° 49′ 5.9″ | 1° 54′ 32.95″ |
| 1 : 12 | 4° 46′ 18.8″ | 2° 23′ 9.4″ |
| 1 : 10 | 5° 43′ 29.3″ | 2° 51′ 44.65″ |
| 1 : 8 | 7° 9′ 9.6″ | 3° 34′ 34.8″ |
| 1 : 7 | 8° 10′ 16.4″ | 4° 5′ 8.2″ |
| 1 : 6 | 9° 31′ 38.2″ | 4° 45′ 49.1″ |
| 1 : 5 | 11° 25′ 16.3″ | 5° 42′ 38.15″ |
| 1 : 4 | 14° 15′ 0.1″ | 7° 7′ 30.05″ |
| 1 : 3 | 18° 55′ 28.7″ | 9° 27′ 44.35″ |
| 1 : 1.866025 | 30° 0′ 0″ | 15° 0′ 0″ |
| 1 : 1.207107 | 45° 0′ 0″ | 22° 30′ 0″ |
| 1 : 0.866025 | 60° 0′ 0″ | 30° 0′ 0″ |
| 1 : 0.651613 | 75° 0′ 0″ | 37° 30′ 0″ |
| 1 : 0.500000 | 90° 0′ 0″ | 45° 0′ 0″ |
| 1 : 0.288675 | 120° 0′ 0″ | 60° 0′ 0″ |
| Метрический конус | ||
| 1 : 20 | 2° 51′ 51.1″ | 1° 25′ 55.55″ |
| Конус Морзе №0 | ||
| 1 : 19.212 | 1° 29′ 27″ | 0° 44′ 43.5″ |
| Конус Морзе №1 | ||
| 1 : 20.047 | 1° 25′ 43″ | 0° 42′ 51.5″ |
| Конус Морзе №2 | ||
| 1 : 20.020 | 1° 25′ 50″ | 0° 42′ 55″ |
| Конус Морзе №3 | ||
| 1 : 19.992 | 1° 26′ 16″ | 0° 43′ 8″ |
| Конус Морзе №4 | ||
| 1 : 19.254 | 1° 29′ 15″ | 0° 44′ 37.5″ |
| Конус Морзе №5 | ||
| 1 : 19.002 | 1° 30′ 26″ | 0° 45′ 13″ |
| Конус Морзе №6 | ||
| 1 : 19.18 | 1° 29′ 36″ | 0° 44′ 48″ |
| Конусность 7:24 | ||
| 1 : 3.42857143 | 16° 35′ 39″ | 8° 17′ 49″ |
| Конусность резьб конических | ||
| 1 : 16 | 3° 34′ 48″ | 1° 47′ 24″ |
Конус 1:500 и 1:200 применяют для изготовления крепежных деталей для неразъемных
соединений, подвергающихся вибрациям и ударной переменной нагрузке, конических оправок.
Конус 1:100 применяют для изготовления крепежных деталей для неразъемных
соединений, подвергающихся вибрациям и спокойной переменной нагрузке, клиновых шпонок, конических оправок.
Конус 1:50 применяют для изготовления конических штифтов, установочных шпилек,
насадных рукояток.
Конус 1:30 применяют для изготовления конусов шеек шпинделей.
Конус 1:20 применяют для изготовления метрических конусов в шпинделях станков, оправок.
Конус 1:16 применяют для изготовления конических резьбовых соединений метрических и дюймовых.
Конус 1:15 применяют для изготовления конических соединений деталей при осевых нагрузках,
соединений поршней со штоками.
Конус 1:12 применяют для изготовления конических закрепительных втолок шарико- и
роликоподшипников.
Конус 1:10 применяют для изготовления конических соединений деталей при нагрузках,
перпендикулярных и параллельных оси, концов валов электрических и других машин, регулируемых
втулок подшипников шпинделей.
Конус 1:7 применяют для кранов в арматуростроении.
Конус 1:5 и 1:3 применяют для изготовления легкоразъемных конических
соединений при нагрузках, перпендикулярных оси, конических фрикционных муфт.
Конус 1:1.5 применяют для изготовления тяжелых винтовых трубных соединений с коническим
уплотнением.
Конус 30° применяют для изготовления фрикционных муфт приводов, зажимных цанг,
головок шинных болтов.
Конус 60° применяют для изготовления центровых отверстий.
Конус 75° применяют для изготовления внутренних конусов нажимных гаек в соединениях труб
высокого давления, наружных центров инструментов диаметром до 10 мм.
Конус 90° применяют для изготовления концов обрабатываемых валов и валиков,
конусов вентилей и клапанов, центровых отверстий для тяжелых работ, потайных головок заклепок диаметром
1 — 10 мм.
Конус 100° применяют для изготовления винтов по дереву.
Конус 120° применяют для изготовления потайных головок заклепок диаметром
2 — 5 мм, внутренних фаскок резьбовых отверстий, конусов под набивку сальников, дроссельных клапанов.

Значок конуса обязательно должен быть направлен в сторону уменьшения диаметра.
Посмотреть какие настройки токарного станка для обработки конуса существуют
можно на этой странице .
starik12 Вы вообще умеете пользоваться таблицами Брадиса? Судя по тому, что вам втолковывают уже несколько дней вы первый раз о них слышали. А зря, дюже полезная книжечка.
1. Берём формулу расчёта которую вам уже дали в 5 или 9 сообщении.
2. Считаем и получаем данные, что tg@= 0.125
3 Берём в руки таблицу Брадиса и смотрим на страницу Тангенсы.
4 Ближайшие к вашим данным это цифры 0.1246 и 0.1263 стоящие в строке напротив левого вертикального столбца где написан угол 7 градусов, записываем его.
Далее высчитываем минуты.
5. До вашего значения 0.1250 первому числу в пункте 4 не хватает 0.0004, а второе больше на 0.0013.
Смотрим на крайние правые колонки. Напротив вашей строки видим цифры 3 6 9. Это поправки на которые надо надбавить или убавить данные таблицы, что бы они совпадали с вашим числом (0.1250) и обозначают они четвёртую цифру после запятой. Наиболее подходит поправка 3 как наиболее близкая к числу 0.1246.
6. Смотрим вертикально вверх от числа 0.1246, видим цифру 6. Это ваши минуты. Запимываем. Далее воспользуемся поправкой 3 про которую я писал в 4 пункте. Смотрим вверх от нее и видим цифру 1. Это число надо прибавить к вашим минутам. Получаем 6+1=7минут. Записываем к вашим градусам.
7. Далее высчитываем секунды. До ваших данных 0.1250 даже с учётом поправок не хватает 0.0001.
Смотрим на поправки. Поправка 4 составляют 1/3 часть между поправками 3 и 6. Смотрим вверх. Там поправка 3 означает 1 минуту, а поправка 6 означает 2 минуты значит поправка 4 означает на 1/3 больше 1минуты, что в конечном итоге составляет 20 секунд.
8. А вот теперь смотрим на бумажку и пишем данные полученные в пунктах 4, 6, и 7. Получаем, что данный ваш угол равен 7 градусов 7 минут 20 секунд.
Потом после того как вы выставите можно проверить способом который предложил Alex_IZA. Я так всегда делаю. Пару тончайших рисок на цилиндрической поверхности и часиками можно спокойно проверить.
Ужас, писал 15 минут, хотя считается это дело в течение 10 -15 секунд.
Содержание
- 1. Понятие о конусе и его элементах
- 2. Способы получения конических поверхностей на токарном станке
- 3. Обработка конических поверхностей поворотом верхней части суппорта
- 4. Обработка конических поверхностей способом поперечного смещения корпуса задней бабки
- 5. Обработка конических поверхностей с применением конусной линейки
- 6. Обработка конических поверхностей широким резцом
- 7. Растачивание и развертывание конических отверстий
- 8. Режимы резания при обработке отверстий коническими развертками
- 9. Измерение конических поверхностей
- 10. Брак при обработке конических поверхностей и меры его предупреждения
- Рекомендованные сообщения
- Создайте аккаунт или войдите в него для комментирования
- Создать аккаунт
- Войти
- Сейчас на странице 0 пользователей
Источник: ГОСТ 8593-81
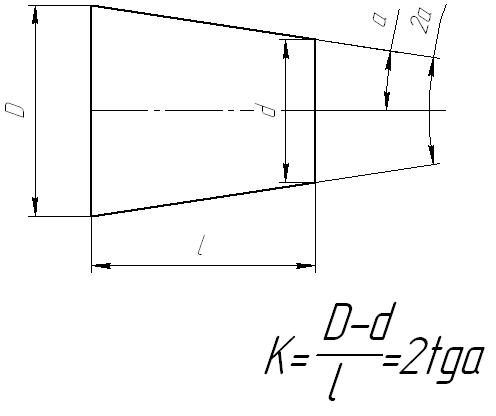
Конусность К есть отношение разности диаметров двух поперечных сечений конуса к расстоянию между ними.
Уклон «i» есть отношение разности размеров двух поперечных сечений к расстоянию между ними.
В машиностроении, наряду с цилиндрическими, широко применяются детали с коническими поверхностями в виде наружных конусов или в виде конических отверстий. Например, центр токарного станка имеет два наружных конуса, из которых один служит для установки и закрепления его в коническом отверстии шпинделя; наружный конус для установки и закрепления имеют также сверло, зенкер, развертка и т. д. Переходная втулка для закрепления сверл с коническим хвостовиком имеет наружный конус и коническое отверстие
1. Понятие о конусе и его элементах
Элементы конуса . Если вращать прямоугольный треугольник АБВ вокруг катета АБ (рис. 202, а), то образуется тело АВГ, называемое полным конусом. Линия АБ называется осью или высотой конуса, линия АВ — образующей конуса. Точка А является вершиной конуса.
При вращении катета БВ вокруг оси АБ образуется поверхность круга, называемая основанием конуса.
Угол ВАГ между боковыми сторонами АВ и АГ называется углом конуса и обозначается 2α. Половина этого угла, образуемая боковой стороной АГ и осью АБ, называется углом уклона конуса и обозначается α. Углы выражаются в градусах, минутах и секундах.
Если от полного конуса отрезать его верхнюю часть плоскостью, параллельной егооснованию (рис. 202, б), то получим тело, называемое усеченным конусом. Оно имеет два основания верхнее и нижнее. Расстояние OO1 по оси между основаниями называется высотой усеченного конуса. Так как в машиностроении большей частью приходится иметь дело с частями конусов, т. е. усеченными конусами, то обычно их просто называют конусами; дальше будем называть все конические поверхности конусами.
Связь между элементами конуса. На чертеже указывают обычно три основных размера конуса: больший диаметр D, меньший — d и высоту конуса l (рис. 203).
Иногда на чертеже указывается только один из диаметров конуса, например, больший D, высота конуса l и так называемая конусность. Конусностью называется отношение разности диаметров конуса к его длине. Обозначим конусность буквой K, тогда
Если конус имеет размеры: D =80 мм, d = 70 мм и l = 100 мм, то согласно формуле (10):
Это значит, что на длине 10 мм диаметр конуса уменьшается на 1 мм или на каждый миллиметр длины конуса разница между его диаметрами изменяется на
Иногда на чертеже вместо угла конуса указывается уклон конуса. Уклон конуса показывает, в какой мере отклоняется образующая конуса от его оси.
Уклон конуса определяется по формуле
где tg α — уклон конуса;
D — диаметр большого основания конуса в мм;
d — диаметр малого основания конуса в мм;
l — высота конуса в мм.
Пользуясь формулой (11), можно при помощи тригонометрических таблиц определить угол а уклона конуса.
Уклон конуса и конусность обычно выражают простой дробью, например: 1 : 10; 1 : 50, или десятичной дробью, например, 0,1; 0,05; 0,02 и т. д.
2. Способы получения конических поверхностей на токарном станке
На токарном станке обработка конических поверхностей производится одним из следующих способов:
а) поворотом верхней части суппорта;
б) поперечным смещением корпуса задней бабки;
в) с помощью конусной линейки;
г) с помощью широкого резца.
3. Обработка конических поверхностей поворотом верхней части суппорта
При изготовлении на токарном станке коротких наружных и внутренних конических поверхностей с большим углом уклона нужно повернуть верхнюю часть суппорта относительно оси станка под углом α уклона конуса (см. рис. 204). При таком способе работы подачу можно производить только от руки, вращая рукоятку ходового винта верхней части суппорта, и лишь в наиболее современных токарных станках имеется механическая подача верхней части суппорта.
Для установки верхней части суппорта 1 на требуемый угол можно использовать деления, нанесенные на фланце 2 поворотной части суппорта (рис. 204). Если угол α уклона конуса задан по чертежу, то верхнюю часть суппорта повертывают вместе с его поворотной частью на требуемое число делений, обозначающих градусы. Число делений отсчитывают относительно риски, нанесенной на нижней части суппорта.
Если на чертеже угол α не дан, а указаны больший и меньший диаметры конуса и длина его конической части, то величину угла поворота суппорта определяют по формуле (11)
Способ обтачивания конических поверхностей поворотом верхней части суппорта имеет следующие недостатки: он допускает обычно применение только ручной подачи, что отражается на производительности труда и чистоте обработанной поверхности; позволяет обтачивать сравнительно короткие конические поверхности, ограниченные длиной хода верхней части суппорта.
4. Обработка конических поверхностей способом поперечного смещения корпуса задней бабки
Для получения конической поверхности на токарном станке необходимо при вращении заготовки вершину резца перемещать не параллельно, а под некоторым углом к оси центров. Этот угол должен равняться углу α уклона конуса. Наиболее простой способ получения угла между осью центров и направлением подачи — сместить линию центров, сдвинув задний центр в поперечном направлении. Путем смещения заднего центра в сторону резца (на себя) в результате обтачивания получают конус, у которого большее основание направлено в сторону передней бабки; при смещении заднего центра в противоположную сторону, т. е. от резца (от себя), большее основание конуса окажется со стороны задней бабки (рис. 205).
Смещение корпуса задней бабки определяют по формуле
где S — смещение корпуса задней бабки от оси шпинделя передней бабки в мм;
D — диаметр большого основания конуса в мм;
d — диаметр малого основания конуса в мм;
L — длина всей детали или расстояние между центрами в мм;
l — длина конической части детали в мм.
Смещение корпуса задней бабки производят, используя деления 1 (рис 206), нанесенные на торце опорной плиты, и риску 2 на торце корпуса задней бабки.
Если на торце плиты делений нет, то смещают корпус задней бабки, пользуясь измерительной линейкой, как показано на рис. 207.
Преимущество обработки конических поверхностей путем смещения корпуса задней бабки заключается в том, что этим способом можно обтачивать конусы большой длины и вести обтачивание с механической подачей.
Недостатки этого способа: невозможность растачивать конические отверстия; потеря времени на перестановку задней бабки; возможность обрабатывать лишь пологие конусы; перекос центров в центровых отверстиях, что приводит к быстрому и неравномерному износу центров и центровых отверстий и служит причиной брака при вторичной установке детали в этих же центровых отверстиях.
Неравномерного износа центровых отверстий можно избежать, если вместо обычного применять специальный шаровой центр (рис. 208). Такие центры используют преимущественно при обработке точных конусов.
5. Обработка конических поверхностей с применением конусной линейки
Для обработки конических поверхностей с углом уклона а до 10—12° современные токарные станки обычно имеют особое приспособление, называемое конусной линейкой. Схема обработки конуса с применением конусной линейки приводится на рис. 209.
К станине станка прикреплена плита 11, на которой установлена конусная линейка 9. Линейку можно поворачивать вокруг пальца 8 под требуемым углом а к оси обрабатываемой детали. Для закрепления линейки в требуемом положении служат два болта 4 и 10. По линейке свободно скользит ползун 7, соединяющийся с нижней поперечной частью 12 суппорта при помощи тяги 5 и зажима 6. Чтобы эта часть суппорта могла свободно скользить по направляющим, ее отсоединяют от каретки 3, вывинчивая поперечный винт или отсоединяя от суппорта его гайку.
Если сообщить каретке продольную подачу, то ползун 7, захватываемый тягой 5, начнет перемещаться вдоль линейки 9. Так как ползун скреплен с поперечными салазками суппорта, то они вместе с резцом будут перемещаться параллельно линейке 9. Благодаря этому резец будет обрабатывать коническую поверхность с углом уклона, равным углу α поворота конусной линейки.
После каждого прохода резец устанавливают на глубину резания с помощью рукоятки 1 верхней части 2 суппорта. Эта часть суппорта должна быть повернута на 90° относительно нормального положения, т. е. так, как это показано на рис. 209.
Если даны диаметры оснований конуса D и d и его длина l, то угол поворота линейки можно найти по формуле (11).
Подсчитав величину tg α, легко определить значение угла α по таблице тангенсов.
Применение конусной линейки имеет ряд преимуществ:
1) наладка линейки удобна и производится быстро;
2) при переходе к обработке конусов не требуется нарушать нормальную наладку станка, т. е. не нужно смещать корпус задней бабки; центры станка остаются в нормальном положении, т. е. на одной оси, благодаря чему центровые отверстия в детали и центры станка не срабатываются;
3) при помощи конусной линейки можно не только обтачивать наружные конические поверхности, но и растачивать конические отверстия;
4) возможна работа е продольным самоходом, что увеличивает производительность труда и улучшает качество обработки.
Недостатком конусной линейки является необходимость отсоединять салазки суппорта от винта поперечной подачи. Этот недостаток устранен в конструкции некоторых токарных станков, у которых винт не связан жестко со своим маховичком и зубчатыми колесами поперечного самохода.
6. Обработка конических поверхностей широким резцом
Обработку конических поверхностей (наружных и внутренних) с небольшой длиной конуса можно производить широким резцом с углом в плане, соответствующим углу α уклона конуса (рис. 210). Подача резца может быть продольная и поперечная.
Однако использование широкого резца на обычных станках возможно только при длине конуса, не превышающей примерно 20 мм. Применять более широкие резцы можно лишь на особо жестких станках и деталях, если это не вызывает вибрации резца и обрабатываемой детали.
7. Растачивание и развертывание конических отверстий
Обработка конических отверстий является одной из наиболее трудных токарных работ; она значительно труднее, чем обработка наружных конусов.
Обработку конических отверстий на токарных станках в большинстве случаев производят растачиванием резцом с поворотом верхней части суппорта и реже с помощью конусной линейки. Все подсчеты, связанные с поворотом верхней части суппорта или конусной линейки, выполняются так же, как при обтачивании наружных конических поверхностей.
Если отверстие должно быть в сплошном материале, то сначала сверлят цилиндрическое отверстие, которое затем растачивают резцом на конус или обрабатывают коническими зенкерами и развертками.
Чтобы ускорить растачивание или развертывание, следует предварительно просверлить отверстие сверлом, диаметр d, которого на 1—2 мм меньше диаметра малого основания конуса (рис. 211, а). После этого рассверливают отверстие одним (рис. 211, б) или двумя (рис. 211, в) сверлами для получения ступеней.
После чистового растачивания конуса его развертывают конической разверткой соответствующей конусности. Для конусов с небольшой конусностью выгоднее производить обработку конических отверстий непосредственно после сверления набором специальных разверток, как показано на рис. 212.
8. Режимы резания при обработке отверстий коническими развертками
Конические развертки работают в более тяжелых условиях, чем цилиндрические: в то время как цилиндрические развертки снимают незначительный припуск небольшими режущими кромками, конические развертки режут всей длиной их режущих кромок, расположенных на образующей конуса. Поэтому при работе коническими развертками применяют подачи и скорости резания меньше, чем при работе цилиндрическими развертками.
При обработке отверстий коническими развертками подачу производят вручную, вращая маховичок задней бабки. Необходимо следить за тем, чтобы пиноль задней бабки перемещалась равномерно.
Подачи при развертывании стали 0,1—0,2 мм/об, при развертывании чугуна 0,2—0,4 мм/об.
Скорость резания при развертывании конических отверстий развертками из быстрорежущей стали 6—10 м/мин.
Для облегчения работы конических разверток и получения чистой и гладкой поверхности следует применять охлаждение. При обработке стали и чугуна применяют эмульсию или сульфофрезол.
9. Измерение конических поверхностей
Поверхности конусов проверяют шаблонами и калибрами; измерение и одновременно проверку углов конуса производят угломерами. На рис. 213 показан способ проверки конуса с помощью шаблона.
Наружные и внутренние углы различных деталей можно измерять универсальным угломером (рис. 214). Он состоит из основания 1, На котором на дуге 130 нанесена основная шкала. С основанием 1 жестко скреплена линейка 5. По дуге основания перемещается сектор 4, несущий нониус 3. К сектору 4 посредством державки 7 может быть прикреплен угольник 2, в котором, в свою очередь, закрепляется съемная линейка 5. Угольник 2 и съемная линейка 5 имеют возможность перемещаться по грани сектора 4.
Путем различных комбинаций в установке измерительных деталей угломера можно производить измерение углов от 0 до 320°. Величина отсчета по нониусу 2′. Отсчет, полученный при измерении углов, производится по шкале и нониусу (рис. 215) следующим образом: нулевой штрих нониуса показывает число градусов, а штрих нониуса, совпадающий со штрихом шкалы основания, — число минут. На рис. 215 со штрихом шкалы основания совпадает 11-й штрих нониуса, что означает 2’Х 11 = 22′. Следовательно, угол в данном случае равен 76°22′.
На рис. 216 показаны комбинации измерительных деталей универсального угломера, позволяющие производить измерение различных углов от 0 до 320°.
Для более точной проверки конусов в серийном производстве применяют специальные калибры. На рис. 217, а показан кониче-ский калибр-втулка для проверки наружных конусов, а на рис. 217, б—конический калибр-пробка для проверки конических отверстий.
На калибрах делаются уступы 1 и 2 на торцах или наносятся риски 3, служащие для определения точности проверяемых поверхностей.
На. рис. 218 приводится пример проверки конического отверстия калибром-пробкой.
Для проверки отверстия калибр (см. рис. 218), имеющий уступ 1 на определенном расстоянии от торца 2 и две риски 3, вводят с легким нажимом в отверстие и проверяют, нет ли качания калибра в отверстии. Отсутствие качания показывает, что угол конуса правилен. Убедившись, что угол конуса правилен, приступают к проверке его размера. Для этого наблюдают, до какого места калибр войдет в проверяемую деталь. Если конец конуса детали совпадает с левым торцом уступа 1 или с одной из рисок 3 или находится между рисками, то размеры конуса правильны. Но может случиться, что калибр войдет в деталь настолько глубоко, что обе риски 3 войдут в отверстие или оба торца уступа 1 выйдут из него наружу. Это показывает, что диаметр отверстия больше заданного. Если, наоборот, обе риски окажутся вне отверстия или ни один из торцов уступа не выйдет из него, то диаметр отверстия меньше требуемого.
Для точной проверки конусности применяют следующий способ. На измеряемой поверхности детали или калибра проводят мелом или карандашом две-три линии вдоль образующей конуса, затем вставляют или надевают калибр на деталь и повертывают его на часть оборота. Если линии сотрутся неравномерно, это значит, что конус детали обработан неточно и необходимо его исправить. Стирание линий по концам калибра говорит о неправильной конусности; стирание линий в средней части калибра показывает, что конус имеет небольшую вогнутость, причиной чего обычно является неточное расположение вершины резца по высоте центров. Вместо меловых линий можно нанести на всю коническую поверхность детали или калибра тонкий слой специальной краски (синьки). Такой способ дает большую точность измерения.
10. Брак при обработке конических поверхностей и меры его предупреждения
При обработке конических поверхностей, помимо упомянутых видов брака для цилиндрических поверхностей, дополнительно возможны следующие виды брака:
1) неправильная конусность;
2) отклонения в размерах конуса;
3) отклонения в размерах диаметров оснований при правильной конусности;
4) непрямолинейность образующей конической поверхности.
1. Неправильная конусность получается главным образом вследствие неточного смещения корпуса задней бабки, неточного поворота верхней части суппорта, неправильной установки конусной линейки, неправильной заточки или установки широкого резца. Следовательно, точной установкой корпуса задней бабки, верхней части суппорта или конусной линейки перед началом обработки можно брак предупредить. Этот вид брака исправим только в том случае, если ошибка во всей длине конуса направлена в тело детали, т. е. все диаметры у втулки меньше, а у конического стержня больше требуемых.
2. Неправильный размер конуса при правильном угле его, т. е. неправильная величина диаметров по всей длине конуса, получается, если снято недостаточно или слишком много материала. Предупредить брак можно только внимательной установкой глубины резания по лимбу на чистовых проходах. Брак исправим, если снято недостаточно материала.
3. Может получиться, что при правильной конусности и точных размерах одного конца конуса диаметр второго конца неправилен. Единственной причиной является несоблюдение требуемой длины всего конического участка детали. Брак исправим, если деталь излишне длинна. Чтобы избежать этого вида брака, необходимо перед обработкой конуса тщательно проверить его длину.
4. Непрямолинейность образующей обрабатываемого конуса получается при установке резца выше (рис. 219, б) или ниже (рис. 219, в) центра (на этих рисунках для большей наглядности искажения образующей конуса показаны в сильно преувеличенном виде). Таким образом, и этот вид брака является результатом невнимательной работы токаря.
Автор: starik12, 30 марта 2012 в Общий
Рекомендованные сообщения
Создайте аккаунт или войдите в него для комментирования
Вы должны быть пользователем, чтобы оставить комментарий
Создать аккаунт
Зарегистрируйтесь для получения аккаунта. Это просто!
Войти
Уже зарегистрированы? Войдите здесь.
Сейчас на странице 0 пользователей
Нет пользователей, просматривающих эту страницу.
Калькулятор и формула для вычисления уклона конуса детали.
Уклон конуса может быть определен как отношение разности наибольшего диаметра конуса и наименьшего диаметра конуса к двойной длине конуса, тогда формула для определения уклона конуса детали будет иметь нижеследующий вид:
Также уклон конуса детали можно вычислить как половину конусности детали, такая формула будет следующей:
Либо уклон конуса можно рассчитать как тангенс угла наклона конуса по нижеследующей формуле:
Для определения уклона конуса необходимо ввести значения наибольшего диаметра конуса, наименьшего диаметра конуса, длины конуса и нажать кнопку «ВЫЧИСЛИТЬ.»
Результатом вычисления будет значение уклона конуса.
При проведении инженерных и других расчетах, а также работе с инженерной графикой и создании чертежей приходится создавать уклон. Конусность получила весьма широкое распространение, она применяется при изготовлении самых различных деталей. Показатель конусности рассчитывается в большинстве случаев при создании деталей, которые получили широкое распространение в сфере машиностроения. Рассмотрим основные параметры, особенности начертания и многие другие моменты подробнее.
Фигура конус
Чтобы понять, как найти образующую конуса, следует дать представление об этой фигуре. Круглым прямым конусом называют фигуру вращения прямоугольного треугольника вокруг одного из его катетов. Рисунок ниже демонстрирует процесс вращения.
Вам будет интересно:Развивающая функция обучения: цель, основные принципы
Полученная пространственная фигура имеет следующие характеристики:
- Сторона AB треугольника является высотой h конуса. Она лежит на оси вращения фигуры.
- Сторона AC треугольника — это радиус r конуса. Круг, который описывает этот радиус, называется основанием фигуры.
- Сторона CB треугольника для конуса является его образующей, или генератрисой. Это название она получила за то, что в процессе вращения она описывает коническую поверхность.
- Вершина B треугольника — это вершина конуса.
Заметим, что высота фигуры пересекает круглое основание в его центре. Это является достаточным условием, чтобы считать конус прямым.
Размеры и допуски углов наружных и внутренних конусов
* Размер для справок.
** Z — базорасстояние конуса задается в стандартах на конкретную продукцию
1 — основная плоскость; 2 — базовая плоскость
| Обозначения конусов |
D | d | Lрасч | Допуск угла, мкм,
конуса ATDпо ГОСТ 8908 |
||||
| 3 | 4 | 5 | 6 | 7 | ||||
| 30 | 31,75 | 17,750 | 48 | 2,5 | 4 | 6 | 10 | 15 |
| 35 | 38,10 | 21,767 | 56 | 2,5 | 4 | 6 | 10 | 15 |
| 40 | 44,45 | 25,492 | 65 | 3,0 | 5 | 8 | 12 | 20 |
| 45 | 57,15 | 32,942 | 83 | 3,0 | 5 | 8 | 12 | 20 |
| 50 | 69,85 | 40,100 | 102 | 4,0 | 6 | 10 | 16 | 25 |
| 55 | 88,90 | 54,858 | 127 | 4,0 | 6 | 10 | 16 | 25 |
| 60 | 107,95 | 60,700 | 162 | 5,0 | 8 | 12 | 20 | 30 |
| 65 | 133,35 | 74,433 | 202 | 5,0 | 8 | 12 | 20 | 30 |
| 70 | 165,10 | 92,183 | 250 | 6,0 | 10 | 16 | 25 | 40 |
| 75 | 203,20 | 113,658 | 307 | 6,0 | 10 | 16 | 25 | 40 |
| 80 | 254,00 | 138,208 | 394 | 8,0 | 12 | 20 | 30 | 50 |
Условное обозначение конусов по ГОСТ 15945 с добавлением степени точности конуса:
Конус 50 АТ5 ГОСТ 15945-82
Предельные отклонения базорасстояния конуса Z следует выбирать из ряда: ± 0,4; ± 0,2; ± 0,1; ± 0,05мм.
Продолжение табл. 10
Вычисление диаметра фигуры через линейные параметры и угол при основании
Описанную пространственную фигуру можно получить, если вращать вокруг любого катета прямоугольный треугольник. Этот факт демонстрирует рисунок ниже.
Из рисунка видно, что два катета AC и AB являются радиусом r и высотой h объемной фигуры соответственно. Генератриса g — это гипотенуза BC. Эти соответствия позволяют записать формулу диаметра конуса через известные g и h:
d = 2*√(g2 — h2)
При записи этой формулы использовалась теорема Пифагора, а также определение диаметра, который в два раза больше радиуса основания конуса.
Если известен угол φ между основанием и любой из образующих g фигуры, тогда диаметр конуса можно определить по следующим формулам:
d = 2*g*cos(φ);
d = 2*h/tg(φ)
Оба равенства являются следствием применения определения тригонометрических функций тангенса и косинуса.
Конусность и уклон: построение, расчет, обозначение
При проведении инженерных и других расчетах, а также работе с инженерной графикой и создании чертежей приходится создавать уклон. Конусность получила весьма широкое распространение, она применяется при изготовлении самых различных деталей. Показатель конусности рассчитывается в большинстве случаев при создании деталей, которые получили широкое распространение в сфере машиностроения. Рассмотрим основные параметры, особенности начертания и многие другие моменты подробнее.
Определение и элементы конуса
Под конусом понимают тело, состоящее из круга и точки, которая удалена от его поверхности на определённое расстояние.
При этом точка соединяется с основанием посредством проведения лучей, которые называются образующими. Линия, соединяющая центр круга с удалённой точкой, является высотой данной фигуры.
Обратите внимание!
Также существует такое понятие, как ось конуса. Это линия, проходящая через его центр и совпадающая с высотой. Образующие строятся относительно оси.
Хотелось бы рассмотреть ещё несколько понятий по этой теме:
1. Под конусностью понимают отношение диаметра основания фигуры и её высоты:
Важно!
Конусность отвечает за угол наклона образующих. Чем больше данный параметр, тем острее угол.
2. Осевое сечение предполагает наличие плоскости, которая будет рассекать фигуру, проходя через ось:
3. Касательная— это плоскость, которая соприкасается с образующей конуса. При этом важно, чтобы она была перпендикулярна осевому сечению.
Развертка прямого кругового конуса
Развертка боковой поверхности прямого кругового конуса представляет собой круговой сектор, радиус которого равен длине образующей конической поверхности l, а центральный угол φ определяется по формуле φ=360*R/l, где R – радиус окружности основания конуса.
В ряде задач начертательной геометрии предпочтительным решением является аппроксимация (замена) конуса вписанной в него пирамидой и построение приближенной развертки, на которую удобно наносить линии, лежащие на конической поверхности.
Алгоритм построения
- Вписываем в коническую поверхность многоугольную пирамиду. Чем больше боковых граней у вписанной пирамиды, тем точнее соответствие между действительной и приближенной разверткой.
- Строим развертку боковой поверхности пирамиды способом треугольников. Точки, принадлежащие основанию конуса, соединяем плавной кривой.
Пример
На рисунке ниже в прямой круговой конус вписана правильная шестиугольная пирамида SABCDEF, и приближенная развертка его боковой поверхности состоит из шести равнобедренных треугольников – граней пирамиды.
Рассмотрим треугольник S0A0B0. Длины его сторон S0A0 и S0B0 равны образующей l конической поверхности. Величина A0B0 соответствует длине A’B’. Для построения треугольника S0A0B0 в произвольном месте чертежа откладываем отрезок S0A0=l, после чего из точек S0 и A0 проводим окружности радиусом S0B0=l и A0B0= A’B’ соответственно. Соединяем точку пересечения окружностей B0 с точками A0 и S0.
Грани S0B0C0, S0C0D0, S0D0E0, S0E0F0, S0F0A0 пирамиды SABCDEF строим аналогично треугольнику S0A0B0.
Точки A, B, C, D, E и F, лежащие в основании конуса, соединяем плавной кривой – дугой окружности, радиус которой равен l.
Онлайн-калькулятор объема конуса
Общее определение конуса
Конус – это тело, образованное совокупностью всех лучей, исходящих из точки пространства и пересекающих плоскость.
Точка, из которой лучи исходят, получила название вершины конуса. В случае, когда основанием конуса является многоугольник, он превращается в пирамиду.
Рассмотрим некоторые важные понятия.
Образующей конуса называется отрезок, который соединяет любую точку границы основания конуса, с его вершиной. Высотой конуса является перпендикуляр, который опущен из вершины к основанию тела.
Конус бывает нескольких типов:
Прямой, если его основание – одна из таких фигур, как эллипс или круг. Обязательным условием является проецирование вершины конуса в центр основания.
Косой – у него центр фигуры, которая находится в основании, не совпадает с проекцией вершины на это самое основание.
Круговой – отталкиваясь от названия, понятно, что в его основании лежит круг.
Усеченный – область конуса, лежащая между основанием и сечением плоскости, которая параллельна основанию и пересекает данный конус.
Вычисление диаметра через площадь поверхности и генератрису
Поверхность рассматриваемого конуса образована конической поверхностью и круглым основанием. Развертка конуса показана ниже.
Общая площадь развертки определяется по следующей формуле:
S = pi*r2 + pi*r*g
Если известна площадь S и генератриса g, тогда это уравнение позволяет вычислить радиус фигуры, а значит, и ее диаметр. Заметим, что речь идет об уравнении второго порядка относительно радиуса r. Решать его следует с использованием дискриминанта. При решении, как правило, получаются два корня, один из которых отрицательный. Он должен быть отброшен, ввиду его не физического значения.
С использованием описанной методики в конце статьи будет решена задача, и будет получен ответ на вопрос о том, чему равен диаметр конуса.
Формула для определения конусности
Провести самостоятельно расчет конусности можно при применении различных формул. Стоит учитывать, что в большинстве случаев показатель указывается в градусах, но может и в процентах – все зависит от конкретного случая. Алгоритм проведения расчетов выглядит следующим образом:
- K=D-d/l=2tgf=2i. Данная формула характеризуется тем, что конусность характеризуется двойным уклоном. Она основана на получении значения большого и меньшего диаметра, а также расстояния между ними. Кроме этого определяется угол.
- Tgf=D/2L. В данном случае требуется протяженность отрезка, который связывает большой и малый диаметр, а также показатель большого диаметра.
- F=arctgf. Эта формула применяется для перевода показателя в градусы. Сегодня в большинстве случаев применяются именно градусы, так как их проще выдерживать при непосредственном проведении построений. Что касается процентов, то они зачастую указываются для возможности расчета одного из диаметров. К примеру, если соотношение составляет 20% и дан меньший диаметр, то можно быстро провести расчет большого.
Как ранее было отмечено, конусность 1:5 и другие показатели стандартизированы. Для этого применяется ГОСТ 8593-81.
На чертеже вычисления не отображаются. Как правило, для этого создается дополнительная пояснительная записка. Вычислить основные параметры довольно просто, в некоторых случаях проводится построение чертежа, после чего измеряется значение угла и другие показатели.
Определение диаметра через объем и высоту
Теперь покажем, как найти диаметр конуса, зная его объем V и высоту h. Для этого необходимо вспомнить, что объем конуса, как и объем любой пирамиды, можно определить, пользуясь следующим равенством:
V = 1/3*S*h
Здесь S — площадь основания. Поскольку площадь основания в рассматриваемом случае является площадью круга, то это выражение можно переписать в таком виде:
V = 1/3*pi*r2*h
Остается выразить отсюда радиус и умножить его в два раза, и мы получим ответ на вопрос о том, как найти диаметр конуса через величины V и h. Имеем:
r = √(3*V/(pi*h));
d = 2*r = 2*√(3*V/(pi*h))
Заметим, что в правой части получается размерность длины. Это доказывает правильность полученной формулы.
Все записанные в статье формулы для диаметра d фигуры также являются справедливыми для радиуса, который будет в два раза меньше диаметра.
Обозначение конусности на чертеже
При создании технической документации должны учитываться все установленные стандарты, так как в противном случае она не может быть использована в дальнейшем. Рассматривая обозначение конусности на чертежах следует уделить внимание следующим моментам:
- Отображается диаметр большого основания. Рассматриваемая фигура образуется телом вращения, которому свойственен диаметральный показатель. В случае конуса их может быть несколько, а изменение показателя происходит плавно, не ступенчато. Как правило, у подобной фигуры есть больший диаметр, а также промежуточной в случае наличия ступени.
- Наносится диаметр меньшего основания. Меньшее основание отвечает за образование требуемого угла.
- Рассчитывается длина конуса. Расстояние между меньшим и большим основанием является показателем длины.
- На основании построенного изображения определяется угол. Как правило, для этого проводятся соответствующие расчеты. В случае определения размера по нанесенному изображению при применении специального измерительного прибора существенно снижается точность. Второй метод применяется в случае создания чертежа для производства неответственных деталей.
Простейшее обозначение конусности предусматривает также отображения дополнительных размеров, к примеру, справочную. В некоторых случаях применяется знак конусности, который позволяет сразу понят о разности диаметров.
Развертка конуса
С помощью данного калькулятора вы сможете рассчитать развертку(раскрой) для вальцовки конуса. При гибке листового материала, внутренняя сторона сжимается, а внешняя растягивается. Есть место на листе, волокна которого не сжимаются и не растягиваются. Это место называют «нейтральной линией». Вот по этой нейтральной линии и необходимо производить расчет. Так же калькулятор выдаст размеры прямоугольника в который вписывается заготовка. Конусы металлические находят широкое применение при изготовлении емкостей, трубопроводов, воздухопроводов, водостоков, зонтов(грибков) на круглые трубы и др.
При расчете используются следующие буквенные обозначения:
- D max — наибольшее основание конуса по нейтральному слою;
- D min — наименьшее основание конуса по нейтральному слою;
- h — высота конуса;
- α — угол конуса;
- R max — внешний диаметр развертки конуса;
- R min — внутренний диаметр развертки конуса;
- β — угол развертки;
- H — одна из сторон прямоугольника , в который вписывается развертка;
- L — вторая из сторон прямоугольника , в который вписывается развертка.
К-фактор — коэффициент, указывающий смещение нейтрального слоя при гибке взависимости от R и S. При построении развертки в инженерной графике К-фактор не учитывают. Диаметры для расчетов развертки принимается наружные. H и L важны при планировании закупки материала. Данные параметры указаны без учета припусков. НЕ ЗАБУДЬТЕ ИХ ЗАЛОЖИТЬ НА СВОЕ УСМОТРЕНИЕ!!!
Формулы, используемые при расчете можно посмотреть здесь
В бежевые ячейки нужно вводить данные, в желтых и зеленых получать результат.
D max D min h α R max R min β H L °
‘
«
Здесь вы можете разбить развертку конуса на несколько частей. Это необходимо бывает, когда заготовка очень большая. Это может быть помехой для вписывания заготовки в стандартный лист. Или ограничение размерами стола плазменной или лазерной установки. Для расчета понадобятся данные: R max, R min, β.
На H и L так же необходимы припуски для планирования закупки материала.
R max R min β n
β2 H L
°
‘
«
Для генерации чертежа конуса необходимо произвести расчет. Генерация развертки пока без размеров и не все углы отработаны (угол развертки меньше 180 точно работает). В случае изменения значений необходимо заново нажать на кнопку генерации чертежа.
центрирование по X и Y X конуса Y конуса
X развертки
Y развертки
Для перемещения изображения конуса изменяйте значения X и Y. Для перемещения изображения развертки изменяйте значения X1 и Y1.
МАСШТАБ КОНУСА :
Для масштабирования изображения конуса изменяйте ячейки масштаба в нужную сторону.
МАСШТАБ РАЗВЕРТКИ :
Для масштабирования изображения развертки изменяйте ячейки масштаба в нужную сторону.
шифр (max 28 символов) наименование (max 18 символов) толщина листа марка стали