Как найти градус угла прямоугольника со сторонами - Исправление недочетов и поиск решений вместе с Examum.ru

Как найти углы прямоугольного треугольника

Главная
/
Математика
/
Геометрия
/
Как найти углы прямоугольного треугольника

Чтобы найти углы прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Чтобы найти острые углы прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

для угла α:

угол β
длины катетов a и b
длину гипотенузы (с) и длину одного из катетов

для угла β:

угол α
длины катетов a и b
длину гипотенузы (с) и длину одного из катетов

Введите их в соответствующие поля и получите результат.

Найти угол α зная угол β и наоборот

Если ∠β = , то ∠α =

Если ∠α = , то ∠β =

Формула

α = 90° — β

β = 90° — α

Найти углы прямоугольного треугольника зная катеты

Катет a =
Катет b =

∠α =

∠β =

Чему равны острые углы (α и β) прямоугольного треугольника если известны оба катета (a и b)?

Формулы

или так:

α = arctg(^a/_b)

β = arctg(^b/_a)

Пример

Для примера определим чему равны углы α и β в градусах если катет a = 5 см, а катет b = 2 см:

∠α = arctg(5/2) = arctg(2.5) ≈ 68.2°

∠β = arctg(2/5) = arctg(0.4) ≈ 21.8°

Найти углы прямоугольного треугольника по катету и гипотенузе

Гипотенуза c =
Катет =

∠α =

∠β =

Чему равны острые углы (α и β) прямоугольного треугольника если известны гипотенуза c и один из катетов (a или b)?

Формулы

sin(α) = ^a/_c

sin(β) = ^b/_c

cos(α) = ^b/_c

cos(β) = ^a/_c

или так:

α = arcsin(^a/_c) = arccos(^b/_c)

β = arcsin(^b/_c) = arccos(^a/_c)

Пример

Для примера определим чему равны углы α и β в градусах если гипотенуза c = 6 см, а катет b = 3 см:

∠α = arccos(3/6) = arccos(0.5) = 60°

∠β = arcsin(3/6) = arcsin(0.5) = 30°

См. также

Источник

Прямоугольник – плоская четырёхугольная геометрическая фигура. Прямоугольник относится к
параллелограммам и обладает некоторыми свойствами:

Все внутренние углы фигуры прямые.
Противолежащие стороны попарно параллельны и равны.
Диагонали прямоугольника (отрезок, соединяющий вершины противоположных внутренних углов) равны.
Точка пересечения делит их на равные отрезки.
Диагональ делит фигуру на 2 одинаковых прямоугольных треугольника.
Диагональ делит внутренний угол (90°) на 2 угла. Накрест лежащие углы при проведенном отрезке
равны.

Острый угол между диагоналями прямоугольника через площадь
и диагональ
Угол между диагоналями прямоугольника через угол между
стороной и диагональю
Острый угол между диагоналями прямоугольника через ширину и
диагональ
Острый угол между диагоналями прямоугольника через длину и
диагональ
Острый угол между диагоналями прямоугольника через ширину и
длину
Тупой угол между диагоналями прямоугольника через длину и
диагональ
Тупой угол между диагоналями прямоугольника через ширину и
диагональ
Тупой угол между диагоналями прямоугольника через длину и
ширину

Острый угол между диагоналями прямоугольника через площадь и диагональ

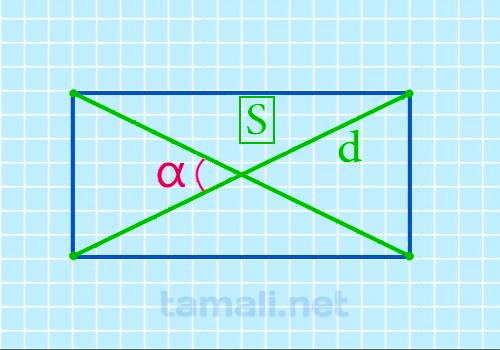
Острый угол (a) между диагоналями, зная площадь (S) и длину диагонали (d) легко можно вычислить по
формуле:

sin a = (2 * S) / d²

где d — диагональ, S — площадь прямоугольника.

Цифр после
запятой:

Результат в:

Через синус находится значение угла. По этой формуле также можно найти тупой угол между диагоналями,
так как 2 данных угла являются смежными, а синусы смежных углов равны.

Пример. Дан прямоугольник, площадь которого равна 108 см², а диагональ – 15 см.
Нужно найти острый угол между диагоналями. Необходимые значения подставляем в формулу sin a = (2 * S) / d² = (2 * 108) / 225 = 0,96. По значению синуса
находится величина острого угла между диагоналями. В данном случае она равна 73,73°.

Угол между диагоналями прямоугольника через угол между стороной и диагональю

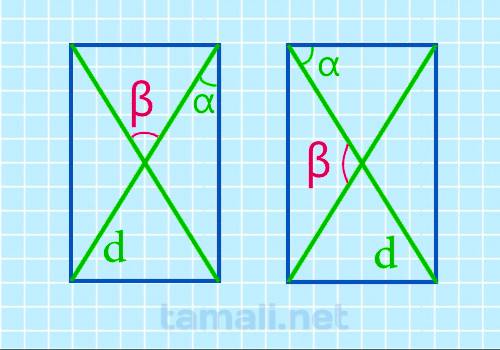
Величина нужного угла (α) в два раза больше угла (β) между стороной и диагональю по свойству углов
равнобедренного треугольника, так как диагонали при пересечении образуют 4 равнобедренных
треугольника. В равнобедренном треугольнике углы при основании (b) равны, а нужный угол является
смежным по отношению к углу при вершине (c), в таком случае c = 180 — α. Сумма углов
треугольника равна 180°. Несложно составить уравнение β+β+180-α=180, которое легко сокращается до
вида

β = 2 * α

где α — угол между стороной и диагональю.

Цифр после
запятой:

Результат в:

Пример. Пусть угол α = 15 (он может быть от 0 до 90º), тогда β = 2 * α = 2 * 15 = 30º

Острый угол между диагоналями прямоугольника через длину и ширину

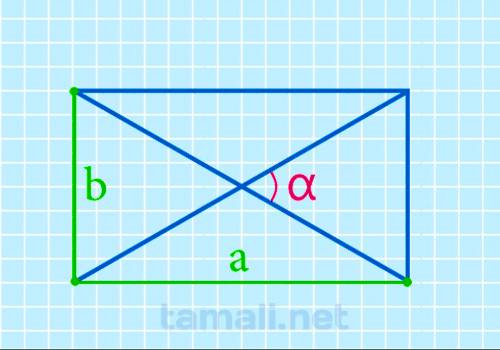
Если в задаче неизвестна длина диагонали, не нужно тратить время на ее поиски. Можно быстро найти
острый угол между диагоналями при помощи длины и ширины прямоугольника по формуле:

α = 2 arctg b / a

где b — ширина прямоугольника, a — длина прямоугольника.

Цифр после
запятой:

Результат в:

Пример. Дан прямоугольник со сторонами 8 см и 6 см. Нужно построить диагонали и
найти острый угол между ними. Угол α = 2 arctg 6 / 8 = 2 arctg 0,75=73,73°.

Острый угол между диагоналями прямоугольника через ширину и диагональ

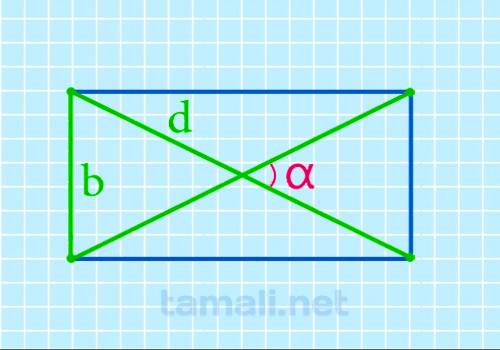
Значение нужного угла можно определить, зная длину диагонали и ширины (B) четырёхугольника, по
формуле:

α = 2 arcsin b / d

где b — ширина прямоугольника, d — диагональ.

Цифр после
запятой:

Результат в:

Пример. Рассмотрим применение формулы в конкретной задаче. Дан прямоугольник, ширина
которого равна 3 мм, а длина диагонали – 5 мм. Необходимо найти острый угол между
диагоналями. Применив данную формулу, находим значение нужного угла: a = 2 * arcsin 0,6 = 73,73°.

Острый угол между диагоналями прямоугольника через длину и диагональ

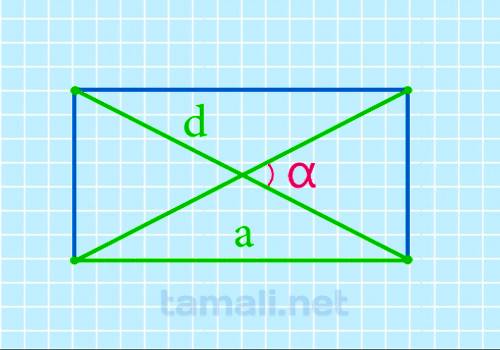
Если неизвестна ширина прямоугольника, но есть значение длины (a), можно также просто найти острый
угол между диагоналями. Формула почти идентична предыдущей:

α = 2 arccos a / d

где a — длина прямоугольника, d — диагональ.

Цифр после
запятой:

Результат в:

Пример. В прямоугольнике с длиной 8 см, в котором проведены диагонали длиной 10 см,
найти острый угол между диагоналями. Угол α = 2arccos 8 / 10 = 2arccos 0,8 = 73,73°.

Тупой угол между диагоналями прямоугольника через ширину и диагональ

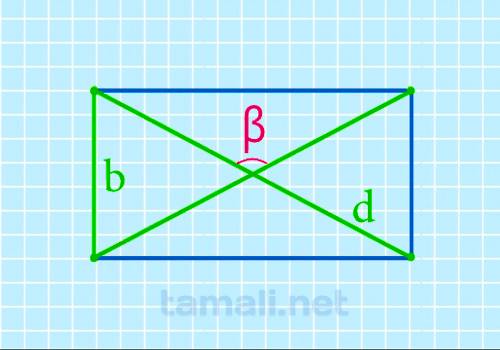
Для того чтобы быстро вычислить значение данного угла при помощи известной ширины и диагонали
прямоугольника, нужно воспользоваться следующей формулой:

β = 2 arccos b / d

где b — ширина прямоугольника, d — диагональ.

Цифр после
запятой:

Результат в:

Пример. Известна ширина прямоугольника, она равна 8 мм. А длина диагонали равна 17
мм. Задача найти значение тупого угла между диагоналями.
Вставив данные в формулу, вы получите
правильный результат. Таким образом, β = 2 arccos 8 / 17 = 2 arccos 0,47 = 123,85°.

Тупой угол между диагоналями прямоугольника через длину и диагональ

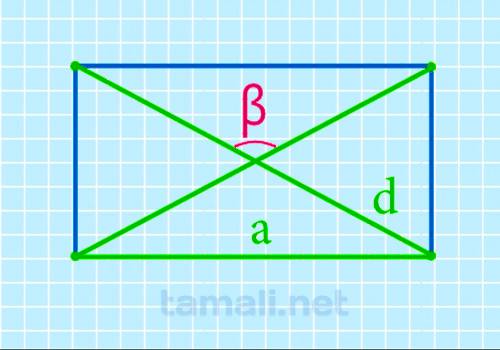
Можно, конечно, применить предыдущую формулу и найти острый угол через длину и диагональ, а потом
вычесть значение из 180°. Но есть упрощенная формула для быстрой скорости решения: тупой угол между
диагоналями

β = 2 arcsin a / d

где a — длина прямоугольника, d — диагональ.

Цифр после
запятой:

Результат в:

Пример. Дан прямоугольник с длиной равной 20 см, в котором проведены диагонали
длиной 25 см. Чтобы найти нужную величину, подставляем значения в формулу: β = 2 arcsin 20 / 25 = 2 arcsin 0,8 = 106°.

Тупой угол между диагоналями прямоугольника через длину и ширину

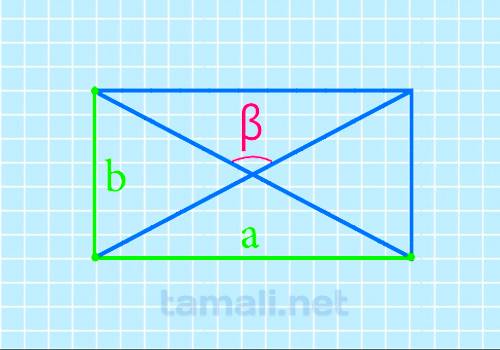
Формула для определения тупого угла между диагоналями прямоугольника через известные значения длины и
ширины такова:

β = 2 arctg a / b

где a — длина прямоугольника, b — ширина прямоугольника.

Цифр после
запятой:

Результат в:

Пример. Дан прямоугольник со сторонами 15 см и 8 см. Вычислим значение тупого угла,
подставив данные в формулу: β = 2arctg 15 / 8 = 2 arctg 0,5= 123,85°.

Стоит отметить, что при использовании указанных в статье правил нужно владеть знаниями о
тригонометрических функциях. Для того чтобы быстро определять углы, образованные пересечением
диагоналей прямоугольника, поможет именно данный список формул, которые необходимо знать наизусть.
Если на решение задач по геометрии дается небольшой промежуток времени, к примеру, контрольная или
экзамен, лучше отложить сложные алгоритмы и воспользоваться упрощенными формулами.

Параллелограмм относится к выпуклым четырехугольным геометрическим фигурам. Его основные
отличительные признаки от других фигур: равные и попарно параллельные противоположные стороны,
равные противолежащие углы. Диагонали фигуры всегда делятся точкой пересечения на равные отрезки, а
также они делят параллелограмм на 2 одинаковых треугольника. Еще одним главным свойством
четырёхугольника является то, что сумма квадратов диагоналей равна двум суммам квадратов смежных
сторон параллелограмма.

Биссектрисы внутренних углов данного четырёхугольника всегда отсекают от него равнобедренный
треугольник, а также они равны между собой. Сумма углов параллелограмма равна 360°, как и у других
четырёхугольников.
К параллелограммам относятся: квадрат (четырёхугольник с равными сторонами и
равными прямыми внутренними углами), прямоугольники и ромбы (параллелограмм с равными сторонами).
Эти фигуры часто встречаются в школьной программе на уроках геометрии.

Для чего необходимо вычисление угла между диагоналями параллелограмма

Для нахождения сторон четырёхугольника (длины и ширины).
Для нахождения площади и периметра фигуры.
Для нахождения углов между стороной и диагональю.
Для нахождения длины диагонали.

Знание свойств геометрических фигур помогает справиться с задачей любой сложности. Постоянная
практика с использованием формул способствует быстрому запоминанию информации, помогает проработать
маршруты и теоремы, которые западают.

Прямоугольник часто встречается в решении задач по геометрии. Важно знать все его свойства и уметь
пользоваться правилами и теоремами для успешного нахождения результата. Упрощенные формулы и
несколько конкретных примеров помогут определить правильный алгоритм решения и быстро найти
ответ.

Источник

Сделано для людей! Красавцы. Спасибо человеческое!

Спасибо хороший сайт

Расчет лестниц секундное дело сейчас, спасибо создателям сайта

Всё работает нормально.

Странно! Находил углы двумя способами, по двум катетам и по катету и гипотенузе при одинаковых значениях получил разные углы.)))

Супер помогли, и не понятно, как это делается. Если один катет 170, а другой 110, поделив их получаем 1,54. Это что? По вашим расчетам правильный угол 57 градусов. И как он получается?

1,54 это значение тангенса угла, прилежащего к катету, находящегося в знаменателе

Не совсем понятно как рассчитывать углы. Ввёл данные катетов, программа запрашивает величину углов! Я для того и обратился к программе, чтобы она мне рассчитала величину углов! А она меня запрашивает

Большое спасибо! Рассчитали лестницу на 2 этаж за полминуты!

Спасибо, очень помогает в расчетах

Спасибо крышу посчитал за пару минут

Спасибо, за онлайн-расчёт. Углы для спусков на ножах рассчитываю. Класс!

Что б я делал без этой услуги?! Рассчитал стропила за минуту!

Спасибо.Строим крышу.

Считаю крышу, очень удобный сервис !
Спасибо !

Спасибо! Пригодилось для нахождения угла конуса (на работе)

Единственный сайт где углы отображены графически, все остальные (особо одаренные) не додумались. Благодарю!

Спасибо большое, а то школьные знания с годами выветрились)))

Спасибо. Быстро, вовремя, без загвоздка.

Отличная программа, очень помогло

Спасибо, сайт очень выручил. Делали перила для лестницы)))

Удобно работать, спасибо

Спасибо, очень пригодилось!

Очень удобно. Спасибо!

Спасибо. Очень удобно. Хорошо продуман интерфейс.

Простой и нормальный сайт

Отличный сайт. Спасибо за помощь

Источник

Загрузить PDF

В геометрии угол — это фигура, которая образована двумя лучами, которые выходят из одной точки (она называется вершиной угла). В большинстве случаев единицей измерения угла является градус (°) — помните, что полный угол или один оборот равен 360°. Найти значение угла многоугольника можно по его типу и значениям других углов, а если дан прямоугольный треугольник, угол можно вычислить по двум сторонам. Более того, угол можно измерить с помощью транспортира или вычислить с помощью графического калькулятора.

1
Сосчитайте число сторон многоугольника. Чтобы вычислить внутренние углы многоугольника, сначала нужно определить, сколько у многоугольника сторон. Обратите внимание, что число сторон многоугольника равно числу его углов.^[1]
- Например, у треугольника 3 стороны и 3 внутренних углов, а у квадрата 4 стороны и 4 внутренних углов.
2
Вычислите сумму всех внутренних углов многоугольника. Для этого воспользуйтесь следующей формулой: (n — 2) x 180. В этой формуле n — это количество сторон многоугольника. Далее приведены суммы углов часто встречающихся многоугольников:^[2]
- Сумма углов треугольника (многоугольника с 3-мя сторонами) равна 180°.
- Сумма углов четырехугольника (многоугольника с 4-мя сторонами) равна 360°.
- Сумма углов пятиугольника (многоугольника с 5-ю сторонами) равна 540°.
- Сумма углов шестиугольника (многоугольника с 6-ю сторонами) равна 720°.
- Сумма углов восьмиугольника (многоугольника с 8-ю сторонами) равна 1080°.
3
Разделите сумму всех углов правильного многоугольника на число углов. Правильный многоугольник это многоугольник с равными сторонами и равными углами. Например, каждый угол равностороннего треугольника вычисляется так: 180 ÷ 3 = 60°, а каждый угол квадрата находится так: 360 ÷ 4 = 90°.^[3]
- Равносторонний треугольник и квадрат — это правильные многоугольники. А у здания Пентагона (Вашингтон, США) и дорожного знака «Стоп» форма правильного восьмиугольника.
4
Вычтите сумму всех известных углов из общей суммы углов неправильного многоугольника. Если стороны многоугольника не равны друг другу, и его углы также не равны друг другу, сначала сложите известные углы многоугольника. Теперь полученное значение вычтите из суммы всех углов многоугольника — так вы найдете неизвестный угол.^[4]
- Например, если дано, что 4 угла пятиугольника равны 80°, 100°, 120° и 140°, сложите эти числа: 80 + 100 + 120 + 140 = 440. Теперь вычтите это значение из суммы всех углов пятиугольника; эта сумма равна 540°: 540 — 440 = 100°. Таким образом, неизвестный угол равен 100°.
Совет: неизвестный угол некоторых многоугольников можно вычислить, если знать свойства фигуры. К примеру, в равнобедренном треугольнике две стороны равны и два угла равны; в параллелограмме (это четырехугольник) противоположные стороны равны и противоположные углы равны.

Реклама

1

Помните, что в любом прямоугольном треугольнике один угол всегда равен 90°. Это так, даже если прямой угол никак не отмечен или его значение не указано. Таким образом, один угол прямоугольного треугольника всегда известен, а другие углы можно вычислить с помощью тригонометрии.^[5]
2

Измерьте длину двух сторон треугольника. Самая длинная сторона прямоугольного треугольника называется гипотенузой. Прилежащая сторона это сторона, которая находится возле неизвестного угла. Противолежащая сторона — это сторона, которая находится напротив неизвестного угла. Измерьте две стороны, чтобы вычислить неизвестные углы треугольника.^[6]

Совет: воспользуйтесь графическим калькулятором, чтобы решить уравнения, или найдите онлайн-таблицу со значениями синусов, косинусов и тангенсов.
3
Вычислите синус угла, если вам известны противолежащая сторона и гипотенуза. Для этого подставьте значения в уравнение: sin(x) = противолежащая сторона ÷ гипотенуза. Например, противолежащая сторона равна 5 см, а гипотенуза равна 10 см. Разделите 5/10 = 0,5. Таким образом, sin(x) = 0,5, то есть x = sin^-1 (0,5).^[7]
- Если у вас есть графический калькулятор, введите 0,5 и нажмите клавишу sin^-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 30°.
4
Вычислите косинус угла, если вам известны прилежащая сторона и гипотенуза. Для этого подставьте значения в уравнение: cos(x) = прилежащая сторона ÷ гипотенуза. Например, прилежащая сторона равна 1,67 см, а гипотенуза равна 2 см. Разделите 1,67/2 = 0,83. Таким образом, cos(x) = 0,83, то есть x = cos^-1 (0,83).^[8]
- Если у вас есть графический калькулятор, введите 0,83 и нажмите клавишу cos^-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 33,6°.
5
Вычислите тангенс угла, если вам известны противолежащая и прилежащая стороны. Для этого подставьте значения в уравнение: tg(x) = противолежащая сторона ÷ прилежащая сторона. Например, противолежащая сторона равна 75 см, а прилежащая сторона равна 75 см. Разделите 75/100 = 0,75. Таким образом, tg(x) = 0,75, то есть x = tg^-1 (0,75).^[9]
- Если у вас есть графический калькулятор, введите 0,75 и нажмите клавишу tg^-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 36,9°.
Реклама

Советы

Названия углов соответствуют их значениям. Угол в 90° — это прямой угол. Угол в 180° — это развернутый угол. Угол, который лежит между 0° и 90° — это острый угол. Угол, который лежит между 90° и 180° — это тупой угол. Угол, который лежит между 180° и 360° — это невыпуклый угол.
Если сумма двух углов равна 90°, они называются дополнительными. Запомните: два острых угла прямоугольного треугольника всегда являются дополнительными. Если же сумма двух углов равна 180°, они называются смежными.

Об этой статье

Эту страницу просматривали 237 189 раз.

Была ли эта статья полезной?

Источник

Как найти острый угол в прямоугольном треугольнике

Прямоугольный треугольник, вероятно, — одна из самых известных, с исторической точки зрения, геометрических фигур. Пифагоровым «штанам» конкуренцию может составить лишь «Эврика!» Архимеда.

Вам понадобится

— чертеж треугольника;
— линейка;
— транспортир.

Инструкция

Как правило, вершины углов треугольника обозначаются заглавными латинскими буквами (A, B, C), а противоположные им стороны маленькими латинскими буквами (a, b, c) или по названиям вершин треугольника, образующих эту сторону (AC, BC, AB).

Сумма углов треугольника составляет 180 градусов. В прямоугольном треугольнике один угол (прямой) всегда будет 90 градусов, а остальные острыми, т.е. меньше 90 градусов каждый. Чтобы определить, какой угол в прямоугольном треугольнике является прямым, измерьте с помощью линейки стороны треугольника и определите наибольшую. Она называется гипотенуза (AB) и располагается напротив прямого угла (C). Остальные две стороны образуют прямой угол и называются катетами (AC, BC).

Когда определили, какой угол является острым, вы можете либо измерить величину угла при помощи транспортира, либо рассчитать с помощью математических формул.

Чтобы определить величину угла с помощью транспортира, совместите его вершину (обозначим ее буквой А) с специальной отметкой на линейке в центре транспортира, катет АС должен совпадать с ее верхним краем. Отметьте на полукруглой части транспортира точку, через которую проходит гипотенуза AB. Значение в этой точке соответствует величине угла в градусах. Если на транспортире указаны 2 величины, то для острого угла нужно выбирать меньшую, для тупого — большую.

Величину угла можно рассчитать, сделав несложные математические вычисления. Вам понадобится знание основ тригонометрии. Если известны длина гипотенузы AB и катета ВС, вычислите значение синуса угла А: sin (A) = BC / AB.

Полученное значение найдите в справочных таблицах Брадиса и определите какому углу соответствует полученное числовое значение. Этим методом пользовались наши бабушки.

В наше время достаточно взять калькулятор с функцией вычисления тригонометрических формул. Например, встроенный калькулятор Windows. Запустите приложение «Калькулятор», в пункте меню «Вид» выберете пункт «Инженерный». Вычислите синус искомого угла, например, sin (A) = BC/AB = 2/4 = 0.5

Переключите калькулятор в режим обратных функций, кликнув по кнопке INV на табло калькулятора, затем кликните по кнопке расчета функции арксинуса (на табло обозначена, как sin в минус первой степени). В окошке расчета появится следующая надпись: asind (0.5) = 30. Т.е. значение искомого угла — 30 градусов.

Источники:

Таблицы Брадиса (синусы, косинусы)

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник