Как найти градусную меру неизвестного угла треугольника

Градусная мера угла

Нам известно, что при измерении отрезков, мы сравниваем измеряемый отрезок с отрезком, который принят за единицу измерения. Аналогично происходит измерение углов: чтобы измерить угол его сравнивают с углом, который принят за единицу измерения — с градусом.

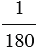
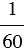
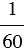
Градус — это угол, который равен части развернутого угла,обозначается знаком

часть градуса называется минутой , обозначается знаком

часть минуты называется секундой , обозначается знаком

Пример: 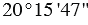(двадцать градусов пятнадцать минут сорок семь секунд)

Градусная мера угла — это положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле.

Пример:

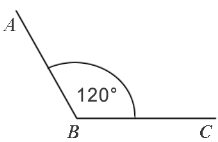
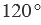
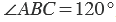
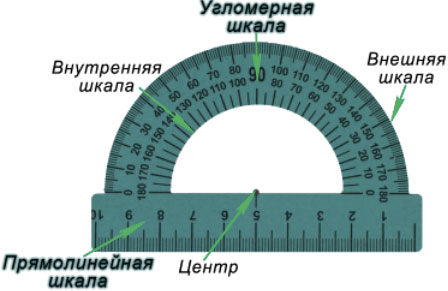
Градусная мера угла ABC равна . Говорят: «Угол ABC равен 120 градусам». Пишут: .

Транспортир — это измерительный инструмент, который используется для измерения и построения углов. Состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы: внутренней и внешней), который разделен на градусы от 0 до .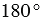

Для того чтобы измерить угол, необходимо совместить вершину угла с центром транспортира, при этом одна из сторон угла должна пройти через нулевое деление шкалы, тогда вторая сторона угла укажет градусную меру угла.

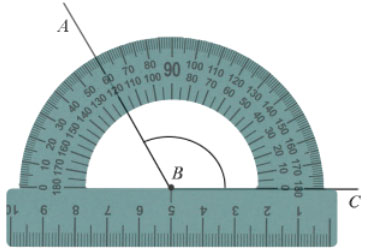
Пример: Измерим угол ABC, для этого совместим точку B с центром транспортира, и расположим транспортир так, чтобы сторона BC прошла через нулевое деление шкалы (обратите внимание отсчёт угла ведётся по той шкале, через нулевое деление которой пройдет одна из сторон угла: в нашем случае по внутренней шкале).

Вторая сторона при этом, как мы видим, проходит через деление шкалы 120, значит: .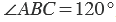

Свойства:

Основные типы углов:

1. Острый угол — угол, градусная мера которого меньше 90 ° .

1. Прямой угол — угол, градусная мера которого равна 90 ° .

1. Тупой угол — угол, градусная мера которого больше 90 °, но меньше 180 ° .

1. Развернутый угол — угол, градусная мера которого равна 180 °.

Поделись с друзьями в социальных сетях:

Углы. Градусная мера угла.

Мерой угла является размер поворота луча около точки как центра вращения.

Что такое градусная мера угла? Градусной мерой угла является число больше нуля, которое показывает,

какое число раз градус и его части — минута и секунда — помещаются в этом угле, т.е. градусная мера —

величина, которая отражает число градусов, минут и секунд между двумя сторонами угла.

У любого угла существует определенная градусная мера, которая больше 0. Развернутый угол = 180°.

Градусная мера угла соответствует сумме градусных мер углов, разбиваемый всяким лучом, который

проходит между его сторонами.

От всякого луча в необходимую полуплоскость есть возможность отложить угол с необходимой градусной

мерой, меньше чем 180°, и только 1.

Мерой плоского угла, который является элементом полуплоскости, является градусная мера угла с теми же

сторонами. Мерой плоского угла, который содержит полуплоскость, является величина 360° – α ,

где α – градусная мера дополнительного плоского угла.

2 угла будут называться равными, когда их градусные меры одинаковы.

Так же как при делении часа, как интервала времени, градус делится на 60 минут — минуты обозначается

знаком ‘, а минуту — на 60 секунд — обозначается знаком ».

Свойства углов.

• У любого угла есть определенная градусную меру, большая нуля. Развернутый угол = 180°.

• Градусная мера угла соответствует сумме градусных мер углов, разбиваемый всяким лучом,

который проходит меж его сторонами.

• От всякого луча в необходимую полуплоскость есть возможность отложить угол с данной градусной

мерой, меньше чем 180°, и только один.

Как найти градусную меру угла?

1 градус (°) — это угол, равный 1/180 части развернутого угла. Если выразиться по другому, если возьмем

развернутый угол и поделим его на 180 одинаковых меж собой частей-углов, то любой такой маленький угол

будет соответствовать 1 градусу. Размер остальных углов вычисляется тем, какой число этих маленьких

углов возможно разместить внутри угла, который измеряется.

Т.о., развернутый угол = 180°, прямой угол = 90°, острые углы меньше, чем 90°, а тупые — больше,

Если угол невозможно измерить точно в целых градусах, то не обязательно использовать минуты и секунды.

Можно пользоваться дробными значениями градуса. Например, 96,5°.

Известно, что минуты и секунды легко переводятся в градусы, выражая их в долях градуса.

Например, 30′ = (30/60)° или 0,5°. А 0,3° = (0,3 * 60)’ или 18′. Т.о., пользоваться минутами и секундами —

Градусная мера угла

Градус — угол, равный 1/180 части развернутого угла. Градусная мера
угла — это положительное число, показывающее сколько раз градус и его части
укладываются в данном угле. Углы измеряют с помощью транспортира.

На рисунке 1 изображен ∠СAB. Градусная мера
которого равна 140°. Обычно записывают кратко: ∠СAB=140°.

Названия определённых частей градуса:

Минута — это 1/60 часть градуса. Секунда — это 1/60 часть минуты.
Минуту обозначают знаком ′, а секунду знаком ″.
Например, угол 45 градусов, 30 минут, 15 секунд обозначают вот так: 45°30′15″.

Равные углы имеют равные градусные меры. Меньший угол имеет меньшую градусную меру.

Мы знаем, что градус составляет 1/180 часть развернутого угла, из этого мы можем сделать вывод, что
развернутый угол равен 180°. Мы также знаем, что неразвернутый угол меньше развернутого угла,
поэтому неразвернутый угол меньше 180 градусов.

Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.
Пример на рисунке 2 — ∠CAH + ∠BAH = ∠CAB ⇒ 60° + 120° = 180°.

Углы называют не только развернутыми и неразвернутыми, но и еще называют
прямыми, острыми и тупыми. Прямым называется угол равный 90°. Острым называется
угол меньше 90°. Тупым называется угол больше 90°, но меньше 180°.

Треугольник – это форма многоугольника, которая имеет три угла, образованных тремя сторонами. Каждая
из трех точек, в которых пересекаются стороны треугольника, называется его вершиной и образует
определенный угол. Стороны треугольника иногда еще называют линейными длинами, а углы – угловыми.
Сторону, противоположную определенному углу, обозначают той же буквой, что характеризует угол как
прилегающий. Стороны обозначаются латинскими буквами a, b, c, а углы – греческими α, β, γ. Зная
определенные параметры треугольника, можно найти его стороны и углы. При этом можно использовать как
линейные формулы, так и обращаться к различным теоремам, например, теореме синусов и косинусов.

Угол треугольника через три стороны

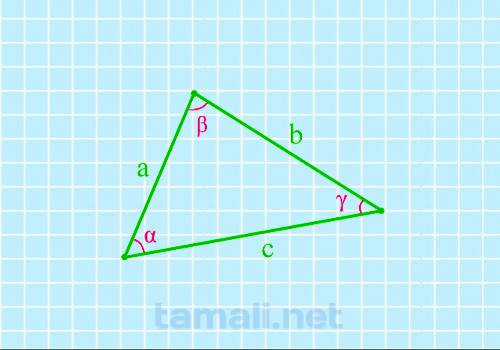
Для того, чтобы найти угол по трем сторонам, нужно вычислить косинус определенного угла. Согласно
теореме косинусов, «квадрат длины стороны треугольника равен сумме квадратов двух других длин его
сторон, минус удвоенное произведение этих длин сторон на косинус угла между ними». Если взять за
предмет вычисления угол β, соответственно, получаем формулу: a² = b² + c² — 2 · b · c · cos (β).
Из полученного равенства можно вычислить

cos(α) = (a² + c² — b²) / 2ac
cos(β) = (a² + b² — c²) /
2ab
cos(γ) = (b² + c² — a²) / 2cb

где a, b, c — стороны треугольника.

Пример. Пусть a = 3, b = 7, c = 6. Cos (β) = (7² + 6² — 3²) : (2 · 7 · 6) = 19/21.
Зная косинус, нужно воспользоваться таблицей Брадиса и по ней найти угол. По таблице Брадиса, если
Cos (β) = 19/21, то β = 58,4°.

Угол прямоугольного треугольника через две стороны

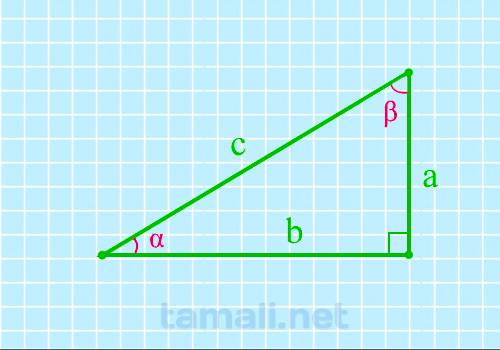
Если известен катет и гипотенуза, угол вычисляется через синус. Если известны катеты и нужно найти
один из острых углов, то можно сделать это через вычисление тангенса.

sin(α) = cos (β) = a / c
sin(β) = cos (α) = b / c
tg(α) = ctg(β) = a
/ b
tg(β) = ctg(α) = b / a

где a, b — катеты, c — гипотенуза.

Пример. В прямоугольном треугольнике есть два катета a = 12, b = 9 и гипотенуза c =
15. Если известны катеты и нужно найти один из острых углов, то можно сделать это через вычисление
тангенса: tg(α) = a / b, то есть tg(α) = 12 / 9. По таблице Брадиса, угол
α = 53, 13°. Если известен катет и гипотенуза, угол вычисляется через синус sin(α) = a / c = 12 / 15 = 0,8. В
этом случае по таблице Брадиса для синусов и косинусов, значение угла – 36, 87°.

Острый угол прямоугольного треугольника через катет и площадь

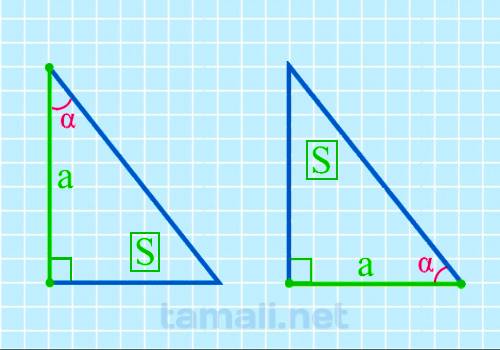
Для того, чтобы вычислить размер острого угла, нужно образовать обратную формулу от площади
прямоугольного треугольника, которая вычисляется через катет и острый угол. Выглядит она следующим
образом: S = (a² * tg β) / 2. Из этих показателей известный площадь S и катет a. Отсюда формула для
нахождения угла будет следующая:

tg(α) = a² / 2S

где a — катет, S — площадь прямоугольного треугольника.

Пример. Пусть S = 34, a = 8. Получается следующее уравнение: tg(α) = a² / 2S = 8² + 2 * 34 = 132.
Таким образом выходит, что по таблице Брадиса, угол с таким тангенсом равен 43°.

Угол треугольника через высоту и катет

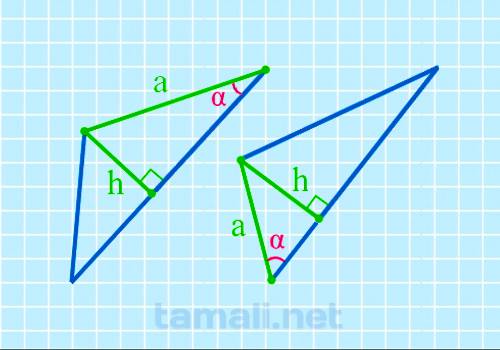
В некоторых прямоугольных треугольниках, в основании которых один острый угол, а второй 90°, один из
катетов (вертикальная прямая, образующая прямой угол) называется также высотой и обозначается как h.
Второй катет a остается со своим обычным названием.

sin α = h / a

где h — высота, a — катет.

Пример. Если высота h = 8, а катет a = 10, то угол α находится по формуле sin α = h / a = 8 / 10 = 0.8 то по таблице Брадиса составляет 53°

Угол при основании равнобедренного треугольника через биссектрису и основание

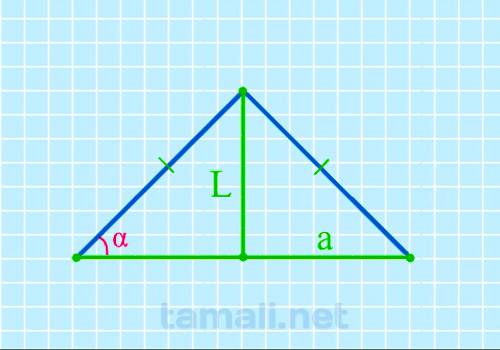
Равнобедренный треугольник ABC с основанием AC имеет биссектрису L (она же CK, делящая основание AC
на два отрезка AK и KB). Также биссектриса L делит угол BCA (он же γ) пополам (каждый из этих
половинок угла γ обозначается как x). То есть γ = 2х. Угол BAC (он же α) = BCA (он же γ), то есть α
= γ. При этом биссектриса L (она же CK) образовала в равнобедренном треугольнике ABC новый
равнобедренный треугольник AKC, в котором AK – это основание, а углы KAC и AKC равны между собой и
равны значению угла γ. Учитывая то, что угол γ равен 2х (то есть двум половинкам угла), то для
треугольника AKC, чтобы вычислить углы при основании, формула будет следующая:

tg α = L / (a/2)

где L — биссектриса, a — основание.

Пример. Пусть биссектриса L равна 15, основание а равно 45, подставив в формулу
получим tg α = L / (a/2) = 15 / (45/2) = 33.69º

Угол при основании равнобедренного треугольника через биссектрису и боковую сторону

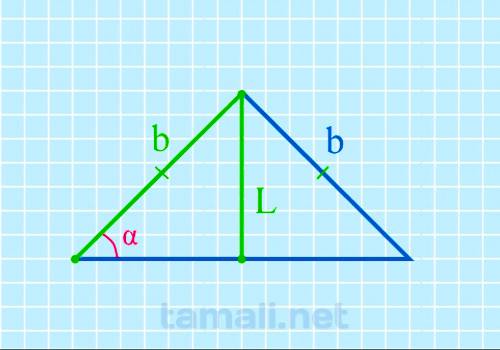
Допустим, что у равнобедренного треугольника ABC углы при основании A (α) и C (γ) равны. Также AB =
BC. Биссектриса L берет начало из вершины А и пересекается с основанием АС, образуя точку
пересечения K, поэтому биссектрису L также можно называть АK. L разделила угол А пополам и основание
поделила на два отрезка: BK и KC. Образовался угол AKC = α (внешний угол для треугольника ABK).
Согласно свойствам внешнего угла:

sin α = L / b

где L — биссектриса, b — боковая сторона.

Пример. Пусть биссектриса L равна 15, боковая сторона b равна 30, подставив в
формулу получим sin α = L / b = 15/30 = 30º.

Угол между боковыми сторонами равнобедренного треугольника через биссектрису и боковую сторону

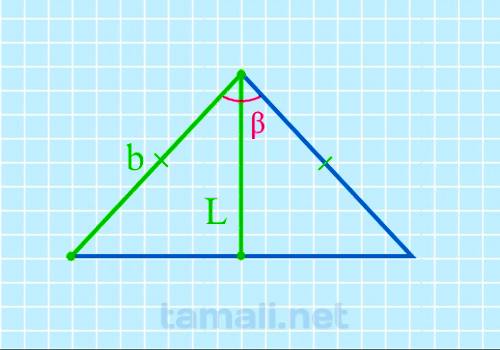
В равнобедренном треугольнике угол ABC (он же β) – это вершина треугольника. Стороны AB и BC равны, и
углы у основания BAC (α) и BCA (γ) тоже равны между собой. Биссектриса L берет начало из вершины B и
пересекается с основанием AC в точке K. Биссектриса BK разделила угол β пополам. Кроме того,
биссектриса разделила треугольник ABC на два прямоугольных треугольника ABK и CBK, так как углы BKA
и BKC – прямые и оба по 90°. Так как треугольники ABK и CBK зеркально одинаковые, для определения
угла β можно взять любой из них. В свою очередь биссектриса BK разделила угол β пополам, например,
на два равных угла х. Оба треугольника, образовавшихся внутри равнобедренного из-за биссектрисы,
прямоугольные, поэтому, чтобы вычислить угол β (он же 2х), нужно взять за правило вычисление угла
через высоту (она в данном случая является также биссектрисой) и катет (это отрезок AK или KC,
которые также равны между собой, так как биссектриса и основание равнобедренного треугольника также
поделила пополам).

2cos(β) = L / b

где L — биссектриса, b — боковая сторона.

Пример. В треугольнике BKC известна биссектриса L = 47 см и боковая сторона b = 64
см. Подставив значения в формулу получим: 2cos(β) = L / b = 47 / 64 = 85.49º

Острый угол между боковыми сторонами равнобедренного треугольника через площадь и боковую
сторону

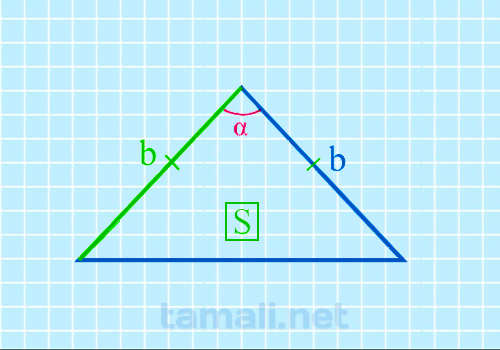
Формула площади равнобедренного треугольника S = 1/2 * bh, где b – это
основание треугольника, а h – это медиана, которая разделила равнобедренный треугольника на два
прямоугольных. Формула для нахождения угла между боковыми сторонами через площадь и боковую сторону
будет следующая:

sin(α) = 2S / b²

где b — боковая сторона равнобедренного треугольника, S — площадь.

Пример. Если площадь равна 48, а сторона 10, то угол между боковыми сторонами можно
вычислить следующим образом: sin(α) = 2S / b² = 2 * 48 / 10² = 73.7º

Вне зависимости от условия задачи, известно, что сумма всех углов треугольника составляет 180°.
Поэтому, элементарно вычислить один из углов можно, когда известны два других. Но для вычисления
углов могут быть использованы и другие показатели. Например, для того, чтобы находить стороны и углы
треугольников, в них можно проводить дополнительные меридианы, биссектрисы, чертить окружности и
использовать эти фигуры как дополнительные вводные, через которые по формулам находятся
неизвестные.

Углы очень удобно вычислять через синусы, косинусы, тангенсы и котангенсы, после чего сопоставлять
данные с таблицей Брадиса, в которой эти величины можно сконвертировать в градусы.

Была ли эта статья полезной?

Как вычислить угол в треугольнике

Из школьного курса планиметрии известно определение: треугольником называется геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой, и трёх отрезков, которые попарно соединяют эти точки. Точки называют вершинами, а отрезки – сторонами треугольника. Разделяют следующие виды треугольников: остроугольные, тупоугольные и прямоугольные. Также треугольники классифицируют по сторонам: равнобедренные, равносторонние и разносторонние.
В зависимости от вида треугольника, существует несколько способов определения его углов, иногда достаточно знать лишь форму треугольника.

Инструкция

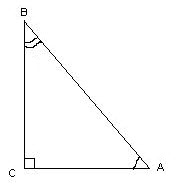
Треугольник называется прямоугольным, если у него есть прямой угол. При измерении его углов можно воспользоваться тригонометрическими вычислениями.

В данном треугольнике угол ∠С = 90º, как прямой, зная длины сторон треугольника, углы ∠A и ∠B вычисляются по формулам: cos∠A = AC/AB, cos∠B = BC/AB. Градусные меры углов можно узнать, обратившись к таблице косинусов.

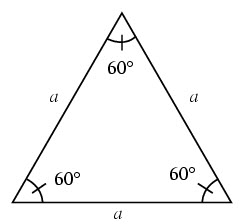
Треугольник называется равносторонним, если у него все стороны равны.

В равностороннем треугольнике все углы равны 60º.

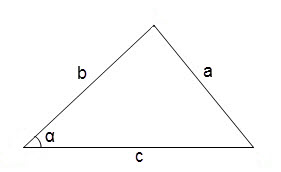
В общем случае, для нахождения углов в произвольном треугольнике можно воспользоваться теоремой косинусов

cos∠α = (b² + c² — a²) / 2 • b • c

Градусную меру угла можно узнать, обратившись к таблице косинусов.

Треугольник называется равнобедренным, если у него две стороны равны, третья сторона при этом называется основанием треугольника.

В равнобедренном треугольнике углы при основании равны, т.е. ∠A = ∠B. Одним из свойств треугольника является то, что сумма его углов всегда равна 180º, поэтому вычислив по теореме косинусов угол ∠С, углы ∠A и ∠B можно вычислить так: ∠A = ∠B = (180º — ∠С)/2

Видео по теме

Источники:

• расчёт угла треугольника

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Решение треугольников онлайн

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:

1. Три стороны треугольника.
2. Две стороны треугольника и угол между ними.
3. Две стороны и угол противостоящий к одному из этих сторон треугольника.
4. Одна сторона и любые два угла.

Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.

Решение треугольника по трем сторонам

Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем .

Решение:

Из теоремы косинусов имеем:

Откуда

Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).

Решение. Из формул (1) и (2) находим:

Используя онлайн калькулятор для arcsin и arccos находим углы A и B:

И, наконец, находим угол C:

Решение треугольника по двум сторонам и углу между ними

Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Решение:

Найдем сторону c используя теорему косинусов:

Далее, из формулы

найдем cosA:

Далее из (3) с помощью калькулятора находим угол A.

Поскольку уже нам известны два угла то находим третий:

Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.

Решение. Иcпользуя теорму косинусов найдем сторону c:

Вычисления выше легко производить инженерным онлайн калькулятором.

Из формулы (3) найдем cosA:

Используя онлайн калькулятор для arcsin и arccos или инженерный онлайн калькулятор находим угол A:

Поскольку уже нам известны два угла то находим третий:

Решение треугольника по стороне и любым двум углам

Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Решение:

Так как, уже известны два угла, то можно найти третий:

Далее, для находждения сторон b и c воспользуемся тероемой синусов:

Откуда

Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.

Решение. Поскольку известны два угла, то легко можно найти третий угол С:

Найдем сторону b. Из теоремы синусов имеем:

Найдем сторону с. Из теоремы синусов имеем:

Ответ: