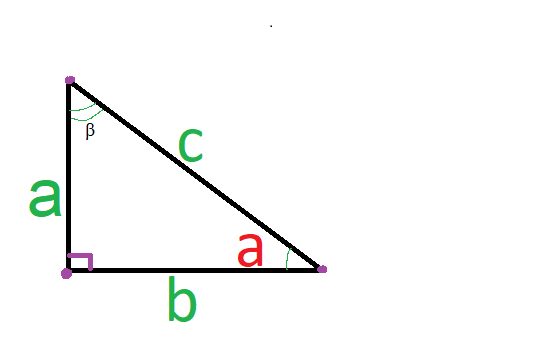Как найти градусную меру угла абс

0

Градусную меру угла абс о центр окружности

Вопрос по геометрии:

найти градусную меру угла ABC, (O-центр окружности)
(ко всем рисункам)

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

4)40
5)130
6)120
7)30
8)45
насчет последней могу ошибаться,а лучше выучи правила я тебе их выделила)

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Центральные и вписанные углы

О чем эта статья:

Центральный угол и вписанный угол

Окружность — замкнутая линия, все точки которой равноудалены от ее центра.

Определение центрального угла:

Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.

На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF

Определение вписанного угла:

Вписанный угол — это угол, вершина которого лежит на окружности.

Вписанный угол равен половине дуги, на которую опирается.

На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC

Свойства центральных и вписанных углов

Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.

• Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:

Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.

• Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:

• Вписанные углы окружности равны друг другу, если опираются на одну дугу:

ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.

• Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:

ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.

Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:

На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.

Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Хорда — отрезок, соединяющий две точки на окружности.

• Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.

AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.

• Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.

ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.

• Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.

ㄥBAC + ㄥBDC = 180°

Примеры решения задач

Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.

Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?

Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°

Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.

Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°

Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?

СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°

Найдите градусную меру угла ABC (о — центр окружности)?

Геометрия | 5 — 9 классы

Найдите градусную меру угла ABC (о — центр окружности).

7 и 8 номер, пожалуйста).

7. ∧CBD опирается на диаметр CD, поэтому∧СBD — 90 гр.

∧ ABC = ∧ABD — ∧CBD = 120 — 90 = 30.

8. ΔABD равнобедренный, поэтому BC — биссектриса,

∧ABO = ∧OBD, но∧ABD прямой(90 гр.

), опирается на диаметр AD,

9. ДостроимΔ DAC.

∧D = ∧С по св — ву равноб.

Δ, вписанный∧ADC = 15 гр.

⇒АС = 30, ∧ABC = ∧ADC, т.

К. опираются на одну и ту жу дугу, откуда∧ABC = 15.

Угол ABC — вписанный и опирается на диаметр окружности с центром в точке O?

Угол ABC — вписанный и опирается на диаметр окружности с центром в точке O.

Найдите градусную меру угла ABC.

Найти градусную меру угла ABC, (O — центр окружности)(ко всем рисункам)?

Найти градусную меру угла ABC, (O — центр окружности)

(ко всем рисункам).

Треугольник abc вписан в окружность с центром в точке 0?

Треугольник abc вписан в окружность с центром в точке 0.

Найдите градусную меру угла с треугольника abc , если угол aob равен 79 градусов.

Треугольник ABC вписан в окружность с центром в точке о?

Треугольник ABC вписан в окружность с центром в точке о.

Найдите градусную меру угла C треугольника ABC, если угол AOB равен 115 градусов.

Треугольник abc вписан в окружность с центром в точке О?

Треугольник abc вписан в окружность с центром в точке О.

Найдите градусную меру угла С треугольника ABC, если угол ABO равен 23 градуса.

Найдите градусную меру угла ABC , если O — центр окружности и угол AOC равен 130 градусам ?

Найдите градусную меру угла ABC , если O — центр окружности и угол AOC равен 130 градусам .

Треугольник abc вписан в окружность с центром в точке о ?

Треугольник abc вписан в окружность с центром в точке о .

Найдите градусную меру угла C , треугольника ABC если угол AOB равен 153.

Треугольник ABC вписан в окружность с центром в точке O?

Треугольник ABC вписан в окружность с центром в точке O.

Найдите градусную меру угла C треугольника ABC, если угол AOB равен 153°.

1)Точка О центр описанной окружности треугольника ABC?

1)Точка О центр описанной окружности треугольника ABC.

Угол BCO = 65 градусов.

Найдите градусную меру угла A треугольника ABC.

2)Точка О центр описанной окружности треугольника ABC.

Угол BCO = 44 градуса.

Найдите градусную меру угла A треугольника ABC.

Треугольник ABC вписан в окружность с центром в точке O?

Треугольник ABC вписан в окружность с центром в точке O.

Найдите градусную меру угла C треугольника ABC, если угол AOB равен 21°.

На странице вопроса Найдите градусную меру угла ABC (о — центр окружности)? из категории Геометрия вы найдете ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

Клетки, несущие генетическую информацию организма. Участвуют в половом размножении 2 особей разного пола одного вида. При слиянии двух клеток вполовом процессеобразуетсязигота, развивающаяся в особь (или группу особей) с наследственными признаками ..

A = b = 4 c = 4√2 R = 2√2 S = πR² = π(2√2)² = 8π.

Vц = п * R ^ 2 * h. Исходя из формулы получаем, что объем второго цилиндра сначала в 4 раза больше (т. К. радиус в квадрате), а затем в 5 раз меньше. Получаем, что V2 = 15 * 4 : 5 = 12.

Это двадцать знаков.

Возьму к примеру — автобус. «Правила поведения при езде в автобусе» — не нужно разговаривать отвлекать водителя от дороги — не толкаться — уступать место пожилым людям — быть вежливым с пассажирами — платить за проезд вовремя — быть бдительным (сл..

Автобус : В автобусе нельзя толкаться , всегда уступать место старшему , не кричать когда разговаривает разговариваешь по телефону .

Sin B = AC / AB = 3 / 5 = 0. 6.

Не уверена на 100%, но мое решение такое : если я правильно поняла, то углы AMN и NMB показаны как равные. Это означает, что они по 45°, т. К. треугольники прямоугольные. Отсюда исходит, что углы MAN и MBN так же по 45°. Значит катеты прямоугольн..

Обозначим угол равный 128 буквой D то угол АВС = половине угла ADB тоесть равен 64 градусам.

Если π = 180°, значит 150° — это 5 / 6π или 5π / 6.

При рассмотрении основных составляющих измерения углов, следует изучить исходные геометрические сведения:

• Угол.
• Развернутый угол, неразвернутый угол.
• Градус, секунда и минута.
• Градусная мера.
• Острый, прямой или тупой.

Геометрическая фигура, которая представляет собой точку — называется вершиной. А исходящие из этой вершины два луча, являются ее сторонами.

Измерение углов производится с помощью градусной меры угла. Углы измеряются таким же способом, как и отрезки, при помощи специальных единиц измерения – градусов.

Равенство градуса таково: [frac{1}{180}] от развернутого угла. Исходя из этого, можно понять, что развернутый угол равен 180 градусам, а неразвернутый угол любой меньше 180 градусов.

Чему равна градусная мера угла

Транспортир используется следующим образом:

• Совместить вершину угла с центром транспортира, при этом одна сторона угла должна пройти по линейке.
• Штрих на шкале транспортира, через который пройдет 2-я сторона, покажет его градусную меру.

Как найти градусную меру угла

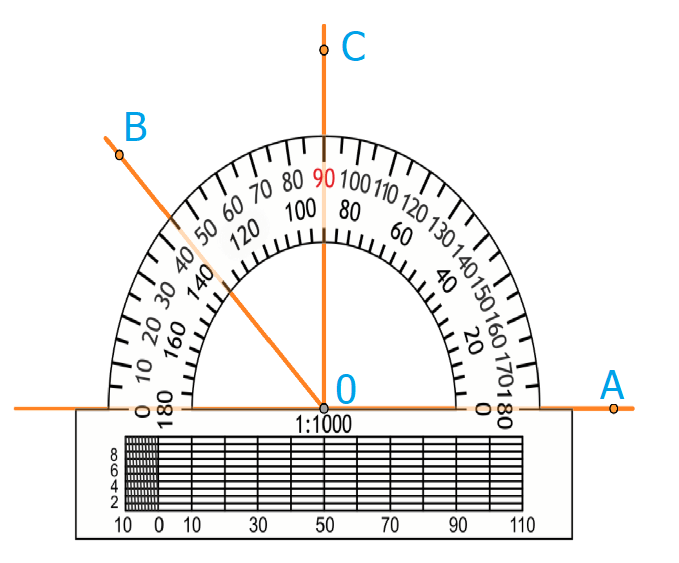
На рисунке угол АОВ = 135 градусов. Угол АОС = 90 градусов, угол ВОС = 45 градусов. Градусная мера углов равна сумме углов, на которые он разбит лучом, который проходит между его сторонами.

Отсюда следует, что величина угла AOB на рисунке 1 равна сумме величин углов AOC и [B O C: angle A O B=angle A O C+angle B O C].

Какие бывают названия углов можно понять, разобравшись со следующими обозначениями.

• Минута – 1/60 часть градуса. Обозначается знаком ‘
• Секунда – 1/60 часть минуты. Обозначают знаком»

Например: угол в 65 градусов, 35 минут,18 секунд записывается так: 75°45’28». Если градусная мера у нескольких углов одинаковая, эти углы считаются равными. Сравнить их можно по размерам – больше или меньше. Развернутый и неразвернутый углы.

Градусная мера вписанного угла

Градусная мера вписанного угла равняется половине градусной меры дуги, опирающуюся на нее, и половине градусной меры угла, находящегося по центру, которая опирается на эту же дугу.

Вписанный угол равняется половине градусной меры дуги, на которую он опирается.

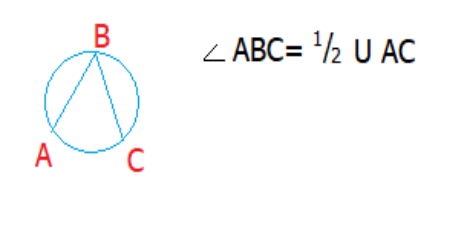
АВ-хорда

ВС-хорда

В-точка окружности.

Углы также различаются несколькими типами:

• Прямыми
• Острыми
• Тупыми

---

Равность прямого угла составляет — 90 градусов. Острый равен цифре меньше 90 градусов. А тупой же – больше 90 и меньше 180 градусов. В чем же заключается важность умения измерения углов и градусной меры в жизни? Оно пригодится в исследованиях, таких как: астрономия. Например, чтобы вычислить положение различных тел в космосе. Чтобы попрактиковаться, необходимо прочертить несколько неразвернутых углов, отличающихся друг от друга. Также важно потренироваться чертить развернутые. А еще, можно при помощи транспортира поупражняться, задавая случайные цифры, в правильности воспроизведения углов.

Существует еще такое понятие, как, биссектриса.

Пример 1. Задача с биссектрисой и развернутым углом.

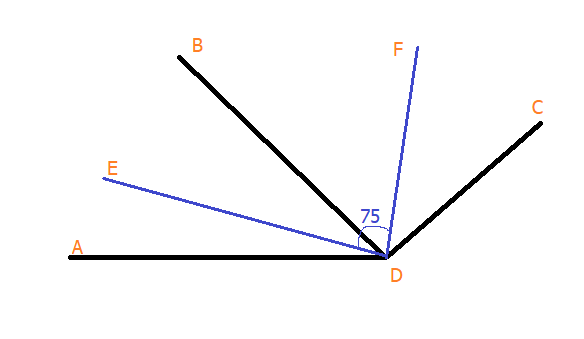
Рис.3 Лучи DЕ и DF – это биссектрисы, которые соответствуют углам ADB и BDC.

Теперь нужно найти угол ADC, при этом угол EDF = 75°

Ответ. Угол EDF имеет по половинке от углов ADB и BDC, это значит, что EDF – это половина самого угла ADC. Теперь получили вычисление угол ADC = 75 умножить на 2 = 150°.

Ответ: 150°

---

Пример 2. Задача с биссектрисой и прямым углом.

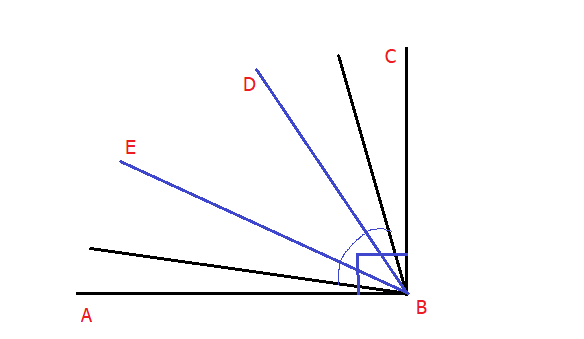
Рисунок 4.  По рисунку 4 видно, что угол АВС прямой, а углы ABE EBD DBC равны. Нужно найти угол, который образовали биссектрисы — ABE и DBC.

Решение будет таким: угол АВС прямой, и исходя из этого, можно понять что он равен 90°. Угол ЕВD=90/3=30°. Согласно правилу, углы ABE EBD DBC равны и поэтому каждый из них будет = 30°. Далее видно, что биссектриса любого из трех углов делит любой из этих углов на 2 угла, которые будут равны 15°. Обе половины углов ABE и DBC относятся к углу, который необходимо найти, то можно смело утверждать, что угол, который мы вычисляем, равен 30+15+15=60°.

Решение: 60°

Градусная мера углов треугольника

У любой геометрической фигуры, кроме округлой, имеются углы. При рассмотрении углов треугольника можно увидеть следующее: Сумма углов треугольника всегда равняется 180°. Если рассматривать прямоугольный треугольник, то можно увидеть, что один из углов равен 90°. А сумма двух других углов тоже равняется 90°.

Поэтому, если известно сколько градусов составляет один из острых углов треугольника, второй угол можно найти по формуле:

[angle a=90^{circ}-angle beta]

У прямоугольного треугольника один из углов прямой, соответственно, два других – острые.

Разъяснение острого угла таково: острым углом называется угол, значение которого составляет менее 90 градусов.

Исходя из вышесказанного, можно отметить, что прямоугольный треугольник — это геометрическая фигура, которая образовалась из трех отрезков. Эти отрезки соединяются между собой тремя точками. Углы у нее все внутренние, а один из них — прямой и равняется 90°. Пример —  рисунок 5.

Ответ:

Объяснение:

A) угол АВС =120° так как вписаный и опирается на дугу АС, которая большая, и равен половине этой дуги, а она будет равна 240, так как вся окружность 360°, а дуга АВС=120° за счет угла АОС-центрального.

Б) угол АВС=90°, так как угол вписаный и опирается на диаметр (180°), и равен половине дуги на которую опирается.

В) угол АВД=120°, угол СВД=90° по пункту Б, значит на угол АВС остается 30° (120-90=30°)

Г) угол АВС=углу АДС=40°, так как они оба вписанные и опираются на одну и туже дугу

Д) угол АВС опирается на большую дугу АДС, вся окружность 360°, угол АДС вписаный и опирается на дугу АВС и равен половине дуги, значит дуга АВС=100°, нам нужна большая часть дуги ю, дуга АДС=360-100=260°, угол АВС вписаный значит равен половине дуги АДС, угол АВС =130°

Е) угол ДВС=90°, аналогично из пункта Б, тогда угол АВС =30°+90°=120°

Ж) угол АВД=90° аналогично из пункта Б. Так как АВ=ВС, то угол ВАД= углу ВДА=45°

Угол ВАО= углу ОВА=45°, так как ОВ=ОА как ради усы, угол АВС и тоже, что и угол ОВА, угол АВС=45°

И) угол СВД опирается на дугу СВ и равен ее половине, тогда дуга СВ=60°, дуга ВСА=180° как половина окружности, угол АВС вписаный и опирается на дугу АДС=180-60=120°, а также угол АВС половина этой дуги, значит угол АВС=60°

К) угол АВС и угол АРС опираются на одну и туже дугу, а значит они равны между собой, тогда угол АВС=38°