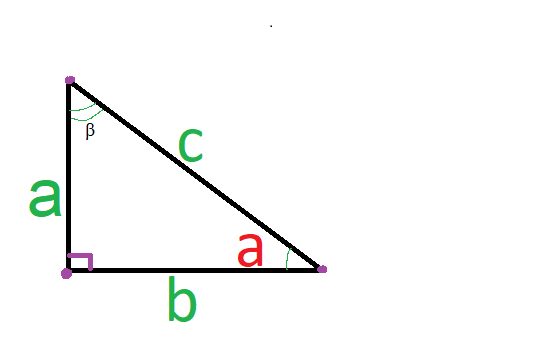Как найти градусную меру угла егэ - Исправление недочетов и поиск решений вместе с Examum.ru

При рассмотрении основных составляющих измерения углов, следует изучить исходные геометрические сведения:

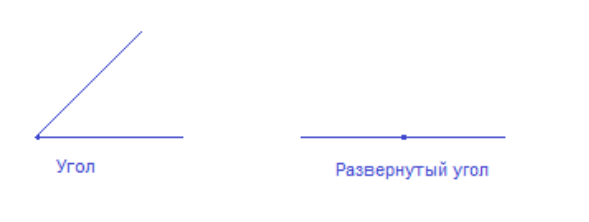
Угол.
Развернутый угол, неразвернутый угол.
Градус, секунда и минута.
Градусная мера.
Острый, прямой или тупой.

Геометрическая фигура, которая представляет собой точку — называется вершиной. А исходящие из этой вершины два луча, являются ее сторонами.

Измерение углов производится с помощью градусной меры угла. Углы измеряются таким же способом, как и отрезки, при помощи специальных единиц измерения – градусов.

Определение

Градус — геометрическая единица измерения, представляющая собой угол, который сравнивается с другими углами.

Равенство градуса таково: [frac{1}{180}] от развернутого угла. Исходя из этого, можно понять, что развернутый угол равен 180 градусам, а неразвернутый угол любой меньше 180 градусов.

Чему равна градусная мера угла

Определение

Градусная мера угла – это положительное число, которое показывает сколько раз градус и его части укладываются в данном углу.

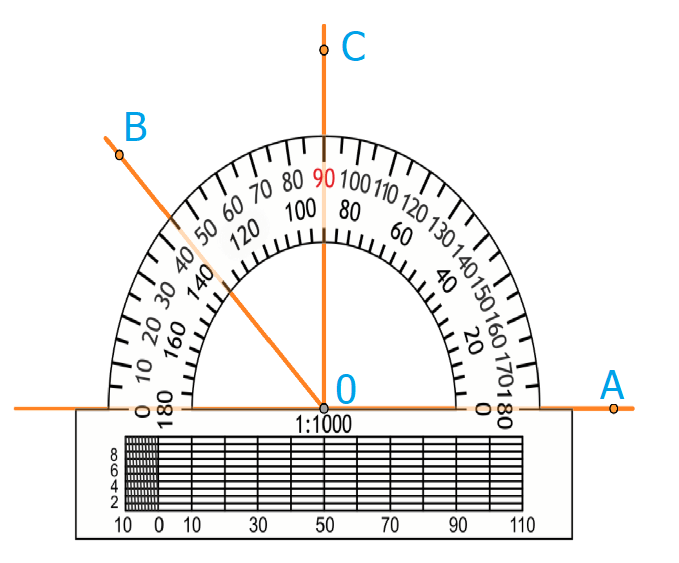
А для их измерения используется инструмент – транспортир.

Рисунок 1. Транспортир

Транспортир используется следующим образом:

Совместить вершину угла с центром транспортира, при этом одна сторона угла должна пройти по линейке.
Штрих на шкале транспортира, через который пройдет 2-я сторона, покажет его градусную меру.

Как найти градусную меру угла

На рисунке угол АОВ = 135 градусов. Угол АОС = 90 градусов, угол ВОС = 45 градусов. Градусная мера углов равна сумме углов, на которые он разбит лучом, который проходит между его сторонами.

Отсюда следует, что величина угла AOB на рисунке 1 равна сумме величин углов AOC и [B O C: angle A O B=angle A O C+angle B O C].

Какие бывают названия углов можно понять, разобравшись со следующими обозначениями.

Минута – 1/60 часть градуса. Обозначается знаком ‘
Секунда – 1/60 часть минуты. Обозначают знаком»

Например: угол в 65 градусов, 35 минут,18 секунд записывается так: 75°45’28». Если градусная мера у нескольких углов одинаковая, эти углы считаются равными. Сравнить их можно по размерам – больше или меньше. Развернутый и неразвернутый углы.

Нет времени решать самому?

Наши эксперты помогут!

Градусная мера вписанного угла

Градусная мера вписанного угла равняется половине градусной меры дуги, опирающуюся на нее, и половине градусной меры угла, находящегося по центру, которая опирается на эту же дугу.

Вписанный угол равняется половине градусной меры дуги, на которую он опирается.

Рисунок.2.

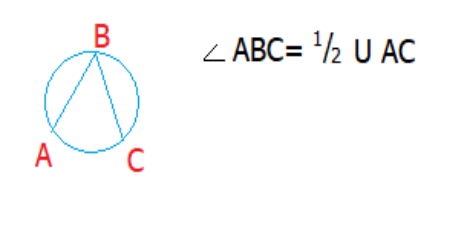
АВ-хорда

ВС-хорда

В-точка окружности.

Углы также различаются несколькими типами:

Прямыми
Острыми
Тупыми

Равность прямого угла составляет — 90 градусов. Острый равен цифре меньше 90 градусов. А тупой же – больше 90 и меньше 180 градусов. В чем же заключается важность умения измерения углов и градусной меры в жизни? Оно пригодится в исследованиях, таких как: астрономия. Например, чтобы вычислить положение различных тел в космосе. Чтобы попрактиковаться, необходимо прочертить несколько неразвернутых углов, отличающихся друг от друга. Также важно потренироваться чертить развернутые. А еще, можно при помощи транспортира поупражняться, задавая случайные цифры, в правильности воспроизведения углов.

Существует еще такое понятие, как, биссектриса.

Определение

Биссектриса— луч, который исходит из вершины этого угла и делит его пополам.

Пример 1. Задача с биссектрисой и развернутым углом.

Рисунок.3.

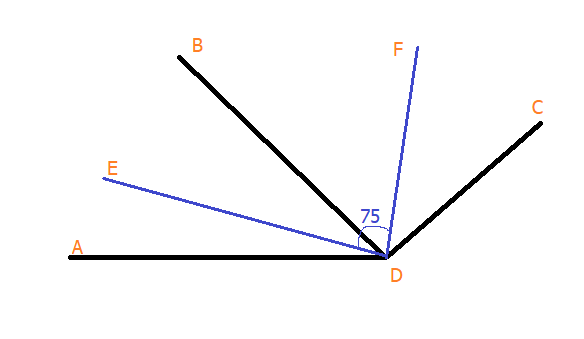
Рис.3 Лучи DЕ и DF – это биссектрисы, которые соответствуют углам ADB и BDC.

Теперь нужно найти угол ADC, при этом угол EDF = 75°

Ответ. Угол EDF имеет по половинке от углов ADB и BDC, это значит, что EDF – это половина самого угла ADC. Теперь получили вычисление угол ADC = 75 умножить на 2 = 150°.

Ответ: 150°

Пример 2. Задача с биссектрисой и прямым углом.

Рисунок.4.

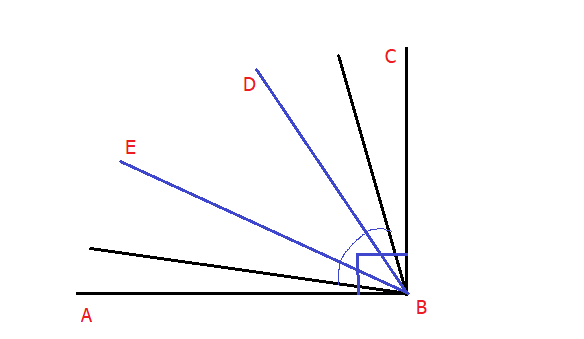
Рисунок 4. По рисунку 4 видно, что угол АВС прямой, а углы ABE EBD DBC равны. Нужно найти угол, который образовали биссектрисы — ABE и DBC.

Решение будет таким: угол АВС прямой, и исходя из этого, можно понять что он равен 90°. Угол ЕВD=90/3=30°. Согласно правилу, углы ABE EBD DBC равны и поэтому каждый из них будет = 30°. Далее видно, что биссектриса любого из трех углов делит любой из этих углов на 2 угла, которые будут равны 15°. Обе половины углов ABE и DBC относятся к углу, который необходимо найти, то можно смело утверждать, что угол, который мы вычисляем, равен 30+15+15=60°.

Решение: 60°

Градусная мера углов треугольника

У любой геометрической фигуры, кроме округлой, имеются углы. При рассмотрении углов треугольника можно увидеть следующее: Сумма углов треугольника всегда равняется 180°. Если рассматривать прямоугольный треугольник, то можно увидеть, что один из углов равен 90°. А сумма двух других углов тоже равняется 90°.

Поэтому, если известно сколько градусов составляет один из острых углов треугольника, второй угол можно найти по формуле:

[angle a=90^{circ}-angle beta]

У прямоугольного треугольника один из углов прямой, соответственно, два других – острые.

Разъяснение острого угла таково: острым углом называется угол, значение которого составляет менее 90 градусов.

Рисунок 5. Прямоугольный треугольник

Исходя из вышесказанного, можно отметить, что прямоугольный треугольник — это геометрическая фигура, которая образовалась из трех отрезков. Эти отрезки соединяются между собой тремя точками. Углы у нее все внутренние, а один из них — прямой и равняется 90°. Пример — рисунок 5.

Источник

Окружность. Центральный и вписанный угол

Центральный угол — это угол, вершина которого находится в центре окружности.

Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают ее.

Отрезок, соединяющий две точки окружности, называется хорда.

Самая большая хорда проходит через центр окружности и называется диаметр.

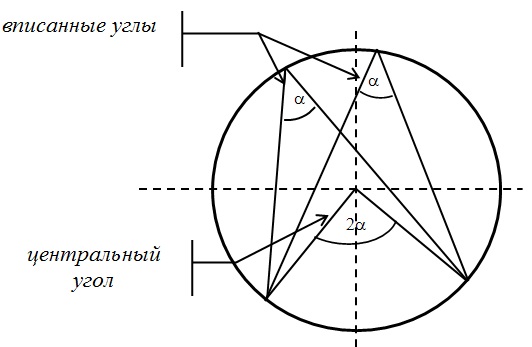
На рисунках — центральные и вписанные углы, а также их важнейшие свойства.

Угол, вершина которого лежит в центре окружности, называется центральным. Величина центрального угла равна угловой величине дуги, на которую он опирается. Угол beta тоже можно назвать центральным. Только он опирается на дугу, которая больше 180 ^circ .

Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. Величина вписанного угла равна половине центрального угла, опирающегося на ту же дугу.

Вписанные углы, опирающиеся на одну и ту же дугу, равны.

Вписанный угол, опирающийся на диаметр, — прямой.

Величина центрального угла равна угловой величине дуги, на которую он опирается. Значит, центральный угол величиной в градусов будет опираться на дугу, равную 90^circ , то есть $displaystyle frac{1}{4}$ круга. Центральный угол, равный 60^circ , опирается на дугу в 60 градусов, то есть на шестую часть круга.

Докажем, что величина вписанного угла в два раза меньше центрального, опирающегося на ту же дугу.

Пусть угол AOC — центральный и опирается на дугу АС, тогда ОА и ОС — радиусы окружности.

Пусть angle ABC — вписанный угол, опирающийся на дугу АС,

АВ и ВС — хорды окружности.

Первый случай: Точка O лежит на BC, то есть ВС — диаметр окружности.

Треугольник AOB — равнобедренный, АО = ОВ как радиусы. Значит,

— внешний угол а внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Получили, что

Второй случай: Центр окружности точка О не лежит на ВС. Построим диаметр BК:

Если точка О лежит внутри вписанного угла АВС, как на рисунке слева, то

Если О лежит вне вписанного угла АВС, как на рисунке справа, то

Мы получили, что в каждом из этих случаев величина центрального угла в два раза больше, чем величина вписанного угла, опирающегося на ту же дугу.

Теорема доказана.

При решении задач по геометрии также применяются следующие теоремы:

1. Равные центральные углы опираются на равные хорды.

2. Равные вписанные углы опираются на равные хорды.

3. Равные хорды стягивают равные дуги.

Докажем теорему 3.

Пусть хорды AB и CD равны. Докажем, что AMB дуги CND имеют одинаковую градусную меру, то есть равны.

Доказательство:

По условию, AB = CD. Соединим концы хорд с центром окружности. Получим: AO = BO = CO = DO = r.

по трем сторонам, отсюда следует, что центральные углы равны, т.е. Значит, и дуги, на которые они опираются, также равны, т.е. дуги AMB и CND имеют одинаковую градусную меру.

Теорема доказана.

Верна и обратная теорема:

Если две дуги окружности равны, то равны и хорды, их стягивающие.

Пусть дуги AMB и CND равны. Тогда как центральные углы, опирающиеся на эти дуги. Значит, треугольники и равны по двум сторонам и углу между ними, и тогда AB=CD, что и требовалось доказать.

Эти две теоремы можно объединить в одну, которая формулируется так:

Хорды окружности равны тогда и только тогда, когда равны дуги, которые они стягивают.

Разберем задачи ЕГЭ и ОГЭ по теме: Окружность, центральный угол, вписанный угол.

Задача 1, ЕГЭ. Чему равен вписанный угол, опирающийся на диаметр окружности? Ответ дайте в градусах.

Вписанный угол, опирающийся на диаметр, — прямой.

Ответ: 90.

Задача 2, ЕГЭ. Центральный угол на больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.

Решение:

Пусть центральный угол равен , а вписанный угол, опирающийся на ту же дугу, равен .

Мы знаем, что x=2y.

Отсюда

y=36.

Ответ: 36.

Задача 3, ЕГЭ. Радиус окружности равен 1. Найдите величину тупого вписанного угла, опирающегося на хорду, равную Ответ дайте в градусах.

Решение:

Пусть хорда AB равна Тупой вписанный угол, опирающийся на эту хорду, обозначим alpha. В треугольнике AOB стороны AO и OB равны 1, сторона AB равна Нам уже встречались такие треугольники. Очевидно, что треугольник AOB — прямоугольный и равнобедренный, то есть угол AOB равен 90 ${}^circ .$ Тогда дуга ACB равна 90 ${}^circ ,$ а дуга AKB равна $360{}^circ - 90{}^circ = 270 {}^circ .$ Вписанный угол alpha опирается на дугу AKB и равен половине угловой величины этой дуги, то есть 135.

Ответ: 135.

Задача 4, ЕГЭ. Хорда AB делит окружность на две части, градусные величины которых относятся как 5 : 7. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.

Решение:

Главное в этой задаче — правильный чертеж и понимание условия. Как вы понимаете вопрос: «Под каким углом хорда видна из точки С?»

Представьте, что вы сидите в точке С и вам необходимо видеть всё, что происходит на хорде AB. Так, как будто хорда AB — это экран в кинотеатре
Очевидно, что найти нужно угол ACB.
Сумма двух дуг, на которые хорда AB делит окружность, равна то есть

Отсюда и тогда вписанный угол ACB опирается на дугу, равную Величина вписанного угла равна половине угловой величины дуги, на которую он опирается, значит, угол ACB равен

Ответ: 105.

Задача 5, ЕГЭ.

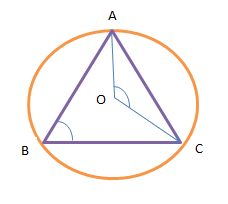
Треугольник ABC вписан в окружность с центром O. Найдите угол BOC, если угол BAC равен 32 ${}^circ .$

Решение:

Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.

$angle BAC=displaystyle frac{1}{2}angle BOC.$

Значит, $angle BOC=2cdot angle BAC=2cdot 32{}^circ =64{}^circ.$

Ответ: 64.

Задача 6, ЕГЭ. Найдите центральный угол AOB, если он на $15{}^circ$ больше вписанного угла ACB, опирающегося на ту же дугу. Ответ дайте в градусах.

Решение:

Пусть величина угла АОВ равна градусов. Величина вписанного угла АСВ равна половине центрального угла, опирающегося на ту же дугу, то есть $displaystyle frac{x}{2}$ градусов.

Получим уравнение: $displaystyle x-frac{1}{2} x = 15{}^circ,$ откуда $x ={30}^circ.$

Ответ: 30.

Задача 7, ЕГЭ. Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

Решение.

Рассмотрим треугольник AOB. Он равносторонний, так как AO = OB = AB = R.

Поэтому угол AOB = 60. Вписанный угол ACB равен половине дуги, на которую он опирается, то есть 30 ${}^circ.$

Ответ: 30.

Задача 8, ЕГЭ.

Дуга окружности AC, не содержащая точки B, составляет 200 ${}^circ.$ А дуга окружности BC, не содержащая точки A, составляет 80 ${}^circ.$ Найдите вписанный угол ACB. Ответ дайте в градусах.

Решение:

Вписанный угол равен половине угловой величины дуги, на которую он опирается. Дуга АВ равна $360{}^circ -200{}^circ -80{}^circ -80{}^circ .$ Тогда $angle ACB=40{}^circ.$

Ответ: 40.

Задачи ОГЭ по теме: Центральный и вписанный угол, градусная мера дуги.

Задача 9, ОГЭ. Центральный угол AOB опирается на хорду AB длиной 6. При этом угол OAB равен ${60}^circ.$ Найдите радиус окружности.

Решение.

Рассмотрим треугольник AOB: он равнобедренный, его боковые стороны равны радиусу окружности.

Углы при основании равнобедренного треугольника равны. Пусть AOB равен , тогда $x + 60{}^circ + 60{}^circ = 180{}^circ,$ где $x = 60{}^circ.$ Треугольник, у которого все углы равны, — равносторонний треугольник; значит, радиус равен 6.

Ответ: 6.

Задача 10, ОГЭ. В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен ${30}^circ.$ Найдите величину угла OAB.

Решение.

Вписанные углы ВСD и ВАD опираются на одну и ту же дугу окружности, поэтому они равны, угол $OAB ={30}^circ.$

Ответ: 30.

Задача 11, ОГЭ. Найдите градусную меру центрального angle MON, если известно, что NP — диаметр, а градусная мера angle MNP равна 18 ${}^circ.$

Решение:

Треугольник MON — равнобедренный. Тогда $angle MON = 180{}^circ$ − $2cdot 18{}^circ = 144{}^circ.$

Ответ: 144.

Задача 12, ОГЭ.

Найдите angle DEF, если градусные меры дуг DE и EF равны ${150}^circ$ и ${68}^circ$ соответственно.

Решение.

Дуга FD, не содержащая точку Е, равна ${360}^circ - {150}^circ - 68{}^circ = 142{}^circ.$ Вписанный угол DEF, опирающийся на эту дугу, равен половине ее угловой величины, $angle DEF = 71{}^circ.$

Ответ: 71.

Задача 13, ОГЭ. В окружности с центром O AC и BD — диаметры. Угол ACB равен ${26}^circ.$ Найдите угол AOD. Ответ дайте в градусах.

Решение.

Угол ACB — вписанный, он равен половине центрального угла, опирающегося на ту же дугу, то есть AОВ = 52 ${}^circ.$ Угол ВОD — развернутый, поэтому угол AOD равен ${180}^circ - 52{}^circ = 128{}^circ.$

Ответ: 128.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Окружность. Центральный и вписанный угол» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

На окружности по разные стороны от диаметра AB отмечены точки D и С. Известно, что угол DBA равен 41°. Найдите угол DCB. Ответ дайте в градусах.

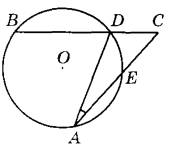
Источник: ЕГЭ 2022. Математика. Базовый уровень. Типовые варианты экзаменационных заданий. 37 вариантов заданий. Под редакцией И. В. Ященко

Задача несложная, если знать про свойства вписанных углов в окружности и правильно нарисовать рисунок.

Рассмотрим 2 решения этой задачи:

Решение 1

1) Нам дан вписанный ∠DBA = 41˚, который опирается на дугу ◡AD. А величина дуги в 2 раза больше вписанного угла на него опирающегося. То есть ◡AD = 2•41˚ = 82˚

2) Дуга ◡AB = 180˚, так как составляет половину окружности, а вся окружность 360˚

3) Дуга ◡ DB = ◡AB — ◡AD = 180˚ — 82˚ = 98˚

4) Искомый ∠DCB = ◡ DB / 2 = 98˚ / 2 = 49˚

Ответ: ∠DCB = 49˚

Решение 2

1) Сделаем дополнительное построение (Соединим точки A и С)

Вписанные углы ∠DCA и ∠DBA опираются на одну дугу AD, а значит они равны ∠DCA = ∠DBA = 41˚

2) Угол ∠ACB — опирается на диаметр, а значит он прямой, то есть ∠ACB = 90˚

3) Искомый ∠DCB = ∠ACB — ∠ACD = 90˚ — 41˚ = 49˚

Ответ: ∠DCB = 49˚

автор вопроса выбрал этот ответ лучшим

Знаете ответ?

Источник

Планиметрия. Углы.

Задание №6 профильного уровня ЕГЭ по математике – решение геометрических задач. В данном задании необходимо справиться с задачей по планиметрии на определение углов.

Теория к заданию №6

Немного стоит напомнить об углах в окружности, так как в задачах это достаточно популярная тематика.

Центральный и вписанный углы:

Разбор типовых вариантов заданий №6 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=”#defae6″]

Треугольник ABC вписан в окружность с центром O. Угол BAC равен 32°. Найдите угол BOC . Ответ дайте в градусах.

[/su_note]

Алгоритм решения:

Выполняем рисунок.
Определяем вид угла.
Применяем свойство вписанных углов и вычисляем искомый угол.
Записываем ответ.

Решение:

1. Выполняем рисунок.

2. Угол, который нужно найти является центральным. Он опирается на ту же дугу, что и угол АВС.

3. Вспомнить правило: “центральный угол в два раза больше вписанного, который опирается на ту же дугу”.

4. Вписанный угол АВС, согласно условию, равен 32⁰. Тогда центральный угол BOC равен 32⁰∙ 2 = 64⁰

Ответ: 64⁰.

Второй вариант задания (из Ященко, №1)

[su_note note_color=”#defae6″]

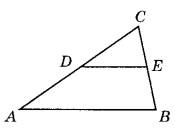
Площадь треугольника ABC равна 152. DE — средняя линия. Найдите площадь треугольника CDE.

[/su_note]

Алгоритм решения:

Устанавливаем подобие треугольников.
Используем свойство площадей подобных треугольников.
Записываем ответ.

Решение:

1. DE – средняя линия треугольника, следовательно, все стороны в треугольнике CDE меньше соответствующих сторон в треугольнике ABC. Это означает, что треугольники подобны, и коэффициент подобия равен 2.

2. Площади подобных фигур относятся как квадраты коэффициентов подобия, следовательно, площадь треугольника CDE в раза меньше, чем площадь треугольника ABC. Имеем:

152 / 4 = 38

Ответ: 38.

Третий вариант задания (из Ященко, №23)

[su_note note_color=”#defae6″]

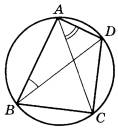
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 36°, угол CAD равен 52°. Найдите угол ABC. Ответ дайте в градусах.

[/su_note]

Алгоритм решения:

Отмечаем на рисунке углы, которые ланы в задаче.
Используем свойство вписанных углов.
Находим угол АВС.
Записываем ответ.

Решение:

1. Отмечаем углы ABD и CAD на рисунке. Эти углы вписаны в окружность.

2. Воспользуемся свойством вписанных в окружность углов: они равны градусной меры дуги, на которую опираются.

Тогда угол ABD, опирающийся на дугу AD. Градусная мера ее равна 36⁰∙2=72⁰, второй – угол CAD опирается на дугу CD с градусной мерой 52⁰∙2=104⁰.

3. Дуга AC=AD+CD. Она имеет градусную меру: АС=72⁰+104⁰=176⁰, а угол АВС, который на нее опирается, определяется как половина величины дуги: 176⁰:2=88⁰.

Ответ: 88.

Четвертый вариант задания (из Ященко, №10)

[su_note note_color=”#defae6″]

Угол АСВ равен 54°. Градусная мера дуги АВ окружности, не содержащей точек D и Е, равна 138°. Найдите угол DAE. Ответ дайте в градусах.

[/su_note]

Алгоритм решения:

Вычисляем угол BDA.
Определяем величину угла ADC,
Рассматриваем треугольник ADC, определяем искомый угол.
Записываем ответ.

Решение:

1. Вычислим угол BDA. Он вписан в окружность, опирается на дугу AB. Тогда по свойству вписанных углов, его градусная мера равна половине градусной величины дуги AB. Тогда .

2. Рассматриваем угол ADC. Он смежный с углом BDA, значит,

3. Рассматриваем треугольник ADC. В нем известны два угла. По свойству суммы углов треугольника третий угол DAC можно найти так:

Из рисунка видно, что угол DAC совпадает с углом DAE, следовательно, угол DAE тоже равен 15⁰.

Ответ: 15⁰.

Даниил Романович | Просмотров: 12.3k

Источник

Видеоурок: Градусная мера дуги окружности

Лекция: Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности

Мерой угла называют величину, на которую отклоняется некоторый луч относительно первоначального положения.

Мера угла может измеряться двумя величинами: градусами и радианами, отсюда и название единиц – градусная и радианная мера угла.

Градусная мера угла

Градусная мера дает возможность оценить, какое количество градусов, минут или секунд помещается в тот или иной угол.

Расчет углов в градусах производится с точки зрения того, что полный поворот луча – это 360°. Половина поворота 180° — развернутый угол, четверть – 90° — прямой угол и т.д.

Радианная мера угла

А теперь давайте же разберемся, что такое радианная мера угла. Как известно из физики, существуют дополнительные единицы. Например, для измерения температуры основной единицей являются Кельвины, а дополнительной градусы Цельсия. Для измерения длины мы используем метры, а англичане используют футы. Данный список можно продолжать и далее. Смысл в том, чтобы Вы поняли, что, кроме градусной меры измерения угла, существует радианная мера, которая так же имеет право на существование.

Для определения радианной меры угла используют окружность. Считается, что радианная мера – это длина дуги окружности, описанная центральным углом.

Напомним, что центральный угол – это угол, вершина которого находится в центре окружности, а лучи опираются на некоторую дугу.

Итак, угол в 1 рад имеет градусную меру в 57,3°. Радианная мера угла описывается либо натуральными числами, или же с использованием числа π ≈ 3,14.

Для геометрии удобнее использовать градусную меру угла, однако для тригонометрии используют радианную меру.

Ниже представлена таблица, позволяющая переходить от градусов к радианам или же наоборот:

Если говорить о длине дуги, то длина дуги в 1 рад равна длине радиуса соответствующей окружности. То есть для определения длины дуги необходимо величину радиуса умножить на градусную меру дуги в радианах.

Источник