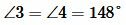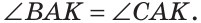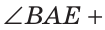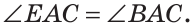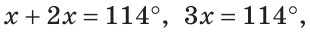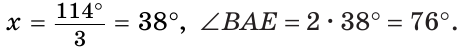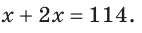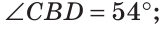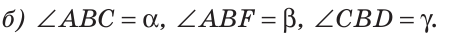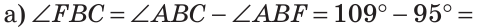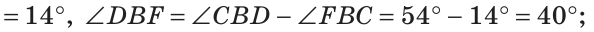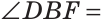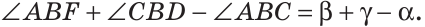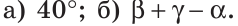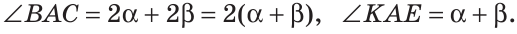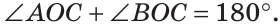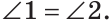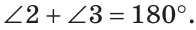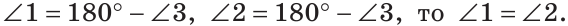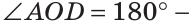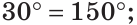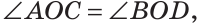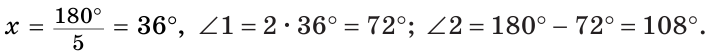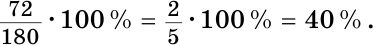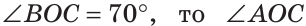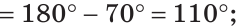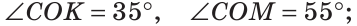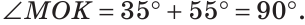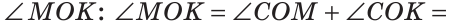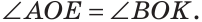Вертикальные углы в геометрии
19 июня 2022
В двух словах: вертикальные углы возникают при пересечении двух прямых, не имеют общих сторон и всегда равны друг другу.
Содержание
- Определение и примеры
- Основная теорема
- Комбинированные задачи
1. Определение и примеры
Определение. Два угла называются вертикальными, если стороны одного из них являются продолжениями сторон другого.
На рисунке ниже пересекаются две прямые: $AB$ и $MN$:
В результате образуются две пары вертикальных углов: $angle ASM$ и $angle BSN$, а также $angle ASN$ $angle BSM$.
Обратите внимание: вертикальные углы образуются только в точке пересечении прямых. Например, углы $ASM$ и $BSN$ на картинке ниже — не вертикальные, даже если они равны:
Если в одной точке пересекается более двух прямых, то вертикальных углов становится очень много:
Я не случайно пометил вертикальные углы одинаковыми дугами. Дело в том, что верна следующая теорема.
2. Основная теорема
Теорема 1. Вертикальные углы всегда равны друг другу.
Доказательство. Рассмотрим «синие» вертикальные $ASN$ и $BSM$. Каждый из них является смежным с углом $BSN$:
Но сумма смежных углов равна 180°, и если $angle BSN=color{red}{x}$, то
[begin{align}angle ASN&={180}^circ -color{red}{x} \ angle BSM&={180}^circ -color{red}{x} end{align}]
Итак, вертикальные углы равны одной и той же величине. Т.е. они равны между собой.
Эта теорема позволяет решать огромное количество задач — от самых простых до весьма нетривиальных. Начнём с простых.
Задача 1. Найдите углы 2, 3 и 4, если $angle 1={134}^circ $.
Решение.
Углы 1 и 3 вертикальные, поэтому они равны: $angle 3=angle 1={134}^circ $.
Углы 1 и 2 смежные, поэтому их сумма равна 180°:
[begin{align}angle 1+angle 2&={180}^circ \ angle 2&={180}^circ -angle 2= \ &={180}^circ -{134}^circ ={46}^circ end{align}]
Углы 2 и 4 вертикальные, поэтому они равны: $angle 4=angle 2={46}^circ $.
Из всех чертежей видно, что при пересечении двух прямых обычно возникает два острых угла и два тупых. Причём острый и тупой угол всегда будут смежными.
Если предположить, что острый угол равен $color{red}{x}$ градусов, то тупой равен $180-color{red}{x}$ градусов.
Задача 2. Найдите углы, образованные при пересечении двух прямых, если разность двух из них равна 68°.
Решение. Пусть острые углы содержат $color{red}{x}$ градусов. Тогда смежные с ними тупые углы содержат по ${180}^circ -color{red}{x}$ градусов.
По условию задачи, разность двух углов равна 68°. Очевидно, речь идёт о смежных углах. Потому что разность вертикальных углов была бы равна нулю. Вычитаем из тупого угла острый и получаем:
[begin{align}{180}^circ -color{red}{x} -color{red}{x} &={68}^circ\ 2color{red}{x}&={112}^circ\ color{red}{x}&={56}^circend{align}]
Итак, острые углы содержат по 56°. Тогда тупые углы содержат по 124°.
Единственный случай, когда все вертикальные углы равны — это когда прямые перпендикулярны, т.е. пересекаются под углом 90°.
Задача 3. На рисунке прямые $a$ и $b$ перпендикулярны, $angle color{red}{1}={36}^circ $. Найдите углы 2, 3 и 4.
Решение.
Углы 1 и 3 вертикальные, поэтому они равны: $angle color{red}{3}=angle color{red}{1}={36}^circ $.
Углы 1 и 2 смежные, поэтому их сумма равна 180°:
[begin{align}angle color{red}{1}+angle color{blue}{2}&={180}^circ \ angle color{blue}{2}&={180}^circ -angle color{red}{1}= \ &={180}^circ -{36}^circ ={144}^circ end{align}]
Углы 3 и 4 вместе образуют прямой угол, поэтому их сумма равна 90°:
[begin{align}angle color{red}{3}+angle color{green}{4}&={90}^circ \ angle color{green}{4}&={90}^circ -angle color{red}{3}= \ &={90}^circ -{36}^circ ={54}^circ end{align}]
Перед тем как переходить к более сложным задачам, рассмотрим ещё одно интересное свойство вертикальных углов.
Теорема 2. Биссектрисы вертикальных углов лежат на одной прямой.
Доказательство. В самом деле, пусть $SC$ и $SD$ — биссектрисы вертикальных углов $ASM$ и $BSN$ соответственно.
Допустим, градусные меры углов $ASM$ и $BSN$ равны $2color{red}{x}$. Тогда градусные меры всех маленьких углов $ASC$, $BSD$ и т.д. равны $color{red}{x}$. Но тогда
[begin{align}angle CSD&=angle CSA+angle ASN+angle NSD= \ &=2color{red}{x}+angle ASN end{align}]
С другой стороны, углы $ASN$ и $ASM=2color{red}{x}$ смежные, поэтому
[2color{red}{x}+angle ASN={180}^circ ]
Итак, угол $angle CSD={180}^circ $, т.е. является развёрнутым. А это как раз и означает, что лучи $SC$ и $SD$ являются дополнительными друг другу и образуют прямую.
3. Комбинированные задачи
Рассмотрим несколько более сложных задач. Тут встречаются вертикальные углы, смежные углы, а также перпендикуляры.
Задача 4. Найдите углы, образованные при пересечении двух прямых, если:
- Сумма двух из них равна 110°.
- Сумма трёх из них равна 308°.
Решение. Для обоих пунктов будем использовать один и тот же чертёж. Пусть острые вертикальные углы содержат по $color{red}{x}$ градусов, тогда два других угла содержат по ${180}^circ -color{red}{x}$ градусов:
1. Если сумма двух углов равна 110°, то, очевидно, речь идёт о вертикальных углах. Потому что сумма смежных углов всегда равна 180°, а не 110°.
Кроме того, это явно острые углы, иначе их сумма была бы больше 180°. Поэтому
[begin{align}color{red}{x}+color{red}{x}&={110}^circ\ 2color{red}{x}&={110}^circ\ color{red}{x}&={55}^circend{align}]
Итак, острые вертикальные углы содержат по 55°. Следовательно, смежные с ними тупые вертикальные углы содержат по 125°.
2. Сумма трёх углов всегда содержит два вертикальных и один смежный с ними. Например, так:
Зелёным пунктиром обозначены три угла, участвующие в сумме. Следовательно, эта сумма равна
[begin{align}left( {180}^circ -color{red}{x} right)+color{red}{x}+left( {180}^circ -color{red}{x} right)&={308}^circ \ {360}^circ -color{red}{x}&={308}^circ\ color{red}{x}&={52}^circend{align}]
Итак, углы равны 52° и 128°.
Эту задачу можно решить по-разному. Взгляните ещё раз на чертёж:
Мы знаем, что «большой зелёный угол» содержит 308°. А «полный оборот» содержит 360°. Но чтобы получить полный оборот, нужно добавить к зелёному сектору небольшой угол $color{red}{x}$. Поэтому
[begin{align}{308}^circ +color{red}{x}&={360}^circ\ color{red}{x}&={52}^circend{align}]
Возможно, такой подход покажется вам более простым и «очевидным».
Заметьте: благодаря введённым обозначениям нам даже не потребовались буквы для обозначения углов.:)
Задача 5. Сумма двух углов, образованных при пересечении двух прямых, равна 250°. Докажите, что эти углы вертикальные.
Решение. Пусть тупой угол $ACN$ содержит $color{blue}{x}$ градусов. Тогда смежный с ним угол $BCN$ содержит ${180}^circ -color{blue}{x}$ градусов, а вертикальный угол $BCM$ тоже равен $color{blue}{x}$ градусов:
Но тогда
[angle ACN+angle BCN={180}^circ ne {250}^circ ]
И это вполне логично, поскольку сумма смежных углов всегда равна 180°. То же самое можно сказать, например, про углы $ACN$ и $ACM$ — они тоже смежные.
Остаётся лишь вариант вертикальных углов $ACN$ и $BCM$. Но эти углы вертикальные, что и требовалось доказать.
В последнем задании мы построили чертёж исходя из следующих соображений. Если искомые углы вертикальные (а именно это мы и пытаемся доказать), то они равны, и каждый из них будет равен 125°. Следовательно, речь идёт о тупых углах, поэтому именно тупые углы мы обозначили за $x$.
Помните: в геометрии важно построить правильный чертёж. И чем сложнее задачи, тем выше требования к качеству чертежей. Иначе на можно просто «не увидеть» алгоритм решения задачи.
Кроме того, в следующих уроках мы будем всё чаще отождествлять углы и их градусные меры. Абсолютно нормально писать и говорить «угол $ABC$ равен $x$» вместо «угол $ABC$ содержит $x$ градусов» — все прекрасно поймут, о чём речь.
Смотрите также:
- Перпендикулярные прямые — определение и свойства
- Что такое смежные углы
- Тест к уроку «Площади многоугольников без координатной сетки» (средний)
- Метод координат в пространстве
- Интегрирование по частям
- Как формулы приведения работают в задаче B11
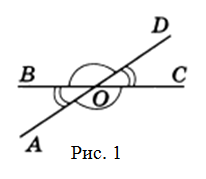
Вертикальные углы. Свойства вертикальных углов
Определение 1. Вертикальными углами называются два угла, у которых стороны одного угла являются продолжениями сторон другого угла.
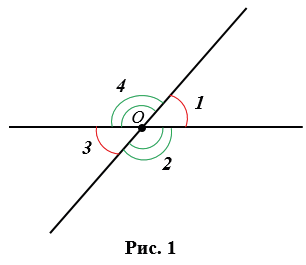
На Рис.1 углы AOB и COD вертикальные. Вертикальные также углы AOD и BOC.
Свойства вертикальных углов
1. Вертикальные углы равны.
2. Две пересекающие прямые образуют две пары вертикальных углов.
Доказательство пункта 1. Поскольку 1, 3 и 2, 3 смежные углы, то имеем
Тогда
Следовательно 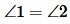
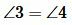
Задачи и решения
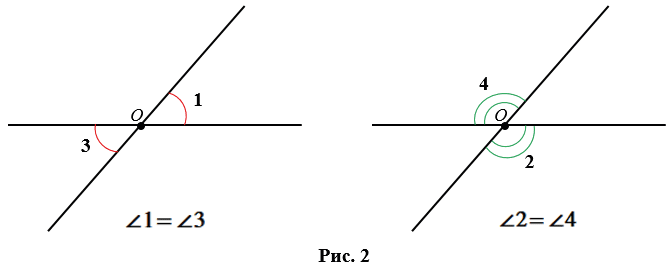
Задание 1. Угол 1 равен 32°. Найти углы 2, 3, 4 (Рис.2).
Решение. Так как углы 1 и 2 вертикальны, то 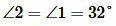
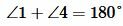
Углы 3 и 4 вертикальные. Тогда
Ответ. 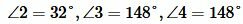
Задание 2. При пересечении двух прямых образовались четыре угла. Сумма двух углов равна 220°. Найти все углы.
Решение. Из образованных четырех углов любые две или смежные, или вертикальные. Поскольку в нашей задаче сумма двух углов равна 220°, то эти углы вертикальные (так как сумма смежных углов равна 180°). Тогда каждый из этих углов равен 220°:2=110°. Смежный по отношению угла 110° , будет угол 180°-110°=70°. Следовательно остальные два угла равны 70°. Отметим, что сумма всех четырех углов равен 360°:
Ответ. 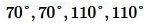
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Начальные геометрические сведения
- Вертикальные углы
Вертикальные углы — это пары углов, имеющие общую вершину и образованные при пересечении двух прямых так, что стороны одного угла являются продолжениями другого.
При пересечении двух прямых получается четыре угла с общей вершиной О (Рис.1), из которых вертикальными будут пары углов 1 и 3, 2 и 4.
Свойство вертикальных углов: вертикальные углы равны (Рис.2).
Советуем посмотреть:
Точки, прямые, отрезки
Провешивание прямой на местности
Луч
Угол
Равенство геометрических фигур
Сравнение отрезков
Сравнение углов
Длина отрезка
Единицы измерения длины, расстояний
Градусная мера угла
Измерение углов на местности
Смежные углы
Перпендикулярные прямые
Построение прямых углов на местности
Начальные геометрические сведения
Правило встречается в следующих упражнениях:
7 класс
Задание 18,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 106,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 117,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 125,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 165,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 166,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 176,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 303*,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 333,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 345,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Содержание:
Определение: Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, и частью плоскости, которую они ограничивают.
Два угла называются равными, если их можно совместить наложением.
Биссектрисой угла называется луч, который выходит из вершины угла и делит его на два равных угла.
Определение. Развернутым углом называется угол, стороны которого являются дополнительными лучами.
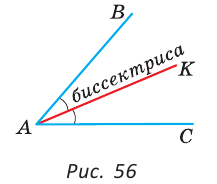
На рисунке 56 луч АК — биссектриса угла ВАС и
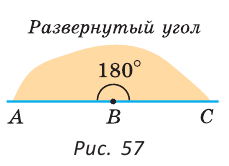
На рисунке 57 угол ABC — развернутый, лучи ВА и ВС — дополнительные. Другая (незакрашенная) полуплоскость относительно прямой АС также задает развернутый угол ABC.
Углы измеряются в градусах, минутах, секундах.
Развернутый угол равен 180°; 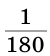
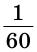
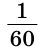
Угол, равный 5 градусов 20 минут и 35 секунд, записывается так: 5°20’35».
Вместо «градусная мера угла равна 20°» часто говорят «угол равен 20°», вместо найти «градусную меру угла» говорят «найти угол».
Определения
Определение: Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, и частью плоскости, которую они ограничивают.
Определение: Угол, равный 90°, называется прямым; угол, меньший 90°, — острым; угол, больший 90°, но меньший 180°, — тупым; угол, равный 360°, называется полным (его стороны совпадают).
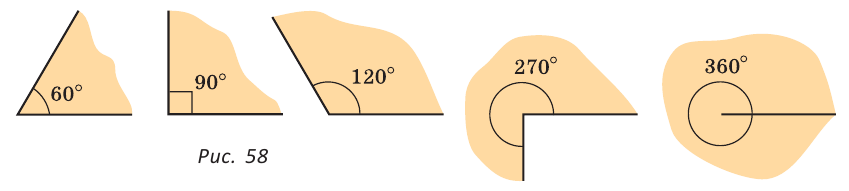
На рисунке 58 последовательно изображены: острый угол, равный 60°; прямой угол, равный 90°; тупой угол, равный 120°; угол, равный 270°; и полный угол, равный 360°.
Градусная мера угла является его важной характеристикой. Свойства градусной меры угла: любой угол имеет градусную меру, выраженную некоторым положительным числом; равным углам соответствуют равные градусные меры, а большему углу — большая градусная мера. И наоборот.
Аксиомы
Аксиома измерения углов. Если внутри угла из его вершины провести луч, то он разобьет данный угол на два угла, сумма градусных мер которых равна градусной мере данного угла.
Аксиома откладывания углов. От любого луча в данную полуплоскость можно отложить угол данной градусной меры, и притом только один.
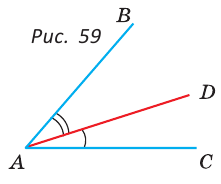
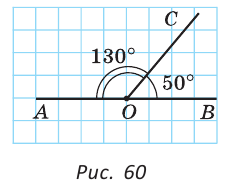
На рисунке 59 луч AD проходит внутри угла ВАС. По аксиоме измерения углов 
Два луча с общим началом задают на плоскости два угла. В дальнейшем будем рассматривать меньший из этих двух углов (если они неразвернутые). Такой угол меньше 180°.
Пример №1
Внутри угла ВАС, равного 114°, из его вершины проведен луч АЕ. Угол ВАЕ в 2 раза больше угла ЕАС. Найти величину угла ВАЕ.
Решение:
Пусть 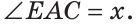
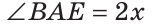
По аксиоме измерения углов
Тогда
Ответ: 76о
Замечания. 1. Возможен другой способ записи решения, когда рядом с буквой 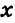
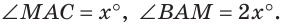
2. В дальнейшем при решении задач не будем ссылаться на аксиому измерения углов.
Пример №2
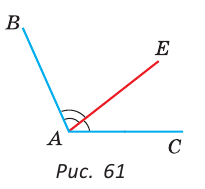
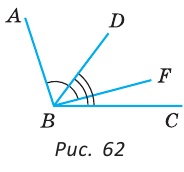
Внутри угла проведены лучи BD и BF (рис. 62).
Найти величину угла DBF, если:
Решение:
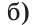
Отсюда
Ответ:
Пример №3
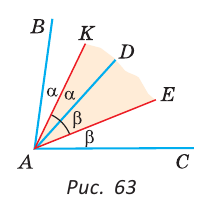
Луч AD делит угол ВАС на два угла BAD и CAD. Доказать, что угол между биссектрисами АК и АЕ углов BAD и CAD равен половине угла ВАС (рис. 63).
Доказательство:
Так как АК иАЕ — биссектрисы, то 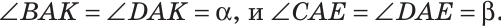
Следовательно, 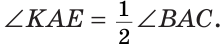
Замечание. В данной задаче мы доказали свойство: «Если внутри угла из его вершины провести луч, то угол между биссектрисами полученных углов равен половине данного угла».
Геометрия 3D
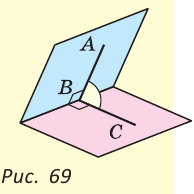
В пространстве при пересечении двух плоскостей образуются двугранные углы. Две полуплоскости с общей границей являются гранями такого двугранного угла, а их граница — его ребром. Измеряется двугранный угол величиной линейного угла, образованного двумя лучами, проведенными в каждой из полуплоскостей из точки на ребре двугранного угла перпендикулярно этому ребру. На рисунке 69 ZABC — линейный угол изображенного двугранного угла.
Геометрия 3D
В пространстве при пересечении двух плоскостей образуются двугранные углы. Две полуплоскости с общей границей являются гранями такого двугранного угла, а их граница — его ребром. Измеряется двугранный угол величиной линейного угла, образованного двумя лучами, проведенными в каждой из полуплоскостей из точки на ребре двугранного угла перпендикулярно этому ребру. На рисунке 69 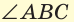
Смежные углы. Вертикальные углы
Определение. Два угла называются смежными, если у них одна сторона общая, а две другие являются дополнительными лучами.
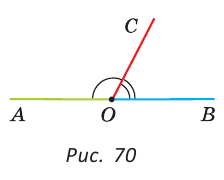
Если на рисунке 70 лучи OA и ОВ дополнительные, то углы АОС и ВОС — смежные.
Теорема (свойство смежных углов). Сумма смежных углов равна 180°.
Дано: 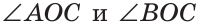
Доказать:
Доказательство:
Из определения смежных углов следует, что лучи OA и ОВ являются дополнительными и поэтому образуют развернутый угол АОВ, равный 180°. Луч ОС проходит между сторонами этого угла, и по аксиоме измерения углов 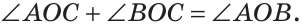
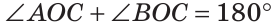
Следствия.
- Если смежные углы равны, то каждый из них прямой.
- Если два угла равны, то равны и смежные с ними углы.
Замечание. Все теоремы курса геометрии 7—9 классов описывают свойства фигур на плоскости.
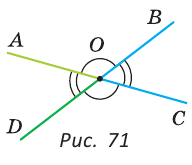
Определение. Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами к сторонам другого.
При пересечении двух прямых АС и DB в точке О (рис. 71) получим, что лучи OA и ОС, О В и OD — дополнительные. Поэтому углы AOD и BОС — вертикальные. Углы АОВ и DOC также вертикальные.
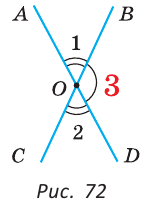
Теорема (свойство вертикальных углов). Вертикальные углы равны.
Дано: 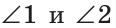
Доказать:
Доказательство:
Углы 1 и 3 смежные, так как лучи OA и OD — дополнительные по определению вертикальных углов. По свойству смежных углов 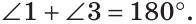
Так как
Теорема доказана.
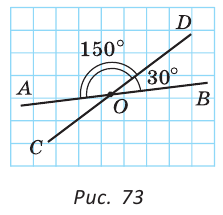
Углом между двумя пересекающимися прямыми называется меньший из образованных ими углов. Если при пересечении прямых АВ и CD (рис. 73) 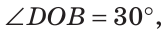
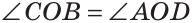
При пересечении двух прямых образуются четыре угла (не считая развернутых). Если один из них 90°, то и остальные по 90° (докажите самостоятельно). Говорят, что прямые пересекаются под прямым углом.
Угол между параллельными прямыми считается равным 0°.
Пример №4
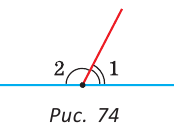
Смежные углы относятся как 2:3. а) Найти величину каждого из углов, б) Определить, сколько процентов развернутого угла составляет меньший угол.
Решение:
а) Пусть 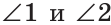
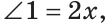
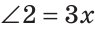
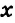
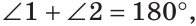
б) Меньшим является 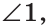
Ответ: 72°, 108°; 40 %.
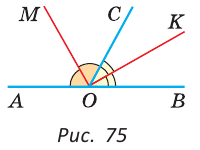
Пример №5
а) Найти угол между биссектрисами ОК и ОМ смежных углов ВОС и АОС (рис. 75), если 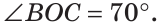
Решение:
а) Если
б) Так как ОМ и ОК — биссектрисы, то
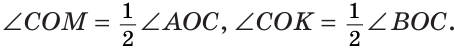
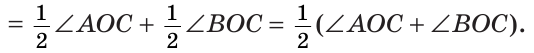
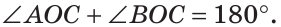
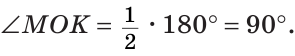
Замечание. Можно было сослаться на ключевую задачу 3* к § 5.
Пример №6
Доказать, что биссектрисы вертикальных углов образуют развернутый угол.
Решение:
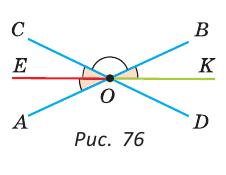
а) Пусть ОЕ и ОК — биссектрисы вертикальных углов АОС и BOD (рис. 76). Докажем, что 
б) 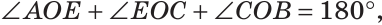
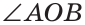
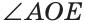
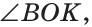
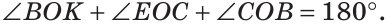

Замечание. Из решения задачи следует свойство: если 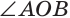
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
- Свойства прямоугольного треугольника
- Расстояние между параллельными прямыми
- Задачи на построение циркулем и линейкой
- Задачи на построение по геометрии
Содержание:
- Определение вертикальных углов
- Примеры решения задач с вертикальными углами
Определение вертикальных углов
Определение
Углы, у которых вершина общая и
стороны которых продолжают друг друга, называются вертикальными углами (рис. 1).
На приведенном рисунке вертикальными есть углы
$AOB$ и
$COD$, а также
$AOC$ и
$BOD$ .
Вертикальные углы образуются при пересечении двух прямых.
Теорема
Вертикальные углы равны.
Примеры решения задач с вертикальными углами
Пример
Задание. Пусть на рисунке 1
$angle COD$ равен
$45^{circ}$. Чему равны углы
$AOB$ и
$AOC$ ?
Решение. Так как углы
$COD$ и
$AOB$ вертикальные, то значит, они равны, а тогда
$$angle A O B=angle C O D=45^{circ}$$
Углы $AOB$ и
$AOC$ смежные, а тогда из
теоремы про смежные углы
получаем, что их сумма равна $180^{circ}$, то есть
$$angle A O B+angle A O C=180^{circ}$$
Отсюда
$$angle A O C=180^{circ}-angle A O B=180^{circ}-45^{circ}=135^{circ}$$
Ответ. $angle A O B=45^{circ}, angle A O C=135^{circ}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Сумма двух вертикальных углов, образованных при пересечении двух прямых, равна
$100^{circ}$. Найти величину каждого из четырех углов,
образованных при пересечении.
Решение. Пусть сумма вертикальных углов
$AOB$ и
$angle COD$ равна
$100^{circ}$ (рис. 1). Как известно, вертикальные углы
равны между собой, поэтому
$$angle A O B=angle C O D$$
Тогда из условия имеем:
$$begin{aligned} angle A O B+angle C O D=100^{circ} & Rightarrow angle C O D+angle C O D=100^{circ} Rightarrow \ & Rightarrow 2 angle C O D=100^{circ} Rightarrow angle C O D=50^{circ} end{aligned}$$
А значит и $angle A O B=50^{circ}$
Углы $AOB$ и
$AOC$ смежные, а значит, их сумма равна
$180^{circ}$:
$$begin{aligned} angle A O B+angle A O C &=180^{circ} Rightarrow angle A O C=180^{circ}-angle A O B=\ &=180^{circ}-50^{circ}=130^{circ} end{aligned}$$
Углы $AOC$ и
$BOD$ вертикальные, а значит
$$angle B O D=angle A O C=130^{circ}$$
Ответ. $50^{circ}, 50^{circ}, 130^{circ}, 130^{circ}$
Читать дальше: что такое синус угла.