Онлайн калькулятор находит какой угол образует минутная и часовая стрелка часов, калькулятор вычисляет наименьший угол между стрелками, для определения наибольшего угла необходимо от 360 градусов отнять наименьший угол.
Отметка 12 часов — это 0°
1 час — 360°:12 = 30° (градусы часовой стрелки)
1 минута — 360°:60 = 6° (градусы минутной стрелки)
Каждую минуту часовая стрелка смещается на 30°:60 = 0.5°
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Часовая и минутная стрелка онлайн.Угол между ними.
| Час и минута разделенные пробелом |
| Угол между стрелками (градусы) |
Обратимся опять к школьным задачам и задачам на сообразительность. Одной из таких задач является узнать, какой угол образуют между собой минутная и часовая стрелка на механических часах в 16 часов 38 минут, или одна из вариаций — сколько времени будет после начала первых суток, когда часовая и минутная стрелка будут образовывать угол в 70 градусов.
Или в самом общем виде «найдите угол между часовой и минутной стрелкой»(с)
Самый простой вопрос, на который много людей умудряются давать неправильный ответ. Какой угол между часовой и минутной стрелкой на часах в 15 часов 15 минут?
Ответ ноль градусов не является правильным ответом 
Давайте разбираться.
Минутная стрелка за 60 минут совершает полный оборот по циферблату, то есть совершит оборот на 360 градусов. За это же самое время (60 минут) часовая стрелка пройдет путь всего одну двенадцатую часть от окружности, то есть сдвинется на 360/12 = 30 градусов
Давайте считать подробно, какой же угол проходит каждая стрелка от 0 часов и нуля минут?
Насчет минутной все очень просто. Составляем пропорцию минуты относятся к пройденному углу как полный оборот(60 минут) к 360 градусам.
Таким образом пройденный угол минутной стрелкой составит минуты/60*360 = минуты*6
Как результат вывод каждая пройденная минута смещает минутную стрелку на 6 градусов
Отлично! Теперь что насчет часовой. А принцип тот же самый, только надо время (часы и минуты) привести к долям часа.
Например 2 часа 30 минут — это 2.5 часа ( 2 часа и его половинка), 8 часов и 15 минут — это 8.25 ( 8 часов и одна четвертинка часа), 11 часов 45 минут — это 11 часов и три четвертинки часа то есть 8.75)
А дальше все просто такая же пропорция: Час(в виде долей часа) относится пройденному углу как 12 часов ( за 12 часов ведь часовая стрелка опишет весь циферблат) к 360 градусам.
Таким образом пройденный угол часовой стрелкой составит часы( в долях часа)*360.12 = часы*30
И как следствие вывод каждая пройденный час смещает часовую стрелку на 30 градусов
Теперь очень легко посчитать угол между стрелками вычислив разницу между углом минутной и часовой стрелки
угол между стрелками = (час+(минуты /60))*30 -минуты*6
где час+(минуты /60) — это положение часовой стрелки
Таким образом ответ к задаче: какой же угол составят стрелки когда на часах 15 часов 15 минут, будет следующим:
15 часов 15 минут это равноценно положению стрелок в 3 часа и 15 минут и таким образом угол составит (3+15/60)*30-15*6=7.5 градуса
В принцие можно считать и так 15.25*30-15*6=367.5 градуса, просто отсюда убираете полные обороты (360 градусов) и получаем тот же самый результат в 7.5 градуса.
Если же у вас есть потребность перевести время в текст то пожалуйста ознаомтесь с материалом Время (часы, минуты, секунды) прописью, а кому часто приходится работать с временными отрезками, складывать минуты и часы, высчитывая простой или наработку на отказ то стоит перейти сюда Суммирование временных отрезков
По углу между стрелками определить время
| Угол, между минутной и часовой стрелкой |
| Время на циферблате когда будет заданный угол |
Это задача сложнее, так как мы решать будем в общем виде, то есть определять все пары (час и минута) когда они будут образовывать заданный угол.
Итак, напомним. Если время выражено в виде HH:MM (час:минута) то угол между стрелками выражается формулой
((HH+cfrac{MM}{60})30-6MM)
Теперь, если обозначим угол буквой U и перевести все в альтернативный вид, то получим следующую формулу
(U=30HH-cfrac{11MM}{2})
Или избавшись от знаменателя, получаем основную формулу связывающая угол между двумя стрелками, и позициями этих стрелок на циферблате.
(2U=60HH-11MM)
заметьте, что угол может быть и отрицательным, то есть в пределах часа у нас может два раза встречаться один и тот же угол, например угол в 7.5 градуса может быть и в 15 часов 15 минут и 15 часов и 17.72727272 минут
Если нам, как в первой задаче был задан угол, то получаем уравнение с двумя переменными. В принципе оно не решается, если не принять условие что час и минута могут быть только целыми числами.
При таком условии мы получаем классическое диофантово уравнение. Решение которого очень простое. Рассматривать мы их пока не будем, а приведем сразу окончательные формулы
где k — произвольное целое число.
Результат часов естественно берем по модулю 24, а результат минут по модулю 60
Посчитаем все варианты когда часовая и минутная стрелка совпадают? То есть когда угол между ними равен 0 градусов.
Как минимум мы знаем две таких точки 0 часов и 0 минут и 12 часов дня 0 минут. А остальные??
Создадим таблицу, положений стрелок когда угол между ними ноль градусов
| k | Часовая стрелка | Минутная стрелка | Пояснения |
|---|---|---|---|
| 0 | 0 | 0 | то есть ровно полночь |
| 1 | 11 | 60 | то есть 12 часов |
| 2 | 22 | 0 | ОШИБКА!! |
Упс! на третьей строке у нас ошибка в 10 часов никак стрелки не совпадают.Это можно убедится взглянув на циферблат. В чём же дело?? Вроде все правильно считали.
А все дело в том, что в промежутке между 10 и 11 часами, для того что бы минутная и часовая стрелка совпадала, минутная стрелка должна находится где то в дробной части какой то минуты.
Это легко проверить по формуле 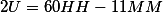
получим, что минутная стрелка будет находится между(!!) делениями 54 и 55 ( совсем точно на позиции 54.545454 минут).
Именно поэтому наши последние формулы не сработали, так как мы подразумевали что часы и минуты числа целые(!).
Задачи, которые встречаются на ЕГЭ
Мы рассмотрим задачи, решения которых есть в интернете, но пойдем другим путем. Возможно это облегчить той части школьников, которые ищут простой и необременительный способ решать задачи.
Ведь чем больше разных вариантов решения задач тем лучше.
Итак, мы знаем только одну формулу 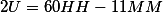
Часы со стрелками показывают 1 час 35 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?
Рассуждения «решателей» на других интернет-ресурсах меня немного утомили и запутали . Вот для таких «утомленных» как я, мы решаем эту задачу по другому.
Определим когда в первом (1) часу минутная и часовая стрелка совпадет (угол 0 градусов)? Подставляем в уравнение изветные числа и получаем
(MM=cfrac{60}{11}=5.45454545)
то есть в 1 час и почти в 5.5 минут. это раньше чем 1 час 35 минут? Да! Отлично, значит этот час мы не учитываем в дальнейших расчетах.
Нам надо найти 10-ое совпадение минутной и часовой стрелки, начинаем анализировать:
в первый раз часовая стрелка будет в 2 часа и сколько то минут,
во второй раз в 3 часа и сколько минут
…
в восьмой раз в 9 часов и сколько то минут
в девятый раз в 10 часов и сколько то минут
в девятый раз в 11 часов и сколько то минут
Теперь осталось найти где будет находится минутная стрелка в 11 часов, так что бы стрелки совпадали
(MM=cfrac{660}{11}=60)
А теперь умножает 10 раз оборота( а это каждый час) на 60 (перведя в минуты) получим 600 минут. и высчитываем разницу между 60 минутами и 35 минутами ( которые были заданы)
Окончательный ответ получили 625 минут.
Что и требовалось доказать. Не надо никаких уравнений, пропорций, ни какая из стрелок с какой скоростью двигалась. Всё это мишура. Достаточно знать одну формулу.
Более интересная и сложная задача звучит так. В 8 часов вечера, угол между часовой и минутной стрелкой составялет 31 градуса . Сколько будет показывать время стрелки, после того как минутная и часовая стрелка образуют прямой угол 5 раз?
Итак в нашей формуле опять известны два из трех параметров 8 и 31 градус. Определяем миунтную стрелку по формуле получим 38 минут.
Когда ближайшее время когда стрелки будут образовывать прямой (90 градусов) угол?
(MM=cfrac{480-180}{11}=27.272727)
(MM=cfrac{480+180}{11}=60)
То есть в 8 часов 27.27272727 минут это первый прямой угол в этом часе и в 8 часов и 60 минут это второй угол в этом часе.
Первый прямой угол уже прошел относительно заданного времени, поэтому его не считаем.
Первый 90 градусов в 8 часов 60 минут ( можно сказать что ровно в 9-00) — раз
в 9 часов и сколько то минут — это два
в 10 часов и сколько минут — это три
еще раз в 10 и сколько минут — это 4-ре, так совпадений в 10 часу два
и в 11 часов и сколько минут это пять.
то есть нам надо посчитать в 11 часу два положения минутной стрелки когда угол равен +90 и -90 градусов. Какое время из этих раньше наступит то и является правильным ответом
Еще проще если мы воспользуемся ботом. Введем 90 градусов и получим следующую таблицу
| Время на циферблате когда будет заданный угол | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
то есть в 11 часо 10.90 минут будет как раз пятый раз когда между часовой и минутной стрелкой вновь образуется прямой угол.
Надеемся данный разбор, поможет Вам как формулировать задачи для учеников, так и легко решать подобные тесты на сообразительность и в ЕГЭ.
Удачи в расчетах!
|
В астрономии принято измерять часовой угол или прямое восхождение звезды не в градусах, а в часовой мере — часах, минутах и секундах. Не вдаваясь в подробности относительно устройства системы небесных координат (а именно, экваториальной системы координат), заметим, что можно перейти от градусов к часовой мере и обратно, используя тот факт, что поворот Земли на 360° происходит за одни сутки, т. е. за 24 ч.
Таким образом получаем соотношения
| Часовая мера | Градусная мера |
|---|---|
| 1 сутки (24 часа) | 360° |
| 1 час | 15° |
| 1 минута | 0°15′ |
| 1 секунда | 0°0’15» |
Калькуляторы ниже можно использовать для соответствующего преобразования
Перевод меры угла из часовой системы в градусную
Перевод меры угла из градусной системы в часовую
Точность вычисления
Знаков после запятой: 2
Для того, чтобы узнать, чему равен угол между минутной и часовой стрелкой, если часы показывают 4:00, нужно провести следующие вычислееия:
1)Так как циферблат разделен еа двеннадцать равных частей, нам нужно 360 разделить на 12 ( чтобы узнать чему равен угол, образующий один сектор: 360/12=30. Следовательно, угол одного сектора составляет 30 градусов.
2) Между минутной стрелки до часовой находятся четыре сектора ( так как минутная стрелка показывает на 12, а часовая на 4). Следовательно, для того, чтобы найти угол между минутной и часовой стрелкой, нам нужно угол одного сектора умножить на количество секторов между стрелками:
30*4=120.
Ответ: угол между стрелками равен 120-ти градусам.
Какой угол образуют стрелки часов, минутная и часовая? Ответ.
В некоторых школьных играх, викторинах, а так же в учебниках по алгебре и геометрии можно встретить задания, в которых вам потребуется определить какой угол образуют стрелки часов, часовая и минутная. На самом деле сделать это довольно просто. Правильные ответы на задания по алгебре представлены ниже.
Так же на картинке вы можете увидеть наглядно углы, которые образуют стрелки. Минутная стрелка — красная, а часовая стрелка — синяя. Для того чтобы самим высчитать углы можно воспользоваться небольшой хитростью. Нужно просто запомнить, что расстояние между минутной и часовой стрелкой в одно деление — это угол в 30 градусов. Так, если между стрелками будет два деления, то между ними будет образован угол в 60 градусов. Если три деления, то образуется угол в 90 градусов. Если 6 делений, то стрелки часов уже образуют угол в 180 градусов.
а) в 3 ч — 90 градусов;
б) в 5 ч — 150 градусов;
в) в 10 ч — 60 градусов;
г) в 11 ч — 30 градусов;
д) в 2 ч 30 мин — 120 градусов;
е) в 5 ч 30 мин — 30 градусов;
ж) в 6 ч — 180 градусов;
з) в 3 ч 45 мин — 180 градусов;
и) в 4 ч — 120 градусов.
Попробуйте теперь отгадать сами. Какой угол образует минутная стрелка если она стоит на числе 12, а часовая стрелка показывает 1 час? А, какой угол образует часовая стрелка, если она стоит на 7, а минутная стрелка стоит на 3? А, какой угол образует минутная и часовая стрелка если обе они показывают на число 12?
Перевод меры угла из часовой системы в градусную и из градусной системы в часовую.
Статья содержит два калькулятора, первый предназначен для перевода угла из часовой меры в градусную, второй — из градусной меры в часовую
В астрономии принято измерять часовой угол или прямое восхождение звезды не в градусах, а в часовой мере — часах, минутах и секундах. Не вдаваясь в подробности относительно устройства системы небесных координат (а именно, экваториальной системы координат), заметим, что можно перейти от градусов к часовой мере и обратно, используя тот факт, что поворот Земли на 360° происходит за одни сутки, т. е. за 24 ч.
Совет 1: Как перевести градусы в минуты.
- Как перевести градусы в минуты
- Как перевести число в радианы
- Как перевести градусы в проценты
- как градусы перевести
Совет 2: Как перевести минуты в секунды.
- — калькулятор или доступ к интернету
Совет 3: Как перевести секунды в часы.
- Калькулятор
Чтобы перевести секунды в часы, достаточно разделить количество секунд на 3600 (так как в одном часу 60 минут, а в каждой минуте 60 секунд). Для этого можно воспользоваться обыкновенным калькулятором. Хватит даже того, который имеется практически в любом сотовом телефоне.
Однако, при этом следует учесть то, что количество часов наверняка окажется дробным (в виде десятичной дроби: x.y часов). Хотя десятичный формат представления времени (особенно временных промежутков) и удобнее при проведении промежуточных вычислений, в качестве окончательного ответа такое представление используется сравнительно редко.
В зависимости от конкретной задачи возможно понадобится указание времени в форме: x часов y секунд. В этом случае достаточно разделить нацело количество секунд на 3600 — целая часть от деления будет количеством часов (x), а остаток от деления количеством секунд (y).
Если в итоге должен получиться конкретный момент времени (показание часов), то решение наверняка потребуется представить в форме: x часов, y минут, z секунд. Для этого количество секунд придется сперва нацело разделить на 3600. Полученное частное будет количеством часов (х). Остаток от деления необходимо снова нацело разделить на 60. Полученное на этом шаге частное будет количеством минут (y), а остаток от деления — количеством секунд (z).
Для того, чтобы решить обратную задачу, т.е. перевести секунды в часы, все вышеописанные действия необходимо проделать в обратном порядке. Соответственно, для первого случая, количество секунд будет x.y*3600, для второго — x*3600+y, а для третьего — x*3600+y*60+z.
Хотя использование вышеописанного способа и не должно вызвать затруднений при единичных расчетах, при больших объемах вычислений (например, обработка экспериментальных данных) этот процесс может занять немало времени, а также привести к ошибкам. В этом случае лучше воспользоваться соответствующими программами.
Например, используя программу MS Excel, достаточно один раз ввести нужные формулы, чтобы получить уже готовые результаты. Составление подходящих формул не потребует от пользователя навыков программирования и доступно даже школьнику. Для примера, составим формулы для нашего случая.
Пусть исходное количество секунд занесено в клетку A1.
Тогда в первом варианте количество часов будет: =A1/3600
Во втором варианте, количество часов и секунд будет: =ЦЕЛОЕ(A1/3600) и =ОСТАТ(A1;3600) соответственно.
В третьем варианте, количество часов, минут и секунд можно посчитать по следующим формулам:
Возможно у Вас есть свои мнения на тему «Как определить градусы по часам»? Напишите об этом в комментариях.

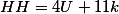
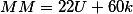
mod24)
mod60)
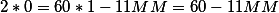
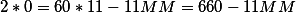
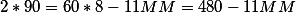
=60*8-11MM=480-11MM)
