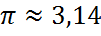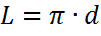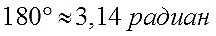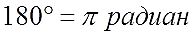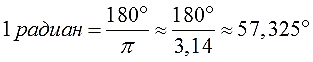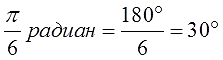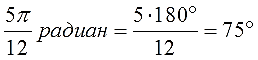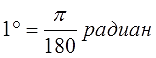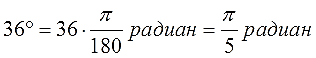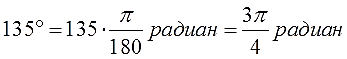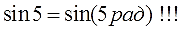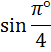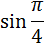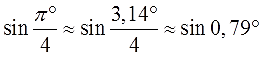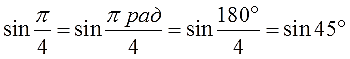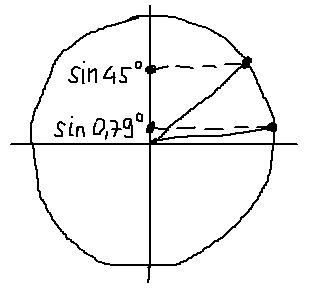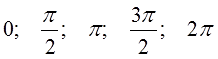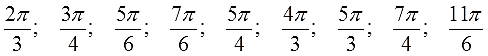Перевод градусов в радианы и обратно: формулы, примеры
Углы измеряются в градусах или в радианах. Важно понимать связь между этими единицами измерения. Понимание этой связи позволяет оперировать углами и осуществлять переход от градусов к радианам и обратно. В данной статье выведем формулу для перевода градусов в радианы и радианов в градусы, а также разберем несколько примеров из практики.
Связь между градусами и радианами
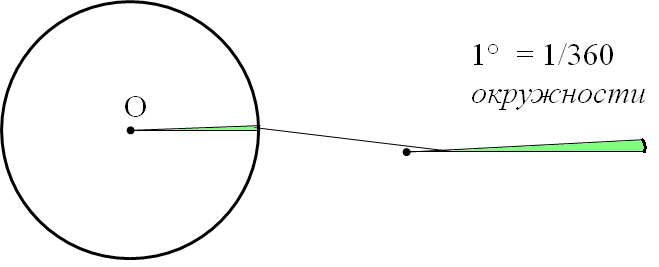
Чтобы установить связь между градусами и радианами, необходимо узнать градусную и радианную меру какого-либо угла. Например, возьмем центральный угол, который опирается на диаметр окружности радиуса r. Чтобы вычислить радианную меру этого угла необходимо длину дуги разделить на длину радиуса окружности. Рассматриваемому углу соответствует длина дуги, равная половине длины окружности π · r . Разделим длину дуги на радиус и получим радианную меру угла: π · r r = π рад.
Итак, рассматриваемый угол равен π радиан. С другой стороны, это развернутый угол, равный 180 ° . Следовательно 180 ° = π рад.
Связь градусов с радианами
Связь между радианами и градусами выражается формулой
Формулы перевода радианов в градусы и наоборот
Из формулы, полученной выше, можно вывести другие формулы для перевода углов из радианов в градусы и из градуов в радианы.
Выразим один радиан в градусах. Для этого разделим левую и правую части радиуса на пи.
1 р а д = 180 π ° — градусная мера угла в 1 радиан равна 180 π .
Также можно выразить один градус в радианах.
1 ° = π 180 р а д
Можно произвести приблизтельные вычисления величин угла в радианах и наоборот. Для этого возьмем значения числа π с точностью до десятитысячных и подставим в полученные формулы.
1 р а д = 180 π ° = 180 3 , 1416 ° = 57 , 2956 °
Значит, в одном радиане примерно 57 градусов
1 ° = π 180 р а д = 3 , 1416 180 р а д = 0 , 0175 р а д
Один градус содержит 0,0175 радиана.
Формула перевода радианов в градусы
x р а д = х · 180 π °
Чтобы перевести угол из радианов в градусы, нужно значение угла в радианах умножить на 180 и разделить на пи.
Примеры перевода градусов в радианы и радианов в градусы
Пример 1. Перевод из радианов в градусы
Пусть α = 3 , 2 рад. Нужно узнать градусную меру этого угла.
Применим формулу перехода от радианов к градусам и получим:
3 , 2 р а д = 3 , 2 · 180 π ° ≈ 3 , 2 · 180 3 , 14 ° ≈ 576 3 , 14 ° ≈ 183 , 4 °
Аналогично можно получить формулу перевода из градусов в радианы.
Формула перевода из градусов в радианы
y ° = y · π 180 р а д
Переведем 47 градусов в радианы.
Согласно формуле, умножим 47 на пи и разделим на 180.
Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
где — целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
Единичная окружность
О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Единичная окружность в тригонометрии
Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.
Поясним, как единичная окружность связана с тригонометрией.
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.
Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.
Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
- Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
- Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
- В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
- В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:
Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.
Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
- 2π радиан = 360°
- 1 радиан = (360/2π) градусов
- 1 радиан = (180/π) градусов
- 360° = 2π радиан
- 1° = (2π/360) радиан
- 1° = (π/180) радиан
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.
Уравнение единичной окружности
При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
http://ege-study.ru/ru/ege/materialy/matematika/trigonometricheskij-krug/
http://skysmart.ru/articles/mathematic/edinichnaya-okruzhnost
урок 2. Математика ЕГЭ
Тригонометрическая окружность
В этой статье мы поговорим об основах тригонометрии — о тригонометрической окружности. С нее начинается изучение тригонометрии в 10-м классе.
Именно тригонометрические уравнения, как правило, попадаются в самом легком задании второй части ЕГЭ по профильной математике. А умение преобразовывать тригонометрические выражения часто бывают и в первой части. Без этой важной темы на ЕГЭ никак не обойтись.
Тригонометрия очень непривычная тема для школьников. А единичная окружность — это основа, если вы разберетесь с ней, то все остальное не будет казаться таким сложным.
Единичная окружность
Чтобы начать пользоваться тригонометрической окружностью, ее нужно построить.
Для начала нарисуем обычную прямоугольную декартову систему координат — ту, в которой вы должны были в младших классах строить различные графики прямых, парабол и т.д. Горизонтальную ось (ось абсцисс), как обычно, обозначим за (x), а вертикальную (ось ординат) за (y). И нарисуем в этой системе координат обыкновенную окружность единичного радиуса с центром в точке с координатами ((0;0)) — начало координат.
Пусть наша единичная окружность пересекает оси абсцисс и ординат в точках (A,B,C,D), как показано на рисунке. Центр окружности обозначим за точку (O).
Тригонометрическая окружность
Сразу обратите внимание, что оси (x) и (y) делят наш круг на четыре части, их называют четвертями. А еще каждой четверти присвоили свой номер так же, как пронумеровано римскими цифрами на рисунке. В школе часто мучают этими четвертями.
Как считать углы на единичной окружности
А теперь мы подобрались к самому главному: будем рисовать углы на окружности. Все углы отсчитываются, начиная с отрезка (OA) ПРОТИВ часовой стрелки. Например, давайте повернем отрезок (OA) против часовой стрелки на угол (30^o) (как стрелку часов) и получим некоторую точку (M), лежащую на окружности. На рисунке хорошо видно, как мы получили угол (angle{AOM}).
Острый угол на единичной окружности
Таким образом, можно получать любые углы, просто поворачивая отрезок (OA). На рисунке 3 кроме угла (angle{AOM}=30^o) я нарисовал углы: (angle{AON}=45^o), (angle{AOK}=60^o), (angle{AOB}=90^o), (angle{AOF}=120^o), (angle{AOL}=135^o), (angle{AOT}=150^o), (angle{AOC}=180^o).
Рис.3. Углы на тригонометрической окружности
Обратите внимание на углы (angle{AOB}=90^o) и (angle{AOC}=180^o): прямой и развернутый углы соответственно. Они нам понадобятся чуть позже.
Но и это еще не все! Оказывается, бывают углы больше чем (180^o). Например, на нашей окружности такими углами будут (angle{AOW}=210^o), (angle{AOQ}=315^o).
Есть даже угол, который соответствует полному обороту (angle{AOA}=360^o) (см. Рис. 4)
Рис.4. Развернутые углы на тригонометрической окружности
Обратите внимание, что абсолютно все углы отсчитываются от отрезка (OA). И каждому углу соответствует своя точка на окружности. В тригонометрии принято все углы на единичной окружности обозначать просто точками. Например, точка (K) на рисунке 3 соответствует углу в (60^o), точка (W) соответствует углу (210^o).
Любознательный читатель может спросить: а существуют ли углы большие (360^o)? И ответом будет – конечно, да. Нам ничто не мешает повернуть отрезок (OA) на (360^o), а потом продолжить поворачивать его, например, еще градусов на (30^o). И тогда мы получим прекрасный угол, соответствующий точке (V=390^o).
Угол больше одного оборота на тригонометрической окружности
Кстати, точка (V) совпадет с точкой (M), соответствующей углу в (30^o). Получается, одна и та же точка может соответствовать сразу нескольким углам!
Действительно, если к любому углу прибавить (360^o), то вы попадете опять в ту же самую точку. Аналогично можно обратить внимание, что точка (A) одновременно соответствует как минимум двум углам: (0^o) и (360^o).
Угол в (720^o) будет соответствовать двум полным оборотам.
А ведь можно к любому углу прибавить не (360^o), а (720^o), что соответствует сразу 2-м полным оборотам. И так добавлять обороты можно до бесконечности. Значит, любой точке на единичной окружности соответствует бесконечное количество углов с шагом в (360^o). Например, углы (60^o, , 420^o, , 780^o, , 1140^o) и т.д. все лежат в одной и той же точке на окружности, так как они все отличаются на один полный оборот – на (360^o). Это важная мысль, в дальнейшем она нам пригодится.
В общем, можно отсчитывать углы от отрезка (OA) сколько угодно большие и можно накручивать круги до бесконечности. Причем каждой точке соответствует бесконечное количество углов.
А еще существуют отрицательные углы! Оказывается, если повернуть отрезок (OA) ПО ЧАСОВОЙ стрелке, то мы получим отрицательный угол. Например, на рисунке показан угол в (-30^o).
Отрицательные углы на единичной окружности
Любой угол, получившийся поворотом по часовой стрелке, будет отрицательным.
Кстати, точка (M) на окружности, соответствующая углу в (-30^o), отсчитанному по часовой стрелке, совпадает с точкой, соответствующей углу в (330^o), отсчитанным против часовой.
Как переводить радианы в градусы?
Все знают, чтобы измерить некоторое расстояние, можно воспользоваться несколькими единицами измерения: сантиметрами, метрами, километрами или даже световыми годами. Точно так же углы можно измерять по-разному. Мы всю свою жизнь углы измеряли градусами и интуитивно уже понимаем, сколько градусов соответствует визуально какому углу. Довольно легко представить угол в (30^o) или (90^o).
Но, к большому сожалению, в математике углы часто измеряют не в градусах, а в радианах. Так просто удобно в некоторых случаях. А нам с вами ничего не остается, как привыкнуть к новой единице измерения углов.
Ничего страшного в этом нет. Первое, с чем нам нужно познакомиться — это иррациональное число Пи:
$$pi=3,14…;$$
Это известная константа, которая обладает интересными свойствами и используется во множестве научных областей. Но об этом в другой раз. Сейчас нам нужно запомнить, что угол в (pi) радиан это тоже самое, что и угол равный (180^o).
$$pi , рад=180^o;$$
Из этого факта легко переводить радианы в градусы и наоборот:
$$ frac{pi}{2}=frac{180}{2}^o=90^o;$$
$$ frac{pi}{3}=frac{180}{3}^o=60^o;$$
$$ frac{pi}{4}=frac{180}{4}^o=45^o;$$
$$ frac{pi}{6}=frac{180}{6}^o=30^o;$$
Для того, чтобы перевести абсолютно любой угол в градусы, удобно воспользоваться пропорцией. Для примера переведем (frac{5pi}{6}) радиан:
$$pi , рад=180^o;$$
$$frac{5pi}{6} , рад=x^o;$$
Пропорции решаются перемножением крест на крест:
$$pi*x=frac{5pi}{6}*180;$$
$$x=frac{frac{5pi}{6}*180}{pi}=frac{5}{6}*180=150^o.$$
Теперь отметим на тригонометрической окружности углы в радианах так же, как мы отмечали углы в градусах:
Радианы на тригонометрической окружности
Чтобы интуитивно воспринимать радианы, важно помнить, что (pi , рад=180^o;) – это равно половине окружности. Тогда (2pi=360^o) – это полный круг. Представьте, что перед вами пирог или пицца, которую вы режете на части. Тогда, помня, что (pi) это ровно половина пирога, легко представить, что, например, (frac{pi}{6}) – это мы половину пирога поделили на 6 одинаковых частей и взяли одну. А (frac{5*pi}{6}) – это опять делим половину пирога на 6 частей, только в этот раз берем 5 частей из 6-ти, считая от 0.
Можно пользоваться такой аналогией, а можно решать пропорции, как вам удобнее.
Мы научились отмечать на единичной окружности углы и познакомились с радианами.
Теперь приступаем к самому важному: какое отношение имеет этот круг единичного радиуса к тригонометрическим функциям?
Прямоугольный треугольник в тригонометрии
$$sin(alpha)=frac{a}{c};$$
$$cos(alpha)=frac{b}{c};$$
И из этих формул и теоремы Пифагора следует одна из самых важных тригонометрических формул:
$$sin^2(alpha)+cos^2(alpha)=1.$$
Раз эти определения вводились для прямоугольного треугольника, то у них есть большой недостаток. Они работают только в прямоугольном треугольнике, а значит только для острых углов. (В прямоугольном треугольнике, один угол прямой, а два другие обязательно острые).
Но синус и косинус можно посчитать на калькуляторе от абсолютно любого угла. Тогда определение из 9-го класса нам не годится.
И вот здесь на помощь приходит тригонометрическая окружность. При помощи нее мы сейчас постараемся определить синус и косинус.
Нарисуем единичную окружность (единичного радиуса) и отметим на ней какой-нибудь острый угол (angle{AOM}=alpha). Точка (M) лежит на дуге этой окружности и соответствует углу в (30^o). Посмотрите внимательно на рисунок: у точки (M) мы можем определить координаты. Пусть по оси (x) координата точки (M) будет (M_{x}), а по оси (y) — (M_{y}).
Точка (M):
$$(M_{x};M_{y});$$
Координаты точки на окружности
Опустим из точки (M) перпендикуляры на оси координат. Перпендикуляр к оси (x) попадет в точку (M_{x}), а перпендикуляр к оси (y) попадет в (M_{y}). Строго говоря, в математике (M_{x}) и (M_{y}) называются проекциями точки (M) на оси координат.
Мы получили прямоугольный треугольник (triangle{MOM}_{x}). По определению из 9-го класса синус (angle{alpha}) – это отношение противолежащего катета (MM_{x}) к гипотенузе (MO) в (triangle{MOM_{x}}):
$$sin(alpha)=frac{MM_{x}}{MO};$$
Обратите внимание, что (MO) это радиус нашей единичной окружности, значит он равен единице:
$$sin(alpha)=frac{MM_{x}}{MO}=MM_{x};$$
Из рисунка видно, что (MM_{x}=OM_{y}) или, другими словами, длина отрезка (MM_{x}) – это координата точки (M) по оси (y).
Это важный момент! Получается, что (sin(alpha)) равен координате точки (M) по оси (y).
Аналогичные рассуждения можно провести и для косинуса. Косинус по определению в прямоугольном треугольнике (triangle{MOM_{x}}) – это отношение прилежащего катета к гипотенузе:
$$cos(alpha)=frac{OM_{x}}{MO}=OM_{x}=M_{x};$$
Косинус (angle{alpha}), оказывается, будет равен координате точки (M) по оси (x).
Точно такие же рассуждения можно сделать для любого другого угла (beta). Из рисунка ниже видно, что синус (angle{beta}) – это координата точки (N) по оси (y). А косинус угла (angle{beta}) – это координата точки (N) по оси (x). (Показано фиолетовым цветом).
Координаты точки на окружности
Данная логика будет справедлива и для тупых углов. Посмотрите на угол (gamma). Значение синуса (angle{gamma}) будет соответствовать координате точки (K) по оси (y), а косинуса – по оси (x).
Тупой угол на единичной окружности
Можно сделать вывод, что значения синуса любого угла на окружности лежат на оси (y), а значения косинуса на (x).
А раз такие дела, то давайте обзовем наши оси координат не (x) и (y), а осями (cos) и (sin) соответственно. На этих осях будут лежать значения косинуса и синуса всех углов на окружности. И в дальнейшем на всех рисунках оси мы будем обозначать (cos) и (sin) соотвественно.
Обратите внимание еще на один факт: координаты любой точки на окружности обязательно будут больше минус единицы и меньше единицы. Это значит, что значения синуса и косинуса лежат в этом же промежутке. Синус и косинус – это ограниченные функции.
$$sin(alpha)in[-1;1];$$
$$cos(alpha)in[-1;1];$$
Пример 1
Изобразить на тригонометрической окружности синус и косинус (frac{pi}{3}=60^o).
Повернем отрезок (OA) против часовой стрелки на (frac{pi}{3}), получим точку (W) на окружности, которая соответствует этому углу. Если выполнять все это на миллиметровке и строить очень точно, то вы увидите, что координата точки (W) по (y) будет (W_{y}=frac{sqrt{3}}{2}approx0,87), а по оси (x) координата будет (W_{x}=frac{1}{2}).
Значения косинуса и синуса на тригонометрической окружности
Исходя из сказанного выше, мы делаем вывод:
$$sin(frac{pi}{3})=frac{sqrt{3}}{2};$$
$$cos(frac{pi}{3})=frac{1}{2};$$
Посмотрев в таблицу стандартных углов тригонометрических функций, понимаем, что мы сделали все правильно.
Тригонометрическая таблица стандартных углов
Вам, конечно, не придется сидеть с миллиметровкой и высчитывать значения тригонометрических функций, вы будете пользоваться таблицей стандартных углов. А тригонометрическая окружность нужна как большой помощник. При дальнейшем изучении тригонометрии вы в этом не раз убедитесь.
Кстати, интересно и очень важно отметить, что значение, например, синуса (frac{pi}{2}=(90^o)) будет равно 1, а косинус (frac{pi}{2}) будет равен 0. Чтобы это понять, необязательно смотреть в таблицу стандартных углов, такой вывод можно сделать при помощи тригонометрической окружности.
Прямой угол на единичной окружности
Действительно, обратите внимание: угол в (frac{pi}{2}=(90^o) соответствует на окружности точке (B). Координата точки (B) по оси (x) будет (0), а по оси (y) (1). А так как координаты точек на окружности, согласно сказанному выше, и есть значения косинуса и синуса угла, то:
$$sin(frac{pi}{2})=1;$$
$$cos(frac{pi}{2})=0;$$
Знаки синуса и косинуса в зависимости от угла
В самом начале мы не просто так разбивали нашу окружность на четверти. Дело в том, что в каждой из этих четвертей тригонометрические функции имеют разные знаки. В школе обычно заставляют учить в какой четверти какой знак. Но мы, как всегда, постараемся вникнуть в суть и понять, как это работает. Тем более, что ничего сложного здесь нет, если разобраться в материале выше.
Мы с вами выяснили, что координаты любой точки на окружности – это и есть значения синуса и косинуса. Рассмотрим первую четверть: возьмем произвольную точку (M), лежащую на дуге в этой четверти, координата точки (M) по (x) будет (M_{x}) и она будет обязательно положительной, так как лежит между нулем и единицей! А это значит, что косинус угла, соответствующего точке (M) тоже будет положительным. Аналогично координата точки (M) по оси (y) тоже лежит от 0 до 1, а значит синус (angle{MOA}) тоже положительный.
Знак синуса и косинуса в первой четверти
И какой бы угол мы не нарисовали в первой четверти, у него будут положительные координаты, а значит, и положительные значения косинуса и синуса!
Рассмотрим теперь вторую четверть. Руководствуясь той же логикой: координаты произвольной точки (K), лежащей на дуге из второй четверти по (x) будут отрицательны, а по (y) положительны. Делаем вывод, что косинус любого угла из второй четверти будет отрицательным, а синус положительным.
Точно так же в третьей четверти и косинус, и синус будут отрицательными.
В четвертой четверти косинус положительный, а синус отрицательный.
Тангенс и котангенс на тригонометрической окружности
Теперь разберемся, как пользоваться тригонометрической окружностью в случае тангенса и котангенса.
Опять из программы 9-го класса вы должны помнить, что в прямоугольном треугольнике тангенс – это отношение противолежащего катета к прилежащему. А котангенс – отношение прилежащего к противолежащему.
$$ tg(alpha)=frac{a}{b};$$
$$ctg(alpha)=frac{b}{a};$$
Отсюда, кстати, следуют несколько простейших тригонометрических формул:
$$tg(alpha)=frac{sin(alpha)}{cos(alpha)};$$
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)};$$
$$tg(alpha)*ctg(alpha)=1.$$
Тангенс и котангенс в прямоугольном треугольнике
Тангенс на окружности и его знаки
Чтобы на окружности можно было пользоваться тангенсом, нам понадобится дополнительная ось. Проведем ее перпендикулярно оси (x) (теперь это у нас ось косинусов) через точку (A):
Тангенс на тригонометрической окружности
Эта ось параллельна оси (y) и полностью ее дублирует. В точке (A) будет координата (0). Отметим на окружности в первой четверти произвольную точку (L). Соединим точку (L) с центром окружности и продлим прямую до пересечения с новой осью в точке (F).
Мы получили прямоугольный треугольник (FOA). В этом прямоугольном треугольнике можем расписать тангенс по определению:
$$tg(angle{FOA})=frac{FA}{OA};$$
А так как (OA) это ни что иное, как радиус единичной окружности:
$$tg(angle{FOA})=FA;$$
А (FA) – это координата точки (F) по нашей новой оси.
Значит (tg(angle{FOA})=tg(angle{LOA})) будет равен координате точки (F) по новой оси.
Аналогичным образом я могу выбрать другую произвольную точку (P) на окружности в первой четверти, продлить до пересечения с новой осью, получить некоторую точку (T). И опять, тангенс получившегося угла (angle{TOA}=angle{POA}) будет равен координате точки (T) на новой оси.
Тут все ясно, но возникает справедливый вопрос: а что, если угол лежит не в первой четверти?
Логика рассуждений сохраняется: произвольному углу (angle{QOA}) соответствует своя точка на окружности (Q), соединим точку (Q) с центром окружности и продлим до пересечения с новой осью в точке (H). Оказывается, тангенс (angle{QOA}) будет равен координате точки (H) по новой оси.
Тангенс на тригонометрической окружности от тупого угла
Общая логика простая – берем точку на окружности, соответствующую некоторому углу (alpha), соединяем ее с центром окружности и продляем до пересечения с осью тангенса. Координата точки пересечения с осью тангенса и будет значением тангенса угла (alpha).
Эта ось называется осью тангенсов, так как на ней лежат значения тангенсов всех углов на окружности.
Стоит обратить внимание на знаки тангенса. Если соединять точки на окружности, лежащие в первой и третьей четвертях с центром окружности, то пересекать ось тангенсов эти прямые будут всегда выше (0). Значение тангенса любых углов из первой и третьей четвертей будет положительно.
А если углы лежат во второй и четвёртой четвертях, то их тангенс будет отрицательным.
Котангенс на окружности и его знаки
С котангенсом ситуация очень похожа на тангенс. Только в этот раз мы проводим горизонтальную ось перпендикулярно оси синусов через произвольную точку (B). Эта ось будет параллельна оси (x) и полностью ее дублировать. Сразу назовем эту ось осью котангенса. Ноль на оси котангенса будет совпадать с точкой (B).
Теперь выберем произвольную точку (N) на окружности, этой точке будет соответствовать угол (angle{NOA}). Соединим точку (N) с центром окружности и продлим получившуюся прямую до пересечения с осью котангенса в точке (Q).
Котангенс на тригонометрической окружности
Обратите внимание, что (angle{NOA}=angle{OQB}), как накрест лежащие при параллельных прямых (оси синуса и котангенса). Рассмотрим прямоугольный треугольник (BOQ) и распишем в нем котангенс (angle{OQB}), как отношение прилежащего катета к противолежащему в прямоугольном треугольнике:
$$ctg(angle{NOA})=ctg(angle{OQB})=frac{QB}{OB}=QB;$$
Мы получили, что котангенс (angle{NOA}) равен координате точки (Q) на оси котангенса.
Аналогичным образом можно выбрать произвольную точку на единичной окружности, соединить ее с центром окружности, продлить получившуюся прямую до пересечения с осью котангенса, координата получившейся точки будет значением котангенса угла, соответствующего точке на окружности.
И у внимательного читателя должен возникнуть вопрос! Ведь не любую точку на окружности возможно соединить с центром окружности и продлить до пересечения с осью тангенса или котангенса.
Действительно, если точки (B) и (D) соединить с центром окружности, то получится прямая параллельная оси тангенса, а значит, она никогда не пересчёт ее. Как же тогда найти значения тангенса углов, соответствующих точкам (B) и (D)? А никак, тангенс этих углов не существует. Точкам (B) и (D) соответствуют углы: (frac{pi}{2}=90^o, , frac{3pi}{2}=270^o, , -frac{pi}{2}=-90^o) и т.д. Каждой точке на окружности, как мы помним, соответствует бесконечное количество углов с периодом (2pi=360^o).
Аналогичные рассуждения с котангенсом. Котангенс не будет существовать от углов: (0, , pi=180^o, , -pi=-180^o, , 2pi) и т.д.
Несколько важных свойств тангенса и котангенса.
- Из построения можно заметить, что для любых углов из первой и третьей четвертей котангенс и тангенс будут положительные, а для второй и четвертой – отрицательные;
- Тангенс и котангенс – неограниченные функции. Это значит, что они могут принимать абсолютно любые значения: (tg(alpha)in(-infty;+infty);) и (ctg(alpha)in(-infty;+infty);)
- Тангенс не существует от углов (frac{pi}{2}*n), где (n in Z) ((n) целое число);
- Котангенс не существует от углов (pi*n), где (n in Z) ((n) целое число);
Пример 2
Изобразить на тригонометрической окружности (ctg(frac{pi}{6})).
Котангенс 30 градусов на тригонометрической окружности
- Рисуем единичную окружность;
- Повернем отрезок (OA) на угол (30^o), что то же самое, что и на (frac{pi}{6}) радиан. Пусть угол пересекает нашу окружность в точке (M);
- Нарисуем ось котангенса параллельно оси косинусов через точку (B);
- Продлим (OM) до пересечения с осью котангенсов в точке (E);
- Координата точки (E) будет соответствовать значению котангенса угла (frac{pi}{6});
- Если делать, опять же, по миллиметровке и измерить аккуратно расстояние (BE), то координата точки (E) будет (sqrt{3}approx1,73;)
- Согласно таблице стандартных углов (ctg(frac{pi}{6})=sqrt{3}). Значит все построено верно;
Симметрия тригонометрических функций
При помощи элементарной геометрии и тригонометрической окружности можно вывести несколько очень важных свойств.
Для начала поговорим про синус и косинус некоторого острого угла (angle{alpha}). Посмотрите на рисунок. Как мы с вами выяснили, значение синуса угла (alpha) будет равно координате точки (M) по оси (y).
Симметричные свойства синуса и косинуса на единичной окружности
Проведем из точки (M) перпендикуляр к оси (y) и продлим до пересечения с окружностью в точке (N). Точка (N) будет соответствовать углу (angle{NOA}).
А так как координаты точек (N) и (M) по (y) равны, то и значения синусов углов (angle{NOA}) и (angle{MOA}) будут равны.
Теперь обратите внимание, что получившаяся картинка симметрична относительно вертикальной оси (y). А значит
$$angle{NOC}=angle{MOA}=angle{alpha};$$
$$angle{NOA}=180-angle{NOC}=180-alpha;$$
А сложив вместе два вывода, получаем:
$$sin(angle{MOA})=sin(angle{NOA}) Rightarrow sin(alpha)=sin(180-alpha);$$
Теперь поговорим про косинус. Координаты у точек (M) и (N) по оси (x) будут одинаковы по модулю, но разные по знаку, так как картинка полностью симметрична относительно оси (y). А это означает, что значения косинусов (angle{MOA}) и (angle{NOA}) будут равны по модулю, но противоположны по знаку:
$$cos(angle{MOA})=-cos(angle{NOA});$$
$$cos(angle{alpha})=-cos(180-angle{alpha});$$
Еще раз нарисуем тригонометрическую окружность и отметим произвольный острый угол (alpha), соответствующий точке (P) на окружности.
Симметричные свойства синуса и косинуса на единичной окружности
Проведем перпендикуляр из точки (P) к оси (x) и продлим до пересечения с окружностью в точке (K). Получили два равных геометрически, исходя из горизонтальной симметрии, угла (angle{POA}=angle{KOA}=angle{alpha}).
Но так как на окружности принято углы, отсчитанные по часовой стрелке, брать со знаком минус, то:
$$angle{KOA}=-angle{alpha};$$
$$angle{POA}=angle{alpha};$$
Обратите внимание, что координаты точек (P) и (K) по оси (x) буду одинаковые, а значит и значения косинусов углов, соответствующих этим точкам, будут одинаковы:
$$cos(angle{POA})=cos(angle{KOA});$$
$$cos(alpha)=cos(-alpha);$$
А вот координаты по оси (y) у точек (P) и (K) будут равны по модулю, но противоположны по знаку. Это дает нам следующее соотношение:
$$sin(-alpha)=-sin(alpha).$$
Кстати, из сказанного выше следует важный вывод, который нам пригодится в дальнейшем при решении тригонометрических уравнений. Из тригонометрической окружности видно, что каждому значению синуса и косинуса соответствует как минимум два угла (кроме единицы и минус единицы).
Теперь обсудим некоторые свойства тангенса и котангенса.
Нарисуем единичную окружность и отметим на ней произвольный угол (angle{LOA}=beta). Продлим сторону (LO) угла до пересечения с осью тангенсов в точке (I) и до пересечения с окружностью с другой стороны в точке (S). Обратите внимание, что значение тангенса углов (angle{LOA}) и тупого угла (angle{SOA}) будут равны! Так как ось тангенсов пересекают в одной точке.
Симметричные свойства тангенса на единичной окружности
$$tg(angle{LOA})=tg(angle{SOA});$$
Кроме этого отметим, что, так как углы (angle{LOA}) и (angle{SOA}) лежат на одной прямой:
$$angle{SOA}=angle{LOA}+180^o=beta+180^o;$$
И получаем:
$$tg(beta)=tg(beta+180);$$
А теперь давайте отметим на рисунке угол (angle{TOA}=-beta). Минус появился потому, что угол (beta) посчитан по часовой стрелке. Продлим (TO) до пересечения с осью тангенса в точке (E). Так как картинка абсолютно симметрична относительно оси (x), то (EA=IA), значит координаты точек (I) и (E) на оси тангенса будут равны по модулю, но противоположны по знаку:
Симметричные свойства тангенса на единичной окружности
$$tg(angle{LOA})=-tg(angle{TOA});$$
$$tg(beta)=-tg(-beta);$$
Абсолютно аналогичные рассуждения можно провести и для котангенса. В качестве тренировки попробуйте это сделать сами:
$$ctg(beta)=ctg(beta+180);$$
$$ctg(beta)=-ctg(180-beta);$$
Выпишем еще раз все полученные формулы:
$$sin(alpha)=sin(180-alpha);$$
$$cos(alpha)=-cos(180-alpha);$$
$$cos(alpha)=cos(-alpha);$$
$$sin(-alpha)=-sin(alpha).$$
$$tg(beta)=tg(beta+180);$$
$$tg(beta)=-tg(-beta);$$
$$ctg(beta)=ctg(beta+180);$$
$$ctg(beta)=-ctg(180-beta);$$
В школе заставляют их учить, но, как видите, достаточно научиться пользоваться тригонометрической окружностью и они легко выводятся.
Краткие правила пользования тригонометрической окружностью
- Углы, отсчитываемые против часовой стрелки, положительны, по часовой – отрицательны;
- Каждой точке на окружности соответствует бесконечное количество углов с периодом (360^o) или (2pi);
- Координата по (x) любой точки на окружности – это значение косинуса угла, координата по (y) – синуса;
- Значения косинуса и синуса принадлежат промежутку ([-1;1]);
- Синус положительный в первой и второй четвертях, отрицательный – в третьей и четвертой;
- Косинус положительный в первой и четвертой, отрицательный – во второй и третьей;
- Чтобы найти тангенс угла, нужно нарисовать ось тангенса параллельно оси (y). Соединить точку на окружности, соответствующую углу, с центром окружности и продлить до пересечения с осью тангенса. Координата полученной точки на оси тангенса и будет значением тангенса угла;
- Чтобы найти котангенс угла, нужно нарисовать ось котангенса параллельно оси (x). Соединить точку на окружности, соответствующую углу, с центром окружности и продлить до пересечения с осью котангенса. Координата полученной точки на оси котангенса и будет значением котангенса угла;
- Тангенс и котангенс положительны в первой и третьей четвертях, отрицательны – во второй и четвертой;
- Тангенс и котангенс могут принимать значения из промежутка ((-infty;+infty)).
Урок с подробным разбором тригонометрических уравнений. Рассмотрим основные методы решения простейших уравнений из тригонометрии, метод замены переменной, однородные уравнения и уравнения с обратными тригонометрическими функциями
Как пользоваться формулами приведения? Правило лошади, единичная окружность и формулы суммы и разности для нахождения формул приведения.
Разбираем тригонометрию с нуля. Синус, косинус, тангенс и котангенс в прямоугольном треугольнике. Таблица стандартных углов и свойства тригонометрических функций.
Подробный разбор метода координат в стереометрии. Формулы расстояния и угла между скрещивающимися прямыми. Уравнение плоскости. Координаты вектора. Расстояние от точки до плоскости. Угол между плоскостями. Выбор системы координат.
Как решать уравнения со степенями. Разбираем основные методы и способы решения простейших показательных уравнений.
Урок по теме логарифмы и их свойства. Разбираемся, что такое логарифм и какие у него свойства. Научимся считать выражения, содержащие логарифмы. И рассмотри несколько возможных заданий №4 из ЕГЭ по профильной математике.
Цикл уроков про степени и логарифмы и их свойства. Учимся решать показательные и логарифмические уравнения и неравенства. Задания №9 и №15 ЕГЭ по профильной математике.
Индивидуальные занятия с репетитором для учеников 6-11 классов. Для каждого ученика я составляю индивидуальную программу обучения. Стараюсь заинтересовать ребенка предметом, чтобы он с удовольствием занимался математикой и физикой.
В прошлый раз мы с вами ответили на первый вопрос, касаемый работы с углами. А именно — как отсчитываются углы. Рассмотрели положительные и отрицательные углы, а также углы, большие 360 градусов. И на круге углы порисовали.)
В этом же уроке настал черёд ответить на второй вопрос, связанный с измерением углов. Здесь мы разберёмся с загадочными радианами и особенно — с пресловутым числом «пи», которое будет мозолить нам глаза на протяжении всего дальнейшего изучения тригонометрии. Поймём, что это за число, откуда оно берётся и как с ним работать. И задания порешаем, само собой. Стандартные и не очень…)
Разберёмся? Ну сколько же можно бояться числа «пи», в конце-то концов!)
Итак, в чём же измеряются углы в математике? Начнём с привычного и знакомого. С градусов.
Что такое один градус? Градусная мера угла.
К градусам вы уже попривыкли. Геометрию изучаете, да и в жизни постоянно сталкиваетесь. Например, «повернул на 90 градусов».) Короче, градус — штука простая и понятная.
Вы и вправду так думаете? Тогда сможете сказать мне, что такое градус? Нет, гуглить и потрошить Википедию не надо. Ну как, слабо с ходу? Вот так-то…
Начнём издалека. С древнейших времён. А именно — с двух очагов древних цивилизаций Вавилона и Египта.)
Градус — это 1/360 часть окружности. И всё!
Смотрим картинку:
Придумали градусы в Древнем Вавилоне.) Как? Очень просто! Просто взяли да разбили окружность на 360 равных кусочков. Почему именно на 360? А не на 100 или на 1000? Вроде бы, число 100 поровнее, чем 360… Вопрос хороший.
Основная версия — астрономическая. Ведь число 360 очень близко к числу дней в году! А для наблюдений за Солнцем, Луной и звёздами это было оч-чень удобно.)
Кроме того, в астрономии (а также строительстве, землемерии и прочих смежных областях) очень удобно делить окружность на равные части. А теперь давайте прикинем чисто математически, на какие числа делится нацело 100 и на какие — 360? И в каком из вариантов этих делителей нацело больше? А людям такое деление очень удобно, да…)
Что такое число «пи»? Как оно возникло?
А теперь переместимся из Древнего Вавилона в Древний Египет. Примерно в то же самое время там разгадывали другую загадку. Не менее интересную, чем вопрос, на сколько частей бить окружность. А именно — во сколько раз длина окружности больше её диаметра? Или по-другому: чему равна длина окружности с диаметром, равным единице?
И так измеряли и сяк… Каждый раз получалось чуть-чуть больше трёх. Но как-то коряво получалось, неровно…
Но они, египтяне, ни в чём не виноваты. После них математики всех мастей продолжали мучиться аж до 18 века! Пока в 1767 году окончательно не доказали, что, как бы мелко ни нарезать окружность на равные кусочки, из таких кусочков сложить точно длину диаметра нельзя. Принципиально нельзя. Только лишь примерно.
Нет, конечно же, во сколько раз длина окружности больше её диаметра установили давным-давно. Но, опять же, примерно… В 3,141592653… раза.
Это число — и есть число «пи» собственной персоной.) Да уж… Корявое так корявое… После запятой — бесконечное число цифр безо всякого порядка, безо всякой логики. В математике такие числа называются иррациональными. И на сегодняшний день доказательство факта иррациональности числа «пи» занимает аж десять (!) лекций на 4-м курсе мехмата МГУ… Этот факт, кстати, и означает, что из одинаковых кусочков окружности её диаметр точно не сложить. Никак. И никогда…
Конечно, рациональные приближения числа «пи» известны людям ещё со времён Архимеда. Например:
22/7 = 3,14285714…
377/120 = 3,14166667…
355/113 = 3,14159292…
Сейчас, в век суперкомпьютеров, погоня за десятичными знаками числа «пи» не стихает, и на сегодняшний день человечеству известно уже два квадриллиона (!) знаков этого числа…
Но нам для практического применения такая сверхточность совершенно не требуется. Чаще всего достаточно запомнить всего лишь две цифры после запятой.
Запоминаем:
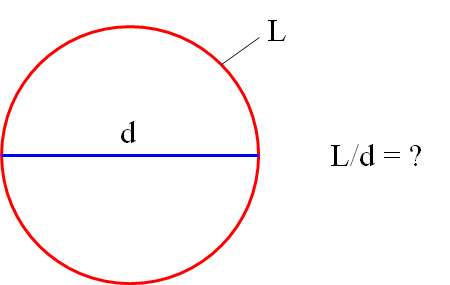
Вот и всё. Раз уж нам ясно, что длина окружности больше её диаметра в «пи» раз, то можно записать (и запомнить) точную формулу для длины окружности:
Здесь L — длина окружности, а d — её диаметр.
В геометрии всяко пригодится.)
Для общего развития скажу, что число «пи» сидит не только в геометрии или тригонометрии. Оно возникает в самых различных разделах высшей математики. В интегралах, например. Или в теории вероятностей. Или в теории комплексных чисел, а также рядов. Само по себе возникает, хотим мы того или нет… Поступите в ВУЗ — убедитесь лично.)
Ну а теперь снова вернёмся к старым добрым градусам. Как мы помним, один градус — это 1/360 часть окружности. С исторической и практической точек зрения людям такое деление на 360 равных частей оказалось очень даже удобно, но…
Как выяснилось гораздо позже Древнего Вавилона, градусы удобны далеко не всем. Например, высшей математике они ой как неудобны! Высшая математика — дама серьёзная. По законам природы устроена. И она справедливо заявляет: «Сегодня вы на 360 частей круг разбили, завтра — на 100 разобьёте, послезавтра — на 250… А мне что делать? Каждый раз под ваши хотелки подстраиваться?»
Против природы не попрёшь… Пришлось прислушаться и уступить. И ввести новую меру угла, не зависящую от наших хотелок. )
Итак, знакомьтесь — радиан!
Что такое один радиан? Радианная мера угла.
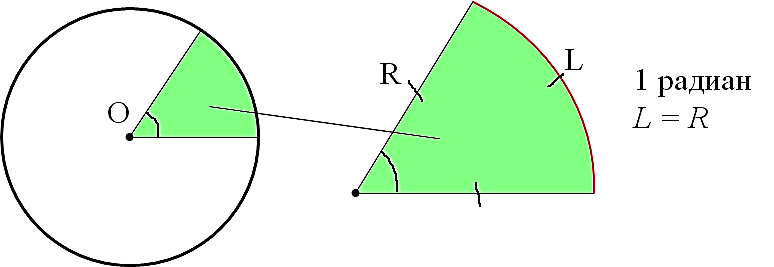
В основе определения радиана — та же самая окружность. Угол в 1 радиан — это угол, который отсекает от окружности дугу, длина которой (L) равна радиусу окружности (R). И всё!
Смотрим картинку:
Причём величина угла в один радиан не зависит от радиуса окружности! Никак. Можно нарисовать очень большую окружность, можно очень маленькую. Но угол, отсекающий от окружности дугу, равную радиусу, никогда не изменит своей величины и будет составлять ровно один радиан. Всегда. Это важно.)
Запоминаем:
Угол в один радиан — это угол, вырезающий из окружности дугу, равную радиусу окружности. Величина угла в 1 радиан не зависит от радиуса окружности.
Кстати говоря, градусная мера угла тоже не зависит от радиуса окружности. Большая окружность, маленькая — углу в один градус без разницы. Но градус — это величина, искусственно придуманная людьми для их личного удобства! Древними вавилонянами, если мы помним.) 1/360 часть окружности. Так уж сложилось чисто исторически. А если бы по каким-то причинам договорились на 100 частей разбить окружность? Или на 200? Кто знает, что тогда называлось бы градусом сегодня… Вот на сколько частей разобьём окружность, такой «градус» и получим. А вот радиан — штука универсальная!) К способу разбиения окружности никак не привязан. Строго дуга, равная радиусу! И чем больше радиус, тем больше (по длине) будет и соответствующая вырезаемая дуга. И наоборот. Но сама величина угла в один радиан не меняется. И разбиение окружности (любой!) радианами — всегда одинаковое. И сейчас мы в этом лично убедимся.)
Как переводить радианы в градусы и обратно?
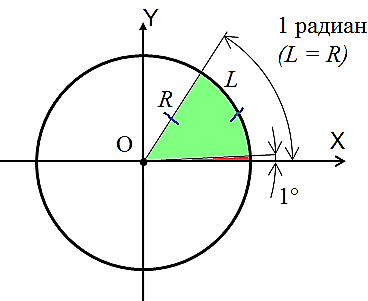
К этому моменту вам уже должно быть интуитивно понятно, что один радиан существенно больше одного градуса. Всё-таки непонятно? Тогда смотрим снова на картинку:
Будем считать, что малюсенький красный угол имеет величину примерно один градус. Совсем крохотный уголок, почти и нет его… А большой зелёный угол — примерно один радиан! Чувствуете разницу?) Конечно же, один радиан сильно больше одного градуса…
А вот теперь начинается самое интересное! Вопрос: а во сколько раз один радиан больше одного градуса? Или сколько градусов в одном радиане? Сейчас выясним!)
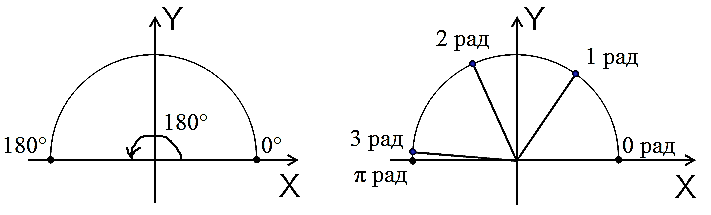
Смотрим на очередные картинки:
На картинке слева изображён полукруг. Обычный развёрнутый угол величиной 180°. А вот на картинке справа — тот же самый полукруг, но нарезанный радианами! Видно, что в 180° помещается примерно три с хвостиком радиана.
Вопрос на засыпку: как вы думаете, чему равен этот хвостик?)
Да! Он равен 0,141592653… Привет, число «пи», вот мы про тебя и вспомнили!)
Стало быть, в 180° укладывается 3,141592653… радиан. Понятное дело, что каждый раз писать такое длинное число неудобно, поэтому пишут приближённо:
Или точно:
Вот и всё. Вот и весь секрет тотального присутствия числа «пи» в тригонометрии. Эту простую формулку надо знать железно. Уловили?)
Так сколько же градусов в одном радиане? Не вопрос! Если в «пи» радианах содержится 180 градусов, то сколько же тогда градусов сидит в одном радиане? Правильно, в «пи» раз меньше! То есть меньше примерно в 3,14 раза.
Вот и делим обе части нашего соотношения на «пи» и получаем один радиан в градусах:
Это приближённое равенство также очень полезно запомнить. В одном радиане примерно 60 градусов. Такой грубой оценки бывает вполне достаточно для ответа на очень многие каверзные вопросы, связанные с углами. Бывает и недостаточно, конечно. В своё время мы такие хитрые задачки рассмотрим.)
Но это не самое главное применение этой формулы!) А самое главное — перевод радианов в градусы и обратно.
Переводим радианы в градусы!
Чаще всего углы в тригонометрии заданы в радианах с числом «пи». Это — самая стандартная ситуация. Если угол задан в радианах с числом «пи», то всё очень просто. Мы знаем, что «пи» радиан — это 180 градусов. Вот и подставляем вместо «пи» радиан — число 180. Сокращаем всё что сокращается и получаем угол в градусах.
Например:
Или более мудрёный угол:
Просто, правда?)
Переводим градусы в радианы!
Обратный перевод градусов в радианы чуть сложнее, но ненамного. Если угол задан в градусах, то сначала нам надо узнать, сколько составляет один градус в радианах. И умножить это значение на количество градусов.) И чему же равен 1° в радианах?
Снова смотрим на нашу формулу и соображаем. Если 180° — это «пи» радиан, то 1° в 180 раз меньше. Вот и делим обе части формулы на 180! Получаем, что 1° в радианах равен:
Вот и все дела. Умножаем дробь π/180 на количество градусов, сокращаем что сокращается и получаем угол в радианах. Например:
Или аналогично:
Вот и всё. Заменять «пи» на примерно 3,14 никакой необходимости нет: его всегда буквой пишут. Что правда, то правда: нас же в заданиях обычно точный ответ интересует! А не приближённый.) Кстати, кому интересен приближённый ответ, посчитайте на калькуляторе. Получите примерно 0,628 и 2,356 радиана соответственно.
Итак, в непринуждённой беседе с лирическими отступлениями мы узнали, что радианы — это очень даже просто, не больно и не страшно.) Да и перевод туда-обратно несложен. И «пи» — не кусается… Так откуда же проблемы?
Что ж, вскрою тайну. Всё дело в том, что в тригонометрии значок градусов — пишется. Всегда и везде. Например, cos30° — это косинус 30 градусов! А вот значок радианов («рад») — не пишется! Он — подразумевается. В чём причина — неизвестно. Может, обленились математики, может ещё что… Но договорились не писать. Например, sin5 — это синус пяти радианов!
Это и приводит к казусам. Человек смотрит на пример, видит «пи» и автоматически считает, что это 180°. Везде и всюду. Кстати, это срабатывает. До поры до времени, пока примеры — типовые. Но любое отклонение примера от шаблона — тут же валит наповал! Почему?
Потому, что само по себе «пи» — это число! А никакие не градусы! Это «пи» радиан = 180°!
Ещё раз запоминаем:
Просто «пи» — это число! «Пи» РАДИАН — это 180°!
Это заклинание надо понимать железно. Причём не просто механически зазубрить, а именно понимать каждое слово и каждый значок! И особенно — слово «радиан». Я не шучу. Ибо, если на вопрос, «Что такое «пи» в тригонометрии?», вы, блистая знаниями, радостно заявляете:
«Пи — это 180 градусов!!!» ,
то это говорит о том, что вы не понимаете до конца смысла этой зелёной фразы. И все дальнейшие беседы уже бессмысленны, да…
Ещё раз: «пи» — это число! Примерно равное 3,14. Точного значения этого числа не знает никто: оно бесконечно длинное, корявое, иррациональное. Но — число! Такое же, как 2 или 7. Можно пройти примерно «пи» километров. Три километра и ещё около 140 метров. Можно купить «пи» килограммов картошки. Если продавец образованный встретится.) Можно выпить «пи» литров кока-колы. Если здоровье не жалко… И так далее…
Всё равно непонятна зелёная запись? Хорошо, вот вам простые житейские фразы:
1 километр — это 1000 метров;
3 часа — это 180 минут;
2 года — это 730 дней;
И тому подобное. Точно так же и с градусами/радианами:
«Пи» радиан — это 180 градусов!
Уяснили, что «пи» — это просто число? Или я уже достал вас этой заезженной фразой? Ну ладно, убедили. Тогда вот вам парочка нестандартных вопросов:
1. Что больше?
или
2. Что меньше?
cos5°
или
cos5
Если у вас случился ступор, не беда. Вспоминаем нашу мантру: «Пи» — это число! В первом синусе нам чётко сказано, что угол — в градусах! Следовательно, машинально заменять «пи» на 180° — нельзя. «Пи» градусов — это примерно 3,14°. Вот и пишем:
Во втором синусе никаких значков нет. Значит, там — радианы. И вот тут замена «пи» на 180° — вполне законна.) Переводим радианы в градусы и получаем:
А теперь сравниваем эти два синуса. Как? По кругу, разумеется! Рисовать углы мы с вами уже умеем, что такое синус угла на круге — тоже знаем. Вперёд! Рисуем круг, углы примерно 0,79° и 45° и смотрим какие синусы у этих углов. Даже на самом корявом круге будет видно, что sin45° гораздо больше, чем sin0,79°.
С косинусами — всё то же самое. Рисуем на круге в правильных четвертях углы примерно 5 градусов и 5 радианов (помним, чему примерно равен один радиан в градусах?). Круг нам всё и подскажет. А именно, что cos5 меньше, чем cos5°.
Вообще, задачки с углами в радианах без «пи» (типа определить знак выражения sin10∙cos20) относятся к разряду нестандартных. В следующем уроке разберём парочку таких.)
Ну что, потренируемся с переводом углов?) Решаем несложные задания.
1. Переведите следующие углы из градусной меры в радианную:
180°; 0°; 360°; 90°; 270°.
Ответы (по возрастанию):
Как вы думаете, что это были за углы? Да! Это углы, которые попадают на координатные оси! Эти опорные значения надо держать в голове надёжно. До автоматизма! Как в градусах, так и в радианах. Зачем? Да всё за тем же! Для правильного распределения любых углов по четвертям.) Это полезное умение — залог успеха в любом задании по тригонометрии. Любом! От примитивных примеров до вполне себе солидных ЕГЭшных задачек части 2 (уравнения с отбором корней, тригонометрические неравенства и прочие хитрые штучки).
Продолжаем развлекаться.
2. Переведите углы в радианную меру:
30°; 45°; 60°.
Ответы (в беспорядке):
Получилось? Рад за вас. Почему я выделил именно эти три угла? По той же самой причине. Эти углы — особые личности в тригонометрии. Потому что именно про эти углы вы обязаны знать всё! И где они находятся и весь комплект их тригонометрических функций. Скажем, значение sin20° вы знать не обязаны. А вот sin30° — уж будьте так добры! Это обязательные значения, без которых во всей остальной тригонометрии делать вообще нечего. Но об этом — в отдельном уроке.)
Продолжим тренировку.
Переведите следующие углы из радианной меры в градусную:
Ответы (в беспорядке):
300°; 225°; 120°; 330°; 240°; 135°; 210°; 315°; 150°.
А это что за углы? Правильно! Это углы, в пределах одного оборота, кратные предыдущим трём! Но не попадающие на оси координат. Такие углы вы также обязаны уметь просчитывать! И более того, все углы, кратные 30, 45 или 60 градусам, вы обязаны уметь просчитывать! Как в пределах одного оборота, так и за его пределами. Как положительные, так и отрицательные… В соответствующем уроке мы научимся с вами проделывать такие полезные вещи.
Если и это получилось, то тогда можно считать, что перевод радианов в градусы и обратно — уже не ваша проблема. Но перевод углов из одной размерности в другую — это лишь ещё один шаг вперёд к успешному постижению тригонометрии. Шаг мощный, но недостаточный. Ведь, чаще всего, с углами надо потом ещё и что-то делать.) Рисовать на круге, например. Или синус/косинус считать. Да и тангенс/котангенс тоже…
Второй серьёзный шаг — это умение правильно определять положение любого угла на тригонометрическом круге. Любого! Как в градусах, так и в радианах. С градусами на круге мы уже плотно поработали в предыдущем уроке. Теперь настал черёд набивать руку в работе с радианами.
Об этом — в следующей теме.
Построение тригонометрической окружности
А теперь сделай вот что: возьми-ка в руки циркуль и нарисуй любую (самую любую, но лучше достаточно немаленькую) окружность.
Получилось?
Ну да ладно, задачка не самая сложная. Так, ты не потерял ту точку, в которой у тебя был центр (куда ты прикладывал острую ножку циркуля)? Я вот у себя потерял, растяпа! Ну ладно, найду!
А что пока делать тебе?
А вот что: проведи через эту точку две линии, которые пересекаются «прямым крестиком», то есть под прямым углом. И пусть их точка пересечения – это центр (который ты не потерял!) окружности.
Нарисовал? У меня получилось что-то вроде вот этого.
Правда я чуть-чуть поторопился и сразу «обозвал» эти прямые ( displaystyle x) и ( displaystyle y) и точку пересечения через ( displaystyle O).
А что такое в таком случае ( displaystyle R)?
Это радиус нашей окружности.
Как называлась наша тема? Единичная окружность.
Тогда будем считать ( но не будем так рисовать!), что ( displaystyle R=1 ).
А рисовать мы так не будем, потому что на такой крошечной картинке ты ничего не разберешь! Ты же понимаешь, что когда инженеры проектируют самолеты, скажем, они не рисуют его в натуральную величину?
Так и мы не будем рисовать единичную окружность в самом деле единичной. Это нам нужно исключительно для удобства.
Теперь отмечаем: ( displaystyle OR=1). Что же мы с тобой на самом деле сделали? А вот что:
Мы поместили нашу окружность в систему координат ( displaystyle mathbf{X0Y}), сделав центр окружности началом координат!
Это позволит изучать свойства такой окружности уже не с геометрической, а с математической точки зрения. Этот подход был придуман хитрым математиком и философом Рене Декартом еще в 17 веке!
Перегнать фигуру в цифры, каково, а?
Но допустим, мы поместили нашу окружность в координаты. В скольких точках она пересекается с осями системы координат?
В четырех. Вот они:
Эти точки ( displaystyle left( A; B; C; D right)) имеют координаты:
( displaystyle Aleft( 1,0 right)); ( displaystyle Bleft( 0,1 right)); ( displaystyle Cleft( -1;0 right)); ( displaystyle Dleft( 0;-1 right)).
Теперь вспомни, как называются области, на которые этот «координатный крестик» делит всю плоскость?
Они называются координатные четверти.
Тогда посмотри на рисунок. Наша окружность тоже оказалась разрезанной на 4 равные дольки. Давай пронумеруем каждую из этих долек против часовой стрелки:
Ты уже можешь догадаться, как называются эти самые дольки:
1 четверть, 2 четверть, 3 четверть, 4 четверть
(Прямо как четверти в школе!)
Углы на тригонометрической окружности
Теперь давай сделаем еще вот что. Снова посмотрим на предыдущую картинку.
Чему на ней равен ( displaystyle angle AOB)?
Он равен ( displaystyle 90{}^circ ).
Также, как и ( displaystyle angle BOC), как и угол ( displaystyle angle COD), и угол ( displaystyle angle DOA).
( displaystyle angle text{AOB}=angle text{BOC}=angle text{COD}=angle text{DOA}=90{}^circ )
Тогда чему равна их сумма?
Она равна ( displaystyle 360{}^circ ).
Вместе же эти 4 угла составляют всю окружность целиком!
Градусная мера окружности равна ( displaystyle 360{}^circ )!
( displaystyle angle Atext{OC}=angle text{AOB}+angle text{BOC}=180{}^circ )
Что еще можно вытянуть? А вот что:
( displaystyle angle Atext{OD}=angle text{AOB}+angle text{BOC}+angle text{COD}=270{}^circ )
Отметим эти значения также на нашей окружности:
Однако, ты нередко можешь увидеть и вот такую картинку:
где вместо привычных нам градусов появляются некие буковки «пи» ( displaystyle pi ) с цифрами.
В чем же тут дело, кто прав и кто виноват?
Ну так вот, кто прав, кто виноват, решать, увы, не нам. Но чтобы «воз не был поныне там», нам нужно уделить этому моменту пару минут времени.
В самом деле, есть два способа измерять углы:
- Через градусы
- Через радианы
Как измерять углы через градусы мы все знаем. Это нам привычно. Однако в некоторых случаях их измеряют по-другому (как в градуснике есть несколько шкал: цельсий, кельвин, фаренгейт и т. д.), а именно: через радианы.
Для того, чтобы перейти от одной формы записи к другой, используется вот такое основное соотношение:
( displaystyle 180{}^circ =pi ~рад.)
И все, больше знать ничего не надо!
По пропорции ты легко получишь, что для того, чтобы пересчитать угол из градусов в радианы, нужно применить вот такую незамысловатую формулу:
( displaystyle P~рад.=frac{alpha {}^circ cdot pi }{180})
И наоборот: от радиан к градусам:
( displaystyle alpha {}^circ =frac{P~рад.cdot 180}{pi })
Ты должен уметь ориентироваться и в той, и в другой форме записи.
Потренируйся на следующих примерах:
- Перевести угол в ( displaystyle 30) градусов в радианы;
- Перевести угол ( displaystyle frac{pi }{4}) радиан в градусы;
- Перевести угол в ( displaystyle 60) градусов в радианы;
- Перевести угол в ( displaystyle frac{pi }{2}) радиан в градусы;
- Перевести угол в ( displaystyle 120) градусов в радианы;
- Перевести угол в ( displaystyle frac{3pi }{4}) радиан в градусы;
- Перевести угол в ( displaystyle 150) градусов в радианы.
Я сделаю только первые два, а остальные реши сам!
- ( P~рад.=frac{30cdot pi }{180}=frac{pi }{6}), тогда угол в ( displaystyle 30) градусов равен углу в ( displaystyle frac{pi }{6}) радиан;
- ( alpha {}^circ =frac{frac{pi }{4}cdot 180}{pi }=frac{45pi }{pi }=45{}^circ ), тогда угол в ( displaystyle frac{pi }{4}) радиан равен углу в ( displaystyle 45) градусов.
Все очень просто, не так ли? Остальные значения ты можешь найти в следующей таблице:
| ( displaystyle 0{}^circ ) | ( displaystyle 30{}^circ ) | ( displaystyle 45{}^circ ) | ( displaystyle 60{}^circ ) | ( displaystyle 90{}^circ ) | ( displaystyle 120{}^circ ) | ( displaystyle 135{}^circ ) | ( displaystyle 150{}^circ ) | ( displaystyle 180{}^circ ) |
| ( displaystyle 0) | ( displaystyle frac{pi }{6}) | ( displaystyle frac{pi }{4}) | ( displaystyle frac{pi }{3}) | ( displaystyle frac{pi }{2}) | ( displaystyle frac{2pi }{3}) | ( displaystyle frac{3pi }{4}) | ( displaystyle frac{5pi }{6}) | ( displaystyle pi ) |
| ( displaystyle 210{}^circ ) | ( displaystyle 225{}^circ ) | ( displaystyle 240{}^circ ) | ( displaystyle 270{}^circ ) | ( displaystyle 300{}^circ ) | ( displaystyle 315{}^circ ) | ( displaystyle 330{}^circ ) | ( displaystyle 360{}^circ ) |
| ( displaystyle frac{7pi }{6}) | ( displaystyle frac{5pi }{4}) | ( displaystyle frac{4pi }{3}) | ( displaystyle frac{3pi }{2}) | ( displaystyle frac{5pi }{3}) | ( displaystyle frac{7pi }{4}) | ( displaystyle frac{11pi }{6}) | ( displaystyle 2pi ) |
Так что впредь не удивляйся, когда ты увидишь вместо привычных градусов углы в радианах. Теперь ты знаешь, что это такое, и с чем его едят!
Синус, косинус, тангенс и котангенс на тригонометрической окружности
Но мы с тобой и так слишком увлеклись. Ты давно уже, наверное, заждался обещанных синусов и косинусов на тригонометрической окружности. Не смею более отвлекаться!
Давай сделаем вот что: совместим два знакомых нам объекта: тригонометрическую окружность (пока в том виде, в котором она у нас есть) и прямоугольный треугольник.
Что нам нужно, чтобы наш треугольник «целиком влез» в окружность?
Его гипотенуза должна быть не более единицы. Пусть же она у нас в точности будет равна единице.
Совместим мы их вот так:
Я нарисовал прямоугольный треугольник с центром в начале координат и гипотенузой равной ( 1). Это так потому, что окружность-то у меня единичная!
Тогда по определению синуса и косинуса:
- ( sin alpha =frac{AB}{OB}=frac{AB}{1}=AB)
- ( cos alpha =frac{OA}{OB}=frac{OA}{1}=OA)
А что же такое отрезки ( OA) и ( OB)? Чему равны их длины?
Смотри, сейчас будет самое главное: мы взяли угол ( alpha ) и провели луч, соединяющий этот угол с точкой на окружности.
Обозначим эту точку через ( B). Пусть ( B) имеет координаты ( Bleft( x,y right)).
Тогда длина отрезка ( OA) равна ( x), а длина отрезка ( AB)–равна ( y).
Но мы с тобой помним, что ( sin alpha =AB), ( cos alpha =OA), тогда:
- ( y=sin alpha )
- ( x=cos alpha )
Ух ты! Это надо еще раз обдумать, что же мы такое получили.
Давай проговорим еще раз: мы выбрали некоторый угол ( alpha ) и хотим найти его синус и косинус.
Что мы делаем?
- Проводим единичную окружность с центром, совпадающим с вершиной угла;
- Ищем точку пересечения нашего угла с окружностью;
- Её «иксовая» координата – это косинус нашего угла;
- Её «игрековая» координата – это синус нашего угла.
Вот и все! Теперь синус и косинус искать стало намного проще! Допустим, мы хотим найти синус, косинус ( 30) градусов.
Отмечаем ( 30) градусов на окружности и «достраиваем» этот угол до треугольника (как показано на рисунке выше).
Как найти ( x) и ( y)?
Да очень просто: в прямоугольном треугольнике катет, лежащий против угла в ( 30) градусов равен половине гипотенузы (это известный факт из геометрии 7 класса).
Так как гипотенуза равна ( 1), то противолежащий ей катет равен ( 0,5), откуда:
( sin 30{}^circ =0,5)
Что касается косинуса: для этого нам потребуется заметить, что выполняется тривиальное утверждение (основное тригонометрическое тождество):
( si{{n}^{2}}alpha +co{{s}^{2}}alpha =1)
Как ты думаешь, откуда оно берется? Да это же пресловутая теорема Пифагора!
Наши катеты в треугольничке равны ( x) и ( y), которые в свою очередь совпадают с ( cos alpha ) и ( sin alpha ). Гипотенуза в треугольнике равна ( 1).
Тогда:
( {{x}^{2}}+{{y}^{2}}=1) или, что то же самое,
( si{{n}^{2}}alpha +co{{s}^{2}}alpha =1)
Эта формула позволит по известному синусу вычислить неизвестный косинус и наоборот.
В частности, если:
( si{{n}^{2}}30{}^circ +co{{s}^{2}}30{}^circ =1) и ( sin 30{}^circ =0,5), то
( frac{1}{4}+co{{s}^{2}}30{}^circ =1)
( displaystyle co{{s}^{2}}30{}^circ =frac{3}{4})
( displaystyle cos 30{}^circ =pm sqrt{frac{3}{4}}=pm frac{sqrt{3}}{2})
Определение знака синуса, косинуса, тангенса и котангенса
Вообще, этот вопрос заслуживает особого внимания, но здесь все просто: у угла ( displaystyle 30) градусов и синус и косинус положительны (смотри рисунок), тогда берем знак «плюс».
( displaystyle cos 30{}^circ =frac{sqrt{3}}{2})
Теперь попробуй на основе вышеизложенного найти синус и косинус углов: ( displaystyle 60{}^circ ) и ( displaystyle 45{}^circ )
Можно схитрить: в частности для угла в ( displaystyle 60{}^circ ) градусов. Так как если один угол прямоугольного треугольника равен ( displaystyle 60{}^circ ) градусам, то второй – ( displaystyle 30{}^circ ) градусам. Теперь вступают в силу знакомые тебе формулы:
( displaystyle sin 30{}^circ =cos 60{}^circ )
( displaystyle sin 60{}^circ =cos 30{}^circ )
Тогда так как ( displaystyle sin 30{}^circ =0,5), то и ( displaystyle cos 60{}^circ =0,5). Так как ( displaystyle cos 30{}^circ =frac{sqrt{3}}{2}), то и ( displaystyle sin 60{}^circ =frac{sqrt{3}}{2}).
C ( displaystyle 45) градусами все еще проще: так если один из углов прямоугольного треугольника равен ( displaystyle 45) градусам, то и другой тоже равен ( displaystyle 45) градусам, а значит такой треугольник равнобедренный.
Значит, его катеты равны. А значит равны его синус и косинус.
Тогда:
( displaystyle si{{n}^{2}}45{}^circ +co{{s}^{2}}45{}^circ =2si{{n}^{2}}45{}^circ =1)
( displaystyle si{{n}^{2}}45{}^circ =co{{s}^{2}}45{}^circ =1/2)
Откуда: ( displaystyle sin 45{}^circ =cos 45{}^circ =sqrt{1/2}=frac{sqrt{2}}{2})
Теперь найди сам по новому определению (через икс и игрек!) синус и косинус углов в ( displaystyle 0) градусов и ( displaystyle 90) градусов. Здесь уже никакие треугольники нарисовать не получится! Уж слишком они будут плоские!
У тебя должно было получиться:
( displaystyle sin 0{}^circ =0), ( displaystyle cos 0{}^circ =1), ( displaystyle sin 90{}^circ =1), ( displaystyle cos 90{}^circ =0).
Тангенс и котангенс ты можешь отыскать самостоятельно по формулам:
( displaystyle text{t}g alpha =frac{sin alpha }{cos alpha }), ( displaystyle ctg alpha =frac{cos alpha }{sin alpha })
Обрати внимание, что на ноль делить нельзя!!
Теперь все полученные числа можно свести в таблицу:
Здесь приведены значения синуса, косинуса, тангенса и котангенса углов I четверти.
Для удобства углы приведены как в градусах, так и в радианах (но ты-то теперь знаешь связь между ними!). Обрати внимание на 2 прочерка в таблице: а именно у котангенса нуля и тангенса ( displaystyle 90) градусов. Это неспроста!
В частности:
( displaystyle ctg 0=frac{cos 0}{sin 0}=frac{1}{0}=?????)
Поэтому мы с тобой будем считать, что тангенс ( displaystyle 90) градусов и котангенс нуля просто-напросто не определены!
Теперь давай обобщим понятие синус и косинус на совсем произвольный угол. Я рассмотрю здесь два случая:
- Угол лежит в пределах от ( displaystyle 0) до ( displaystyle 360) градусов;
- Угол больше ( displaystyle 360) градусов.
Честно говоря, я скривил немного душой, говоря про «совсем все» углы. Они бывают также и отрицательными! Но этот случай мы с тобой рассмотрим чуть позже. Вначале остановимся на первом случае.
Если угол лежит в 1 четверти – то тут все понятно, мы этот случай уже рассмотрели и даже таблицы нарисовали.
Теперь же пусть наш угол больше ( displaystyle 90) градусов и не больше чем ( displaystyle 360).
Это значит, что он расположен либо во 2, либо в 3 или же в 4 четверти.
Как мы поступаем? Да точно так же!
Давай рассмотрим вместо вот такого случая…
…вот такой:
То есть рассмотрим угол ( displaystyle alpha ), лежащий во второй четверти. Что мы можем сказать про него?
У точки ( displaystyle {{M}_{1}}), которая является точкой пересечения луча и окружности по-прежнему имеет 2 координаты (ничего сверхъестественного, правда?). Это координаты ( displaystyle {{x}_{1}}) и ( displaystyle {{y}_{1}}).
Причем первая координата отрицательная, а вторая – положительная! Это значит, что у углов второй четверти косинус отрицателен, а синус – положителен!
Удивительно, правда? До этого мы еще ни разу не сталкивались с отрицательным косинусом.
Да и в принципе этого не могло быть, когда мы рассматривали тригонометрические функции как отношения сторон треугольника.
Кстати, подумай, у каких углов косинус равен ( displaystyle -1)? А у каких ( displaystyle -1) равен синус?
Аналогично можно рассмотреть углы во всех остальных четвертях. Я лишь напомню, что угол отсчитывается против часовой стрелки! (так, как это показано на последнем рисунке!).
Конечно, можно и отсчитывать в другую сторону, но вот подход к таким углам будет уже несколько другой.
Исходя из приведенных выше рассуждений, можно расставить знаки у синуса, косинуса, тангенса (как синус деленный на косинус) и котангенса (как косинус деленный на синус) для всех четырех четвертей.
Но еще раз повторюсь, нет смысла запоминать этот рисунок. Все, что тебе нужно знать:
Синус – это игрек. Косинус – это икс. Тангенс – это синус деленный на косинус. Котангенс – это косинус деленный на синус.
Углы больше 360 градусов
А как быть с углами, большими чем ( displaystyle 360) градусов?
Возьму я, скажем, угол в ( displaystyle 30) градусов (( displaystyle frac{pi }{6}) радиан) и пойду от него против часовой стрелки…
На рисунке я нарисовал спираль, но ты-то понимаешь, что на самом деле у нас нет никакой спирали: у нас есть только окружность.
Так куда же мы попадем, если стартуем от определенного угла и пройдем полностью весь круг (( displaystyle 360) градусов или ( displaystyle 2pi ) радиан)?
Куда мы придем? А придем мы в тот же самый угол!
Это же, конечно, справедливо и для любого другого угла:
Взяв произвольный угол ( displaystyle alpha ) и пройдя полностью всю окружность, мы вернемся в тот же самый угол ( displaystyle alpha ).
Что же нам это даст? А вот что: если ( displaystyle sin alpha =y,~cos alpha =x), то
( displaystyle sin left( alpha +2pi k right)=y), ( displaystyle cos left( alpha +2pi k right)=x), откуда окончательно получим:
( displaystyle sin left( alpha +2pi k right)=sinalpha )
( displaystyle cos left( alpha +2pi k right)=cosalpha )
Для любого целого ( displaystyle k). Это значит, что синус и косинус являются периодическими функциями с периодом ( displaystyle 2pi ).
Таким образом, нет никакой проблемы в том, чтобы найти знак теперь уже произвольного угла: нам достаточно отбросить все «целые круги», которые умещаются в нашем угле и выяснить, в какой четверти лежит оставшийся угол.
Например, найти знак:
- ( displaystyle text{sin}1000{}^circ ),
- ( displaystyle text{cos} 605{}^circ ),
- ( displaystyle text{cos}frac{16pi }{7}),
- ( displaystyle text{sin}frac{19pi }{4}).
Проверяем:
Отрицательные углы
Отрицательные углы в тригонометрии откладываются на тригонометрическом круге вниз от начала, по направлению движения часовой стрелки:
Давай вспомним, как мы до этого откладывали углы на тригонометрической окружности.
Мы шли от положительного направления оси ( displaystyle Ox) против часовой стрелки:
Тогда на нашем рисунке построен угол, равный ( displaystyle 180+45=225{}^circ ). Аналогичным образом мы строили все углы.
Однако ничего нам не запрещает идти от положительного направления оси ( displaystyle Ox) по часовой стрелке.
Мы будем тоже получать различные углы, но они будут уже отрицательными:
А следующей картинке изображено два угла, равные по абсолютной величине (если не знаешь, что это такое, читай здесь про «Модуль числа»), но противоположные по знаку:
В целом правило можно сформулировать вот так:
- Идем против часовой стрелки – получаем положительные углы
- Идем по часовой стрелке – получаем отрицательные углы
Схематично правило изображено вот на этом рисунке:
Ты мог бы задать мне вполне резонный вопрос: ну углы нам нужны для того, чтобы измерять у них значения синуса, косинуса, тангенса и котангенса.
Так есть ли разница, когда у нас угол положительный, а когда – отрицательный? Я отвечу тебе: как правило есть.
Однако ты всегда можешь свести вычисление тригонометрической функции от отрицательного угла к вычислению функции в угле положительном.
Посмотри на следующую картинку:
Я построил два угла, они равны по абсолютному значению, но имеют противоположный знак. Отметим для каждого из углов его синус и косинус на осях.
Что мы с тобой видим? А вот что:
Синусы у углов ( displaystyle alpha ) и ( displaystyle -alpha ) противоположны по знаку!
Тогда если ( displaystyle text{sin} text{ }!!alpha!!text{ }=text{y}),
то ( displaystyle sin left( -text{ }!!alpha!!text{ } right)=-text{y})
( displaystyle sin left( -text{ }!!alpha!!text{ } right)=-text{sin} text{ }!!alpha!!text{ }).
Косинусы у углов ( displaystyle alpha ) и ( displaystyle -alpha ) совпадают!
Тогда если ( displaystyle text{cos} text{ }!!alpha!!text{ }=text{x}),
то и ( displaystyle cos left( -text{ }!!alpha!!text{ } right)=text{x})
( displaystyle cos left( -text{ }!!alpha!!text{ } right)=text{cos} text{ }!!alpha!!text{ })
Так как ( displaystyle text{tg}left( -text{ }!!alpha!!text{ } right)=frac{text{sin}left( -text{ }!!alpha!!text{ } right)}{text{cos}left( -text{ }!!alpha!!text{ } right)}=frac{-text{sin}left( text{ }!!alpha!!text{ } right)}{text{cos}left( text{ }!!alpha!!text{ } right)}), то:
( displaystyle text{tg}left( -text{ }!!alpha!!text{ } right)=-text{tg }!!alpha!!text{ })
Так как ( displaystyle text{ctg}left( -text{ }!!alpha!!text{ } right)=frac{text{cos}left( -text{ }!!alpha!!text{ } right)}{text{sin}left( -text{ }!!alpha!!text{ } right)}=frac{text{cos}left( text{ }!!alpha!!text{ } right)}{-text{sin}left( text{ }!!alpha!!text{ } right)}), то:
( displaystyle text{ctg}left( -text{ }!!alpha!!text{ } right)=-text{ctg} text{ }!!alpha!!text{ })
Таким образом, мы всегда можем избавиться от отрицательного знака внутри любой тригонометрической функции: либо просто уничтожив его, как у косинуса, либо поставив его перед функцией, как у синуса, тангенса и котангенса.
Кстати, вспомни-ка, как называется функция ( displaystyle f(x)), у которой для любого допустимого ( displaystyle x) выполняется:( displaystyle f(-x)=-f(x))?
Такая функция называется нечетной.
А если же для любого допустимого ( displaystyle x) выполняется: ( displaystyle f(-x)=f(x))? То в таком случае функция называется четной.
Таким образом, мы с тобой только что показали, что:
Синус, тангенс и котангенс – нечетные функции, а косинус – четная.
Таким образом, как ты понимаешь, нет никакой разницы, ищем ли мы синус от положительного угла или отрицательного: справиться с минусом очень просто. Так что нам не нужны таблицы отдельно для отрицательных углов.
С другой стороны, согласись, было бы очень удобно зная только тригонометрические функции углов первой четверти, уметь вычислять аналогичные функции и для остальных четвертей.
Можно ли это сделать? Конечно, можно!
У тебя есть по крайней мере 2 пути: первый – строить треугольник и применять теорему Пифагора (так мы с тобой и отыскали значения тригонометрических функций для основных углов первой четверти)
Второй – запомнив значения функций для углов в первой четверти и некое несложное правило, уметь вычислять тригонометрические функции для всех остальных четвертей.
Второй способ избавит тебя от долгой возни с треугольниками и с Пифагором, поэтому мне он видится более перспективным:
Итак, данный способ (или правило) называется формулами приведения.
Формулы приведения
Грубо говоря, эти формулы помогут тебе не запоминать вот такую таблицу (она между прочим содержит 98 чисел!):
…если ты помнишь вот эту (всего на 20 чисел):
То есть ты сможешь не забивать себе голову совершенно ненужными 78 числами! Пусть, например, нам нужно вычислить ( displaystyle text{sin} 855{}^circ ). Ясно, что в маленькой таблице такого нет. Что же нам делать? А вот что:
Во-первых, нам понадобятся следующие знания:
Синус и косинус имеют период ( displaystyle 2pi ) (( displaystyle 360) градусов)
То есть
( displaystyle sinleft( 2pi k+x right)=sin x)
( displaystyle cosleft( 2pi k+x right)=cos x)
Тангенс (котангенс) имеют период ( displaystyle pi ) (( displaystyle 180) градусов)
( displaystyle tgleft( pi k+x right)=tg x)
( displaystyle ctgleft( pi k+x right)=ctg x)
( displaystyle k) – любое целое число
Синус и тангенс – функции нечетные, а косинус – четная:
( displaystyle sinleft( -x right)=-sin x)
( displaystyle tgleft( -x right)=-tgleft( x right))
( displaystyle cosleft( -x right)=cosleft( x right))
Первое утверждение мы уже доказали с тобой, а справедливость второго установили совсем недавно.
Непосредственно правило приведения выглядит вот так:
Если мы вычисляем значение тригонометрической функции от отрицательного угла – делаем его положительным при помощи группы формул о четности.
Например:
( displaystyle sinleft( -855{}^circ right)=-sin855{}^circ),
( displaystyle cosleft( -855{}^circ right)=cos855{}^circ).
Отбрасываем для синуса и косинуса его периоды: ( displaystyle 2pi k) (по ( displaystyle 360) градусов), а для тангенса – ( displaystyle pi k) (( displaystyle 180) градусов).
Например:
( displaystyle sin 855{}^circ =sinleft( 2cdot 360{}^circ +135{}^circ right)=sin 135{}^circ )( displaystyle tg 225{}^circ =tgleft( 180{}^circ +45{}^circ right)=tg 45{}^circ )
Если оставшийся «уголок» меньше ( displaystyle 90) градусов, то задача решена: ищем его в «малой таблице».
Иначе ищем, в какой четверти лежит наш угол ( displaystyle alpha ): это будет 2, 3 или 4 четверть. Смотрим, какой знак имеет искомая функция в четверти. Запомнили этот знак!!!
Представляем угол ( displaystyle alpha )в одной из следующих форм:
- ( displaystyle alpha =90+beta ) (если во второй четверти)
- ( displaystyle alpha =180-beta ) (если во второй четверти)
- ( displaystyle alpha =180+beta ) (если в третьей четверти)
- ( displaystyle alpha =270-beta ) (если в третьей четверти)
- ( displaystyle alpha =270+beta ) (если в четвертой четверти)
- ( displaystyle alpha =360-beta ) (если в четвертой четверти)
…так, чтобы оставшийся угол ( displaystyle beta ) был больше нуля и меньше ( displaystyle 90) градусов.
Например:
( displaystyle 135{}^circ =180{}^circ -45{}^circ )
( displaystyle 135{}^circ =90{}^circ +45{}^circ )
( displaystyle 315{}^circ =270{}^circ+45{}^circ )
( displaystyle 240{}^circ =180{}^circ +60{}^circ )
( displaystyle 240{}^circ =270{}^circ -30{}^circ )…
В принципе не важно, в какой из двух альтернативных форм для каждой четверти ты представишь угол. На конечном результате это не скажется.
Теперь смотрим, что у нас получилось: если ты выбрал запись через ( displaystyle 180) или ( displaystyle 360) градусов плюс минус что-либо, то знак функции меняться не будет: ты просто убираешь ( displaystyle 180) или ( displaystyle 360) и записываешь синус, косинус или тангенс оставшегося угла.
Если же ты выбрал запись через ( displaystyle 90) или ( displaystyle 270) градусов, то синус меняем на косинус, косинус на синус, тангенс на котангенс, котангенс – на тангенс.
Ставим перед получившимся выражением знак, который мы запомнили.
Угол может измеряться следующими величинами:
- Градусами (и соответствующими ему величинами: угловыми минутами и секундами);
- Радианами.
Градусная мера угла
Если взять развернутый угол (это два прямых угла) и поделить его на 180 частей, то одна такая часть будет называться одним градусом. Для того, чтобы измерить градусную меру угла, необходимо посчитать, сколько раз 1 градус входит в данный угол. Полученное число и будет ответом.
Если угол таков, что его нельзя измерить целым числом, либо же он меньше единичного угла, то используют такие меры измерения как угловые минуты и секунды.
Если градус поделить на 60 частей, то одной такой частью будет минута. В свою же очередь, если минуту разделить на те же 60 частей, то полученным числом будет 1 секунда.
Радианная мера угла
Радианом называют угол, образованный дугой окружности длинной равной радиусу этой окружности.
Длина окружности равна:
l=2⋅π⋅rl=2cdotpicdot r,
где rr — радиус этой окружности.
Тогда, разделив на радиус, получаем, что полный угол в радианах равен:
lr=2⋅π⋅rr=2⋅π радианfrac{l}{r}=frac{2cdotpicdot r}{r}=2cdotpitext{ радиан}
В градусах этот же угол равен, как известно, 360∘360^{circ}.
Отсюда находим связь между радианами и градусами:
2⋅π радиан=360∘2cdotpitext{ радиан}=360^{circ}
Это та главная формула, которая нужна, чтобы переводить градусы в радианы и наоборот.
Один радиан равен:
1 радиан=360∘2⋅π≈57.3∘1text{ радиан}=frac{360^{circ}}{2cdotpi}approx57.3^{circ}
Один радиан в минутах:
1 радиан=360∘2⋅π⋅60≈3438′1text{ радиан}=frac{360^{circ}}{2cdotpi}cdot60approx3438′
Один радиан в секундах:
1 радиан=360∘2⋅π⋅60⋅60≈206280′′1text{ радиан}=frac{360^{circ}}{2cdotpi}cdot60cdot60approx206280»
Перевод градусов в радианы
Если по условию известна градусная мера угла, то чтобы перевести ее в радианную, нужно сделать следующие действия: умножить ее на πpi и разделить на 180.
y радиан=π180⋅xytext{ радиан}=frac{pi}{180}cdot x
xx — значение угла в градусах;
yy — значение того же угла в радианах.
Переведите 45 градусов в радианную меру измерения. Ответ округлите до десятой доли.
Решение
45∘=π180⋅45 радиан≈0.8 радиан45^{circ}=frac{pi}{180}cdot 45text{ радиан}approx0.8text{ радиан}
Ответ
0.8 радиан0.8text{ радиан}
Земля совершила треть от половины оборота вокруг Солнца. На какой угол в радианах она повернулась?
Решение
Найдем сначала этот угол в градусах. Полный угол составляет 360∘360^circ. Половина от полного оборота это 180∘180^{circ}. Нам же нужна треть этого угла, то есть:
180∘3=60∘frac{180^circ}{3}=60^circ
Земля отклонилась на угол 60∘60^circ от своего начального положения. Переведем теперь этот угол в радианы:
60∘=π180⋅60 радиан≈1 радиан60^circ=frac{pi}{180}cdot 60text{ радиан}approx1text{ радиан}
Решение
1 радиан1text{ радиан}
Перевод радиан в градусы
Чтобы перевести радианы в градусы, нужно умножить угол в радианах на 180 и разделить на πpi.
y∘=180π⋅xy^{circ}=frac{180}{pi}cdot x
xx — значение угла в радианах;
yy — значение того же угла в градусах.
Переведите 3 радиана в градусную меру угла.
Решение
3 радиана=180π⋅3≈172∘3text{ радиана}=frac{180}{pi}cdot3approx172^circ
Ответ
172∘172^circ
Ищете, где можно заказать задачу по математике недорого? Обратитесь к нашим экспертам в данной области!