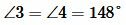Вертикальные углы в геометрии
19 июня 2022
В двух словах: вертикальные углы возникают при пересечении двух прямых, не имеют общих сторон и всегда равны друг другу.
Содержание
- Определение и примеры
- Основная теорема
- Комбинированные задачи
1. Определение и примеры
Определение. Два угла называются вертикальными, если стороны одного из них являются продолжениями сторон другого.
На рисунке ниже пересекаются две прямые: $AB$ и $MN$:
В результате образуются две пары вертикальных углов: $angle ASM$ и $angle BSN$, а также $angle ASN$ $angle BSM$.
Обратите внимание: вертикальные углы образуются только в точке пересечении прямых. Например, углы $ASM$ и $BSN$ на картинке ниже — не вертикальные, даже если они равны:
Если в одной точке пересекается более двух прямых, то вертикальных углов становится очень много:
Я не случайно пометил вертикальные углы одинаковыми дугами. Дело в том, что верна следующая теорема.
2. Основная теорема
Теорема 1. Вертикальные углы всегда равны друг другу.
Доказательство. Рассмотрим «синие» вертикальные $ASN$ и $BSM$. Каждый из них является смежным с углом $BSN$:
Но сумма смежных углов равна 180°, и если $angle BSN=color{red}{x}$, то
[begin{align}angle ASN&={180}^circ -color{red}{x} \ angle BSM&={180}^circ -color{red}{x} end{align}]
Итак, вертикальные углы равны одной и той же величине. Т.е. они равны между собой.
Эта теорема позволяет решать огромное количество задач — от самых простых до весьма нетривиальных. Начнём с простых.
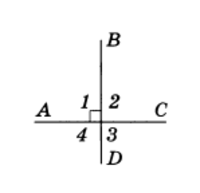
Задача 1. Найдите углы 2, 3 и 4, если $angle 1={134}^circ $.
Решение.
Углы 1 и 3 вертикальные, поэтому они равны: $angle 3=angle 1={134}^circ $.
Углы 1 и 2 смежные, поэтому их сумма равна 180°:
[begin{align}angle 1+angle 2&={180}^circ \ angle 2&={180}^circ -angle 2= \ &={180}^circ -{134}^circ ={46}^circ end{align}]
Углы 2 и 4 вертикальные, поэтому они равны: $angle 4=angle 2={46}^circ $.
Из всех чертежей видно, что при пересечении двух прямых обычно возникает два острых угла и два тупых. Причём острый и тупой угол всегда будут смежными.
Если предположить, что острый угол равен $color{red}{x}$ градусов, то тупой равен $180-color{red}{x}$ градусов.
Задача 2. Найдите углы, образованные при пересечении двух прямых, если разность двух из них равна 68°.
Решение. Пусть острые углы содержат $color{red}{x}$ градусов. Тогда смежные с ними тупые углы содержат по ${180}^circ -color{red}{x}$ градусов.
По условию задачи, разность двух углов равна 68°. Очевидно, речь идёт о смежных углах. Потому что разность вертикальных углов была бы равна нулю. Вычитаем из тупого угла острый и получаем:
[begin{align}{180}^circ -color{red}{x} -color{red}{x} &={68}^circ\ 2color{red}{x}&={112}^circ\ color{red}{x}&={56}^circend{align}]
Итак, острые углы содержат по 56°. Тогда тупые углы содержат по 124°.
Единственный случай, когда все вертикальные углы равны — это когда прямые перпендикулярны, т.е. пересекаются под углом 90°.
Задача 3. На рисунке прямые $a$ и $b$ перпендикулярны, $angle color{red}{1}={36}^circ $. Найдите углы 2, 3 и 4.
Решение.
Углы 1 и 3 вертикальные, поэтому они равны: $angle color{red}{3}=angle color{red}{1}={36}^circ $.
Углы 1 и 2 смежные, поэтому их сумма равна 180°:
[begin{align}angle color{red}{1}+angle color{blue}{2}&={180}^circ \ angle color{blue}{2}&={180}^circ -angle color{red}{1}= \ &={180}^circ -{36}^circ ={144}^circ end{align}]
Углы 3 и 4 вместе образуют прямой угол, поэтому их сумма равна 90°:
[begin{align}angle color{red}{3}+angle color{green}{4}&={90}^circ \ angle color{green}{4}&={90}^circ -angle color{red}{3}= \ &={90}^circ -{36}^circ ={54}^circ end{align}]
Перед тем как переходить к более сложным задачам, рассмотрим ещё одно интересное свойство вертикальных углов.
Теорема 2. Биссектрисы вертикальных углов лежат на одной прямой.
Доказательство. В самом деле, пусть $SC$ и $SD$ — биссектрисы вертикальных углов $ASM$ и $BSN$ соответственно.
Допустим, градусные меры углов $ASM$ и $BSN$ равны $2color{red}{x}$. Тогда градусные меры всех маленьких углов $ASC$, $BSD$ и т.д. равны $color{red}{x}$. Но тогда
[begin{align}angle CSD&=angle CSA+angle ASN+angle NSD= \ &=2color{red}{x}+angle ASN end{align}]
С другой стороны, углы $ASN$ и $ASM=2color{red}{x}$ смежные, поэтому
[2color{red}{x}+angle ASN={180}^circ ]
Итак, угол $angle CSD={180}^circ $, т.е. является развёрнутым. А это как раз и означает, что лучи $SC$ и $SD$ являются дополнительными друг другу и образуют прямую.
3. Комбинированные задачи
Рассмотрим несколько более сложных задач. Тут встречаются вертикальные углы, смежные углы, а также перпендикуляры.
Задача 4. Найдите углы, образованные при пересечении двух прямых, если:
- Сумма двух из них равна 110°.
- Сумма трёх из них равна 308°.
Решение. Для обоих пунктов будем использовать один и тот же чертёж. Пусть острые вертикальные углы содержат по $color{red}{x}$ градусов, тогда два других угла содержат по ${180}^circ -color{red}{x}$ градусов:
1. Если сумма двух углов равна 110°, то, очевидно, речь идёт о вертикальных углах. Потому что сумма смежных углов всегда равна 180°, а не 110°.
Кроме того, это явно острые углы, иначе их сумма была бы больше 180°. Поэтому
[begin{align}color{red}{x}+color{red}{x}&={110}^circ\ 2color{red}{x}&={110}^circ\ color{red}{x}&={55}^circend{align}]
Итак, острые вертикальные углы содержат по 55°. Следовательно, смежные с ними тупые вертикальные углы содержат по 125°.
2. Сумма трёх углов всегда содержит два вертикальных и один смежный с ними. Например, так:
Зелёным пунктиром обозначены три угла, участвующие в сумме. Следовательно, эта сумма равна
[begin{align}left( {180}^circ -color{red}{x} right)+color{red}{x}+left( {180}^circ -color{red}{x} right)&={308}^circ \ {360}^circ -color{red}{x}&={308}^circ\ color{red}{x}&={52}^circend{align}]
Итак, углы равны 52° и 128°.
Эту задачу можно решить по-разному. Взгляните ещё раз на чертёж:
Мы знаем, что «большой зелёный угол» содержит 308°. А «полный оборот» содержит 360°. Но чтобы получить полный оборот, нужно добавить к зелёному сектору небольшой угол $color{red}{x}$. Поэтому
[begin{align}{308}^circ +color{red}{x}&={360}^circ\ color{red}{x}&={52}^circend{align}]
Возможно, такой подход покажется вам более простым и «очевидным».
Заметьте: благодаря введённым обозначениям нам даже не потребовались буквы для обозначения углов.:)
Задача 5. Сумма двух углов, образованных при пересечении двух прямых, равна 250°. Докажите, что эти углы вертикальные.
Решение. Пусть тупой угол $ACN$ содержит $color{blue}{x}$ градусов. Тогда смежный с ним угол $BCN$ содержит ${180}^circ -color{blue}{x}$ градусов, а вертикальный угол $BCM$ тоже равен $color{blue}{x}$ градусов:
Но тогда
[angle ACN+angle BCN={180}^circ ne {250}^circ ]
И это вполне логично, поскольку сумма смежных углов всегда равна 180°. То же самое можно сказать, например, про углы $ACN$ и $ACM$ — они тоже смежные.
Остаётся лишь вариант вертикальных углов $ACN$ и $BCM$. Но эти углы вертикальные, что и требовалось доказать.
В последнем задании мы построили чертёж исходя из следующих соображений. Если искомые углы вертикальные (а именно это мы и пытаемся доказать), то они равны, и каждый из них будет равен 125°. Следовательно, речь идёт о тупых углах, поэтому именно тупые углы мы обозначили за $x$.
Помните: в геометрии важно построить правильный чертёж. И чем сложнее задачи, тем выше требования к качеству чертежей. Иначе на можно просто «не увидеть» алгоритм решения задачи.
Кроме того, в следующих уроках мы будем всё чаще отождествлять углы и их градусные меры. Абсолютно нормально писать и говорить «угол $ABC$ равен $x$» вместо «угол $ABC$ содержит $x$ градусов» — все прекрасно поймут, о чём речь.
Смотрите также:
- Перпендикулярные прямые — определение и свойства
- Что такое смежные углы
- Тест к уроку «Площади многоугольников без координатной сетки» (средний)
- Метод координат в пространстве
- Интегрирование по частям
- Как формулы приведения работают в задаче B11
Вертикальные углы. Свойства вертикальных углов
Определение 1. Вертикальными углами называются два угла, у которых стороны одного угла являются продолжениями сторон другого угла.
На Рис.1 углы AOB и COD вертикальные. Вертикальные также углы AOD и BOC.
Свойства вертикальных углов
1. Вертикальные углы равны.
2. Две пересекающие прямые образуют две пары вертикальных углов.
Доказательство пункта 1. Поскольку 1, 3 и 2, 3 смежные углы, то имеем
Тогда
Следовательно 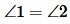
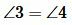
Задачи и решения
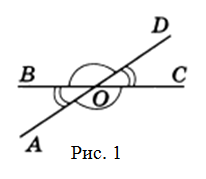
Задание 1. Угол 1 равен 32°. Найти углы 2, 3, 4 (Рис.2).
Решение. Так как углы 1 и 2 вертикальны, то 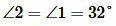
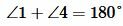
Углы 3 и 4 вертикальные. Тогда
Ответ. 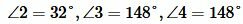
Задание 2. При пересечении двух прямых образовались четыре угла. Сумма двух углов равна 220°. Найти все углы.
Решение. Из образованных четырех углов любые две или смежные, или вертикальные. Поскольку в нашей задаче сумма двух углов равна 220°, то эти углы вертикальные (так как сумма смежных углов равна 180°). Тогда каждый из этих углов равен 220°:2=110°. Смежный по отношению угла 110° , будет угол 180°-110°=70°. Следовательно остальные два угла равны 70°. Отметим, что сумма всех четырех углов равен 360°:
Ответ. 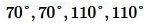
Содержание:
- Определение вертикальных углов
- Примеры решения задач с вертикальными углами
Определение вертикальных углов
Определение
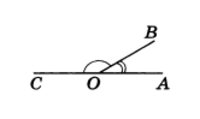
Углы, у которых вершина общая и
стороны которых продолжают друг друга, называются вертикальными углами (рис. 1).
На приведенном рисунке вертикальными есть углы
$AOB$ и
$COD$, а также
$AOC$ и
$BOD$ .
Вертикальные углы образуются при пересечении двух прямых.
Теорема
Вертикальные углы равны.
Примеры решения задач с вертикальными углами
Пример
Задание. Пусть на рисунке 1
$angle COD$ равен
$45^{circ}$. Чему равны углы
$AOB$ и
$AOC$ ?
Решение. Так как углы
$COD$ и
$AOB$ вертикальные, то значит, они равны, а тогда
$$angle A O B=angle C O D=45^{circ}$$
Углы $AOB$ и
$AOC$ смежные, а тогда из
теоремы про смежные углы
получаем, что их сумма равна $180^{circ}$, то есть
$$angle A O B+angle A O C=180^{circ}$$
Отсюда
$$angle A O C=180^{circ}-angle A O B=180^{circ}-45^{circ}=135^{circ}$$
Ответ. $angle A O B=45^{circ}, angle A O C=135^{circ}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Сумма двух вертикальных углов, образованных при пересечении двух прямых, равна
$100^{circ}$. Найти величину каждого из четырех углов,
образованных при пересечении.
Решение. Пусть сумма вертикальных углов
$AOB$ и
$angle COD$ равна
$100^{circ}$ (рис. 1). Как известно, вертикальные углы
равны между собой, поэтому
$$angle A O B=angle C O D$$
Тогда из условия имеем:
$$begin{aligned} angle A O B+angle C O D=100^{circ} & Rightarrow angle C O D+angle C O D=100^{circ} Rightarrow \ & Rightarrow 2 angle C O D=100^{circ} Rightarrow angle C O D=50^{circ} end{aligned}$$
А значит и $angle A O B=50^{circ}$
Углы $AOB$ и
$AOC$ смежные, а значит, их сумма равна
$180^{circ}$:
$$begin{aligned} angle A O B+angle A O C &=180^{circ} Rightarrow angle A O C=180^{circ}-angle A O B=\ &=180^{circ}-50^{circ}=130^{circ} end{aligned}$$
Углы $AOC$ и
$BOD$ вертикальные, а значит
$$angle B O D=angle A O C=130^{circ}$$
Ответ. $50^{circ}, 50^{circ}, 130^{circ}, 130^{circ}$
Читать дальше: что такое синус угла.
Какие углы называются вертикальными: определение и свойства
Содержание:
- Вертикальные углы — что это такое в геометрии, определение
- Свойства вертикальных углов
- Равны или нет, доказательство теоремы
-
Примеры решения задач
- Задача 1
- Задача 2
Вертикальные углы — что это такое в геометрии, определение
Определение
Вертикальные углы – пара углов с общей вершиной, которые образованы при пересечении двух прямых таким образом, что стороны одного из них являются продолжением сторон другого. Иными словами – они противоположны.
Свойства вертикальных углов
- Когда две прямые пересекаются, то образуется две пары вертикальных углов.
- Синусы, косинусы и тангенсы их равны.
- В сумме два вертикальных угла создают полный угол. Его градус равняется 360^circ.
Равны или нет, доказательство теоремы
Особенность вертикальных углов в том, что они абсолютно идентичны.
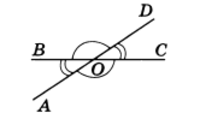
Убедимся в справедливости этого свойства. Докажем его: на чертеже 1 и 2, 2 и 3, 3 и 4, 4 и 1 являются смежными, 1 и 3, 2 и 4 – вертикальные.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
По свойству смежных углов, в сумме они дают (180^circ). Используем этот признак и получаем:
(angle1+angle2=180^circ и angle2+angle3=180^circ)
Отсюда выведем, что:
(angle1=180^circ-angle2, angle3=180^circ-angle2)
Уравнение доказало равенство углов 1 и 3.
Примеры решения задач
Задача 1
Дано
(angle1=45^circ)
Найти: значения (angle2, angle3, angle4)
Решение
(angle1) и (angle3) вертикальные. Значит (angle1=angle3=45^circ.)
(angle1) и (angle4) смежные. По правилу о смежных углах:
(angle1+angle4=180^circ)
(angle4=180^circ-angle1=180^circ-45^circ=135^circ)
Так как (angle4) и (angle2) вертикальные, то (angle4=angle2=135^circ.)
Ответ: величина (angle3=45^circ,) величина (angle2) и (angle4=135^circ.)
Задача 2
Дано
Две прямые пересеклись и сформировали четыре угла. Сумма двух из них составляет (140^circ.)
Найти: значения всех углов, образовавшихся при пересечении прямых.
Решение
Поскольку по условию пара углов образует (140^circ), это дает право сделать вывод – они вертикальные, так как смежные в сумме должны достигать (180^circ).
Так как вертикальные углы равны, то значение каждого из них соответствует:
(140/2=70=70^circ)
Оставшиеся углы – смежные к вертикальным и вертикальные по отношению друг к другу. Для того, чтобы их вычислить, выполним следующее действие:
(180-70=110=110^circ)
Ответ: (70^circ), (110^circ), (70^circ), (110^circ).
Насколько полезной была для вас статья?
Рейтинг: 3.50 (Голосов: 2)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.
Сумма смежных углов равна 180°
Рис.1
Теорема 1. Сумма смежных углов равна 180°.
Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .
Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.
Вертикальные углы равны
Рис.2
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).
Теорема 2. Вертикальные углы равны.
Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1
∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.
Отсюда заключаем, что ∠ АОВ = ∠ COD.
Следствие 1. Угол, смежный с прямым углом, есть прямой угол.
Рис.3
Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.
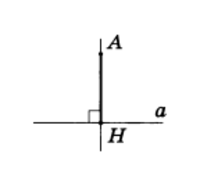
АН — перпендикуляр к прямой
Рис.4
Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
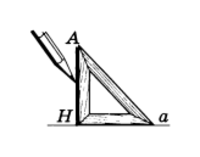
Чертежный угольник
Рис.5
Справедлива следующая теорема.
Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).
Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.
Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».
Пример 1. Один из смежных углов равен 44°. Чему равен другой?
Решение. Обозначим градусную меру другого угла через x, тогда согласно теореме 1.
44° + х = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.
Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?
Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.
∠ АОС = 180° — ∠ COD = 180° — 45° = 135°.
Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.
Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Значит, смежные углы равны 45° и 135°.
Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.
Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол
АОС) смежный с углом COD, и, значит, по теореме 1
∠ BOD = ∠ АОС = 180° — 50° = 130°.
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°.
Найдите величину угла ABC . Ответ дайте в градусах.
Отыскание смежных углов треугольника.