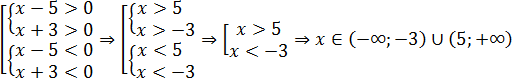Как найти графическим методом интервалов

Решение уравнений с помощью графиков

Решение линейных уравнений

Как ты уже знаешь, графиком линейного уравнения является прямая линия, отсюда и название данного вида.

Линейные уравнения достаточно легко решать алгебраическим путем – все неизвестные переносим в одну сторону уравнения, все, что нам известно – в другую и вуаля! Мы нашли корень.

Сейчас же я покажу тебе, как это сделать графическим способом.

Итак, у тебя есть уравнение: ( displaystyle 2{x} -10=2)

Как его решить?

Вариант 1, и самый распространенный – перенести неизвестные в одну сторону, а известные в другую, получаем:

Иными словами, у нас будет:

Как ты думаешь, что является корнем нашего уравнения? Правильно, координата ( displaystyle x) точки пересечения графиков:

Наш ответ: ( displaystyle x=6)

Вот и вся премудрость графического решения. Как ты с легкостью можешь проверить, корнем нашего уравнения является число ( displaystyle 6)!

Вариант 1. Напрямую

Просто строим параболу по данному уравнению: ( displaystyle {{x}^{2}}+2{x} -8=0)

Чтобы сделать это быстро, дам тебе одну маленькую подсказку: удобно начать построение с определения вершины параболы. Определить координаты вершины параболы помогут следующие формулы:

Посчитал? Какие координаты вершины параболы у тебя получились? Давай разбираться вместе:

И вот мы знаем уже координаты вершины, а для построения параболы нам нужно еще … точек. Как ты думаешь, сколько минимум точек нам необходимо? Правильно, ( displaystyle 3).

Ты знаешь, что парабола симметрична относительно своей вершины, например:

Соответственно, нам необходимо еще две точки по левой или правой ветви параболы, а в дальнейшем мы эти точки симметрично отразим на противоположную сторону:

Возвращаемся к нашей параболе.

Для нашего случая точка ( displaystyle Aleft( -1;-9 right)). Нам необходимо еще две точки, соответственно, ( displaystyle x) можно взять положительные, а можно взять отрицательные? Какие точки тебе удобней?

Мне удобней работать с положительными, поэтому я рассчитаю при ( displaystyle x=0) и ( displaystyle x=2).

Как ты думаешь, что является решением уравнения?

Правильно, точки, в которых ( displaystyle y=0), то есть ( displaystyle x=2) и ( displaystyle x=-4). Потому что ( displaystyle {{x}^{2}}+2{x} -8=0).

И если мы говорим, что ( displaystyle y={{x}^{2}}+2{x} -8), то значит, что ( displaystyle y) тоже должен быть равен ( displaystyle 0), или ( displaystyle y={{x}^{2}}+2{x} -8=0).

Просто? Это мы закончили с тобой решение уравнения сложным графическим способом, то ли еще будет!

Конечно, ты можешь проверить наш ответ алгебраическим путем – посчитаешь корни через теорему Виета или Дискриминант.

Что у тебя получилось? То же самое?

Вот видишь! Теперь посмотрим совсем простое графическое решение, уверена, оно тебе очень понравится!

Решение смешанных неравенств

Теперь перейдем к более сложным неравенствам!

Как тебе такое:

Первое, с чего мы начнем, – это с построения двух графиков:

Расписал? Теперь строй два графика.

Сравним наши рисунки?

У тебя так же? Отлично!

Теперь расставим точки пересечения и цветом определим, какой график у нас по идее должен быть больше, то есть ( displaystyle {{y}_{2}}={{x}^{3}}).

Смотри, что получилось в итоге:

А теперь просто смотрим, в каком месте у нас выделенный график находится выше, чем график ( displaystyle {{y}_{1}}=4x)? Смело бери карандаш и закрашивай данную область! Она и будет решением нашего сложного неравенства!

На каких промежутках по оси ( displaystyle Ox) у нас ( displaystyle {{y}_{2}}={{x}^{3}}) находится выше, чем ( displaystyle {{y}_{1}}=4x)? Верно, ( displaystyle xin left( -2;0 right)cup left( 2;+infty right)).

Это и есть ответ!

Ну вот, теперь тебе по плечу и любое уравнение, и любая система, и уж тем более любое неравенство!

Метод интервалов, решение неравенств

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение квадратного неравенства

Неравенство — алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.

Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит найти множество, для которых оно выполняется.

Квадратное неравенство выглядит так:

где x — переменная,

Квадратное неравенство можно решить двумя способами:

• графический метод;
• метод интервалов.

Решение неравенства графическим методом

При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax 2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.

Как дискриминант влияет на корни уравнения:

1. D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
2. D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два различных корня;
3. D 2 + bx + c.

Если требуется найти числовой промежуток, на котором квадратный трехчлен ax 2 + bx + c больше нуля, то этот числовой промежуток находится там, где парабола лежит выше оси ОХ.

Если нужно найти числовой промежуток, на котором квадратный трехчлен ax 2 + bx + c меньше нуля — это числовой промежуток, где парабола лежит ниже оси ОХ.

Если квадратное неравенство нестрогое, то корни входят в числовой промежуток. А если строгое — не входят.

Обучение на курсах по математике в онлайн-школе Skysmart сделает сложные темы понятными, а высокий балл на экзаменах — достижимым!

Решение неравенства методом интервалов

Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.

Если неравенство строгое, нужно отметить корни пустыми (выколотыми) точками. Если нестрогое — обычными точками. Именно эти точки разбивают координатную ось на промежутки.

Определить, какие знаки имеют значения трехчлена на каждом промежутке (если на первом шаге нашли нули) или на всей числовой прямой (если нулей нет). И проставить над этими промежутками + или − в соответствии с определенными знаками.

Если квадратное неравенство со знаком > или ≥ — наносим штриховку над промежутками со знаками +.

Если неравенство со знаком 2 + 4x — 5, его корнями являются числа -5 и 1, они разбивают числовую ось на три промежутка: (-∞, -5), (-5, 1) и (1, +∞).

Определим знак трехчлена x 2 + 4x — 5 на промежутке (1, +∞). Для этого вычислим значение данного трехчлена при некотором значении x из этого промежутка. Можно брать любое значение переменной, главное — чтобы вычисления были простыми. В нашем случае, возьмем x = 2. Подставим его в трехчлен вместо переменной x:

• 2 2 + 4 * 2 — 5 = 4 + 8 — 5 = 7.

7 — положительное число. Это значит, что любое значение квадратного трехчлена на интервале (1, +∞) будет положительным. Так мы определили знак плюс.

Определим знаки на оставшихся двух промежутках. Начнем с интервала (-5, 1). Из этого интервала можем взять x = 0 и вычислить значение квадратного трехчлена при этом значении переменной:

• 0 2 + 4 * 0 — 5 = 0 + 0 — 5 = -5.

Так как -5 — отрицательное число, то на этом интервале все значения трехчлена будут отрицательными. Так мы определили знак минус.

Осталось определиться со знаком на промежутке (-∞, -5). Возьмем x = -6, подставляем:

• (-6) 2 + 4 * (-6) — 5 = 36 — 24 — 5 = 7.

Следовательно, искомый знак — плюс.

Можно расставить знаки быстрее, если запомнить эти факты:

Плюс или минус: как определить знаки

Можно сделать вывод о знаках по значению старшего коэффициента a:

если a > 0, последовательность знаков: +, −, +,

если a 0, последовательность знаков: +, +,

если a 2 — 7 не имеет корней и на промежутке (−∞, +∞) его значения отрицательны, так как коэффициент при x 2 есть отрицательное число -4, и свободный член -7 тоже отрицателен.

• Когда квадратный трехчлен при D > 0 имеет два корня, то знаки его значений на промежутках чередуются. Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −.
• Если квадратный трехчлен при D = 0 имеет один корень, то этот корень разбивает числовую ось на два промежутка, а знаки над ними будут одинаковыми. Это значит, что достаточно определить знак над одним из них и над другим поставить такой же. При этом получится, либо +, +, либо −, −.
• Когда квадратный трехчлен корней не имеет (D

Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.

Пример 1. Решить неравенство методом интервалов: x^2 — 5x + 6 ≥ 0.

Разложим квадратный трехчлен на множители.

Неравенство примет вид:

Проанализируем два сомножителя:

Первый: х — 3. Этот сомножитель может поменять знак при х = 3, значит при х 0 принимает положительные значения: х — 3 > 0.

Второй: х — 2. Для этого сомножителя такая «знаковая» точка: х = 2.

Вывод: знак произведения (х — 3) * (х — 2) меняется только при переходе переменной через значения х = 3 и х = 2.

В этом весь смысл метода интервалов: определить интервалы значений переменной, на которых ситуация не меняется и рассматривать их как единое целое.

Построим чертеж.

Рассмотрим интервалы в том же порядке, как пишем и читаем: слева направо.

Отобразим эти данные на чертеже:

2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.

• (25 — 3) (25 — 2) = 22*23 = 506 > 0

Вывод: при х > 3 верно неравенство (х — 3) * (х — 2) > 0. Внесем эти данные в чертеж.

Исходное неравенство: (х — 3) * (х — 2) ≥ 0.

Если (х — 3) * (х — 2) > 0:

Если (х — 3) (х — 2) = 0 — при х1 = 3, х2 = 2.

Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.

Ответ: х ≤ 0, х ≥ 3.

Пример 2. Применить метод интервалов для решения неравенства х2+4х+3

Графический метод в задачах с параметром

Данный метод используется не только в задачах с параметром, но и для решения обыкновенных уравнений, систем уравнений или неравенств. Он входит в стандартный курс школьной программы и наверняка вы с ним сталкивались, но в несколько упрощенном варианте. Сначала я кратко напомню, в чем заключается этот метод. Затем разберем, как его применять для решения задач с параметром, и рассмотрим несколько типовых примеров.

Для начала рассмотрим уравнение с одной переменной (f(x)=0). Для того, чтобы решить его графическим методом, нужно построить график функции (y=f(x)). Точки пересечения графика с осью абсцисс (ось (х)) и будут решениями нашего уравнения.

Или рассмотрим уравнение (f(x)=g(x)). Точно так же строим на одной координатной плоскости графики функций (y=f(x)) и (y=g(x)), абсциссы точек их пересечения будут решениями уравнения.

Стоит отдельно отметить, что для решения графическим методом необходимо выполнять очень качественный и точный рисунок.

Решить графическим методом уравнение (x^2+3x=5x+3).

Решение: Построим на одной координатной плоскости графики функций (y=x^2+3x) и (y=5x+3). См. рис.1.

(y=5x+3) – красный график; (y=x^2+3x) – синий график.

Из Рис.1 видно, что графики пересекаются в точках ((-1;2)) и ((3;18)). Таким образом, решением нашего уравнения будут: (_<1>=-1; _<2>=3).

Теперь рассмотрим уравнение с двумя переменными (f(x,y)=0). Решением этого уравнения будет множество пар точек ((x,y)), которые можно изобразить в виде графика на координатной плоскости ((xOy)). Если решать это уравнение аналитически, то, как правило, мы выражаем одну переменную через другую ((x,y=f(x))) или ((x=f(y),y)).

В качестве примера рассмотрим обыкновенное линейное уравнение (2x-5y=10). (1) Выражаем (x=frac<10+5y><2>) – это называется общим решением уравнения. Изобразим его на координатной плоскости, построив график (Рис. 2):

Методика организации решения уравнений графическим способом как средство формирования графических умений у учащихся

Разделы: Математика

Графический метод обладает рядом преимуществ:

• он часто проще аналитического;
• обладает наглядностью. Особенно когда нет решений или требуется установить количество корней.
• он красив и доставляет эстетическое наслаждение. Выполнять графики нужно в цвете. Это помогает в выборе ответа.

Умение строить графики функций не является самоцелью. Часто построение графиков связано с исследованием поведения функций. Однако необходимость построения графиков облегчают нахождение решений уравнений и неравенств, сокращая или упрощая аналитические выкладки и часто при этом являются единственным методом решения таких задач. Графический метод решения способствует лучшему усвоению ряда понятий: функции, корней уравнения и неравенства, систем уравнений. При этом целесообразно при графическом решении уравнений устанавливать связи с такими свойствами функций как возрастание и убывание, знакопостоянство, обращение функции в ноль и т.д., что помогает глубже понять функциональную зависимость между величинами. Изучение поведения функций и построение их графиков является важным разделом математики. Свободное владение техникой построения графиков часто помогает решать многие задачи и порой является единственным средством их решения. Кроме того, умение строить график представляет большой самостоятельный интерес. Материал, связанный с построением графиков функций, в средней школе изучается недостаточно полно с точки зрения требований, предъявляемых на экзаменах. Поэтому задачи на построение графиков нередко вызывают затруднения у учащихся.

Для того, чтобы по графикам можно было получать достаточно приемлемые числовые ответы, графики должны быть особенно тщательно построены. Решается задача организации работы таким образом, чтобы выработать навыки быстрого построения графиков элементарных функций и их преобразований. Работа над формированием графических умений начинается с 5-го класса.

Изящно выполненная работа способствует развитию чувства красоты, удовлетворения от проделанной работы.

Изучение поведения функций и построение их графиков являются важным разделом школьного курса. Свободное владение техникой построения графиков часто помогает решать сложные задачи, а порой является единственным средством их решения. Кроме того, умение строить графики функций представляет большой интерес для самих учащихся. Однако на базе основной школы материал, связанный с этим вопросом, представлен несколько хаотично, изучается недостаточно полно, многие важные моменты не входят в программу.

Цель – прояснить и дополнить школьный материал, связанный с функциями и построение их графиков, применением их к решению уравнений, их систем.

В требованиях к уровню подготовки выпускников по разделу «Функции и графики» прописано:

• решать уравнения, системы уравнений, используя свойства функций и их графические представления;
• находить приближённые решения уравнений и их систем, используя графический метод.

В преподавание алгебры по учебнику под редакцией А.С.Теляковского. Линейная функция и функции у=х 2 , у=х 3 изучаются в 7 классе. Практически не вырабатываются навыки в применении графиков этих функций. Единственное упражнение: найти координаты точек пересечения графиков функций у=8,5х и у=0,5х-19,5. графики линейных функций только иллюстрируют решение систем линейных уравнений.

Автор вводит некоторые упражнения, необходимые в дальнейшем при решении уравнений и их систем:

— постройте в одной и той же координатной плоскости а) у=х 2 ; у=4; б) у=х 2 ; у=2х.

— изобразите схематически графики функций у = -0,9х + 4; у = 2,3х; у = х/10 . Но упражнения вводятся как дополнительные. И в «Задачах повышенной трудности» (в конце учебника) есть уравнения, которые тоже можно решать графическим способом: |х -3| = 7; |х+2| = 9; |4 — х| = 1,5.

В 8 классе изучаются функции у = к/х; у =. Представлены функции у = 4/|х|, у = -6/|х|.

— Могут ли графики функций у=к/х и у = ах +в пересекаться

а) в одной точке;

б) в двух точках;

в) в трёх точках.

— Могут ли графики функций у = к/х и у = ах +в пересекаться в двух точках, лежащих

а) в одной четверти;

б) в первой и второй четвертях;

в) в первой и третьей четвертях.

Опять же эти упражнения в дополнительных.

В 8 классе обучающихся знакомят с графическим способом решения уравнений (8/х = -х+6; (8/х = х 2 ). Появляются уравнения третьей степени, которые не решаются аналитическим способом. (х 3 — х + 1 = 0; х 3 + 2х — 4=0) На изучение этой темы отводится 1 час.

В 9 классе подробно изучается квадратичная функция и её график. Получены обучающимися представления о преобразовании графического объекта относительно осей координат. Именно в это время отрабатываются навыки в построении параболы. Но данные преобразования почти не переносятся на преобразования других графических объектов. Хотя есть два упражнения, которые соотносятся с заданиями, встречающимися в материалах ЕГЭ.

На рисунке изображён график одной их функций . Какой именно?

— Какой из трёх графиков, изображённых на рисунке, является графиком функции у = |х -2|

Сделаны попытки преобразования графических объектов.

— Какие преобразования надо выполнить, чтобы

а) из графика функции у=х 3 получить графики функций у = — х 3 ; у = (х-3) 3 ; у = х 3 + 4.

б) из графика функции у = получить графики функций у = — ;

— Постройте в одной координатной плоскости графики функций у = | х|; у =|х -4| ; у = |х -4|-3.

В учебнике 9 класса в главе «Целое уравнение и его корни» упоминается графический способ уравнений третьей и более высокой степени как один из способов наряду с разложением на множители.

Поэтому: уже в 7 классе строим графики функций у = | х| — 3, у = 4 — | х|; у =|х +4|; у = | х — 3|.

При построении параболы вводим первые преобразования:

— построить графики функций у = х 2 +3; у=х 2 -5, где смещение по оси ординат. А затем у = (х+2) 2 ; у = (х-1) 2 . Конечно, не все ученики усваивают, впрочем, как и всё содержание материала. Для успешных учеников это не сложно. Тем более это только пропедевтика.

В 8-м классе: Урок-практикум.

Тема: «График функции у = . Графический способ решения иррациональных уравнений»

Цель: отработать навыки в преобразовании графика функции у = , закрепить умения графически решать иррациональные уравнения.

I. Фронтально

1). Схематически в одной системе координат изобразить графики функций

2). Решить уравнения

II. Построить графики функций

III. Решение уравнений

X 2 -3 =

В 8 классе строим преобразования гиперболы и графика функции у = .

Упражнения взяты из «Сборника задач по алгебре 8-9 класса» М.Л.Галицкого, А.И.Звавича. Уже на факультативных занятиях или занятиях кружка решаем уравнения с параметром |х 2 -2х-3| = а. Определить, при каком а уравнение имеет три корня. Строим графики функций у = |х 2 -2х-3|; у = а. Получаем ответ а = 4.

В 9 классе больше занимаемся исследованием квадратного трёхчлена. Формулы функций усложняю. Рассматриваем графики вида у = (х 2 -2) 2 — (х 2 -1) 2 ;

Необычность конструкций, разрыв графиков, удаление точек вызывает некоторую удивлённость. Тем самым преодолевается стандартность мышления, развивается воображение, повышается интерес: а что ещё может получиться? В каких случаях?

Уравнения, решаемые графическим способом.

I. Решение уравнений Р(х) = 0, где Р(х) – многочлен степени большей 2.

источники:

http://sigma-center.ru/graphical_method

http://urok.1sept.ru/articles/672912

Выполнила Дзюба Светлана Ивановна, учитель математики МБОУ «Средняя школа №53 города Макеевки».

Метод интервалов

Решение неравенств

Для начала: определение квадратного неравенства.

• Неравенство — алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.
• Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.
• Решение — значение переменной, при котором неравенство становится верным.
• Решить неравенство значит найти множество, для которых оно выполняется.
• Квадратное неравенство выглядит так:

где x — переменная,

a, b, c — числа,

при этом а ≠ 0.

Квадратные неравенства можно решить двумя способами:

Графический метод

Метод интервалов

Примеры решения

Графический метод

Повторим

0 . Если дискриминант больше нуля, тогда у квадратного уравнения есть два корня ; D . Если дискриминант меньше нуля, тогда у квадратного уравнения нет корней . В зависимости от полученных корней и знака коэффициента a , возможно одно из шести расположений графика функции у = ax² + bx + c . » width=»640″

Решение неравенства графическим методом

При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax² + bx + c = 0 . Чтобы найти корни, нужно найти дискриминант данного уравнения.

Как дискриминант влияет на корни уравнения:

• D = 0 . Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень ;
• D 0 . Если дискриминант больше нуля, тогда у квадратного уравнения есть два корня ;
• D . Если дискриминант меньше нуля, тогда у квадратного уравнения нет корней .

В зависимости от полученных корней и знака коэффициента a , возможно одно из шести расположений графика функции у = ax² + bx + c .

Решение неравенства графическим методом (продолжение)

Если требуется найти числовой промежуток, на котором квадратный трехчлен ax² + bx + c больше нуля, то этот числовой промежуток находится там, где парабола лежит выше оси ОХ .

Если нужно найти числовой промежуток, на котором квадратный трехчлен ax² + bx + c меньше нуля — это числовой промежуток, где парабола лежит ниже оси ОХ .

Если квадратное неравенство нестрогое, то корни входят в числовой промежуток. А если строгое — не входят.

Метод интервалов

, Сейчас мы узнаем про интервалы в контексте решения квадратных неравенств. Интервал — это некий промежуток числовой прямой, то есть все возможные числа, заключенные между двумя числами — концами интервала. Представить эти промежутки не так просто, поэтому интервалы принято рисовать. » width=»640″

Решение неравенства методом интервалов

Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.

Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: ,

Сейчас мы узнаем про интервалы в контексте решения квадратных неравенств.

Интервал — это некий промежуток числовой прямой, то есть все возможные числа, заключенные между двумя числами — концами интервала. Представить эти промежутки не так просто, поэтому интервалы принято рисовать.

Алгоритм решения квадратных неравенств методом интервалов:

• Найти нули квадратного трехчлена ax² + bx + c из левой части квадратного неравенства.
• Изобразить координатную прямую и при наличии корней отметить их на ней. Если неравенство строгое, нужно отметить корни пустыми (выколотыми) точками. Если нестрогое — обычными точками. Именно эти точки разбивают координатную ось на промежутки.
• Определить, какие знаки имеют значения трех- члена на каждом промежутке (если на первом шаге нашли нули) или на всей числовой прямой (если ну- лей нет) . И проставить над этими промежутками + или − в соответствии с определенными знаками.

или ≥ — наносим штриховку над промежутками со знаками +. Если неравенство со знаком В результате получаем геометрический образ некоторого числового множества — это и есть решение неравенства. Либо вместо штриховки можно нарисовать «арки» для интервалов. Справа налево, начиная с +, проставить чередуя знаки + и −. Выбрать необходимые интервалы и записать ответ. » width=»640″

Алгоритм решения квадратных неравенств методом интервалов (продолжение):

• Если квадратное неравенство со знаком или ≥ — наносим штриховку над промежутками со знаками +. Если неравенство со знаком

• В результате получаем геометрический образ некоторого числового множества — это и есть решение неравенства.
• Либо вместо штриховки можно нарисовать «арки» для интервалов. Справа налево, начиная с +, проставить чередуя знаки + и −.

• Выбрать необходимые интервалы и записать ответ.

Немного подробнее про 3 шаг алгоритма

Для примера возьмем трехчлен x² + 4x — 5 , его корнями являются числа -5 и 1, они разбивают числовую ось на три промежутка: (-∞, -5), (-5, 1) и (1, +∞).

Определим знак трехчлена x² + 4x — 5 на промежутке (1, +∞) . Для этого вычислим значение данного трехчлена при некотором значении x из этого промежутка. Можно брать любое значение переменной, главное — чтобы вычисления были простыми. В нашем случае, возьмем x = 2 . Подставим его в трехчлен вместо переменной x :

• 2² + 4 * 2 — 5 = 4 + 8 — 5 = 7.

7 — положительное число. Это значит, что любое значение квадратного трехчлена на интервале (1, +∞) будет положительным. Так мы определили знак плюс.

Определим знаки на оставшихся двух промежутках. Начнем с интервала (-5, 1) . Из этого интервала можем взять x = 0 и вычислить значение квадратного трехчлена при этом значении переменной:

• 0² + 4 * 0 — 5 = 0 + 0 — 5 = -5.

Так как -5 — отрицательное число, то на этом интервале все значения трехчлена будут отрицательными. Так мы определили знак минус.

Осталось определиться со знаком на промежутке (-∞, -5) . Возьмем x = -6 , подставляем:

• (-6)² + 4 * (-6) — 5 = 36 — 24 — 5 = 7.

Следовательно, искомый знак — плюс.

0 , последовательность знаков: +, −, +, если a , последовательность знаков: −, +, −. Можно также сделать вывод о знаках по значению старшего коэффициента a : если a 0, последовательность знаков: +, +, если a Например -4x^2 — 7 не имеет корней и на промежутке (−∞, +∞) его значения отрицательны, так как коэффициент при x² есть отрицательное число -4, и свободный член -7 тоже отрицателен. Когда квадратный трехчлен при D 0 имеет два корня, то знаки его значений на промежутках чередуются. Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −. Если квадратный трехчлен при D = 0 имеет один корень, то этот корень разбивает числовую ось на два промежутка, а знаки над ними будут одинаковыми. Это значит, что достаточно определить знак над одним из них и над другим поставить такой же. При этом получится, либо +, +, либо −, −. Когда квадратный трехчлен корней не имеет (D a , так и со знаком свободного члена c . » width=»640″

Плюс или минус: как определить знаки

Можно сделать вывод о знаках по значению старшего коэффициента a :

если a 0 , последовательность знаков: +, −, +,

если a , последовательность знаков: −, +, −.

Можно также сделать вывод о знаках по значению старшего коэффициента a :

если a 0, последовательность знаков: +, +,

если a

Например -4x^2 — 7 не имеет корней и на промежутке (−∞, +∞) его значения отрицательны, так как коэффициент при x² есть отрицательное число -4, и свободный член -7 тоже отрицателен.

• Когда квадратный трехчлен при D 0 имеет два корня, то знаки его значений на промежутках чередуются. Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −.
• Если квадратный трехчлен при D = 0 имеет один корень, то этот корень разбивает числовую ось на два промежутка, а знаки над ними будут одинаковыми. Это значит, что достаточно определить знак над одним из них и над другим поставить такой же. При этом получится, либо +, +, либо −, −.
• Когда квадратный трехчлен корней не имеет (D a , так и со знаком свободного члена c .

0. Второй: х — 2. Для этого сомножителя такая «знаковая» точка: х = 2. Вывод: знак произведения (х — 3) * (х — 2) меняется только при переходе переменной через значения х = 3 и х = 2. Построим чертеж . » width=»640″

Пример 1. Решить неравенство методом интервалов: x² — 5x + 6 ≥ 0.

• Как решаем:

• Разложим квадратный трехчлен на множители .

Неравенство примет вид:

(х — 3) * (х — 2) ≥ 0

• Проанализируем два сомножителя :

Первый: х — 3. Этот сомножитель может поменять знак при х = 3, значит при х 0 принимает положительные значения: х — 3 0.

Второй: х — 2. Для этого сомножителя такая «знаковая» точка: х = 2.

Вывод: знак произведения (х — 3) * (х — 2) меняется только при переходе переменной через значения х = 3 и х = 2.

• Построим чертеж .

0 (2,5 — 3) (2,5 — 2) = -0,5 * 0,5 = — 0,25 Вывод: при х 0. Отобразим эти данные на чертеже: Вывод: при 2 » width=»640″

Пример 1. Решить неравенство методом интервалов: x² — 5x + 6 ≥ 0.

• Рассмотрим интервалы в том же порядке, как пишем и читаем: слева направо.

• 2

• х

Подставляем:

(-1 — 3) * (-1 — 2) = -4 * (-3) = 12; 12 0

(2,5 — 3) (2,5 — 2) = -0,5 * 0,5 = — 0,25

Вывод: при х 0. Отобразим эти данные на чертеже:

Вывод: при 2

3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25. Исходное неравенство : (х — 3) * (х — 2) ≥ 0. Если (х — 3) * (х — 2) 0: Подставляем: (x — 3) * (x + 3/2) 0. (25 — 3) (25 — 2) = 22*23 = 506 0 Если (х — 3) (х — 2) = 0 — при х1 = 3, х2 = 2. Вывод : при х 3 верно неравенство (х — 3) * (х — 2) 0. Внесем эти данные в чертеж. Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми. Ответ: х ≤ 0, х ≥ 3. » width=»640″

Пример 1. Решить неравенство методом интервалов: x² — 5x + 6 ≥ 0.

• х 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.

• Исходное неравенство : (х — 3) * (х — 2) ≥ 0. Если (х — 3) * (х — 2) 0:

Подставляем:

(x — 3) * (x + 3/2) 0.

(25 — 3) (25 — 2) = 22*23 = 506 0

Если (х — 3) (х — 2) = 0 — при х1 = 3, х2 = 2.

Вывод : при х 3 верно неравенство (х — 3) * (х — 2) 0. Внесем эти данные в чертеж.

Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.

Ответ: х ≤ 0, х ≥ 3.

(самостоятельно)

Примените метод интервалов для решения неравенства х²+4х+3

• Как решить неравенство методом интервалов нам уже известно. Поэтому можем оформить решение кратко:

Ответ: -3

Пример 2. Выполнить решение квадратного неравенства методом интервалов:

• Находим корни квадратного трехчлена, который находится в левой части:

• Так как мы решаем строгое неравенство, то на координатной прямой изображаем выколотую точку с координатой 7:
• Теперь определим знаки на двух полученных промежутках (−∞, 7) и (7, +∞). Это легко сделать, потому что дискриминант квадратного трехчлена равен нулю, а старший коэффициент со знаком минус. Фиксируем знаки: −, −:
• Так как мы решаем неравенство со знаком
• Очевидно, решениями являются оба промежутка (−∞, 7), (7, +∞).

Ответ: (−∞, 7), (7, +∞).

На этом урок завершён, спасибо за внимание!



2.6. Метод интервалов

Объяснять буду сразу на конкретном примере: . Кстати, все ли до конца

понимают то, что нам предстоит сделать? Здесь нужно определить при каких «икс» квадратный трёхчлен

будет больше нуля. Итак, как решить это неравенство?

На первом шаге нужно решить соответствующее уравнение, а также определить все недопустимые значения

«икс». Что касаемо недопустимых значений, то их здесь нет, поскольку квадратный трёхчлен  определён для всех «икс». А вот с розыском корней придётся потрудиться – решаем квадратное уравнение .

Используя стандартный алгоритм, рассчитываем дискриминант:
 – отлично, извлекаем корень:
 и находим сами корни:

Не забываем о проверке!  – мысленно подставляем значения   в уравнение  и

убеждаемся, что получаются верные равенства.

На втором шаге отмечаем на числовой прямой все «нелегальные» точки и все корни. Поскольку наше неравенство строгое, то корни «выкалываем»:

Теперь нужно определить знаки, в нашем случае трёхчлена , на полученных интервалах. Как это сделать? Если квадратный трёхчлен больше (либо

меньше) нуля в какой-либо точке интервала, то он больше (либо меньше) нуля и во всех точках этого

интервала. В этом и состоит суть метода интервалов:

1) Рассмотрим интервал . Выберем любое значение,

принадлежащее этому интервалу, выгодно взять , и подставим его в

трёхчлен:
, значит трёхчлен больше нуля и во всех точках

этого интервала.

2) Рассмотрим интервал  и подставим в трёхчлен наиболее удобное

значение :   , значит,  трёхчлен меньше нуля и во всех точках интервала.

3) И, наконец, интервал  с подопытной точкой :
, значит, трёхчлен положителен и во всех

точках этого интервала.

Перечисленные подстановки выполняют устно, а результаты (полученные знаки) отмечают на чертеже. При этом нужные интервалы удобно

заштриховать:

Таким образом, решением неравенства  являются два интервала, и ответ часто записывают в виде объединения промежутков: , если
Используя метод интервалов, решим неравенство  – здесь

нужно найти все значения «икс», при которых дробь будет меньше либо равна нулю.

Сначала определим недопустимые значения «икс» и корни соответствующего уравнения: . И те и другие точки виднЫ невооружённым глазом: у нас есть нелегальное значение , которое обращает знаменатель в ноль, и корни . Первую точку следует «выколоть», а вот корни «затушевать» – по той причине, что неравенство нестрогое:

Теперь определим знаки дроби  на полученных

интервалах:
1) Подставим значение  из интервала
, значит, дробь больше нуля и во всех точках этого

интервала

2) Из интервала  удобно выбрать значение :
, значит, дробь меньше нуля и на всём

интервале.

3) Из интервала  я выберу точку :
, значит, дробь отрицательна и на этом интервале.

4) И, наконец, из интервала  возьмём значение поменьше, а

именно :
 – заметьте, что для определения знака зачастую не

обязательно проводить вычисления или доводить их до конца.

Отмечаем на чертеже знаки и штрихуем нужные нам интервалы:

Ответ: , если

Что делать, если справа не ноль, а что-то другое? С помощью преобразований получить справа ноль :). Возможно, потребуется ещё «причесать» левую часть: привести дроби к общему знаменателю, привести подобные слагаемые и т.п.

А что делать, если нет ни «плохих» значений, ни корней? Тут всё просто – у нас один интервал (вся числовая прямая) и мы подставляем в

неравенство любое значение «икс». Если получено верное числовое неравенство, то решением является вся числовая прямая. Если

же получено неверное неравенство, то неравенство не имеет решений. Решим, например, неравенство  . У соответствующего уравнения  нет корней, поскольку дискриминант отрицателен: . И мы

просто подставляем в неравенство любое «икс», проще всего взять ноль:

 – в результате получено неверное числовое неравенство,

следовательно, неравенство  не имеет решений.
Ну и легко понять, что решением неравенства  будет любое

«икс».

Иногда из области рассмотрения следует исключить целые промежутки. Забегая вперёд, приведу неравенство с натуральным логарифмом: . «Начинка» любого логарифма строго положительна: , а значит, нам нужно рассмотреть не всю числовую прямую, а лишь участок, где: . Дорешаем позже!

2.7. Уравнения и неравенства с модулем

2.5. Действия с неравенствами

| Оглавление |



Метод интервалов: решение простейших строгих неравенств

12 ноября 2017

• Домашнее задание
• Ответы

Для начала — немного лирики, чтобы почувствовать проблему, которую решает метод интервалов. Допустим, нам надо решить вот такое неравенство:

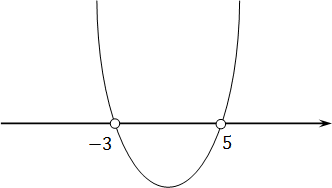
(x − 5)(x + 3) > 0

Какие есть варианты? Первое, что приходит в голову большинству учеников — это правила «плюс на плюс дает плюс» и «минус на минус дает плюс». Поэтому достаточно рассмотреть случай, когда обе скобки положительны: x − 5 > 0 и x + 3 > 0. Затем также рассмотрим случай, когда обе скобки отрицательны: x − 5 < 0 и x + 3 < 0. Таким образом, наше неравенство свелось к совокупности двух систем, которая, впрочем, легко решается:

Более продвинутые ученики вспомнят (может быть), что слева стоит квадратичная функция, график которой — парабола. Причем эта парабола пересекает ось OX в точках x = 5 и x = −3. Для дальнейшей работы надо раскрыть скобки. Имеем:

x² − 2x − 15 > 0

Теперь понятно, что ветви параболы направлены вверх, т.к. коэффициент a = 1 > 0. Попробуем нарисовать схему этой параболы:

Функция больше нуля там, где она проходит выше оси OX. В нашем случае это интервалы (−∞ −3) и (5; +∞) — это и есть ответ.

Обратите внимание: на рисунке изображена именно схема функции, а не ее график. Потому что для настоящего графика надо считать координаты, рассчитывать смещения и прочую хрень, которая нам сейчас совершенно ни к чему.

Почему эти методы неэффективны?

Итак, мы рассмотрели два решения одного и того же неравенства. Оба они оказались весьма громоздкими. В первом решении возникает — вы только вдумайтесь! — совокупность систем неравенств. Второе решение тоже не особо легкое: нужно помнить график параболы и еще кучу мелких фактов.

Это было очень простое неравенство. В нем всего 2 множителя. А теперь представьте, что множителей будет не 2, а хотя бы 4. Например:

(x − 7)(x − 1)(x + 4)(x + 9) < 0

Как решать такое неравенство? Перебирать все возможные комбинации плюсов и минусов? Да мы уснем быстрее, чем найдем решение. Рисовать график — тоже не вариант, поскольку непонятно, как ведет себя такая функция на координатной плоскости.

Для таких неравенств нужен специальный алгоритм решения, который мы сегодня и рассмотрим.

Что такое метод интервалов

Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f (x) > 0 и f (x) < 0. Алгоритм состоит из 4 шагов:

1. Решить уравнение f (x) = 0. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;
2. Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов;
3. Выяснить знак (плюс или минус) функции f (x) на самом правом интервале. Для этого достаточно подставить в f (x) любое число, которое будет правее всех отмеченных корней;
4. Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется.

Вот и все! После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f (x) > 0, или знаком «−», если неравенство имеет вид f (x) < 0.

На первый взгляд может показаться, что метод интервалов — это какая-то жесть. Но на практике все будет очень просто. Стоит чуть-чуть потренироваться — и все станет понятно. Взгляните на примеры — и убедитесь в этом сами:

Задача. Решите неравенство:

(x − 2)(x + 7) < 0

Работаем по методу интервалов. Шаг 1: заменяем неравенство уравнением и решаем его:

(x − 2)(x + 7) = 0

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:

x − 2 = 0 ⇒ x = 2;
x + 7 = 0 ⇒ x = −7.

Получили два корня. Переходим к шагу 2: отмечаем эти корни на координатной прямой. Имеем:

Теперь шаг 3: находим знак функции на самом правом интервале (правее отмеченной точки x = 2). Для этого надо взять любое число, которое больше числа x = 2. Например, возьмем x = 3 (но никто не запрещает взять x = 4, x = 10 и даже x = 10 000). Получим:

f (x) = (x − 2)(x + 7);
x = 3;
f (3) = (3 − 2)(3 + 7) = 1 · 10 = 10;

Получаем, что f(3) = 10 > 0, поэтому в самом правом интервале ставим знак плюс.

Переходим к последнему пункту — надо отметить знаки на остальных интервалах. Помним, что при переходе через каждый корень знак должен меняться. Например, справа от корня x = 2 стоит плюс (мы убедились в этом на предыдущем шаге), поэтому слева обязан стоять минус.

Этот минус распространяется на весь интервал (−7; 2), поэтому справа от корня x = −7 стоит минус. Следовательно, слева от корня x = −7 стоит плюс. Осталось отметить эти знаки на координатной оси. Имеем:

Вернемся к исходному неравенству, которое имело вид:

(x − 2)(x + 7) < 0

Итак, функция должна быть меньше нуля. Значит, нас интересует знак минус, который возникает лишь на одном интервале: (−7; 2). Это и будет ответ.

Задача. Решите неравенство:

(x + 9)(x − 3)(1 − x) < 0

Шаг 1: приравниваем левую часть к нулю:

(x + 9)(x − 3)(1 − x) = 0;
x + 9 = 0 ⇒ x = −9;
x − 3 = 0 ⇒ x = 3;
1 − x = 0 ⇒ x = 1.

Помните: произведение равно нулю, когда хотя бы один из множителей равен нулю. Именно поэтому мы вправе приравнять к нулю каждую отдельную скобку.

Шаг 2: отмечаем все корни на координатной прямой:

Шаг 3: выясняем знак самого правого промежутка. Берем любое число, которое больше, чем x = 1. Например, можно взять x = 10. Имеем:

f (x) = (x + 9)(x − 3)(1 − x);
x = 10;
f (10) = (10 + 9)(10 − 3)(1 − 10) = 19 · 7 · (−9) = − 1197;
f (10) = −1197 < 0.

Шаг 4: расставляем остальные знаки. Помним, что при переходе через каждый корень знак меняется. В итоге наша картинка будет выглядеть следующим образом:

Вот и все. Осталось лишь выписать ответ. Взгляните еще раз на исходное неравенство:

(x + 9)(x − 3)(1 − x) < 0

Это неравенство вида f (x) < 0, т.е. нас интересуют интервалы, отмеченные знаком минус. А именно:

x ∈ (−9; 1) ∪ (3; +∞)

Это и есть ответ.

Замечание по поводу знаков функции

Практика показывает, что наибольшие трудности в методе интервалов возникают на последних двух шагах, т.е. при расстановке знаков. Многие ученики начинают путаться: какие надо брать числа и где ставить знаки.

Чтобы окончательно разобраться в методе интервалов, рассмотрим два замечания, на которых он построен:

1. Непрерывная функция меняет знак только в тех точках, где она равна нулю. Такие точки разбивают координатную ось на куски, внутри которых знак функции никогда не меняется. Вот зачем мы решаем уравнение f (x) = 0 и отмечаем найденные корни на прямой. Найденные числа — это «пограничные» точки, отделяющие плюсы от минусов.
2. Чтобы выяснить знак функции на каком-либо интервале, достаточно подставить в функцию любое число из этого интервала. Например, для интервала (−5; 6) мы вправе брать x = −4, x = 0, x = 4 и даже x = 1,29374, если нам захочется. Почему это важно? Да потому что многих учеников начинают грызть сомнения. Мол, что если для x = −4 мы получим плюс, а для x = 0 — минус? А ничего — такого никогда не будет. Все точки на одном интервале дают один и тот же знак. Помните об этом.

Вот и все, что нужно знать про метод интервалов. Конечно, мы разобрали его в самом простом варианте. Существуют более сложные неравенства — нестрогие, дробные и с повторяющимися корнями. Для них тоже можно применять метод интервалов, но это тема для отдельного большого урока.

Теперь хотел бы разобрать продвинутый прием, который резко упрощает метод интервалов. Точнее, упрощение затрагивает только третий шаг — вычисление знака на самом правом куске прямой. По каким-то причинам этот прием не проходят в школах (по крайней мере, мне никто такого не объяснял). А зря — ведь на самом деле этот алгоритм очень прост.

Итак, знак функции на правом куске числовой оси. Этот кусок имеет вид (a; +∞), где a — самый большой корень уравнения f (x) = 0. Чтобы не взрывать мозг, рассмотрим конкретный пример:

(x − 1)(2 + x)(7 − x) < 0;
f (x) = (x − 1)(2 + x)(7 − x);
(x − 1)(2 + x)(7 − x) = 0;
x − 1 = 0 ⇒ x = 1;
2 + x = 0 ⇒ x = −2;
7 − x = 0 ⇒ x = 7;

Мы получили 3 корня. Перечислим их в порядке возрастания: x = −2, x = 1 и x = 7. Очевидно, что наибольший корень — это x = 7.

Для тех, кому легче рассуждать графически, я отмечу эти корни на координатной прямой. Посмотрим, что получится:

Требуется найти знак функции f (x) на самом правом интервале, т.е. на (7; +∞). Но как мы уже отмечали, для определения знака можно взять любое число из этого интервала. Например, можно взять x = 8, x = 150 и т.д. А теперь — тот самый прием, который не проходят в школах: давайте в качестве числа возьмем бесконечность. Точнее, плюс бесконечность, т.е. +∞.

«Ты че, обкурился? Как можно подставить в функцию бесконечность?» — возможно, спросите вы. Но задумайтесь: нам ведь не нужно само значение функции, нам нужен только знак. Поэтому, например, значения f (x) = −1 и f (x) = −938 740 576 215 значат одно и то же: функция на данном интервале отрицательна. Поэтому все, что от вас требуется — найти знак, который возникает на бесконечности, а не значение функции.

На самом деле, подставлять бесконечность очень просто. Вернемся к нашей функции:

f (x) = (x − 1)(2 + x)(7 − x)

Представьте, что x — это очень большое число. Миллиард или даже триллион. Теперь посмотрим, что будет происходить в каждой скобке.

Первая скобка: (x − 1). Что будет, если из миллиарда вычесть единицу? Получится число, не особо отличающееся от миллиарда, и это число будет положительным. Аналогично со второй скобкой: (2 + x). Если к двойке прибавить миллиард, по получим миллиард с копейками — это положительное число. Наконец, третья скобка: (7 − x). Здесь будет минус миллиард, от которого «отгрызли» жалкий кусочек в виде семерки. Т.е. полученное число мало чем будет отличаться от минус миллиарда — оно будет отрицательным.

Осталось найти знак всего произведения. Поскольку в первых скобках у нас был плюс, а в последней — минус, получаем следующую конструкцию:

(+) · (+) · (−) = (−)

Итоговый знак — минус! И неважно, чему равно значение самой функции. Главное, что это значение — отрицательное, т.е. на самом правом интервале стоит знак минус. Осталось выполнить четвертый шаг метода интервалов: расставить все знаки. Имеем:

Исходное неравенство имело вид:

(x − 1)(2 + x)(7 − x) < 0

Следовательно, нас интересуют интервалы, отмеченные знаком минус. Выписываем ответ:

x ∈ (−2; 1) ∪ (7; +∞)

Вот и весь прием, который я хотел рассказать. В заключение — еще одно неравенство, которое решается методом интервалов с привлечением бесконечности. Чтобы визуально сократить решение, я не буду писать номера шагов и развернутые комментарии. Напишу только то, что действительно надо писать при решении реальных задач:

Задача. Решите неравенство:

x(2x + 8)(x − 3) > 0

Заменяем неравенство уравнением и решаем его:

x(2x + 8)(x − 3) = 0;
x = 0;
2x + 8 = 0 ⇒ x = −4;
x − 3 = 0 ⇒ x = 3.

Отмечаем все три корня на координатной прямой (сразу со знаками):

Справа на координатной оси стоит плюс, т.к. функция имеет вид:

f (x) = x(2x + 8)(x − 3)

А если подставить бесконечность (например, миллиард), получим три положительных скобки. Поскольку исходное выражение должно быть больше нуля, нас интересуют только плюсы. Осталось выписать ответ:

x ∈ (−4; 0) ∪ (3; +∞)

Смотрите также:

1. Метод интервалов: случай нестрогих неравенств
2. Тест по методу интервалов для строгих неравенств
3. Сводный тест по задачам B12 (2 вариант)
4. Профильный ЕГЭ-2022, задание 6. Геометрический смысл производной
5. Формулы приведения: ускоряем вычисления в тригонометрии
6. Задачи B4: перевозка груза тремя фирмами