2D XY
- 2D XY
- Horizontal Bar
- Vertical Bar
- Pie/Doughnut
- Polar
- Ternary
- Map with Scale
- Distance
- Angle
- Area
Pro
Go PRO
Instructions
About
Contact
Instruction
Use the online PlotDigitizer tool to extract data from graphs, charts, 2D plots, and other images.
- Upload or drag-drop the desired image in png, jpg, svg, or gif format.
- Calibrate the axes by drag-dropping x1, x2, y1, & y2 and insert their values. Then, select the axes type: linear, date/time, or log10.
- Mark the data points by left-clicking. You can use the zoom panel to increase precision while marking.
- You can always readjust x1, x2, y1, and y2 if necessary.
- To delete the data points, right-click on them.
- Export the extracted points using the export options to CSV, MS Excel, JSON, & Python List.
Click to upload or drag-and-drop your image here
—
X-AXIS
Linear
Linear
Date/Time
Log10
Reciprocal
Loge
Pro
Y-AXIS
Linear
Linear
Date/Time
Log10
Reciprocal
Loge
Pro
X-AXIS
Linear
Linear
Date/Time
Log10
Reciprocal
Loge
Pro
Y-AXIS
Linear
Linear
Date/Time
Log10
Reciprocal
Loge
Pro
AXIS
Linear
Linear
Date/Time
Log10
Reciprocal
Loge
Pro
Radius
Linear
Linear
Date/Time
Log10
Reciprocal
Loge
Pro
Tip
Thank you for using PlotDigitizer
If you find it helpful, consider sharing with others.
Статистический анализ по картинке
Время на прочтение
7 мин
Количество просмотров 2.8K
Название звучит как «приворот по фото», но я о чём — захотел я как-то проанализировать пару графиков, найти корреляции и столкнулся с парой сложностей:
Оцифровка аналоговых графиков
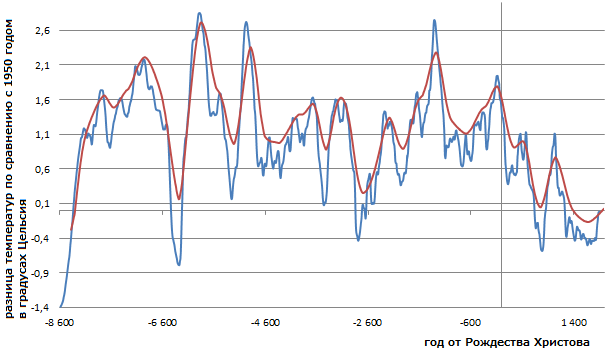
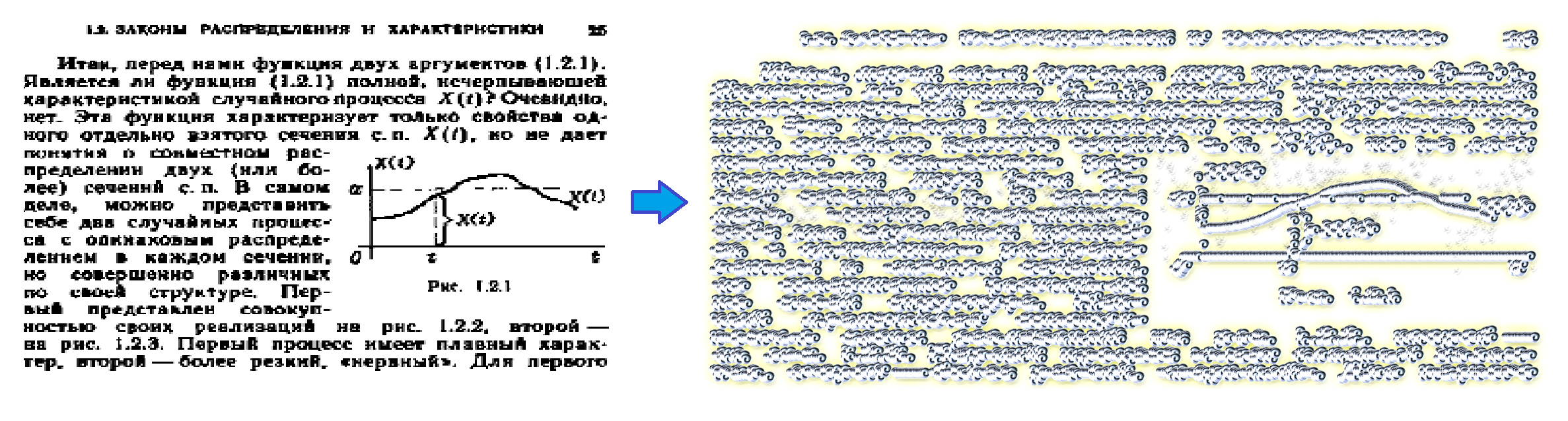
I. У меня был только график — картинка (аналоговое представление данных), самих данных (значений) не было. Принялся я по нему вычислять хотя бы наиболее важные точки — в итоге получилось ужасно долго и просто ужасно (человеский глаз и осознанный мозг не может предоставить точность больше 10% деления, а ещё случаются незамеченные ошибки):
Поэтому, я написал специальную, программу, с которой вами делюсь: скачать можно здесь
С её помощью получается почти идеальный вариант:
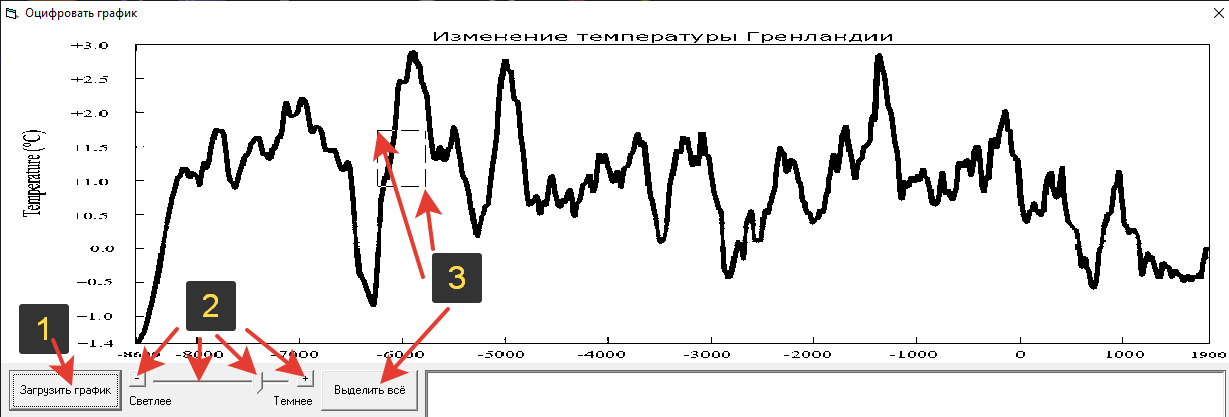
Рассказываю как пользоваться, чтобы оцифровать значения графика:
-
(Желательно предварительно подрехтовать картинку, чтобы график был тёмный, других тёмных элементов не было, рамка чтоб была серая, но это необязательно). Загружаем график, он сразу превращается в чёрно-белый
-
Регулируем яркость (светлее/темнее), чтобы лишние элементы с области значений ушли, а график и рамка осталась (не нужно если область значений во всю картинку).
-
Выделяем область значений, либо не касаясь рамки, либо повторяем пункт 2, чтобы она тоже исчезла
-
Вписываем диапазон значений для рамки и нажимаем «Получить значения»
-
Дожидаемся результата и копируем его куда хотите, например, в Excel.
Поиск корреляций и оценка их значимости на временных рядах
II. Вторая проблема, с которой я столкнулся — это то, что как мне подсказали, указав на эту очень важную статью — Корреляция между временными рядами: что может быть проще? — на случайных процессах (коими являются большинство графиков) по большей части не будут работать знакомые нам формулы из базовой теории вероятности (особенно на немарковских процессах).
К сожалению, при применении статистических методов на этот нюанс часто не обращают внимания. Однако, именно эта "мелочь" приводит к очень серьезным и нетривиальным следствиям с точки зрения обработки таких сигналов. Самые обычные формулы, описанные во всех учебниках, внезапно отказываются работать. А попытки их применения "в лоб" иногда дают, мягко говоря, весьма неожиданные результаты. Например, статистическая связь между числом пиратов и глобальным потеплением оказывается не просто "значимой", а "практически достоверной". Что удивительно, столкнувшись с такой ситуацией, даже достаточно грамотные исследователи не всегда понимают, где же тут "порылась собака". Данные вроде бы правильные, ... А результат – ни в какие ворота... А Вы твердо уверены, что всегда правильно оцениваете значимость таких корреляций? — Корреляция между временными рядами: что может быть проще?
Поэтому даже корреляция в 90% может быть обыденностью и ничего не значить) — её азы написаны для случайных величин (а не процессов, где Y зависит от Х), поэтому для начала нужно найти функцию распределения случайного процесса, в зависимости от которой нужно применять специальные, ей подходящие, законы. Это задача намного сложнее предыдущей, однако, моя программа, я думаю, хоть и не решит её полностью — может помочь:
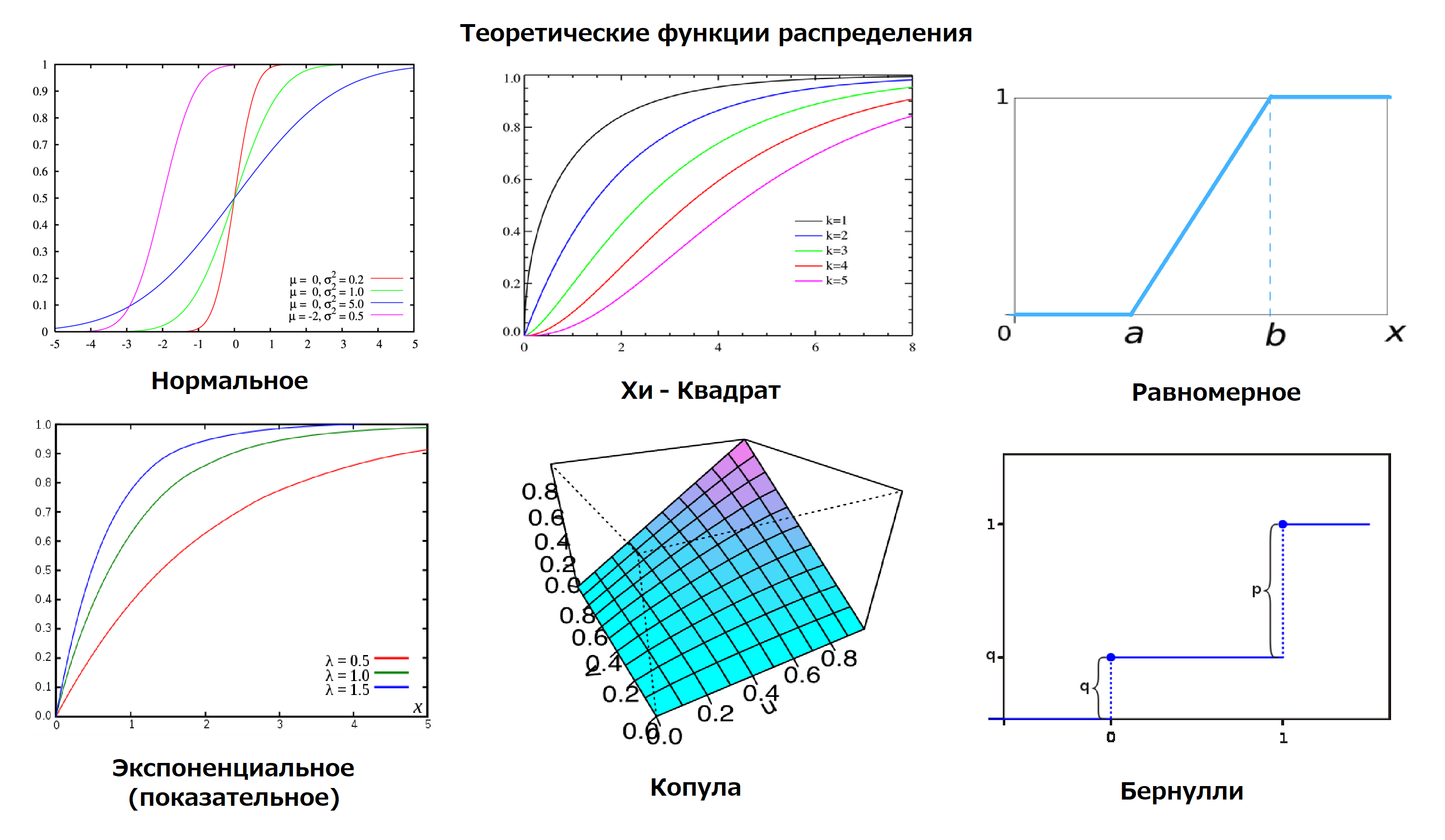
Для правильного выбора доверительных интервалов, критических значений признака проверяемых гипотез — в общем чтобы результаты исследования опирались на математику, а не на первые найденные формулы в интернете — необходимо знать какое распределение у значений — нормальное, показательное, равномерное, какое-то ещё? И в зависимости от распределения пользоваться соответсвующими формулами, таблицами, ограничениями и т.д.
Для этого прежде чем приступать к анализу, первым делом желательно вычислить эмпирическую функцию распределения и сравнить её с теоретической:
Итак, для «затравки» — вычисление графика эмпирической функции распределения для случайных величин:
Вы можете спросить — это что за график такой, где Y не зависит от Х? Вот несколько примеров:
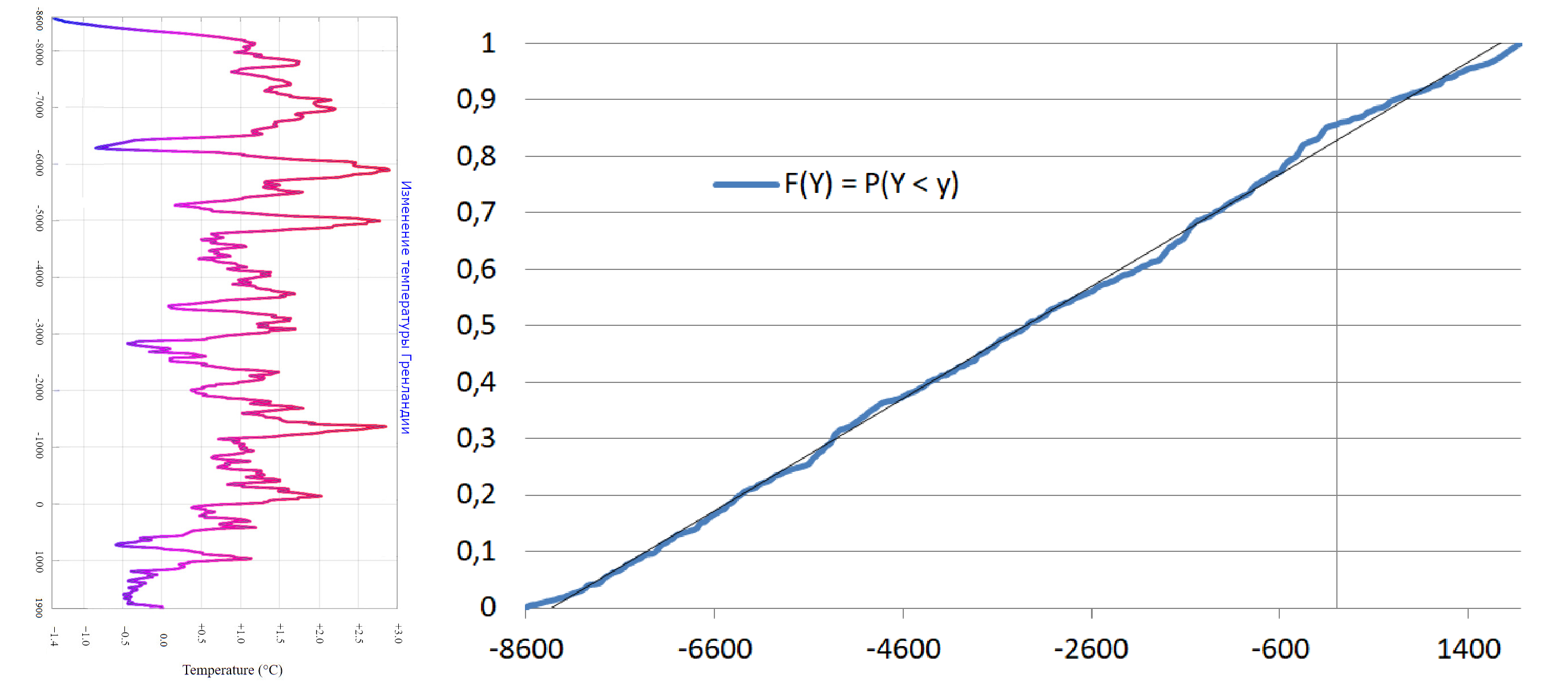
а) просто повернуть наш исходный график разницы температур от года на 90°, поменяв местами Х и Y (который будет уже не графиком, а плоской кривой) — зная год, можно узнать среднегодовую температуру, а вот зная температуру — не всегда можно однозначно сказать какой это год (этакая хеш-функция получается)
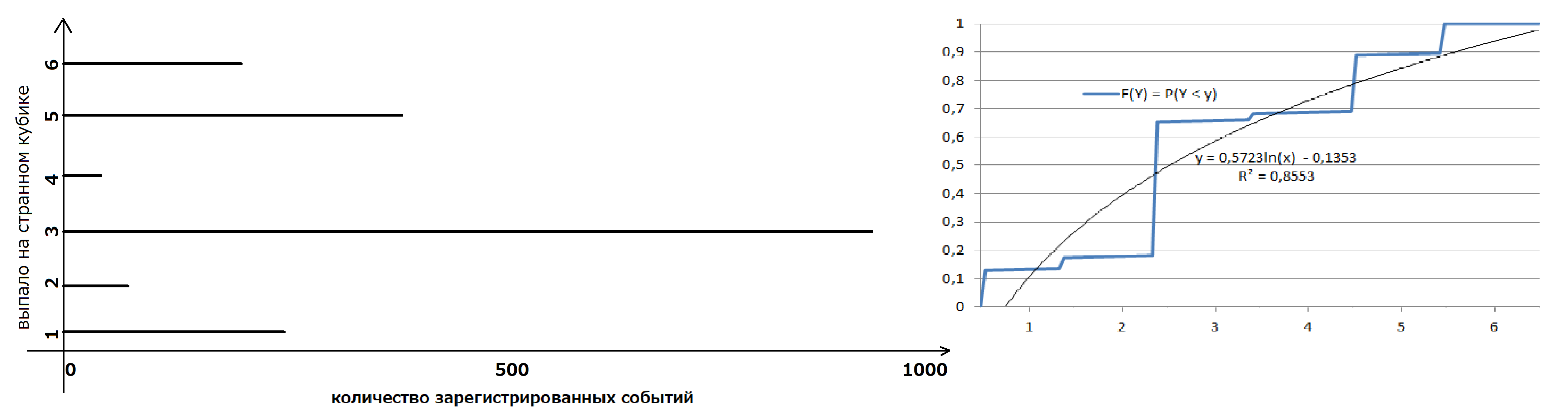
б) Вот следующее изображение, иллюстрирующее результаты опыта с броском игрового кубика со смещённым центром тяжести:
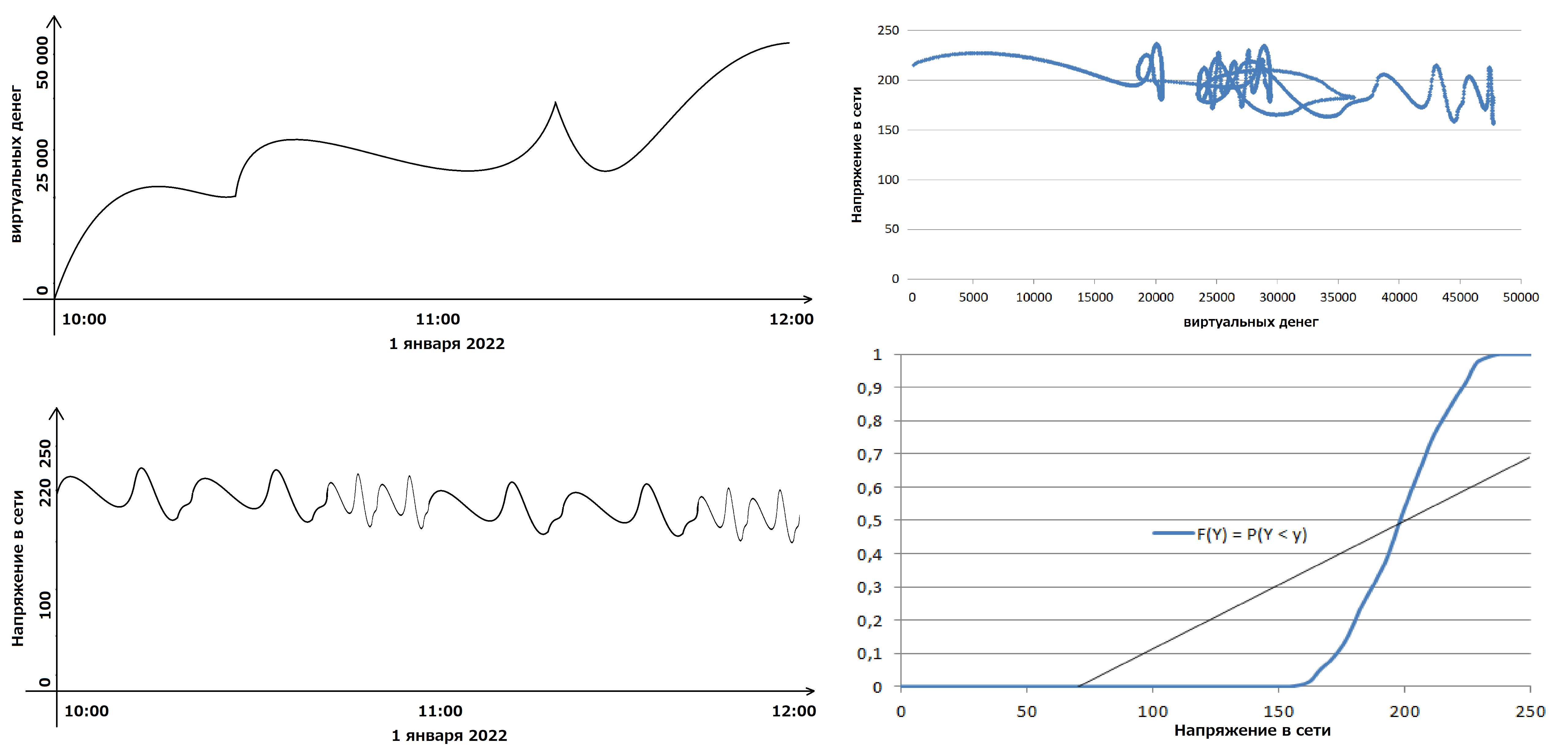
в) связать два графика через время:
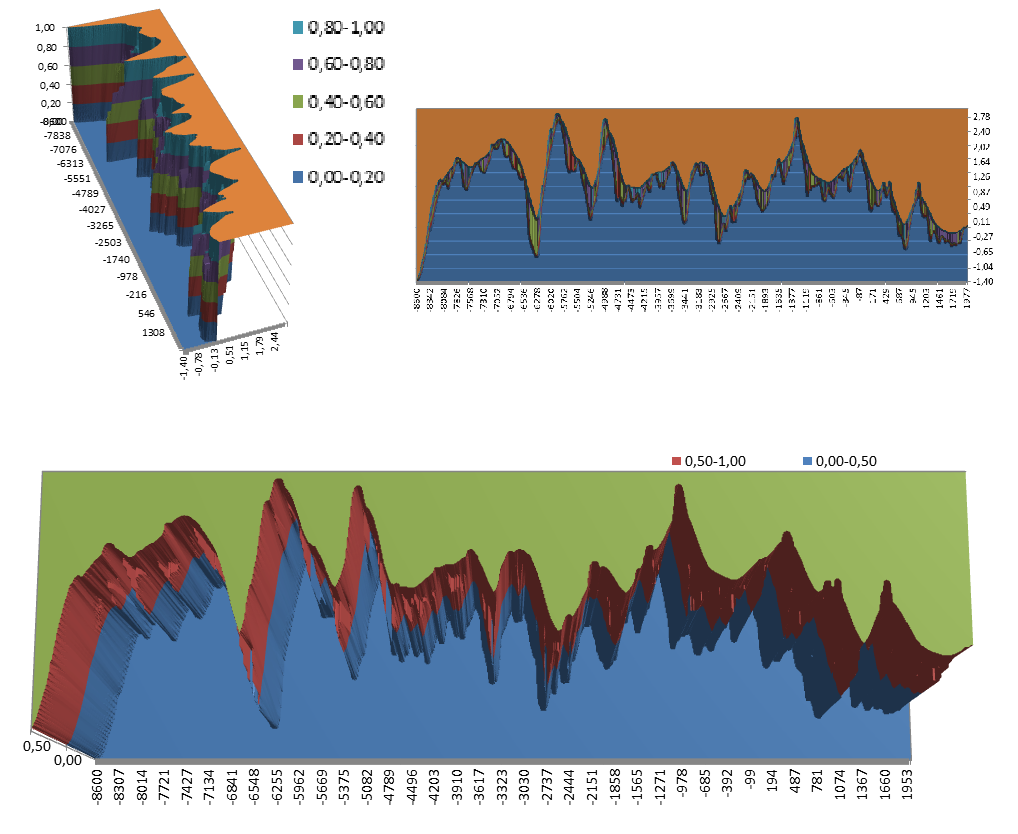
На графиках слева показаны сколько денег в игре на смартфоне, не подключенном к сети электропитания, у конкретного мальчика в Калининграде, и какое напряжение в сети в конкретном доме в Анадыре в одно и то же время. Справа получившаяся пересекающаяся кривая этого напряжения от вышеупомянутых виртуальных денег. Поскольку напряжение не зависит от виртуальных денег (хотя апофенисты могут и тут придумать связь — чем я и занимался в прошлой моей статье Взаимосвязь температуры и населения (там можно скачать данные по температуре и населению за 10 000 лет), хоть и не утверждал, что мои выводы верны -, и действительно на некоторых участках она видна), эту кривую можно считать геометрическим представлением случайной величины, а не процесса. И можно восстановить функцию распределения напряжения — последний график, который показывает, что напряжение распределено не равномерно, а имеет место быть нормальное распределение. Это можно было выяснить и из второго графика, однако, если у Вас в наличии только пересекающаяся кривая — моя программа Вам в этом поможет.
Переходим далее к функции распределения случайных процессов:
Во-первых, здесь ограничение в том, что графиков на одной картинке должно быть несколько, где каждый график представляет собой конкретную реализацию этого случайного процесса. Однако, очень часто у нас есть только одна реализация на конкретном временном отрезке (у нас пока одна планета, например). В таком случае, конечно, Вы можете проводить исследования, находить закономерности, корреляции — и математика Вам этого запретить не может. Но нужно понимать, что смысла в этом столько же, сколько в том, чтобы подбросить монетку один раз в полдень, и на основе результатов только этого эксперимента судить о том с какой вероятностью выпадает орёл, решка, монета встаёт на ребро, теряется, если её подбросить ровно в полдень. Поэтому, например, если Вы собираете данные об изменении глобальной температуры планеты за несколько тысячелетий, а они остались только в ледниках, возьмите хотя бы данные с нескольких ледников, чем больше — тем лучше, точнее и адекватнее будут результаты Ваших исследований.
Во-вторых, полная функция распределения случайного процесса многомерна: для одной реализации — она трёхмерна, для двух — уже пятимерна и так далее. Моя программа может дать значения только графика трёхмерной проекции функции распределения, поэтому это неполная информация о ней, однако и они могут дать некоторое представление. В теории, можно усовершенствовать программу и для больших измерений, но для ПК это будет чрезвычайно долго (уже трёхмерная проекция — без параллелизации, конечно, но — строится десятки минут), а также, я не представляю что могут дать только значения функции, без её формул, для больших измерений, которые мы даже посмотреть не сможем — Вы сможете представить себе хотя бы пятимерную поверхность, даже если построить всевозможные её проекции?
И, завершая тему функции распределения спрошу — есть математики статанализа в этом самолёте, который без пилота вряд ли долетит куда надо?
Для математически верного доказательства значимости любых корреляций двух временных рядов между собой нужно знать ответы на некоторые вопросы. Итак, мы с @adeshere (мы не математики, а программист и физик) спрашиваем:
Пусть у нас есть случайный процесс вида x(t), где t-время. Все, что мы знаем про этот процесс — это то, что для почти любой его реализации спектр полученного временного ряда (ведь реализация случайного процесса — это временной ряд) имеет степенной вид. То есть, спектральная мощность W в первом приближении зависит от частоты f, как W(f) =Cf^(-b), где C - это некоторая константа, а степенной параметр b лежит в диапазоне от 0.5 до 2.0. То есть, чем выше частота, тем меньше спектральная мощность, и наоборот. Так вот, теперь возьмем две реализации такого случайного процесса (два временных ряда), определенные на интервале времени T. Обозначим их, как Х1 и Х2. (Задача со звёздочкой - если взять не две реализации одного процесса, а много двух разных случайных процессов Х1 и Х2, также удовлетворяющих требованиям - спектр имеет степенной вид, C - константа, b ∈ [0.5,2.0]) И посчитаем формально в пределах интервала T статистику, ПОХОЖУЮ на коэффициент корреляции: R12=cov(x1,x2)/(s1s2), где cov(x1,x2) — это аналог ковариации, а s1 и s2 — аналоги стандартных отклонений для Х1 и Х2.
Вопросы такие:
1) Можно ли найти функцию распределения R12(b1,b2), зная только степенные параметры исходных случайных процессов b1 и b2? Если да, то какая она будет? Или хотя бы для случая b1 = b2? Или зная ещё и константы C?
2) Если этих знаний недостаточно, то какие еще ограничения на случайные процессы надо наложить, чтобы вычисление этой функции распределения стало возможным?
3) Еще интересный вопрос — доказать, что функция распределения случайной величины R12 не зависит от T. Я подозреваю, что в силу автомодельности случайных процессов зависимости быть не должно. Но это надо доказывать. Или все же зависит?
Очень надеемся на ответы в Ваших комментариях или ссылкой на статью. Заранее благодарны!
А мы продолжаем с программой:
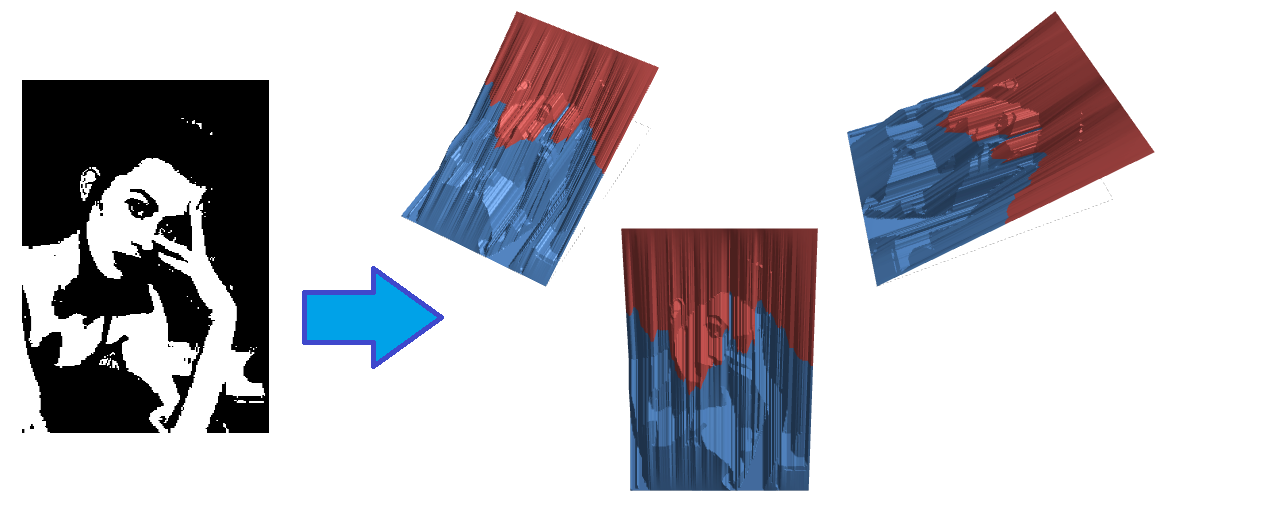
Бонусом с помощью неё можно добиться интересных (не относящихся к математике) результатов, если вместо графика загрузить скриншот текста или фото:
График линейной функции, его свойства и формулы
О чем эта статья:
Понятие функции
| Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции. |
|---|
Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:
Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.
Графический способ — наглядно. Его мы и разберем в этой статье.
| График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу. |
|---|
Понятие линейной функции
| Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент. |
|---|
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Нам дана функция: у = 0,5х — 2. Значит:
если х = 0, то у = -2;
если х = 2, то у = -1;
если х = 4, то у = 0 и т. д.
Для удобства результаты можно оформлять в виде таблицы:
Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.
| Функция | Коэффициент k | Коэффициент b |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.
Свойства линейной функции
Область определения функции — множество всех действительных чисел.
Множеством значений функции является множество всех действительных чисел.
График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.
Функция не имеет ни наибольшего, ни наименьшего значений.
Четность и нечетность линейной функции зависят от значений коэффициентов k и b:
b ≠ 0, k = 0, значит, y = b — четная;
b = 0, k ≠ 0, значит, y = kx — нечетная;
b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;
b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.
Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.
График функции пересекает оси координат:
ось абсцисс ОХ — в точке (−b/k; 0);
ось ординат OY — в точке (0; b).
x = −b/k — является нулем функции.
Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.
Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.
Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).
При k 0, то этот угол острый, если k
Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
если k > 0, то график наклонен вправо;
если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
если b 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Если k > 0 и b
В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.
Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.
Например, график уравнения х = 3:
Условие параллельности двух прямых:
График функции y = k1x + b1 параллелен графику функции y = k2x + b2, если k1 = k2.
Условие перпендикулярности двух прямых:
График функции y = k1x + b1 перпендикулярен графику функции y = k2x + b2, если k1k2 = −1 или k1 = −1/k2.
Точки пересечения графика функции y = kx + b с осями координат:
С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
Координаты точки пересечения с осью OY: (0; b).
С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.
Координаты точки пересечения с осью OX: (−b/k; 0).
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.
В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
Таким образом, нам надо построить график функции y = -4x — 10
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
Поставим эти точки в координатной плоскости и соединим прямой:
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.
Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
Вычтем из второго уравнения системы первое, и получим k = 3.
Подставим значение k в первое уравнение системы, и получим b = -2.
Ответ: уравнение прямой y = 3x — 2.
Алгоритм определения формулы линейной функции по графику
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Выполнила учительница математики МБОУ Башкирский лицей № 1 муниципального района Учалинский район Республики Башкортостан Хидиятова Залифа Даутовна
Алгоритм определения формулы линейной функции по графику»
На рисунке представлен график функции у = kx +b.
Записать формулу линейной функции, соответствующей данному графику.
1) Так как ордината точки пересечения графика функции с осью Оy равна 1, следовательно, b=1.
Значит, у = kx+ 1
2) Выбираем на графике произвольную точку, например, А (2;2) и определяем её координаты: если x = 2, то у = 2. Подставим в нашу формулу вместо Х и У и получим уравнение относительно k.
2 = 2k+1
2k=1
k = 0.5 Записываем формулу линейной функции: у = 0,5х + 1.
Написать ФОРМУЛУ линейной функции У= КХ+В, график которой изображен на рисунке :
Это ВПР задание 
ВНИМАНИЕ : задание на сегодня 16 апреля
Внимание : вот эти следующие задания пока НЕ РЕШАТЬ.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 930 человек из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 687 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 304 человека из 68 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 594 534 материала в базе
Материал подходит для УМК
«Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А.
16. Линейная функция и её график
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 16.09.2020
- 201
- 11
- 31.03.2020
- 1171
- 30
- 16.03.2020
- 227
- 1
- 16.03.2020
- 192
- 1
- 08.03.2020
- 282
- 6
- 20.02.2020
- 1254
- 72
- 21.01.2020
- 180
- 0
- 09.12.2019
- 424
- 13
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 30.09.2020 16256
- DOCX 549.2 кбайт
- 155 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Хидиятова Залифа Даутовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 5 лет и 3 месяца
- Подписчики: 0
- Всего просмотров: 39036
- Всего материалов: 37
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной
Время чтения: 0 минут
Школы смогут вносить данные в портфолио школьника в «МЭШ»
Время чтения: 2 минуты
Минобрнауки и Минпросвещения запустили горячие линии по оказанию психологической помощи
Время чтения: 1 минута
В Ростовской и Воронежской областях организуют обучение эвакуированных из Донбасса детей
Время чтения: 1 минута
В Швеции запретят использовать мобильные телефоны на уроках
Время чтения: 1 минута
Минпросвещения России подготовит учителей для обучения детей из Донбасса
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Как определить a, b и c по графику параболы
Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.
1 способ – ищем коэффициенты на графике
Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.
Коэффициент (a) можно найти с помощью следующих фактов:
— Если (a>0), то ветви параболы направленных вверх, если (a 1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.
Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:
Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.
Решаем систему.
Пример:
Вычтем из второго уравнения первое:
Подставим (9a) вместо (b):
Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:
Подставим в первое уравнение (a):
Получается квадратичная функция: (y=-x^2-9x-15).
Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).
Таким образом имеем систему:
Сложим 2 уравнения:
Подставим во второе уравнение:
Теперь найдем точки пересечения двух функций:
Теперь можно найти ординату второй точки пересечения:
3 способ – используем преобразование графиков функций
Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.
Главный недостаток этого способа — вершина должна иметь целые координаты.
Сам способ базируется на следующих идеях:
График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).
– Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
– Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз.
– График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
— График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц.
График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.
У вас наверно остался вопрос — как этим пользоваться? Предположим, мы видим такую параболу:
Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).
А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).
То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:
Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:
Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).
Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).
Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).
http://infourok.ru/algoritm-opredeleniya-formuly-linejnoj-funkcii-po-grafiku-4463697.html
http://cos-cos.ru/ege/zadacha203/378/
Поиск изображения по графику оригинала
Пр.9
По данному графику оригинала найти
изображение.
Построим аналитическое
выражение для данной функции,
на
основе общего уравнения прямой, проходящей
через
две
точки (t1,
y1)
, (t2,
y2)
=
( 5 )
и
свойств единичной функции
(t
— а) =
(t)
(t)
—
(t
— а)
Решение.
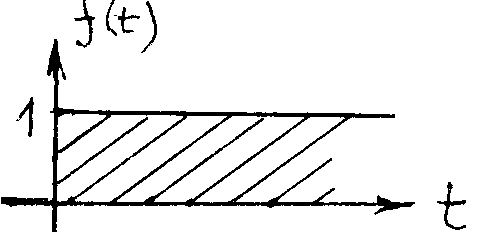
Функцию на интервале [0 , a]
описывает разность двух единичных
функций
(t)
—
(t
— а) . Первую наклонную определим из ( 5
) по точкам (2а,
0), (а,
1): y
=-
(t
– 2a).
Для перехода от бесконечной прямой к
отрезку на интервале [a,
3a]
умножим уравнение на разность(t
-а) —(t
-3а)
Вторую наклонную определим из ( 5 ) по
точкам (4а,0)
, (3а,-1):
y
=(t
– 4a),
и умножим уравнение на
(t
— 3а).
Сумма этих трех выражений определит
аналитический вид функции
f(t)
=
(t)
—
(t
— а) —
(t
– 2a)
[(t
— а) —
(t
— 3а)]
+
(t
– 4a)
[(t
— 3а)]
Представим
f(t)
в виде суммы слагаемых двух типов
(t
— b)
и (t
– b)(t
— b)
f(t)
=(t)
—(t
— а) —(t
– a)(t
— а) +(t
— а) +(t
– 3a)(t
— 3а)
+(t
— 3а)+
+
(t
– 3a)
(t
— 3а)
—
(t
— 3а)
=
(t)
—
(t
– a)(t
— а)
+
(t
–
3a)(t
— 3а)
С
помощью соотношений Пр.8 совершим
переход к искомому изображению
F(t)
=:
—
+
.
Таблица
изображений
-
№
f(t)
при t>0F(p)
№
f(t)
при t>0F(p)
1
1
9
t
cos at2
10
t
sin at3
eat
11
4
cos
at12
5
sin
at13
6
ezt
cos at14
7
ezt
sin at15
8
eat16
Отыскание оригинала по изображению
Если
изображение является дробно-рациональной
функцией F(p)
=
и m
< n
,
то многочлен
знаменателя представим в виде произ-ведения
линейных множителей
=
.
Корни
многочлена pi
могут
быть
действительными числами, комплексными
числами и кратными. Комплексные корни
входят сопряженными парами и приводят
к трехчленам типа ( p2
+
p
+
).
В результате F(p)
представ-ляется в виде суммы
элементарных
дробей типа
,
(метод неопределенных коэффициентов).
Комбинируя эти дроби, можно пытаться
построить изображения основных
элементарных функций и затем по таблице
восстановить оригинал.
Пр.
10 Найти оригинал функции F(p)
=
.
=
=
+ ½=:
etcos
2t
+ ½ etsin
2t
Пр.
11 Найти оригинал функции F(p)
=
.
=
=
+
= =
p2
| A + B = 0
p1
| 2A – 2B + C = 0
A = 1/12 , B = -1/12 , C = — 1/3
p0
| 4A – 2C = 1
=
—
=
—
Из
формул
№ 3, 6, 7
оригинал
f(t)
=e2t
—
e-t
(cos t+
sin t)
.
Если
в F(p)
только простые нули :
=
,
то разложение
изображения упрощается
F(p)
=
, где
( 6 )
Пр.12
Найти оригинал функции F(p)
=
Вычисляем
производную от знаменателя
= [ p(p
– 1)(p
– 2)(p
– 3) ]` =
=
(p
– 1)(p
– 2)(p
– 3) + p(p
– 2)(p
– 3) + p(p
– 1)(p
– 3) +
p(p
– 1)(p
– 2),
находим
её значения в нулевых точках v4`(0)
= — 6 , v4`(1)
= 2 , v4`(2)
= — 2 , v4`(3)
= 6 , определяем коэффициенты A0
= — 1/6 , A1
= 1, A2
= — 3/2, A3
= 2/3
и
по формуле ( 6 ) расписываем разложение
изображения на простые дроби
F(p)
=
=:
+
—
+
.
Если
F(p)
разлагается в сходящийся ряд
F(p)
=
+
+
+ . . . +
+ . . . ,
то
его оригинал находится по формуле
f(t)
=
+
+
+ . . . +
+ . . .
Этот
ряд сходится при всех значениях t
.
Пр.13
Найти оригинал функции F(p)
=
.
Используем
формулу для суммы бесконечной
геометрической прогрессии
=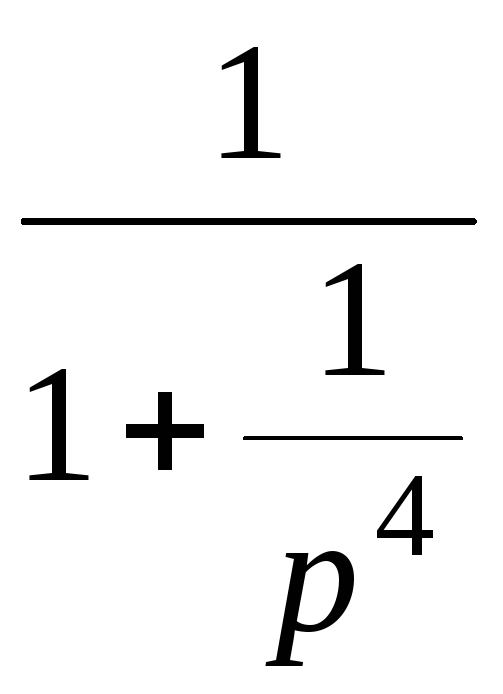
—
+
— . . . Этот ряд сходится при |p|
> 1
По
формуле № 2 получаем оригинал f(t)
=
—
+
—
+ . . .
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Интегральное преобразование Лапласа онлайн, калькулятор изображения функций.
Теория функций комплексного переменного.
: x^a
модуль x: abs(x)
: Sqrt[x]
: x^(1/n)
: a^x
: Log[a, x]
: Log[x]
: cos[x] или Cos[x]
 : sin[x] или Sin[x]
: sin[x] или Sin[x] : tan[x] или Tan[x]
: tan[x] или Tan[x] : cot[x] или Cot[x]
: cot[x] или Cot[x] : sec[x] или Sec[x]
: sec[x] или Sec[x] : csc[x] или Csc[x]
: csc[x] или Csc[x] : ArcCos[x]
: ArcCos[x] : ArcSin[x]
: ArcSin[x] : ArcTan[x]
: ArcTan[x] : ArcCot[x]
: ArcCot[x] : ArcSec[x]
: ArcSec[x] : ArcCsc[x]
: ArcCsc[x] : cosh[x] или Cosh[x]
: cosh[x] или Cosh[x] : sinh[x] или Sinh[x]
: sinh[x] или Sinh[x] : tanh[x] или Tanh[x]
: tanh[x] или Tanh[x] : coth[x] или Coth[x]
: coth[x] или Coth[x] : sech[x] или Sech[x]
: sech[x] или Sech[x] : csch[x] или Csch[е]
: csch[x] или Csch[е] : ArcCosh[x]
: ArcCosh[x] : ArcSinh[x]
: ArcSinh[x] : ArcTanh[x]
: ArcTanh[x] : ArcCoth[x]
: ArcCoth[x] : ArcSech[x]
: ArcSech[x] : ArcCsch[x]
: ArcCsch[x]





















 : x^a
: x^a : Sqrt[x]
: Sqrt[x]![sqrt[n]{x}](https://upload.wikimedia.org/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png) : x^(1/n)
: x^(1/n) : a^x
: a^x : Log[a, x]
: Log[a, x] : Log[x]
: Log[x] : cos[x] или Cos[x]
: cos[x] или Cos[x]