Построение графика заданной функции по точкам имеет целью получение точного рисунка нужных размеров, который можно было бы использовать в публикациях, технической документации, презентациях и т.п.
Чтобы получить графическое изображение заданной функции y=f(x)y = f(x) на заданном отрезке [a,b][a, b] в прямоугольной системе координат, необходимо выполнить следующие действия:
- выбрать количество точек для построения nn;
- вычислить шаг табуляции аргумента xx по формуле h=(b–a)/(n–1)h = (b–a) / (n–1);
- найти все nn значений xx, для которых должны быть вычислены значения функции, то есть x1=ax_{1} = a; xi+1=xi+hx_{i+1} = x_{i} + h, i=1,2,…,n–2i = 1,2,…,n–2; xn=bx_{n} = b;
- построить таблицу значений функции, вычислив yi=f(xi)y_{i} = f(x_{i}), i=1,2,…,ni = 1,2,…,n;
| i | 1 | 2 | n–1n – 1 | n |
|---|---|---|---|---|
| xix_i | x1x_1 | x2x_2 | xn–1x_{n–1} | xnx_n |
| yiy_i | y1y_1 | y2y_2 | yn–1y_{n–1} | yny_n |
- вычислить масштабы по осям координат OxO_x и OyO_y по формулам mx=(b–a)/Lxm_{x} = (b – a) / Lx, my=(ymax–ymin)/Lym_{y} = (y_{max} – y_{min}) / L_{y} соответственно, где LxL_x и LyL_y – заданные размеры графика по осям координат, ymaxy_{max} и yminy_{min} – наибольшее и наименьшее значения функции, выбранные из таблицы; значения масштабов следует округлить;
- на поле размером Lx×LyL_{x} × L_{y} изобразить оси координат OxO_x и OyO_y в пределах промежутков [a,b][a, b] и [ymin,ymax][y_{min}, y_{max}] соответственно, на осях проставить масштабные деления, нанести точки графика (xi,yi)(x_{i}, y_{i}) и соединить их плавной линией.
Пример построения графика функции по точкам
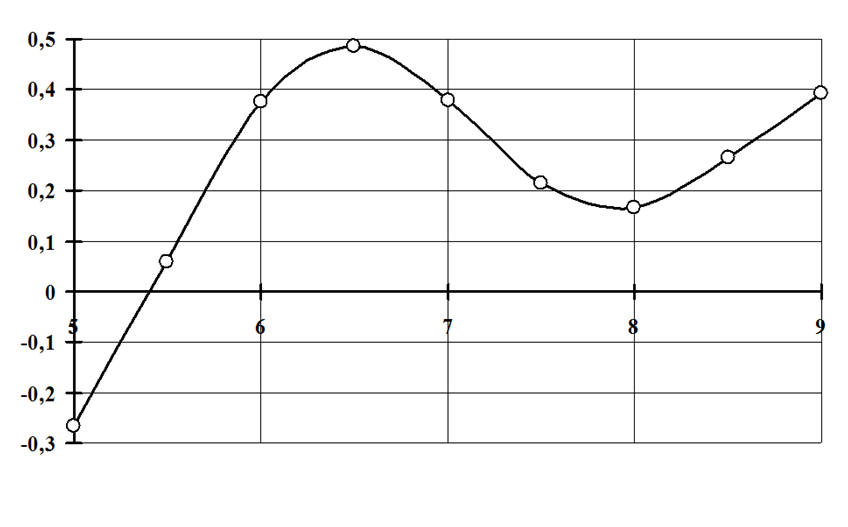
Построим график функции y=(3⋅sinx+x⋅cos2x)/(2⋅ln3x+1)y = (3·sinx + x·cos^2x) / (2·ln^3x +1) на отрезке [5, 9] размером Lx=16L_{x} = 16 см по горизонтали и Ly=7,5L_{y} = 7,5 см по вертикали.
Выбираем количество точек для построения n=9n = 9. Вычисляем шаг табуляции по аргументу x:h=(9–5)/(9–1)=0,5x: h = (9 – 5) / (9 – 1) = 0,5. Находим значения аргумента и строим таблицу значений функции:
| ii | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| xix_i | 5 | 5,5 | 6 | 6,5 | 7 | 7,5 | 8 | 8,5 | 9 |
| yiy_i | -0,265 | 0,059 | 0,375 | 0,485 | 0,378 | 0,214 | 0,165 | 0,266 | 0,392 |
Вычисляем масштабы: mx=(9–5)/16=0,25m_{x} = (9 – 5) / 16 = 0,25 единиц на 1 см (или 1 единица на 4 см) по оси OxO_x; my=(0,485–(–0,265))/7,5=0,1m_{y} = (0,485 – (–0,265)) / 7,5 = 0,1 единиц на 1 см по оси OyO_y.
Выполняем построение графика:
Тест на тему “Построение графика функции по точкам”
Как по точкам найти функцию
Во многих случаях данные статистики или измерений какого-либо процесса бывают представлены в виде набора дискретных значений. Но для того, чтобы на их основе построить непрерывный график, нужно по этим точкам найти функцию. Сделать это можно путем интерполяции. Для этого хорошо подходит полином Лагранжа.
Вам понадобится
- — бумага;
- — карандаш.
Инструкция
Определите степень полинома, который будет использован для интерполирования. Он имеет вид: Кn*Х^n + К(n-1)*Х^(n-1) +… + К0*Х^0. Число n здесь на 1 меньше количества известных точек с различными Х, через которые должна проходить результирующая функция. Поэтому просто пересчитайте точки и отнимите от полученного значения единицу.
Определите общей вид искомой функции. Поскольку Х^0 = 1, то она примет вид: f(Хn) = Кn*Х^n + К(n-1)*Х^ (n-1) +… + К1*Х + К0, где n — найденное на первом шаге значение степени полинома.
Начните составление системы линейных алгебраических уравнений с целью нахождения коэффициентов интерполирующего полинома. Исходный набор точек задает ряд соответствий значений координат Хn искомой функции по оси абсцисс и оси ординат f(Хn). Поэтому поочередная подстановка величин Хn в полином, значение которого будет равно f(Хn), позволяет получить нужные уравнения:
Кn*Хn^n + К(n-1)*Хn^ (n-1) +… + К1*Хn + К0 = f(Хn)
Кn*Х(n-1)^n + К(n-1)*Х(n-1)^ (n-1) +… + К1*Х(n-1) + К0 = f(Х(n-1))
…
Кn*Х1n + К(n-1)*Х1^ (n-1) + … + К1*Х1 + К0 = f(Х1).
Представьте систему линейных алгебраических уравнений в удобном для решения виде. Вычислите значения Хn^n… Х1^2 и Х1…Хn, а затем подставьте их в уравнения. При этом значения (также известные) перенесите в левую часть уравнений. Получится система вида:
Сnn*Кn + Сn(n-1)*К(n-1) +… + Сn1*К1 + К0 — Сn = 0
С(n-1)n*Кn + С(n-q)(n-1)*К(n-1) +… + С(n-1)1*К1 + К0 — С(n-1) = 0
…
С1n*Кn + С1(n-1)*К(n-1) +… + С11*К1 + К0 — С1 = 0
Здесь Сnn = Хn^n, а Сn = f(Хn).
Решите систему линейных алгебраических уравнений. Используйте любой известный способ. Например, метод Гаусса или Крамера. В результате решения будут получены значения коэффициентов полинома Кn…К0.
Найдите функцию по точкам. Подставьте коэффициенты Кn…К0, найденные в предыдущем шаге, в полином Кn*Х^n + К(n-1)*Х^ (n-1) +… + К0*Х^0. Данное выражение и будет являться уравнением функции. Т.е. искомая f(Х) = Кn*Х^n + К(n-1)*Х^ (n-1) +… + К0*Х^0.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Вывести уравнение прямой по координатам двух точек
По введенным пользователем координатам двух точек вывести уравнение прямой, проходящей через эти точки.
Общее уравнение прямой имеет вид y = kx + b . Для какой-то конкретной прямой в уравнении коэффициенты k и b заменяются на числа, например, y = 4x — 2 . Задача сводится именно к нахождению этих коэффициентов.
Так как координаты точки это значения x и y , то мы имеем два уравнения. Пусть, например, координаты точки А(3;2), а координаты B(-1;-1). Получаем уравнения:
2 = k*3 + b,
-1 = k*(-1) + b.
Решая полученную систему уравнений находим значения k и b :
b = 2 — 3k
-1 = -k + 2 — 3k
4k = 3
k = 3/4 = 0.75
b = 2 — 3 * 0.75 = 2 — 2.25 = -0.25
Таким образом, получается уравнение конкретной прямой, проходящей через указанные точки: y = 0.75x — 0.25.
Алгоритм решения данной задаче на языке программирования будет таков:
- Получить значения координат первой точки и присвоить их переменным, например x1 и y1 .
- Получить значения координат ( x2, y2 ) второй точки.
- Вычислить значение k по формуле k = (y1 — y2) / (x1 — x2) .
- Вычислить значение b по формуле b = y2 — k * x2 .
- Вывести на экран полученное уравнение.
Аппроксимация функции одной переменной
Калькулятор использует методы регрессии для аппроксимации функции одной переменной.
Данный калькулятор по введенным данным строит несколько моделей регрессии: линейную, квадратичную, кубическую, степенную, логарифмическую, гиперболическую, показательную, экспоненциальную. Результаты можно сравнить между собой по корреляции, средней ошибке аппроксимации и наглядно на графике. Теория и формулы регрессий под калькулятором.
Если не ввести значения x, калькулятор примет, что значение x меняется от 0 с шагом 1.
Аппроксимация функции одной переменной
Линейная регрессия
Коэффициент линейной парной корреляции:
Средняя ошибка аппроксимации:
Квадратичная регрессия
Система уравнений для нахождения коэффициентов a, b и c:
Коэффициент корреляции:
,
где
Средняя ошибка аппроксимации:
Кубическая регрессия
Система уравнений для нахождения коэффициентов a, b, c и d:
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Степенная регрессия
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Показательная регрессия
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Гиперболическая регрессия
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Логарифмическая регрессия
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Экспоненциальная регрессия
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Вывод формул
Сначала сформулируем задачу:
Пусть у нас есть неизвестная функция y=f(x), заданная табличными значениями (например, полученными в результате опытных измерений).
Нам необходимо найти функцию заданного вида (линейную, квадратичную и т. п.) y=F(x), которая в соответствующих точках принимает значения, как можно более близкие к табличным.
На практике вид функции чаще всего определяют путем сравнения расположения точек с графиками известных функций.
Полученная формула y=F(x), которую называют эмпирической формулой, или уравнением регрессии y на x, или приближающей (аппроксимирующей) функцией, позволяет находить значения f(x) для нетабличных значений x, сглаживая результаты измерений величины y.
Для того, чтобы получить параметры функции F, используется метод наименьших квадратов. В этом методе в качестве критерия близости приближающей функции к совокупности точек используется суммы квадратов разностей значений табличных значений y и теоретических, рассчитанных по уравнению регрессии.
Таким образом, нам требуется найти функцию F, такую, чтобы сумма квадратов S была наименьшей:
Рассмотрим решение этой задачи на примере получения линейной регрессии F=ax+b.
S является функцией двух переменных, a и b. Чтобы найти ее минимум, используем условие экстремума, а именно, равенства нулю частных производных.
Используя формулу производной сложной функции, получим следующую систему уравнений:
Для функции вида частные производные равны:
,
Подставив производные, получим:
Откуда, выразив a и b, можно получить формулы для коэффициентов линейной регрессии, приведенные выше.
Аналогичным образом выводятся формулы для остальных видов регрессий.
Как найти функцию зная только точки?
Судя по всему, то, о чем Вы говорите — аппроксимация функции. В Википедии более подробна статья про интерполяцию.
По сути, Ваша задача сводится к 2м шагам:
1. По точкам и общим зависимостям выбирается форма функции (например, полиномиальная, экспоненциальная и.т.п).
2. Строится модель, в которой задаётся функция с неизвестными параметрами. Задача — найти такие параметры, чтобы минимизировать функцию невязки(часто это квадрат разности между реальными значениями в заданых точках и значениями модельной функции, см. МНК).
http://planetcalc.ru/5992/
http://qna.habr.com/q/5823
Построение графиков функций

В данном пособии рассматриваются различные способы построения графиков функций. Приводятся примеры построения графиков различными методами, задания для самостоятельной работы.Пособие рекомендовано для учащихся старших классов и учителей школ, гимназий, лицеев для организации работы, как на уроке, так и на факультативах и дополнительных занятиях по данной теме, а также для подготовки к экзаменам.
Оглавление
Построение графика функции по точкам
Построение графика функции по точкам выполняется в следующем порядке:
1. составляется таблица значений аргумента и функции на основе данной формулы;
2. в выбранной системе координат строятся точки, координатами которых являются соответствующие значения переменных, содержащиеся в таблице;
3. полученные точки соединяются плавной линией.
При задании значений аргумента следует учитывать область определения функции.
Пример 1. Построить график функции у=х (6-х), где — 1 <х <5.
Решение. Функция у=х (6-х) определена на всем указанном интервале. Составим таблицу значений аргумента и функции:
На координатной плоскости отметим полученные точки и соединим их плавной линией.
Получим график функции у=х (6-х) на интервале — 1 <х <5.
При построении графика функции по точкам иногда указывают шаг, т.е. число, через которое выбирается последующее значение аргумента. Чем меньше шаг, тем точнее получается график.
Задание 1. Постойте по точкам график функции…
Пример 2. Постройте график функции у=х2—3, на интервале [ — 4; 4] с шагом 1.
Решение. Функция у=х2—3 определена на всем интервале. Составим таблицу значений. Первое значение аргумента — 4. Следующее с учетом шага — 4+1=-3 и т. д. пока не получим последнее значение 4.
Отметим точки на координатной плоскости и построим график:
Задание 2. Постройте график функции на заданном интервале с указанным шагом…

Смотрите также
Судя по всему, то, о чем Вы говорите — аппроксимация функции. В Википедии более подробна статья про интерполяцию.
По сути, Ваша задача сводится к 2м шагам:
1. По точкам и общим зависимостям выбирается форма функции (например, полиномиальная, экспоненциальная и.т.п).
2. Строится модель, в которой задаётся функция с неизвестными параметрами. Задача — найти такие параметры, чтобы минимизировать функцию невязки(часто это квадрат разности между реальными значениями в заданых точках и значениями модельной функции, см. МНК).
Если известны некоторые значения x и y на графике, то можно найти коэффициент и свободный член данной функции. Допустим линейная зависимость y=kx+b. Например нам известно, что при x = 2, y = 5 и при х = 3, у = 4,5. Составим систему уравнений, подставив известные значения х и у: {2k+b=5; 3k+b=4,5}, решив систему, нетрудно догадаться, что k=-0,5; b=6;
В итоге наша функция принимает вид y=-0,5x+6
Да, это численные методы. Ищите по словам «Аппроксимация» и «Интерполяция». Из книг могу порекомендовать: Дьяконов В.П. Справочник по алгоритмам и программам на языке Бейсик для персональных ЭВМ. У меня бумажное издание 1989 года. В Гугле можно найти в DJVU. Примеры на Бейсике позволяет запрограммировать нужный метод на вашем любимом языке программирования, даже не вникая в их суть. А вообще если есть время и желание, разберитесь, это довольно интересно