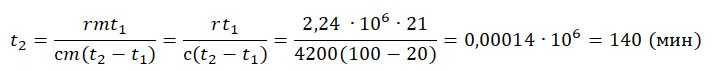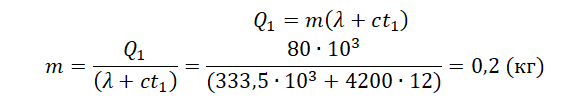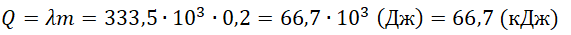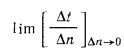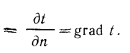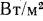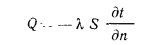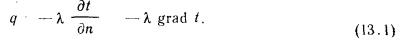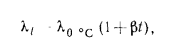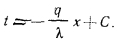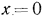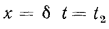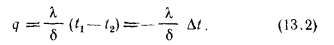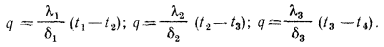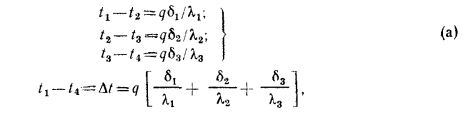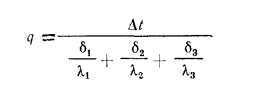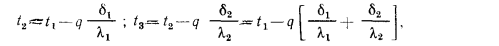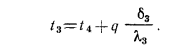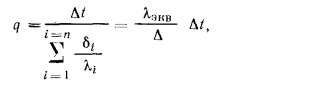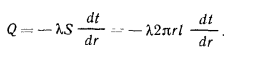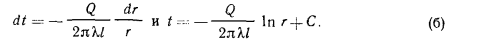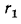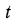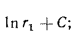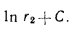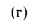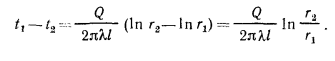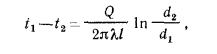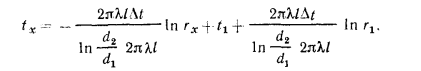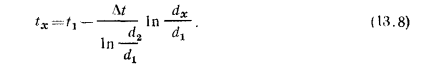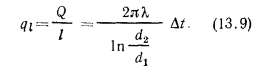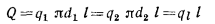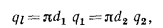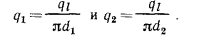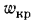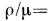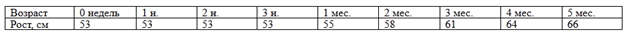17 февраля 2011
Пожалуй, самая простая задача из всех, которые встречаются в ЕГЭ. В ней проверяется умение интерпретировать графики, извлекать из них простейшую числовую информацию и делать необходимые выводы.
В задаче B3 используются данные, полученные в результате реальных измерений, наблюдений и опытов. Эти данные представлены в форме графиков, которые условно делятся на два типа:
- Непрерывные, в которых значение функции определено для каждой точки графика. Как правило, такие графики представляют собой плавные линии, описывающие постоянно меняющееся значение функции. Наиболее типичный пример — график изменения температуры.
- Дискретные, где функция определена лишь для конечного числа точек. В остальных точках функция не существует. Для наглядности эти точки могут быть соединены или представлены в виде столбцов.
Правильное определение типа графика позволит избежать классических ошибок при решении задания B3. Например, довольно часто на дискретных графиках рассматриваются лишние точки, которые не являются значениями функции.
Задача. Определить тип графиков, представленных на рисунке:
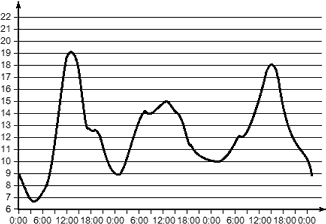
- Изменение температуры за три дня, начиная с 0:00.
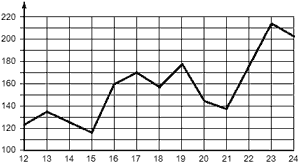
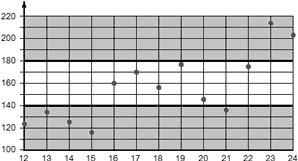
- Количество изготовленных на станке деталей по дням, с 12 по 24 сентября.

Очевидно, первый график является непрерывным, т.к. в любой момент времени, отмеченный на горизонтальной оси, мы можем определить значение функции. И неважно, что это определение будет довольно приблизительным.
Второй график является дискретным, поскольку количество деталей можно определить лишь для нескольких конкретных дней. Например, 16 сентября было изготовлено 160 деталей, 17 сентября — 170, но любое значение между 16 и 17 сентября не имеет никакого смысла — точки соединены исключительно для наглядности.
Непрерывные графики
Работа с непрерывными графиками, как правило, не вызывает затруднений, поскольку существует эффективный метод решения таких задач: отсечь ненужную информацию.
Например, очень часто встречаются задачи, где требуется определить максимальное или минимальное значение температуры в заданный день. При этом на графике показано изменение температуры в течение сразу нескольких дней.
Чтобы решить подобную задачу, сначала необходимо удалить с графика все, что не относится к рассматриваемому дню. Например, закрыть рукой, линейкой или листом бумаги. Только не зачеркиваете график ручкой — в случае ошибки восстановить его первоначальный вид не получится!
Затем на оставшейся части графика выбираем требуемую точку. Минимальное значение достигается в нижней точке графика, а максимальное — наоборот, в самой высокой.
Задача. На графике показано изменение температуры воздуха в течение трех суток, начиная со вторника, 0:00. Определите, до какой наибольшей температуры прогрелся воздух в среду.

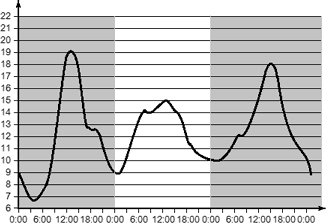
Для начала отсечем всю лишнюю информацию. Нас интересует только среда. Учитывая, что график начинается со вторника, закрасим серым цветом лишние дни:
На оставшейся части графика надо отыскать наибольшую температуру. Очевидно, она равна 15 °C — такое значение достигается ближе к середине дня.
Некоторые преподаватели предлагают довольно эффективный способ поиска максимального и минимального значения на участке графика, который остается после отсечения ненужной информации. Для поиска минимального значения надо приложить горизонтальную полоску бумаги к нижней части картинки и двигать ее вверх до тех пор, пока полоска не пересечет график. Аналогично, для поиска максимального значения надо приложить полоску сверху и двигать вниз.
Дискретные графики
Но как решать задачу B3, если в ней встретился дискретный график? Для начала надо избавиться от соединительных линий, если они есть. Помните: дискретный график — это просто набор точек, остальная информация только мешает решению задачи.
Задача. На дискретном графике показано количество изготовленных на станке деталей в период 12—24 сентября. Очистить этот график от лишней информации.

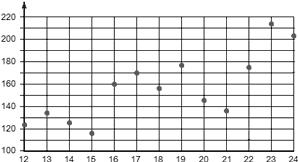
Очевидно, значимой информацией являются только точки, лежащие на вертикальных линиях разметки. Они показывают, сколько деталей было изготовлено в конкретный день. Например, 17 сентября было изготовлено 170 деталей. Уберем отрезки, соединяющие эти точки, и получим следующую картинку:
Обратите внимание на крайние точки графика: в самом начале (12 сентября) и конце (24 сентября). Многие забывают про них, однако на исходном графике эти точки были, и поэтому должны учитываться в решении.
Когда на графике останется только нужная информация, можно решать саму задачу. Здесь применяется уже знакомый метод отсечения, который для дискретных графиков имеет две формы:
- Вертикальное — указание диапазона точек, которые будут участвовать в решении. Например, если нас интересует только период с 16 до 20 сентября, то все другие точки надо «удалить». Этот прием аналогичен отсечению ненужной информации для непрерывных графиков.
- Горизонтальное — указание требуемого диапазона значений. Аналога в непрерывных графиках не имеет. Ограничения могут накладываться снизу, сверху или с обеих сторон. Точки, выпадающие из диапазона, не участвуют в дальнейшем решении.
Например, выясним по графику, приведенному выше, сколько раз на станке изготавливалось больше 150 деталей в день. Очевидно, требование «больше 150» — это ограничение снизу. Проведем горизонтальную черту на уровне 150 деталей и удалим все точки, которые оказались ниже. Остальные точки можно легко подсчитать — читателю предлагается сделать это в качестве упражнения.
Задача. На графике показано деталей, изготовленных на станке, в период 12—24 сентября. Определите, сколько раз на станке изготавливалось от 140 до 180 деталей в день.

Уберем отрезки, соединяющие отдельные точки, поскольку это лишняя информация. Затем проведем горизонтальное отсечение, для чего установим границы на уровнях 140 и 180 деталей. Нас интересует только то, что находится между этими границами. Получим следующую картинку:
Все, что выпадает из диапазона, закрашено серым цветом. Осталось лишь подсчитать количество «правильных» точек — очевидно, их шесть.
Дополнительные соображения
Условие задачи B3 с дискретным графиком всегда нужно понимать буквально. Если требуется найти, сколько раз значение функции находилось «в пределах от 2 до 7», то следует учитывать все числа из отрезка [2, 7]. Обратите внимание: границы отрезка, т.е. числа 2 и 7, тоже учитываются! Игнорирование это факта — очень частая ошибка на экзамене.
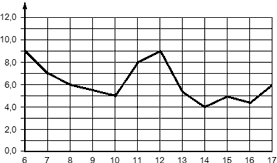
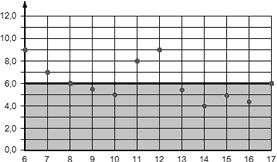
Задача. На рисунке изображен график среднесуточной температуры в Саратове в период с 6 по 17 октября 1969 г. На оси абсцисс откладываются числа, на оси ординат — температура в градусах Цельсия. Определить по графику, сколько дней из указанного периода средняя температура была не ниже 6,0 °C.

Очевидно, это дискретный график. Избавимся от ненужной информации, убрав все соединительные линии. На полученном наборе точек выполним горизонтальное отсечение, проведя черту на уровне 6,0 °C. Все, что ниже этой границы, нас не интересует, поэтому закрашено серым цветом. Имеем:
Подсчитаем точки, попадающие в диапазон — их оказалось шесть. Обратите внимание, что 8 и 17 октября температура равна 6 °C. Эти дни тоже учитываются в итоговом расчете.
Еще раз напомним, что B3 — это самая простая задача ЕГЭ по математике. В ней проверяется умение извлекать из графика и обрабатывать числовую информацию. Требуются именно практические навыки, а не умение работать с формальными теоретическими построениями.
В этих задачах нет сложных и двусмысленных формулировок. Если требуется определить наивысшую точку графика, такая точка будет только одна. А если, например, просят найти минимальную ночную температуру, то по графику будет видно, что самая низкая температура была именно ночью. Не придется размышлять о том, когда именно заканчивается ночь и начинается день.
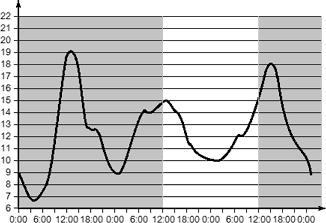
Задача. На графике показано изменение температуры воздуха на протяжении трех суток, начиная с 0 часов вторника. На оси абсцисс отмечается время суток в часах, на оси ординат — значение температуры в градусах. Определите по графику наименьшую температуру воздуха в ночь со среды на четверг.

Это непрерывный график. Для решения задачи необходимо отбросить всю лишнюю информацию, проведя вертикальные границы. Проблема в том, что фраза «ночь со среды на четверг» не дает четких границ.
Попробуем установить эти границы. Так, 12:00 среды — это точно еще не ночь, а 12:00 четверга — это уже не ночь. Чем ближе мы подходим к указанным моментам, тем выше температура. Очевидно, в этой задаче 12:00 среды и 12:00 четверга могут служить вертикальными границами. Проведем их и получим следующую картинку:
То, что закрашено серым цветом, нас не интересует. На оставшейся части графика минимальная температура равна 10 °C. Это значение достигается как раз ночью — примерно в 0:00 — и поэтому является ответом.
Смотрите также:
- Введение системы координат
- Тест к уроку «Десятичные дроби» (2 вариант)
- Типичные задачи B12 с функциями
- Координаты вершин правильного тетраэдра
Как построить температурный график
Бывает необходимо знать температуру не только в конкретный момент, но и в динамике. Это может относится и к температуре воздуха, и человека, например, при его лечении. Во всех этих случаях используется температурный график. Как же его составить?

Вам понадобится
- — показатели температуры;
- — бумага;
- — ручка;
- — компьютер.
Инструкция
Соберите данные по температуре. Важно, чтобы она измерялась в сходных условиях. Например, температура воздуха должна определяться по градуснику, находящемуся на одной и той же высоте от земли и с теневой стороны. Температуру больного человека желательно изменять в одно и то же время, например, с утра. Для повышения точности желательно также использовать одни и те же измерительные приборы.
Выберите, к каких единицах вы будете фиксировать температуру — в градусах Цельсия, Фаренгейта или кельвинах. Это зависит от целей измерения и используемого оборудования.
Начертите на бумаге двухмерную систему координат. По абсциссе будет определяться дата или время измерения температуры, а по ординате — градусы. Сделайте на них соответствующие отметки в виде шкалы.
Занесите в график свои данные. Для начала отметьте точки,которые по оси X будут соответствовать температуре в градусах, а по оси Y — дате измерения. Затем соедините получившиеся точки линиями. У вас получился график, показывающий изменение температуры.
Если вам удобнее работать на компьтере, оформите график в виде таблицы через редактор для составления таблиц Excel. Создайте новый файл, а в нем — таблицу с двумя столбцами — x и y. В первый столбец заносите данные о дате измерения в виде числа, а во второй — о температуре. После заполнения зайдите в раздел меню «Вставка», а затем — «Диаграмма». Выберите вид графика, наиболее удобный для вас, и вид разметки шкалы, а затем нажмите на кнопку «Готово». Система сформирует для вас график температуры в соответствии с вашими пожеланиями.
Полезный совет
Для составления более сложных температурных графиков, например, для расчета показателей систем теплоснабжения, лучше использовать специальные компьютерные программы, например, ZuluThermo или другие.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
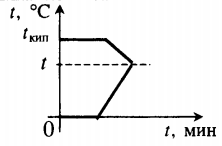 Уравнение теплового баланса:
Уравнение теплового баланса:
− r m п + c в m п ( t − t к и п ) + λ m л + c в m л ( t − t п л ) = 0
Пример №2. В кастрюлю, где находится вода объемом 2 л при температуре 25 о С, долили 3 л кипятка. Какая температура воды установилась?
Количество теплоты, отданное кипятком, равно количеству теплоты, принятому более прохладной водой. Поэтому:
c m 1 ( t − t 0 ) = − c m 2 ( t − t к и п )
m 1 ( t − t 0 ) = − m 2 ( t − t к и п )
m 1 t + m 2 t = m 1 t 0 + m 2 t к и п
( m 1 + m 2 ) t = m 1 t 0 + m 2 t к и п
t = m 1 t 0 + m 2 t к и п m 1 + m 2 . .
t = 2 · 25 + 3 · 100 2 + 3 . . = 350 5 . . = 70 ( ° C )
Взаимные превращения механической и внутренней энергии
Если в тексте задачи указан процент одного вида энергии, перешедший в другой, то он указывается в виде десятичной дроби перед этой энергией, которой тело обладало вначале.
Частные случаи закона сохранения энергии
m v 2 2 . . = c m Δ t
0 , 5 ( m v 2 0 2 . . − m v 2 2 . . ) = c m Δ t
m v 2 2 . . = c m Δ t + λ m
0 , 6 m g h = c m Δ t + r m
q m т о п = m р g h
0 , 25 q m т о п m с v 2 2 . .
Пример №3. Свинцовая дробинка, летящая со скоростью 100 м/с, попадает в доску и входит в нее. 52% кинетической энергии дробинки идет на ее нагревание. На сколько градусов нагрелась дробинка? Удельная теплоемкость свинца 130 Дж/(кг∙К).
Запишем закон сохранения энергии для этого случая:
0 , 52 m v 2 2 . . = c m Δ t
Δ t = 0 , 52 v 2 2 c . . = 0 , 52 · 100 2 2 · 130 . . = 20 ( К )
Примеры КПД
| При неупругом ударе о стенку пуля нагрелась |
| Тело падает с некоторой высоты и в момент падения нагревается |
| В результате того, что пуля пробивает стену, ее скорость уменьшается, 50% выделившейся при этом энергии идет на нагревание пули |
| Летящая пуля при ударе о стенку расплавилась. Начальная температура пули меньше температуры плавления |
| Капля воды, падая с некоторой высоты, в момент удара испарилась. Температура капли у поверхности земли меньше температуры кипения. На нагрев пошло 60% выделившейся механической энергии |
| Вследствие сгорания топлива ракета поднялась на некоторую высоту |
| Вследствие сгорания топлива снаряд приобрел некоторую скорость, и на это было затрачено 25% энергии |
Q п о л е з н = c m Δ T
Q п о л е з н = c m Δ T + r m
( п р о и з в е д е н и е м о щ н о с т и н а в р е м я )
η = c m Δ T P t . . 100 %
Q п о л е з н = c m Δ T
Q з а т р = q m т о п
η = c m Δ T q m т о п . . 100 %
A п о л е з н = N t = N s v . .
Q з а т р = q m т о п
η = c m Δ T v q m т о п . . 100
E п о л е з н = m v 2 2 . .
Q з а т р = q m п о р
η = m v 2 2 q m п о р . . 100
Внимание! Если в задаче указано время, в течение которого происходит один тепловой процесс, а спрашивают о времени протекания другого, то считайте, что мощность нагревателя или холодильника постоянна:
Q 1 t 1 . . = Q 2 t 2 . .
Пример №4. Для нагревания на электроплитке некоторого количества воды от 20 до 100 о С потребовалась 21 минута. Сколько времени после этого необходимо для полного испарения воды? Удельная теплоемкость воды 4200 Дж (кг∙К), удельная теплота парообразования 2,24 МДж/кг.
Будем считать, что мощность электроплитки постоянна. Поэтому:
Q 1 t 1 . . = Q 2 t 2 . .
Количество теплоты, сообщенное воде при нагревании:
Q 1 = с m ( t 2 − t 1 )
Количество теплоты, которое нужно сообщить, чтобы вода полностью испарилась:
с m ( t 2 − t 1 ) t 1 . . = r m t 2 . .
Кусок льда, имеющий температуру 0°С, помещён в калориметр с электронагревателем. Чтобы превратить этот лёд в воду с температурой 12°С, требуется количество теплоты 80 кДж. Какая температура установится внутри калориметра, если лёд получит от нагревателя количество теплоты 60 кДж? Теплоёмкостью калориметра и теплообменом с внешней средой пренебречь.
Алгоритм решения
Решение
Запишем исходные данные:
Составим уравнение теплового баланса для первого случая:
Q 1 = λ m + c m t 1
Внимание! Вместо разности температур используется значение только конечной температуры, так как начальная температура равна 0.
Найдем массу льда из уравнения теплового баланса для первого случая. Учтем что:
Чтобы расплавить кусок льда массой 0,5 кг, нужно затратить следующее количество теплоты:
Лед не расплавится весь, так как ему будет сообщено лишь 60 кДж теплоты. Поэтому в калориметре температура будет равна 0 о С.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Внимательно прочитайте текст задания и выберите верный ответ из списка
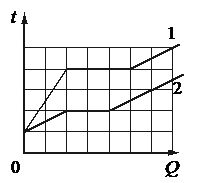
Используя данные графиков, выберите из предложенного перечня два верных утверждения и укажите их номера. Ответ: а) Температура плавления первого тела в 1,5 раза больше, чем второго. б) Тела имеют одинаковую удельную теплоёмкость в твёрдом агрегатном состоянии. в) Удельная теплоёмкость второго тела в твёрдом агрегатном состоянии в 3 раза больше, чем первого. г) Оба тела имеют одинаковую удельную теплоту плавления. д) Тела имеют одинаковую удельную теплоёмкость в жидком агрегатном состоянии.
Алгоритм решения
- Проанализировать каждое из утверждений.
- Проверить истинность утверждений с помощью графика.
- Выбрать и записать верные утверждения.
Решение
Проверим первое утверждение, согласно которому, температура плавления первого тела в 1,5 раза больше, чем второго.
Если это было бы так, то количество клеток до горизонтального участка графика 1 относилось к количеству клеток до горизонтального участка графика 2 как 3 к 2. Но мы видим, что до 1 графика 4 клетки, до 1 — 2. Следовательно, температура плавления первого тела в 2 раза больше, чем второго.
Первое утверждение неверно.
Проверим второе утверждение, согласно которому тела имеют одинаковую удельную теплоёмкость в твёрдом агрегатном состоянии.
Если бы это было так, то соответствующие участки графиков совпадали бы. Только в таком случае температура тел увеличивалась на одну и ту же температуру при получении одного и того же количества теплоты. Но мы видим, что это не так.
Второе утверждение неверно.
Проверим третье утверждение, согласно которому удельная теплоёмкость второго тела в твёрдом агрегатном состоянии в 3 раза больше, чем первого.
Если это было бы так, то первое тело при сообщении телам одинакового количества теплоты нагревалось бы втрое быстрее второго. И это действительно так, потому что температура второго во время нагревания в твердом состоянии увеличилась только на 1 клетку, в то время как температура первого тела — на 2 клетки.
Третье утверждение верно.
Проверим четвертое утверждение, согласно которому оба тела имеют одинаковую удельную теплоту плавления.
Если это было бы так, то протяженность горизонтальных участков обоих графиков была бы одинаковой. Но это не так. Протяженность этого участка для тела 1 составляет 3 клетки, для тела 2 — 2 клетки.
Четвертое утверждение верно.
Проверим пятое утверждение, согласно которому тела имеют одинаковую удельную теплоёмкость в жидком агрегатном состоянии.
Если бы это было так, то соответствующие участки графиков были параллельными. Только при таком условии при повышении температуры на одно и то же количество градусов тела бы получли одинаковое количество теплоты. И это действительно так.
Пятое утверждение верно.
Вывод: верным утверждения «в» и «д».
pазбирался: Алиса Никитина | обсудить разбор | оценить
В сосуде лежит кусок льда. Температура льда t 1 = 0 «> t 1 = 0 °C. Если сообщить ему количество теплоты Q = 50 «> Q = 50 кДж, то 3/4 льда растает. Какое количество теплоты q надо после этого сообщить содержимому сосуда дополнительно, чтобы весь лёд растаял и образовавшаяся вода нагрелась до температуры t 2 = 20 «> t 2 = 20 °C? Тепловыми потерями на нагрев сосуда пренебречь.
Теплотехника
Теплотехника (нем. Wärmetechnik) — общетехническая дисциплина, изучающая методы получения, преобразования, передачи и использования теплоты, а также принцип действия и конструктивные особенности тепло- и парогенераторов тепловых машин, агрегатов и устройств. wikipedia.org/wiki/Теплотехника
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Введение в теплотехнику
Теплотехника представляет собой науку, которая изучает законы распространения и передачи теплоты между телами. Вместе с термодинамикой учение о теплообмене составляет теоретические основы теплотехники.
Различают три вида теплообмена: теплопроводность (или кондук-ция), конвекция и тепловое излучение. Теплопроводностью называется перенос теплоты, возникающий при непосредственном соприкосновении между частицами тела.
В жидкостях наряду с теплопроводностью теплота может распространяться также путем перемещения и перемешивания между собой более или менее нагретых частиц самой жидкости. Такой вид распространения теплоты называется конвекцией. В целом явление передачи теплоты при соприкосновении стенки с жидкостью путем теплопроводности и дальнейшее распространение ее в жидкости за счет конвекции (а также процесс, протекающий в обратном направлении) называется конвективным теплообменом, или теплоотдачей.
Тепловым излучением, или лучеиспусканием, называется перенос энергии в виде электромагнитных волн между двумя взаимно излучающими поверхностями. При этом происходит двойное превращение энергии: тепловой энергии в лучистую на поверхности тела, излучающего теплоту, и лучистой энергии в тепловую на поверхности тела, поглощающего лучистую теплоту.
Частные процессы переноса теплоты
Частные процессы переноса теплоты — теплопроводность, конвекция и лучеиспускание обычно происходят одновременно. Например, в топочных устройствах различных технологических установок конвективный перенос теплоты сопровождается тепловым излучением. В этом случае процесс переноса теплоты называется сложным теплообменом.
В теплообменных аппаратах, как правило, происходят одновременно различные виды теплообмена. Например, в паровом котле теплота передается от продуктов сгорания топлива к стенкам кипятильных труб путем излучения и конвекции, через металл стенок труб теплота распространяется путем теплопроводности, и далее осуществляется процесс теплоотдачи кипящей воде или пару. Такой процесс переноса теплоты от греющей среды через стенку к нагреваемой среде называется теплопередачей.
Необходимо отметить, что в тепловых установках, используемых в производстве строительных материалов и изделий, процессы теплообмена являются решающими, так как интенсивность и качество тепловой обработки строительных изделий в значительной мере зависят от правильной работы теплоиспользующей аппаратуры. Очень важно при организации теплообмена в промышленных условиях обеспечить равномерность тепловой обработки во всем объеме камеры или на отдельных
участках непрерывно действующих установок. В противном случае в общей массе обработанной продукции будет содержаться как перегретый, так и недогретый материал. При этом нужно иметь в виду, что тепловая обработка многих строительных изделий сопровождается сложными физико-химическими процессами экзо- или эндотермического характера, учет которых в расчете теплообмена обязателен.
Известно, что процесс распространения теплоты в пространстве неразрывно связан с распределением температуры в нем. Совокупность значений температуры в каждый момент времени для всех точек рассматриваемого пространства называется температурным полем.
Математически оно выражается уравнением 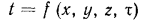

Температурное поле может быть функцией трех, двух и одной координаты. Соответственно оно называется трех, двух- и одномерным. Наиболее простой вид имеет уравнение одномерного стационарного температурного поля t=f(x). Все точки пространства, имеющие одинаковую температуру, образуют изотермическую поверхность.
Естественно, что изменение температуры в теле может наблюдаться лишь в направлениях, пересекающих изотермические поверхности (например, направление х, (рис. 13.1). При этом наиболее резкое изменение получается в направлении нормали n к изотермическим поверхностям. Предел отношения изменения температуры 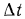
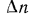
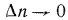
Частная производная применена здесь потому, что в общем случае температура может изменяться не только в пространстве, но и во времени (при нестационарном режиме).
Температурный градиент
Температурный градиент — это вектор с положительным знаком при возрастании температуры и с отрицательным при ее падении. Градиент температуры численно равен производной температуры по нормали.
Количество переносимой теплоты в единицу времени называют тепловым потоком Q, который измеряется вДж/с (Вт). Тепловой поток, отнесенный в единице поверхности тела, называют по верх постной плотностью теплового потока (или просто плотностью теп-
лового потока) q Q/S, которая измеряется в
Величина q является вектором, направление которого противоположно направлению градиента температуры, так как тепловая энергия самостоятельно распространяется всегда только в сторону убывания температуры (см. рис. 13.1).
Исследуя явления теплопроводности в твердых телах, Фурье установил, что тепловая мощность, передаваемая теплопроводностью, пропорциональна градиенту температуры и площади сечения, перпендикулярного направлению теплового потока, т. е.
Множитель пропорциональности 

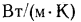
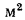
Возможно эта страница вам будет полезна:
Для различных тел теплопроводность имеет определенное значение и зависит от структуры, плотности, влажности, давления и температуры веществ этих тел. Точные значения 

Таким образом, наиболее высокая теплопроводность у металлов, значительно ниже у неметаллических строительных материалов и самые низкие значения у пористых материалов, применяемых специально для тепловой изоляции. У теплоизоляционных материалов 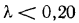
У большинства металлов с повышением температуры теплопроводность убывает. Содержание примесей в металлах резко снижает их теплопроводность. Например, для стали при 0,1% углерода 

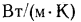

где 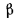

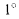
У различных строительных материалов в интервале температур 0—100° С 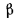
У газов с повышением температуры теплопроводность возрастает и практически не зависит от давления, за исключением очень высоких (более 200МПа) и очень низких (менее 0,003 МПа) давлений. На теплопроводность влияют общая пористость материала, размер и степень замкнутости пор.
Для пористых материалов теплопроводность находится в обратной зависимости от их общей пористости и в прямой— от размеров пор. Это объясняется увеличением передачи теплоты конвекцией и излучением в общем процессе теплообмена пористого материала и свидетельствует о том, что теплоизоляционные материалы, используемые при высоких температурах, должны иметь мелкопористое строение.
Поры, сообщающиеся между собой и с поверхностью материала, создают более благоприятные условия для увлажнения материала и тем самым для увеличения его теплопроводности, поэтому теплоизоляционные материалы должны иметь по возможности замкнутые поры.
Для пористых материалов 

Материалы с большей плотностью, как правило, обладают большей теплопроводностью, однако нужно иметь в виду, что теплопроводные свойства материала зависят не только от объема воздуха, заключенного в порах, но главным образом от равномерного распределения воздуха в пористом материале.
С этой точки зрения крупнопористый материал будет менее эффективным теплоизолятором, чем мелкопористый материал с той же плотностью. Среди строительных материалов встречаются такие, которые, имея меньшую плотность, обладают большей теплопро-
водностью, чем материалы с большей плотностью. Примерами могут служить минеральная вата, торфяная крошка, употребляемая в качестве теплоизоляционного сыпучего материала, и др. В частности, у минеральной ваты при плотности около 125 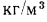
При меньшей плотности теплопроводность возрастает в результате увеличения передачи теплоты конвекцией в порах вследствие меньшего уплотнения ваты.
Теплопроводность строительных материалов
Теплопроводность строительных материалов резко возрастает при их увлажнении, гак как значительно отличаются теплопроводности воздуха и воды: теплопроводность воздуха в порах материала 0,025— 0,028, а воды 0,55 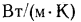
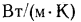
Повышение теплопроводности влажных материалов обусловливается также увеличением контактирующих поверхностей частиц основного вещества материала. Это приводит к тому, что теплопроводность влажного материала значительно выше, чем сухого и воды в отдельности.
Например, для сухого кирпича 
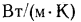
Для анизотропных материалов, которые имеют неодинаковую структуру в различных направлениях (древесина, волокнистые и прессованные материалы, кристаллы), теплопроводность зависит от направления теплового потока. Например, у сосновой древесины при направлении теплового потока параллельно направлению волокон 
- Это объясняется тем, что при направлении, перпендикулярном волокнам, тепловому потоку приходится пересекать большое количество воздушных зазоров, находящихся как внутри волокон древесины, так и между ними и оказывающих сопротивление прохождению теплоты. При направлении теплового потока параллельно волокнам влияние воздуха, заключенного в древесине,, будет значительно меньше.
Расчетные формулы при стационарной теплопроводности
Рассмотрим формулы, по которым можно рассчитать количество-теплоты, передаваемой путем теплопроводности через стенки различной конфигурации (плоскую, цилиндрическую; сферическую), и установим для них уравнения температурных полей.
Однородная плоская стенка. Рассмотрим явление теплопроводности в однородной плоской стенке толщиной 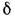

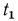
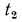
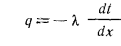
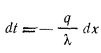
Постоянная интегрирования С определяется из граничных условий: при 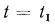
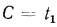
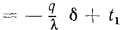
Разность температур 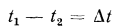
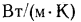
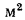
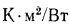
термическим сопротивлением стенки, которое определяет падение температуры при прохождении через стенку теплового потока плотностью, равной единице. Подобное название 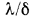
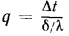
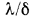
Если в выражение 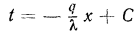
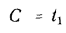
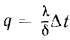
Уравнение (13.3) показывает, что при постоянном значении 
Зная по уравнению (13.2) величину q, легко определить и общее количество теплоты Q, переданное через плоскую стенку с площадью поверхности S в течение времени 
Многослойная плоская стенка. В строительстве наиболее распространенный тип ограждения — многослойные конструкции. Например, стены жилых домов на основном кирпичном слое с одной стороны имеют внутреннюю штукатурку, а с другой — внешнюю облицовку. Обмуровка топок и печей, используемых в промышленности строительных материалов, также обычно состоит из нескольких слоев: слоя огнеупорной кладки, слоя обычного кирпича и слоя тепловой изоляции.
Рассмотрим плоскую стенку, составленную из нескольких например трех, разнородных, плотно прилегающих друг к другу слоев (рис. 13.3). Толщины слоев и соответствующие значения теплопроводности составляют 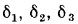
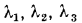
Кроме того, заданы температуры наружных поверхностей стенки 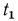
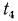
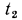
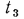
Исходя из написанных уравнений, находим изменения температуры в каждом слое и, складывая их, получим температурный напор 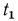
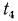
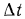
По аналогии для n-слойной стенки расчетную формулу можно написать так:
Из полученного уравнения следует, что общее термическое сопротивление многослойной стенки равно сумме частных термических сопротивлений.
Если значение теплового потока, определенного по формуле (13.5), подставить в равенство (а), можно найти неизвестные температуры 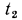
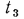
Внутри каждого слоя температура изменяется по закону прямой линии (при 

Возможно эта страница вам будет полезна:
В некоторых случаях многослойную стенку рассчитывают как однослойную однородную стенку с такой же толщиной 
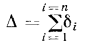
При этом в расчет вводится так называемая эквивалентная теплопроводность 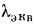
Однослойная цилиндрическая стенка
Рассмотрим однородную цилиндрическую стенку (трубу) длиной l с внутренним диаметром 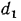
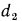

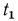
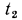
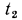
Разделяя переменные и интегрируя, получим:
Используя граничные условия, находим: при 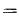
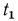
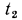
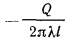
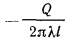
Вычитая из равенства (в) равенство (г), получим:
Полученное уравнение является расчетной формулой теплопроводности цилиндрической стенки. Оно будет справедливо и при 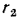
Для определения закона изменения температуры по толщине цилиндрической стенки подставим в равенство 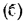
Равенство (13.8) представляет собой уравнение логарифмической кривой. При 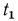
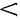
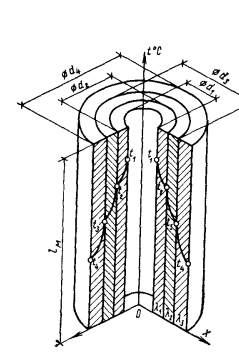
Плотность теплового потока для цилиндрической стенки может быть отнесена к единице внутренней поверхности 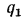
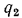
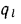
Соотношения между 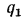
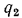
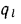
Величину 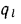
Факторы, влияющие на процесс теплоотдачи
Процесс теплообмена между жидкостью и стенкой, которую эта жидкость омывает, называется конвективным теплообменом, или процессом теплоотдачи. В этом процессе теплота передается одновременно путем теплопроводности и конвекции, и поэтому такой вид теплообмена представляет собой сложный процесс, зависящий от большего числа факторов по сравнению с процессом чистой теплопроводности.
- Конвективный теплообмен характерен для большинства процессов тепловой обработки строительных материалов и изделий, связанных с прохождением газов через слой материала, через садку изделий, над уровнями жидкостей при сушке и т. д.
Факторы, влияющие на процесс теплоотдачи, условно можно разделить на следующие группы.
I. Природа возникновения движения жидкости вдоль стенки.В зависимости от причины, вызывающей движение жидкости, различают два вида движения — свободное и вынужденное. Свободное движение, называемое иначе естественной конвекцией, вызывается подъемной силой, обусловленной разностью плотностей холодных и нагретых частиц жидкости. Интенсивность свободного движения зависит от вида жидкости, разности температур между отдельными ее частицами и объема пространства, в котором протекает процесс.
Вынужденное движение жидкости, или вынужденная конвекция, обусловлено работой внешних агрегатов (насоса, вентилятора и т. п.). Движущая сила при этом виде движения возникает вследствие разности давлений, устанавливающихся на входе и выходе из канала, по которому перемещается жидкость. Если скорость вынужденного движения небольшая и есть разница температур между отдельными частицами жидкости, то наряду с вынужденным движением может наблюдаться и свободное движение.
II. Режим движения жидкости. Движение жидкости может иметь ламинарный или турбулентный характер. В первом случае частицы жидкости в форме отдельных несмешивающихся струй следуют очертаниям канала или стенки и профиль скоростей на достаточном удалении от начала трубы имеет вид правильной параболы. Подобное распределение установившихся скоростей обусловливается наличием сил внутреннего трения (вязкости) между частицами жидкости. При этом максимальная скорость движения частиц жидкости, перемещающейся по оси трубы, в 2 раза больше средней скорости их движения, получаемой в результате деления секундного объема жидкости на площадь поперечного сечения трубы (рис. 14.1, а).
Турбулентный режим движения характеризуется непостоянством скорости движения частиц жидкости в рассматриваемой точке пространства. Из-за непрерывного перемешивания жидкости в ней нельзя выделить отдельные струи, и такое движение лишь условно можно назвать стационарным, считая для каждой частицы жидкости характерными не мгновенные, а усредненные за некоторый промежуток времени значения скорости. В этом случае профиль скоростей по сечению трубы будет иметь вид усеченной параболы и максимальная скорость, наблюдаемая у частиц жидкости, движущихся по оси трубы, будет всего в 1,2— 1,3 раза больше средней скорости. Характерно, что не все частицы жидкости при турбулентном режиме имеют неупорядоченное движение. Вблизи стенок, ограничивающих потоки, вследствие вязкости жидкости пульсации скорости уменьшаются, и около самой стенки сохраняется тонкий пограничный слой, движущийся ламинарно. В пределах этого слоя, который имеет толщину не более нескольких тысячных долей диаметра трубы, скорость движения частиц жидкости резко меняется от нуля на самой стенке до 0,4—0,7 средней скорости на условной границе с турбулентным ядром потока (рис. 14.1, б).
Строго говоря, турбулентные пульсации проникают и в ламинарный подслой и затухают в нем вследствие действия сил вязкости. Поэтому термин «ламинарный подслой» правильнее заменять термином «вязкий подслой».
Английский физик Рейнольдс установил, что при движении жидкости в трубах переход из ламинарного режима в турбулентный определяется значением безразмерного комплекса 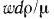
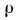
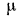
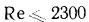
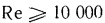
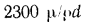
Следует также отметить, что наряду с описанным процессом формирования гидродинамического пограничного слоя происходит аналогичный процесс формирования и теплового пограничного слоя, в пределах
которого температура меняется от 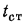
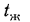
При ламинарном течении перенос теплоты между слоями жидкости осуществляется путем теплопроводности. В турбулентном пограничном слое основное изменение температуры происходит в пределах тонкого вязкого подслоя около стенки, через который теплота также передается путем теплопроводности.
В турбулентном ядре пограничного слоя вследствие интенсивного перемешивания жидкости температура изменяется незначительно (см. рис. 14.2, б) и поле температур имеет ровный пологий характер, т. е. отмечается качественное сходство в пограничном слое между распределением температур и скоростей.
III. Физические свойства жидкостей. На процесс теплоотдачи непосредственно влияют следующие физические параметры жидкостей: теплопроводность 
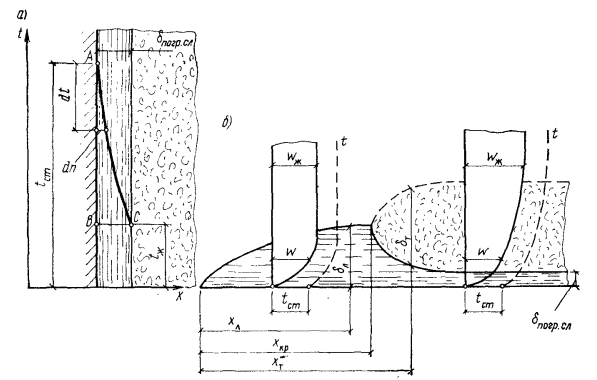
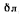
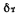
плотность р, а также вязкость и температуропроводность. Известно, что все жидкости обладают вязкостью, т. е. между отдельными частицами или слоями, перемещающимися с различными скоростями, всегда возникает сила внутреннего трения, противодействующая движению. По закону Ньютона, эта сила F, отнесенная к единице поверхности, пропорциональна градиенту скорости 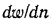
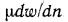
Коэффициент пропорциональности jx в этом уравнении называется коэффициентом . внутреннего трения или динамической вязкостью. При 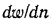
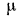
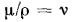
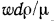
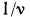
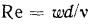
- Понятие температуропроводности тел связано с протеканием в них нестационарных тепловых процессов, наблюдаемых обычно при нагревании или охлаждении.
Скорость теплового процесса при нестационарном режиме определяется отношением 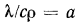
Единицей измерения динамической (абсолютной) вязкости 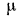
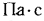
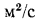
В настоящее время опытное определение коэффициента теплоотдачи производится, как правило, не на самих образцах тепловых устройств, а на их упрощенных моделях, более удобных для экспериментирования.
Результаты опытов, проведенных на моделях, обобщают, используя тепловую теорию подобия. Основной вывод, который делают на основе этой теории, заключается в том, что нет необходимости искать зависимость коэффициента теплоотдачи от каждого из тех факторов, которые на него влияют, а достаточно найти зависимость между определенными безразмерными комплексами величин, характерных для рассматриваемых условий процесса теплоотдачи.
Эти безразмерные комплексы величин называют критериями подобия. Составленные из размерных величин критерии подобия отражают физическую сущность, или, как говорят, модель процесса. Следовательно, задача заключается в том, чтобы найти вид зависимостей между критериями подобия, называемых критериальными уравнениями.
Теория из учебников тут.
Составляют критерии подобия с помощью дифференциальных уравнений конвективного теплообмена, т. е. уравнений, которые дают аналитическую зависимость между параметрами, характеризующими процесс теплоотдачи в дифференциальной форме.




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
источники:
http://spadilo.ru/fazovye-perexody-i-uravnenie-teplovogo-balansa/
http://lfirmal.com/predmet-teplotekhnika/
| Устройство | Полезная энергия (работа), затраченная энергия (полная работа) | КПД |
| Электронагреватель, электроплитка, электрочайник, кипятильник. | ||
| Газовая горелка, паровая турбина, спиртовка, плавильная печь. | ||
| Двигатель автомобиля, самолета. | ||
| Ружье с пороховым зарядом, пушка |
Изопроцессы в МКТ — это процессы, протекающие в газах с каким-нибудь неизменным параметром. Для начала мы рассмотрим газ, у которого постоянная масса и химический состав. То есть в газе не меняется количество вещества ν . В этом случае мы можем упростить уравнение Менделеева-Клайперона.
Я не буду углубляться в названия газовых законов, вы это прочтете в учебниках. Займемся чистой математикой
Итак, у нас есть некий газ постоянной массы. Основные характеристики его состояния определяются . То есть, если мы будем на этот газ как-то воздействовать, меняя его характеристики, то
Получается, что все три его характеристики связаны. Но можно рассмотреть случаи, когда один из этих компонентов не меняется. это и будут изопроцессы. Посмотрим, как будут выглядеть графики изопроцессов в осях p(V), p(T), V(T).
Теперь рассмотрим график конкретного циклического процесса, представленного на рисунке в координатах V-T :

ВC: Изохора
CD: Изобара
DA: Изотерма

А теперь можно построить этот же циклический процесс на графиках с другими координатами.
Обратите внимание, что значения в эти графики из риунка1 можно перенести только на оси температуры и объема. Значения для давления произвольные, но… ВС — изохора, следовательно, прямая, ей соответствующая, обязательно должна начинаться в нуле в осях Р-Т! В осях P-V изотерма DA — кривая (гипербола)
Разбор некоторых задач →
График функции. Примеры функциональных зависимостей в реальных процессах и явлениях
Функция — это одно из основных общенаучных и математических понятий, выражающее зависимость между переменными величинами. Это закон, по которому каждому значению элемента x из некоторого множества X ставится в соответствие единственный элемент y из множества Y.
Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у. Переменную х называют независимой переменной или аргументом, а переменную у — зависимой переменной. Значение у, соответствующее заданному значению х, называют значением функции.
Записывают: у = f (х). Буквой f обозначается данная функция, т. е. функциональная зависимость между переменными х и у; f (х) есть значение функции, соответствующее значению аргумента х. Говорят также, что f (х) есть значение функции в точке х. Все значения, которые принимает независимая переменная, образуют область определения функции. Все значения, которые принимает функция f (х) (при х, принадлежащих области ее определения), образуют область значений функции.
Способы задания функции
Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у = f (х),
где f (х) — некоторое выражение с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически.
Пусть функция задана аналитически формулой у = f (х). Если на координатной плоскости отметить все точки, обладающие следующим свойством: абсцисса точки принадлежит области определения функции, а ордината равна соответствующему значению функции, то множество точек (х; f (x)) есть график функции. В физике и технике функции нередко задаются графически, причем иногда гарфик является единственным доступным средством задания функции. Чаще всего это бывает при употреблении самопишущих приборов, автоматически записывающих изменение одной величины в зависимости от изменения другой. В результате на ленте прибора получается линия, графически задающая регистрируемую прибором функцию.
Также функцию можно задать таблично. Рассмотрим примеры функциональной зависимости в реальной жизни.
Пример 1
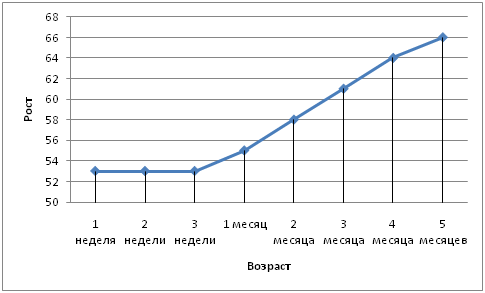
Таблицей заданы данный о росте ребенка в течении первых 5 месяцев жизни:
Имея таблицу значений функциональной зависимости роста от возраста, можно по точкам построить график:
Пример 2
Вот яркий пример функции, заданной графически. На графике можно увидеть максимум и минимум, фрагменты линейной функции, сглаживание линий и т.д.
Кардиограмма — график работы сердца.
Кардиограмма — это запись сокращений сердца человека, которая осуществляется при помощи какого-либо инструментального способа. Во время сокращения сердце передвигается в пределах грудной клетки, оно вращается вокруг своей оси слева направо.
Суть электрографии заключается в том, чтобы зарегистрировать разности потенциала во времени. Кривая, которая показывает нам эти изменения и есть кардиограмма. Прибор, который записывает эту кривую, именуется электрокардиографом. Кардиограмма сердца показывает возбуждение сердца и его сокращение. Во время снятия кардиограммы к телу человека прикрепляются специальные электроды, благодаря которым аппарат и получает необходимые данные.
Суть обработки сигналов данного исследования заключается в том, чтобы диагностировать имеющиеся проблемы в работе сердечных мышц, используя при этом различные аналитические методы.
Пример 3
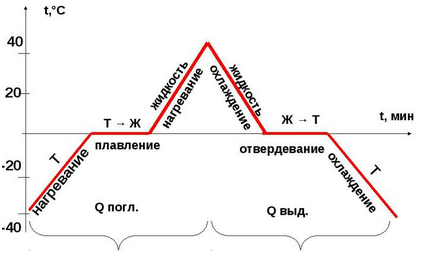
Переход вещества из твердого состояние в жидкое называется плавлением. Для того чтобы тело начало плавиться, его необходимо нагреть до определенной температуры. Температура, при которой вещество плавится, называют температурой плавления вещества.
Каждое вещество имеет свою температуру плавления. У каких-то тел она очень низкая, например, у льда. А у каких-то тел температура плавления очень высокая, например, железо. Плавление кристаллического тела это сложный процесс.
На рисунке представлен известный из курса физики график плавления льда.
График показывает зависимость температуры льда от времени, которое его нагревают. На вертикальной оси отложена температура, по горизонтальной — время.
Из графика видно, что изначально температура льда была -40 градусов. Потом его начали нагревать. С течением времени, температура увеличилась до 0 градусов. Эта температура считается температурой плавления льда. При этой температуре лед начал плавиться, но при этом перестала возрастать его температура, хотя при этом лед также продолжали нагревать. Затем, когда весь лед расплавился и превратился в жидкость, температура воды снова стала увеличиваться. Во время плавления температура тела не изменяется, так как вся поступающая энергия идет на плавление. После нагревания (пик графика) жидкость стали охлаждать, процесс пошел в обратную сторону до затвердевания.
Рассмотрим задачу
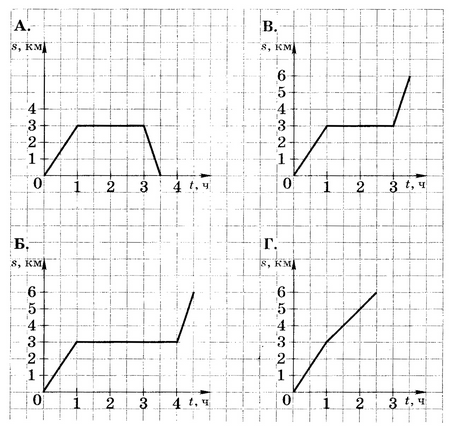
Туристы отправились с турбазы на озеро, провели там 2 часа и вернулись обратно. Выберите график, описывающий зависимость пройденного расстояния от времени:
Верным будет ответ А., т.к. в течении двух часов туристы находились на озере, добравшись до него, а затем снова вернулись в лагерь, т.е. в нулевую точку отсчета.