Как найти график некоторой функции

Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.

Содержание страницы:

Декартова система координат

Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.

Координатные оси – прямые, образующие систему координат.

Ось абсцисс (ось x ) – горизонтальная ось.

Ось ординат (ось y ) – вертикальная ось.

Функция

Функция – это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.

Прямая

Линейная функция – функция вида y = a x + b где a и b – любые числа.

Графиком линейной функции является прямая линия.

Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :

Если a > 0 , прямая будет проходить через I и III координатные четверти.

b – точка пересечения прямой с осью y .

Если a < 0 , прямая будет проходить через II и IV координатные четверти.

b – точка пересечения прямой с осью y .

Если a = 0 , функция принимает вид y = b .

Отдельно выделим график уравнения x = a .

Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».

Гипербола

Графиком функции y = k x является гипербола.

Характерная особенность гиперболы в том, что у неё есть асимптоты.

Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.

Ось x – горизонтальная асимптота гиперболы

Ось y – вертикальная асимптота гиперболы.

На графике асимптоты отмечены зелёной пунктирной линией.

Если коэффициент k > 0 , то ветви гиперолы проходят через I и III четверти.

Если k     <     0, ветви гиперболы проходят через II и IV четверти.

Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y .

Квадратный корень

Функция y     =     x имеет следующий график:

Возрастающие/убывающие функции

Функция y   =   f ( x ) возрастает на интервале, если большему значению аргумента (большему значению x ) соответствует большее значение функции (большее значение y ) .

То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)

Примеры возрастающих функций:

Функция y   =   f ( x ) убывает на интервале, если большему значению аргумента (большему значению x ) соответствует меньшее значение функции (большее значение y ) .

То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).

Примеры убывающих функций:

Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наибольшим значением функции.

Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наименьшим значением функции.

Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.

Скачать домашнее задание к уроку 5.

1. Дробно-линейная функция и ее график

Функция вида y = P(x) / Q(x), где P(x) и Q(x) – многочлены, называется дробно-рациональной функцией.

С понятием рациональных чисел вы уже наверняка знакомы. Аналогично рациональные функции – это функции, которые можно представить как частное двух многочленов.

Если дробно-рациональная функция представляет собой частное двух линейных функций – многочленов первой степени, т.е. функцию вида

y = (ax + b) / (cx + d), то ее называют дробно-линейной.

Заметим, что в функции y = (ax + b) / (cx + d), c ≠ 0 (иначе функция становится линейной y = ax/d + b/d) и что a/c ≠ b/d (иначе функция константа). Дробно-линейная функция определена при всех действительных числах, кроме x = -d/c. Графики дробно-линейных функций по форме не отличаются от известного вам графика y = 1/x. Кривая, являющаяся графиком функции y = 1/x, называется гиперболой. При неограниченном увеличении x по абсолютной величине функция y = 1/x неограниченно уменьшается по абсолютной величине и обе ветки графика приближаются к оси абсцисс: правая приближается сверху, а левая – снизу. Прямые, к которым приближаются ветки гиперболы, называются ее асимптотами.

Пример 1.

y = (2x + 1) / (x – 3).

Решение.

Выделим целую часть: (2x + 1) / (x – 3) = 2 + 7/(x – 3).

Теперь легко видеть, что график этой функции получается из графика функции y = 1/x следующими преобразованиями: сдвигом на 3 единичных отрезка вправо, растяжением вдоль оси Oy в 7 раз и сдвигом на 2 единичных отрезка вверх.

Любую дробь y = (ax + b) / (cx + d) можно записать аналогичным образом, выделив «целую часть». Следовательно, графики всех дробно-линейных функций есть гиперболы, различным образом сдвинутые вдоль координатных осей и растянутые по оси Oy.

Для построения графика какой-нибудь произвольной дробно-линейной функции совсем не обязательно дробь, задающую эту функцию, преобразовывать. Поскольку мы знаем, что график есть гипербола, будет достаточно найти прямые, к которым приближаются ее ветки – асимптоты гиперболы x = -d/c и y = a/c.

Пример 2.

Найти асимптоты графика функции y = (3x + 5)/(2x + 2).

Решение.

Функция не определена, при x = -1. Значит, прямая x = -1 служит вертикальной асимптотой. Для нахождения горизонтальной асимптоты, выясним, к чему приближаются значения функции y(x), когда аргумент x возрастает по абсолютной величине.

Для этого разделим числитель и знаменатель дроби на x:

y = (3 + 5/x) / (2 + 2/x).

При x → ∞ дробь будет стремиться к 3/2. Значит, горизонтальная асимптота – это прямая y = 3/2.

Пример 3.

Построить график функции y = (2x + 1)/(x + 1).

Решение.

Выделим у дроби «целую часть»:

(2x + 1) / (x + 1) = (2x + 2 – 1) / (x + 1) = 2(x + 1) / (x + 1) – 1/(x + 1) =

= 2 – 1/(x + 1).

Теперь легко видеть, что график этой функции получается из графика функции y = 1/x следующими преобразованиями: сдвигом на 1 единицу влево, симметричным отображением относительно Ox и сдвигом на 2 единичных отрезка вверх по оси Oy.

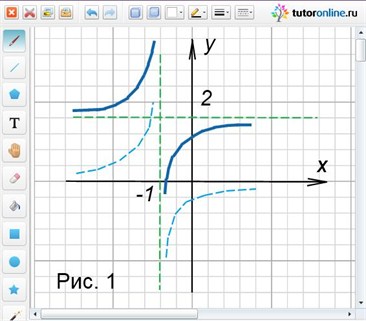
Область определения D(y) = (-∞; -1)ᴗ(-1; +∞).

Область значений E(y) = (-∞; 2)ᴗ(2; +∞).

Точки пересечения с осями: c Oy: (0; 1); c Ox: (-1/2; 0). Функция возрастает на каждом из промежутков области определения.

Ответ: рисунок 1.

2. Дробно-рациональная функция

Рассмотрим дробно-рациональную функцию вида y = P(x) / Q(x), где P(x) и Q(x) – многочлены, степени выше первой.

Примеры таких рациональных функций:

y = (x³ – 5x + 6) / (x⁷ – 6) или y = (x – 2)²(x + 1) / (x² + 3).

Если функция y = P(x) / Q(x) представляет собой частное двух многочленов степени выше первой, то ее график будет, как правило, сложнее, и построить его точно, со всеми деталями бывает иногда трудно. Однако, часто достаточно применить приемы, аналогичные тем, с которыми мы уже познакомились выше.

Пусть дробь – правильная (n < m). Известно, что любую несократимую рациональную дробь можно представить, и притом единственным образом, в виде суммы конечного числа элементарных дробей, вид которых определяется разложением знаменателя дроби Q(x) в произведение действительных сомножителей:

P(x)/Q(x) = A₁/(x – K₁)^m1 + A₂/(x – K₁)^m1-1 + … + A_m1/(x – K₁) + …+

+ L₁/(x – K_s)^ms + L₂/(x – K_s)^ms-1 + … + L_ms/(x – K_s) + …+

+ (B₁x + C₁) / (x² +p₁x + q₁)^m1 + … + (B_m1x + C_m1) / (x² +p₁x + q₁) + …+

+ (M₁x + N₁) / (x² +p_tx + q_t)^m1 + … + (M_m1x + N_m1) / (x² +p_tx + q_t).

Очевидно, что график дробно-рациональной функции можно получить как сумму графиков элементарных дробей.

Построение графиков дробно-рациональных функций

Рассмотрим несколько способов построения графиков дробно-рациональной функции.

Пример 4.

Построить график функции y = 1/x².

Решение.

Используем график функции y = x² для построения графика y = 1/x² и воспользуемся приемом «деления» графиков.

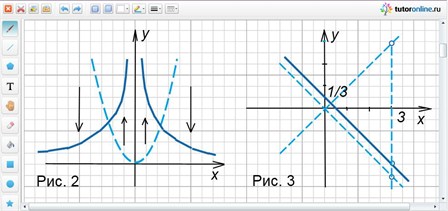
Область определения D(y) = (-∞; 0)ᴗ(0; +∞).

Область значений E(y) = (0; +∞).

Точек пересечения с осями нет. Функция четная. Возрастает при все х из интервала (-∞; 0), убывает при x от 0 до +∞.

Ответ: рисунок 2.

Пример 5.

Построить график функции y = (x² – 4x + 3) / (9 – 3x).

Решение.

Область определения D(y) = (-∞; 3)ᴗ(3; +∞).

y = (x² – 4x + 3) / (9 – 3x) = (x – 3)(x – 1) / (-3(x – 3)) = -(x – 1)/3 = -x/3 + 1/3.

Здесь мы использовали прием разложения на множители, сокращения и приведения к линейной функции.

Ответ: рисунок 3.

Пример 6.

Построить график функции y = (x² – 1)/(x² + 1).

Решение.

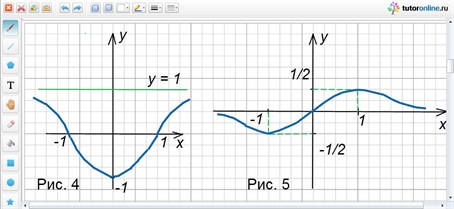
Область определения D(y) = R. Так как функция четная, то график симметричен относительно оси ординат. Прежде чем строить график, опять преобразуем выражение, выделив целую часть:

y = (x² – 1)/(x² + 1) = 1 – 2/(x² + 1).

Заметим, что выделение целой части в формуле дробно-рациональной функции является одним из основных при построении графиков.

Если x → ±∞, то y → 1, т.е. прямая y = 1 является горизонтальной асимптотой.

Ответ: рисунок 4.

Пример 7.

Рассмотрим функцию y = x/(x² + 1) и попробуем точно найти наибольшее ее значение, т.е. самую высокую точку правой половины графика. Чтобы точно построить этот график, сегодняшних знаний недостаточно. Очевидно, что наша кривая не может «подняться» очень высоко, т.к. знаменатель довольно быстро начинает «обгонять» числитель. Посмотрим, может ли значение функции равняться 1. Для этого нужно решить уравнение x² + 1 = x, x² – x + 1 = 0. Это уравнение не имеет действительных корней. Значит, наше предположение не верно. Чтобы найти самое большое значение функции, надо узнать, при каком самом большом А уравнение А = x/(x² + 1) будет иметь решение. Заменим исходное уравнение квадратным: Аx² – x + А = 0. Это уравнение имеет решение, когда 1 – 4А² ≥ 0. Отсюда находим наибольшее значение А = 1/2.

Ответ: рисунок 5, max y(x) = ½.

 Остались вопросы? Не знаете, как строить графики функций?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© devblog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

В научных исследованиях при решении практических задач всегда рассматривают изменения одних величин в зависимости от изменений других. Например, в электрической цепи величина тока меняется в зависимости от величины сопротивления, объем шара меняется в зависимости от его радиуса и т.д.

Взаимосвязь изменяемых величин в математике описывают с помощью функций.

Формальное определение выглядит следующим образом.

Функция

Пусть существует некоторый закон ff, по которому каждому числовому значению переменной xx ставится в соответствие единственное определенное числовое значение другой переменной yy. Такой закон называется функцией от xx и символически записывается в виде y=f(x)y = f(x).

При этом переменную xx называют независимой переменной или аргументом, переменную yy – зависимой переменной или функцией. Буква ff в записи y=f(x)y = f(x) обозначает правило или совокупность действий, которые нужно произвести над значением аргумента xx, чтобы получить значение функции yy.

Согласно определению функции, каждому числовому значению переменной xx должно ставиться в соответствие единственное числовое значение другой переменной yy. Чтобы подчеркнуть эту особенность, такую функцию называют однозначной. Но существуют также функции, в которых одному значению аргумента соответствуют два и более значений функции. Такие функции называются многозначными.

Способы задания функции

Существуют аналитический, табличный и графический способы задания функции.
Аналитический способ представляет собой задание функции с помощью формулы. Это самый удобный способ, так как формулу можно исследовать по полной программе. К сожалению, далеко не всегда изменения одних величин в зависимости от изменений других могут быть описаны в виде формулы.

При табличном способе задания в определенном порядке выписываются значения аргумента x1x_1, x2x_2, …, xnx_n и соответствующие значения функции y1y_1, y2y_2, …, yny_n. В таком виде часто получают функции во время измерительных экспериментов. Кроме того, таблицы значений разнообразных специальных функций мы можем видеть в справочниках.

Кроме аналитического и табличного способов задания функции, существует еще и графический, который позволяет «увидеть» функцию.

График функции

Графиком функции y=f(x)y = f(x) называется множество всех точек плоскости, для которых значения аргумента принадлежат области определения функции, а ординаты равны соответствующим значениям из области значений функции. Другими словами, график функции y=f(x)y = f(x) – это множество всех точек плоскости, координаты xx, у которых удовлетворяют соотношению y=f(x)y = f(x).

Графики позволяют выполнять предварительный визуальный анализ функций, дают возможность видеть характерные особенности их поведения. При этом можно обнаружить такие характерные свойства функций, как монотонность, ограниченность, четность или нечетность, а также периодичность.

Системы координат для построения графиков функций

Для построения графиков функций на плоскости используют декартову прямоугольную систему координат и полярную систему координат.

Прямоугольная система координат позволяет отображать функционально зависимые пары чисел xx и yy. Эта система координат образована двумя взаимно перпендикулярными осями, которые называются осями координат.

Точка пересечения осей координат называется началом координат и обозначается буквой OO. Горизонтальная ось направлена слева направо, называется осью абсцисс и обозначается OxO_x. Вертикальная ось направлена снизу вверх, называется осью ординат и обозначается OyO_y. С целью указания числовых значений координат на обоих осях выбирають масштабную единицу (одинаковую или разную).

При указанных условиях расположение любой точки M(x,y)M(x, y) на плоскости полностью определяется её координатами. Первая координата xx (абсцисса) точки MM указывает положение точки M1M_1 на оси OxO_x. Вторая координата y (ордината) точки MM указывает положение точки M2M_2 на оси OyO_y.

Оси координат делят плоскость на четыре части, которые называются четвертями или квадрантами. Квадранты нумеруют римскими цифрами против часовой стрелки. Знаки координат в каждом из квадрантов следующие:

– I квадрант – x>0x > 0, y>0y > 0;
– II квадрант – x<0x < 0, y>0y > 0;
– III квадрант – x<0x < 0, y<0y < 0;
– IV квадрант – x>0x > 0, y<0y < 0.

Точки на оси OyO_y имеют координату x=0x = 0, точки на оси OxO_x имеют координату y=0y = 0.

Начало координат имеет нулевые значения обеих координат.

На плоскости, кроме декартовой прямоугольной системы координат, используют также полярную систему координат. Это связано с тем, что сложность аналитических представлений многих кривых зависит от системы координат. Поэтому при удачном выборе системы координат можно существенно упростить решение той или иной задачи. Например, уравнение окружности радиуса RR с центром в начале координат в прямоугольной системе координат имеет вид: x2+y2=R2x^2 + y^2 = R^2. Уравнение той же окружности в полярной системе координат: ρ=Rρ = R.

Способы построения графиков функций

Известны следующие основные способы построения графиков функций:

1. построение графика функции по точкам;
2. построение графика функции посредством сложения графиков элементарных функций;
3. построение графика сложной функции посредством преобразования графика элементарной функции
4. построение графика функции на основе результатов её исследования.

Графическое изображение функции непосредственно чаще всего можно получить в тех или иных физических экспериментах, например, на экране осциллографа. В большинстве других случаев для построения графика функции необходимо иметь либо аналитическое, либо табличное её представление.

Тест по теме «Построение графика функции»

Функции и их графики — одна из самых увлекательных тем в школьной математике. Жаль только, что проходит она… мимо уроков и мимо учеников. На нее вечно не хватает времени в старших классах. А те функции, которые проходят в 7-м классе, — линейная функция и парабола — слишком просты и незамысловаты, чтобы показать все разнообразие интересных задач.

Умение строить графики функций необходимо для решения задач с параметрами на ЕГЭ по математике. Это одна из первых тем курса математического анализа в вузе. Это настолько важная тема, что мы в ЕГЭ-Студии проводим по ней специальные интенсивы для старшеклассников и учителей, в Москве и онлайн. И часто участники говорят: «Жаль, что мы не знали этого раньше».

Но это не все. Именно с понятия функции и начинается настоящая, «взрослая» математика. Ведь сложение и вычитание, умножение и деление, дроби и пропорции — это все-таки арифметика. Преобразования выражений — это алгебра. А математика — наука не только о числах, но и о взаимосвязях величин. Язык функций и графиков понятен и физику, и биологу, и экономисту. И, как сказал Галилео Галилей, «Книга природы написана на языке математики».

Точнее, Галилео Галилей сказал так:«Математика есть алфавит, посредством которого Господь начертал Вселенную».

Темы для повторения:

Понятие функции

Типы элементарных функций

Преобразования графиков функций

Производная функции

Асимптоты. Поведение функции в бесконечности

1. Построим график функции

Знакомая задача! Такие встречались в вариантах ОГЭ по математике. Там они считались сложными. Но сложного ничего здесь нет.

Упростим формулу функции:

при

График функции — прямая с выколотой точкой

2. Построим график функции

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, применяемый в решении неравенств, построении графиков и оценке целых величин в задачах на числа и их свойства. Он встретится вам также на первом курсе, когда придется брать интегралы.

3. Построим график функции

Он получается из графика функции растяжением в 2 раза, отражением по вертикали и сдвигом на 1 вверх по вертикали

4. Построим график функции

Главное — правильная последовательность действий. Запишем формулу функции в более удобном виде:

Действуем по порядку:

1) График функции y=sinx сдвинем на влево;

2) сожмем в 2 раза по горизонтали,

3) растянем в 3 раза по вертикали,

4) сдвинем на 1 вверх

Сейчас мы построим несколько графиков дробно-рациональных функций. Чтобы лучше понять, как мы это делаем, читайте статью «Поведение функции в бесконечности. Асимптоты».

5. Построим график функции

Область определения функции:

Нули функции: и

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Прямая x = 0 (ось Y) — вертикальная асимптота функции. Асимптота — прямая, к которой бесконечно близко подходит график функции, но не пересекает ее и не сливается с ней (смотри тему «Поведение функции в бесконечности. Асимптоты»)

Есть ли другие асимптоты у нашей функции? Чтобы выяснить это, посмотрим, как ведет себя функция, когда x стремится к бесконечности.

Раскроем скобки в формуле функции:

Если x стремится к бесконечности, то стремится к нулю. Прямая является наклонной асимптотой к графику функции.

6. Построим график функции

Это дробно-рациональная функция.

Область определения функции

Нули функции: точки — 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты:

Если x стремится к бесконечности, то у стремится к 1. Значит, — горизонтальная асимптота.

Вот эскиз графика:

Еще один интересный прием — сложение графиков.

7. Построим график функции

Если x стремится к бесконечности, то стремится к нулю и график функции будет бесконечно близко подходить к наклонной асимптоте

Если x стремится к нулю, то функция ведет себя как Это мы и видим на графике:

Вот мы и построили график суммы функций. Теперь график произведения!

8. Построим график функции

Область определения этой функции — положительные числа, поскольку только для положительных x определен

Значения функции равны нулю при (когда логарифм равен нулю), а также в точках, где то есть при

При значение cos x равно единице. Значение функции в этих точках будет равно при

9. Построим график функции

Функция определена при Она четная, поскольку является произведением двух нечетных функций и График симметричен относительно оси ординат.

Нули функции — в точках, где то есть при при

Если x стремится к бесконечности, стремится к нулю. Но что же будет, если x стремится к нулю? Ведь и x, и sin x будут становиться меньше и меньше. Как же будет вести себя частное ?

Оказывается, что если x стремится к нулю, то стремится к единице. В математике это утверждение носит название «Первого замечательного предела».

А как же производная? Да, наконец-то мы до нее добрались. Производная помогает более точно строить графики функций. Находить точки максимума и минимума, а также значения функции в этих точках.

10. Построим график функции

Область определения функции — все действительные числа, поскольку

Функция нечетна. Ее график симметричен относительно начала координат.

При x=0 значение функции равно нулю. При значения функции положительны, при отрицательны.

Если x стремится к бесконечности, то стремится к нулю.

Найдем производную функции
По формуле производной частного,

если или

В точке производная меняет знак с «минуса» на «плюс», — точка минимума функции.

В точке производная меняет знак с «плюса» на «минус», — точка максимума функции.

Найдем значения функции при x=2 и при x=-2.

Графики функций удобно строить по определенному алгоритму, или схеме. Помните, вы изучали ее в школе?

Общая схема построения графика функции: 

1. Область определения функции

2. Область значений функции

3. Четность — нечетность (если есть)

4. Периодичность (если есть)

5. Нули функции (точки, в которых график пересекает оси координат)

6. Промежутки знакопостоянства функции (то есть промежутки, на которых она строго положительна или строго отрицательна).

7. Асимптоты (если есть).

8. Поведение функции в бесконечности

9. Производная функции

10. Промежутки возрастания и убывания. Точки максимума и минимума и значения в этих точках.

Графики функций с модулями

Покажем полезные примеры построения графиков модулей функций. Такие графики с модулями встречаются на ЕГЭ в задачах с параметрами.

11. Построим графики функций:

а)

б)

в)

Решение:
а) Первый график построить легко. Выделим полный квадрат в формуле функции

График – квадратичная парабола, сдвинутая на 3 влево и на 1 вверх и перевернутая ветвями вниз.

б) Чтобы построить график функции зеркально отражаем относительно оси Х те части первого графика, которые лежали под ней. А та часть первого графика, которая лежала выше оси Х, остается на месте. Точки (2; 0) и (4; 0), в которых график пересекал ось Х, также остаются на месте.

в) Теперь график функции

Он тоже получается из графика первой функции, но преобразования другие. Часть первого графика, лежащая справа от оси Y, остается на месте. Действительно, модуль неотрицательного числа равен самому этому числу. Получили график функции для неотрицательных . И отражаем его зеркально относительно оси Y в левую полуплоскость.

12. Построим график функции

Функция определена при всех действительных х.

Нули функции:

Функция получается из элементарной функции в результате следующих преобразований:

1) Сдвиг на 2 единицы вниз,
2) Отражение части графика, лежащей ниже оси ОХ, в верхнюю полуплоскость. Стандартный прием при построении графика модуля функции.

13. Построим график функции

Ее график получается из графика функции сдвигом на 5 единиц вниз вдоль оси ОУ и симметричным отображением части графика, лежащей ниже оси ОХ, в верхнюю полуплоскость.

– вертикальная асимптота графика, — горизонтальная асимптота.

Читайте также: Асимптоты. Поведение функции в бесконечности

Исследование функции и построение графика

На этой странице мы постарались собрать для вас наиболее полную информацию об исследовании функции. Больше не надо гуглить! Просто читайте, изучайте, скачивайте, переходите по отобранным ссылкам.

Что будет дальше?

Общая схема исследования

Для чего нужно это исследование, спросите вы, если есть множество сервисов, которые построят график онлайн для самых замудренных функций? Для того, чтобы узнать свойства и особенности данной функции: как ведет себя на бесконечности, насколько быстро меняет знак, как плавно или резко возрастает или убывает, куда направлены «горбы» выпуклости, где не определены значения и т.п.

А уже на основании этих «особенностей» и строится макет графика — картинка, которая на самом-то деле вторична (хотя в учебных целях важна и подтверждает правильность вашего решения).

Начнем, конечно же, с плана. Исследование функции — объемная задача (пожалуй, самая объемная из традиционного курса высшей математики, обычно от 2 до 4 страниц с учетом чертежа), поэтому, чтобы не забыть, что в каком порядке делать, следуем пунктам, описанным ниже.

Алгоритм

1. Найти область определения. Выделить особые точки (точки разрыва).
2. Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
3. Найти точки пересечения с осями координат.
4. Установить, является ли функция чётной или нечётной.
5. Определить, является ли функция периодической или нет (только для тригонометрических функций).
6. Найти точки экстремума и интервалы монотонности.
7. Найти точки перегиба и интервалы выпуклости-вогнутости.
8. Найти наклонные асимптоты. Исследовать поведение на бесконечности.
9. Выбрать дополнительные точки и вычислить их координаты.
10. Построить график и асимптоты.

В разных источниках (учебниках, методичках, лекциях вашего преподавателя) список может иметь отличный от данного вид: некоторые пункты меняются местами, объединяются с другими, сокращаются или убираются. Учитывайте требования/предпочтения вашего учителя при оформлении решения.

Схема исследования в формате pdf: скачать.

Полный пример решения онлайн

Провести полное исследование и построить график функции
$$
y(x)=frac{x^2+8}{1-x}.
$$

1) Область определения функции. Так как функция представляет собой дробь, нужно найти нули знаменателя.
$$1-x=0, quad Rightarrow quad x=1.$$
Исключаем единственную точку $x=1$ из области определения функции и получаем:
$$
D(y)=(-infty; 1) cup (1;+infty).
$$

2) Исследуем поведение функции в окрестности точки разрыва. Найдем односторонние пределы:

Так как пределы равны бесконечности, точка $x=1$ является разрывом второго рода, прямая $x=1$ — вертикальная асимптота.

3) Определим точки пересечения графика функции с осями координат.

Найдем точки пересечения с осью ординат $Oy$, для чего приравниваем $x=0$:

Таким образом, точка пересечения с осью $Oy$ имеет координаты $(0;8)$.

Найдем точки пересечения с осью абсцисс $Ox$, для чего положим $y=0$:

Уравнение не имеет корней, поэтому точек пересечения с осью $Ox$ нет.

Заметим, что $x^2+8>0$ для любых $x$. Поэтому при $x in (-infty; 1)$ функция $y>0$ (принимает положительные значения, график находится выше оси абсцисс), при $x in (1; +infty)$ функция $ylt 0$ (принимает отрицательные значения, график находится ниже оси абсцисс).

4) Функция не является ни четной, ни нечетной, так как:

5) Исследуем функцию на периодичность. Функция не
является периодической, так как представляет собой дробно-рациональную функцию.

6) Исследуем функцию на экстремумы и монотонность. Для этого найдем первую производную функции:

Приравняем первую производную к нулю и найдем стационарные точки (в которых $y’=0$):

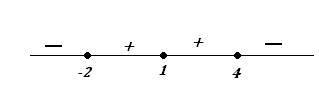
Получили три критические точки: $x=-2, x=1, x=4$. Разобьем всю область определения функции на интервалы данными точками и определим знаки производной в каждом промежутке:

При $x in (-infty; -2), (4;+infty)$ производная $y’ lt 0$, поэтому функция убывает на данных промежутках.

При $x in (-2; 1), (1;4)$ производная $y’ >0$, функция возрастает на данных промежутках.

При этом $x=-2$ — точка локального минимума (функция убывает, а потом возрастает), $x=4$ — точка локального максимума (функция возрастает, а потом убывает).

Найдем значения функции в этих точках:

Таким образом, точка минимума $(-2;4)$, точка максимума $(4;-8)$.

7) Исследуем функцию на перегибы и выпуклость. Найдем вторую производную функции:

Приравняем вторую производную к нулю:

Полученное уравнение не имеет корней, поэтому точек перегиба нет. При этом, когда $x in (-infty; 1)$ выполняется $y» gt 0$, то есть функция вогнутая, когда $x in (1;+infty)$ выполняется $y» lt 0$, то есть функция выпуклая.

Исследуем поведение функции на бесконечности, то есть при .

Так как пределы бесконечны, горизонтальных асимптот нет.

Попробуем определить наклонные асимптоты вида $y=kx+b$. Вычисляем значения $k, b$ по известным формулам:

Получили, у что функции есть одна наклонная асимптота $y=-x-1$.

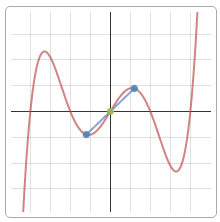
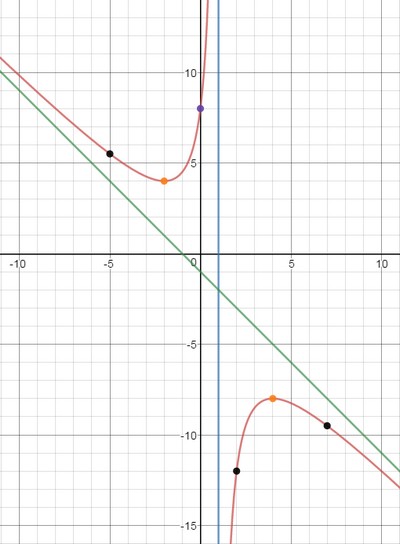
9) Дополнительные точки. Вычислим значение функции в некоторых других точках, чтобы точнее построить график.

$$
y(-5)=5.5; quad y(2)=-12; quad y(7)=-9.5.
$$

10) По полученным данным построим график, дополним его асимптотами $x=1$ (синий), $y=-x-1$ (зеленый) и отметим характерные точки (фиолетовым пересечение с осью ординат, оранжевым экстремумы, черным дополнительные точки):

Примеры решений по исследованию функции

Разные функции (многочлены, логарифмы, дроби) имеют свои особенности при исследовании (разрывы, асимптоты, количество экстремумов, ограниченная область определения), поэтому здесь мы пострались собрать примеры из контрольных на исследование функций наиболее часто встречающихся типов. Удачи в изучении!

Задача 1. Исследовать функцию методами дифференциального исчисления и построить график.

$$y=frac{e^x}{x}.$$

Задача 2. Исследовать функцию и построить ее график.

$$y=-frac{1}{4}(x^3-3x^2+4).$$

Задача 3. Исследовать функцию с помощью производной и построить график.

$$y=ln frac{x+1}{x+2}.$$

Задача 4. Провести полное исследование функции и построить график.

$$y=frac{x}{sqrt{x^2+x}}.$$

Задача 5. Исследовать функцию методом дифференциального исчисления и построить график.

$$y=frac{x^3-1}{4x^2}.$$

Задача 6. Исследовать функцию на экстремумы, монотонность, выпуклость и построить график.

$$y=frac{x^3}{x^2-1}.$$

Задача 7. Проведите исследование функции с построением графика.

$$y=frac{x^3}{2(x+5)^2}.$$

Задача 8. Построить график функции $y=y(x)$, заданной параметрически

$$x=frac{t^2}{t+1}, y=frac{1}{t}-frac{t^3}{3}.$$

Задача 9. Исследовать функцию и построить ее график $r=1+tg phi$.

Задача 10. Исследовать функцию и построить ее график $(x^2+y^2)^3=4x^2y^2$.

Задача 11. Провести полное исследование периодической функции
$y = cos 3x – 2 sin 6x$ и построить её график.

Задача 12. Провести полное исследование и построить график функции $y=f(x)$ с помощью Excel. Найти наибольшее и наименьшее значения функции на отрезке $[-3; -1]$.

$$y=frac{4-x^3}{x^2}.$$

Задача 13. Провести полное исследование и построить график функции.

$$f(x)=frac{x}{2}-arccosfrac{2x}{1+x^2}.$$

Еще примеры исследования функции (контрольные работы)

Как построить график онлайн?

Даже если преподаватель требует вас сдавать задание, написанное от руки, с чертежом на листке в клеточку, вам будет крайне полезно во время решения построить график в специальной программе (или сервисе), чтобы проверить ход решения, сравнить его вид с тем, что получается вручную, возможно, найти ошибки в своих расчетах (когда графики явно ведут себя непохоже).

Ниже вы найдете несколько ссылок на сайты, которые позволяют построить удобно, быстро, красиво и, конечно, бесплатно графики практически любых функций. На самом деле таких сервисов гораздо больше, но стоит ли искать, если выбраны лучшие?

Графический калькулятор Desmos

Desmos.com

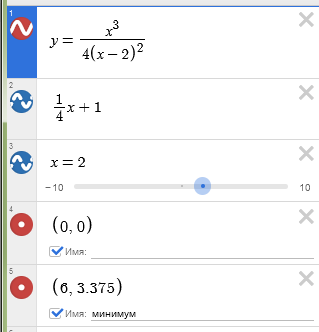
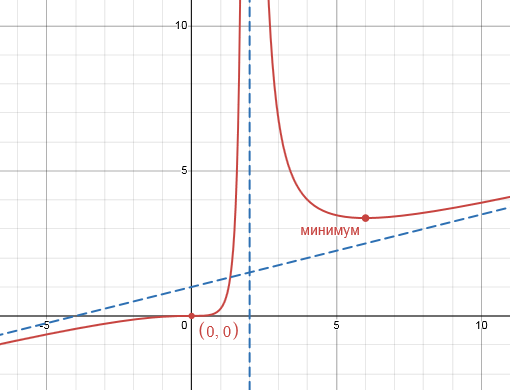
Невероятно гибкий и функциональный графический калькулятор. Интутивно понятно вводятся формулы (прямо на ходу преобразуются), автоматически подбираются масштаб и цвета графика для максимальной наглядности. Например, для функции $y(x)=frac{x^3}{4(x-2)^2}$ буквально за минуту построены основной график и асимптоты, вот что получилось:

При этом сайт сам пометил важные точки на графике (см. серым): локальный экстремум, пересечение с осями.

Вы можете менять масштаб, цвета, вид линий; добавлять на график точки, линии, кривые, табличные данные и даже анимацию!

Посмотрите, какую красоту Desmos умеет рисовать (точнее, его пользователи):

Сайт для построения графиков y(x).ru

y(x).ru

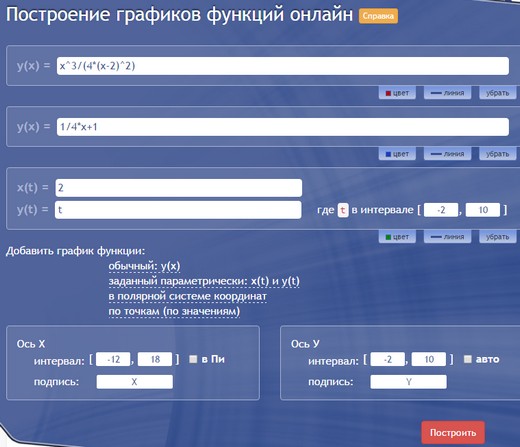
Это уже наш продукт, возможно, не такой красивый и интерактивный, но вполне подходящий для учебных целей. Можно строить онлайн несколько графиков одновременно, при этом выбирать и обычный, и параметрический вид, и даже задание в полярных координатах. Цвет и масштаб можно менять вручную. Вот так вводятся графики:

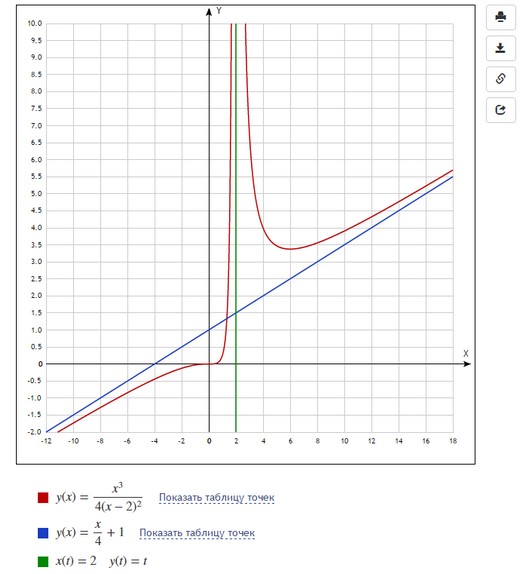
И такой график получается в итоге:

Из минусов можно заметить, что вводить, например, горизонтальные асимптоты не так просто: если в Desmos мы просто написали $x=2$, то здесь пришлось вводить параметрическую функцию $x(t)=2, y(t)=t$. Цвета и масштаб тоже пришлось подбирать вручную (иначе все графики оказались бы красными и мелкими).

Другие сайты

Еще несколько сервисов, которые обладают меньшим удобством/функциональностью, но тоже достойны внимания:

• ru.numberempire.com Можно построить сразу несколько функций, цвета подбираются автоматически, график интерактивный (положение и масштаб меняются мышкой).
• mathsolution.ru Можно строить несколько графиков, выбирая толщину линий и цвет, скрывать/отображать сетку, менять масштаб, сохранять картинки в файл.
• easyto.me При построении нескольких графиков на одном поле предыдущие не редактируются. В остальном функции как у прежних: выбор цвета, толщины линии, масштаба чертежа.
• grafikus.ru Кроме обычных графиков можно также строить трехмерные (3d). Можно построить несколько графиков разного типа (обычный,параметрический, в полярных координатах). Цвет и толщину линии выбрать нельзя. Интерактивности нет

Больше знаний: теория и практика

Еще немного ссылок для тех, кто хочет углубиться в тему. Первая ссылка на теоретический материал, где вы найдете и подробные примеры, и отсылки к предыдущим разделам теории (а исследовать функцию не зная пределов, производных, понятия непрерывности и т.п. нельзя) с не менее подробным объяснением. Все это сдобрено порцией юмора, отчего очень «съедобно» даже для полного чайника в математике: Исследование функций от Александра Емелина.

Вторая ссылка практическая, для тех, кто хочет научиться строить красивые графики в Desmos.com (см. выше описание): Полная инструкция по работе с Desmos. Эта инструкция довольно старая, с тех пор интерфейс сайта поменялся в лучшую сторону, но основы остались неизменными и помогут быстро разобраться с важными функциями сервиса.

Официальные инструкции, примеры и видео-инструкции на английском можно найти тут: Learn Desmos.

Решебник

Срочно нужна готовая задача? Более сотни разных функций с полным исследованием уже ждут вас. Подробное решение, быстрая оплата по SMS и низкая цена — около 50 рублей. Может, и ваша задача уже готова? Проверьте!

Полезные видео-ролики

Вебинар по работе с Desmos.com. Это уже полноценный обзор функций сайта, на целых 36 минут. К сожалению, он на английском языке, но базовых знаний языка и внимательности достаточно, чтобы понять большую часть.

Классный старый научно-популярный фильм «Математика. Функции и графики». Объяснения на пальцах в прямом смысле слова самых основ.