Как найти грани функции

0

Берем производную, для того чтобы найти экстремумы. Имеем $$f'(x)=1-1/x^2$$ или $$x^2=1.$$ Поскольку $$x>0,$$ имеем $$x=1.$$ В точке x=1 $$f(x)=1+1=2.$$ Несложно увидеть, что при $%x$%, стремящемся к бесконечности или к нулю, значение функции стремится к бесконечности, то есть функция не ограничена сверху. А нижняя грань 2 (экстремум в этом случае единствен, и он будет минимумом). ссылка отвечен 23 Окт ’14 23:23 Василий16 1.1k●1●17 изменен 24 Окт ’14 14:41 Виталина 99●1●7 10|600 символов нужно символов осталось

1. Определение предела функции в точке
   по Коши.

Определение предела функции
в точке a по
Коши. Пусть f(x)
определена на множестве X,
и a — предельная точка
X. Число b
называется пределом f(x)
при x 
a, если для 
 >
0  
> 0 такое, что для 
x 
{0 < x
— a<
}:
f(x)
— b
< .

1. Определение предела функции f(x)
   при x
   по Коши.

Определение. Число А
называется пределом функции f(x)
при x ,
если для 
> 0 B()
> 0: x
такого, что x
> B

1. Определение неограниченной в точке
   функции.

1. Определение бесконечно малой функции
   в точке.

Определение. Функция f(x)
называется бесконечно малой в точке x
= a (при x
 a),
если

f(x)=
0.

Эквивалентное определение. f(x)
называется бесконечно малой в точке a,
если

  > 0 
 >
0,  x
 {0 <
| x — a
| < 
}: | f(x)
| < .

1. Определение бесконечно большой
   функции в точке.

Определение. Функция f(x)
называется бесконечно большой в точке
x = a
(при x 
a), если

 A > 0 

> 0, 
x 
{0 < | x
— a | <

}: | f(x)
| > A.

Обозначение:

f(x)
= .

1. Определение непрерывной функции в
   точке.

Определение 1. Пусть f(x)
определена в некоторой окрестности
точки а. f(x)
называется непрерывной в точке а
если

f(x)
= f(а)

Определение 2. f(x)
называется непрерывной в точке а,
если  
> 0 
 >
0: | f(x)
— f(а) | < 
при | х — а | < .

1. Классификация точек разрыва функции.

Определение. Предельные точки
области определения функции, в которых
эта функция не является непрерывной,
называются точками её разрыва.

1). Устранимый разрыв. Точка а
называется точкой устранимого разрыва
функции f(x),
если 

f(x),
но

f(x)
 f(a)
, либо в точке а функция f(x)
вообще не определена.

2). Разрыв 1-го рода. Точка a
называется точкой разрыва 1-го рода,
если в этой точке функция f(x)
имеет конечные, но не равные друг другу
правое и левое предельные значения:

или

3). Разрыв 2-го рода. Точка a
называется точкой разрыва 2-го рода,
если в этой точке функция f(x)
не имеет по крайней мере одного из
односторонних предельных значений или
если хотя бы одно из них бесконечно.

1. Определение точной верхней грани
   функции.

(Я, на всякий случай, привожу определения
и верхней, и нижней граней)

Определение 1. Пусть f(x)-
ограниченна сверху (снизу) на X,
то есть 
M (m)
,  x
 X:
f(x)
 M (f(x)
 m)
. Число М (m)
называется верхней
(нижней) гранью функции f(x)
на множестве Х. Наименьшая (наибольшая)
из верхних (нижних) граней ограниченной
сверху (снизу) на X
f(x)
называется её точной верхней (точной
нижней) гранью и обозначается
f(x)
(
f(x)).

Эквивалентное определение. Число
M (число m)
называется точной верхней (точной
нижней) гранью функции f(x)
на множестве X,
если выполнены следующие два требования:
1) для 
x 
X: f(x)
 M (f(x)
 m),
2) для 

> 0 x
 X,
для которого справедливо неравенство

()

1. Определение производной функции в
   точке.

Определение. Производной
функции f(x)
в данной фиксированной точке x
называется предел при x
0 разностного отношения

(при условии, что этот предел существует).

1. Определение дифференцируемости
   функции.

Определение. Функция f(x)
называется дифференцируемой в данной
точке x , если
приращение y
этой функции в точке x,
соответствующее приращению аргумента
x,
может быть представлено в виде

,

где A – некоторое
число, не зависящее от x,
а  — функция
аргумента x,
являющаяся бесконечно малой при x

0.

Т.к. произведение двух
бесконечно малых x
является бесконечно малой более высокого
порядка, чем x,
то можно определение переписать

(А = f’(x)).

1. Определение дифференциала функции.

Определение. Дифференциалом
функции

в точке x, соответствующим
приращению аргумента x,
называют главную линейную относительно
x
часть приращения этой функции в точке
x.

Принято обозначать дифференциал функции

символом dy,

.

Дифференциалом независимой переменной
х называется приращение этой
переменной: dx = x.
Таким образом, dy = f
‘(x)dx,
или

1. Определение производной вектор-функции.

Если каждому числу t
из некоторого множества T
поставлен в соответствие вектор,
то говорят, что на множестве T,
определена векторная функция (или вектор
— функция) и пишут:
=(t),
t 
T. |(t)
| — скалярная функция.

Определение. Векторназывается
пределом вектор-функции
=(t)
при t 
t₀ если |(t)
—|
 0 при
t t₀,

(t)
=.

Зафиксируем какое-нибудь значение t,
а затем дадим приращение t
 0
аргументу t. =

(t
+ t)
—
(t)

Определение производной вектор-функции.
Если существует
,
то он называется производной вектор-функции
в точке t и обозначается
‘(t).

1. Определение предела последовательности.

Определение. Число А называется
пределом последовательности
,
если для

  n>N
x_n
— A
< 

Обозначение:
.

1. Определение бесконечно большой
   последовательности.

Определение. Последовательность

называется бесконечно большой, если
для А >
0 N:
n 
N x_n
> A.

1. Определение неограниченной
   последовательности.

Определение.
Последовательность {x_n}
называется неограниченной, если 
A > 0 
n: x_n
> A.

1. Определение фундаментальной
   последовательности.

Определение. Последовательность
{x_n}
называется фундаментальной, если для
 
> 0  N:
 n
>N и 
натурального p:
x_n+p—x_n
< .

1. Определение предельной точки числовой
   последовательности.

Определение 1. Число a
называется предельной точкой
последовательности {x_n},
если из последовательности {x_n}
можно выделить подпоследовательность,
сходящуюся к a.

Определение 2. Число a
называется предельной точкой
последовательности {x_n},
если в любой -окрестности
точки a содержится
бесконечно много членов последовательности
{x_n}.

1. Определение предела функции в точке
   по Гейне.

Определение предела
функции в точке a
по Гейне. Число b
называется пределом f(x)
при x 
a, если для 
{x_n}
 a
(x_n
 a):
{f(x_n)}
 b.

1. Определение предела функции f(x)
   при x
   по Гейне.

Определение (по Гейне). Число b
называется пределом f(x)
при x 
+, если 
{x_n}
 +:
{f(x_n)}
 b.

1. Определение первообразной и
   неопределенного интеграла.

Определение 1. Функция F(x)
называется первообразной для функции
f(x)
на X, если 
xX:
F‘(x)
= f(x).

Определение 2. Множество всех
первообразных для функции f(x)
на промежутке X
называется неопределенным интегралом
от этой функции на промежутке X
и обозначается

.

f(x)
называется подынтегральной функцией.

f(x)dx
называется подынтегральным выражением.

1. Определение равномерно непрерывной
   функции.

Определение. Функция f(x)
называется равномерно непрерывной на
множестве {x}, если для
 
> 0 ()
> 0 такое, что для любых двух
точек x’
и x’’
множества {x},
удовлетворяющих условию

выполняется условие
.

Примеры:

— равномерно непрерывна на полупрямой
x 
1,

— не является равномерно
непрерывной на множестве x 
1,

не является равномерно
непрерывной на интервале (0,
1).

1. Определение точки локального экстремума
   функции.

Определение. Пусть функция f(x)
определена всюду в некоторой окрестности
точки с.
Говорят, что функция f(x)
имеет в точке с
локальный максимум (минимум), если
существует такая окрестность точки с,
в пределах которой значение f(с)
является наибольшим (наименьшим).

Локальный максимум и минимум объединяются
общим названием экстремум.

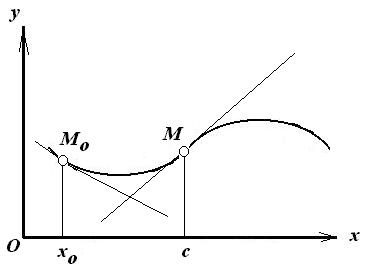
1. Определение наклонной асимптоты к
   графику функции.

Определение. Говорят, что прямая

(1)

является наклонной
асимптотой графика
функции

при
,
если функция f(x)
представима в виде

,
где

(2)

___________________________________________________________________________________

Определение. Говорят, что
прямая x = a является вертикальной
асимптотой графика функции
,
если хотя бы одно из предельных значений

или

равно +
или —.

1. Определение точки перегиба графика
   функции.

Определение.
Точка

графика функции

называется точкой
перегиба этого графика,
если существует такая окрестность точки
с оси
абсцисс, в пределах которой график
функции

слева и справа от с
имеет разные направления выпуклости.
(см. рисунок).

Иногда при определении
точки перегиба графика функции

дополнительно требуют, чтобы этот график
всюду в пределах достаточно малой
окрестности точки с оси абсцисс слева
и справа от с лежал по разные стороны
от касательной к этому графику в точке
.

1. Определение направления выпуклости
   графика функции.

Предположим, что функция f(x)
дифференцируема в любой точке интервала
.
Тогда существует
касательная к графику функции
,
проходящая через любую точку

этого графика
,
причем эта касательная не параллельна
оси Oy.

Определение. График функции

имеет на интервале

выпуклость, направленную вниз (вверх),
если график этой функции в пределах
указанного интервала лежит не ниже (не
выше) любой своей касательной.

1. Определение условно сходящегося
   ряда.

Определение. Ряд

называется условно сходящимся, если
этот ряд сходится , а соответствующий
ряд из модулей

расходится.

1. Определение абсолютно сходящегося
   ряда.

Определение. Ряд

называется абсолютно сходящимся, если
сходится ряд
.

Соседние файлы в папке 67 вопросов

• #
• #
• #

Теорема Вейерштрасса о непрерывной функции на отрезке

30 декабря 2021

Теорема Вейерштрасса — фундаментальная теорема матанализа, которая состоит из двух частей:

1. Теорема об ограниченности;
2. Теорема о достижении максимума и минимума.

Сейчас мы сформулируем и докажем обе эти теоремы. Прежде всего дадим определения, на которые будем опираться:

Определение 1. Функция $fleft( x right)$ непрерывна в точке $x=a$, если $limlimits_{xto a}fleft( x right)=fleft( a right)$.

Определение 2. Функция $fleft( x right)$ непрерывна на интервале $left[ a;b right]$, если она непрерывна в каждой точке этого отрезка. При этом на концах отрезка речь идёт об односторонней непрерывности.

Всё это подробно разобрано в уроке про непрерывность функции в точке. Перейдём к теоремам.

1. Теорема Вейерштрасса об ограниченности функции

Теорема 1. (об ограниченности непрерывной функции) Функция, непрерывная на отрезке $left[ a;b right]$, ограничена на этом отрезке.

Другими словами, найдётся $Min mathbb{R}$ такое, что

[forall left( xin left[ a;b right] right)quad left| fleft( x right) right| lt M]

Приведу два доказательства — выбирайте то, которое больше нравится именно вам (или вашему преподу).

1.1. Доказательство методом Больцано

Предположим противное: пусть $fleft( x right)$ не ограничена на $left[ a;b right]$. Обозначим середину этого отрезка ${{c}_{1}}={left( a+b right)}/{2};$ и рассмотрим два новых отрезка:

[left[ a;{{c}_{1}} right]quad left[ {{c}_{1}};b right]]

Вместе эти отрезки покрывают отрезок $left[ a;b right]$. Следовательно, функция $fleft( x right)$ не ограничена как минимум на одном из них. Иначе если $fleft( x right)$ ограничена на обоих отрезках, то она будет ограничена и на из объединении, что противоречит нашему предположению.

Обозначим тот отрезок, на котором $fleft( x right)$ не ограничена, как ${{I}_{1}}=left[ {{a}_{1}};{{b}_{1}} right]$. Найдём середину этого отрезка ${{c}_{2}}={left( {{a}_{1}}+{{b}_{1}} right)}/{2};$. Вновь рассмотрим пару отрезков $left[ {{a}_{1}};{{c}_{1}} right]$ и $left[ {{c}_{1}};{{b}_{1}} right]$. Как минимум на одном из них функция $fleft( x right)$ будет не ограничена. Обозначим этот отрезок как ${{I}_{2}}=left[ {{a}_{2}};{{b}_{2}} right]$.

Проделаем эту операцию много раз. Получим последовательность стягивающихся отрезков:

[{{I}_{1}}supset {{I}_{2}}supset ldots supset {{I}_{n}}supset ldots ]

Длина отрезка ${{I}_{n}}$ равна $left| {{I}_{n}} right|=left| b-a right|cdot {{2}^{-n}}$ и стремится к нулю при $nto +infty $. По лемме о стягивающихся отрезках существует точка ${{x}_{0}}in mathbb{R}$ такая, что ${{x}_{0}}in {{I}_{n}}$ для любого $nin mathbb{N}$.

Кроме того, ${{x}_{0}}in left[ a;b right]$, поэтому функция $fleft( x right)$ непрерывна в т.ч. и в точке $x={{x}_{0}}$:

[limlimits_{xto {{x}_{0}}}fleft( x right)=fleft( {{x}_{0}} right)]

Вспомним определение предела функции в точке:

[begin{align} & limlimits_{xto {{x}_{0}}} fleft( x right)=fleft( {{x}_{0}} right)Rightarrow\ & forall left( varepsilon gt 0 right)quad exists left( delta =delta left( varepsilon right) gt 0 right): \ & xin {{overset{circ }{mathop{U}},}_{delta }}left( {{x}_{0}} right)Rightarrow left| fleft( x right)-fleft( {{x}_{0}} right) right| lt varepsilon\ end{align}]

Возьмём $varepsilon =1$. Следовательно, найдётся $delta =delta left( 1 right) gt 0$ такое, что в проколотой $delta $-окрестности точки ${{x}_{0}}$ выполняется условие $left| fleft( x right)-fleft( {{x}_{0}} right) right| lt 1$. Но тогда

[begin{align} left| fleft( x right) right|&=left| fleft( x right)-fleft( {{x}_{0}} right)+fleft( {{x}_{0}} right) right|le\ & le left| fleft( x right)-fleft( {{x}_{0}} right) right|+left| fleft( {{x}_{0}} right) right| lt \ & lt 1+left| fleft( {{x}_{0}} right) right| \ end{align}]

Получается, что внутри $delta $-окрестности функция ограничена числом $M=1+left| fleft( {{x}_{0}} right) right|$. Но поскольку $delta gt 0$ — фиксированное положительное число, а длины отрезков $left| {{I}_{n}} right|=left| b-a right|cdot {{2}^{-n}}$ стремятся к нулю, начиная с какого-то момента эти отрезки будут полностью лежать внутри этой $delta $-окрестности:

Мы даже можем приблизительно вычислить этот момент — достаточно потребовать, чтобы величина $delta $ оказалась больше длины $left| {{I}_{n}} right|$:

[begin{align} delta& gt left| b-a right|cdot {{2}^{-n}} \ {{2}^{n}} & gt {left| b-a right|}/{delta }; \ n& ge left[ {{log }_{2}}{left| b-a right|}/{delta }; right]+1 \ end{align}]

Здесь $left[ l right]$ следует понимать как «целая часть числа $l$» (подробнее об этом — в уроке «Что такое предел последовательности»).

Но тогда для всякого такого отрезка, полностью лежащего в $delta $-окрестности точки ${{x}_{0}}$, одновременно выполняется два условия:

1. Функция $fleft( x right)$ ограничена на этом отрезке, потому что $left| fleft( x right) right| lt left| fleft( {{x}_{0}} right) right|+1$;
2. Функция $fleft( x right)$ не ограничена на этом отрезке, потому что мы так выбрали ${{I}_{n}}$.

Получили противоречие. Следовательно, исходное предположение не верно. Теорема доказана.

1.2. Доказательство по Гейне

Рассмотрим более хитрое доказательство, которое опирается на теорема Больцано-Вейерштрасса о сходящейся подпоследовательности.

Итак, нужно доказать, что функция, непрерывная на отрезке $left[ a;b right]$, будет ограничена на этом отрезке. Вновь предположим, что это не так: пусть функция $fleft( x right)$ не ограничена, т.е.

[begin{align} & forall left( cin mathbb{R} right)quad exists left( xin left[ a;b right] right): \ & left| fleft( x right) right| gt c \ end{align}]

Рассмотрим натуральные значения $c$.

Пусть $c=1$. Тогда найдётся ${{x}_{1}}in left[ a;b right]$ такое, что $left| fleft( {{x}_{1}} right) right| gt 1$.

Пусть $c=2$. Тогда найдётся ${{x}_{2}}in left[ a;b right]$ такое, что $left| fleft( {{x}_{2}} right) right| gt 2$.

Продолжаем так много раз. Пусть $c=n$. Тогда найдётся ${{x}_{n}}in left[ a;b right]$ такое, что $left| fleft( {{x}_{n}} right) right| gt n$.

Получили последовательность $left{ {{x}_{n}} right}$, которая бесконечна и ограничена: $ale {{x}_{n}}le b$. По теореме Больцано-Вейерштрасса из неё можно выбрать сходящуюся подпоследовательность $left{ {{x}_{{{n}_{k}}}} right}$:

[limlimits_{kto +infty } {{x}_{{{n}_{k}}}}=xi ]

Но поскольку члены последовательности $ale {{x}_{{{n}_{k}}}}le b$, её предел $xi in left[ a;b right]$ (почему это так — смотрите свойства предела последовательности), и функция $fleft( x right)$, непрерывная на $left[ a;b right]$, будет непрерывна и в точке $x=xi $.

Согласно определению непрерывности функции по Гейне имеем

[limlimits_{kto +infty } fleft( {{x}_{{{n}_{k}}}} right)=fleft( xi right)]

С другой стороны, последовательность [left{ {{x}_{{{n}_{k}}}} right}] сконструирована таким образом, что

[left| fleft( {{x}_{{{n}_{k}}}} right) right| gt {{n}_{k}}ge k]

Но тогда предел

[limlimits_{kto +infty } fleft( {{x}_{{{n}_{k}}}} right)=infty ]

Получаем, что один и тот же предел одновременно равен и $fleft( xi right)in mathbb{R}$, и $infty notin mathbb{R}$. Чего не может быть, поскольку если предел существует, то он единственный.

Вновь получили противоречие. Следовательно, исходное предположение не верно. Теорема Вейерштрасса об ограниченности функции доказана.

1.3. Важное замечание

Эту теорему можно обобщить, рассмотрев вместо отрезка произвольный компакт.

С другой стороны, если вместо отрезка рассмотреть интервал (или любое другое открытое множество), то теорема будет не верна!

Пример 1. Функция $y= operatorname{tg}x$, где $xin left( -frac{pi }{2};frac{pi }{2} right)$.

Тангенс непрерывен в каждой точке указанного интервала, однако неограниченно возрастает при $xto {pi }/{2};$ и неограниченно убывает при $xto -{pi }/{2};$.

Принципиально важно, чтобы функция была определена на концах отрезка $left[ a;b right]$, т.е. принимала бы конкретные значения $fleft( a right)$ и $fleft( b right)$. И следовательно, была бы ограниченна в некоторой $delta $-окрестности этих концов.

2. Теорема Вейерштрасса о достижении максимума и минимума

В матанализе есть понятие локального максимума и минимума (смотрите раздел про производные), поэтому при формулировке теоремы Вейерштрасса лучше говорить о точной верхней грани и точной нижней грани значений функции на отрезке:

[suplimits_{xin left[ a;b right]}fleft( x right)quad inflimits_{xin left[ a;b right]}fleft( x right)]

Теорема 2. (о достижении точной верхней и нижней грани) Функция, непрерывная на отрезке $left[ a;b right]$, достигает своей точной верхней грани и точной нижней грани:

[begin{align} & exists left( {{x}_{1}}in left[ a;b right] right): & fleft( {{x}_{1}} right)=underset{xin left[ a;b right]}{mathop{sup }},fleft( x right) \ & exists left( {{x}_{2}}in left[ a;b right] right): & fleft( {{x}_{2}} right)=underset{xin left[ a;b right]}{mathop{inf }},fleft( x right) \ end{align}]

Докажем эту теорему только для точной верхней грани. Затем достаточно рассмотреть функцию $gleft( x right)=-fleft( x right)$ и заметить, что

[inflimits_{xin left[ a;b right]} fleft( x right)=-suplimits_{xin left[ a;b right]} gleft( x right)]

2.1. Доказательство для точной верхней грани

Пусть функция $fleft( x right)$ непрерывна на $left[ a;b right]$. Тогда по теореме Вейерштрасса об ограниченности, которую мы доказали выше, найдётся такое $Min mathbb{R}$, что

[forall left( xin left[ a;b right] right)quad left| fleft( x right) right| lt M]

Но тогда существует точная верхняя грань

[A=suplimits_{xin left[ a;b right]} fleft( x right)]

Докажем теорему от противного. Пусть $Ane fleft( x right)$ для любого $xin left[ a;b right]$. Тогда очевидно, что $A gt fleft( x right)$ при каждом $xin left[ a;b right]$.

Рассмотрим функцию $gleft( x right)=A-fleft( x right)$. Она непрерывна на отрезке $left[ a;b right]$. Кроме того для всякого $xin left[ a;b right]$

[gleft( x right)=A-fleft( x right) gt 0]

Следовательно, функция

[{{g}_{1}}left( x right)=frac{1}{gleft( x right)}=frac{1}{A-fleft( x right)} gt 0]

тоже непрерывна на отрезке $left[ a;b right]$ и принимает лишь положительные значения. Но тогда ${{g}_{1}}left( x right)$ ограничена на $left[ a;b right]$. Следовательно, найдётся число $B gt 0$ такое, что

[begin{align} left| {{g}_{1}}left( x right) right| & lt B \ 0 lt frac{1}{A-fleft( x right)}& lt B \ end{align}]

Но тогда

[begin{align} A-fleft( x right) & gt frac{1}{B} gt 0 \ fleft( x right) & lt A-frac{1}{B} \ end{align}]

Получается, что мы нашли верхнюю грань $A-{1}/{B};$, которая меньше точной верхней грани $A=suplimits_{xin left[ a;b right]} fleft( x right)$.

Но это противоречит определению точной меньшей грани. Следовательно, исходное предположение неверно. Теорема доказана.

Смотрите также:

1. Теорема о промежуточном значении функции
2. Непрерывность функции в точке
3. Тест к уроку «Что такое логарифм» (средний)
4. Тест к уроку «Площади многоугольников без координатной сетки» (средний)
5. Как решать биквадратное уравнение
6. Задача B4: экономика

1. Понятие числовой функции.

   Начать изучение
   

2. Равенство функций. Операции над функциями.

   Начать изучение
   

3. Способы задания функции.

   Начать изучение
   

4. График функции.

   Начать изучение
   

5. Четные и нечетные функции.

   Начать изучение
   

6. Ограниченные и неограниченные функции.

   Начать изучение
   

7. Монотонные функции.

   Начать изучение
   

8. Периодические функции.

   Начать изучение
   

9. Обратная функция.

   Начать изучение
   

10. Неявные функции. Параметрически заданные функции.

    Начать изучение
    

Понятие числовой функции.

Пусть дано числовое множество (Xsubsetmathbb{R}). Если каждому (xin X) поставлено в соответствие по некоторому правилу число (y). то говорят, что на множестве (X) определена числовая функция.

Правило, устанавливающее соответствие, обозначают некоторым символом, например, (f) и пишут
$$
y=f(x),;xin X,label{ref1}
$$
а множество (X) называют областью определения функции и обозначают (D(f)), то есть (X=D(f)).

(x) часто называют аргументом или независимой переменной, а (y) — зависимой переменной. Числа (x) из множества (D(f)) называют значениями аргумента. Число (y_0), соответствующее значению (x_{0}in D(f)), называют значением функции при (x=x_{0}) (или значением функции в точке (x_0)) и обозначают (f(x_0)) или (f(x)|_{x=x_{0}}). Совокупность всех значений, которые функция принимает на множестве (D(f)), называют множеством значений функции и обозначают (E(f)). Заметим, что если (y_0in E(f)), то существует по крайней мере одно число (x_{0}in D(f)) такое, что (f(x_0)=y_0).

Функцию часто обозначают только символом ((f,;varphi,;F) и т. д.), который определяет правило (закон) соответствия. Для обозначения функции используются также записи вида (xmapsto f(x),;f:;Xrightarrow Y). Под словом «функция» часто понимают зависимую переменную (у), значения которой определяются значениями независимой переменной (x) и правилом (f), или даже само это правило. Термин «функция» имеет синонимы: отображение, преобразование, морфизм. Например, говорят, что функция (f) отображает множество (X=D(f)) на множество (Y=E(f)), и называют множество (Y) образом множества (X) при отображении (f). Если (E(f)subset E_1), то говорят, что функция (f) отображает (X) в (E_1).

---

Равенство функций. Операции над функциями.

Функции (f) и (g) называют равными или совпадающими, если они имеют одну и ту же область определения (X) и для каждого (xin X) значения этих функций совпадают. В этом случае пишут (f(x)=g(x), xin X) или (f=g).

Например, если (f(x)=sqrt{x^{2}},  xinmathbb{R}),и (g(x)=|x|, xinmathbb{R}), то (f=g), так как при всех (xinmathbb{R}) справедливо равенство (sqrt{x^{2}}=|x|).

Если (E’subset D(f)) , то функцию (g(x)=f(x),;xin E’), называют сужением функции f на множество (E’). Например, если (E’=[0, +infty),) то функция ( q(x)=x,  xin E’), является сужением функции (f(x)=|x|), (xinmathbb{R}) , на множество (E’).

Если равенство (f(x)=g(x)) верно при всех (xin E’), где (E’subset D(f)cap D(g)), то есть сужения функций f и g на множество (E’) совпадают, то в этом случае говорят, что функции (f) и (g) равны на множестве (E’). Например, функции (sqrt{x^{2}}) и (x) равны на множестве ( E’=[0,+infty)).

Естественным образом для функций вводятся арифметические операции. Пусть функции (f) и (g) определены на одном и том же множестве (E). Тогда функции, значения которых в каждой точке (xin E) равны (f(x)+g(x),;f(x)-g(x),;f(x)g(x),;f(x)/g(x)(g(x)neq 0) для всех (xin E)) , называют соответственно суммой, разностью, произведением и частным функций (f) и (g) и обозначают (f+g,;f-g,;fg,;f/g).

Введем понятие сложной функции. Пусть функции (y=varphi(x)) и (z=f(y)) определены на множествах (X) и (Y) соответственно, причем множество значений функции (varphi) содержится в области определения функции (f). Тогда функцию, принимающую при каждом (xin X) значение (F(x)=f(varphi(x))), называют сложной функцией или суперпозицией (композицией) функций (varphi) и (f) и обозначают ( fcirc varphi ).  Например, функция (z=sqrt{4-x^2},;xin [-2,2]), является композицией функций (y=4-x^2,;xin [-2,2]) и (z=sqrt{y},;yin [0,+infty)) . Эта функция относится к совокупности элементарных функций, то есть функций, которые можно получить из основных элементарных функций с помощью конечного числа арифметических операций и композиций. К основным элементарным функциям относят постоянную, степенную, логарифмическую, тригонометрические и обратные тригонометрические функции. Например, элементарными являются функции:

1. линейная (y=ax+b, aneq 0;)
2. квадратичная (y=ax^2+bx+c, aneq 0);
3. многочлен степени n, то есть функция , где (y=P_n(x)), где (P_n(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+ldots+a_{1}x+a_0;)
4. рациональная функция, то есть функция вида (y=frac{P_{n}(x)}{Q_{m}(x)}) где (P_{n}) и (Q_{m}) — многочлены степени n и m, ( mneq 0).

---

Способы задания функции.

Числовые функции чаще всего задаются при помощи формул. Такой способ задания называют аналитическим. Например, функции (y=x^2, y=|x|^{3/2}, y=sin^3{3x}) заданы на множестве (mathbb{R}) аналитически.

Если числовая функция f задана формулой и не указана область ее определения (D(f)) , то принято считать, что (D(f)) — множество всех тех значений аргумента, при которых эта формула имеет смысл, и результатом каждой операции, указанной в формуле, является вещественное число. Например, если (f(x)=sqrt{9-x^2}), то (D(f)=[-3,3]), а если (f(x)=sqrt{operatorname{lg} sin{x}}), то (D(f)) — множество корней уравнения (sin x=1) то есть множество чисел (x_{k}=pi/2.+2pi k), где (kin Z).

Следует отметить, что функция может быть задана различными формулами на разных промежутках. Например, функция
$$
f(x)=left{begin{array}{l}-x,quad если;x;<;0,\x^{2},quad если;0leq xleq1,\2-sqrt{x},quad если;x>1,end{array}right.nonumber
$$
задана аналитическим способом на (mathbb{R}) с помощью трех различных формул.

Иногда функциональная зависимость описывается с помощью таблицы, содержащей лишь некоторые значения аргумента и соответствующие значения функции. Для значений аргумента, не содержащихся в таблице, значения функции обычно находят приближенно.

На практике часто соответствие между значениями аргумента и значениями функции задается с помощью рисунка. Например, в медицине при изучении работы сердца получают электрокардиограммы — кривые, отражающие изменение с течением времени электрических импульсов в мышце сердца. В практике физических измерений функциональная зависимость часто задается с помощью эскиза графика, снимаемого, например, с экрана осциллографа.

---

График функции.

Графиком функции (y=f(x), xin D(f),) в прямоугольной системе координат (Oxy)-называют множество всех точек плоскости с координатами ((x,f(x)overline{)}), где (xin D(f)).

Для каждого (x_0in D(f)) прямая, (x=x_{0}), параллельная оси (Oy), пересекает график функции (y=f(x)) , (xin D(f)), в одной точке (M_{0}(x_{0},y_{0})) , где (y_{0}=f(x_{0})) — значение функции f при (x=x_{0}). Значениях (x=a), при котором (f(a)=0), называют нулем функции (f(x)). Если (x=a) — нуль функции (f(x)), то график функции (y=f(x)) пересекает ось (Ox) при (x=a) то есть в точке М((a,0)).

Строго говоря, следует различать график функции, точное определение которого дано выше, и эскиз части графика, принимаемый нередко за график.

График функции (y=f(x)) иногда можно получить преобразованием известного графика другой функции (y=g(x)).

Функция (y=f(x))	Преобразование графика функции (y=g(x))
(y=g(x)+A)	Сдвиг (параллельный перенос) вдоль оси ординат на A
(y=g(x-a))	Сдвиг вдоль оси абсцисс на а
(y=g(-x))	Симметрия относительно оси ординат
(y=-g(x))	Симметрия относительно оси абсцисс
(y=Bg(x))	Умножение каждой ординаты на B, где (bneq 0)
(y=g(kx))	Деление каждой абсциссы на k, где (kneq 0)

Приведем примеры применения преобразований, указанных в таблице.

В частности, если (y=displaystyle frac{3-2x}{x+1}), то (y=displaystyle frac{5-2(x+1)}{x+1}=-2+frac{5}{x+1}).

Поэтому график этой функции можно получить сдвигом графика гиперболы (y=displaystyle frac{5}{x}) вдоль оси (Ox) на -1 и вдоль оси (Oy) на -2 (рис. 9.4). Отсюда следует, что график функции (y=displaystyle frac{3-2x}{x+1}) симметричен относительно точки ((-1, -2)).

Отметим еще, что график функции (y=|f(x)|) можно получить из графика функции (у=f(x)) следующим образом:

1. часть графика функции (f(x)), лежащую выше оси (Ox) и на этой оси, оставить без изменения;
2. часть графика функции f(x),лежащую ниже оси (Ox,) симметрично отразить относительно Ox.

---

Четные и нечетные функции.

Функция f, определенная на множестве X, называется:

1. четной, если для любого (xin X) выполняются условия (-xin X) и (f(-x)=f(x));
2. нечетной, если для любого (xin X) выполняются условия (-xin X) и (f(-x)=-f(x)).

Четными являются, например, следующие функции: (displaystyle y=x^{4},;y=cosfrac{x}{2},;y=lg |x|,;y=frac{sin x}{x}), а нечетными — функции (y=displaystyle frac{1}{x^{3}}, y=sin^{5}2x, y=x^{2}displaystyle operatorname{tg}frac{x}{2}, y=arcsin(sin x)).

График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.

На рис. 9.8 изображен график нечетной функции (y=x^{3}.)

---

Ограниченные и неограниченные функции.

Функцию f называют ограниченной снизу на множестве (Xsubset D(f)), если существует число (С_1) такое, что для любого (xin X) выполняется неравенство (f(x) geq C_1).

Используя символы (exists) и (forall), это определение можно записать так:
$$
exists C_{1}:forall xin Xrightarrow f(x)geq C_{1}.nonumber
$$
Аналогично функцию f называют ограниченной сверху на множестве (Xsubset D(f)), если
$$
exists C_{2}:forall xin Xrightarrow f(x)leq C_{2}.nonumber
$$

Функцию, ограниченную и сверху, и снизу на множестве X, называют ограниченной на этом множестве.

Функция f является ограниченной на множестве X тогда и только тогда, когда
$$
exists c>0:forall xin Xrightarrow|f(x)|leq C.label{ref4}
$$

Если неравенство (|f(x)|leq C) выполняется для всех (xin D(f)), говорят, что функция f ограничена.

Геометрически ограниченность функции f на множестве X означает, что график функции (y=f(x), xin X,) лежит в полосе ({-Cleq yleq C}.)

Например, функция (y=displaystyle sinfrac{1}{x}), определенная при (xinmathbb{R}, xneq 0), ограничена, так как
$$
|sinfrac{1}{x}|leq 1nonumber
$$

Функция f не ограничена на множестве X, если условие eqref{ref4} не выполняется, то есть
$$
forall C>0 exists x_{C}in X:|f(x_{C})|geq C.label{ref5}
$$

Если (X= D(f)) и выполнено условие eqref{ref5}, то говорят, что функция f не ограничена.

Пусть Y — множество значений, которые функция f принимает на множестве (Xsubset D(f)) . Тогда точную верхнюю грань множества Y называют точной верхней гранью функции f на множестве X и обозначают (sup_{xin X}{f(x)}), а точную нижнюю грань множества Y — точной нижней гранью функции f на множестве X и обозначают (displaystyle inf_{xin X}{f(x)}).
Если X=D(f), то в этих определениях указание на множество X опускают.

Пусть существует точка (x_{0}in Xsubset D(f)) такая, что для всех (xin X) выполняется неравенстве (f(x) leq f(x_0)).Тогда говорят, что функция f принимает в точке (x_{0}) наибольшее (максимальное) значение на множестве X и пишут (f(x_{0})=displaystyle max_{xin X}f(x)) В этом случае (displaystyle sup_{xin X}{f(x)}=f(x_{0}) )

Аналогично, если (exists x_{0}in Xsubset D(f):forall xin Xrightarrow f(x)geq f(x_{0})) , то говорят, что функция f принимает в точке (x_0) наименьшее (минимальное) значение на множестве X, и пишут (f(x_{0})=displaystyle min_{xin X}f(x)). В этом случае (displaystyle inf_{xin X}f(x)=f(x_{0})).

Максимальные и минимальные значения называют экстремальными.

Например, если (f(x)=sin x), то (displaystyle sup_{xinmathbb{R}}f(x)=max_{xinmathbb{R}}f(x)=f(x_{k})), где (x_{k}=displaystyle frac{pi}{2}+2pi k,;kinmathbb{Z},;inf_{xinmathbb{R}}f(x)=min_{xinmathbb{R}}{f}(x)=f(widetilde{x}_{k}),) где (widetilde{x}_{k}=-frac{pi}{2}+2pi k,;kinmathbb{Z}).

---

Монотонные функции.

Функцию (f) называют возрастающей (неубывающей) на множестве (Xsubset D(f)), если для любых точек (x_1 in X, x_{2}in X) таких, что (x_{1};<;x_{2}), выполняется неравенство ( f(x_1)leq f(х_2)).Если это неравенство является строгим ((f(x_{1});<;f(x_{2}))), то функцию (f) называют строго возрастающей на множестве (X).

Таким образом, функция (f) называется:

1. возрастающей (неубывающей) на множестве (X), если
   $$
   forall x_{1}in Xquad forall x_{2}in X:;x_{1};<;x_{2}rightarrow f(x_{1})leq f(x_{2});nonumber
   $$
2. строго возрастающей на множестве (X), если
   $$
   forall x_{1}in Xquad forall x_{2}in X:;x_{1};<;x_{2}rightarrow f(x_{1});<;f(x_{2}).nonumber
   $$

Аналогично функция (f) называется:

1. убывающей (невозрастающей) на множестве (X), если
   $$
   forall x_{1}in Xquadforall x_{2}in X:;x_{1};<;x_{2}rightarrow f(x_{1})geq f(x_{2});nonumber
   $$
2. строго убывающей на множестве (X), если
   $$
   forall x_{1}in Xquadforall x_{2}in X:;x_{1};<;x_{2}rightarrow f(x_{1})>f(x_{2}).nonumber
   $$

Убывающие и возрастающие функции объединяют названием монотонные, а строго возрастающие и строго убывающие — названием строго монотонные.

Если (X=D(f)), то в этих определениях указание на множество (X) обычно опускают.

---

Периодические функции.

Число (Tneq 0) называют периодом функции (f), если для любого (xin D(f)) значения (x+T) и (x-T) также принадлежат (D(f)) и выполняется равенство
$$
f(x-T)=f(x)=f(x+T).nonumber
$$
Функцию, имеющую период (T), называют периодической с периодом (Т).

Отметим, что если (T) — период функции (f), то каждое число вида (nT), где (ninmathbb{Z},;nneq 0), также является периодом этой функции.

Примерами периодических функций могут служить тригонометрические функции. При этом число (2pi) — наименьший положительный период функций (sin x,;cos x,) a (pi) — наименьший положительный период функций tg x и ctg x.

---

Обратная функция.

Пусть задана числовая функция (y=f(x),;xin D(f)). Тогда каждому числу (x_0in D(f))соответствует единственное число (y_{0}=f(x_{0})in E(f)) . Нередко приходится по заданному значению функции (y_0) находить соответствующее значение аргумента, то есть решать относительно (x) уравнение
$$
f(x)=y_{0},quad y_{0}in E(f).label{ref8}
$$

Это уравнение может иметь не одно, а несколько и даже бесконечно много решений. Решениями уравнения eqref{ref8} являются абсциссы всех точек, в которых прямая (y=y_0) пересекает график функции (y=f(x)).

Например, если (f(x)=x^{2}), то уравнение
$$
x^{2}=y_{0},quad y_{0}>0,nonumber
$$
имеет два решения: (x_{0}=displaystyle sqrt{y_0}) и ({widetilde x}_0=sqrt{y_0}). Если (f(x)=sin x), то уравнение
$$
sin{x}=y_{0},quad |y_{0}|leq 1,nonumber
$$
имеет бесконечно много решений вида (x_n=(-1)^{n}x_{0}+pi n), где (ninmathbb{Z};x_0) — одно из решений этого уравнения.

Однако существуют функции, для которых уравнение eqref{ref8} при каждом (y_{0}in E(f)) однозначно разрешимо, то есть имеет единственное решение (x_0in D(f)). Этим свойством обладают, например, следующие функции:

1. (f(x)=3x+4,;D(f)=mathbb{R});
2. (f(x)=x^{3},;D(f)=mathbb{R});
3. (f(x)=displaystyle frac{1}{x},quad D(f)={xinmathbb{R},;xneq 0}).

Если функция (f) такова, что при каждое значение (y_{0}in E(f)) она принимает только при одном значении (x_{0}in D(f)) , то эту функцию называют обратимой. Для такой функции уравнение
$$
f(x)=ynonumber
$$
можно при любом (уin Е(f))однозначно разрешить относительно (x), то есть каждому (yin Е(f)) соответствует единственное значение (xin D(f)).

Это соответствие определяет функцию, которую называют обратной к функции (f) и обозначают символом (f^{-1}).

Заметим, что прямая (y=y_0) для каждого (y_{0}in E(f)) пересекает график обратимой функции (y=f(x)) в единственной точке ((x_0,;y_0)), где (f(x_{0})=y_{0}).

Обозначая, как обычно, аргумент обратной функции буквой (x), а ее значения — буквой (y), обратную для (f) функцию записывают в виде
$$
y=f^{-1}(x),quad xin D(f^{-1}).nonumber
$$

Для упрощения записи вместо символа (f^{-1}) будем употреблять букву (g).

Отметим следующие свойства, которые показывают, как связаны данная функция и обратная к ней:

1. если (g) — функция, обратная к (f), то и (f) — функция, обратная к (g); при этом
   $$
   D(g)=E(f),quad E(g)=D(f),nonumber
   $$
   то есть область определения функции (g) совпадает с множеством значений функции (f) и наоборот;
2. для любого (xin D(f)) справедливо равенство
   $$
   g(f(x))=x,nonumber
   $$
   а для любого (хin Е(f)) справедливо равенство
   $$
   f(g(x))=x;nonumber
   $$
3. график функции (y=g(x)) симметричен графику функции (y=f(x)) относительно прямой (y=x);
4. если нечетная функция обратима, то обратная к ней функция также является нечетной;
5. если (f) — строго возрастающая (строго убывающая) функция, то она обратима, причем обратная к ней функция (g) также является строго возрастающей (строго убывающей).

Свойства 1) и 2) следуют непосредственно из определения обратной функции, 4) и 5) — из определений обратной и соответственно нечетной и строго монотонной функции.

Рассмотрим свойство 3). Пусть точка ((x_{0},y_{0})) принадлежит графику функции (y=f(x)), то есть (y_{0}=f(x_0)). Тогда (x_{0}=g(y_{0})), то есть точка ((x_{0},y_{0})) принадлежит графику обратной функции (g). Так как точки ((x_{0},y_{0})) и ((y_{0},x_{0})) симметричны относительно прямой (y=x) (рис. 9.9), то график функции (у=g(х)) симметричен графику функции относительно этой прямой.

На рис. 9.10 изображены графики взаимно обратных функций (y=x^{2},;xgeq 0), и (y=sqrt{x}), а на рис. 9.11 — графики взаимно обратных функций (y=x^{2},;xleq 0), и (y=-sqrt{x}).

---

Неявные функции. Параметрически заданные функции.

Пусть Е — множество точек (M(x,y)) плоскости (Oxy). Если каждой точке (Min E) поставлено в соответствие по некоторому правилу (закону) число z, то говорят, что на множестве E задана числовая функция от переменных (x) и (y), и пишут (z=f(x,y),;(x,y)in E).

Например, объем конуса (v) есть функция от переменных r и h, где r — радиус основания, h — высота конуса. Эта функция задается формулой (v=displaystyle frac{1}{3}pi r^{2}h).

Аналогично вводится понятие функции от трех и большего числа переменных.

Пусть функция (F(x,y)) определена на некотором множестве точек плоскости. Рассмотрим уравнение
$$
F(x,y)=0.label{ref9}
$$

Графиком уравнения eqref{ref9} в прямоугольной системе координат называют множество всех точек плоскости, координаты которых удовлетворяют этому уравнению. Например, графиком уравнения
$$
x^{2}+y^{2}-1=0label{ref10}
$$
является единичная окружность (рис. 9.12).

Естественной является постановка вопроса о том, можно ли уравнение eqref{ref9} однозначно разрешить относительно (y), то есть найти единственную функцию (y=f(x)) такую, что (F(x,f(x))=0), где (x) принимает значения из некоторого промежутка.

Обратимся к уравнению eqref{ref10}. Если (|x|>1), то не существует значений (y) таких, что пара чисел ((x,y)) удовлетворяет уравнению eqref{ref10}. Если (|x|leq 1), то, решая это уравнение относительно y, получаем
$$
y=pmsqrt{1-x^{2}}.label{ref11}
$$

Таким образом, если (|x|;<1), то из уравнения eqref{ref10} (y) выражается через (х) неоднозначно: каждому значению (x) соответствуют два различных значения (y), а именно (y_{1}=-sqrt{1-x^{2}}quad y_{2}=sqrt{1-x^{2}}quad (y_{1}=y_{2}) при (x=-1;x=1)).

Отсюда следует, что всякая функция (y=f(x)), которая в точке (xin[-1,1]) принимает либо значение (y_{1}), либо значение (y_{2}), удовлетворяет уравнению eqref{ref10}, то есть
$$
x^{2}+f^{2}(x)-1=0,quad xin[-1,1].nonumber
$$

Например, функция (y=f(x)), принимающая значение (y_1) при (xin[-1,alpha)), где (-1;<;alpha;<1), и значение (y_2) при (хin[alpha,1]), удовлетворяет уравнению eqref{ref10}. Меняя (alpha), можно получить бесконечное множество функций, удовлетворяющих на отрезке ([-1,1]) уравнению eqref{ref10}.

Будем теперь рассматривать уравнение eqref{ref10} в прямоугольнике
$$
K_{1}={(x,y):-1leq xleq 1,;0leq yleq 1}.nonumber
$$

В этом случае существует единственная функция (y=y_{1}=sqrt{1-x^{2}},;-1leq xleq 1), удовлетворяющая уравнению eqref{ref10} и такая, что (yin[0,1]). Эту функцию называют неявной функцией, определяемой уравнением eqref{ref10} в прямоугольнике (K_1).

Аналогично в прямоугольнике (K_{1}={(x,y):-1leq xleq 1,;-1leq yleq 0}) неявная функция, определяемая уравнением eqref{ref10}, задается формулой (y=y_{2}=-sqrt{1-x^{2}},;-1leq xleq 1).

Вернемся к уравнению eqref{ref9}. Пусть прямоугольник (K={(x,y):|x-x_{0}|leq a,;|y-у_0|leq b) содержится в области определения функции (F(х,у)), и пусть (F(х_0,y_0)=0). Если на отрезке (Delta=lceil x_{0}-a,x_{0}+arceil) существует единственная функция (y=f(x)) такая, что (f(x)inlceil y_0-b,y_0+brceil) и
$$
F(x,f(x))=0,quad xinDelta,nonumber
$$
то говорят, что уравнение eqref{ref9} определяет в прямоугольнике (K) переменную y как неявную функцию переменной (x).

Достаточные условия существования неявной функции и другие вопросы, связанные с неявными функциями, рассматриваются далее в параграфе 28.

Функция одной переменной может быть задана не только в явном виде (y=f(x)) или неявно уравнением (F(х,у)=0), но также параметрически. Этот способ задания состоит в следующем.

Пусть функции (x=varphi(t)) и (varphi(t)) определены на некотором множестве (E), и пусть (E_1) — множество значений функции (varphi). Предположим, что функция (varphi) обратима на множестве (E), и пусть (t=varphi^{-1}(x)) — обратная к ней функция. Тогда на множестве (E_1) определена сложная функция (y=psi(varphi^{-1}(x))=f(x)), которую называют параметрически заданной формулами (уравнениями) (х=varphi(t),quad y=psi(t)).

Например, уравнениях (x=cos t,;y=sin t), где (tinleft [0,displaystyle frac{pi}{2}right ]), определяют параметрически заданную функцию (y=f(x)). В данном случае (t=arccos x,;y=sin(arccos x)=sqrt{1-x^{2}}).

Сначала разберемся, какие значения может принимать функция целой части числа на рассматриваемом отрезке.

Если , то

Если принадлежит полуинтервалу , то , так как (), поэтому

---

Нетрудно догадаться, что точной нижней гранью в этом случае является число . Действительно, при любом из отрезка . Это видно по расшифровке выше. Помимо этого, не существует большей нижней границы, ведь тогда, взяв , получим противоречие определению нижней границы. По определению это обозначает, что — точная нижняя грань .

Немного сложнее, но все же достаточно просто догадаться, что точная верхняя грань равна . К этой грани стремится при стремлении к . Докажем это.

является верхней границей, потому что для любого из выполняется неравенство (на самом деле, в нашем случае выполняется даже строгое неравенство).

Рассмотрим теперь следующую последовательность -ов:

Каждый член этой последовательности находится в полуинтервале , на котором, как мы показали выше, .

Последовательность значений функции имеет вид:

Найдем, к чему она стремится:

Здесь мы воспользовались тем, что . Это элементарный предел (см. прото-задачу П-ссылка).

По определению это означает, что какое-бы число мы не взяли, всегда найдется бесконечно много значений функции, которые лежат в интервале . Это значит, что не существует верхней границы, которая была бы меньше . То есть, — наименьшая верхняя грань функции .