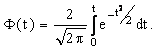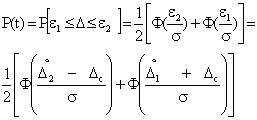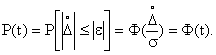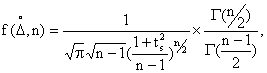Как найти границы доверительного интервала метрология

Наиболее
полный показатель точности – размер
интервала возможных погрешностей. Этот
интервал носит название доверительного.
Степень доверия тому,что погрешность
не выйдет за его пределы, определяется
доверительной
вероятностью.

абсолютная
погрешность,

t_p
– аргумент ф-ии вероятности: Рt=f(t_p)
X=

Нахождение
t_p
при заданном значении доверительной
вер-ти
р_t:

а)
для случая нормального распределения
пользуются таблицей Лапласа и находят
t_p;

б)
при числе измерений n<20
значение t_p
находят
по таблицам Стьюдента;

в)
при n>30
и неизвестном законе распределения
пользуются неравенством Чебышева,
вычисляя t_p
из уравнения: р_t=1-1/t_p²

Определив
t_p,
находят границы доверительного интервала
для случайной погрешности:
Окончательный результат записывают в
виде
при доверительной вероятности р_t.
рt=1-q,
q
– уровень значимости, если рt0,997
и q=0.003,
то событие считается достоверным.

24. Доверительный интервал: критерий Чебышева, область его применения

Доверительный
интервал
— это интервал, построенный с помощью
случайной выборки из распределения с
неизвестным параметром, такой, что он
содержит данный параметр с заданной
вероятностью.

При
n>30
и неизвестном законе распределения
пользуются неравенством Чебышева,
вычисляя
t_p
из уравнения:

р_t=1-1/t_p²

Определив
t_p,
находят границы доверительного интервала
для случайной погрешности:

Окончательный
результат записывают в виде
при доверительной вероятности р_t

26. Правило «трех сигм» в метрологии. Общая взаимосвязь величины доверительного интервала и вероятности отклонения отсчета от его математического ожидания

Правило
«трех сигм» в метрологии

Грубые
погрешности измерений (промахи) могут
сильно иска­зить
,
и доверительный интервал, поэтому их
исключение из серии измерений обязательно.
Обычно в ряду по­лученных результатов
они сразу видны, но в каждом конкретном
случае это не­обходимо доказать.
Существует ряд критериев для оценки
прома­хов.
Критерий
З
служит
для выявления и сиключения грубых
погрешностей и промахов. Применяется
этот критерий, если выборка результатов
измерений подчинятся нормальному закону
распределения и N>20…50
и более. В
этом случае считается, что результат,
возника­ющий с вероятностью Р
< 0,003,
нереален и его можно рассматривать как
промах, т. е. сомнительный результата
отбрасыва­ется, если
Величиныи
и вычисляют без учета х_i(результат
измерений, поставленный под сомнение).

—
приближенное значение

=
Σ
Qi-оценка
мат.ожидания

n→∞,

→m
(m
– истинное значение)

При
отсутствии систематической погрешности
Δс = 0

υi
= (Qi
—
)
→ Συi=0;
Συi=min

(υi
– случайная погрешность)

При
n→∞,

→m
можно рассчитать дисперсию.

(Q)=
σ=

Σ(Qi-)=
Σ
υi/(n-1)

=— оценка ср. квадр. Отклонения

(Q)-оценка
дисперсии.
(Q)=
=

=

28. Распределение Стьюдента в метрологии

Семейство
распределения Стьюдента в метрологии.
Распределение
Стьюдента используется для точечного
оценивания, построения доверительных
интервалов и тестирования гипотез,
касающихся неизвестного среднего…
выборки из нормального распределения.
Распределение Стьюдента в метрологии
применяют в методе серий. Этот метод
позволяет выявлять систематические
погрешности посредствам анализа серий
измерений. Если есть 2 ряда измерений
п₁
и п_2,
и их средние арифметические
и,
то вероятность того, что разностьявляется
случайной величиной, определяется
равенством,где

Величина
Р
определяется
по таблице Стьюдента.

Если
полученная вероятность Р
> 0,95,
то разность
носит систематический характер.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Доверительный интервал и доверительная вероятность

Наряду с точечными широко применяют интервальные оценки числовых характеристик случайных величин, выражающеся границами интервала, внутри которого с определенной вероятностью заключено истинное значение результата измерения. Вероятность того, что погрешность не выйдет за границы некоторого интервала, определяется по площади, ограниченной кривой распределения и границами этого интервала, отложенными по оси абсцисс (квантилями), что показано на рис. 1.10.

Рис.1.10.

Таким образом, интервал , за границы которого погрешность не выйдет с некоторой вероятностью, называется доверительным интервалом, а характеризующая его вероятность — доверительной вероятностью. Границы этого интервала называются доверительными значениями погрешности. При измерениях можно задаваться доверительным интервалом и по нему определять доверительную вероятность, либо, наоборот, по доверительной вероятности подсчитывать доверительный интервал. Чем больше доверительная вероятность, тем шире доверительный интервал; поэтому на практике обычно выбирают доверительную вероятность 0,95 и даже 0,90.

Доверительный интервал обычно выражают через относительную величину в долях среднего квадратического отклонения (“кратность”) . Для нормального закона доверительную вероятность определяют по значениям интеграла вероятности (функции Лапласа), который в математической справочной литературе обозначается и определяется

Зная доверительные границы и можно определить доверительную вероятность

Если значения доверительных границ и симметричны, т.е.

, то и .

Тогда

Для наиболее часто встречающихся значений доверительной вероятности в табл. 1.3 указаны соответствующие значения кратности.                                   Таблица 1.3

При нормальном законе распределения доверительный интервал имеет доверительную вероятность =0,9973, что означает, что из 370 случайных погрешностей только одна по абсолютному значению будет больше . На основании этого основан один из критериев грубых погрешностей, когда остаточная погрешность какого-либо результата измерения превышает значение , то этот результат считается промахом и исключается из ряда измерений.

Пример. Для известного числа измерений получены значения и . Определить вероятность того, что имеет место неравенство 1,261,28.

Так как , то 0,01/0,025=0,4. Используя таблицу интеграла вероятности, находим . Следовательно, около 30% общего числа измерений будут иметь случайную погрешность , не превышающую ±0,01.

Распределение Стьюдента

При малом числе повторных измерений 20 используется распределение случайных погрешностей, предложенное Стьюдентом. Плотность вероятности по этому закону зависит от значения случайной погрешности и от числа измерений:

где (,)-плотность вероятности случайной погрешности при заданном числе измерений ; -гамма-функция; s=/ — коэффициент Стьюдента (“кратность” случайной погрешности).

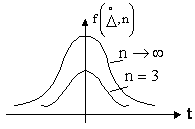
На рис.1.11 показаны графики кривых распределения случайных погрешностей по закону Стьюдента для двух значений . При →∞ распределение Стьюдента совпадает с нормальным, а при 20 всё более и более от него отличается.

Доверительный интервал и доверительная вероятность s также зависят от числа измерений. Соответствующие значения s при заданном значении и приводятся в таблицах.

Рис.1.11

Коэффициент Стьюдента s определяется из соотношения s= =,где -СКО ряда измерений, -доверительный интервал.

Пример. Для числа измерений =6 среднее арифметическое значения =35,4, а СКО ряда наблюдений. Определить доверительную вероятность s , если отличается от истинного значения на величину доверительного интервала т.е. 35,2≤35,6.

Определим коэффициент Стьюдента s==.По таблицам распределения Стьюдента находим = 0,9. Следовательно, случайная погрешность результата измерения в 90% случаев не выйдет за пределы доверительного интервала.

6.5. доверительная вероятность и доверительный интервал

Рассмотренные точечные оценки параметров распределения дают оценку в виде числа, наиболее близкого к значению неизвестного параметра. Такие оценки используют только при большом числе измерений. Чем меньше объем выборки, тем легче допустить ошибку при выборе параметра. Для практики важно не только получить точечную оценку, но и определить интервал, называемый доверительным, между границами которого с заданной дове рителъной вероятностью

где q — уровень значимости; хн, хв— нижняя и верхняя границы интервала, находится истинное значение оцениваемого параметра.

В общем случае доверительные интервалы можно строить на основе неравенства Чебышева. При любом законе распределения случайной величины, обладающей моментами первых двух порядков, верхняя граница вероятности попадания отклонения случайной величины х от центра распределения Хц в интервал tSx описывается неравенством Чебышева

где Sx — оценка СКО распределения; t — положительное число.

Для нахождения доверительного интервала не требуется знать закон распределения результатов наблюдений, но нужно знать оценку СКО. Полученные с помощью неравенства Чебышева интервалы оказываются слишком широкими для практики. Так, доверительной вероятности 0,9 для многих законов распределений соответствует доверительный интервал 1,6SX. Неравенство Чебышева дает в данном случае 3,16SX. В связи с этим оно не получило широкого распространения.

В метрологической практике используют главным образом кван-тильные оценки доверительного интервала. Под 100P-процентным квантилем хр понимают абсциссу такой вертикальной линии, слева от которой площадь под кривой плотности распределения равна Р%. Иначе говоря, квантиль — это значение случайной величины (погрешности) с заданной доверительной вероятностью Р. Например, медиана распределения является 50%-ным квантилем х0,5.

На практике 25и 75%-ный квантили принято называть сгибами, или квантилями распределения. Между ними заключено 50% всех возможных значений случайной величины, а остальные 50% лежат вне их. Интервал значений случайной величины х между х0 05 и х0 95 охватывает 90% всех ее возможных значений и называется интерквантильным промежутком с 90%-ной вероятностью. Его протяженность равна d0,9= х0,95 х0,05.

На основании такого подхода вводится понятие квантильных значений погрешности, т.е. значений погрешности с заданной доверительной вероятностью Р — границ интервала неопределенности ± DД = ± (хр х1-р)/2 = ± dp/2. На его протяженности встречается Р% значений случайной величины (погрешности), a q = (1Р)% общего их числа остаются за пределами этого интервала.

Для получения интервальной оценки нормально распределенной случайной величины необходимо:

• определить точечную оценку МО х̅ и СКО Sx случайной величины по формулам (6.8) и (6.11) соответственно;

• выбрать доверительную вероятность Р из рекомендуемого ряда значений 0,90; 0,95; 0,99;

• найти верхнюю хв и нижнюю хн границы в соответствии с уравнениями

полученными с учетом (6.1). Значения хн и хв определяются из таблиц значений интегральной функции распределения F(t) или функции Лапласа Ф(1).

Полученный доверительный интервал удовлетворяет условию

           (6.13)

где n — число измеренных значений; zp — аргумент функции Лапласа Ф(1), отвечающей вероятности Р/2. В данном случае zp называется квантильным множителем. Половина длины доверительного интервала  называется доверительной границей погрешности результата измерений.

Пример 6.1. Произведено 50 измерений постоянного сопротивления. Определить доверительный интервал для МО значения постоянного сопротивления, если закон распределения нормальный с параметрами mx = R = 590 Ом, Sx= 90 Ом при доверительной вероятности Р = 0,9.

Так как гипотеза о нормальности закона распределения не противоречит опытным данным, доверительный интервал определяется по формуле

Отсюда Ф(zр) = 0,45. Из таблицы, приведенной в приложении 1, находим, что zp= 1,65. Следовательно, доверительный интервал запишется в виде

  или 590 21 < R < 590 + 21. Окончательно 509 Ом < R < 611 Ом.

При отличии закона распределения случайной величины от нормального необходимо построить его математическую модель и определять доверительный интервал с ее использованием.

Рассмотренный способ нахождения доверительных интервалов справедлив для достаточно большого числа наблюдений n, когда s = Sx. Следует помнить, что вычисляемая оценка СКО Sx является лишь некоторым приближением к истинному значению s. Определение доверительного интервала при заданной вероятности оказывается тем менее надежным, чем меньше число наблюдений. Нельзя пользоваться формулами нормального распределения при малом числе наблюдений, если нет возможности теоретически на основе предварительных опытов с достаточно большим числом наблюдений определить СКО.

Расчет доверительных интервалов для случая, когда распределение результатов наблюдений нормально, но их дисперсия неизвестна, т.е. при малом числе наблюдений п, возможно выполнить с использованием распределения Стьюдента S(t,k). Оно описывает плотность распределения отношения (дроби Стьюдента):

где Q — истинное значение измеряемой величины. Величины х̅, Sx. и Sx̅ вычисляются на основании опытных данных и представляют собой точечные оценки МО, СКО результатов измерений и СКО среднего арифметического значения.

Вероятность того, что дробь Стьюдента в результате выполненных наблюдений примет некоторое значение в интервале (tp; + tp)

 (6.14)

где k — число степеней свободы, равное (п 1). Величины tp (называемые в данном случае коэффициентами Стьюдента), рассчитанные с помощью двух последних формул для различных значений доверительной вероятности и числа измерений, табулированы (см. таблицу в приложении 1). Следовательно, с помощью распределения Стьюдента можно найти вероятность того, что отклонение среднего арифметического от истинного значения измеряемой величины не превышает   

В тех случаях, когда распределение случайных погрешностей не является нормальным, все же часто пользуются распределением Стьюдента с приближением, степень которого остается неизвестной. Распределение Стьюдента применяют при числе измерений n < 30, поскольку уже при n = 20, …,30 оно переходит в нормальное и вместо уравнения (6.14) можно использовать уравнение (6.13). Результат измерения записывается в виде: ; P = Рд, где Рд — конкретное значение доверительной вероятности. Множитель t при большом числе измерений n равен квантильному множителю zp. При малом n он равен коэффициенту Стьюдента.

Полученный результат измерения не является одним конкретным числом, а представляет собой интервал, внутри которого с некоторой вероятностью Рд находится истинное значение измеряемой величины. Выделение середины интервала х вовсе не предполагает, что истинное значение ближе к нему, чем к остальным точкам интервала. Оно может быть в любом месте интервала, а с вероятностью 1 Рд даже вне его.

Пример 6.2. Определение удельных магнитных потерь для различных образцов одной партии электротехнической стали марки 2212 дало следующие результаты: 1,21; 1,17; 1,18; 1,13; 1,19; 1,14; 1,20 и 1,18 Вт/кг. Считая, что систематическая погрешность отсутствует, а случайная распределена по нормальному закону, требуется определить доверительный интервал при значениях доверительной вероятности 0,9 и 0,95. Для решения задачи использовать формулу Лапласа и распределение Стьюдента.

По формулам (6.8) в (6.11) находим оценки среднего арифметического значения и СКО результатов измерений. Они соответственно равны 1,18 и 0,0278 Вт/кг. Считая, что оценка СКО равна самому отклонению, находим:

Отсюда, используя значения функции Лапласа, приведенные в таблице приложения 1, определяем, что zp = 1,65. Для Р = 0,95 коэффициент zp =1,96. Доверительные интервалы, соответствующие Р = 0,9 и 0,95, равны 1,18 ± 0,016 и 1,18±0,019 Вт/кг.

В том случае, когда нет оснований считать, что СКО и его оценка равны, доверительный интервал определяется на основе распределения Стьюдента:

По таблице приложения 1 находим, что t0,9 = 1,9 и t0,95 = 2,37. Отсюда доверительные интервалы соответственно равны 1,18±0,019 и 1,18±0,023 Вт/кг.

Контрольные вопросы.

1. При каких условиях погрешность измерения может рассматриваться как случайная величина?

2. Перечислите свойства интегральной и дифференциальной функций распределения случайной величины.

3. Назовите числовые параметры законов распределения.

4. Каким образом может задаваться центр распределения?

5. Что такое моменты распределения? Какие из них нашли применение в метрологии?

6. Назовите основные классы распределений, используемых в метрологии.

7. Дайте характеристику распределениям, входящим в класс трапецеидальных распределений.

8. Что такое экспоненциальные распределения? Каковы их свойства и характеристики?

9. Что такое нормальное распределение? Почему оно играет особую роль в метрологии?

10. Что такое функция Лапласа и для чего она используется?

11. Как описывается и где используется семейство распределений Стьюдента?

12. Какие точечные оценки законов распределения вы знаете? Какие требования предъявляются к ним?

13. Что такое доверительный интервал? Какие «способы его задания вам известны?