Двойные интегралы используют в математике, механике, физике. С его помощью можно решить огромное количество непростых задач. Ниже приведено 10 примеров на двойные и тройные интегралы, которые в значительной степени облегчат подготовку к контрольной работе или экзамену. Примеры взяты из индивидуальной работы по высшей математики.
ВАРИАНТ — 12
Двойной интеграл
ЗАДАНИЕ 1.18 Изменить порядок интегрирования в двойном интеграле:
Решение: Сначала записываем область интегрирования, которая ограничена границами
где y=2/x — гипербола.
y=-x2-4x-3 — парабола с вершиной в точке S (-2;1), ветками вниз.
Чтобы знать, как расставить пределы интегрирования при изменении порядка интегрирования изобразим область интегрирования на плоскости
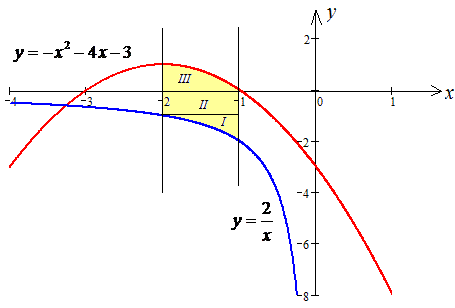
y=2/x, отсюда x=2/y; y=-x2-4x-3, отсюда 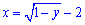
Из рисунка видим, что при изменении порядка интегрирования область необходимо разделить на три части: D=D1+D2+D3.
Расставим пределы интегрирования в каждой области:
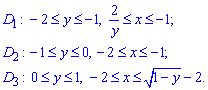
Изменяем порядок интегрирования функции
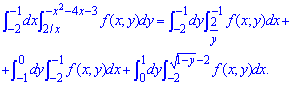
ЗАДАНИЕ 2.19 Найти площадь плоской фигуры, заданной следующими условиями, : y=2x, y=5, 2x-2y+3=0.
Решение: Прежде всего выполняем построение всех кривых, чтобы видеть как будут изменяться пределы интегрирования
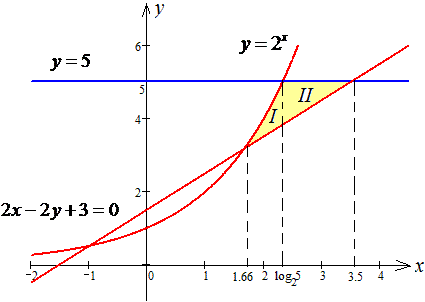
1 и 2
отсюда
Дальше точки пересечения 2 и 3 функций
отсюда
Напоследок пересечение 1 и 3 ф-й
отсюда
Заданную область будем разбивать на две области: D=D1+D2.
Расставим пределы для каждой из областей:
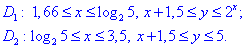
Через двойной интеграл находим площадь фигуры которая ограничена заданными кривыми, :
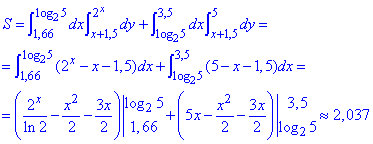
При округлении площадь криволинейной трапеции равна 2,037 единиц квадратных.
ЗАДАНИЕ 3.20 Найти двойной интеграл 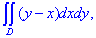
Решение: Найдем точки пересечения графиков заданных функций: y=x2-1 и y=3:
3=x2-1, x2-4=0, (x-2)(x+2)=0, x=-2; x=2.
Параболу и прямую изобразим графически
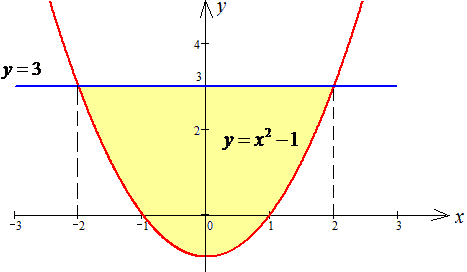
Вычислим двойной интеграл по области которая ограничена параболой и прямой:
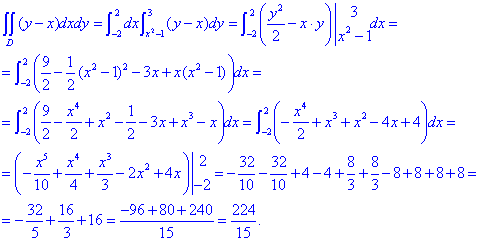
ЗАДАНИЕ 4.21 Найти двойной интеграл, используя полярные координаты:
Решение: Построим область интегрирования, которая ограничена кривыми
где 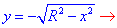
Получили круг с центром в точке O (0;0) и радиусом R (нижняя половина).
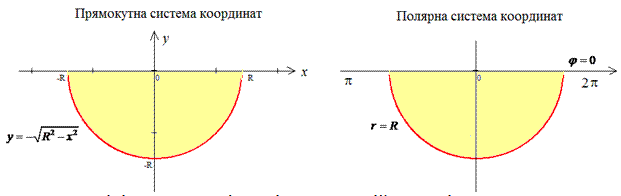
перейдем к полярной системе координат (СК).
При этом подынтегральную функцию следует умножить на якобиан перехода, который находим через определитель из производных:
Перепишем подинтегральную функцию в полярной СК :
Пределы интегрирования при переходе к полярной системе координат изменятся на следующие:
Вычислим двойной интеграл:
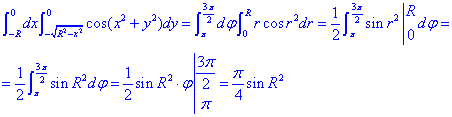
ЗАДАНИЕ 5.22 Вычислить площадь области D, ограниченной указанными линиями: D: x3=3y, y2=3x.
Решение: Найдем точку пересечения двух графиков 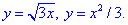
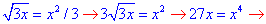
Графики кривой в декартовой системе координат имеет вид
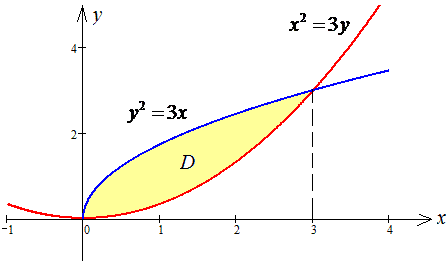
Найдем площадь криволинейной трапеции которая ограничена указанными линиями:
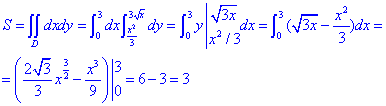
ЗАДАНИЕ 6.23 Используя двойной интеграл, вычислить, перейдя к полярным координатам, площадь плоской фигуры : (x2+y2)3=4a2xy (x2-y2).
Решение: Сначала построим чотирёх лепесток
Перейдем к полярной системе координат:
Якобиан перехода из предыдущих примеров равен I=r.
Найдем пределы интегрирования в новой системе координат
Переменные приобретают значение:
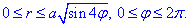
Расставляем пределы интегрирования в двойном интеграле, таким образом найдем четверть площади плоской фигуры.
Дальше результат умножим на 4:
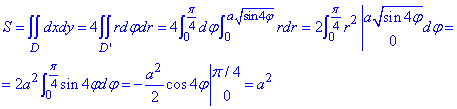
Внимательно проанализируйте как определять пределы интегрирования. Это тяжелее всего, что может быть в подобных задачах.
Как вычислить определенный интеграл, как правило, должны знать все студенты. Здесь лишь расширяется его приложение.
Тройной интеграл
ЗАДАНИЕ 8.25 Расставить пределы интегрирования в тройном интеграле 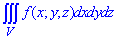
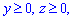
Нарисовать область интегрирования.
Решение: Уравнение поверхности в пространстве z=4 (x2+y2) — эллиптический параболоид.
График параболоида и проекция в декартовую плоскость тела имеют вид
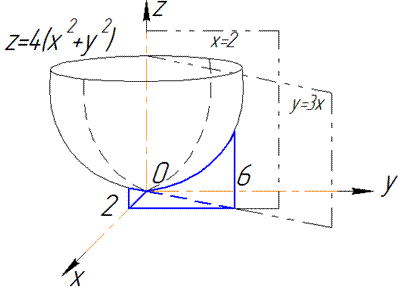
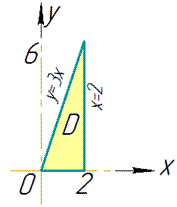
V:
Расставляем пределы интегрирования в соответствии с областью
ЗАДАНИЕ 9.6 Вычислить тройные интегралы:
где V:
Решение: Выполним построение области интегрирования
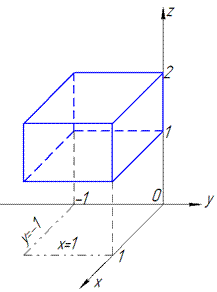
Вычисления не сложны, поэтому превращение в формуле проанализируйте самостоятельно.
6
ЛЕКЦИЯ 1
Двойные
интегралы. Определение
двойного интеграла и его свойства.
Повторные интегралы. Сведение двойных
интегралов к повторным. Расстановка
пределов интегрирования. Вычисление
двойных интегралов в декартовой системе
координат.
1.
ДВОЙНЫЕ ИНТЕГРАЛЫ
1.1.
Определение двойного интеграла
Двойной интеграл
представляет собой обобщение понятия
определенного интеграла на случай
функции двух переменных. В этом случае
вместо отрезка интегрирования будет
присутствовать какая-то плоская фигура.
Пусть
D
– некоторая замкнутая ограниченная
область, а f(x,y)
– произвольная функция, определенная
и ограниченная в этой области. Будем
предполагать, что границы области D
состоят из конечного числа кривых,
заданных уравнениями вида y=f(x)
или x=g(y),
где f(x)
и g(y)
– непрерывные функции.
Р
Рис.
1.1
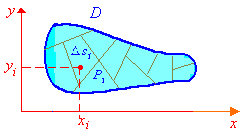
азобьем область D
произвольным образом на n
частей. Площадь i-го
участка обозначим символом si.
На каждом участке произвольно выберем
какую-либо точку Pi,
и пусть она в какой-либо фиксированной
декартовой системе имеет координаты
(xi,yi).
Составим интегральную
сумму для функции
f(x,y)
по области D,
для этого найдем значения функции во
всех точках Pi,
умножим их на площади соответствующих
участков si
и просуммируем все полученные результаты:
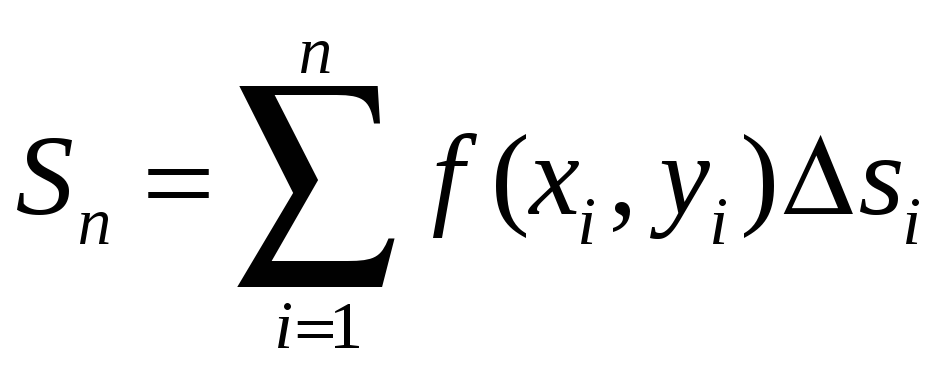
(1.1)
Назовем
диаметром
diam(G)
области G
наибольшее расстояние между граничными
точками этой области.
Двойным
интегралом
функции
f(x,y)
по
области
D
называется
предел, к которому стремится
последовательность интегральных
сумм
(1.1) при
неограниченном увеличении числа
разбиений
n
(при
этом
).
Это
записывают следующим образом
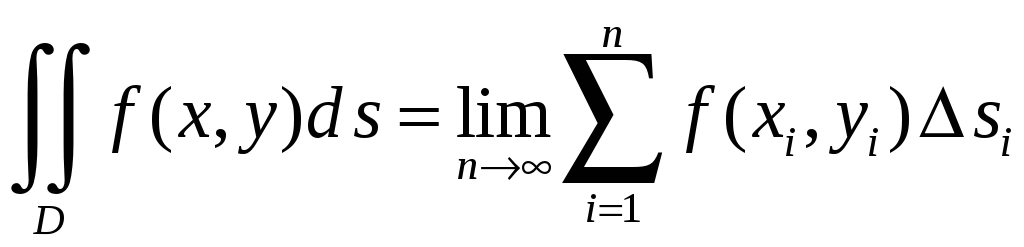
(1.2)
Заметим,
что, вообще говоря, интегральная сумма
для заданной функции и заданной области
интегрирования зависит от способа
разбиения области D
и выбора точек Pi.
Однако если двойной интеграл существует,
то это означает, что предел соответствующих
интегральных сумм уже не зависит от
указанных факторов. Для
того чтобы двойной интеграл существовал
(или, как говорят, чтобы
функция
f(x,y)
была
интегрируемой
в области D),
достаточно чтобы подынтегральная
функция была непрерывной
в заданной области интегрирования.
П
Рис.
1.2
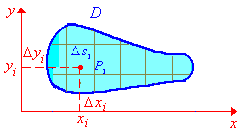
усть функция f(x,y)
интегрируема в области D.
Поскольку предел соответствующих
интегральных сумм для таких функций не
зависит от способа разбиения области
интегрирования, то разбиение можно
производить при помощи вертикальных
и горизонтальных линий. Тогда большинство
участков области D
будет иметь прямоугольный вид, площадь
которых равна si=xiyi.
Поэтому дифференциал площади можно
записать в виде ds=dxdy.
Следовательно, в
декартовой системе координат
двойные
интегралы можно
записывать в виде
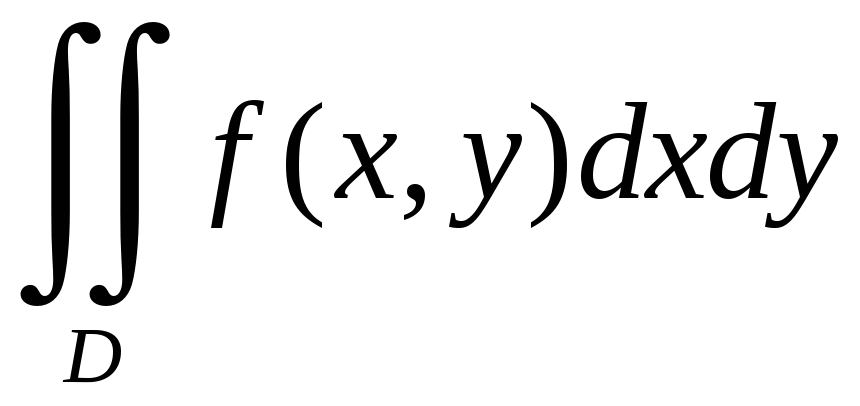
(1.3)
Замечание.
Если
подынтегральная функция
f(x,y)1,
то
двойной интеграл будет равен площади
области интегрирования:
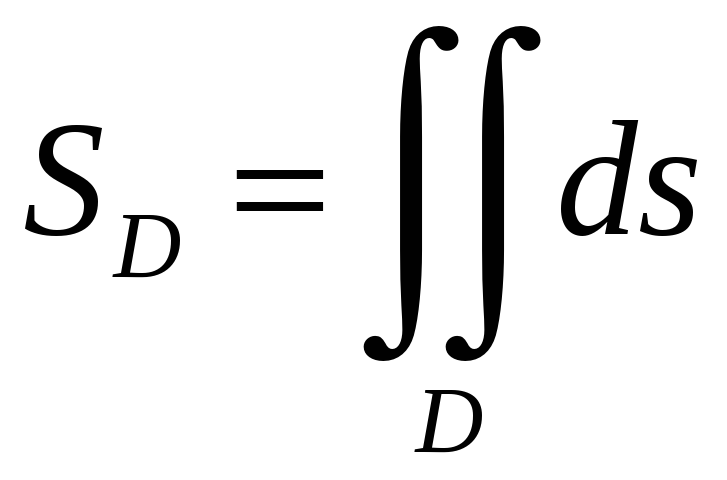
(1.4)
Отметим,
что двойные интегралы обладают такими
же свойствами, что и определенные
интегралы. Отметим некоторые из них.
Свойства
двойных интегралов.
10.
Линейное свойство.
Интеграл от
суммы функций равен сумме интегралов:
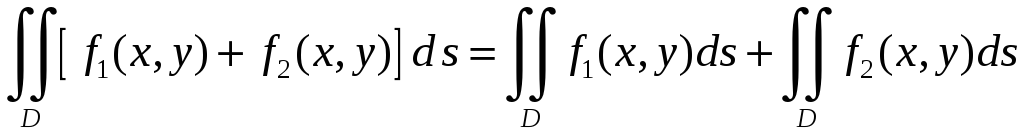
и
постоянный множитель можно выносить
за знак интеграла:

20.
Аддитивное свойство.
Если
область интегрирования D
разбить на две части, то двойной интеграл
будет равен сумме интегралов по каждой
этой части:
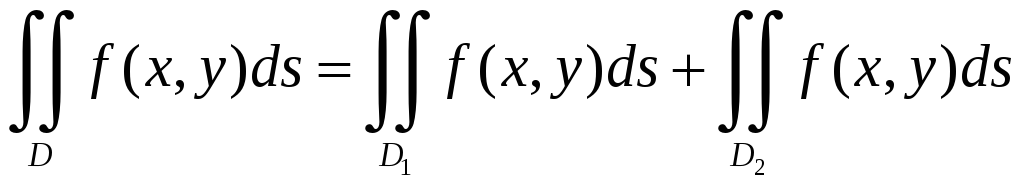
30.
Теорема о среднем.
Если
функция f(x,y)
непрерывна в области D,
то в этой области найдется такая точка
(),
что:
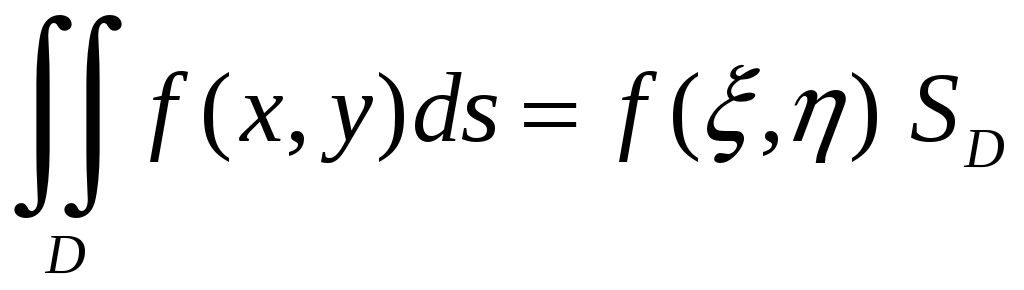
Далее возникает
вопрос: как вычисляются двойные интегралы?
Его можно вычислить приближенно, с этой
целью это разработаны эффективные
методы составления соответствующих
интегральных сумм, которые затем
вычисляются численно при помощи ЭВМ.
При аналитическом вычислении двойных
интегралов их сводят к двум определенным
интегралам.
1.2.
Повторные интегралы
Повторными
интегралами называются интегралы вида
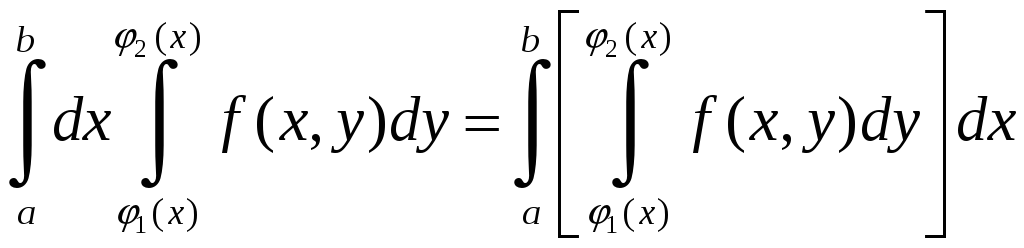
(1.5)
В
этом выражении сначала вычисляется
внутренний интеграл, т.е. производится
сначала интегрирование по переменной
y
(при этом переменная
x
считается постоянной величиной). В
результате интегрирования по y
получится некоторая функция по x:
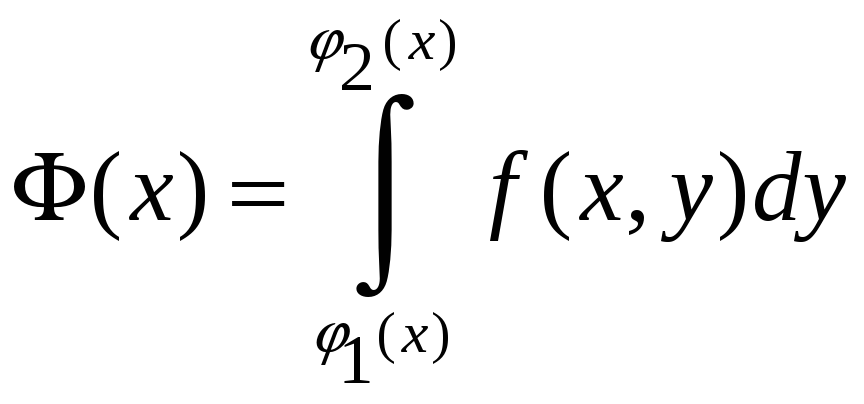
Затем
полученную функцию интегрируют по x:
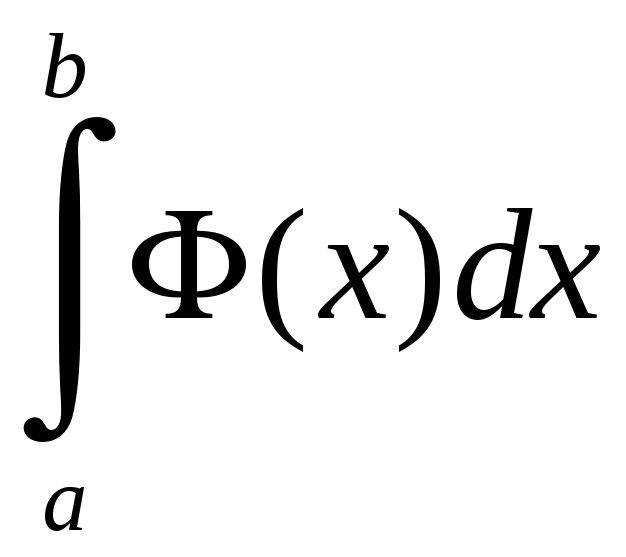
Пример
1.1.
Вычислить интегралы:
а)
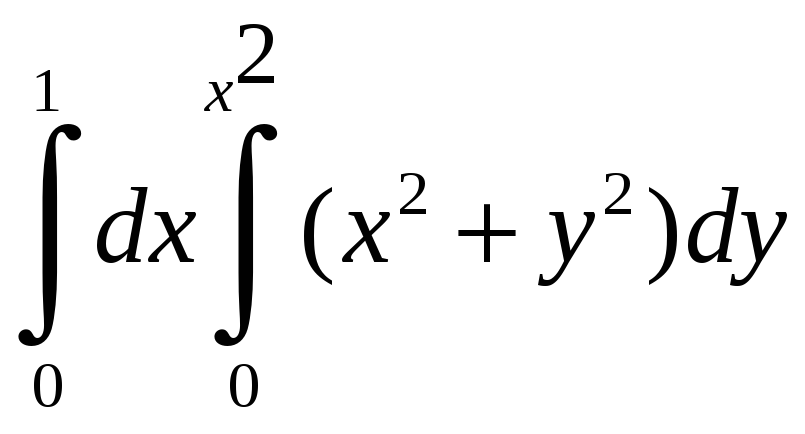
б)
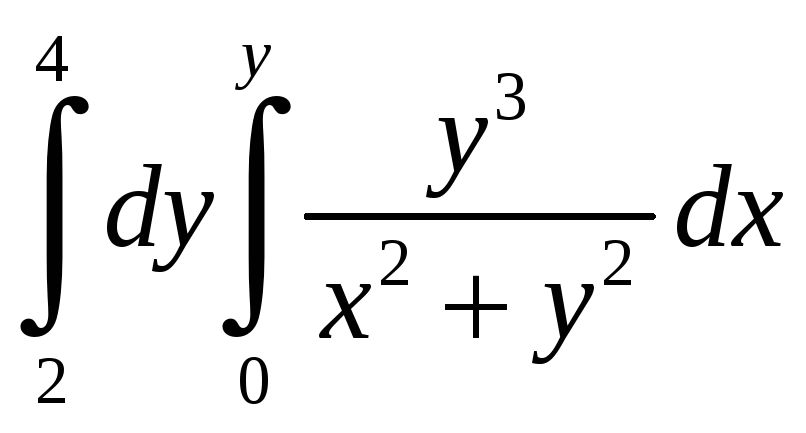
Решение.
а) Произведем интегрирование по y,
считая, что переменная x=const.
После этого вычисляем интеграл по x:
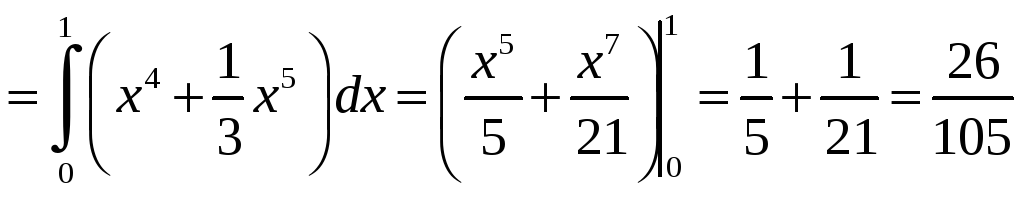
б)
Так как во внутреннем интеграле
интегрирование производится по переменной
x,
то y3
можно вынести во внешний интеграл как
постоянный множитель. Поскольку y2
во внутреннем интеграле считается
постоянной величиной, то этот интеграл
будет табличным. Производя последовательно
интегрирование по y
и x,
получаем
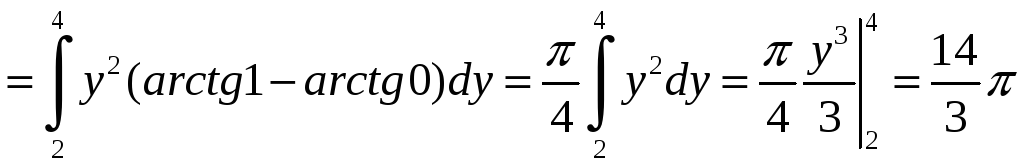
Между
двойными и повторными интегралами
существует взаимосвязь, но сначала
рассмотрим простые и сложные области.
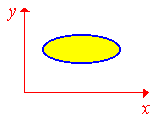
Область называется простой
в каком-либо направлении, если любая
прямая, проведенная в этом направлении,
пересекает границу области не более
чем в двух точках. В декартовой системе
координат обычно рассматривают
направления вдоль осей Ox
и Oy.
Если область является простой в обоих
направлениях, то говорят коротко –
простая область, без выделения направления.
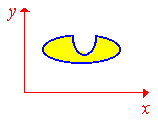
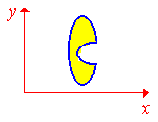
Если область не является простой, то
говорят, что она сложная.
Л
а
б
Рис.
1.4
юбую сложную область можно
представить в виде суммы простых
областей. Соответственно, любой двойной
интеграл можно представить в виде суммы
двойных интегралов по простым областям.
Поэтому в дальнейшем мы будем рассматривать,
в основном, только интегралы по простым
областям.
Теорема.
Если
область интегрирования D
– простая в направлении оси Oy
(см. рис.1.4а), то двойной интеграл можно
записать в виде повторного следующим
образом:
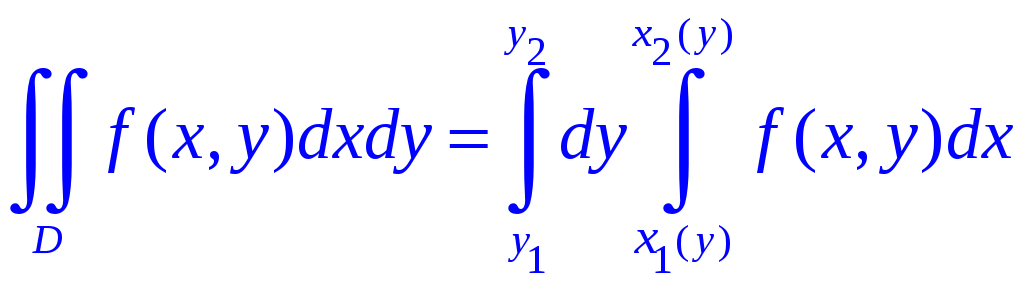
(1.6)
если
область интегрирования D
– простая в направлении оси Ox
(см. рис.1.4б), то двойной интеграл можно
записать в виде повторного следующим
образом:
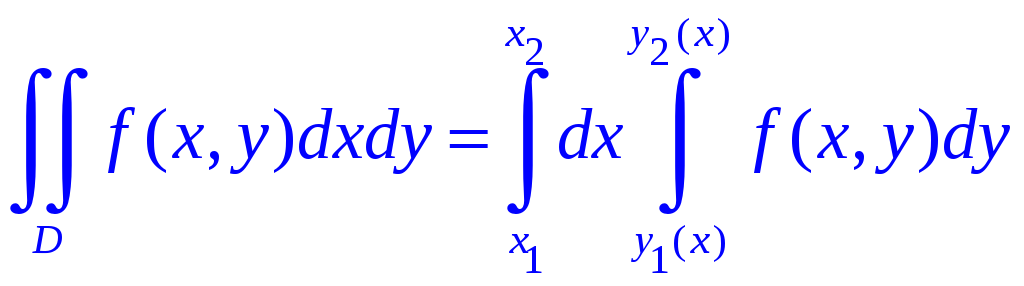
(1.7)
Е
|
простая |
простая |
простая |
сложная |
Рис.
1.3
сли область интегрирования
является правильной в обоих направлениях,
то можно произвольно выбирать вид
повторного интеграла, в зависимости от
простоты интегрирования.
1.3.
РАССТАНОВКА ПРЕДЕЛОВ ИНТЕГРИРОВАНИЯ
1.3.1.
Прямоугольная область интегрирования
П
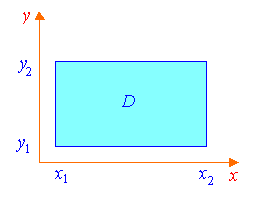
1.5
ри сведении двойных интегралов к
повторным, основная трудность возникает
при расстановке пределов во внутренних
интегралах. Наиболее просто это сделать
для прямоугольных областей (см. рис.
1.5).
Пример
1.2.
Вычислить двойной интеграл
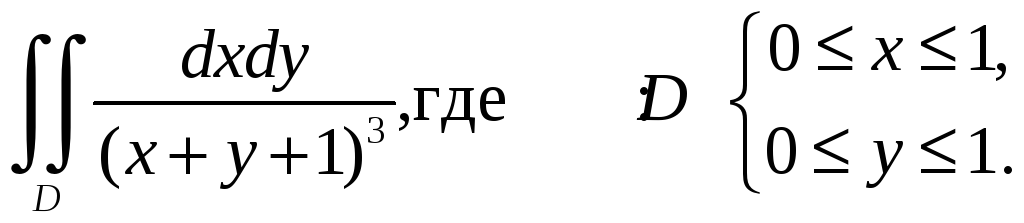
Решение.
Запишем двойной интеграл в виде
повторного:
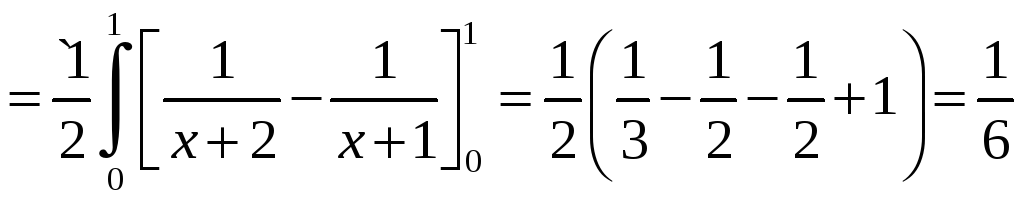
1.3.2.
Произвольная область интегрирования
Для того, чтобы
перейти от двойного интеграла к повторному
следует:
-
построить
область интегрирования; -
расставить
пределы в интегралах, при этом следует
помнить, что пределы внешнего интеграла
должны быть постоянными величинами
(т.е. числами) независимо от того, по
какой переменной вычисляется внешний
интеграл.
Пример
1.3.
Расставить пределы интегрирования в
соответствующих повторных интегралах
для двойного интеграла
,
если а)
б)
Р
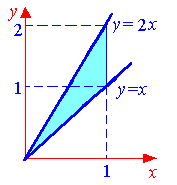
1.6
ешение.
а)
Изобразим область интегрирования D
(см. рис.1.6). Пусть интегрирование во
внешнем интеграле производится по
переменной x,
а во внутреннем – по y.
Расстановку
пределов всегда нужно начинать с внешнего
интеграла, в данном
случае с переменной x.
Из рисунка видно, что x
изменяется от 0 до 1, при
этом значения переменной y
будут изменяться от значений на прямой
y=x
до значений на прямой y=2x.
Таким образом, получаем
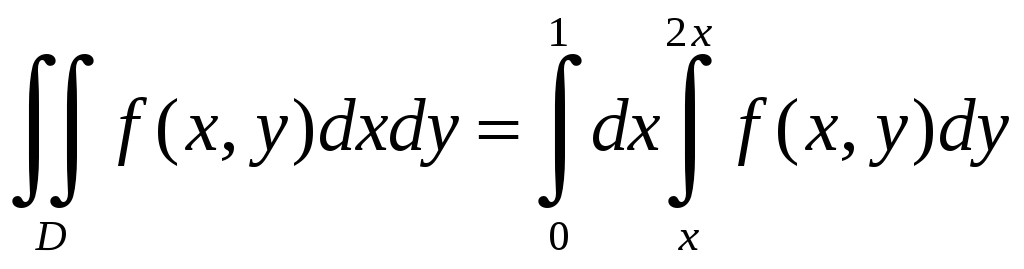
Пусть
теперь интегрирование во внешнем
интеграле производится по y,
а во внутреннем – по x.
В этом случае значения y
будут изменяться от 0 до 2. Однако тогда
верхняя граница изменений значений
переменной x
будет состоять из двух участков x=y/2
и x=1.
Это означает, что область интегрирования
нужно разбить на две части прямой y=1.
Тогда в первой области y
изменяется от 0 до 1, а x
от прямой x=y/2
до прямой x=y.
Во второй области y
изменяется от 1 до 2, а x
– от прямой x=y/2
до прямой x=1.
В результате получим
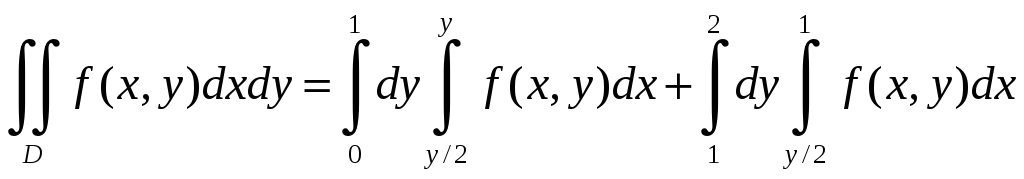
б
Рис.
1.7
) Построим область
интегрирования D
(см. рис.1.7). Пусть во внешнем интеграле
интегрирование производится по x,
а во внутреннем – по y.
В этом случае при изменении x
от –1 до 1 изменения переменной y
сверху будут ограничены двумя линиями:
окружностью и прямой. На отрезке [–1;0]
y
изменяется от y=0
до
;
на отрезке [0;1] переменная y
изменяется от y=0
до y=1–x.
Таким образом,
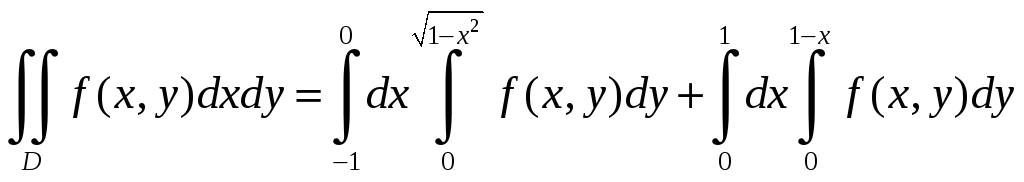
Пусть
теперь во внешнем интеграле интегрирование
производится по y,
а во внутреннем – по x.
В этом случае y
будет изменяться от 0 до 1, а переменная
x
– от дуги окружности
до
прямой x=1–y.
В результате получим
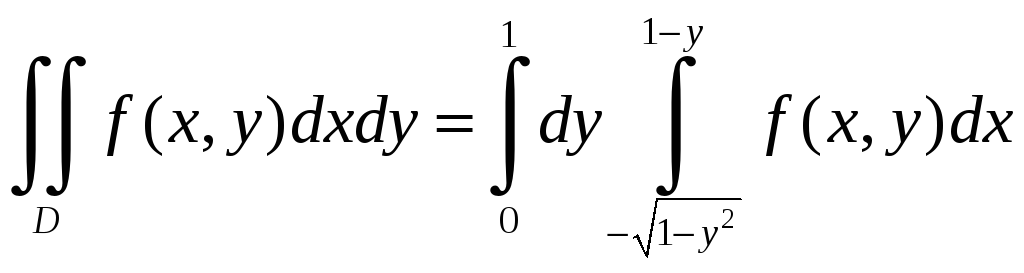
Данные примеры
показывают, как важно правильно выбирать
порядок интегрирования.
Пример
1.4.
Изменить порядок интегрирования
а)
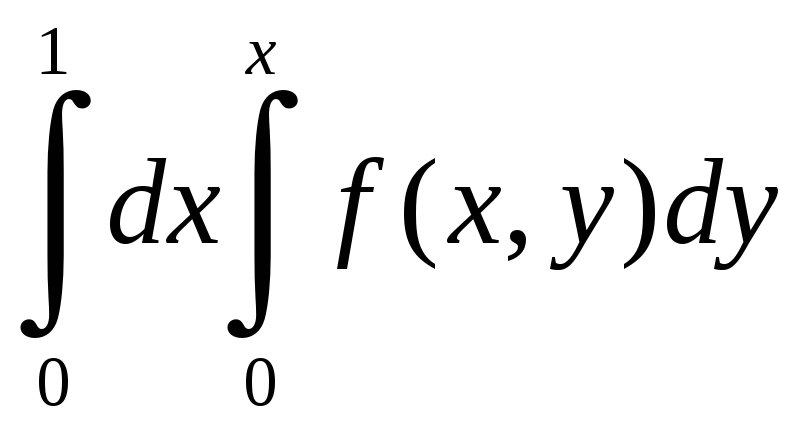
б)
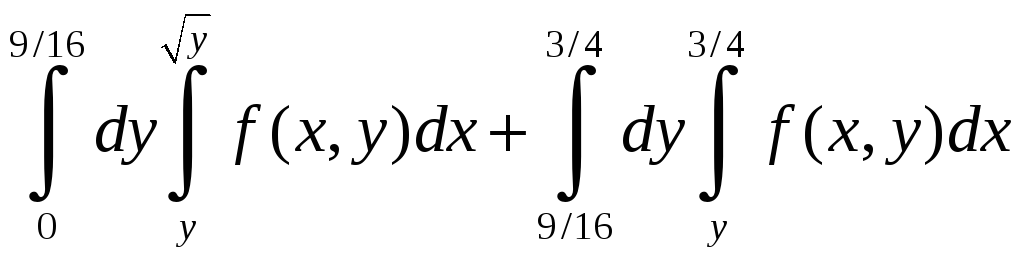
Р
1.8
ешение.
а)
Построим область интегрирования. На
отрезке [0;1] для x
переменная y
изменяется от прямой y=0
до прямой y=x.
В результате получается следующая
область интегрирования (см. рис.1.8). На
основании построенного рисунка,
расставляем пределы интегрирования
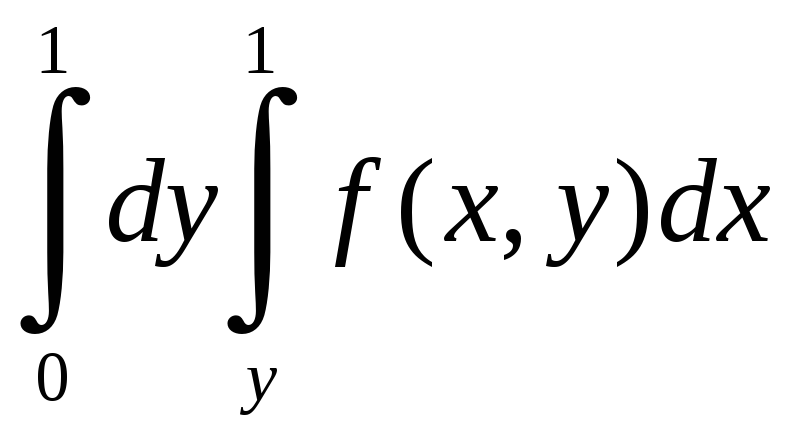
б)
Построим область интегрирования. На
отрезке [0;9/16] для y
переменная x
изменяется от прямой x=y
до параболы
;
на отрезке [9/16;3/4] – от прямой x=y
до прямой x=3/4.
В результате получается следующая
область интегрирования (см. рис.1.9). На
основании построенного рисунка,
расставляем пределы интегрирования,
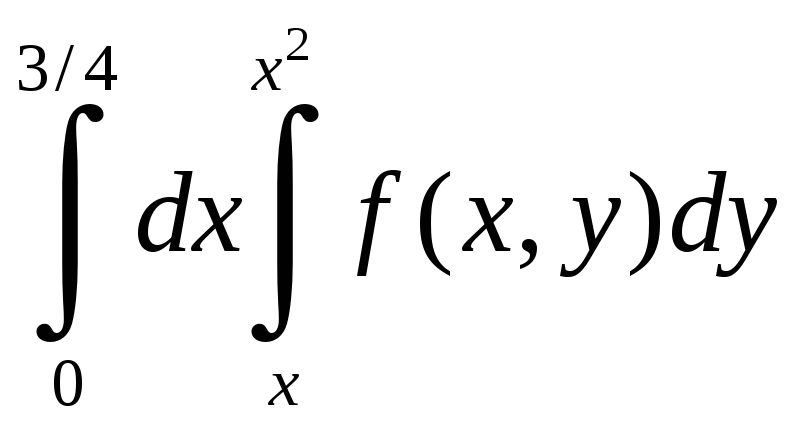
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Занятие 27. Тема «Двойной интеграл и его свойства. Приложение двойного интеграла»
План лекции:
-
Понятие двойного интеграла
-
Свойства двойного интеграла
-
Правила вычисления двойного интеграла
Понятие двойного интеграла
Определение: Двойной интеграл представляет собой обобщение понятия определенного интеграла на случай функции двух переменных. В этом случае вместо отрезка интегрирования будет присутствовать какая-то плоская фигура.
Двойной интеграл в общем виде записывается следующим образом:
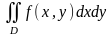
– знак двойного интеграла;
D – область интегрирования (плоская фигура);
f(x;y) – подынтегральная функция двух переменных;
dx, dy – элементы площади интегрирования.
Пусть D – некоторая замкнутая ограниченная область, а f(x,y) – произвольная функция, определенная и ограниченная в этой области. Будем предполагать, что границы области D состоят из конечного числа кривых, заданных уравнениями вида y=f(x) или x=g(y), где f(x) и g(y) – непрерывные функции.
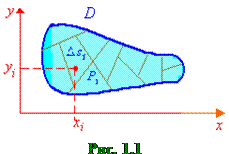
Свойства двойного интеграла
-
Если С – числовая константа, то
,
-
-
Если область D “разбита” на области D1 и D2, то
-
.
Правила вычисления двойного интеграла
-
Чтобы вычислить двойной интеграл, нужно для начала построить область D в системе координат и определить границы этой области по оси Ох и по оси Оу. Затем выбрать один из видов области интегрирования по правилу 2, подставить в функцию и вычислить двойной интеграл по 3 правилу.
-
Различают два основных вида области интегрирования.
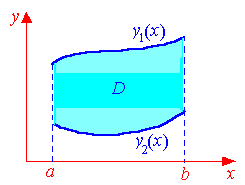
-
Область интегрирования D ограничена слева и справа прямыми х=а и х=b (ab), а снизу и сверху – непрерывными кривыми y=
и y=
(
).
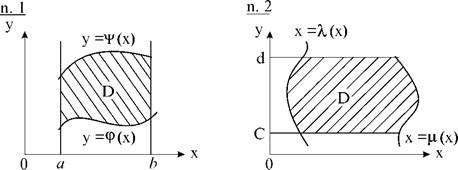
Для такой области интеграл вычисляется следующим образом 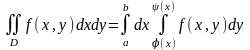
-
Область интегрирования D ограничена снизу и сверху прямыми у=с и y=d (cd), а слева и справа – непрерывными кривыми x=
и y=
(
)

Для такой области интеграл вычисляется следующим образом 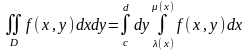
-
При вычислении двойного интеграла сначала вычисляется внутренний интеграл, используя формулу Ньютона-Лейбница, считая одну из переменных постоянным числом:
-
здесь х считается постоянным числом.
-
здесь у считается постоянным числом.
Затем, вычисляется внешний интеграл также по формуле Ньютона-Лейбница.
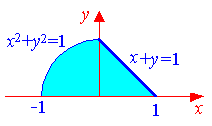
Пример1. Вычислить двойной интеграл , где
Решение. 1. Строим область интегрирования D
2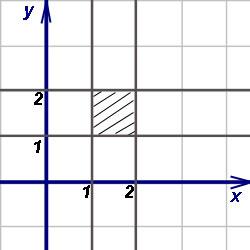
3. Выбираем вид области интегрирования .
Вычисляем внутренний (правый) интеграл, считая у — числом, которое можно вынести за знак интеграла. Получаем 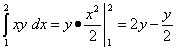
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
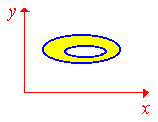
Пример 2. Вычислить двойной интеграл ,
где .
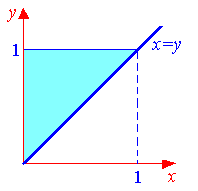
Решение. 1. Строим область интегрирования D
2. Находим границы области, то есть пределы интегрирования 1xy
3. Выбираем вид области интегрирования
Вычисляем внутренний (правый) интеграл, считая х — число. Получаем.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Ответить на контрольные вопросы:
-
Что называется двойным интегралом?
-
Перечислите основные свойства двойного интеграла.
-
На какие виды делится область интегрирования?
-
Каким образом вычисляется двойной интеграл?
-
Что делать с переменной, если она в интеграле не является интегрируемой?
-
Пользуясь учебником П.Е. Данко «Высшая математика в упражнениях и задачах» часть 2, разобрать №4 стр.8 рис.3, выписать в тетрадь.
Выполненное задание отправить на адрес электронной почты преподавателя. Имя файла – фамилия студента и номер занятия. (например Петров-27)

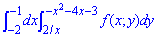
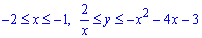
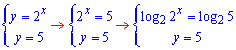
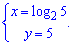
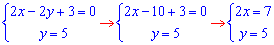
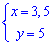
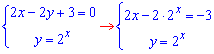
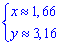
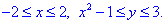
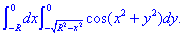
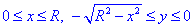
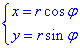
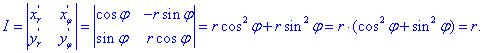
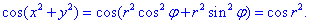
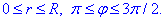
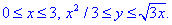
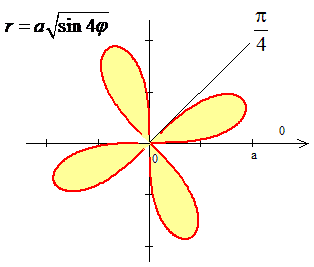
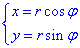
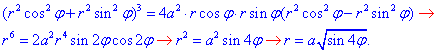
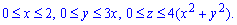
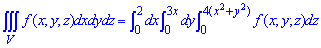
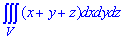
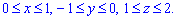
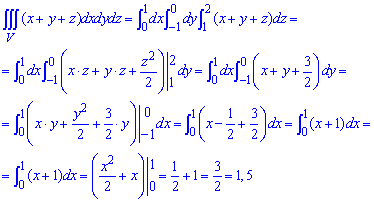
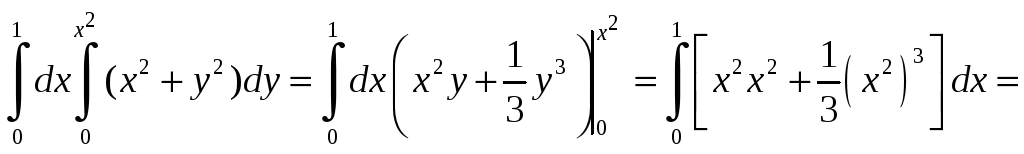
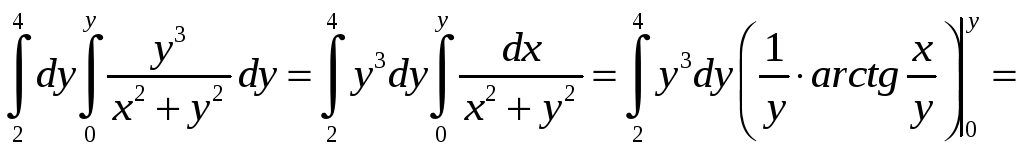

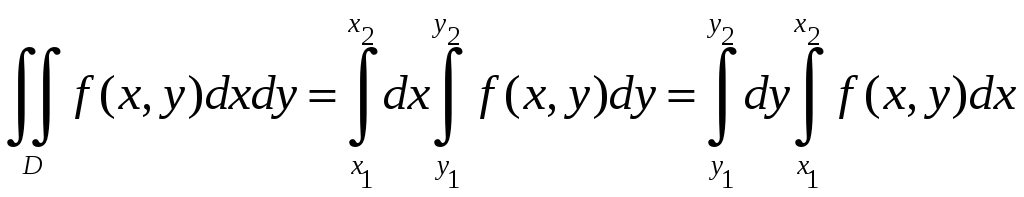
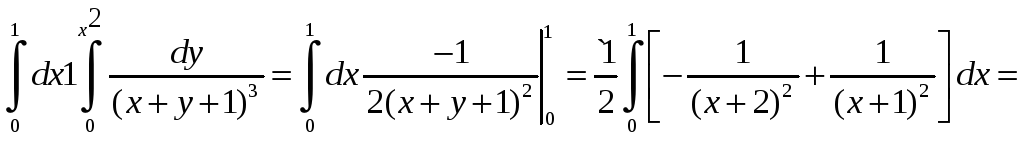

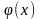 и y=
и y=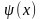 (
(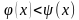 ).
). 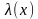 и y=
и y=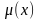 (
(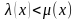 )
)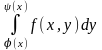 здесь х считается постоянным числом.
здесь х считается постоянным числом.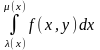 здесь у считается постоянным числом.
здесь у считается постоянным числом.