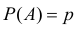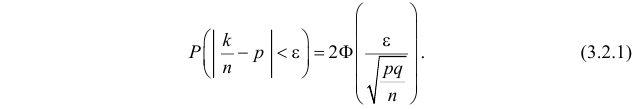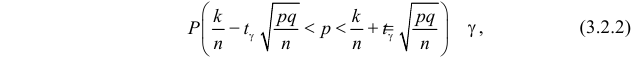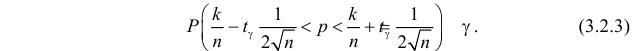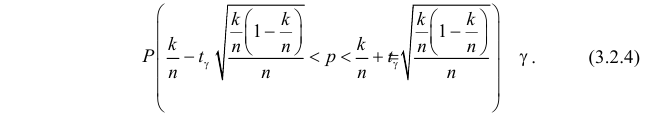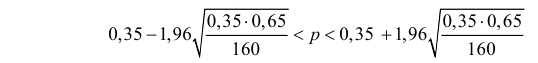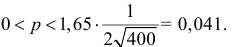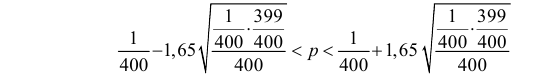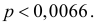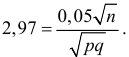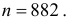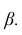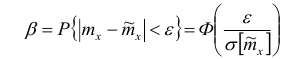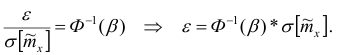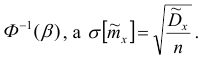From Wikipedia, the free encyclopedia
Probability bounds analysis (PBA) is a collection of methods of uncertainty propagation for making qualitative and quantitative calculations in the face of uncertainties of various kinds. It is used to project partial information about random variables and other quantities through mathematical expressions. For instance, it computes sure bounds on the distribution of a sum, product, or more complex function, given only sure bounds on the distributions of the inputs. Such bounds are called probability boxes, and constrain cumulative probability distributions (rather than densities or mass functions).
This bounding approach permits analysts to make calculations without requiring overly precise assumptions about parameter values, dependence among variables, or even distribution shape. Probability bounds analysis is essentially a combination of the methods of standard interval analysis and classical probability theory. Probability bounds analysis gives the same answer as interval analysis does when only range information is available. It also gives the same answers as Monte Carlo simulation does when information is abundant enough to precisely specify input distributions and their dependencies. Thus, it is a generalization of both interval analysis and probability theory.
The diverse methods comprising probability bounds analysis provide algorithms to evaluate mathematical expressions when there is uncertainty about the input values, their dependencies, or even the form of mathematical expression itself. The calculations yield results that are guaranteed to enclose all possible distributions of the output variable if the input p-boxes were also sure to enclose their respective distributions. In some cases, a calculated p-box will also be best-possible in the sense that the bounds could be no tighter without excluding some of the possible distributions.
P-boxes are usually merely bounds on possible distributions. The bounds often also enclose distributions that are not themselves possible. For instance, the set of probability distributions that could result from adding random values without the independence assumption from two (precise) distributions is generally a proper subset of all the distributions enclosed by the p-box computed for the sum. That is, there are distributions within the output p-box that could not arise under any dependence between the two input distributions. The output p-box will, however, always contain all distributions that are possible, so long as the input p-boxes were sure to enclose their respective underlying distributions. This property often suffices for use in risk analysis and other fields requiring calculations under uncertainty.
History of bounding probability[edit]
The idea of bounding probability has a very long tradition throughout the history of probability theory. Indeed, in 1854 George Boole used the notion of interval bounds on probability in his The Laws of Thought.[1][2] Also dating from the latter half of the 19th century, the inequality attributed to Chebyshev described bounds on a distribution when only the mean and variance of the variable are known, and the related inequality attributed to Markov found bounds on a positive variable when only the mean is known. Kyburg[3] reviewed the history of interval probabilities and traced the development of the critical ideas through the 20th century, including the important notion of incomparable probabilities favored by Keynes.
Of particular note is Fréchet’s derivation in the 1930s of bounds on calculations involving total probabilities without dependence assumptions. Bounding probabilities has continued to the present day (e.g., Walley’s theory of imprecise probability.[4])
The methods of probability bounds analysis that could be routinely used in
risk assessments were developed in the 1980s. Hailperin[2] described a computational scheme for bounding logical calculations extending the ideas of Boole. Yager[5] described the elementary procedures by which bounds on convolutions can be computed under an assumption of independence. At about the same time, Makarov,[6] and independently, Rüschendorf[7] solved the problem, originally posed by Kolmogorov, of how to find the upper and lower bounds for the probability distribution of a sum of random variables whose marginal distributions, but not their joint distribution, are known. Frank et al.[8] generalized the result of Makarov and expressed it in terms of copulas. Since that time, formulas and algorithms for sums have been generalized and extended to differences, products, quotients and other binary and unary functions under various dependence assumptions.[9][10][11][12][13][14]
Arithmetic expressions[edit]
Arithmetic expressions involving operations such as additions, subtractions, multiplications, divisions, minima, maxima, powers, exponentials, logarithms, square roots, absolute values, etc., are commonly used in risk analyses and uncertainty modeling. Convolution is the operation of finding the probability distribution of a sum of independent random variables specified by probability distributions. We can extend the term to finding distributions of other mathematical functions (products, differences, quotients, and more complex functions) and other assumptions about the intervariable dependencies. There are convenient algorithms for computing these generalized convolutions under a variety of assumptions about the dependencies among the inputs.[5][9][10][14]
Mathematical details[edit]
Let 

A p-box is a quintuple
where 


If a function satisfies all the conditions above it is said to be inside the p-box. In some cases, there may be no information about the moments or distribution family other than what is encoded in the two distribution functions that constitute the edges of the p-box. Then the quintuple representing the p-box ![{displaystyle {B_{1},B_{2},[-infty ,infty ],[0,infty ],mathbb {D} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/639f77fff8f6ce0293698932b7b7ad4fbe3a090f)
The notation 

Let us generalize the tilde notation for use with p-boxes. We will write X ~ B to mean that X is a random variable whose distribution function is unknown except that it is inside B. Thus, X ~ F ∈ B can be contracted to X ~ B without mentioning the distribution function explicitly.
If X and Y are independent random variables with distributions F and G respectively, then X + Y = Z ~ H given by
This operation is called a convolution on F and G. The analogous operation on p-boxes is straightforward for sums. Suppose
If X and Y are stochastically independent, then the distribution of Z = X + Y is inside the p-box
Finding bounds on the distribution of sums Z = X + Y without making any assumption about the dependence between X and Y is actually easier than the problem assuming independence. Makarov[6][8][9] showed that
These bounds are implied by the Fréchet–Hoeffding copula bounds. The problem can also be solved using the methods of mathematical programming.[13]
The convolution under the intermediate assumption that X and Y have positive dependence is likewise easy to compute, as is the convolution under the extreme assumptions of perfect positive or perfect negative dependency between X and Y.[14]
Generalized convolutions for other operations such as subtraction, multiplication, division, etc., can be derived using transformations. For instance, p-box subtraction A − B can be defined as A + (−B), where the negative of a p-box B = [B1, B2] is [B2(−x), B1(−x)].
Logical expressions[edit]
Logical or Boolean expressions involving conjunctions (AND operations), disjunctions (OR operations), exclusive disjunctions, equivalences, conditionals, etc. arise in the analysis of fault trees and event trees common in risk assessments. If the probabilities of events are characterized by intervals, as suggested by Boole[1] and Keynes[3] among others, these binary operations are straightforward to evaluate. For example, if the probability of an event A is in the interval P(A) = a = [0.2, 0.25], and the probability of the event B is in P(B) = b = [0.1, 0.3], then the probability of the conjunction is surely in the interval
- P(A & B) = a × b
-
-
- = [0.2, 0.25] × [0.1, 0.3]
- = [0.2 × 0.1, 0.25 × 0.3]
- = [0.02, 0.075]
-
-
so long as A and B can be assumed to be independent events. If they are not independent, we can still bound the conjunction using the classical Fréchet inequality. In this case, we can infer at least that the probability of the joint event A & B is surely within the interval
- P(A & B) = env(max(0, a+b−1), min(a, b))
-
-
- = env(max(0, [0.2, 0.25]+[0.1, 0.3]−1), min([0.2, 0.25], [0.1, 0.3]))
- = env([max(0, 0.2+0.1–1), max(0, 0.25+0.3–1)], [min(0.2,0.1), min(0.25, 0.3)])
- = env([0,0], [0.1, 0.25])
- = [0, 0.25]
-
-
where env([x1,x2], [y1,y2]) is [min(x1,y1), max(x2,y2)]. Likewise, the probability of the disjunction is surely in the interval
- P(A v B) = a + b − a × b = 1 − (1 − a) × (1 − b)
-
-
- = 1 − (1 − [0.2, 0.25]) × (1 − [0.1, 0.3])
- = 1 − [0.75, 0.8] × [0.7, 0.9]
- = 1 − [0.525, 0.72]
- = [0.28, 0.475]
-
-
if A and B are independent events. If they are not independent, the Fréchet inequality bounds the disjunction
- P(A v B) = env(max(a, b), min(1, a + b))
-
-
- = env(max([0.2, 0.25], [0.1, 0.3]), min(1, [0.2, 0.25] + [0.1, 0.3]))
- = env([0.2, 0.3], [0.3, 0.55])
- = [0.2, 0.55].
-
-
It is also possible to compute interval bounds on the conjunction or disjunction under other assumptions about the dependence between A and B. For instance, one might assume they are positively dependent, in which case the resulting interval is not as tight as the answer assuming independence but tighter than the answer given by the Fréchet inequality. Comparable calculations are used for other logical functions such as negation, exclusive disjunction, etc. When the Boolean expression to be evaluated becomes complex, it may be necessary to evaluate it using the methods of mathematical programming[2] to get best-possible bounds on the expression. A similar problem one presents in the case of probabilistic logic (see for example Gerla 1994). If the probabilities of the events are characterized by probability distributions or p-boxes rather than intervals, then analogous calculations can be done to obtain distributional or p-box results characterizing the probability of the top event.
Magnitude comparisons[edit]
The probability that an uncertain number represented by a p-box D is less than zero is the interval Pr(D < 0) = [F(0), F̅(0)], where F̅(0) is the left bound of the probability box D and F(0) is its right bound, both evaluated at zero. Two uncertain numbers represented by probability boxes may then be compared for numerical magnitude with the following encodings:
- A < B = Pr(A − B < 0),
- A > B = Pr(B − A < 0),
- A ≤ B = Pr(A − B ≤ 0), and
- A ≥ B = Pr(B − A ≤ 0).
Thus the probability that A is less than B is the same as the probability that their difference is less than zero, and this probability can be said to be the value of the expression A < B.
Like arithmetic and logical operations, these magnitude comparisons generally depend on the stochastic dependence between A and B, and the subtraction in the encoding should reflect that dependence. If their dependence is unknown, the difference can be computed without making any assumption using the Fréchet operation.
Sampling-based computation[edit]
Some analysts[15][16][17][18][19][20] use sampling-based approaches to computing probability bounds, including Monte Carlo simulation, Latin hypercube methods or importance sampling. These approaches cannot assure mathematical rigor in the result because such simulation methods are approximations, although their performance can generally be improved simply by increasing the number of replications in the simulation. Thus, unlike the analytical theorems or methods based on mathematical programming, sampling-based calculations usually cannot produce verified computations. However, sampling-based methods can be very useful in addressing a variety of problems which are computationally difficult to solve analytically or even to rigorously bound. One important example is the use of Cauchy-deviate sampling to avoid the curse of dimensionality in propagating interval uncertainty through high-dimensional problems.[21]
Relationship to other uncertainty propagation approaches[edit]
PBA belongs to a class of methods that use imprecise probabilities to simultaneously represent aleatoric and epistemic uncertainties. PBA is a generalization of both interval analysis and probabilistic convolution such as is commonly implemented with Monte Carlo simulation. PBA is also closely related to robust Bayes analysis, which is sometimes called Bayesian sensitivity analysis. PBA is an alternative to second-order Monte Carlo simulation.
Applications[edit]
P-boxes and probability bounds analysis have been used in many applications spanning many disciplines in engineering and environmental science, including:
- Engineering design[22]
- Expert elicitation[23]
- Analysis of species sensitivity distributions[24]
- Sensitivity analysis in aerospace engineering of the buckling load of the frontskirt of the Ariane 5 launcher[25]
- ODE models of chemical reactor dynamics[26][27]
- Pharmacokinetic variability of inhaled VOCs[28]
- Groundwater modeling[29]
- Bounding failure probability for series systems[30]
- Heavy metal contamination in soil at an ironworks brownfield[31][32]
- Uncertainty propagation for salinity risk models[33]
- Power supply system safety assessment[34]
- Contaminated land risk assessment[35]
- Engineered systems for drinking water treatment[36]
- Computing soil screening levels[37]
- Human health and ecological risk analysis by the U.S. EPA of PCB contamination at the Housatonic River Superfund site[38][39]
- Environmental assessment for the Calcasieu Estuary Superfund site[40]
- Aerospace engineering for supersonic nozzle thrust[41]
- Verification and validation in scientific computation for engineering problems[42]
- Toxicity to small mammals of environmental mercury contamination[43]
- Modeling travel time of pollution in groundwater[44]
- Reliability analysis[45]
- Endangered species assessment for reintroduction of Leadbeater’s possum[46]
- Exposure of insectivorous birds to an agricultural pesticide[47]
- Climate change projections[31][48][49]
- Waiting time in queuing systems[50]
- Extinction risk analysis for spotted owl on the Olympic Peninsula[51]
- Biosecurity against introduction of invasive species or agricultural pests[52]
- Finite-element structural analysis[53][54][55]
- Cost estimates[56]
- Nuclear stockpile certification[57]
- Fracking risks to water pollution[58]
See also[edit]
- Probability box
- Robust Bayes analysis
- Imprecise probability
- Second-order Monte Carlo simulation
- Monte Carlo simulation
- Interval analysis
- Probability theory
- Risk analysis
References[edit]
- ^ a b Boole, George (1854). An Investigation of the Laws of Thought on which are Founded the Mathematical Theories of Logic and Probabilities. London: Walton and Maberly.
- ^ a b c Hailperin, Theodore (1986). Boole’s Logic and Probability. Amsterdam: North-Holland. ISBN 978-0-444-11037-4.
- ^ a b Kyburg, H.E., Jr. (1999). Interval valued probabilities. SIPTA Documention on Imprecise Probability.
- ^ Walley, Peter (1991). Statistical Reasoning with Imprecise Probabilities. London: Chapman and Hall. ISBN 978-0-412-28660-5.
- ^ a b Yager, R.R. (1986). Arithmetic and other operations on Dempster–Shafer structures. International Journal of Man-machine Studies 25: 357–366.
- ^ a b Makarov, G.D. (1981). Estimates for the distribution function of a sum of two random variables when the marginal distributions are fixed. Theory of Probability and Its Applications 26: 803–806.
- ^ Rüschendorf, L. (1982). Random variables with maximum sums. Advances in Applied Probability 14: 623–632.
- ^ a b Frank, M.J., R.B. Nelsen and B. Schweizer (1987). Best-possible bounds for the distribution of a sum—a problem of Kolmogorov. Probability Theory and Related Fields 74: 199–211.
- ^ a b c Williamson, R.C., and T. Downs (1990). Probabilistic arithmetic I: Numerical methods for calculating convolutions and dependency bounds. International Journal of Approximate Reasoning 4: 89–158.
- ^ a b Ferson, S., V. Kreinovich, L. Ginzburg, D.S. Myers, and K. Sentz. (2003). Constructing Probability Boxes and Dempster–Shafer Structures Archived 22 July 2011 at the Wayback Machine. SAND2002-4015. Sandia National Laboratories, Albuquerque, NM.
- ^ Berleant, D. (1993). Automatically verified reasoning with both intervals and probability density functions. Interval Computations 1993 (2) : 48–70.
- ^ Berleant, D., G. Anderson, and C. Goodman-Strauss (2008). Arithmetic on bounded families of distributions: a DEnv algorithm tutorial. Pages 183–210 in Knowledge Processing with Interval and Soft Computing, edited by C. Hu, R.B. Kearfott, A. de Korvin and V. Kreinovich, Springer (ISBN 978-1-84800-325-5).
- ^ a b Berleant, D., and C. Goodman-Strauss (1998). Bounding the results of arithmetic operations on random variables of unknown dependency using intervals. Reliable Computing 4: 147–165.
- ^ a b c Ferson, S., R. Nelsen, J. Hajagos, D. Berleant, J. Zhang, W.T. Tucker, L. Ginzburg and W.L. Oberkampf (2004). Dependence in Probabilistic Modeling, Dempster–Shafer Theory, and Probability Bounds Analysis. Sandia National Laboratories, SAND2004-3072, Albuquerque, NM.
- ^ Alvarez, D. A., 2006. On the calculation of the bounds of probability of events using infinite random sets. International Journal of Approximate Reasoning 43: 241–267.
- ^ Baraldi, P., Popescu, I. C., Zio, E., 2008. Predicting the time to failure of a randomly degrading component by a hybrid Monte Carlo and possibilistic method. IEEE Proc. International Conference on Prognostics and Health Management.
- ^ Batarseh, O. G., Wang, Y., 2008. Reliable simulation with input uncertainties using an interval-based approach. IEEE Proc. Winter Simulation Conference.
- ^ Roy, Christopher J., and Michael S. Balch (2012). A holistic approach to uncertainty quantification with application to supersonic nozzle thrust. International Journal for Uncertainty Quantification 2 (4): 363–81 doi:10.1615/Int.J.UncertaintyQuantification.2012003562.
- ^ Zhang, H., Mullen, R. L., Muhanna, R. L. (2010). Interval Monte Carlo methods for structural reliability. Structural Safety 32: 183–190.
- ^ Zhang, H., Dai, H., Beer, M., Wang, W. (2012). Structural reliability analysis on the basis of small samples: an interval quasi-Monte Carlo method. Mechanical Systems and Signal Processing 37 (1–2): 137–51 doi:10.1016/j.ymssp.2012.03.001.
- ^ Trejo, R., Kreinovich, V. (2001). Error estimations for indirect measurements: randomized vs. deterministic algorithms for ‘black-box’ programs. Handbook on Randomized Computing, S. Rajasekaran, P. Pardalos, J. Reif, and J. Rolim (eds.), Kluwer, 673–729.
- ^ Aughenbaugh, J. M., and C.J.J. Paredis (2007). Probability bounds analysis as a general approach to sensitivity analysis in decision making under uncertainty Archived 2012-03-21 at the Wayback Machine. SAE 2007 Transactions Journal of Passenger Cars: Mechanical Systems, (Section 6) 116: 1325–1339, SAE International, Warrendale, Pennsylvania.
- ^ Flander, L., W. Dixon, M. McBride, and M. Burgman. (2012). Facilitated expert judgment of environmental risks: acquiring and analysing imprecise data. International Journal of Risk Assessment and Management 16: 199–212.
- ^ Dixon, W.J. (2007). The use of Probability Bounds Analysis for Characterising and Propagating Uncertainty in Species Sensitivity Distributions. Technical Report Series No. 163, Arthur Rylah Institute for Environmental Research, Department of Sustainability and Environment. Heidelberg, Victoria, Australia.
- ^ Oberguggenberger, M., J. King and B. Schmelzer (2007). Imprecise probability methods for sensitivity analysis in engineering. Proceedings of the 5th International Symposium on Imprecise Probability: Theories and Applications, Prague, Czech Republic.
- ^ Enszer, J.A., Y. Lin, S. Ferson, G.F. Corliss and M.A. Stadtherr (2011). Probability bounds analysis for nonlinear dynamic process models. AIChE Journal 57: 404–422.
- ^ Enszer, Joshua Alan, (2010). Verified Probability Bound Analysis for Dynamic Nonlinear Systems. Dissertation, University of Notre Dame.
- ^ Nong, A., and K. Krishnan (2007). Estimation of interindividual pharmacokinetic variability factor for inhaled volatile organic chemicals using a probability-bounds approach. Regulatory Toxicology and Pharmacology 48: 93–101.
- ^ Guyonnet, D., F. Blanchard, C. Harpet, Y. Ménard, B. Côme and C. Baudrit (2005). Projet IREA—Traitement des incertitudes en évaluation des risques d’exposition, Annexe B, Cas «Eaux souterraines». Rapport BRGM/RP-54099-FR, Bureau de Recherches Géologiques et Minières, France. Archived 2012-03-11 at the Wayback Machine
- ^ Fetz, Thomas; Tonon, Fulvio (2008). «Probability bounds for series systems with variables constrained by sets of probability measures». International Journal of Reliability and Safety. 2 (4): 309. doi:10.1504/IJRS.2008.022079.
- ^ a b Augustsson, A., M. Filipsson, T. Öberg, B. Bergbäck (2011). Climate change—an uncertainty factor in risk analysis of contaminated land. Science of the Total Environment 409: 4693–4700.
- ^ Baudrit, C., D. Guyonnet, H. Baroudi, S. Denys and P. Begassat (2005). Assessment of child exposure to lead on an ironworks brownfield: uncertainty analysis. 9th International FZK/TNO Conference on Contaminated Soil – ConSoil2005, Bordeaux, France, pages 1071–1080.
- ^ Dixon, W.J. (2007). Uncertainty Propagation in Population Level Salinity Risk Models. Technical Report Technical Report Series No. 164, Arthur Rylah Institute for Environmental Research. Heidelberg, Victoria, Australia
- ^ Karanki, D.R., H.S. Kushwaha, A.K. Verma, and S. Ajit. (2009). Uncertainty analysis based on probability bounds (p-box) approach in probabilistic safety assessment. Risk Analysis 29: 662–75.
- ^ Sander, P., B. Bergbäck and T. Öberg (2006). Uncertain numbers and uncertainty in the selection of input distributions—Consequences for a probabilistic risk assessment of contaminated land. Risk Analysis 26: 1363–1375.
- ^ Minnery, J.G., J.G. Jacangelo, L.I. Boden, D.J. Vorhees and W. Heiger-Bernays (2009). Sensitivity analysis of the pressure-based direct integrity test for membranes used in drinking water treatment. Environmental Science and Technology 43(24): 9419–9424.
- ^ Regan, H.M., B.E. Sample and S. Ferson (2002). Comparison of deterministic and probabilistic calculation of ecological soil screening levels. Environmental Toxicology and Chemistry 21: 882–890.
- ^ U.S. Environmental Protection Agency (Region I), GE/Housatonic River Site in New England
- ^ Moore, Dwayne R.J.; Breton, Roger L.; Delong, Tod R.; Ferson, Scott; Lortie, John P.; MacDonald, Drew B.; McGrath, Richard; Pawlisz, Andrzej; Svirsky, Susan C.; Teed, R. Scott; Thompson, Ryan P.; Whitfield Aslund, Melissa (2016). «Ecological risk assessment for mink and short-tailed shrew exposed to PCBS, dioxins, and furans in the Housatonic River area». Integrated Environmental Assessment and Management. 12 (1): 174–184. doi:10.1002/ieam.1661. PMID 25976918.
- ^ U.S. Environmental Protection Agency (Region 6 Superfund Program), Calcasieu Estuary Remedial Investigation Archived January 20, 2011, at the Wayback Machine
- ^ Roy, C.J., and M.S. Balch (2012). A holistic approach to uncertainty quantification with application to supersonic nozzle thrust. International Journal for Uncertainty Quantification 2: 363-381.
doi:10.1615/Int.J.UncertaintyQuantification.2012003562. - ^ Oberkampf, W.L., and C. J. Roy. (2010). Verification and Validation in Scientific Computing. Cambridge University Press.
- ^ Regan, H.M., B.K. Hope, and S. Ferson (2002). Analysis and portrayal of uncertainty in a food web exposure model. Human and Ecological Risk Assessment 8: 1757–1777.
- ^ Ferson, S., and W.T. Tucker (2004). Reliability of risk analyses for contaminated groundwater. Groundwater Quality Modeling and Management under Uncertainty, edited by S. Mishra, American Society of Civil Engineers Reston, VA.
- ^ Crespo, Luis G.; Kenny, Sean P.; Giesy, Daniel P. (2013). «Reliability analysis of polynomial systems subject to p-box uncertainties». Mechanical Systems and Signal Processing. 37 (1–2): 121–136. Bibcode:2013MSSP…37..121C. doi:10.1016/j.ymssp.2012.08.012.
- ^ Ferson, S., and M. Burgman (1995). Correlations, dependency bounds and extinction risks. Biological Conservation 73: 101–105.
- ^ Ferson, S., D.R.J. Moore, P.J. Van den Brink, T.L. Estes, K. Gallagher, R. O’Connor and F. Verdonck. (2010). Bounding uncertainty analyses. Pages 89–122 in Application of Uncertainty Analysis to Ecological Risks of Pesticides, edited by W. J. Warren-Hicks and A. Hart. CRC Press, Boca Raton, Florida.
- ^ Kriegler, E., and H. Held (2005). Utilizing belief functions for the estimation of future climate change. International Journal of Approximate Reasoning 39: 185–209.
- ^ Kriegler, E. (2005). Imprecise probability analysis for integrated assessment of climate change, Ph.D. dissertation, Universität Potsdam, Germany.
- ^ Batarseh, O.G.Y., (2010). An Interval Based Approach to Model Input Uncertainty in Discrete-event Simulation. Ph.D. dissertation, University of Central Florida.
- ^ Goldwasser, L., L. Ginzburg and S. Ferson (2000). Variability and measurement error in extinction risk analysis: the northern spotted owl on the Olympic Peninsula. Pages 169–187 in Quantitative Methods for Conservation Biology, edited by S. Ferson and M. Burgman, Springer-Verlag, New York.
- ^ Hayes, K.R. (2011). Uncertainty and uncertainty analysis methods: Issues in quantitative and qualitative risk modeling with application to import risk assessment ACERA project (0705). Report Number: EP102467, CSIRO, Hobart, Australia.
- ^ Zhang, H., R.L. Mullen, and R.L. Muhanna (2010). Finite element structural analysis using imprecise probabilities based on p-box representation. Proceedings of the 4th International Workshop on Reliable Engineering Computing (REC 2010).
- ^ Zhang, H., R. Mullen, R. Muhanna (2012). Safety Structural Analysis with Probability-Boxes.
International Journal of Reliability and Safety 6: 110–129. - ^ Patelli, E; de Angelis, M (2015). «Line sampling approach for extreme case analysis in presence of aleatory and epistemic uncertainties». Safety and Reliability of Complex Engineered Systems. pp. 2585–2593. doi:10.1201/b19094-339. ISBN 978-1-138-02879-1.
- ^ Mehl, Christopher H. (2013). «P-boxes for cost uncertainty analysis». Mechanical Systems and Signal Processing. 37 (1–2): 253–263. Bibcode:2013MSSP…37..253M. doi:10.1016/j.ymssp.2012.03.014.
- ^ Sentz, K., and S. Ferson (2011). Probabilistic bounding analysis in the quantification of margins and uncertainties. Reliability Engineering and System Safety 96: 1126–1136.
- ^ Rozell, Daniel J., and Sheldon J. Reaven (2012). Water pollution risk associated with natural gas extraction from the Marcellus Shale. Risk Analysis 32: 1382–1393.
Further references[edit]
- Bernardini, Alberto; Tonon, Fulvio (2010). Bounding Uncertainty in Civil Engineering: Theoretical Background. Berlin: Springer. ISBN 978-3-642-11189-1.
- Ferson, Scott (2002). RAMAS Risk Calc 4.0 Software : Risk Assessment with Uncertain Numbers. Boca Raton, Florida: Lewis Publishers. ISBN 978-1-56670-576-9.
- Gerla, G. (1994). «Inferences in Probability Logic». Artificial Intelligence. 70 (1–2): 33–52. doi:10.1016/0004-3702(94)90102-3.
- Oberkampf, William L.; Roy, Christopher J. (2010). Verification and Validation in Scientific Computing. New York: Cambridge University Press. ISBN 978-0-521-11360-1.
External links[edit]
- Probability bounds analysis in environmental risk assessments
- Intervals and probability distributions
- Epistemic uncertainty project
- The Society for Imprecise Probability: Theories and Applications
Анализ границ вероятности (PBA ) — это набор методов распространения неопределенности для качественного и количественные расчеты с учетом различного рода неопределенностей. Он используется для проецирования частичной информации о случайных величинах и других величинах с помощью математических выражений. Например, он вычисляет надежные границы распределения суммы, произведения или более сложной функции, учитывая только надежные границы распределений входных данных. Такие границы называются ячейками вероятности и ограничивают кумулятивные распределения вероятностей (а не плотности или функции масс ).
Этот подход ограничения позволяет аналитикам производить расчеты, не требуя чрезмерно точных предположений о значениях параметров, зависимости между переменными или даже форме распределения. Анализ границ вероятности, по сути, представляет собой комбинацию методов стандартного интервального анализа и классической теории вероятностей. Анализ границ вероятности дает тот же ответ, что и интервальный анализ, когда доступна только информация о диапазоне. Он также дает те же ответы, что и моделирование Монте-Карло, когда информации достаточно, чтобы точно указать входные распределения и их зависимости. Таким образом, это обобщение как интервального анализа, так и теории вероятностей.
Разнообразные методы, включающие анализ границ вероятности, предоставляют алгоритмы для оценки математических выражений при наличии неопределенности относительно входных значений, их зависимостей или даже формы самого математического выражения. Вычисления дают результаты, которые гарантированно включают все возможные распределения выходной переменной, если входные p-блоки также обязательно включают соответствующие распределения. В некоторых случаях вычисленный p-блок также будет наилучшим из возможных в том смысле, что границы не могут быть более жесткими без исключения некоторых возможных распределений.
P-блоки обычно просто ограничивают возможные распределения. Границы часто также включают распределения, которые сами по себе невозможны. Например, набор распределений вероятностей, которые могут возникнуть в результате добавления случайных значений без предположения о независимости от двух (точных) распределений, обычно является правильным подмножеством всех распределений, заключенных в p-блок, вычисляемый для суммы. То есть внутри выходного p-блока есть распределения, которые не могут возникнуть ни при какой зависимости между двумя входными распределениями. Однако выходной p-блок всегда будет содержать все возможные распределения, при условии, что входные p-блоки обязательно включают соответствующие базовые распределения. Этого свойства часто бывает достаточно для использования в анализе риска и других областях, требующих вычислений в условиях неопределенности.
Содержание
- 1 История ограничивающей вероятности
- 2 Арифметические выражения
- 2.1 Математические детали
- 3 Логические выражения
- 4 Сравнение величин
- 5 Вычисление на основе выборки
- 6 Связь с другие подходы к распространению неопределенности
- 7 Приложения
- 8 См. также
- 9 Ссылки
- 10 Дополнительные ссылки
- 11 Внешние ссылки
История ограниченной вероятности
Идея ограничивающей вероятности имеет очень давнюю традицию на протяжении всей истории теории вероятностей. Действительно, в 1854 году Джордж Буль использовал понятие интервальных границ вероятности в своей Законы мысли. Неравенство , также относящееся ко второй половине XIX века,, приписываемое Чебышеву, описывает границы распределения, когда известны только среднее значение и дисперсия переменной, а также связанные неравенство, приписываемое Маркову, обнаружило границы положительной переменной, когда известно только среднее значение. Кибург рассмотрел историю интервальных вероятностей и проследил развитие критических идей в течение 20-го века, включая важное понятие несравнимых вероятностей, одобренное Кейнсом. Особо следует отметить вывод Фреше в 1930-х годах ограничений на вычисления, включающие полные вероятности без предположений о зависимости. Ограничение вероятностей продолжается и по сей день (например, теория Уолли неточной вероятности.)
Методы анализа границ вероятности, которые можно было бы регулярно использовать при оценке риска, были разработаны в 1980-х годах. Хайлперин описал вычислительную схему для ограничивающих логических вычислений, расширяющую идеи Буля. Ягер описал элементарные процедуры, с помощью которых могут быть вычислены границы сверток в предположении независимости. Примерно в то же время Макаров и независимо от него Рюшендорф решили проблему, первоначально поставленную Колмогоровым, о том, как найти верхнюю и нижнюю границы для распределения вероятностей суммы случайных величин, маргинальные распределения которых но не их совместное распространение, известно. Франк и др. обобщил результат Макарова и выразил его в терминах связок. С того времени формулы и алгоритмы для сумм были обобщены и расширены на различия, произведения, частные и другие двоичные и унарные функции при различных предположениях зависимости.
Арифметические выражения
Арифметические выражения, включающие такие операции, как в качестве сложения, вычитания, умножения, деления, минимума, максимума, степени, экспоненты, логарифма, квадратного корня, абсолютного значения и т. д. обычно используются в анализе риска и моделировании неопределенности. Свертка — это операция нахождения распределения вероятностей суммы независимых случайных величин, заданных распределениями вероятностей. Мы можем расширить этот термин до нахождения распределений других математических функций (продуктов, различий, частных и более сложных функций) и других предположений о взаимозависимостях переменных. Существуют удобные алгоритмы для вычисления этих обобщенных сверток при различных предположениях о зависимостях между входными данными.
Математические детали
Пусть D { displaystyle mathbb {D}}

- D = { D | D: R → [0, 1], D (x) ≤ D (y) для всех x < y }. {displaystyle mathbb {D} ={D|D:mathbb {R} to [0,1],D(x)leq D(y){text{ for all }}x
p-блок — это пятерка
- {F ¯, F _, m, v, F}, { displaystyle left {{ overline {F}}, { underline {F}}, m, v, mathbf {F} right },}
где F ¯, F _ ∈ D, m, v { displaystyle { overline {F}}, { underline {F}} in mathbb {D}, m, v}


- ∀ x ∈ R: F ¯ (x) ≤ F (x) ≤ F _ (x) ∫ R xd F (x) ∈ m условие ожидания ∫ R x 2 d F (x) — (∫ R xd F (x)) 2 ∈ v условие дисперсии { displaystyle { begin {align} forall x in mathbb {R}: qquad { overline {F}} (x) leq F (x) leq { underline {F}} (x) \ [6pt] int _ { mathbb {R}} xdF (x) in m { text {условие ожидания}} \ int _ { mathbb {R}} x ^ {2} dF (x) — left ( int _ { mathbb {R}} xdF (x) right) ^ {2} in v { text {условие отклонения}} end {выровнено}}}
Если функция удовлетворяет всем вышеперечисленным условиям, то говорят, что она находится внутри p-блока. В некоторых случаях может отсутствовать информация о моментах или семействе распределения, кроме того, что закодировано в двух функциях распределения, которые составляют края p-блока. Тогда пятерка, представляющая p-блок {B 1, B 2, [- ∞, ∞], [0, ∞], D} { displaystyle {B_ {1}, B_ {2}, [- infty, infty], [0, infty], mathbb {D} }}![{ displaystyle {B_ {1}, B_ {2}, [- infty, infty], [0, infty], mathbb {D} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/639f77fff8f6ce0293698932b7b7ad4fbe3a090f)
Обозначение X ∼ F { displaystyle X sim F}

- {F: R → [0, 1] x ↦ Pr (X ≤ x) { displaystyle { begin {cases} F: mathbb {R} to [0,1] \ x mapsto Pr (X leq x) end {cases}}}
Давайте обобщим обозначение тильды для использования с p-блоками. Мы будем писать X ~ B, чтобы обозначать, что X — случайная величина, функция распределения которой неизвестна, за исключением того, что она находится внутри B. Таким образом, X ~ F ∈ B можно свести к X ~ B без явного упоминания функции распределения.
Если X и Y — независимые случайные величины с распределениями F и G соответственно, то X + Y = Z ~ H задается формулой
- H (z) = ∫ z = x + y F (x) G (y) dz = ∫ RF (x) G (z — x) dx = F ∗ G. { Displaystyle H (z) = int _ {z = x + y} F (x) G (y) dz = int _ { mathbb {R}} F (x) G (zx) dx = F * G.}
Эта операция называется сверткой над F и G. Аналогичная операция над p-блоками проста для сумм. Предположим, что
- X ∼ A = [A 1, A 2] и Y ∼ B = [B 1, B 2]. { displaystyle X sim A = [A_ {1}, A_ {2}], quad { text {and}} quad Y sim B = [B_ {1}, B_ {2}].}
Если X и Y стохастически независимы, то распределение Z = X + Y находится внутри p-блока
- [A 1 ∗ B 1, A 2 ∗ B 2]. { displaystyle left [A_ {1} * B_ {1}, A_ {2} * B_ {2} right].}
Нахождение границ распределения сумм Z = X + Y без каких-либо предположений о зависимость между X и Y на самом деле проще, чем проблема, предполагающая независимость. Макаров показал, что
- Z ∼ [sup z = x + y max (F (x) + G (y) — 1, 0), inf z = x + y min (F (x) + G (y), 1)] { Displaystyle Z sim влево [ sup _ {z = x + y} max (F (x) + G (y) -1,0), inf _ {z = x + y} min (F (x) + G (y), 1) right]}
Эти границы подразумеваются границами Фреше – Хоффдинга копула. Проблема также может быть решена с использованием методов математического программирования.
Свертка при промежуточном предположении, которое имеют X и Y, также легко вычисляется, как и свертка при экстремальных предположениях совершенного положительного или зависимости между X и Y.
Обобщенные свертки для других операций, таких как вычитание, умножение, деление и т. Д., Могут быть получены с использованием преобразований. Например, вычитание p-блока A — B может быть определено как A + (-B), где отрицательное значение p-блока B = [B 1, B 2 ] равно [B 2 (-x), B 1 (-x)].
Логические выражения
Логические или логические выражения, включающие союзы (AND операции), дизъюнкции (OR операций), исключительные дизъюнкции, эквивалентности, условия и т. д. возникают при анализе деревьев отказов и деревьев событий, общих для оценок риска. Если вероятности событий характеризуются интервалами, как, среди прочего, предложено Boole и Кейнсом, эти двоичные операции легко оценить. Например, если вероятность события A находится в интервале P (A) = a = [0,2, 0,25], а вероятность события B находится в P (B) = b = [0,1, 0,3], то вероятность соединения обязательно находится в интервале
- P (A B) = a × b
-
-
- = [0,2, 0,25] × [0,1, 0,3]
- = [0,2 × 0,1, 0,25 × 0,3]
- = [0,02, 0,075]
-
-
при условии, что A и B можно считать независимыми событиями. Если они не являются независимыми, мы все же можем оценить конъюнкцию, используя классическое неравенство Фреше. В этом случае мы можем сделать вывод, по крайней мере, о том, что вероятность совместного события A и B, несомненно, находится в интервале
- P (A B) = env (max (0, a + b − 1), min (a, b))
-
-
- = env (max (0, [0,2, 0,25] + [0,1, 0,3] -1), min ([0,2, 0,25], [0,1, 0,3]))
- = env ([max (0, 0,2 + 0,1–1), max (0, 0,25 + 0,3–1)], [min (0,2,0,1), min (0,25, 0,3)])
- = env ([0,0], [0.1, 0.25])
- = [0, 0.25]
-
-
где env ([x 1,x2], [y 1,y2]) равно [min ( x 1,y1), max (x 2,y2)]. Точно так же вероятность дизъюнкции обязательно находится в интервале
- P (A v B) = a + b — a × b = 1 — (1 — a) × (1 — b)
-
-
- = 1 — (1 — [0,2, 0,25]) × (1 — [0,1, 0,3])
- = 1 — [0,75, 0,8] × [0,7, 0,9]
- = 1 — [0,525, 0,72]
- = [0,28, 0,475]
-
-
, если A и B являются независимыми событиями. Если они не являются независимыми, неравенство Фреше ограничивает дизъюнкцию
- P (A v B) = env (max (a, b), min (1, a + b))
-
-
- = env (max ([0.2, 0,25], [0,1, 0,3]), мин (1, [0,2, 0,25] + [0,1, 0,3]))
- = env ([0,2, 0,3], [0,3, 0,55])
- = [0.2, 0.55].
-
-
Также возможно вычислить границы интервала для конъюнкции или дизъюнкции при других предположениях о зависимости между A и B. Например, можно предположить, что они положительно зависимы, в этом случае результирующий интервал будет не таким узким, как ответ, предполагающий независимость, но более узким, чем ответ, данный неравенством Фреше. Сравнимые вычисления используются для других логических функций, таких как отрицание, исключительная дизъюнкция и т. Д. Когда вычисляемое логическое выражение становится сложным, может потребоваться вычислить его с помощью методов математического программирования, чтобы получить наилучшие границы выражения. Похожая проблема возникает в случае вероятностной логики (см., Например, Gerla 1994). Если вероятности событий характеризуются распределениями вероятностей или p-блоками, а не интервалами, то аналогичные вычисления могут быть выполнены для получения результатов распределения или p-блоков, характеризующих вероятность главного события.
Сравнение величин
Вероятность того, что неопределенное число, представленное p-блоком D, меньше нуля, — это интервал Pr (D < 0) = [F(0), F̅ (0)], где F̅ (0) — левая граница вероятностного бокса D, а F (0) — его правая граница, оба оцениваются как ноль. Два неопределенных числа, представленные вероятностными квадратами, затем можно сравнить по числовой величине следующие кодировки:
- A < B = Pr(A − B < 0),
- A>B = Pr (B — A < 0),
- A ≤ B = Pr (A — B ≤ 0) и
- A ≥ B = Pr (B — A ≤ 0).
Таким образом, вероятность того, что A меньше B, равна вероятности того, что их разница меньше нуля, и эту вероятность можно назвать значением выражения A < B.
Подобно арифметическим и логическим операциям, эти сравнения величин обычно зависят от стохастической зависимости между A и B, и вычитание при кодировании должно отражать эту зависимость. Если их зависимость неизвестна, разницу можно вычислить без каких-либо предположений, используя th e Операция Фреше.
Вычисление на основе выборки
Некоторые аналитики используют подходы на основе выборки для вычисления границ вероятности, включая моделирование Монте-Карло, методы латинского гиперкуба или выборка по важности. Эти подходы не могут гарантировать математическую строгость результата, поскольку такие методы моделирования являются приближениями, хотя их производительность, как правило, можно улучшить, просто увеличив количество повторений в моделировании. Таким образом, в отличие от аналитических теорем или методов, основанных на математическом программировании, вычисления на основе выборки обычно не могут дать проверенных вычислений. Однако методы, основанные на выборке, могут быть очень полезны при решении множества задач, которые с вычислительной точки зрения трудно решить аналитически или даже строго связать. Одним из важных примеров является использование выборки с отклонением Коши, чтобы избежать проклятия размерности при распространении неопределенности интервала через проблемы большой размерности.
Связь с распространением другой неопределенности подходы
PBA принадлежит к классу методов, которые используют неточные вероятности для одновременного представления алеаторической и эпистемической неопределенности. PBA — это обобщение как интервального анализа, так и вероятностной свертки, например, что обычно реализуется с помощью моделирования Монте-Карло. PBA также тесно связан с надежным байесовским анализом, который иногда называют анализом байесовской чувствительности. PBA — альтернатива.
Приложения
P-box и анализ границ вероятности использовались во многих приложениях, охватывающих многие дисциплины в области инженерии и экологии, включая:
- Инженерное проектирование
- Экспертное заключение
- Анализ распределений чувствительности видов
- Анализ чувствительности в аэрокосмической технике изгибающей нагрузки передней юбки Ariane 5 пусковая установка
- ODE модели химического реактора динамика
- Фармакокинетика изменчивость вдыхаемых ЛОС
- Моделирование подземных вод
- Граничное нарушение вероятность для серийных систем
- Загрязнение почв тяжелыми металлами на заводе заброшенном месторождении
- Распространение неопределенности для моделей риска засоления
- Оценка безопасности системы электроснабжения
- Оценка риска загрязненных земель
- Инженерные системы для питьевой очистки воды
- Вычисление уровней скрининга почвы
- Здоровье человека и экологи анализ рисков, проведенный США. EPA загрязнения ПХБ на участке Housatonic River Superfund
- Экологическая оценка для Calcasieu Estuary Superfund сайт
- Аэрокосмическая техника для сверхзвукового сопла тяги
- Проверка и валидация в научных расчетах для инженерных задач
- Токсичность для мелких млекопитающих окружающей среды ртуть загрязнение
- Моделирование времени прохождения загрязнения в подземных водах
- Анализ надежности
- Вымирающие виды оценка повторного внедрения опоссума Ледбитера
- Воздействие насекомоядные птицы на сельскохозяйственный пестицид
- Изменение климата прогнозы
- Время ожидания в системах очередей
- исчезновение анализ риска пятнистой совы на Олимпийском полуострове
- Биозащита от интродукции инвазивных видов или сельскохозяйственных видов
- Конечный элемент структурный анализ
- Смета
- Nucl запас ушей сертификация
- гидроразрыв риски загрязнения воды
См. также
Ссылки
Дополнительные ссылки
- Бернардини, Альберто; Тонон, Фульвио (2010). Граничная неопределенность в гражданском строительстве: теоретические основы. Берлин: Springer. ISBN 978-3-642-11189-1.
- Ферсон, Скотт (2002). Программное обеспечение RAMAS Risk Calc 4.0: оценка рисков с неопределенными числами. Бока-Ратон, Флорида: Lewis Publishers. ISBN 978-1-56670-576-9.
- Герла Г. (1994). «Выводы в вероятностной логике». Искусственный интеллект. 70 (1–2): 33–52. doi : 10.1016 / 0004-3702 (94) 90102-3.
- Оберкампф, Уильям Л.; Рой, Кристофер Дж. (2010). Проверка и подтверждение в научных вычислениях. Нью-Йорк: Издательство Кембриджского университета. ISBN 978-0-521-11360-1.
Внешние ссылки
Определяя
для средней арифметической (или
относительной) величины два крайних
значения: минимально возможное и
максимально возможное, находят пределы,
в которых может быть искомая величина
генерального
параметра. Эти
пределы называют доверительными
границами.
Доверительные
границы — границы
средних (или относительных) величин,
выход за пределы которых вследствие
случайных колебаний имеет незначительную
вероятность.
Вероятность
попадания средней или относительной
величины в доверительный интервал
называется доверительной
вероятностью.
Доверительные
границы средней
арифметической генеральной совокупности
определяют по формуле:
Мген
= Мвыб
±
t
· mM
Доверительные
границы относительной величины в
генеральной совокупности определяют
по следующей формуле:
Рген
= Рвыб ± t
· mр
Где:
Мген
и Рген
— значения средней и
относительной величин, полученных для
генеральной совокупности;
Мвыб
и Рвыб
— значения средней и
относительной величин, полученных для
выборочной совокупности;
mM
и mр
— ошибки
репрезентативности выборочных величин;
t
— доверительный критерий,
который зависит от величины безошибочного
прогноза, устанавливаемого при
планировании исследования.
Произведение
t
· m
(Δ)
— предельная ошибка показателя, полученного
при данном выборочном исследовании.
Размеры
предельной ошибки зависят от коэффициента
t,
который избирает сам
исследователь, исходя из заданной
вероятности безошибочного прогноза.
Величина
критерия t
связана с вероятностью
безошибочного прогноза (Р)
и числом наблюдений в
выборочной совокупности (табл. 4.1).
Таблица
4.1
Зависимость
доверительного критерия t
от степени
вероятности
безошибочного прогноза
Р (при n
> 30)
|
Степень вероятности |
Доверительный |
|
95,0 |
2 |
|
99,0 |
2,6 |
|
99,9 |
3,3 |
Для большинства
медико-биологических и социальных
исследований достоверными считаются
доверительные границы, установленные
с вероятностью безошибочного прогноза
= 95% и более.
Чтобы
найти критерий t
при числе наблюдений
(n) < 30,
необходимо пользоваться специальной
таблицей Н.А.Плохинского (табл. 4.2), в
которой слева показано число наблюдений
— единица (n
— 1), а сверху (Р)
— степень вероятности
безошибочного прогноза.
При
определении доверительных границ
сначала надо решить вопрос о том, с какой
степенью вероятности безошибочного
прогноза необходимо представить
доверительные границы средней или
относительной величины. Избрав
определенную степень вероятности,
соответственно этому находят величину
доверительного критерия t
при данном числе
наблюдений. Таким образом, доверительный
критерий устанавливается заранее, при
планировании исследования.
Таблица 4.2
Значение
критерия t
для трех степеней
вероятности (по Н.А.Плохинскому)
|
Р n = n-1 |
95% |
99% |
99,9% |
|
1 |
12,7 |
63,7 |
37,0 |
|
2 |
4,3 |
9,9 |
31,6 |
|
3 |
3,2 |
5,8 |
12,9 |
|
4 |
2,8 |
4,6 |
8,6 |
|
5 |
2,6 |
4,0 |
6,9 |
|
6 |
2,4 |
3,7 |
6,0 |
|
7 |
2,4 |
3,5 |
5,3 |
|
8 |
2,3 |
3,4 |
5,0 |
|
9 |
2,3 |
3,3 |
4,8 |
|
10 |
2,2 |
3,2 |
4,6 |
|
11 |
2,2 |
3,1 |
4,4 |
|
12 |
2,2 |
3,1 |
4,3 |
|
13 |
2,3 |
3,0 |
4,1 |
|
14-15 |
2,1 |
3,0 |
4,1 |
|
16-17 |
2,1 |
2,9 |
4,0 |
|
18-20 |
2,1 |
2,9 |
3,9 |
|
21-24 |
2,1 |
2,8 |
3,8 |
|
25-29 |
2,0 |
2,8 |
3,7 |
Любой параметр
(средняя или относительная величина)
может оцениваться с учетом доверительных
границ, полученных при расчете.
Например:требуется определить доверительные
границы среднего уровня пепсина у
больных гипертериозом с 95% вероятностью
безошибочного прогноза. Если известно,
что:
n
= 49;
Мвыб
=1г%;
mм
= ± 0,05г%
1.Определение
доверительных границ средней величины
в генеральной совокупности:
Мген
= Мвыб
±
t
· mM
= 1г% ± 2 ·
0,05г%
1г%
+ 0,1г% = 1,1 г%
Мген
=
1г%
— 0,1г% = 0,9 г%
Заключение:
установлено с вероятностью безошибочного
прогноза 95%, что средний уровень пепсина
в генеральной совокупности у больных
гипертериозом находится в пределах от
1,1 г% до 0,9 г%.
Как видно,
доверительные границы зависят от размера
доверительного интервала.
Анализ
доверительных интервалов указывает,
что при заданных степенях вероятности
и n
> 30 — t
имеет неизменную величину
и при этом доверительный интервал
зависит от величины ошибки репрезентативности.
С уменьшением
величины ошибки суживаются доверительные
границы средних и относительных величин,
полученных на выборочной совокупности,
т.е. уточняются результаты исследования,
которые приближаются к соответствующим
величинам генеральной совокупности.
Если ошибка большая, то получают для
выборочной величины большие доверительные
границы, которые могут противоречить
логической оценке искомой величины в
генеральной совокупности. В подобном
случае надо искать резервы сокращения
размаха доверительных границ в размере
величины ошибки репрезентативности.
Доверительные
границы Мвыб
и Рвыб
зависят не только от
средних ошибок этих величин, но и от
избранной исследователем степени
вероятности безошибочного прогноза.
При большой степени вероятности размах
доверительных границ увеличивается.
3.
Определение достоверности разности
средних (или относительных) величин (по
критерию t
— Стъюдента).
В медицине и
здравоохранении по разности параметров
оценивают средние и относительные
величины, полученные для разных групп
населения по полу, возрасту, а также
групп больных и здоровых и т.д. Во всех
случаях при сопоставлении двух
сравниваемых величин возникает
необходимость не только определить
их разность, но и оценить ее достоверность.
Достоверность
разности величин, полученных при
выборочных исследованиях, означает,
что вывод об их различии может быть
перенесен на соответствующие генеральные
совокупности.
Достоверность
разности выборочной совокупности
измеряется доверительным критерием,
который рассчитывается по специальным
формулам для средних и относительных
величин.
Формула оценки
достоверности разности сравниваемых
средних величин:
M1
— M2
t
= ——————
m12
+ m22
Для относительных
величин:
Р1
— Р2
t
= ——————
m12
+ m22
Где:
M1;
M2
; Р1;
Р2
— параметры,
полученные при выборочных исследованиях;
m1;
m2
— их средние ошибки;
t
— критерий достоверности
(Стъюдента).
Разность
статистически достоверна при t
≥ 2, что соответствует
вероятности безошибочного прогноза,
равной 95% и более.
Для большинства
исследований, проводимых в медицине и
здравоохранении, такая степень вероятности
является вполне достаточной.
При
величине критерия достоверности t
< 2 степень вероятности
безошибочного прогноза составляет Р <
95%. При такой степени
вероятности нельзя утверждать, что
полученная разность показателей
достоверна с достаточной степенью
вероятности. В этом случае необходимо
получить дополнительные данные, увеличив
число наблюдений.
Иногда при увеличении
численности выборки разность продолжает
оставаться не достоверной. Если при
повторных исследованиях разность
остается недостоверной, можно считать
доказанным, что между сравниваемыми
совокупностями не обнаружено различий
по изучаемому признаку.
Например:требуется определить, достоверны ли
различия в уровне пепсина в желудочном
соке больных гипертериозом и здоровых
лиц. Обследуются на пепсин две группы:
49 больных гипертериозом и 50 здоровых
людей (контрольная группа). Результаты
представлены в таблице 4.3.
Таблица
4.3
Сравнение среднего
уровня пепсина в желудочном соке больных
гипертериозом и здоровых лиц
|
Сравниваемые |
N |
М (г%) |
m (г%) |
t |
Уровень вероятности |
|
Больные |
49 |
1,0 |
± 0,3 |
10,0 |
< 99,9 |
|
Здоровые |
50 |
4,0 |
± 0,1 |
M1
— M2
t
= ——————
m12
+ m22
4
— 1
t
= —————- = 10,0
0,32
+ 0,12
Заключение:
при гипертериозе наблюдается снижение
уровня пепсина, что подтверждается с
большой степенью вероятности безошибочного
прогноза (Р > 99,9%).
Следовательно, снижение уровня пепсина
может быть использовано в качестве
одного из симптомов для подтверждения
диагностики гипертериоза.
Подобным же образом
оценивают достоверность разности
сравниваемых относительных величин.
Указанная методика
оценки достоверности и разности
результатов исследования позволяет
проводить только сравнение групп по
парам, при обязательном наличии обобщающих
параметров — средних арифметических
или относительных величин и их средних
ошибок.
Соседние файлы в папке По вопросам
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Загрузить PDF
Загрузить PDF
Доверительный интервал является показателем точности измерений. Это также показатель того, насколько стабильна полученная величина, то есть насколько близкую величину (к первоначальной величине) вы получите при повторении измерений (эксперимента). Выполните следующие действия, чтобы вычислить доверительный интервал для нужных величин.
Шаги
-
1
Запишите задачу. Например: средний вес студента мужского пола в университете АВС составляет 90 кг. Вы будете тестировать точность предсказания веса студентов мужского пола в университете АВС в пределах данного доверительного интервала.
-
2
Составьте подходящую выборку. Вы будете использовать ее для сбора данных для тестирования гипотезы. Допустим, вы уже случайно выбрали 1000 студентов мужского пола.
-
3
Рассчитайте среднее значение и стандартное отклонение этой выборки. Выберите статистические величины (например, среднее значение и стандартное отклонение), которые вы хотите использовать для анализа вашей выборки. Вот как вычислить среднее значение и стандартное отклонение:
- Для расчета среднего значения выборки сложите значения весов 1000 выбранных мужчин и разделите результат на 1000 (число мужчин). Допустим, получили средний вес, равный 93 кг.
- Для расчета стандартного отклонения выборки необходимо найти среднее значение. Затем нужно вычислить дисперсию данных или среднее значение квадратов разностей от среднего. Найдя это число, просто возьмите квадратный корень из него. Допустим, в нашем примере стандартное отклонение равно 15 кг (заметим, что иногда эта информация может быть дана вместе с условием статистической задачи).
-
4
Выберите нужный доверительный уровень. Наиболее часто используемые доверительные уровни: 90 %, 95 % и 99 %. Он также может быть дан вместе с условием задачи. Допустим, вы выбрали 95 %.
-
5
Рассчитайте предел погрешности. Вы можете найти предел погрешности с помощью следующей формулы: Za/2 * σ/√(n). Za/2 = коэффициент доверия (где а = доверительный уровень), σ = стандартное отклонение, а n = размер выборки. Это формула показывает, что вы должны умножить критическое значение на стандартную ошибку. Вот как вы можете решить эту формулу, разбив ее на части:
- Вычислите критическое значение или Za/2. Доверительный уровень равен 95 %. Преобразуйте проценты в десятичную дробь: 0,95 и разделите ее на 2, чтобы получить 0,475. Затем посмотрите в таблицу Z-оценок, чтобы найти соответствующее значение для 0,475. Вы найдете значение 1,96 (на пересечении строки 1,9 и столбца 0,06).
- Возьмите стандартную ошибку (стандартное отклонение): 15 и разделите ее на квадратный корень из размера выборки: 1000. Вы получите: 15/31,6 или 0,47 кг.
- Умножьте 1,96 на 0,47 (критическое значение на стандартную ошибку), чтобы получить 0,92 — предел погрешности.
-
6
Запишите доверительный интервал. Чтобы сформулировать доверительный интервал, просто запишите среднее значение (93) ± погрешность. Ответ: 93 ± 0,92. Вы можете найти верхнюю и нижнюю границы доверительного интервала, прибавляя и вычитая погрешность к/от средней величины. Итак, нижняя граница составляет 93 — 0,92 или 92,08, а верхняя граница составляет 93 + 0,92 или 93,92.
- Вы можете использовать следующую формулу для вычисления доверительного интервала: x̅ ± Za/2 * σ/√(n), где x̅ — среднее значение.
Реклама
Советы
- И t-оценки и z-оценки можно рассчитать вручную, а также с помощью графического калькулятора или статистических таблиц, которые часто встречаются в учебниках по статистике. Также доступны онлайн-инструменты.
- Критическое значение, используемое для расчета погрешности, является постоянным и выражается либо через t-оценку, либо через z-оценку. T-оценка обычно более предпочтительна в условиях, когда стандартное отклонение выборки неизвестно или когда используется маленькая выборка.
- Ваша выборка должна быть достаточной (по размеру) для того, чтобы вычислить правильный доверительный интервал.
- Доверительный интервал не указывает на вероятность получения того или иного результата. Например, если вы на 95 % уверены, что среднее значение вашей выборки лежит между 75 и 100, то доверительный интервал в 95 % не означает, что среднее значение попадает в ваш диапазон.
- Есть много методов, таких как простая случайная выборка, систематический отбор и стратифицированная выборка, с помощью которых вы можете собрать репрезентативную выборку для тестирования.
Реклама
Что вам понадобится
- Выборка
- Компьютер
- Доступ в интернет
- Учебник статистики
- Графический калькулятор
Об этой статье
Эту страницу просматривали 264 906 раз.
Была ли эта статья полезной?
Доверительный интервал для вероятности события:
Пусть вероятность
По заданному уровню надежности 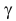
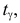
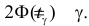
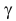
откуда 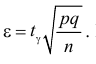
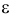
К сожалению, в формуле (3.2.2) доверительные границы для вероятности 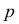
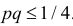
Оценка 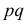
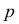
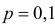
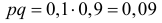
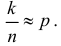
Пример:
Для обследования большой партии изделий (несколько тысяч штук) наугад выбрано 160 изделий. Среди них оказалось 56 изделий низкого сорта. Оценить долю изделий низкого сорта в этой партии с надежностью 0,95.
Решение. Так как партия изделий крупная, то для упрощения можно считать, что по мере выбора изделий состав партии заметно не изменяется и вероятность выбрать наугад изделие низкого сорта равна доле низкосортных изделий в этой партии. Тогда задача сводится к построению доверительного интервала для вероятности выбрать из этой партии изделие низкого сорта. Частота изделий низкого сорта в выборке равна 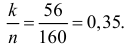
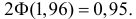
или 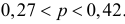
Ответ. От 27% до 42%.
Пример:
Было проведено 400 испытаний механизма катапультирования. В этих испытания не зарегистрировано ни одного отказа. С надежностью 0,95 оценить вероятность отказа механизма катапультирования.
Решение. В данной серии испытаний частота появления отказа 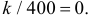
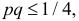
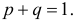
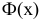
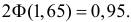
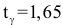
Еще раз подчеркнем, что доверительный интервал (3.2.3) построен в расчете на худший вариант, когда вероятность события близка к 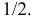
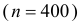
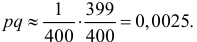
или 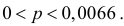
Ответ.
Пример:
При штамповке 70% деталей выходит первым сортом, 20% – вторым и 10% – третьим. Определить, сколько нужно взять деталей, чтобы с вероятностью равной 0,997 можно было утверждать, что доля первосортных среди них будет отличаться от вероятности изготовления первосортной детали не более чем на 0,05 в ту или другую сторону? Ответить на тот же вопрос, если процент первосортных деталей неизвестен.
Решение. Изготовление каждой детали можно считать независимым испытанием с вероятностью «успеха» 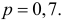
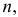
По таблице функции Лапласа (см. прил., табл. П2) находим, что 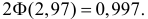
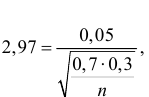
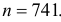
Учитывая, что 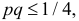
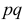
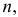
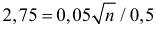
Ответ. 741; 882.
Доверительные вероятности, доверительные интервалы
В материалах сегодняшней лекции мы рассмотрим доверительные вероятности и доверительные интервалы.
При статистической обработке результатов наблюдений необходимо знать не только точечную оценку 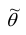
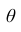
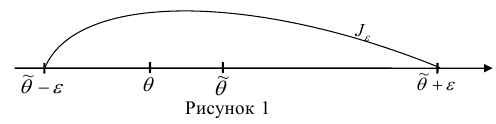
Доверительным интервалом для параметра 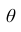
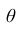
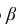
Число 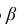
Пусть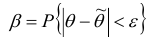
0,95,…).
Так как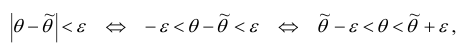
интервал 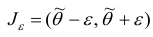
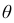
Интервал 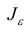
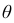
Покажем, как найти доверительный интервал для математического ожидания 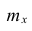
Пусть 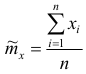
Используя центральную предельную теорему, можно считать, что случайная величина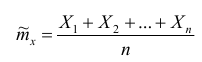
Тогда
Отсюда
Здесь 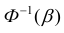
значению 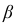
Таким образом, доверительный интервал для математического ожидании имеет вид
Заключение по лекции:
В лекции мы рассмотрели доверительные вероятности и доверительные интервалы.
- Проверка гипотезы о равенстве вероятностей
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Проверка статистических гипотез
- Вероятность и риск
- Определения вероятности событий
- Предельные теоремы теории вероятностей
- Точечные оценки, свойства оценок

![{displaystyle mathbb {D} ={D|D:mathbb {R} to [0,1],D(x)leq D(y){text{ for all }}x<y}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/173c1ccf960f10cf05977467c066c4dd5ed4e5e5)

![{displaystyle {begin{aligned}forall xin mathbb {R} :qquad &{overline {F}}(x)leq F(x)leq {underline {F}}(x)\[6pt]&int _{mathbb {R} }xdF(x)in m&&{text{expectation condition}}\&int _{mathbb {R} }x^{2}dF(x)-left(int _{mathbb {R} }xdF(x)right)^{2}in v&&{text{variance condition}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c36134180b8d189741c472bfecc6b971d50f998)
![{displaystyle {begin{cases}F:mathbb {R} to [0,1]\xmapsto Pr(Xleq x)end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/699eda9b337e4d7f765e752f6796e875d5a5b97e)

![{displaystyle Xsim A=[A_{1},A_{2}],quad {text{and}}quad Ysim B=[B_{1},B_{2}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4749447e0fab28de80afe70cfe490e024c06bcaa)
![{displaystyle left[A_{1}*B_{1},A_{2}*B_{2}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42b46a7fa9b744b3e3583e2a53e9f6f7f3f26105)
![{displaystyle Zsim left[sup _{z=x+y}max(F(x)+G(y)-1,0),inf _{z=x+y}min(F(x)+G(y),1)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4048dcecff5cd096ca9860f5c43cc8483b7a889c)