Библиографическое описание:
Баладжонзода, Сулаймончони Додарджон. Доказательство значения постоянной всемирного тяготения относительно движения Луны вокруг Земли / Сулаймончони Додарджон Баладжонзода, Саидхуджаи Чурабег Одиназода. — Текст : непосредственный // Молодой ученый. — 2022. — № 22 (417). — С. 445-448. — URL: https://moluch.ru/archive/417/91927/ (дата обращения: 25.05.2023).
Все тела в природе притягиваются друг к другу. Закон, которому подчиняется эта гравитация, был установлен Ньютоном и называется законом всемирного тяготения. Здесь G — гравитационная постоянная, которую также называют коэффициентом пропорциональности, цель постоянного доказательства гравитации — определить движение Луны вокруг Земли и использовать его для решения задач.
Впервые числовое значение постоянной гравитации было определено английским ученым Г. Кавендиш в 1798 году с помощью очень редкого метода крутильных весов.
Два свинцовых шарика массой m (каждый из них 729 г) закреплены на концах коромысла возле проволочных шаров M (по 158 кг каждый) (см.: к рисунку 1 а, б). Коромысло висит на гибкой веревке, через которую можно измерить гравитационную силу шаров. Расстояние между штоками можно изменить с помощью рулевой тяги. Наиболее точное значение определяется различными методами, которая равно G = 6,67 10–
11
Н
м
2
/кг
2
а)б)
Рис. 1
Если m
1
= m
2
=1 кг, а r = 1 м, то G число будет равно F. То есть две сферы массой 1 кг, расположенные на расстоянии 1 м друг от друга, притягиваются друг к другу силой 6,67 10–
11
Н.
Этот закон был принят после появления теории Коперника и законов Кеплера, которые определяются как таковые.
Первый закон Кеплера
. Все планеты движутся по эллипсу, и в одной из его вершин находится Солнце.
Второй закон Кеплера
. Радиусы планет в равные моменты времени рисуют большие равные друг с другом области.
Третий закон Кеплера
. Квадраты звездного круга планет вокруг Солнца пропорциональны кубам их эллиптических полутонов. В математическом виде пишется таким образом.
Используя выше упомянутые законы английский ученый И. Ньютон открыл постоянную гравитации, перед учеными того времени встал вопрос: Почему планеты постоянно вращаются вокруг Солнца и меняют свою скорость, как по направлению, так и по величине?».
Ньютон дал полный ответ на этот вопрос. На основании второго закона динамики он установил, что скорость тела изменится тогда, когда к нему будет приложена внешняя сила. Так как Луна вращается вокруг Земли и меняет свою скорость, то можно с уверенностью сказать, что на нее действует какая-то центральная сила, и под действием этой силы тело приобретает ускорение
Чтобы определить гравитационную постоянную, мы принимаем орбиту движения Луны вокруг Земли по кругу. Затем в качестве центробежной силы мы принимаем гравитационную силу между Землей и Луной. Величина этой силы равна модулю центробежной силы. Здесь окружность орбиты Луны вокруг Земли равна 27,32 суток, расстояние между Землей и Луной равно 384400 км, а масса Земли равна 6•1024 кг.
Методика доказательства всемирного тяготения
Дано: Решение:
T=27,32с.т =2360448с В соответствии с вышеизложенным
r=3,844
м пишем: F
т
=
: F
ц
M=6
здесь сила тяготения, равная центробежной силе
Fт =Fц
G-?
— умножив обе стороны формулы на
, получим такую формулу:
; (1)
, то есть:
(2)
Ставим значение выражения (2) в (1):
;(1)
Обе стороны умножаем на —
, находим —
.
(3) Здесь заменяем
, тоесть
(4) Ставим значение выражения (4) в (3) и рассчитываем:
Видно, что значение гравитационной постоянной посредством движения Луны вокруг Земля равна
.
Образец:
Задача №
1
На каком расстоянии друг от друга находятся два одинаковых шара массами по 20 т, если сила тяготения между ними 6,67•10
–5
Н?
Задача №
2
Масса Сатурна 5,7•10
26
кг, а его радиус— 6•10
7
м. Определите ускорение свободного падения на Сатурне.
Задача № 3
Вычислите ускорение свободного падения и первую космическую скорость у поверхности Луны.
Задачи для самостоятельной работы.
Задача № 1. С какой силой притягивается к центру Земли тело массой m, находящееся в глубокой шахте, если расстояние от центра Земли до тела равно г? Плотность Земли считайте всюду одинаковой и равной р.
Задача №
2.
Масса Марса 6,4•1023 кг, а его радиус— 3,4•107 м. Определите ускорение свободного падения на Марс.
Литература:
- М.Саъдулоева “Механика, физикаи молекулавӣ ва термодинамика: Дастури таълим барои мактабҳои олӣ. Душанбе: Маориф,1984с.
- Воронсов.В “ Астраномия” Душанбе.Маориф,1990с.
- А. П. Рымкевич “ Маҷмӯаи масъалаҳо аз физика” Душанбе. Маориф 1991с
- Касянов В.А “ Учебник физика-10” ООО “Дрофа” 2001
- Громов.С.В “ Учебник физика-10” Москва : Просвещение 2003
- Фриш “ Курс общей физика” Москва : Просвещение 1987
- Бакулин П. И., Кононович Э. В., Мороз В. И. Курс общей астрономии.
- Баратов Р. Б., Новиков В. П. Каменное чудо Таджикистана. — Душанбе, Ирфон, 1988. 216 с.
- Виноградов И. М. Основы теории чисел: Учебник. 2001.
- Волькенштейн В. С. Сборник задач по общему курсу физики.
- Воронцов-Вельяминов Б. А., Страут Е. К. Астрономия. 11 класс.
Основные термины (генерируются автоматически): друг, свободное падение, центробежная сила, всемирное тяготение, движение Луны, задача, Земля, значение выражения, сила тяготения, центр Земли.
Уравнение гравитации земли и луны
В данной главе мы рассмотрим, как Луна воздействует своим гравитационным полем собственно на саму Землю, т.е. на ее тело и ее движение по орбите. Последствия данного воздействия для различных земных сфер — литосферы, гидросферы, ядра, атмосферы, магнитосферы и др., а также для биосферы будут рассмотрены в следующих главах.
ВНИМАНИЕ!
Графики гравитационного взаимодействия Луны и Земли см. с помощью сервиса
ЛУННЫЙ ФАКТОР
3.1. ПАРАМЕТРЫ ЛУННОЙ ГРАВИТАЦИИ.
Расчетные соотношения и константы
Для расчета гравитационного воздействия Луны воспользуемся формулой классической физики, определяющей силу F взаимного притяжения двух тел с массами M1 и M2, центры масс которых находятся друг от друга на расстоянии R:
(1) F (н) = (G x M1 x M2) / R 2 ,
где G = 6,67384 х 10 -11 — гравитационная постоянная.
Данная формула дает значение силы притяжения в единицах системы СИ — ньютонах (н). Для целей нашего трактата удобнее и понятнее будет оперировать килограммами силы (кгс), которые получаются делением F на коэффициент 9,81, т.е.:
(2) F (кгс) = (G x M1 x M2) / (9,81 х R 2 )
Для дальнейших расчетов нам потребуются следующие константы:
- масса Луны — 7,35 х 10 22 кг;
- среднее расстояние от Земли до Луны — 384400 км;
- средний радиус Земли — 6371 км;
- масса Солнца — 1,99 х 10 30 кг;
- среднее расстояние от Земли до Солнца — 149,6 млн. км;
Сила лунного притяжения на Земле
В соответствии с формулой (2), сила притяжения Луной тела массой 1 кг, находящегося в центре Земли, при расстоянии между Луной и Землей, равном его среднему значению, равна:
(3) F = (6,67 х 10 -11 х 7,35 х 10 22 х 1) / (9,81 х 384400000 2 ) = 0, 000003382 кгс
т.е. всего 3,382 микрограмма. Для сравнения расчитаем силу притяжения того же тела Солнцем (также для среднего расстояния):
(4) F = (6,67 х 10 -11 х 1,99 х 10 30 х 1) / (9,81 х 149600000000 2 ) = 0, 000604570 кгс,
т.е. 604,570 микрограмм, что почти в 200 (двести!) раз больше, чем сила притяжения Луной.
Кроме того, вес тела, находящегося на поверхности Земли, изменяется в гораздо более существенных пределах из-за отклонения формы Земли от идеальной, неравномерности рельефа и плотности, а также влияния центробежных сил. Так, например, вес тела массой в 1 кг на полюсах больше веса на экваторе примерно на 5,3 грамма, причем одна треть этой разницы обусловлена сплюснутостью Земли с полюсов, а две трети — центробежной силой на экваторе, направленной против силы тяжести.
Как видно, прямое гравитационное воздействие Луны на конкретное тело, находящееся на Земле, является в прямом смысле микроскопическим и при этом существенно уступает гравитационному воздействию Солнца и геофизических аномалий.
Градиент силы лунного притяжения
Обратимся к рис.3.1. Для среднего значения расстояния Земля — Луна сила притяжения Луной тела массой 1 кг, расположенного на поверхности Земли в ближайшей к Луне точке составляет 3,495 микрограмм, что на 0,113 микрограмм больше, чем сила притяжения того же тела, но расположенного в центре Земли. Сила же притяжения тела, находящегося на поверхности Земли, Солнцем (также для среднего значения расстояния) составит 604,622 микрограмма, что больше силы притяжения того же тела, но расположенного в центре Земли, на 0,052 микрограмма.
Рис.3.1 Лунная и солнечная гравитация
Т.о, несмотря на неизмеримо меньшую массу Луны по сравнению с Солнцем, градиент силы ее тяготения на орбите Земли в среднем в два с лишним раза больше градиента силы тяготения Солнца.
3.2. ВЛИЯНИЕ НА ТЕЛО ЗЕМЛИ
Для иллюстрации воздействия гравитационного поля Луны на тело Земли обратимся к рис. 3.2.
Рис.3.2 Влияние гравитационного поля Луны на тело Земли.
Данный рисунок представляет весьма и весьма упрощенную картину реакции тела Земли на воздействие лунной гравитации, но достоверно отражает суть процесса — изменение формы земного шара под воздействием т.н. приливных (или приливообразующих) сил, направленных вдоль оси Земля — Луна, и противодействующих им сил упругости тела Земли. Приливные силы возникают из-за того, что точки Земли, расположенные ближе к Луне, притягиваются к ней сильнее, чем точки, расположенные дальше от нее. Иными словами, деформация тела Земли является следствием градиента силы притяжения Луны и противодействующих ему сил упругости тела Земли. В результате действия этих сил размер Земли увеличивается в направлении действия приливных сил и уменьшается в поперечном направлении, вследствие чего на поверхности образуется волна, именуемая приливной. Эта волна имеет два максимума, находящиеся на оси Земля — Луна и перемещающиеся по поверхности Земли в направлении, противоположном направлению ее вращения. Амплитуда волны зависит от широты местности и текущих параметров орбиты Луны и может достигать нескольких десятков сантиметров. Максимальное значение она будет иметь на экваторе при прохождении Луной ее перигея.
Солнце также вызывает приливную волну в теле Земли, но существенно меньшую из-за меньшего градиента силы его тяготения. Совместное гравитационное воздействие Луны и Солнца на тело Земли зависит от их взаимного расположения. Максимально значение приливных сил и, соответственно, максимальная амплитуда приливной волны достигается при расположении всех трех объектов на одной оси, т.е. в состоянии т.н. сизигии (выравнивания), что имеет место при новолунии (Луна и Солнце в «соединении») или при полнолунии (Луна и Солнце в «оппозиции»). Данные конфигурации иллюстрируются рис. 3.3 и 3.4.
Рис.3.3 Совместное влияние гравитационных полей Луны и Солнца на тело Земли
в «соединении» (в новолуние).
Рис.3.4 Совместное влияние гравитационных полей Луны и Солнца на тело Земли
в «оппозиции» (в полнолуние).
По мере отклонения Луны и Солнца от линии сизигии вызываемые ими приливные силы и, соответственно, приливные волны начинают приобретать самостоятельный характер, их сумма уменьшается, а степень их противодействия друг другу растет. Противодействие достигает максимума, когда угол между направлениями на Луну и Солнце из центра Земли равен 90°, т.е. данные тела находятся в «квадрате», а Луна, соответственно, находится в фазе четверти (первой или последней). В этой конфигурации приливные силы Луны и Солнца действуют на форму тела Земли строго противоположно, соответствующие приливные волны на поверхности максимально разнесены, а их амплитуда минимальна, что иллюстрируется рис. 3.5.
Рис.3.5 Совместное влияние гравитационных полей Луны и Солнца на тело Земли в «квадрате».
Примечание. «Соединение», «оппозиция», «квадрат» (или «квадратура») — термины, используемые в астрономии и астрологии для определения геометрии взаимного расположения двух небесных тел или точек относительно Земли. Подробнее см. Лунные аспекты.
Физика земных приливных процессов под воздействием гравитационных полей Луны и Солнца весьма сложна и требует учета большого числа параметров. На эту тему было разработано большое число различных теорий, проведено много экспериментальных исследований, написано огромное количество статей, монографий и диссертаций. Даже на сегодняшней день в этой области остается много «белых» пятен, противоречащих друг другу точек зрения и альтернативных подходов. Для желающих углубиться в проблематику земных приливов можно рекомендовать фундаментальное исследование П. Мельхиора «Земные приливы» (пер. с англ., М., «Мир», 1968 г. 483 страницы).
3.3. ВЛИЯНИЕ НА ОРБИТУ ЗЕМЛИ
Как было отмечено в п.1.1 главы 1, Луна для естественного спутника планеты обладает аномально большой массой, поэтому более корректно считать, что Земля и Луна образуют двойную планетную систему, вращающуюся вокруг общего центра масс, который смещен относительно центра Земли в среднем на 4670 км. Вследствие этого Земля, вращаясь вокруг своей центральной оси, одновременно вращается и вокруг этого центра масс с периодом, равным синодическому лунному месяцу, т.е. 29,530588 солнечных суток. В результате на эллиптическую орбиту Земли накладывается переменнная «модулирующая» составляющая с соответствующей амплитудой и периодом (см. рис.3.6).
Рис.3.6 Модуляция орбиты Земли лунной гравитацией
Эта составляющая изменяет расстояние от Земли до Солнца, что приводит к колебаниям солнечной гравитации примерно на ± 450 мкгс, практически не влияя на ее градиент. Кроме того, она создает определенные силы инерции, внося дополнительный вклад в изменение силы тяжести в зависимости от положения тела на поверхности Земли, а также незначительно влияет на величину достигающей Земли солнечной энергии (см. здесь).
3.4. КРАТКОЕ РЕЗЮМЕ
Следствием воздействия лунной гравитации на Землю являются два фундаментальных явления:
- Лунные приливы на поверхности Земли — периодических изменений уровня земной поверхности, синхронизированные с суточным вращением Земли и перемещением Луны по орбите.
- Наложение на земную орбиту переменной составляющей, синхронизированной с вращением системы Земля — Луна вокруг общего центра масс.
Данные явления являются главными механизмами воздействия Луны на земные сферы — литосферу, гидросферу, земное ядро, атмосферу, магнитосферу и др. Более подробно об этом — в следующей главе.
Взаимное притяжение Земли и Луны
Что такое притяжение Земли и Луны? Это сила и взаимодействие материи, свойственное всем телам и предметам в нашей Вселенной. По другому, называется гравитацией или всемирным тяготением.
Безусловно, каждый слышал это понятие, но не все понимают его значение и роль в окружающем нас мире. Хотя во многом благодаря силам гравитации этот мир и существует в таком виде, каким мы его наблюдаем вокруг себя. Можно сказать, что земная жизнь напрямую зависит от данного явления.

Сила гравитации на Земле
Гравитационное поле Земли представляет собой поле силы тяжести, которое формируется земным тяготением и центробежной силой планеты, вызванной её вращение вокруг своей оси.
Гравитацию можно рассчитать, если знать массу тел и расстояние между их центрами. Также следует учитывать, гравитационное поле. Поскольку чем оно сильнее, тем больше будет масса тела и, соответственно, его ускорение.
С какой силой притягивается к Земле или точнее, как рассчитать силы гравитации, можно ознакомиться тут.
Притяжение Земли и Луны
Не секрет, что Луна является естественным спутником нашей планеты. То есть сила притяжения Земли удерживает её возле себя. Однако учёные установили, что расстояние до спутника ежегодно увеличивается почти на 4 см. Почему это происходит, рассмотрим ниже.
Поскольку лунные значения размера и массы меньше нашей планеты, то его сила притяжения намного слабее.

Как стало известно, существует взаимное притяжение Земли и Луны. Разумеется, взаимодействие земной и лунной стороны не проходит незаметно для обоих. По данным учёных, гравитационное поле нашего спутника влияет на разные земные сферы.
Главным образом, лунная гравитация формирует на Земле периодические изменения уровня земной поверхности. Прежде всего, такие изменения связаны с вращением планеты вокруг совей оси и движением Луны по орбите. По-другому их называют лунными приливами.

Что такое лунные приливы и отливы?
Как оказалось, два раза за сутки происходит повышение и понижение уровня воды на водных просторах Земли. Это связано с притяжением Луной отдельных частиц с земной поверхности. То есть, те элементы, которые находятся ближе к ней, притягиваются сильнее (расстояние между ними уменьшается), и наоборот. А так как наша планета беспрерывно вращается, то и влияние на определенные частицы меняется. Наибольшее влияние оказывается на водную оболочку.
Так вот, сторона, обращенная к Луне в определенный промежуток времени, испытывает большую силу притяжения к ней. В результате вода на этой стороне поднимается, образуя прилив, тем самым снижая уровень воды на противоположной стороне, формируя отлив.
Кроме того, из-за земного вращения приливная волна движется в направлении с запада на восток. А также она опережает лунное движение. В свою очередь, эта борьба на опережение увеличивает скорость движения Луны. Собственно говоря, вот и причина её удаления от Земли.
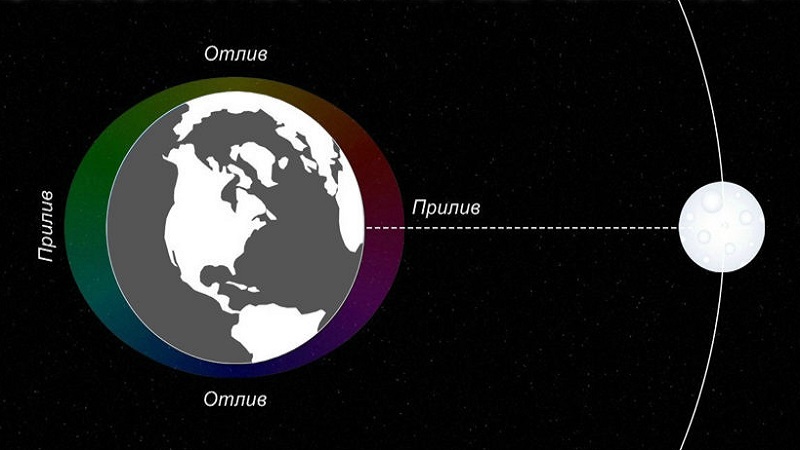
Однако, перемещение воды в океанах влияет и на саму планету. Поскольку приливная волна практически постоянно наталкивается на материки, что создает для неё препятствия. В итоге, эти преграды, вращение планеты и лунная гравитация вызывают силу, которая действует противоположно земной поверхности.
Как результат, происходит уменьшение скорости вращения Земли вокруг своей оси. Поэтому мы наблюдаем увеличение продолжительности оборота планеты, и соответственно увеличение продолжительности дня. Конечно, процесс данного роста протекает очень медленно. Но его наличие отрицать сложно.
Как видно, любой происходящий процесс на планете, нашей или любой другой, обязательно связан с какими-либо процессами на других объектах. Это могут быть как земные, скажем ближние, объекты, так и космические тела. Все во Вселенной взаимосвязанно и непрерывно. Вероятно, наша задача не просто узнать и изучить взаимодействие, но и использовать накопленные знания для поддержания и сохранения жизни.
Идеальное одиночество и покой — лучшее, что способен подарить людям единственный спутник Земли.
Моделирование динамических систем: Как движется Луна?
Светлой памяти моего учителя — первого декана физико-математического факультета Новочеркасского политехнического института, заведующего кафедрой «Теоретическая механика» Кабелькова Александра Николаевича
Введение
Август, лето подходит к концу. Народ яростно рванул на моря, да оно и неудивительно — самый сезон. А на Хабре, тем временем, буйным цветом распускается и пахнет лженаука. Если говорить о теме данного выпуска «Моделирования. », то в нем мы совместим приятное с полезным — продолжим обещанный цикл и совсем чуть-чуть поборемся с этой самой лженаукой за пытливые умы современной молодежи.
А вопрос ведь действительной не праздный — со школьных лет мы привыкли считать, что наш ближайший спутник в космическом пространстве — Луна движется вокруг Земли с периодом 29,5 суток, особенно не вдаваясь в сопутствующие подробности. На самом же деле наша соседка своеобразный и в какой-то степени уникальный астрономический объект, с движением которого вокруг Земли не всё так просто, как, возможно хотелось бы некоторым моим коллегам из ближайшего зарубежья.
Итак, оставив полемику в стороне, попытаемся с разных сторон, в меру своей компетенции, рассмотреть эту безусловно красивую, интересную и очень показательную задачу.
1. Закон всемирного тяготения и какие выводы мы можем из него сделать
где m1, m2 — массы, соответственно Луны и Земли; G = 6,67e-11 м 3 /(кг * с 2 ) — гравитационная постоянная; r1,2 — расстояние между центрами Луны и Земли. Если принимать во внимание только эту силу, то, решив задачу о движении Луны как спутника Земли и научившись рассчитывать положение Луны на небе на фоне звезд, мы довольно скоро убедимся, путем прямых измерений экваториальных координат Луны, что в нашей консерватории не всё так гладко как хотелось бы. И дело здесь не в законе всемирного тяготения (а на ранних этапах развития небесной механики такие мысли высказывались весьма нередко), а в неучтенном возмущении движения Луны со стороны других тел. Каких? Смотрим на небо и наш взгляд сразу упирается в здоровенный, массой аж 1,99e30 килограмм плазменный шар прямо у нас под носом — Солнце. Луна притягивается к Солнцу? Ещё как, с силой, равной по модулю
где m3 — масса Солнца; r1,3 — расстояние от Луны до Солнца. Сравним эту силу с предыдущей
Возьмем положение тел, в котором притяжение Луны к Солнцу будет минимальным: все три тела на одной прямой и Земля располагается между Луной и Солнцем. В этом случае наша формула примет вид:
где , м — среднее расстояние от Земли до Луны; , м — среднее расстояние от Земли до Солнца. Подставим в эту формулу реальные параметры
Вот это номер! Получается Луна притягивается к Солнцу силой, более чем в два раза превышающей силу её притяжения к Земле.
Подобное возмущение уже нельзя не учитывать и оно определенно повлияет на конечную траекторию движения Луны. Пойдем дальше, принимая во внимание допущение о том, что орбита Земли круговая с радиусом a, найдем геометрическое место точек вокруг Земли, где сила притяжения любого объекта к Земле равна силе его притяжения к Солнцу. Это будет сфера, с радиусом
смещенная вдоль прямой, соединяющей Землю и Солнце в сторону противоположенную направлению на Солнце на расстояние
где — отношение массы Земли к массе Солнца. Подставив численные значения параметров получим фактические размеры данной области: R = 259300 километров, и l = 450 километров. Эта сфера носит название сферы тяготения Земли относительно Солнца.
Известная нам орбита Луны лежит вне этой области. То есть в любой точке траектории Луна испытывает со стороны Солнца существенно большее притяжение, чем со стороны Земли.
2. Спутник или планета? Гравитационная сфера действия
Эта информация, часто порождает споры, о том, что Луна не спутник Земли, а самостоятельная планета Солнечной системы, орбита которой возмущена притяжением близкой Земли.
Оценим возмущение, вносимое Солнцем в траекторию Луны относительно Земли, а так же возмущение, вносимое Землей в траекторию Луны относительно Солнца, воспользовавшись критерием, предложенным П. Лапласом. Рассмотрим три тела: Солнце (S), Землю (E) и Луну (M).
Примем допущение, что орбиты Земли относительно Солнца и Луны относительно Земли являются круговыми.
С другой стороны, в соответствии с теоремой Кориолиса, абсолютное ускорение Луны
где — переносное ускорение, равное ускорению Земли относительно Солнца; — ускорение Луны относительно Земли. Ускорения Кориолиса здесь не будет — выбранная нами система координат движется поступательно. Отсюда получаем ускорение Луны относительно Земли
Часть этого ускорения, равная обусловлена притяжением Луны к Земле и характеризует её невозмущенное геоцентрическое движение. Оставшаяся часть
ускорение Луны, вызванное возмущением со стороны Солнца.
Если рассматривать движение Луны в гелиоцентрической инерциальной системе отсчета, то всё намного проще, ускорение характеризует невозмущенное гелиоцентрическое движение Луны, а ускорение — возмущение этого движения со стороны Земли.
При существующих в текущую эпоху параметрах орбит Земли и Луны, в каждой точке траектории Луны справедливо неравенство
что можно проверить и непосредственным вычислением, но я сошлюсь на источник, дабы излишне не загромождать статью.
Что означает неравенство (1)? Да то, что в относительном выражении эффект от возмущения Луны Солнцем (причем очень существенно) меньше эффекта от притяжения Луны к Земле. И наоборот, возмущение Землей геолиоцентрической траектории Луны оказывает решающее влияние на характер её движения. Влияние земной гравитации в данном случае более существенно, а значит Луна «принадлежит» Земле по праву и является её спутником.
Интересным является другое — превратив неравенство (1) в уравнение можно найти геометрическое место точек, где эффекты возмущения Луны (да и любого другого тела) Землей и Солнцем одинаковы. К сожалению это у же не так просто, как в случае со сферой тяготения. Расчеты показывают, что данная поверхность описывается уравнением сумасшедшего порядка, но близка к эллипсоиду вращения. Всё что мы может сделать без лишних заморочек, это оценить общие габариты этой поверхности относительно центра Земли. Решая численно уравнение
относительно расстояния от центра Земли до искомой поверхности на достаточном количестве точек, получаем сечение искомой поверхности плоскостью эклиптики
Для наглядности здесь показаны и геоцентрическая орбита Луны и, найденная нами выше сфера тяготения Земли относительно Солнца. Из рисунка видно, что сфера влияния, или сфера гравитационного действия Земли относительно Солнца есть поверхность вращения относительно оси X, сплющенная вдоль прямой, соединяющей Землю и Солнце (вдоль оси затмений). Орбита Луны находится глубоко внутри этой воображаемой поверхности.
Для практических расчетов данную поверхность удобно аппроксимировать сферой с центром в центра Земли и радиусом равным
где m — масса меньшего небесного тела; M — масса большего тела, в поле тяготения которого движется меньшее тело; a — расстояние между центрами тел. В нашем случае
Вот этот недоделанный миллион километров и есть тот теоретический предел, за который власть старушки Земли не распространяется — её влияние на траектории астрономических объектов настолько мало, что им можно пренебречь. А значит, запустить Луну по круговой орбите на расстоянии 38,4 млн. километров от Земли (как делают некоторые лингвисты) не получится, это физически невозможно.
Эта сфера, для сравнения, показана на рисунке синей пунктирной линией. При оценочных расчетах принято считать, что тело, находящееся внутри данной сферы будет испытывать тяготение исключительно со стороны Земли. Если тело находится снаружи данной сферы — считаем что тело движется в поле тяготения Солнца. В практической космонавтике известен метод сопряжения конических сечений, позволяющий приближенно рассчитать траекторию космического аппарата, используя решение задачи двух тел. При этом всё пространство, которое преодолевает аппарат разбивается на подобные сферы влияния.
Например, теперь понятно, для того чтобы иметь теоретическую возможность совершить маневры для выхода на окололунную орбиту, космический аппарат должен попасть внутрь сферы действия Луны относительно Земли. Её радиус легко рассчитать по формуле (3) и он равен 66 тысяч километров.
Таким образом, Луна справедливо может считаться спутником Земли. Однако, ввиду существенно влияния гравитационного поля Солнца она движется не в центральном гравитационном поле, а значит её траектория не является коническим сечением.
3. Задача трех тел в классической постановке
Итак, рассмотрим модельную задачу в общей постановке, известную в небесной механике как задача трех тел. Рассмотрим три тела произвольной массы, расположенных произвольным образом в пространстве и движущихся исключительно под действием сил взаимного гравитационного притяжения
Тела считаем материальными точками. Положение тел будем отсчитывать в произвольном базисе, с которым связана инерциальная система отсчета Oxyz. Положение каждого из тел задается радиус-вектором соответственно , и . На каждое тело действует сила гравитационного притяжения со стороны двух других тел, причем в соответствии с третьей аксиомой динамики точки (3-й закон Ньютона)
Запишем дифференциальные уравнения движения каждой точки в векторной форме
В соответствии с законом всемирного тяготения, силы взаимодействия направлены вдоль векторов
Вдоль каждого из этих векторов выпустим соответствующий орт
тогда каждая из гравитационных сил рассчитывается по формуле
С учетом всего этого система уравнений движения принимает вид
Введем обозначение, принятое в небесной механике
— гравитационный параметр притягивающего центра. Тогда уравнения движения примут окончательный векторный вид
4. Нормирование уравнений к безразмерным переменным
Довольно популярным приемом при математическом моделировании является приведение дифференциальных уравнений и прочих соотношений, описывающих процесс, к безразмерным фазовым координатам и безразмерному времени. Нормируются так же и другие параметры. Это позволяет рассматривать, хоть и с применением численного моделирования, но в достаточно общем виде целый класс типовых задач. Вопрос о том, насколько это оправдано в каждой решаемой задаче оставляю открытым, но соглашусь, что в данном случае такой подход вполне справедлив.
Итак, введем некое абстрактное небесное тело с гравитационным параметром , такое, что период обращения спутника по эллиптической орбите с большой полуосью вокруг него равен . Все эти величины, в силу законов механики, связаны соотношением
Введем замену параметров. Для положения точек нашей системы
где — безразмерный радиус-вектор i-й точки;
для гравитационных параметров тел
где — безразмерный гравитационный параметр i-й точки;
для времени
где — безразмерное время.
Теперь пересчитаем ускорения точек системы через эти безразмерные параметры. Применим прямое двукратное дифференцирование по времени. Для скоростей
При подстановке полученных соотношений в уравнения движения всё элегантно схлопывается в красивые уравнения:
Данная система уравнений до сих пор считается не интегрируемой в аналитических функциях. Почему считается а не является? Потому что успехи теории функции комплексного переменного привели к тому, что общее решение задачи трех тел таки появилось в 1912 году — Карлом Зундманом был найден алгоритм отыскания коэффициентов для бесконечных рядов относительно комплексного параметра, теоретически являющихся общим решением задачи трех тел. Но… для применения рядов Зундмана в практических расчетах с требуемой для них точностью требует получения такого числа членов этих рядов, что эта задача во много превосходит возможности вычислительных машин даже на сегодняшний день.
Поэтому численное интегрирование — единственный способ анализа решения уравнения (5)
5. Расчет начальных условий: добываем исходные данные
Как я уже писал ранее, прежде чем начинать численное интегрирование, следует озаботится расчетом начальных условий для решаемой задачи. В рассматриваемой задаче поиск начальных условий превращается в самостоятельную подзадачу, так как система (5) дает нам девять скалярных уравнений второго порядка, что при переходе к нормальной форме Коши повышает порядок системы ещё в 2 раза. То есть нам необходимо рассчитать целых 18 параметров — начальные положения и компоненты начальной скорости всех точек системы. Где мы возьмем данные о положении интересующих нас небесных тел? Мы живем в мире, где человек ходил по Луне — естественно человечество должно обладать информацией, как эта самая Луна движется и где она находится.
То есть, скажете вы, ты, чувак, предлагаешь нам взять с полок толстые астрономические справочники, сдуть с них пыль… Не угадали! Я предлагаю сходить за этими данными к тем, кто собственно ходил по Луне, к NASA, а именно в Лабораторию реактивного движения, Пасадена, штат Калифорния. Вот сюда — JPL Horizonts web interface.
Здесь, потратив немного времени на изучение интерфейса, мы добудем все необходимые нам данные. Выберем дату, например, да нам всё равно, но пусть это будет 27 июля 2018 года UT 20:21. Как раз в этот момент наблюдалась полная фаза лунного затмения. Программа выдаст нам огромную портянку
Бр-р-р, что это? Без паники, для того, кто хорошо учил в школе астрономию, механику и математику тут боятся нечего. Итак, самое главное конечное искомые координаты и компоненты скорости Луны.
Да-да-да, они декартовы! Если внимательно прочесть всю портянку, то мы узнаем, что начало этой системы координат совпадает с центром Земли. Плоскость XY лежит в плоскости земной орбиты (плоскости эклиптики) на эпоху J2000. Ось X направлена вдоль линии пересечения плоскости экватора Земли и эклиптики в точку весеннего равноденствия. Ось Z смотрит в направлении северного полюса Земли перпендикулярно плоскости эклиптики. Ну а ось Y дополняет всё это счастье до правой тройки векторов. По-умолчанию единицы измерения координат: астрономические единицы (умнички из NASA приводят и величину автрономической единицы в километрах). Единицы измерения скорости: астрономические единицы в день, день принимается равным 86400 секундам. Полный фарш!
Аналогичную информацию мы можем получить и для Земли
Здесь в качестве начала координат выбран барицентр (центр масс) Солнечной системы. Интересующие нас данные
Для Луны нам понадобятся координаты и скорость относительно барицентра Солнечной системы, мы можем их посчитать, а можем попросит NASA дать нам такие данные
Чудесно! Теперь необходимо слегка обработать полученные данные напильником.
6. 38 попугаев и одно попугайское крылышко
Для начала определимся с масштабом, ведь наши уравнения движения (5) записаны в безразмерной форме. Данные, предоставленные NASA сами подсказывают нам, что за масштаб координат стоит взять одну астрономическую единицу. Соответственно в качестве эталонного тела, к которому мы будем нормировать массы других тел мы возьмем Солнце, а в качестве масштаба времени — период обращения Земли вокруг Солнца.
Все это конечно очень хорошо, но мы не задали начальные условия для Солнца. «Зачем?» — спросил бы меня какой-нибудь лингвист. А я бы ответил, что Солнце отнюдь не неподвижно, а тоже вращается по своей орбите вокруг центра масс Солнечной системы. В этом можно убедится, взглянув на данные NASA для Солнца
Взглянув на параметр RG мы увидим, что Солнце вращается вокруг барицентра Солнечной системы, и на 27.07.2018 центр звезды находится от него на расстоянии в миллион километров. Радиус Солнца, для справки — 696 тысяч километров. То есть барицентр Солнечной системы лежит в полумиллионе километров от поверхности светила. Почему? Да потому что все остальные тела, взаимодействующие с Солнцем так же сообщают ему ускорение, главным образом, конечно тяжеленький Юпитер. Соответственно у Солнца тоже есть своя орбита.
Мы конечно можем выбрать эти данные в качестве начальных условий, но нет — мы же решаем модельную задачу трех тел, и Юпитер и прочие персонажи в неё не входят. Так что в ущерб реализму, зная положение и скорости Земли и Луны мы пересчитаем начальные условия для Солнца, так, чтобы центр масс системы Солнце — Земля — Луна находился в начале координат. Для центра масс нашей механической системы справедливо уравнение
Поместим центр масс в начало координат, то есть зададимся , тогда
Перейдем к безразмерным координатам и параметрам, выбрав
Дифференцируя (6) по времени и переходя к безразмерному времени получаем и соотношение для скоростей
где
Теперь напишем программу, которая сформирует начальные условия в выбранных нами «попугаях». На чем будем писать? Конечно же на Питоне! Ведь, как известно, это самый лучший язык для математического моделирования.
Однако, если уйти от сарказма, то мы действительно попробуем для этой цели питон, а почему нет? Я обязательно приведу ссылку на весь код в моем профиле Github.
7. Интегрирование уравнений движения и анализ результатов
Тогда введя вектор состояния системы
сводим (7) и (5) к одному векторному уравнению
Для интегрирования (8) с имеющимися начальными условиями напишем немного, совсем немного кода
Посмотрим что у нас получилось. Получилась пространственная траектория Луны на первые 29 суток от выбранной нами начальной точки
а так же её проекция в плоскость эклиптики.
«Эй, дядя, что ты нам впариваешь?! Это же окружность!».
Во-первых, таки не окружность — заметно смещение проекции траектории от начала координат вправо и вниз. Во-вторых — ничего не замечаете? Не, ну правда?
Обещаю подготовить обоснование того (на основе анализа погрешностей счета и данных NASA), что полученное смещение траектории не есть следствие ошибок интегрирования. Пока предлагаю читателю поверить мне на слово — это смещение есть следствие солнечного возмущения лунной траектории. Крутанем-ка еще один оборот
Во как! Причем обратите внимание на то, что исходя из начальных данных задачи Солнце находится как раз в той стороне, куда смещается траектория Луны на каждом обороте. Да это наглое Солнце ворует у нас наш любимый спутник! Ох уж это Солнце!
Можно сделать вывод, что солнечная гравитация влияет на орбиту Луны достаточно существенно — старушка не ходит по небу дважды одним и тем же путём. Картинка за полгода движения позволяет (по крайней мере качественно) убедится в этом (картинка кликабельна)
Интересно? Ещё бы. Астрономия вообще наука занятная.
Постскриптум
В вузе, где я учился и работал без малого семь лет — Новочеркасском политехе — ежегодно проводилась зональная олимпиада студентов по теоретической механике вузов Северного Кавказа. Трижды мы принимали и Всероссийскую олимпиаду. На открытии, наш главный «олимпиец», профессор Кондратенко А.И., всегда говорил: «Академик Крылов называл механику поэзией точных наук».
Я люблю механику. Всё то хорошее, чего я добился в своей жизни и карьере произошло благодаря этой науке и моим замечательным учителям. Я уважаю механику.
Поэтому, я никогда не позволю издеваться над этой наукой и нагло эксплуатировать её в своих целях никому, будь он хоть трижды доктор наук и четырежды лингвист, и разработал хоть миллион учебных программ. Я искренне считаю, что написание статей на популярном публичном ресурсе должно предусматривать их тщательную вычитку, нормальное оформление (формулы LaTeX — это не блажь разработчиков ресурса!) и отсутствие ошибок, приводящих к результатам нарушающим законы природы. Последнее вообще «маст хэв».
Я часто говорю своим студентам: «компьютер освобождает ваши руки, но это не значит, что при этом нужно отключать и мозг».
Ценить и уважать механику я призываю и вас, мои уважаемые читатели. Охотно отвечу на любые вопросы, а исходный текст примера решения задачи трех тел на языке Python, как и обещал, выкладываю в своем профиле Github.
http://habr.com/ru/post/420133/
В современной формулировке закона всемирного тяготения присутствует коэффициент , называющийся гравитационной постоянной и стоящий перед формулой особняком. Интересно, что Ньютон, открывший закон притяжения, не использовал явную форму константы, численно она была определена больше века спустя со дня смерти учёного.
Содержание
- Что такое и чему равна гравитационная постоянная
- В чём измеряется гравитационная постоянная
- Как найти гравитационную постоянную – история открытия
- Работы Ньютона
- Как была экспериментально определена гравитационная постоянная – эксперимент Кавендиша
- Измерение гравитационной постоянной
- Современная история изменений гравитационной постоянной
Что такое и чему равна гравитационная постоянная
Формула закона всемирного тяготения, известная по курсу школьной механики:
G – коэффициент пропорциональности или гравитационная постоянная;
m1, m2 – массы двух тел, испытывающих взаимное притяжение;
r – расстояние между ними.
Коэффициент пропорциональности G обозначает силу, с которой притягивается пара килограммовых объектов, расположенных друг от друга на метровом расстоянии. Значение константы обычно принимается равным:
Столь маленькое число объясняет, почему несмотря на постоянное действие гравитации люди, находящиеся рядом, не чувствуют силу тяготения – она проявляется на объектах огромных масс, имеющих высокие порядки, например, массе планет, Солнца, других звёзд.
В чём измеряется гравитационная постоянная
Несмотря на то, что гравитационная постоянная численно равна силе, её единицы измерения не ньютоны. Размерность коэффициента может показаться страшной –
, но её возникновение легко объясняется.
Согласно Международной системе единиц (системе интернациональной или СИ), сила измеряется в ньютонах, причём
то есть 1 ньютон – сила, изменяющая скорость килограммового объекта на 1 м/с за одну секунду.
После открытия закона тяготения определено: пара килограммовых тел притягивается друг к другу силой со значением, зависящим обратно пропорционально от квадрата расстояния между объектами.
То есть единица измерения гравитационной силы –
и размерность не совпадает с привычной . Требуется коэффициент, который должен уравнять единицы измерения привычной силы и силы гравитационного взаимодействия.
Проведём математические вычисления самостоятельно.
Нужно уравнять
и 
Для этого нужно разделить на 1с2 и 1кг, а также умножить на м3, получим:
Получилась требуемая размерность.
Следовательно, постоянная имеет размерность .
Как найти гравитационную постоянную – история открытия
Коэффициент G – универсальная константа, измерение которой осуществляется экспериментальным путём. Доподлинно неизвестно, кто открыл значение гравитационной постоянной, первое употребление в «Трактате по механике» Пуассона датируется 1811 годом.
Работы Ньютона
При публикации закона тяготения в трактате Ньютона отсутствовало явное обозначение константы, характеризующее гравитацию и её действие. Коэффициент не появлялся в работах по физике вплоть до конца восемнадцатого века, его точное значение не было вычислено.
Вместо известной сегодня постоянной присутствовал гравитационный параметр:
M – масса объекта, причём, масса планеты или звезды, так как гравитационный параметр нашёл широкое распространение в астрофизике.
Сегодня для объектов Солнечной системы значение параметра рассчитано точнее, чем гравитационная постоянная G и масса по отдельности, так как она не требует серьёзных экспериментов, вычисляется на основании астрономических наблюдений.
Например:
Подробнее о использовании закона всемирного тяготения в астрономии вы можете прочитать в нашей статье.
Как была экспериментально определена гравитационная постоянная – эксперимент Кавендиша
Естествоиспытатель Джон Митчел придумал эксперимент для определения массы Земли при помощи крутильных весов, однако не реализовал его. После его смерти идея опыта и аппаратура перешли к английскому физику и химику Генри Кавендишу, который, усовершенствовав прибор, провёл ряд экспериментов и осуществил задумку своего предшественника.
Главенствующая роль в опытах отводилась установке. На метровой нити из меди подвешивалось коромысло длиной 1,8 метра, на его концах устанавливалась пара свинцовых шариков диаметром 5 сантиметров, массой 775 грамм. Чуть выше крепилась поворотная ферма, причём тщательно соблюдалось требование совпадения оси вращения фермы с медной нитью. На концах поворотной штанги находилось по одному большому свинцовому шару диаметром 20 сантиметров, массой 49,5 килограмм. Чтобы избежать влияния конвекционных воздушных потоков, вся установка накрывалась плотным деревянным кожухом. Вследствие взаимодействия лёгкие шарики притягивались к тяжёлым, закручивая нить и отклоняя коромысло. Угол отклонения фиксировался двумя телескопами, а сила упругости нити приравнивалась гравитационному взаимодействию шаров.
Величина определённой силы притяжения составляла 0,17 микроньютона. Если сравнивать это значение с весом маленького шара, то оно меньше последнего примерно в 45 миллионов раз.
В результате своего эксперимента Генри Кавендиш рассчитал среднюю плотность Земли, причём его эксперимент был точным – погрешность измеренного значения в сравнении с современным значением составляет всего 0,7%. Именно Кавендишу приписывают открытие значения гравитационной постоянной, однако он никогда не задавался подобной целью при проведении своих опытов. Очевидно, величина константы определена на основании результатов его эксперимента, но кто сделал это первым, неизвестно.
Измерение гравитационной постоянной
Значение константы, полученное по измеренной Кавендишем плотности, по разным источникам разнится. Британская энциклопедия называет число, равное , с каковым некоторые современные физики. Леон Нил Купер утверждает, что экспериментально полученное число равно

.
Коэффициент пропорциональности определяли после Генри Кавендиша, причём зачастую его установку модернизировали новыми материалами. Например, в 1872 году Корню и Байль для измерения гравитационной постоянной использовали платиновые маленькие шарики и стеклянные, наполненные ртутью, большие. Результаты опыта показали значение

Современная история изменений гравитационной постоянной
Гравитационная постоянная – десятичная дробь, её значение постоянно уточняется, причём измерение коэффициента G происходит путём усовершенствования прибора Митчела и улучшения методов наблюдения. Например, в 2018 году учёные из России и Китая проводили опыты на установках разной конструкции. В первой группе применялся метод «time of swing» (TOS), где коэффициент пропорциональности зависит от колебательной частоты весов. Во второй – метод «angular acceleration feedback» (AAF), где угловое ускорение независимо вращающихся коромысел шаров измеряется системой управления с обратной связью, при этом нить поддерживается незакрученной.
По результатам команды первый метод продемонстрировал значение гравитационной постоянной , второй метод –
. Относительная погрешность составила 11,6*10-6
Комитет по данным для науки и техники (CODATA) рекомендовал на 2020 год значение коэффициента пропорциональности, равное:
Таким образом, гравитационная постоянная всё время уточняется, требуя новые, более точные способы измерения и вычисления.
Гравитационная Постоянная. Массы Земли, Луны, Солнца.
Гравитационная константа может по праву считаться самой старой физической константой.
Казалось бы, что сейчас она должна быть одной из наиболее точных констант.
Эх, как хотелось бы!
Но, увы!
Точность гравитационной постоянной в последние годы скачет.
До 1999 года предлагаемый диапазон её значений был: (6.67174 — 6.67344)·10-11
м3кг-1c-2,
с 1999 года её точность упала на два порядка: (6.663 — 6.683)·10-11 м3кг-1c-2,
с 2002 года её уточнили на порядок: (6.6732 — 6.6752)·10-11 м3кг-1c-2,
с 2006 года её ещё уточнили: (6.67361 — 6.67428)·10-11 м3кг-1c-2.
Это же можно записать короче:
до 1999 года G=6.67259(85)·10-11 м3кг-1c-2,
с 1999 года G = 6.673(10)·10-11 м3кг-1c-2,
с 2002 года G = 6.6742(10)·10-11 м3кг-1c-2,
с 2006 года G = 6.67428(67)·10-11 м3кг-1c-2.
Я малость ленив, и в этой работе я не пишу цифры в скобках, а просто подчеркиваю
сомнительные цифры в числах, к примеру, так: В 1999 году точность G упала от четырех
верных знаков 6.67259·10-11 м3кг-1c-2,
до двух верных знаков 6.673·10-11 м3кг-1c-2.
Что же произошло с гравитационной константой? Развитие космонавтики? Космические
корабли не вписываются в расчетные траектории? Не склеились какие-то расчеты? На
самом деле, 1999 год здесь указан чисто символически. Просто в 1999 году CODATA
внёс «уточнение» в рекомендованное значение гравитационной постоянной, а причиной
этого «уточнения» послужили эксперименты, проведенные в разных лабораториях мира,
которые дали сильно отличающиеся результаты. К примеру, группа немецких физиков
под руководством W.Michaelis получила значение G на 0.6% больше принятого. Марк
Фитцжеральд с сотрудниками определили G, которое оказалось на 0.1% ниже. Группа
российских физиков [В.П. Измайлов, О.В. Карагиоз, В.А. Кузнецов, В.Н. Мельников,
А.Е. Росляков. Measurement Techniques 36, 1065 (1993)] указали на наличие странных
вариаций в G до 0.7%.
The Controversy over
Newton’s Gravitational Constant
Precise Calibration
of the Intrinsic Strength of Gravity and Measuring the Mass of the Earth
Вместе с изменением точности гравитационной константы изменяется точность масс
планет. Так, до 1999 года на web-сайте ASTROPHYSICAL CONSTANTS
http://pdg.lbl.gov/ мы видели
следующие значения для гравитационной константы, масс Солнца и Земли:
G = 6.67259(85)·10-11м3кг-1c-2,
MSun = 1.98892(25)·1030 кг,
MEarth = 5.97370(76)·1024 кг;
то с 1999 по 2002 было:
G = 6.673(10)·10-11м3кг-1c-2,
MSun = 1.9889(30)·1030 кг,
MEarth = 5.974(9)·1024 кг.
с 2002 по сегодня (апрель 2006):
G = 6.673(10)·10-11м3кг-1c-2,
MSun = 1.98844(30)·1030 кг,
MEarth = 5.9723(9)·1024 кг.
А если взглянуть на один из сайтов NASA
http://nssdc.gsfc.nasa.gov/planetary/factsheet/sunfact.html,
то для масс Солнца и Земли мы увидим значения (2006):
MSun = 1 989 100·1024 кг,
MEarth = 5.9736·1024 кг.
Возникает вопрос: «А для какого G верны эти значения масс?» Очевиден ответ: «Истину
сейчас нужно искать не в G и не в M, а в произведении GM. Так, на сайте NASA мы
видим:
GMSun = 132 712·106 км3/с2,
GMEarth = 0.3986·106 км3/с2.
Зато на сайте ASTROPHYSICAL CONSTANTS мы находим очень точные комбинации, содержащие
произведение GM, а именно, шварцшильдовские радиусы Солнца и Земли (2GM/c2):
2GMSun/c2 = 2.95325008 км,
2GMEarth/c2 = 8.87005622 мм.
Точность последних величин удивляет. Никто конечно Землю и Солнце не превращал
в черные дыры, но очевидно, что шварцшильдовские радиусы получены не через массы
и гравитационную константу, а через правую сторону закона Кеплера, содержащую период
обращения спутника по орбите и её большую полуось. А последние величины действительно
можно измерить с высокой точностью. Тем не менее, двум последним цифрам в этих значениях
лично я не доверяю. (Ниже мы получим шварцшильдовские радиусы, чуть-чуть отличающиеся
от приведенных, а пока вернемся к гравитационной константе.)
А не получить ли нам теоретическое значение гравитационной константы? Это делается
элементарно. Можно даже получить не одну, а две, три, десять G. Красота. Но вот
проблема. А какая же из них ближе к истине. Оставим сомнения пока в стороне. Время
покажет, стоило ли это делать. Приведем несколько выводов G.
Один из выводов достаточно точного значения G был получен мной в феврале этого
года (2006) и я его помещу чуть ниже. А здесь поместим вывод гравитационной константы,
полученный мной в 2001 году. Назовем его метод G-2001. Замечание: в 2001 году фундаментальные
константы (e, m,..) имели значения, чуть-чуть отличающиеся от сегодняшних. Перерасчет
в связи с этим я не делаю, а оставляю результаты такими какими они были в 2001 году.
Вывод гравитационной константы «Метод G-2001» и массы Солнца,
Земли, Луны.
Текст от 1 апреля 2001 года: Подойдем к этой проблеме гравитационной константы
другой стороны. Может быть, G действительно испытывает значительные вариации. Может
быть, это связано с распространением гравитационных волн длиной в несколько дней.
А в этой работе, кстати, предсказан максимум гравитационных колебаний длиной волны
порядка 6 световых дней. Этот максимум есть зеркальное отражение относительно граничной
частоты между фотоном и гравитоном. Этот максимум, по моему убеждению, ответственен
за наличие циклонов и антициклонов, за периодичность в изменении погоды. См.
Пространственно- временная симметрия. Тем не менее, среднестатистическое
значение гравитационной постоянной должно быть очень точным.
В настоящей работе развиты Нормированные Единицы, в
которых граничная частота n0, граничная длина
волны l0, граничный период колебаний t0
приняты равными единицам. Гравитационная постоянная в нормированных единицах безразмерна,
обозначена той же буквой G, но со штрихом G’, и может быть получена по формулам:
если определяющая гравитирующая частица — протон то
1. G’ = Gt02mpr/l03
= 3.0398508967·10-60,
2. G’ = N(fgr/fel)pr-el/(2p2)
= 3.0398508967·10-60,
3. G’ = (a/e0/G)1/2e/mel/2
= 3.0398508967·10-60,
4. G’ = 1/Exp(a+1/a) =
3.0398508967·10-60;
или:
если определяющая гравитирующая частица — атом водорода то
1. G’ = Gt02mH/l03
= 3.043933809·10-60,
2. G’ = N(fgr/fel)H-el/(2p2)
= 3.043933809·10-60,
3. G’ = (a/e0/G)1/2e/mel/2
= 3.043933809·10-60,
4. G’ = 1/(sExp(1/a))
= 3.062114896E-60 / s = 3.043933809·10-60.
Последние результаты, полученные в январе феврале 2001 года, показали, что второй
вариант, где определяющей гравитирующей частицей является атом водорода, оказывается
предпочтительней. Поэтому, далее мы исследуем именно второй вариант. Но что же прячется
за буквой s в последней формуле. В случае протона, как
определяющей частицы, мы вводили релятивистскую поправку в формулу G’ = 1/Exp(1/a).
В результате формула изуродовалась, а её хорошее приближение приобрело вид G’ =
1/Exp(a+1/a). В случае с водородом
этого делать не хочется, и мы попробуем поискать, а что же должно быть на месте
s?
Отношение 3.062114896·10-60 / 3.043933809·10-60
= 1.0059730 = s.
Отношение ln(1/G’) / (1/a) = 1.00004345664
= 1 +a ln(s).
Разложим по полочкам приведенные выше формулы, содержащие G’.
Формула 1: G’ = Gt02mH/l03
G’ — гравитационная константа в нормированных единицах,
безразмерна; точнее — сократимая комбинация вспышек: [!ОБ/пр], [!/!];
G — гравитационная константа в метрических единицах размерная: [Н·м2/кг2]
или [м3/кг/c2];
mH — масса атома водорода; mH
= 1,67·10-27кг в метрических единицах, или mH = 1 нормированных
единиц массы;
n0, l0, t0
— граничные величины (частота, длина волны, период) между фотоном и гравитоном,
или между электромагнитными и гравитационными волнами. Эти же величины являются
коэффициентами перехода от нормированных величин к метрическим.
Пример 1: L = 3000 метров, L’ = L/l0 =
3000м / 408181м/! = 0.00735! То есть, 3000 метров приближенно равно 0.00735
вспышек.
Пример 2: T = 3000 секунд, T’ = T/t0 = 3с / 0.00136с/! = 2203! То
есть, 3 секунды приближенно равно 2203 вспышек.
Пример 3: G = 6.672606660·10-11 м3/кг/c2,
G’ = Gt02mH/l03
= 3.043933809·10-60.
Итак, простейший смысл первой из приведенных формул заключается в обычном переводе
G из метрических единиц в нормированные. Более глубокий смысл этой формулы заключается
в приведении этой формулы к третьему закону Кеплера
G’ = Gt02mH/l03;
GmH/G’= l03/t02;
mH ~ mpr+mel;
G(mpr+mel) = l03/t2*G’
Сравни: G(M+m) = 4p2a3/t2.
Формула 2 и 3: G’ = N(fgr/fel)H-el/(2p2)
= (a/e0/G)1/2e/mel/2
Эти формулы связывают электромагнитные и гравитационные взаимодействия и
являются просто разной формой записи одного и того же, то есть, это не система
из двух уравнений. В эти формулы входят следующие величины:
N — Число Инерциальных Систем Отсчета в точке для mH; N — размеры
Вселенной в нормированных единицах; N — число уровней энергии нормированной
единицы массы mH в пространстве. Единицы измерения частное от вспышек
разного уровня: вспышек на оборот; !/об; вспышка нашего масштаба на вселенскую
вспышку. Вспышка есть акт пространственно-временной синхронизации. N определяется
через решение одного из уравнений N = sqr(mHc2/(hH)),
N = sqr(ap(fel/fgr)el-el),
где fel/fgr)e-e отношение электрических сил
к гравитационным между двумя электронами.
(fgr/fel)H-el — эту величину в случае,
если определяющей массой является атом водорода, не назовешь отношением сил
между атомом водорода и электроном. Лучше сказать, что это комбинация констант:
(fgr/fel)H-el = (GmHmel/R2)
/ (e2/(4pe0R2))
= (GmHmel) / (e2/(4pe0))
= 4pe0GmHmel/e2.
(Последнее является слабым местом в выборе между протоном и атомом водорода
на роль определяющей массы частицы во Вселенной.)
Формула 4: 1/G’ = sExp(1/a)
Эмпирическая формула. Так действительно должно быть. Гравитация и электромагнетизм
симметричны друг другу. И это находит своё отражение в связи между безразмерными
константами электрического и гравитационного взаимодействия. Форма записи была
бы изумительна без корявого коэффициента s. (Вспомним
лямбда-коэффициент ОТО.) Поэтому, a есть постоянная
тонкой структуры электромагнитных взаимодействий, а G’ есть постоянная тонкой
структуры гравитационных взаимодействий.Итак, нам еще предстоит выяснить, что же такое:
ln(1/G’) / (1/a) = 1.00004345664 = 1 +a
ln(s), или
(1/Exp(1/a)) / G’ = 3.062114896·10-60
/ 3.043933809·10-60 = 1.0059730 = s.Массы Земли, Луны, Солнца
Здесь мы попытаемся получить массы Земли, Луны, Солнца несколько нетрадиционным
способом. Прежде всего, укажем, что эти массы сильно отличаются от справочника к
справочнику. Поместим значения из разных справочников в таблицу. В последнюю колонку,
красным цветом я ввожу свои данные, которые мы получим ниже, при условии нескольких
«ЕСЛИ». То есть, результаты верны, ЕСЛИ такие-то предположение верны… А сначала
в таблице идут значения, приведенные в современных справочных сайтах по состоянию
на март 2001 года.
1. http://pdg.lbl.gov/
2. http://www.seds.org/nineplanets/nineplanets/earth.html
3. http://nssdc.gsfc.nasa.gov/planetary/factsheet/sunfact.html
4. «устаревшие значения» из энциклопедического словаря по физике за 1983 год, который
переиздан в 1999 году.
5. Мои результаты (2001).
| . | 1 | 2 | 3 | 4 | 5 (если…!) |
| MEarth (*1024 кг) | 5.974(9) | 5.972 | 5.9736 | 5.976 | 5.973538542 |
| MMoon (*1022 кг) | — | 7.35 | 7.349 | 7.35 | 7.3463 |
| MSun (*1030 кг) | 1.9889(30) | 1.989 | 1.9891 | 1.989 | 1.988909058 |
| LSun (*1026 Вт) | 3.846(8) | 3.86 | 3.846 | 3.826 | 3.841740089 |
| GMSun (*1017 м3/с2) | — | — | 1.32712 | — | 1.327120783 |
| 2GMSun /c2 (км) | 2.95325008 | — | — | — | 2.953242026 |
| GMEarth (*1014 м3/с2) | — | — | 3.986 | — | 3.985907306 |
| 2GMEarth /c2 (мм) | 8.87005622 | — | — | — | 8.869839976 |
Давайте попытаемся постулировать следующие утверждения:
Мир предельно симметричен. Для того, чтобы на планете Земля в Солнечной системе
развилась разумная жизнь необходимо чтобы: Солнце миллиарды лет имело неизменную
мощность, строго определяемую по формуле L = GMSun2H/(4l0).
А Земля должна миллиарды лет занимать одну и ту же резонансную орбиту с
квантовым числом пять, точно. Следовательно, формула
H = GMEarth/(5r)2/c верна точно. Пятерка несколько раз
входит в качестве простого множителя в отношение сил между электронами, то есть,
гипотеза «(fgr/fel)electron-electron = 2.4·10-43
точно» верна. Следовательно, N = 1022(ap/24)1/2
= 3.090665321·1020 (точность зависит только от
a).
А через N, по формуле Gtheory = e2a
/(4e0N2mel2)
мы уточняем гравитационную константу 1986 года на 4 знака, или G1999
уточняем на 6 знаков:
G1999 = 6.673·10-11м3кг-1c-2.
G1986 = 6.67259·10-11м3кг-1c-2.
Gtheory = 6.672606660·10-11м3кг-1c-2.
По формуле H = c2mH / (N2h) получим константу
Хаббла:
H = 2.376378745E-18 об/секунду, или, поскольку 1 парсек = 3.0856775807E+16
метров, то: H = 73.32738618 км/с/Мпк. (Результат «Ключевого Проекта»
на телескопе Хаббла дал:
72 = +/- 8 km/s/Mpc)
По формуле MEarth = 52r2Hc/G, где: r — большая
полуось земной орбиты, получим массу Земли (r = 149597870660 м):
MEarth = 5.973538542·1024 кг.
GMEarth = 3.985907306·1014 м3/с2.С Луной дело обстоит сложнее. Точное квантовое резонансное число для неё
пока не найдено (март, 2001). Получается нечто вроде 216, но не точно! Заметим
что 216=63. Кроме того, известно, что MEarth / MMoon
~ 81 = 34 . Но это опять же не точно.На странице
Moon
Fact Sheet мы находим отношение масс Луны и Земли: 0.0123, или мы можем
записать: 0.0123 =1/81.3008. Или читаем у П.И. Бакулина «Курс Общей Астрономии»
стр.105:»…По возмущениям в движениях искусственных спутников Земли отношение
масс Луны и Земли получилось равным 1/81.30…» Это будет 0.01230012.
А на странице http://www.solarviews.com/eng/moon.htm
мы находим, что это отношение равно 0.012298. А радиус орбиты: 384403 км. Можно
ли доверять этой страничке? Бог знает. Рискнём. Сомнительные цифры для Луны
мы жирно подчеркнём. Пусть MMoon / MEarth = 0.012298.
Тогда:
MMoon = 7.3463·1022 кг.
Теперь найдем массу Солнца, пользуясь законом Кеплера. G(M+m)/(4p2)=
a3/T2,где a = 149597870660 метров, — большая полуось земной
орбиты, или астрономическая единица; T = 31558149.8 секунд = 365.256 дней —
сидерический год. (Сидерический год: от фиксированной звезды до фиксированной
звезды; тропический год от эквинокса до эквинокса, точки весеннего равноденствия).В левой части закона Кеплера стоит две массы. Но мы то знаем, что там стоит
не две массы, а пять масс, которые можно представить как два тела. Первое тело,
— это Солнце и внутренние планеты: Меркурий и Венера. А второе тело, — это система
Земля-Луна. Подставляя все эти массы в закон Кеплера, мы уменьшаем массу Солнца
в шестом-седьмом знаке и чуть-чуть удаляемся от «точного» результата шварцшильдовского
радиуса 2GMSun/c2 = 2.95325008 км, который мы «откопали»
на сайте ASTROPHYSICAL CONSTANTS. Наша масса Солнца получается:
MSun = 1.988909058·1030 кг.
Или совокупная внутренняя масса, влияющая на движение системы Земля Луна:
MInt = MSun + MVen +
MMer = 1.988914257·1030 кг.
Другие понятные величины:
GMSun =1.327120783·1017 м3/с2.
GMInt = 1.327124251·1017 м3/с2.
2GMSun/c2 =2.953242026 км.
2GMInt/c2 = 2.953249746 км.
Имеем в виду, что полученные результаты верны, если работают допущения
«ЕСЛИ«.
Выводы гравитационной константы
«Метод G-1999», «Метод G-2006».
На моей странице Физические Константы можно увидеть,
как получено нормированное (безразмерное) значение гравитационной константы G’.
G’=3.04171(68)·10-60.
Если взять логарифм от этого числа, то получим число 137.04268(22).
Сравни с постоянной тонкой структуры a=1/137.03599911(46).
А еще лучшее сходство получается для величины a+1/a=137.04329646(46).
Поскольку G известна с малой точностью, и предполагая, что формула G’=1/Exp(a+1/a)
верна, можно получить сначала G’, а из этого значения получим G1999_t
= 6.671480(24)·10-11м3кг-1c-2.
Если же верна G’=1/Exp(1/a), то G1999_0 =
6,718976(24)·10-11м3кг-1c-2.
Эти результаты получены в 1999 году. Результат G1999_0 довольно сильно
отличается от наблюдаемого значения гравитационной константы. Однако, если предположить,
что это аналог электрической постоянной, а в закон Ньютона входит ещё и гравитационная
проницаемость среды, по аналогии с электрической проницаемостью среды в законе Кулона,
то различие становится не избыточным, а необходимым. Этот вариант проанализирован
на странице Ядро Земли — раскаленная пустота; Объединение
взаимодействий.
В феврале 2006 года было замечено еще одно свойство в семье констант.
Для того, чтобы свести данные по G к одному и тому же числу, необходимо либо увеличить
массу протона в число близкое к 1.001153, либо стартовую G в 1.001154,
либо и т.п. в 1.00115x раз.
Что же это за число, 1.00115?
И встречалось ли оно раньше?
Магнетон Бора — это простая комбинация констант и он должен соответствовать магнитному
моменту электрона.
Но согласно CODATA-2002 истинное значение магнитного момента электрона отличается
от магнетона Бора в -1.0011596521859(38) раз.
Тогда можно допустить, что получаемое G’=1/Exp(1/a)
есть «комбинация констант», а истинное значение G ослаблено в 1.0011596521859(38)x
раз. Таким образом, мы получаем более точное значение для G.
Расчет дает:
G2006=6,6730102(37)·10-11м3кг-1c-2,
G2009=6,6730079(15)·10-11м3кг-1c-2.
Наша G в 300 раз точнее, чем величина, предлагаемая CODATA2009: G=6,67428(67)·10-11
м3/(сек2кг).
Наш результат имеет достаточно высокую достоверность, думаю, порядка 95%. Это
следует из анализа движения образа и прообраза электрона в VB-программе
http://darkenergy.narod.ru/SR2007.exe
Описание программы: 1, 2.
А также из анализа Exel-программы
http://darkenergy.narod.ru/data.xls.
Сейчас (май 2009) стало понятно, почему магнитная аномалия элементарного заряда
оказывает влияние на гравитационную константу.
В результате нормировки физических величин, все физические константы удивительно
красиво выразились через число N, через постоянную тонкой структуры
a, и через отношение масс протона и электрона
D. Прекрасно, всего лишь три числа (N, a, D),
и все константы у нас в руках! Лишь гравитационная постоянная не выражалась красиво
через эти числа (N, a, D). Одна красивая формула
была замечена: G’ = 1/Exp(1/a), но поскольку она
не давала точного совпадения, раннее использовалось приближение к ней: G’ = 1/Exp(a+1/a).
В 2006 году была найдена точная формула для вывода гравитационной константы, а в
этом году 2009 она была логически обоснована. Нормированная гравитационная константа
действительно может быть записана так: G» = 1/Exp(1/a),
но измеряемая величина, которую мы назовем аномальной нормированной гравитационной
константой, есть G’ = 1 / (Exp(1/a)
δ6), где:
δ — отношение магнитного момента электрона к магнетону Бора. Как известно,
величина δ теоретически выводится через
два числа (p и
α), следовательно, наша G» тоже
выражается через эти же числа. Найдя G’ или
G», мы можем получить
G:
G=ch(αG’/D2)2/3/21/3/m2
=ch(αG»/D2)2/3/21/3/mμ2,
где: c — скорость света, h — постоянная Планка, D — отношение
масс протона и электрона, m — масса электрона, mμ
— «аномальная масса электрона». «Аномальная масса электрона» это величина,
равная сумме масс электрона и «вакуумных добавок», получаемая из равенства mμc2
= pB, где p — магнитный момент электрона; B — магнитная индукция, создаваемая током
«вращающегося электрона». Магнитный момент электрона превосходит магнетон Бора в
δ раз. Это превосходство как раз и обеспечивается
«вакуумными добавками». С учетом того, что магнитный момент контура с током определяется
по формуле p = IS; а магнитная индукция B = μ0I
/ 2R, где в обе формулы входит один и тот же ток I, мы заключаем, что величина превосходит
Боровский аналог величины pB в δ2
раз. Учитывая также, что спиновой магнитный момент превосходит орбитальный
момент в два раза, мы добавим в формулу p = IS коэффициент 2. Проделав выкладки,
получим mμc2 = mδ2c2,
или: mμ = mδ2.
Поскольку гравитационные взаимодействия осуществляются посредством того же электрон-позитронного
вакуума, и поскольку в закон Ньютона входят две массы взаимодействующих тел, то
обе эти массы обретают экранировку, учитываемую в нашей гравитационной константе,
содержащей либо δ4 в коэффициенте
mμ2, формулы
G=ch(αG»/D2)2/3/21/3/mμ2,
либо 1/δ6 в коэффициенте (G’)2/3
формулы G=ch(αG’/D2)2/3/21/3/m2,
что в сущности равноправно.
Сайт создан 10 июня 1998 г.
Эта страница создана 1 апреля 2001 года.
К другим разделам Космической Генетики
Иван
Горелик.
From Wikipedia, the free encyclopedia
Radial gravity anomaly at the surface of the Moon in mGal
The acceleration due to gravity on the surface of the Moon is approximately 1.625 m/s2, about 16.6% that on Earth’s surface or 0.166 ɡ.[1] Over the entire surface, the variation in gravitational acceleration is about 0.0253 m/s2 (1.6% of the acceleration due to gravity). Because weight is directly dependent upon gravitational acceleration, things on the Moon will weigh only 16.6% (= 1/6) of what they weigh on the Earth.
Gravitational field[edit]
The gravitational field of the Moon has been measured by tracking the radio signals emitted by orbiting spacecraft. The principle used depends on the Doppler effect, whereby the line-of-sight spacecraft acceleration can be measured by small shifts in frequency of the radio signal, and the measurement of the distance from the spacecraft to a station on Earth. Since the gravitational field of the Moon affects the orbit of a spacecraft, one can use this tracking data to detect gravity anomalies.
Most low lunar orbits are unstable. Detailed data collected has shown that for low lunar orbit the only «stable» orbits are at inclinations near 27°, 50°, 76°, and 86°.[2] Because of the Moon’s synchronous rotation it is not possible to track spacecraft from Earth much beyond the limbs of the Moon, so until the recent Gravity Recovery and Interior Laboratory (GRAIL) mission the far-side gravity field was not well mapped.
The missions with accurate Doppler tracking that have been used for deriving gravity fields are in the accompanying table. The table gives the mission spacecraft name, a brief designation, the number of mission spacecraft with accurate tracking, the country of origin, and the time span of the Doppler data. Apollos 15 and 16 released subsatellites. The Kaguya/SELENE mission had tracking between 3 satellites to get far-side tracking. GRAIL had very accurate tracking between 2 spacecraft and tracking from Earth.
| Mission | ID | Number | Source | Years |
|---|---|---|---|---|
| Lunar Orbiter 1 | LO1 | 1 | US | 1966 |
| Lunar Orbiter 2 | LO2 | 1 | US | 1966–1967 |
| Lunar Orbiter 3 | LO3 | 1 | US | 1967 |
| Lunar Orbiter 4 | LO4 | 1 | US | 1967 |
| Lunar Orbiter 5 | LO5 | 1 | US | 1967–1968 |
| Apollo 15 Subsatellite | A15 | 1 | US | 1971–1972 |
| Apollo 16 Subsatellite | A16 | 1 | US | 1972 |
| Clementine | Cl | 1 | US | 1994 |
| Lunar Prospector | LP | 1 | US | 1998–1999 |
| Kaguya/SELENE | K/S | 3 | Japan | 2007–2009 |
| Chang’e 1 | Ch1 | 1 | China | 2007–2009 |
| GRAIL | G | 2 | US | 2012 |
| Chang’e 5T1 | Ch1T1 | 1 | China | 2015–2018 |
The accompanying table below lists lunar gravity fields. The table lists the designation of the gravity field, the highest degree and order, a list of mission IDs that were analyzed together, and a citation. Mission ID LO includes all 5 Lunar Orbiter missions. The GRAIL fields are very accurate; other missions are not combined with GRAIL.
| Designation | Degree | Mission IDs | Citation |
|---|---|---|---|
| LP165P | 165 | LO A15 A16 Cl LP | [3] |
| GLGM3 | 150 | LO A15 A16 Cl LP | [4] |
| CEGM01 | 50 | Ch 1 | [5] |
| SGM100h | 100 | LO A15 A16 Cl LP K/S | [6] |
| SGM150J | 150 | LO A15 A16 Cl LP K/S | [7] |
| CEGM02 | 100 | LO A15 A16 Cl LP K/S Ch1 | [8] |
| GL0420A | 420 | G | [9] |
| GL0660B | 660 | G | [10] |
| GRGM660PRIM | 660 | G | [11] |
| GL0900D | 900 | G | [12] |
| GRGM900C | 900 | G | [13] |
| GRGM1200A | 1200 | G | [14] |
| CEGM03 | 100 | LO A15 A16 Cl LP Ch1 K/S Ch5T1 | [15] |
A major feature of the Moon’s gravitational field is the presence of mascons, which are large positive gravity anomalies associated with some of the giant impact basins. These anomalies significantly influence the orbit of spacecraft around the Moon, and an accurate gravitational model is necessary in the planning of both crewed and uncrewed missions. They were initially discovered by the analysis of Lunar Orbiter tracking data:[16] navigation tests prior to the Apollo program showed positioning errors much larger than mission specifications.
Mascons are in part due to the presence of dense mare basaltic lava flows that fill some of the impact basins.[17] However, lava flows by themselves cannot fully explain the gravitational variations, and uplift of the crust-mantle interface is required as well. Based on Lunar Prospector gravitational models, it has been suggested that some mascons exist that do not show evidence for mare basaltic volcanism.[3] The huge expanse of mare basaltic volcanism associated with Oceanus Procellarum does not cause a positive gravity anomaly. The center of gravity of the Moon does not coincide exactly with its geometric center, but is displaced toward the Earth by about 2 kilometers.[18]
Mass of Moon[edit]
The gravitational constant G is less accurate than the product of G and masses for Earth and Moon. Consequently, it is conventional to express the lunar mass M multiplied by the gravitational constant G. The lunar GM = 4902.8001 km3/s2 from GRAIL analyses.[12][11][19] The mass of the Moon is M = 7.3458 × 1022 kg and the mean density is 3346 kg/m3. The lunar GM is 1/81.30057 of the Earth’s GM.[20]
Theory[edit]
For the lunar gravity field, it is conventional to use an equatorial radius of R = 1738.0 km. The gravity potential is written with a series of spherical harmonic functions Pnm. The gravitational potential V at an external point is conventionally expressed as positive in astronomy and geophysics, but negative in physics. Then, with the former sign,
where r is the radius to an external point with r ≥ R, φ is the latitude of the external point, and λ is the east longitude of the external point. Note that the spherical harmonic functions Pnm can be normalized or unnormalized affecting the gravity coefficients Jn, Cnm, and Snm. Here we will use unnormalized functions and compatible coefficients. The Pn0 are called Legendre polynomials and the Pnm with m≠0 are called the Associated Legendre polynomials, where subscript n is the degree, m is the order, and m ≤ n. The sums start at n = 2. The unnormalized degree-2 functions are
Note that of the three functions, only P20(±1)=1 is finite at the poles. More generally, only Pn0(±1)=1 are finite at the poles.
The gravitational acceleration of vector position r is
where er, eφ, and eλ are unit vectors in the three directions.
Gravity coefficients[edit]
The unnormalized gravity coefficients of degree 2 and 3 that were determined by the GRAIL mission are given in Table 1.[12][11][19] The zero values of C21, S21, and S22 are because a principal axis frame is being used. There are no degree-1 coefficients when the three axes are centered on the center of mass.
| nm | Jn | Cnm | Snm |
|---|---|---|---|
| 20 | 203.3 × 10−6 | — | — |
| 21 | — | 0 | 0 |
| 22 | — | 22.4 × 10−6 | 0 |
| 30 | 8.46 × 10−6 | — | — |
| 31 | — | 28.48 × 10−6 | 5.89 × 10−6 |
| 32 | — | 4.84 × 10−6 | 1.67 × 10−6 |
| 33 | — | 1.71 × 10−6 | −0.25 × 10−6 |
The J2 coefficient for an oblate shape to the gravity field is affected by rotation and solid-body tides whereas C22 is affected by solid-body tides. Both are larger than their equilibrium values showing that the upper layers of the Moon are strong enough to support elastic stress. The C31 coefficient is large.
Simulating lunar gravity[edit]
In January 2022 China was reported by the South China Morning Post to have built a small (60 centimeters in diameter) research facility to simulate low lunar gravity with the help of magnets.[21][22] The facility was reportedly partly inspired by the work of Andre Geim (who later shared the 2010 Nobel Prize in Physics for his research on graphene) and Michael Berry, who both shared the Ig Nobel Prize in Physics in 2000 for the magnetic levitation of a frog.[21][22]
See also[edit]
- Magnetic field of the Moon
- Micro-g environment
References[edit]
- ^ C. Hirt; W. E. Featherstone (2012). «A 1.5 km-resolution gravity field model of the Moon». Earth and Planetary Science Letters. 329–330: 22–30. Bibcode:2012E&PSL.329…22H. doi:10.1016/j.epsl.2012.02.012. Retrieved 2012-08-21.
- ^ Bell, Trudy E. (November 6, 2006). Phillips, Tony (ed.). «Bizarre Lunar Orbits». Science@NASA. NASA. Retrieved 2017-09-08.
- ^ a b
A. Konopliv; S. Asmar; E. Carranza; W. Sjogren; D. Yuan (2001). «Recent gravity models as a result of the Lunar Prospector mission». Icarus. 50 (1): 1–18. Bibcode:2001Icar..150….1K. CiteSeerX 10.1.1.18.1930. doi:10.1006/icar.2000.6573. - ^ Mazarico, E.; Lemoine, F. G.; Han, Shin-Chan; Smith, D. E. (2010). «GLGM-3: A degree-150 lunar gravity model from the historical tracking data of NASA Moon orbiters». Journal of Geophysical Research. 115 (E5): E05001, 1–14. Bibcode:2010JGRE..115.5001M. doi:10.1029/2009JE003472. ISSN 0148-0227.
- ^ Jianguo, Yan; Jinsong, Ping; Fei, Li; Jianfeng, Cao; Qian, Huang; Lihe, Fung (2010). «Chang’E-1 precision orbit determination and lunar gravity field solution». Advances in Space Research. 46 (1): 50–57. Bibcode:2010AdSpR..46…50J. doi:10.1016/j.asr.2010.03.002.
- ^ Matsumoto, K.; Goossens, S.; Ishihara, Y.; Liu, Q.; Kikuchi, F.; Iwata, T.; Namiki, N.; Noda, H.; Hanada, H.; et al. (2010). «An improved lunar gravity field model from SELENE and historical tracking data: Revealing the farside gravity features». Journal of Geophysical Research. 115 (E6): E06007, 1–20. Bibcode:2010JGRE..115.6007M. doi:10.1029/2009JE003499. ISSN 0148-0227.
- ^ Mazarico, E.; Lemoine, F. G.; Han, Shin-Chan; Smith, D. E. (2010). «GLGM-3: A degree-150 lunar gravity model from the historical tracking data of NASA Moon orbiters». Journal of Geophysical Research. 115 (E5): E05001, 1–14. Bibcode:2010JGRE..115.5001M. doi:10.1029/2009JE003472. ISSN 0148-0227.
- ^ Yan, Jianguo; Goossens, Sander; Matsumoto, Koji; Ping, Jinsong; Harada, Yuji; Iwata, Takahiro; Namiki, Noriyuki; Li, Fei; Tang, Geshi; et al. (2012). «CEGM02: An improved lunar gravity model using Chang’E-1 orbital tracking data». Planetary and Space Science. 62 (1): 1–9. Bibcode:2012P&SS…62….1Y. doi:10.1016/j.pss.2011.11.010.
- ^ Zuber, M. T.; Smith, D. E.; Neumann, G. A.; Goossens, S.; Andrews-Hanna, J. C.; Head, J. W.; Kiefer, W. S.; Asmar, S. W.; Konopliv, A. S.; et al. (2016). «Gravity field of the Orientale basin from the Gravity Recovery and Interior Laboratory Mission». Science. 354 (6311): 438–441. Bibcode:2016Sci…354..438Z. doi:10.1126/science.aag0519. ISSN 0036-8075. PMC 7462089. PMID 27789835.
- ^ Konopliv, Alex S.; Park, Ryan S.; Yuan, Dah-Ning; Asmar, Sami W.; Watkins, Michael M.; Williams, James G.; Fahnestock, Eugene; Kruizinga, Gerhard; Paik, Meegyeong; et al. (2013). «The JPL lunar gravity field to spherical harmonic degree 660 from the GRAIL Primary Mission». Journal of Geophysical Research: Planets. 118 (7): 1415–1434. Bibcode:2013JGRE..118.1415K. doi:10.1002/jgre.20097. hdl:1721.1/85858. S2CID 16559256.
- ^ a b c Lemoine, Frank G.; Goossens, Sander; Sabaka, Terence J.; Nicholas, Joseph B.; Mazarico, Erwan; Rowlands, David D.; Loomis, Bryant D.; Chinn, Douglas S.; Caprette, Douglas S.; Neumann, Gregory A.; Smith, David E. (2013). «High‒degree gravity models from GRAIL primary mission data». Journal of Geophysical Research: Planets. 118 (8): 1676–1698. Bibcode:2013JGRE..118.1676L. doi:10.1002/jgre.20118. ISSN 2169-9097.
- ^ a b c Konopliv, Alex S.; Park, Ryan S.; Yuan, Dah-Ning; Asmar, Sami W.; Watkins, Michael M.; Williams, James G.; Fahnestock, Eugene; Kruizinga, Gerhard; Paik, Meegyeong; Strekalov, Dmitry; Harvey, Nate (2014). «High-resolution lunar gravity fields from the GRAIL Primary and Extended Missions». Geophysical Research Letters. 41 (5): 1452–1458. Bibcode:2014GeoRL..41.1452K. doi:10.1002/2013GL059066.
- ^ Lemoine, Frank G.; Goossens, Sander; Sabaka, Terence J.; Nicholas, Joseph B.; Mazarico, Erwan; Rowlands, David D.; Loomis, Bryant D.; Chinn, Douglas S.; Neumann, Gregory A.; Smith, David E.; Zuber, Maria T. (2014). «GRGM900C: A degree 900 lunar gravity model from GRAIL primary and extended mission data». Geophysical Research Letters. 41 (10): 3382–3389. Bibcode:2014GeoRL..41.3382L. doi:10.1002/2014GL060027. ISSN 0094-8276. PMC 4459205. PMID 26074638.
- ^ Goossens, Sander; et, al. (2016). «A global degree and order 1200 model of the lunar gravity field using GRAIL mission data» (PDF).
{{cite web}}: CS1 maint: url-status (link) - ^ Yan, Jianguo; Liu, Shanhong; Xiao, Chi; Ye, Mao; Cao, Jianfeng; Harada, Yuji; Li, Fei; Li, Xie; Barriot, Jean-Pierre (2020). «A degree-100 lunar gravity model from the Chang’e 5T1 mission». Astronomy & Astrophysics. 636: A45, 1–11. Bibcode:2020A&A…636A..45Y. doi:10.1051/0004-6361/201936802. ISSN 0004-6361. S2CID 216482920.
- ^ P. Muller; W. Sjogren (1968). «Mascons: Lunar mass concentrations». Science. 161 (3842): 680–84. Bibcode:1968Sci…161..680M. doi:10.1126/science.161.3842.680. PMID 17801458. S2CID 40110502.
- ^ Richard A. Kerr (12 April 2013). «The Mystery of Our Moon’s Gravitational Bumps Solved?». Science. 340 (6129): 138–39. doi:10.1126/science.340.6129.138-a. PMID 23580504.
- ^ Nine Planets
- ^ a b Williams, James G.; Konopliv, Alexander S.; Boggs, Dale H.; Park, Ryan S.; Yuan, Dah-Ning; Lemoine, Frank G.; Goossens, Sander; Mazarico, Erwan; Nimmo, Francis; Weber, Renee C.; Asmar, Sami W. (2014). «Lunar interior properties from the GRAIL mission». Journal of Geophysical Research: Planets. 119 (7): 1546–1578. Bibcode:2014JGRE..119.1546W. doi:10.1002/2013JE004559. S2CID 7045590.
- ^ Park, Ryan S.; Folkner, William M.; Williams, James G.; Boggs, Dale H. (2021). «The JPL Planetary and Lunar Ephemerides DE440 and DE441». The Astronomical Journal. 161 (3): 105. Bibcode:2021AJ….161..105P. doi:10.3847/1538-3881/abd414. ISSN 1538-3881. S2CID 233943954.
- ^ a b «China building «Artificial Moon» that simulates low gravity with magnets». Futurism.com. Recurrent Ventures. Retrieved 17 January 2022.
Interestingly, the facility was partly inspired by previous research conducted by Russian physicist Andrew Geim in which he floated a frog with a magnet. The experiment earned Geim the Ig Nobel Prize in Physics, a satirical award given to unusual scientific research. It’s cool that a quirky experiment involving floating a frog could lead to something approaching an honest-to-God antigravity chamber.
- ^ a b Stephen Chen (12 January 2022). «China has built an artificial moon that simulates low-gravity conditions on Earth». South China Morning Post. Retrieved 17 January 2022.
It is said to be the first of its kind and could play a key role in the country’s future lunar missions. Landscape is supported by a magnetic field and was inspired by experiments to levitate a frog.

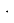
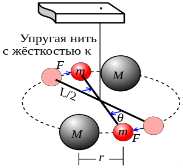
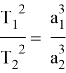
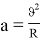
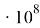
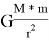
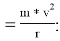
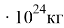
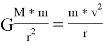

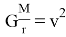
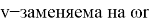
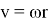
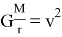
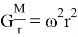
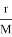
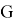
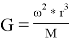
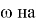
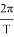
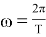

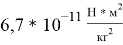







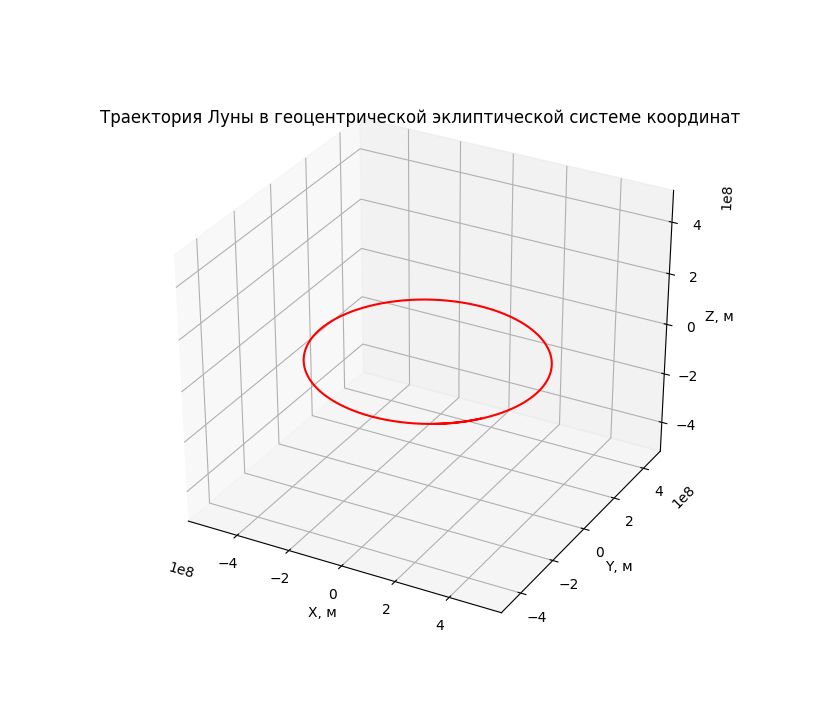
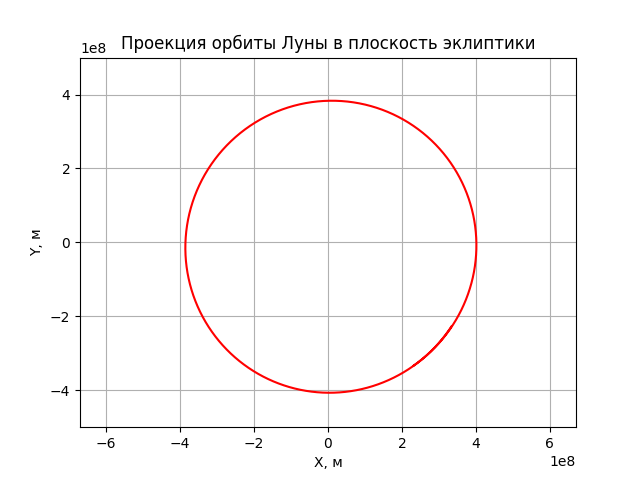


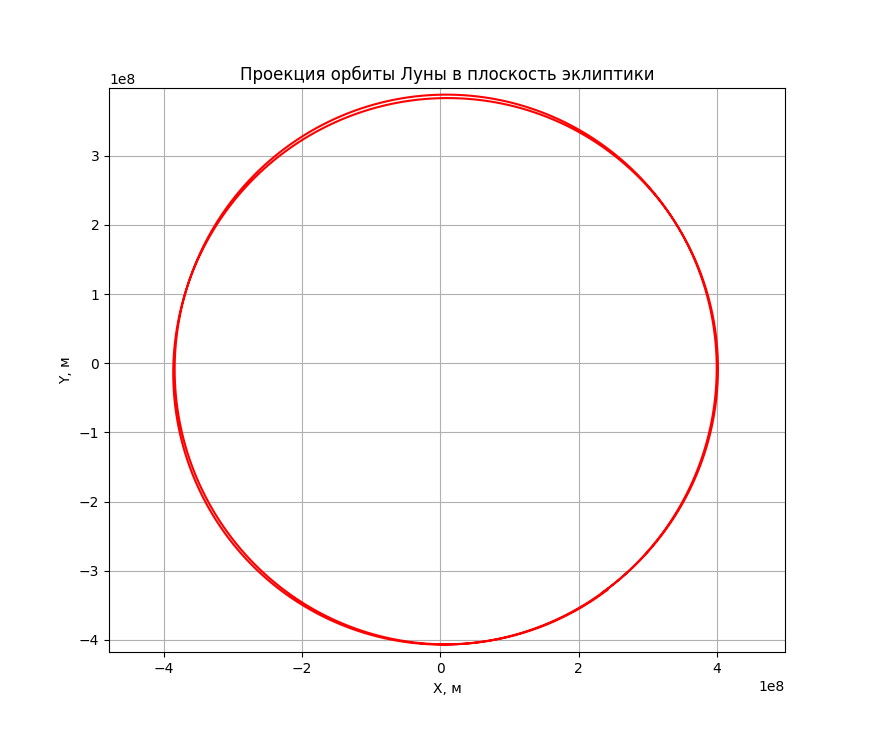


















![{displaystyle V=left({frac {GM}{r}}right)-left({frac {GM}{r}}right)sum left({frac {R}{r}}right)^{n}J_{n}P_{n,0}(sin phi )+left({frac {GM}{r}}right)sum left({frac {R}{r}}right)^{n}[C_{n,m}P_{n,m}(sin phi )cos(mlambda )+S_{n,m}P_{n,m}(sin phi )sin(mlambda )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb4e57eaed82bfc3d5bfa628e063fe3d965f99a1)
![{displaystyle {begin{aligned}P_{2,0}&={frac {3}{2}}sin ^{2}!phi -{frac {1}{2}}\[1ex]P_{2,1}&=3sin phi cos phi \[1ex]P_{2,2}&=3cos ^{2}phi end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9efdca9b526b8464ba88ed5603edd93e29b6f804)
![{displaystyle {begin{aligned}{frac {d^{2}r}{dt^{2}}}&=nabla V\[1ex]&={partial V over partial r}e_{r}+{frac {1}{r}}{partial V over partial phi }e_{phi }+{frac {1}{rcos phi }}{partial V over partial lambda }{e_{lambda }}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/054d8a6bb16f2bba5470889b0a9afab61b01605f)